Chapter Three
Changing the Order of Quantifiers
3.1.1 Löwenheim begins the proof of his theorem by showing that every formula is logically equivalent to a formula which has a certain normal form. A formula is in (Löwenheim) normal form if it is in prenex form and every existential quantifier precedes every universal quantifier.1 Obviously, the central step in obtaining the normal form of a formula involves moving the existential quantifiers in front of the universal quantifiers, preserving logical equivalence. Löwenheim takes this step by generalizing and applying a transformation introduced by Schröder in the third volume of Vorlesungen.
Schröder only considers the problem of changing the order of quantifiers for the case of two quantifiers. In the middle of a particular proof, he realizes that it is impossible to continue without a law which allows for the order of quantifiers to be changed. He stops the proof and introduces the equations
which, in his opinion, transform 
and 
into logically equivalent formulas which begin with 
) and 
respectively (Vorlesungen III, pp. 513–516). After explaining and proving these equations, Schröder finishes the proof he had interrupted, using only
(3.2). He then applies (3.2) in an analogous proof (Vorlesungen III, p. 519) and does not use either equation again at any time in the rest of the book.
One equation is the dual of the other (although at first sight they do not appear so, due to the prefixes of the formulas on the right), so thatit suffices to prove only one of them. Schröder prefers to explain and prove equation (3.2), as it is the one that he needs for the proof that he is performing, but I will refer at all times to (3.1), as it is the one that Löwenheim uses in his proof of the theorem. The clarifications and arguments I present are dual to those given by Schröder. Whenever I quote him in this section I will write in double brackets the text on which my commentary is based.
3.1.2 Schröder starts by clarifying the meaning of what he calls the “enigmatic operators”: 
and . First of all, he notes that 
is not an “authentic” quantifier, but is conventionally written to indicate the presence of a string of quantifiers which
may be existential or universal, depending on whether it precedes 
. or IIm
. The string will have as many quantifiers as the domain of interpretation has elements (the symbol II is used precisely for
this reason). Thus, these operators act like a kind of schema which gives rise to strings that differ according to the cardinality
of the domain. For example, if the domain is denumerable, 
) represents the string
When the domain is uncountable, Schröder says that it is not possible to express the meaning of 
) explicitly, but that this poses no difficulty since it suffices to suppose that for each element of the domain there is
a different existential quantifier. The fact that 
is in any case a string of existential quantifiers explains why—contrary to initial impressions—equation (3.1) allows to
change the order of the quantifiers.
To understand fully the meaning of the formula
a further clarification is necessary. Schröder warns that the variables and i should take values in parallel. To explain what he means, he presents the following example: if we suppose that the
domain is denumerable and denote the individuals in the domain by i1, i2, i3,...., then the meaning of (3.3) is given by
Again, if the domain is not countable, it should also be understood, that for each element r—which we can suppose to be denoted
by ir—there are an existential quantifier 
and a formula A(ir,mr) as factor. The order of the quantifiers is of no importance.
3.1.3 
After these clarifications, Schröder goes on to prove the two equations, distinguishing between various cases according to
the cardinality of the domain. First he examines the case of a denumerable domain. As we saw above, equation (3.1) in this
case takes the form
Now, the supposition that the individuals of the domain are denoted by i1, i2 i3,... allows us to affirm that
Hence, what has to be proven is the equality
According to Schröder, for this proof it suffices to observe that, for any r, mr does not occur in the formulas previous and subsequent to ΣmrA(ir,mr), and, therefore, the schema
can be applied. This proves the equation for the case of a denumerable domain. The same argument can be used to show by induction that (3.1) is valid for any finite domain.
To conclude the proof, Schröder considers the case of a particular uncountable domain: the continuum. He affirms that if the variables take values over the continuum, it suffices to observe that
each term of a 
can also be presented as an authentic component of a (binary) “sum” (in the strict sense) of which the other component may
be denoted by a, as independent of the m that occurs in that term, which must observe the schema 
]] Etc. q.e.d.2
Schröder's argument is not easy to understand. It seems to run as follows: if v is any element of the domain and IIuB(u) any product of type II, then B(v) can be written as a separate factor of a binaryproduct of type B · C whose second factor is the type II product; explicitly, for each element r (which, as always, we denote by ir), the following equation holds:
Now, assuming that IIiΣmA(i,m) does not depend on mr (i.e., mr does not occur in IIiΣmA(i,m)), the schema
can be applied to the formula on the right side to obtain
Surprisingly, after this remark, Schröder goes on to affirm “Etc. q.e.d.”
3.1.4 I will now comment on Schröder's proposal for the change of order of the quantifiers, beginning with a particularly obscure
point—the relation between and i.
For the validity of the whole of Schröder's reasoning it is fundamental that the development of formula (3.3) has an existential
quantifier for each element of the domain. That is to say, it is essential that for each value of i there be a different existential
quantifier in the formula developed. Schröder's problem lies in finding a formula with this property. The solution that he
proposes is, as we saw, quite artificial. He fixes the subscript to the variable m and adopts the ad hoc convention that and i should take values in parallel. Schröder does not clarify whether is a variable of the same type as i, although most of the time he speaks as if were not a true individual variable, but a subscript whose range can be put into one-to-one correspondence with the domain
and every time that i takes a value, takes the corresponding value.
Apparently, everything would be much simpler if we used only the variable i and replaced (3.3) with
This would avoid the existence of two variables which must take the same value (or be modified in parallel), and would at the same time retain the idea to be reflected, that is, that for each value of i there must be a different existential quantifier. Of course, this expression would conventionally be attributed the same meaning as the previous one. Nevertheless, Schröder explicitly rejects this alternative. In his opinion, if we made this modification, the resulting schema (the equation) would be “false and illusory”:
Because then in its last part, 
)]] would enter as a general factor of II [[general summand of Σ]], and the latter would have to show a value that was totally
independent of i; bear in mind that the letter i functions there only as a substitute of the values attributed to it that
are extracted from the range of i. Accordingly, mi could no longer occur as such in its interpreted expression. (Analogously
to the way in which a defined integral is independent of its integration variables!) This would remove totally the operator
)]] which precedes the term, in accordance with the tautological law IIa = a [[Σa = a]], and our schema would be simplified
enormously. That this simplification is not permissible in general can be shown by exemplifying.3
In outline, what Schröder maintains in this obscure paragraph is that
and, in consequence, the schema is reduced in this case to the equality
which does not always hold.
I will now analyze this argument. That (3.6) does not always hold can be seen by exemplifying, as Schröder says. Let us suppose that the domain has only two elements, denoted by 1 and 2. Then (3.6) can be written as follows:
But then the m1 and m2 occurring on the right-hand side are, speaking in our terms, free variables, and we can therefore choose their denotation in any way that suits us. Accordingly, it may be that
is true, but A(1;m1) ·A(2;m2) is false (because the elements denoted by m1 and m2 are not among those that make the quantified formula true).
The argument with which Schröder intends to prove (3.5) is expressed rather obscurely, so our first task is to formulate it
more clearly. Schröder begins by observing that (3.4) is a sum (an existential formula) whose general summand (the formula
that constitutes the scope of the existential quantifier) is 
. In addition, the role of i in 
is the same as that of in 
); that is, to refer to a string of existential quantifiers. In other words, the development of the operator is always the
same, regardless of the variable that we use. Applied to the case of a denumerable domain, this means that (3.4) refers to
But then it is obvious that mi does not occur in the development of 
). As a result, all the existential quantifiers of the development can be removed because for all r
since mr does not occur in 
. Therefore the operator 
) does not play any role, and we can omit it.
The weakness of Schröder's argument is to be found at its startingpoint. If we accept his approach, the argument is beyond
dispute. There is an important difference between the ways in which Schröder interprets (3.3) and (3.4). In the case of the
former, he never considers the possibility of developing 
independently of 
because the two expressions are linked by , and he has established the additional convention that and i should take values at the same time. However, the argument that proves the necessity of using a variable other than
i is based on the consideration of what happens when we develop 
but not 
:
From today's perspective, there does not appear to be any reason for this difference of interpretation; it would suffice to stipulate that these operators cannot be developed independently of the quantifierthat follows them. With the introduction of these “enigmatic operators” what Schröder does is to widen his language with a new type of expression; nothing prevents him from attributing the same meaning to (3.3) as to (3.4). Consequently, his argument fails to convince.
At the end of this chapter I will come back to this argument to explain why Schröder reasons in the way he does.
3.1.5 I will now analyze Schröder's proof of equation (3.2). As it is the proof of a logical equivalence between two formulas, one of which begins with an “enigmatic operator,” it seems essential to clarify the operator's semantics before we judge the proof. I have not yet made this clarification. This does not, however, prevent us from analyzing the structure of the proof, as basically it consists in showing that the expanded formulas (in which the operators no longer intervene) are logically equivalent. I will explain the semantics of the operators later.
As we saw above, when the domain is denumerable, Schröder first reduces the problem to showing the equivalence of the formulas
and then states that we can go from (3.7) to (3.8) by applying the schema
There are two problems here that deserve comment. First, the schema is, strictly speaking, insufficient, since it is not applicable to the first quantifier. If we wanted to go from (3.7) to (3.8) by applying a series of equivalences (or equations), as Schröder appears to be trying to do, we would need also to use the equation
(assuming that m does not occur in B). But this detail has no importance whatsoever, because the fact is that we cannot go from (3.7) to (3.8) simply by applying equations of this type. This is the second difficulty that I would point out. Schröder's argument (leaving aside the point about the schema) only shows that any quantifier of (3.7) can be carried to the beginning of the formula, but this does not prove that we can place all the quantifiers at the beginning. Nor would resorting to induction be of any help in this case. We could prove by induction that any finite number of quantifiers can be placed at the beginning,but we would still not have shown what interests us. Schröder is arguing as if the formulas had a finite length or, equivalently, as if the domain were finite.
There are no objections to Schröder's proof when the domain is finite. Indeed, the reasoning used for the case of a denumerable domain makes it possible to prove by induction that, for all finite domains, the formulas corresponding to (3.7) and (3.8) will be logically equivalent.
Schröder's argument in the case in which the domain is the continuum is extremely surprising. The type of proof is the same as in the previous cases: we first obtain the formulas most suited to the domain, and then show that it is possible to go from one formula to the other by applying a series of equivalences. The problem is: what are the formulas that now correspond to (3.7) and (3.8)? When the domain is countable, the well-ordering of the natural numbers makes it possible to write the formulas in question in some way, and this is all that Schröder believes is necessary for applying the equivalences. However, as he says, in the case of the continuum the corresponding formulas cannot be written. But his argument requires that there be a formula to which the equivalences are to be applied. Schröder believes that, if we had a way of referring to any quantifier, we could use it as in the case of a countable domain, and the proof would be complete. This is exactly what he does. He first observes that the equality
makes possible the explicit reference that he was looking for, and then he merely indicates that the formula on the right side is equal to
(assuming, as always, that mk does not occur in 
)). After this step Schröder concludes with “etc.,” as an analogous argument can be applied to all the quantifiers.
Once we clarify what Schröder means, there is not much more to say. Taken literally, his argument does not quite make sense, as it is based on the transformation of formulas that do not, strictly speaking, exist. Even without this problem his argument would be unacceptable, because (as in the case of a denumerable domain) Schröder seeks to prove that all the quantifiers can be moved to the front of a formula, but his argument only permits us to conclude that any quantifier can be moved to the front of a formula. Moreover, if his argument were right, it would not be necessary to distinguish cases according to the cardinality of the domain.
The only infinite domains that Schröder considers are the set of natural numbers and the continuum. This is understandable because Cantor had only recently established the existence of sets of cardinality greater than the continuum. Nevertheless, if his proof were correct, there would be no objection to accepting it in its complete generality, because the argument is the same for any infinite domain (which does not mean that Schröder, due to the type of reasoning that he uses, would not have seen different problems in domains of greater cardinality, but that is another matter).
This may seem overcritical; perhaps it would be fairer to Schröder to consider his proof as a reasoning dealing with elements of the domain. I believe that Schröder saw that the equations were true because he thought semantically. But the way in which one approaches a problem and reaches conclusions is one thing, and the proof that one later offers for them is quite another. I do not think that there are any important errors in the way in which Schröder conceives the problem, but I think that the proof that he offers is syntactic in type. Schröder makes it very clear that the proof consists in going from one formula to another via the application of certain equations, and this is basically a proof of a syntactic nature (even though the proof of the equations used is not). The type of proof that Schröder has in mind is the one that is usually followed in elementary algebra to prove an equality: going from one side to another by applying equations already proved. The point is that in this case this type of reasoning cannot be applied. The short argument for the case of the continuum is so schematic and obscure that it allows multiple interpretations, but there is no reason for adopting a different approach for this case (indeed, there are reasons for not doing so).
3.2.1 Löwenheim does not seem to have been convinced by Schröder's reasons for writing instead of i. In the proof of his theorem, Löwenheim formulates equation (3.1) in the following way:
As is clear, it is 
that corresponds to 4 
According to Löwenheim, the 
on the right side is written to indicate that for each¸ 
ranges over all the elements of the domain. In consequence, 
is an n-fold quantifier, where n is the cardinality of the domain (n may be transfinite).
If we compare (3.1) and (3.9), we will see that Löwenheim ignores Schröder's indications; otherwise he would have written
) rather than 
5 I do not know what Schröder would have thought of this way of writing the equation, but he would probably have seen in it
the same, or similar, problems as the ones he found in (3.5). In any case, a few lines below (3.9), Löwenheim pays no attention
to Schröder's warnings and writes
A little further on, he again uses the same notation as in (3.9). Observe that his fluctuations in notation are limited to
the variables 
attached to §, and he always writes the rest of the formula as in (3.9).
Löwenheim calls terms of the form ki fleeing indices (Fluchtindizes) and says that these indices are characterized by the fact that their subindices are universally quantified variables (“Über Möglichkeiten,” p. 454 (238)), but in fact he also gives that name to the indices generated by a fleeing index when its universally quantified variables take values on a domain.
In what follows, I shall call fleeing indices terms of the form kr1...rn, whether r1,...,rn are indices or (canonical names
of) elements of the domain. Observe that the numerals 1,...,n occurring in kr1...rn do not denote elements of the domain;
for the purpose of avoiding potential ambiguities, I shall say that r1,...,rn are the subindices (not the subscripts) of the
fleeing index and that 1,...,n are the subscripts of r1,...,rn. In order to simplify the notation, I will write 
instead of 
.
Löwenheim generalized Schröder's procedure to formulas with multiple quantifiers. The generalization is easy and Schröder could have introduced it if he had needed it. The equation
for the case of two universal quantifiers suggests clearly how we can generalize the procedure to the case in which the existential quantifier is in the scope of n universal quantifiers.
3.2.2 The difference I have just signaled between the equations of Löwenheim and Schröder only affects the notation; it does not affect the idea that they aim to express. Löwenheim attributes the same meaning to his equation as Schröder does to his. Löwenheim explains the meaning of (3.9) in the following way:
In order to make the formula above [[(3.9)]] more intelligible, I want once to expand in part the 
and II that occur in it, that is, I want to use the symbol + and juxtaposition (or dots) for these in one exceptional case
here (contrary to the stipulation on page ...). I shall denote the indices by 1, 2, 3,.... Then the formula reads
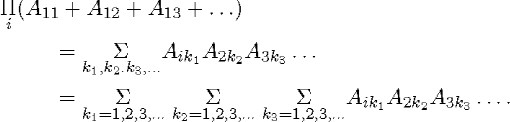
(“Über Möglichkeiten,” pp. 451–452 (236); my italics)
Before commenting this quotation, I will introduce some terminology. If D is any domain, the expansion of a formula of the
form 
) (or 
on D is the iterated conjunction (or disjunction) of all formulas A(a), for a 
D (assuming that we identify the elements of D with their canonical name in the language).
As we can see, Löwenheim explains the meaning of (3.9) by means of expansions,6 but warns that by so doing he is contravening the stipulations on language. Importantly, this transgression does not depend on whether the domain is finite or not, that is, on whether the formula resulting from the expansion has finite length or not. A few lines after the above quotation, Löwenheim performs a couple of expansions on finite domains and repeats exactly the same warning about the use of · and +.
The way in which the above quotation has traditionally been understood is reflected in the paragraphs that I shall analyze now. These paragraphs make reference to Löwenheim's theorem, which I mentioned at the beginning of this chapter. For the discussion that follows it suffices to know that
is the normal form of 
) and that the references to the normal form can be taken as references to (3.10).
In his introduction to Löwenheim's paper, van Heijenoort comments:
In Löwenheim's theorem the number of existential quantifiers depends on the number of individuals in the Denkbereich. For domains of different cardinalities, the original formula is replaced by different formulas; for infinite domains there are infinitely many quantifiers, and the formula is replaced by what now is sometimes called an infinitely long expression, which no longer satisfies Löwenheim's own definition of Zählausdruck (“Σ and II occur only a finite number of times”). (From Frege, pp. 229–230)
To quote another well-known historian, Moore states that:
At this juncture Löwenheim advanced beyond Hilbert and Müller by combining first-order expressions not only with infinite conjunctions and disjunctions but with transfinitely many quantifiers as well. These infinitary propositions occurred in his proof of the “Löwenheim-Skolem theorem,” which he stated in the following fashion: if a first-order expression is satisfied in every finite domain but not in every domain, then it is not satisfied in some denumerable domain. To begin his demonstration, he showed that every first-order expression can be transformed into an equivalent one having a normal form such that all the existential quantifiers precede the universal ones. However this string of quantifiers might be infinite—with one such quantifier for each element in the domain under consideration. (Moore [1980], pp. 100–101)
I will make a small comment here before going on to discuss the central point. As Moore speaks of infinite strings of quantifiers, we need to make it clear that these strings are only of existential quantifiers. Löwenheim does not consider any formula in which there occur infinite strings of universal quantifiers. Moore overlooks this detail and especially Löwenheim's definition of Relativausdruck (quoted at the beginning of the next section) when, a little later on, he states that Löwenheim “developed an infinitary logic” which he used to provehis theorem (see also Moore [1988], p. 121 and Moore [1997], p. 76). Even if it were true that formulas of infinite length resulting from performing expansions actually intervene in Löwenheim's proof, it would be an exaggeration to conclude from this alone that Löwenheim developed an infinitary logic. Indeed, Moore gives no reason in favor of his claim.
Let us now look at the central aspects of the interpretation of (3.10). The views of van Heijenoort and Moore coincide on the essential points (though Moore goes much further in certain aspects). We can summarize their interpretation as follows: (3.10) is a schema of formulas which produces different formulas depending on the cardinality of the domain under consideration; in each case, (3.10) should be replaced by the corresponding expansion; when the domain is infinite the result of the expansion is a formula of infinite length.7
This interpretation—which I will call “the traditional one”—leaves out two important points. First, in 1911 (see note 24 in chapter 2) Löwenheim warned that the rules of calculation for infinite sums and products of propositions had not been proved yet. This strongly suggests that he would never use infinite expansions in a proof as long as those rules remained unproven. Did Löwenheim think that they had been demonstrated when he wrote “Über Möglichkeiten”? No answer to this question can be found in the traditional commentaries. The second point is more important, because it precisely concerns Löwenheim's explanation of (3.10). When he performs the expansion with which he explains the meaning of (3.10) he warns that he is going to do something that is contrary to the stipulations (the sentence in italics in the quotation). The traditional interpretation does not explain this warning; in no commentary is there the slightest reference to it. Van Heijenoort speaks of a transgression of the stipulations (i.e., the characterization of Zählausdruck) but does not specify whether this transgression is the one that Löwenheim refers to, or a different one. In fact it must be a different one because, as I said above, Löwenheim offers the same warning in the case of an expansion on a finite domain in which there can only occur a finite number of quantifiers.
The traditional view cannot be accepted unreservedly as it does not give an interpretation of this warning. Expression (3.10) cannot be held to be a schema of formulas without accounting for why Löwenheim warns that he is doing something contrary to the stipulations each time he performs an expansion. In addition, Löwenheim makes it clear that the purpose of the expansion of (3.10) (with the help of an informal explanation, since he is contravening the stipulations) is to facilitate the understanding of (3.10) itself or, more precisely, the understanding of (3.9) (because he expands both sides of this equation). I do not think that he meant to indicate which formula would replace (3.10) in the case of a denumerable domain.
Everything depends on Löwenheim's opinion of expansions. As I have said, Löwenheim repeats the same warning each time he uses connectives to develop quantifiers, that is, whenever he performs an expansion, finite or infinite. This warning then could mean that in Löwenheim's opinion performing expansions is wrong; in this case we should conclude that he does not think that (3.10) is a schema of formulas.
In the next section I shall propose an interpretation of the warning and analyze the extent to which it can explain certain assertions that Löwenheim made. The examination of the repercussions of this interpretation for the traditional view will allow us to analyze this view in some detail and to evaluate the arguments that support it.
3.2.3 As we will see, it is not at all necessary to use expansions to understand Löwenheim's proof of his well-known theorem. Contrary to the generally held view, Löwenheim's proof is independent of whether (3.10) is or is not a schema of formulas. We can therefore proceed without taking sides on this question. Of course, if for the proof it were essential to consider (3.10) as a schema of formulas, we should accept the traditional view.
Expansions are a rather rough and ready way of expressing the semantics of quantified formulas. In the logic of relatives they are used to make explicit the meaning of these formulas. I do not mean that they are only used on these occasions, but I think that Löwenheim performed expansions of (3.10) with this aim in mind. Today's technical and expressive devices allow us to give the meaning of (3.10) without recourse to expansions. Let us suppose that S is a solution in a domain D and, for the sake of simplicity, that (3.10) has no free variables. Then
(3.11)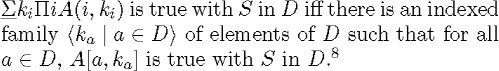
8
The idea behind the explanations of Löwenheim and Schröder is expressed in (3.11) and is all we need to account for Löwenheim's arguments in which (3.10) intervenes. In saying this I am not taking up a position on whether Löwenheim thought that (3.10) was a schema of formulas; I am saying that (3.11) is an updated way of expressing what Löwenheim and Schröder meant.9 A different problem is whether Löwenheim thought that expansions were a useful way (though not a rigorous one) of giving the meaning of (3.10), or whether, on the contrary, he thought they were full-fledged formulas which did allow a rigorous expression of its meaning.
I believe that the traditional interpretation of (3.10) is applicable to Schröder, but very possibly is not applicable to
Löwenheim. Schröder attributes to 
) the meaning that Löwenheim attributes to (3.10), but Schröder thinks of (3.10) as a schema of formulas. Schröder's proof
of the equation cannot be reproduced without forcing it unduly, by resorting to (3.11), precisely because it depends on expansions.
Nonetheless, there is nothing in Löwenheim's proof that makes it necessary to use the expansion of (3.10). Indeed, in the
cases in which he expands a formula he warns that he is proceeding contrary to the stipulations on language. These two facts
suggest that Löwenheim did not see (3.10) as a schema of formulas, but as a formula whose interpretation gives (3.11), although
we cannot accept this conclusion fully without analyzing the meaning of his warning about expansions.
3.3.1 The essential point in the stipulations that Löwenheim refers to in the quotation in subsection 3.2.2 is this:
In what follows we shall always understand by relative expression [[Relativausdruck]] an expression that is formed from relatives or (not necessarily binary) relative coefficients and in which Σ and II occur only a finite number of times, each Σ and II ranging either over the indices—thatis, over all individuals of the domain of the first degree, which, following Schröder, we call 11—or over all relatives that can be formed by means of this domain. All sums and products that do not range over the individuals of 11 or over all the relatives are assumed to be finite and will always be denoted by + or · (or the juxtaposition of factors) and never by Σ or by II. (“Über Möglichkeiten,” pp. 447–448 (232))
As we can see, not all the stipulations are of the same nature. Some can be considered as rules of a syntactic character: the number of quantifiers and connectives must be finite. Others, in contrast, are semantic: the quantifiers range over all the elements (or individuals, to use Schröder's terminology) of the domain, and the sums and products that do not range over all the elements of the domain should be denoted by + or ·, never by quantifiers. The semantic character of this latter stipulation is clear. It suffices to note that the stipulation is of no use in determining whether an expression is well formed or not; it is only useful for deciding whether a certain idea is correctly expressed. It is not unusual that Löwenheim should mix the two aspects in his stipulations, since no clear distinction was made between syntactic and semantic aspects at that time.
When Löwenheim warns that he is about to do something contrary to the stipulations each time he performs an expansion, he is not referring to a problem of a syntactic nature. An expansion can only be syntactically incorrect if it has infinite length, but, as I said above, Löwenheim sees the same type of problem in finite expansions. What appears to be contrary to the stipulations is the use of connectives to develop quantifiers; this is not a syntactic problem. In conclusion, if in the stipulations there is something that is contrary to making expansions, they must contain something more than syntactic rules. This corroborates the idea that not all stipulations are of the same nature, and demonstrates that we should concentrate our attention on their semantic aspect.
The problem is that there does not appear to be anything in the stipulations that prevents using the connectives to develop the quantifiers. What they prohibit is the use of the quantifiers to express sums and products that do not range over all the elements of the domain, but what happens in expansions is exactly the opposite: connectives are used to express sums and products that do range over all the elements of the domain.
There is a way of interpreting the stipulations which makes it possible to account for Löwenheim's warning. He may mean more
than he actually says. Löwenheim states that sums and products which do not range over all the individuals of the domain should
be denoted by + or by ·, but he may also mean that these symbols should only be used in this case. That is to say, for the
sums and products that range over all the elements of the domain, the use of quantifiers is obligatory. Let us consider, for
example, the formula 
), and let us suppose that the domain is {1, 2, 3}. What would be contrary to the stipulations would be to express the sum
(which does not range over all the elements of the domain) by means of 
and also to express the latter by means of its expansion in {1, 2, 3}:
In other words, 
) cannot be replaced equivalently by (3.12), nor A(1) + A(3) by .
Understood in this way, the role of the stipulations which I have called “semantic” would be to attribute distinct expressive functions to connectives and quantifiers, and to prohibit the use of certain symbols to carry out the role that corresponds to others. In expansions (finite or infinite) the connectives are used to express sums and products that range over all the elements of the domain, and it is this that is contrary to the stipulation, because it is the function of the quantifiers to express these sums.
3.3.2 Supposing that this interpretation of the stipulations is correct, we now have to inquire about the reasons that might have
led Löwenheim to introduce a stipulation that prohibited using expansions in a proof, although they can be used to informally
elucidate, for example, the meaning of quantifiers. I will suggest a possible explanation. In the logic of relatives it is
tacitly accepted that, for the domain in which the expansion is made, the final formula (the expanded formula) expresses the
same as the initial one. Naturally, an essential assumption in any expansion is that both formulas are interpreted in the
same domain. For example, it is accepted that 
) and (3.12) express the same for the domain {1, 2, 3} (or for any domain with three elements that are held to be denoted
by 1, 2, and 3; logicians of the algebraic school did not distinguish clearly betweenthe two alternatives, and spoke indiscriminately
of one or the other). The essential assumption in this example is that 1, 2, and 3 are (or denote) the elements of the domain
or, in Löwenheim's words, that the sum in (3.12) ranges over all elements of the domain. Löwenheim might have realized that
this assumption is not reflected in (3.12), because nothing prevents us from considering, for example, that the domain has
more than three elements or that 1, 2 and 3 denote the same element.10 Accordingly, he might have concluded that sums and products that range over all the elements of a given domain cannot strictly
be expressed by a + sum and, therefore they cannot be expressed by an expansion on the domain.
As we will see, in the proof of his theorem Löwenheim introduces numerals that denote elements of a certain domain, but with the peculiarity that two distinct numerals can denote the same individual. The problem posed by the treatment of these numerals is, roughly speaking, the one that I have just described. Löwenheim does not consider that these numerals alone determine another domain, because the equalities and inequalities between them are not fixed. One of the most important parts of his proof aims to determine these equalities. For this reason, Löwenheim may conceivably have intuited the problem that the development of the quantifiers could present. Perhaps Löwenheim's proof is the first one in the history of logic where numerals are used as individual constants instead of as canonical names of individuals.
3.3.3 Before examining the arguments against this interpretation of the stipulations, I would like to make clear what its consequences
are. First, it cannot be maintained that for Löwenheim (3.10) is a schema of formulas, or that 
represents strictly a string of as many existential quantifiers as there are elements in the domain. If with his stipulations
Löwenheim meant what this interpretation proposes, then he must have thought that (3.10) was a formula and a single quantifier with certain special characteristics. This would explain why he saw no contradiction between (3.10) and
the stipulation according to which formulas must have a finite number of quantifiers. Those of his claims which are usually
interpreted in terms of expansions should be seen in this case exclusively as representing ways (perhaps the only ones at
his disposal) of explaining intuitively the meaning of (3.10).
The other consequence is in fact a conjecture. Löwenheim must have held Schröder's proof of the equation to be wrong, not only because Schröder's argument was inconclusive, but because his approach presupposes that, given a domain, a formula can be replaced equivalently by an expansion. Löwenheim may also have made a semantic reading of Schröder's proof, but, as I have already stated, I do not believe such a reading to be possible.11
3.3.4 Let us turn now to the arguments that could be used against my interpretation of the stipulations, or, more precisely, against the consequences I have just mentioned. The first argument consists in maintaining that since Löwenheim makes no reference to what Schröder says it is reasonable to believe that he agrees with him. In my view this argument is weak. First, it is not that Löwenheim refers to Schröder without warning that he disagrees with him; in fact, he does not even mention Schröder here. Second, we have seen that Löwenheim introduces modifications in an aspect which Schröder considers essential and does not draw attention to these modifications. Recall that Schröder would have considered Löwenheim's equation to be false, or, at least, he would have said that written in this way (3.10) does not express the idea that it should express. Perhaps the reason that Löwenheim did not refer to Schröder was that he could not, halfway through a proof, explain why he wrote the equation in a way which appeared incorrect to Schröder. There may be other reasons, because he could merely have said that the idea was Schröder's. In any case, it is clear that we cannot draw conclusions about Löwenheim's approach by basing ourselves on what Schröder says.
The second argument is that Löwenheim himself states that is an n-fold quantifier, and this can only mean that is a string of as many existential quantifiers as there are elements in the domain. But, of course, it only makes sense to
speak of a string of quantifiers in the context of the expansion; so if is a string of quantifiers, (3.10) is a schema of formulas.
This statement should be borne in mind, but we need not necessarily make a syntactic reading of it. Let us suppose that at
the same time Löwenheim said explicitly that it was incorrect to perform expansions. For him, the two statements could be
perfectly compatible. The point is that, as I said above, Löwenheim cannot explain the meaning of (3.10) in any way other
than the one he follows. He may thus think that is a single quantifier, that expansions are not correct (in the sense that I have explained), and at the same time use them
to explain the meaning of (3.10). With the assertion that is an n-fold quantifier, Löwenheim may only be claiming that has the meaning that we intuitively assign to a string of quantifiers.
Indeed, it would not be surprising if Löwenheim thought that was a single quantifier. He may have seen it as a kind of generalization of the concept of multiple quantifier, and, as I said
in subsection 2.5.2 of chapter 2, in the logic of relatives multiple quantifiers are thought of as a single quantifier. This
would explain why the special nature of passed unnoticed.
The third argument (strictly, inseparable from the previous one—I have separated them for the sake of simplicity) appears to be decisive: Löwenheim performs expansions, and so we cannot attribute to him an interpretation of his stipulations that prohibits them. All the commentaries with which I am familiar (including Skolem's, which I will mention shortly) state that in this paper Löwenheim dealt with formulas of infinite length and performed expansions with a nondenumerable number of terms. The examples which are invariably used proceed from the proof of his famous theorem. I am not saying that these expansions are held to be the only ones in his paper, but that the specific examples are taken from there.
The only expansions in the proof of the theorem are the three I mentioned in subsection 3.2.2 of this chapter: the one that I quoted, and two more on finite domains. As I said, the three are accompanied by the warning that performing expansions is contrary to the stipulations. I do not think that there is anything in the way Löwenheim speaks that supports the claim that (3.10) is a schema of formulas. His expansion is not intended to mean that (3.10) should be replaced by
in the case of a denumerable domain, but rather to make clear the meaning of (3.10). Löwenheim says so openly at the beginning of the quotation, but even if he had not, the fact that he then writes the values taken by k1, k2,k3,... below the quantifiers suggests this;12 it isa completely unnecessary clarification, only there because Löwenheim wanted to make the idea as evident as possible.
The fact that the above expansions had a didactic purpose does not show that Löwenheim had something against expansions or that for him (3.10) was not a schema of formulas. What it shows is that these expansions cannot be adduced as evidence of what he thought about (3.10) or about the value he gave to expansions in general (especially when no mention is made of the warning that accompanies them). It could be replied that my arguments are only applicable to what Löwenheim thought, but, as I myself said referring to Schröder, what one thinks is one thing and the way one argues quite another. What I mean is that, regardless of what he thought, we could say that for Löwenheim (3.10) was a schema of formulas, if this were the only way of accounting for his arguments (which it would be if in some case he replaced (3.10) with his expansion). In the absence of a clear notion of formal language it would not be surprising if this type of inconsistency occurred, but the point is that this does not happen. The only expansions in the whole of the paper which have to do with (3.10) are the ones that I have mentioned.
3.3.5 Finally, against the interpretation that we are discussing, one may quote Skolem:
Löwenheim's proof is unnecessarily complicated, and moreover the complexity is rather essential to his argument, since he introduces subscripts when he expands infinite logical sums or products; in this way he obtains logical expressions with a nondenumerably infinite number of terms.Thus he must make a detour, so to speak, through the nondenumerable. (Skolem [1923], p. 140, (293))
In other papers, Skolem makes similar remarks. As can be seen, Skolem's opinion coincides with the traditional one. Indeed, I believe that some of the commentaries simply repeat what Skolem said. I have left Skolem's opinion till last, as the criteria for evaluating the opinion of a historian and that of a logician who initially worked in the field of the logic of relatives are different, even when the opinions coincide.
With regard to Skolem's comments I can only repeat what I said before, that Löwenheim's proof does not depend on expansions. It does not contain any formulas with a uncountable (nondenumerable) number of terms, contrary to what Skolem's words suggest. What Löwenheim does is to write a part of an expansion. I will give an example. The formula
can be seen, speaking informally, as a fragment of the expansion of 
in a certain domain (uncountable or not). This is the type of formula that intervenes in the proof and, clearly, these formulas
do not contravene the stipulations even if we interpret them in the way we are discussing here. I will argue for this when
I comment on the proof of the theorem.
Although what I have just said may appear to suggest the contrary, I do not think that my interpretation of Löwenheim's proof differs greatly from Skolem's. In fact it is the traditional interpretation that is entirely different from Skolem's, as I will show later. My divergences from Skolem are limited to the above quotation (or others in which he states the same idea), and even on this point they may be less important than they appear.
Löwenheim's proof does not depend on expansions, but it is true that he gives the impression that he is thinking in terms of expansions when he reasons. There are even occasions when the terminology seems to be suggested by expansions. When Löwenheim writes formulas like the one above, he speaks as if he had in mind the whole expansion in an uncountable domain and as if he were writing a part of it. In this regard, we could say that the above formula proceeds from an expansion. This may be all that the last sentences in the quote from Skolem actually mean.
Another point is that we can read Löwenheim's arguments and explanations in a way that Skolem could not. I think that everyone would accept that the meaning that Löwenheim gives to (3.10) is the same as the one that (3.11) attributes to it. But we should remember that (3.11) is a more or less updated form of expressing what Löwenheim meant. Neither Löwenheim nor Skolem could have expressed it in that form because (3.11) presupposes that a clear distinction is made between syntax and semantics. It is in consequence normal that Skolem ignores the definition of Relativausdruck and describes Löwenheim's use of (3.10) in terms of expansions.
3.4.1 Schröder's procedure for changing the order of quantifiers is generally considered to be the origin of the concept of the Skolemfunction, and
as the current way of writing (3.10). This quotation from Hao Wang is a typical example of this opinion:
The use of “Skolem functions” seems to go back to logicians of the Schröder school to which Löwenheim and Korselt belong. They speak of a general logic law (a distributive law) which, in modern notation, states:
(Wang [1970], p. 27)
The logic law to which he refers is equation (3.1) or (3.9). Van Heijenoort (From Frege, p. 230), Largeault ([1972], p.114), and Brady ([200], p. 193) say something similar. Moore ([1988], p. 122) asserts that Löwenheim uses the above equivalence (though interpreted in an infinitary way) in his proof and Vaught ([1974], p. 156), who is more cautious, says that “Löwenheim's proof involves a strange way of thinking in dealing with what we would call Skolem functions.” The following quotation from Goldfarb seems to me to be more accurate, because it stresses what in my opinion is the principal aspect of the procedure devised by Schröder:
The use of choice functions was foreshadowed by Schröder [1895, § 29] and by Löwenheim [1915] in their introduction of double subscripts into relative equations. Although in the end double subscripts represent functions on the universe, these authors did not connect quantification over double subscripts with (second-order) quantification over functions. (Golfarb [1979], p. 357, note 12; my italics)
In this section I aim to show that, as Goldfarb says, neither Schröder nor Löwenheim associated the procedure for changing the order of quantifiers with quantification over functions. We will see that Skolem did not make this association either; indeed it is debatable whether fleeing terms are functional terms (i.e., terms of the form ft1,...,tn, where t1,...,tn are terms and f is an n-place function symbol). Finally, we will see that the interpretation of (3.10) in terms of what today we call Skolem functions does not clarify why Schröder andLöwenheim reasoned as they did, nor does it explain Skolem's statements.
3.4.2 The first point I will discuss is whether ki is a functional term or not, that is, whether its logical behavior is like the behavior that we attribute today to fx. Both Löwenheim and Schröder made a purely instrumental use of fleeing indices; these indices were never completely inserted in the theory. Too many aspects of their nature are unclear and it is difficult, not to say impossible, to know how Löwenheim and Schröder would have considered them.
I will begin by looking at syntactic aspects. In what we can consider as the standard use, ki occurs in formulas in which the variable i is universally quantified, such as IIiA(i,ki) or 
). When the variable i ranges over the elements of the domain, ki gives rise to different terms, as many as the domain has elements. Apart from alphabetical variants, the possibility of replacing
the variable i with terms that are not elements of the domain is not considered. As I explained in chapter 2, once a domain
is fixed, we can consider that the language is expanded with individual constants which play the role of elements of the domain.
When we say that the domain is, for instance, {1, 2}, we consider the language whose only individual constants are 1 and 2.
My point is that in this example it is only expected that the variable i will take 1 and 2 as values (or be replaced by them)
to produce the terms k1 and k2. Probably for the sake of convenience, Löwenheim still calls these indices “fleeing indices.”
This ability to generate a different term for each element of the domain is the main characteristic of fleeing indices, for both Schröder and Löwenheim. Schröder's notation strained the syntax considerably and did not clearly reflect this characteristic. As we saw, Löwenheim was aware of this problem and solved it, ignoring Schröder's indications.
The terms which ki generates when the variable i ranges over the elements of the domain behave like simple (not fleeing) indices. It makes sense
to debate whether or not 
represents a string of as many existential quantifiers as there are elements in the domain, simply because we can quantify
the terms that ki generates. This is a significant difference between the syntactical behavior of ki and of fx.
When we think of the syntax of fleeing indices, an immediate question is whether or not a fleeing index can occur as a subindex—that is, whether or not indices of the type kk1 are admissible. More exactly, the question is whether to accept this formation rule: if t is an index (fleeing or not), kt is a fleeing index. As I said, fleeing indices are devised to solve a specific problem in which these expressions do not occur and therefore are not considered. Löwenheim mentioned this problem in passing, when he came up against it. He did not give a conclusive response, but his reasoning is worth examining.
As we will see in the following chapter, when Löwenheim explains the method of obtaining the normal form of a formula, he discusses the problem of how to change the order of the quantifiers in a case of the type
In this context, he states that it is possible to write lkh instead of l(kh). He says not that it is wrong to write the latter, but that it is possible to write the former. The above formula is logically equivalent to
Löwenheim makes a couple of expansions to show that it does not matter which of the two types of terms we write. He does not intend thereby to offer a proof, but to make it clear that either of the alternatives can be adopted. One of the two expansions, also simplified, is the following:
There is no other reference to l(kh), nor does he make the expansion for this alternative. At first sight, it seems surprising that Löwenheim thinks that with this expansion he has shown what it was his purpose to show. I think that he offers no more clarifications because what he means is trivial. The idea is that the subindices have no other function than to differentiate the terms; from this perspective it does not matter whether we write l12 or l12 . The choice between one and the other is simply a matter of notation. Using other variables would have given the same result, and, in fact, this is exactly what Löwenheim does.
We might think that if it were solely a matter of notation, Löwenheim would not mention it and would just adopt one of the
alternatives. But he is obliged to mention it. In the case we are examining he considers for the first time the problem of
placing a in front of a II. There is actually no equation that we can apply in this case, but Löwenheim believes that (3.9) can be
applied, because he considers that behaves essentially like any existential quantifier. Since the result of applying (3.9) would seem to be
Löwenheim must explain why he writes the subindices in a different way. He notes that it does not matter which alternative is adopted and, in my opinion, simply chooses the one that is more convenient. (We should remember that he does not write A(h, k, lkh), but Ahklkh.)
Nothing in this argument has anything to do with functions. If we interpret the above formulas in terms of functions, we will not understand anything of what Löwenheim intends to say with his expansion. If we think of fleeing indices as functional terms, what Löwenheim maintains, in today's notation, is that
is logically equivalent to
where f is a unary function symbol and g is a binary one. It is not clear what the counterpart of (3.13) is in terms of functions; there is probably no point in asking this question. The above equivalence is true, and, as we know, it is proved with the aid of the axiom of choice, but with this approach what Löwenheim says becomes incomprehensible. I have never seen any commentary on the transformation that I have just mentioned (in general, there is never any commentary on Löwenheim's method of obtaining of the normal form of a formula). I think that in part this is due to the fact that this method receives an “updated” reading (in terms of Skolem functions). Many of Löwenheim's commentaries then become inexplicable, but as the conclusions he reaches are in general correct, commentators have preferred not to go into detail.
The two mentioned facts (that the terms generated from ki are treated as variables and that the substitution of the fleeing indices by Skolem functions makes the details of Löwenheim's argumentation incomprehensible) suggest that fleeing indices are not functional terms, but a suggestion is not a conclusive proof. What these facts do prove is that neither Löwenheim nor Schröder connected fleeing indices with the idea of function. Later I will present further arguments in favor of this claim, but first let us examine whether fleeing indices behave semantically like functional terms.
3.4.3 Function symbols, like fleeing indices, make it possible to form terms from others. In the case of function symbols, the value assigned to the new terms does not depend on their component terms but on the value assigned to them. If x and y take the same value, fx and fy will also take the same value. This characterizes functional terms. The question is whether fleeing indices have this characteristic—or, more precisely, whether ki and ki can denote different elements when i and j denote the same element. If the answer is “yes,” then fleeing indices are not functional terms. The point is not that Löwenheim and Schröder did not associate them with the idea of function, but that they are not functional terms. If the answer is “no,” we can say that they are functional terms although Löwenheim and Schröder did not identify them as such. The issue here is to determine the semantics of fleeing indices.
Nothing we have seen so far answers the question that I have just posed. If Löwenheim and Schröder see in k1 and k2 two distinct variables, then they are taking their value to be independent of the value of their subindices. Therefore k1 and k2 do not appear to be functional terms. This detail is indicative, but it does not resolve the problem because 1 and 2 are two distinct elements of the domain and we need to know what happens when the subindices have the same value, or if we prefer, when they denote the same element.
Neither Löwenheim nor Schröder considered the possibility that two distinct subindices of a fleeing index could denote the same element. This is understandable. First, in the normal use of fleeing indices this question is not considered because the subindices are replaced by elements of the domain. Second, it is difficult to consider the problem abstractly if we do not make certain distinctions. In the logic of relatives there are no individual constants, so neither Löwenheim nor Schröder could have asked what would happen when in ki the variable i is replaced by two distinct constants that denote the same individual.The same question can be asked using variables, but I do not think that Löwenheim or Schröder could have posed it due to the lack of a clear separation between syntax and semantics. The expression “i and j take the same value” is used with the same meaning as “i and j are the same element of the domain.” In this way, the question whether ki and kj can denote distinct elements when i and j denote the same individual becomes a triviality. In any case, it does not matter whether or not Löwenheim and Schröder were in a position to pose this question; the important point is that they did not.
They did not explicitly consider the question, but Löwenheim came across it by chance. Simplifying the situation, in the proof
of his wellknown theorem there occur terms of the form k1 and k2 which arise from replacing the variable i with 1 and 2 in ki; in this case, 1 and 2 are not elements of the domain. Löwenheim
insists repeatedly that 1 and 2 can denote the same element in this case. He therefore replaces k1 with 3 and k2 with 4 and, for reasons which are not relevant here, says that all possible equalities and inequalities between 1, 2, 3;
and 4 should be considered. This is precisely the situation that interests us, since 1, 2, 3; and 4 behave entirely like individual
constants of the language and the problem that we posed was whether it could happen that 1 = 2 and k1
k2, or, equivalently, that 
12= 1 and k1k2 = 0 (34 = 0). It is clear that if ki is a functional term, then it 12 = 1 and 34 = 0.
If Löwenheim had clarified which equalities were possible, the question of whether or not ki is a functional term would be definitively resolved, but unfortunately he did not. His exposition is compatible with either alternative. In my view, however, there are reasons for believing that the only limitations to which the systems of equalities are subject are those imposed by the properties of equality. In other words, I think there are reasons for maintaining that fleeing indices are not functional terms.
First, in this part of the proof Löwenheim puts great emphasis on the interpretation of atomic sentences of the form nm. For instance, he repeats time and again that one should not presuppose that different numerals denote different elements.14 It is reasonable then to think that he would also make explicit mention of any restriction which should be taken into account
in establishing which systems of equalities were possible. If Löwenheim gives no other warnings, it is probably because the
systems of equalities that are possible are all those that are compatible with the properties of equality, and for this reason
no clarification is necessary.
Second, the fact that Löwenheim replaces k1 and k2 with different constants suggests that they are simply different terms; since when they are replaced by constants, the dependence on the subindices is lost, and their possible functional character as well. If k1 and k2 can be replaced by 3 and 4, it is because their value does not depend on the value of their subindex. When we think of the equalities possible between 1, 2, 3; and 4, it is natural is to consider them as distinct,unrelated terms; and, as I have just said, since this is natural, no clarification is needed. Any system of equalities acceptable between 1, 2, 3; and 4 must also be acceptable between 1, 2, k1, and k2. In consequence, they must simply be distinct terms.
Third, in the context we are examining Löwenheim makes certain assertions which at first sight appear to support a functional interpretation of fleeing indices, but, in my opinion, this is not so. Referring only to cases in which the subindex is a variable, Löwenheim affirms that fleeing indices are functions of their subindices. Löwenheim also calls k1 and k2 “fleeing indices,” but warns that they are no longer functions of the subindex. (Remember that now 1 and 2 can denote the same element of the domain.) This does not mean that for Löwenheim fleeing indices are functional terms in our sense; he only means that, when the variable i takes different values, ki gives rise to different terms. Thus, ki is a kind of generator of terms, and as such behaves syntactically as a (one-to-one) function of i. When the variables that figure as subindices take values, the terms that result are no longer functions of their subindices because the subindices no longer take values. Hence, k1 and k2 are no longer functions of the subindex (they do not generate other terms) but simply distinct terms, or, in Löwenheim's words, they denote specific elements (just like the free variables of a formula).
3.4.4 I have not seen any arguments in favor of the idea that fleeing indices are functional terms. This is probably because it is considered so obvious that it is not thought to be necessary to argue for it.
The supposed proof of their being functional terms is almost certainly to be found in the meaning of (3.10). I said above
that (3.11) formulates the appropriate semantics for (3.10), and all the commentators are in agreement on this point. Since
(3.11) asserts the existence of an indexed family, and families are functions, the conclusion is that 
is a quantifier over functions and ki a functional term. This is why all the commentators see in (3.10) the origin of the
concept of the Skolem function.
In my view, whether or not is a quantifier over functions is one question, and whether or not ki is a functional term quite another. Indeed, asserts the existence of an indexed family of elements of the domain, and in this respect it is a quantifier over functions.
Nevertheless, this does not imply that ki must of necessity be considered as a functional term. As I said above, (3.11) is completely neutral as to whether fleeing
indices are functional terms or not; contrary to appearances, it gives no information about this problem. It is possibleto
adopt a precise formulation of (3.11) that does not oblige us to consider fleeing indices as functional terms. I have adopted
a formulation of this type in the technical reconstruction that I present in the final appendix,15 but we need not mention it here. All I mean to show is that there are reasons, albeit not conclusive, for thinking that fleeing
indices are not functional terms and that there is no need to consider them as such.
3.4.5. Whether fleeing indices are functional in nature or not, it is evident that Schröder and Löwenheim did not connect them with
the idea of function. If we identify with 
, we are unable to understand the way in which they deal with fleeing indices. Their arguments are difficult to understand
precisely because they did not think of fleeing indices as functional terms. However, these arguments can be understood when
we see them as arguments based on an informal view of the notion of indexed family, that is, arguments in which indexed families
are vaguely considered as sets of objects (elements or indices) such that each object carries a subindex indicating the element
of the domain with which it is associated. As I explained in subsection 3.4.2, the way in which Löwenheim argues that it is
not necessary to write subsubindices is a clear example of what I have said here. I will now give another example which shows
even more clearly that Schröder and Löwenheim did not associate the ideas of indexed family and function.
At the beginning of this chapter I mentioned how strange and unconvincing Schröder's reasons are for writing instead of i
in the formula 
). I claim that his reasons are comprehensible (although still not very convincing) if we think of them with regard 
to indexed families.
Schröder saw clearly that (3.11) also expressed the meaning of 
. More explicitly, he saw that, for any domain D and any solution S in D, the statement
for all 
there exists 
such that A[a, b] is true with S in D
is equivalent to (3.11), that is, to the statement
there is an indexed family (ma | of elements of such that for all A[a, ma] is true with S in D.
To reflect approximately the way in which Schröder could have formulated these ideas, we will use the same letters for the variables over elements of the domain as for the indices, and omit references to the domain and to the solutions. The above statements can then be reformulated as follows:
(3.14) for all 
there exists 
such that A[i, m] is true in D;
(3.15) there exists an indexed family (mi | 
such that for all A[i, m] is true in D.
It is clear now that 
) is the literal translation to symbols of (3.14) and that between this statement and (3.15) there is an important difference:
the order of the quantifiers has changed. So we can imagine Schröder's problem as having to find a reformulation of (3.15)
which can be directly expressed in symbols in the same sense that 
) is the literal expression in symbols of (3.14). Of course, it is easy for us to express (3.15) in a second-order language,
but this so is because:
1. we have a precise concept of formal language, and
2. we identify an indexed family with a function of a certain kind.
Let us now try to put ourselves in the place of someone who, like Schröder, does not have a precise concept of formal language and does not associate the concept of indexed family with the concept of function. The problem is how to express in a way that can be directly translated to symbols what we mean by “there exists an indexed family,” since (3.15) has the appropriate form for the other concerns.
Bearing in mind the informal concept of indexed family, the expression
there exists an indexed family 
,
could be replaced, in an initial attempt, by
for all 
there exists mi.
But let us see what happens when we make the substitution. Statement (3.15) then becomes:
for all there exists mi such that for all ,A[i,mi] is true in D.
Unfortunately, now the variable i is quantified twice, and we cannot discard either of the quantifiers. If we discard the
first, we lose the idea of indexed family. If we discard the second, we return to the beginning, that is, with no change in
the order of the quantifiers. Further, if the two quantifiers are maintained, the statement becomes somewhat confused, and
there is a problem with the scope of the quantifiers. For this reason Schröder considers that 
) plays no role in 
). One way of avoiding these problems is to change the variable. Let us consider the following possibility:
(3.16) for all there exists m such that for all 
].
But again there are problems. If we take (3.16) literally (i.e., considering that all the quantifiers are of the same type),
(3.15) and (3.16) do not have the same meaning. For example, if 
, then from (3.16) we can deduce that
there exists ma such that for all 
, A(i, ma),
which clearly is not a consequence of (3.15). For (3.16) and (3.15) to express the same, we must
1. postulate that and i will take values at the same time, and
2. bear in mind that the role of “for all ” is to tell us that there is an indexed family there, and, therefore, it is not an authentic quantifier (that is to say,
it is not a quantifier of the same type as “for all i”).
With these conventions, the formalization or literal expression in symbols of (3.16) is 
:
I think that the reconstruction I have just presented makes it clear that, when we see Schröder's arguments as dealing with indexed families, we reach an understanding of them which would be impossible if we interpreted them as functional terms.
3.4.6 Skolem did not associate fleeing indices with the idea of function either. This point is especially significant because Skolem acquired his logical training inside the algebraic tradition.
In Löwenheim's proof of his theorem, equation (3.9) and, more precisely the fleeing indices play an important role. In Skolem's first proof of Löwenheim's theorem we read:
Löwenheim proves his theorem by means of Schröder's “development” of products and sums, a procedure that takes a II symbol across and to the left of a Σ symbol, or vice versa. But this procedure is somewhat involved and makes it necessary to introduce for individuals symbols that are subindices on the relative coefficients. In what follows I want to give a simpler proof, in which such subindices are avoided ... (Skolem [1920], p. 103 (254))
As this quotation shows, Skolem saw that Schröder's procedure for changing the order of quantifiers complicated Löwenheim's proof. His intention (or, at least, one of his intentions) was precisely to avoid the use of fleeing indices. If we present the proof using the traditional reformulation of (3.9) (in terms of functions), Skolem's words are irrelevant because the problems that he mentions disappear.
It is important to stress that the difficulties mentioned by Skolem in the above quotation are not due to notation (as his reference to subindices might suggest). The complications are essential to Löwenheim's argument and disappear or are reduced when functions are used. In support of these two assertions we could repeat the quote in subsection 3.3.5, in which Skolem makes the same remark (and it is not the only time he made it). In 1938, when Skolem had proved the theorem in different ways (including the one that uses the functions that today bear his name) he stated:
Löwenheim's proof is very arduous because of the use of the logical expressions II and Σ, following Schröder's notation with an infinite or indeterminate set of terms. But his reasonings can be simplified by using the “Belegungsfunktionen” (i.e., functions of individuals whose values are individuals), bearing in mind the fact that a proposition such as
can be transformed into
(Skolem (1938], pp. 455–456)
If we formulate (3.9) in terms of functions, the version that we will give of Löwenheim's proof must, of necessity, be in terms of Belegungs-funktionen. How then do we explain what Skolem thought, and what did his contribution consist in? Understanding Löwenheim's proof depends on our understanding how he reasoned with fleeing indices and, judging from Skolem's words, seeing them as functional terms does not seem to be the right way of approaching the proof.
1In fact, Löwenheim speaks of equations, but since they are equations of the form A = 0, which are considered to be in normal form when A is in normal form, we can ignore this detail.
Recall that a formula is in prenex form if it is of the form Q1i1 ... QninA, where each Qp (1 ≤ p ≤ n) is a quantifier and A is a quantifierfree formula.
2Vorlesungen III, p. 516. German text:
jeder Term einer “Σ” auch darstellbar ist als wirkliches Gleid einer (binären) “Summe” (in engsten Sinne), deren andres Glied alsdann, als unabhängig von dem in jenem Term auftretenden m mit a bezeichnet, dem Schema IImf(m) + a = IIm {f(m) + a} unterworfen sein muss. Etc. q.e.d.
3Vorlesungen III, p. 516. German text:
Denn in seinem letzten Teile würde alsdann Σif(i,mi) als allgemeiner Faktor der II auftreten, und dieses müsste einen von i gänzlich unabh ängigen Wert aufweisen, sintemal der Buchstabe i darin blos als Stellvertreter funktionirt für die ihm aus dem Erstreckungsbereich des i beizulegenden Werte. Es könnte darnach auch mi als solches in seinem ausgewerteten Ausdrucke nicht mehr vorkommen. (Analog wie ein bestimmtes Integral unabhängig ist von seiner Integrationsvariablen!) Darnach käme der dem Term vorangehende Operator IIi(IImi) ganz in Wegfall, gemäss dem Tautologiegesetze IIa = a, und unser Schema müsste sich noch ausserordentlich vereinfachen! Das solche Vereinfachung im Allgemeinen nicht zulässig, würde sich exemplificando darthun lassen.
4“Über Möglichkeiten,” p. 451 (236). For typographical reasons, I replace the symbol used by 
Löwenheim by 
.
5Löwenheim probably intends to avoid expressions as unintuitive as IIiA(i; k
), where it should be supposed that the variable is bounded by the quantifier. Due to the use of two different variables Schröder is obliged to reason with this type of expression
when he applies his equations (Vorlesungen III, p. 517).
6IIi(Ai1 + Ai2 + Ai3 + ...) is the (partial) expansion of IIiΣkAik in the domain and Σk1k2k3...A1k1 A2k2 A3k3 ... that of 
. The third formula merely makes more explicit the values taken by the variables.
7It is not clear if this view can also be ascribed to Vaught, because he only says that Schröder and Löwenheim “seem to have
interpreted” 
as 
, where A is the domain; see Vaught [1974], p. 165.
8Recall that a solution in a domain D is a function that assigns 0 or 1 to therelative coefficients in the domain D. An indexed family (ka | a 
D) of elements of D is a function k from D into D, where ka is the value assigned to a. By A[a; ka] I mean that i takes the value a and ki the value ka. It is not necessary here to give a completely precise formulation of
this idea (I will do so in the appendix).
9For reasons that will be discussed in chapter 5, even if Löwenheim had wanted to give the meaning of (3.10) in a way analogous to (3.11), certain limitations of the logic of relatives would have prevented him from doing so.
10To prove that ΣiA(i) and (3.12) are equivalent formulas we only need the premise IIi(i1 + i2 + i3), but if 1, 2, and 3 are not different from each other, then (3.12) is not an expansion.
11Since Löwenheim offers no proof of equation (3.9), we may wonder why he considered it correct. This question is of interest
in relation to the implicit use of the axiom of choice in mathematical arguments. Specifically, did Löwenheim consider it
evident that, if for every a D there exists b D such that 
(a; b); then there exists an indexed family (ba | a Di such that (a; ba), for every a D?
12Remember that Löwenheim equates the previous formula with
Σk1=1,2,3,...Σk2=1,2,3,Σk2=1,2,3,... . . . A1k1 A2k2 A3k3....
13Schröder does not consider any case of this type.
14Löwenheim's insistence is significant and, as we will see, important for the proof of the theorem. If he had given no warning,
it would be assumed that 1 and 2 are different elements of the domain and, accordingly, that 12 = 0, since this is the normal use of numerals in the logic of relatives.
15Although I do not introduce the quantification over fleeing indices, in the corresponding section I indicate the way to extend the definition of satisfaction for these quantifiers.