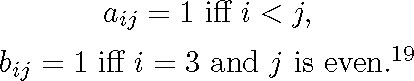Chapter Two

The Theory of Relatives

2.1 INTRODUCTION

2.1.1 The study of the logic of relatives (or of relations) was begun by A. De Morgan in his 1859 paper “On the syllogism IV and on the logic of relations.” If Boole can be considered the founder of mathematical logic, De Morgan deserves acknowledgment as the first logician to appreciate the limitations of traditional logic and to recognize the importance to logic of the study of relations. De Morgan, for a number of reasons, did not establish the foundations of a theory of relations.According to Tarski ([1941], p. 73), the creator of the theory of binary relations is Peirce. Without denying his debt to De Morgan, whom he considered as “one of the best logicians that ever lived and unquestionably the father of the logic of relatives,” in 1903 Peirce had this to say of his own work:

In 1870 I made a contribution to this subject [[logic]] which nobody who masters the subject can deny was the most important excepting Boole's original work that ever has been made.¹

Modesty was not one of Peirce's virtues,² but there is no doubt that he established the basis of the theory of relations (later developed by Schröder) and that this contribution has an extraordinary importance in the history of logic.

Peirce studied relative terms for the first time in his already mentioned [1870]. The complete title of this paper clearly describes his purpose: “Description of a notation for the logic of relatives, resultingfrom an amplification of the conceptions of Boole's calculus of logic.” Peirce worked on the development of this new calculus between 1870 and 1883. In accordance with the title, the calculus of relatives was the extension of the calculus of classes obtained by adding to it the definitions (axioms) corresponding to certain operations characteristic of relatives (mainly inversion, relative sum, and relative product).

The calculus of relatives was never to Peirce's liking, because he thought that it became highly complicated when class operations occurred together with relative ones (Peirce [1883], p. 464). In [1882] (“Brief description of the algebra of relatives”), Peirce made use of quantifiers in order to define relative operations in terms of operations on certain kind of coefficients and thus established the basis of what we could consider an algebraic theory of relatives. Peirce did not develop this theory, and the only advantage he saw in these definitions was that they allowed a simplification of the calculus of relatives (in spite of which he continued to hold that it was excessively complicated).

As I said in the previous chapter, between 1883 and 1885 Peirce lost interest in the algebraic focus of logic. In [1883] (“The logic of relatives”) he was still trying to develop the calculus of relatives using the results of [1882], but at the end of the paper there are a number of indications of what his new point of view was to be. From [1885] onwards he concentrated on what he later called the general algebra of logic.³ Peirce gave it this name because he thought he was describing a different type of algebra, but from today's perspective, the nearest thing to the general algebra of logic is an informal, elementary exposition of first-order logic. Thus, Peirce conceived his new algebra as a language and saw that from this perspective there was no need for relative operations. Peirce was always convinced that one of the main advantages of his new algebra was that it meant that relative operations could be dispensed with completely.

As was the case with the calculus of classes, Schröder systematized the contributions made by Peirce between 1870 and 1885, developing them substantially. The result of this work was the theory of relatives, which Schröder presented in the third volume of Vorlesungen Essentially, this theory is the one that underpins Löwenheim's “Über Möglichkeiten” (short for “Über Möglichkeiten im Relativkalkül”).

2.1.2 In the next two sections I will introduce the basic concepts and postulates of the theory of relatives. I do not intend to offer a historical vision explaining the ideas that Schröder takes from Peirceand identifying the specific contributions of each one (although some of these details are mentioned in the notes).⁴ My aim is to present as clearly and systematically as possible the theory of relatives as it emerges in the third volume of Vorlesungen, because it is here that the most complete and detailed exposition of the theory is found, and, in fact, it is here that the logicians of the time (and later scholars such as Tarski) studied it.

Schröder based the theory on 31 conventional stipulations (Festsetzungen) which can be taken as its fundamental propositions. If the theory were axiomatized, some of these stipulations would be axioms of the theory, but they should not be thought of as such; rather, they should be understood as accompanied by a series of clarifications and complementary rules that are explained informally, and without which they could not be used.⁵ In what I call basic postulates I include Schröder's stipulations and some laws of quantification which he considers proven, but which cannot be justified solely with his stipulations.

In the fourth section I will try to explain how the theory of relatives allows Löwenheim to obtain the first results of model theory. In the last section I will specify certain aspects that should be borne in mind in the analysis of the proof that Löwenheim made of his theorem.

2.2 BASIC CONCEPTS OF THE THEORY OF RELATIVES

2.2.1 First-order domain. Indices

Schröder begins the exposition of the theory of relatives assuming the existence of a pure and consistent manifold of given elements:

Let us think of the “elements” or individuals

A, B, C, D, E, . . .

of a “usual” manifold (compare v. 1, p. 342) as given and in some way conceptually determined. They should be regarded without exception as different from each other and from the nothing (from 0). They must be compatible (consistent) with each other so that positing one of them should not prevent the conceivability of another, and theymust exclude each other (be mutually disjoint), so that none of the elements can be interpreted as a class that embraces some other of them.⁶

The starting manifold is called first-order domain (Denkbereich der ersten Ordnung) and is denoted by 1¹. As we saw in the previous chapter, the elements of a manifold are its unit subclasses. Thus, says Schröder, if the elements are A, B, C, D,..., then

Schröder maintains that the first-order domain must have more than one element.⁷ He states that this condition is necessary for the validity of almost all the theorems of the theory; this is probably an exaggeration. The condition should be taken into account in order to understand why Schröder asserts the validity of certain formulas, but it does not affect the basic postulates of the theory, and it was not taken into consideration by later logicians. Indeed, in “Über Möglichkeiten” Löwenheim says that Schröder errs in considering as valid a formula that is only false when the first-order domain has one element. ⁸

In the theory of relatives the term index is used to refer to variables that range over the elements of the first-order domain. It should of course be understood that these are not elements in our sense. In the example above, the indices take the values A, B, C,.... As indices the letters h, i, j, k, l, and m are the most frequently used.

2.2.2 Ordered pairs and relatives

An ordered pair is the result of taking two elements of the first-order domain together in a particular order. If i and j are elements of the first-order domain, the pair that results from taking first i and then j is denoted by (i : j). This is how Schröder explains informally what an ordered pair is (Vorlesungen III, p. 8). His explanation is the one we give today when speaking informally. However, he does not mean what we mean, because in the theory of relatives an ordered pair is an individual (see subsection 1.4.2.1 in chapter 1). Specifically, what he calls “ordered pair” is, in our terms, a unit class whose element is an ordered pair.⁹

Ordered pairs are also called individual relatives. A relative (binary or dual) is an identical sum of individual relatives. The word “relative” is short for “relative term” and refers to what we call “relation.”

The second-order domain (Denkbereich der zweiten Ordnung) is the identical sum of all the individual relatives that can be formed with the elements of the first-order domain and is denoted by 1². The individual relatives (the ordered pairs) are therefore the elements (individuals) of 1². If, for example, 1¹ = A + B + C + ..., then

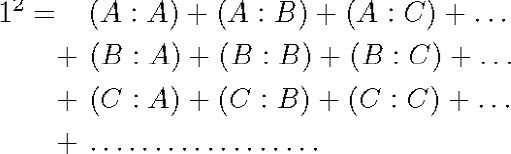
The theory of relatives only deals with binary relatives, on the assumption that taking into account non-binary relatives would not increase the expressive power of the theory.¹⁰

In what follows, I will use the word “domain” as short for “first-order domain” and the expression “domain of the relatives” instead of “second-order domain.”

2.2.3 Modules

A module (Modul) is a special kind of relative. There are four modules: two identical (or absolute) modules and two relative ones. The identical modules (1 and 0) are the ones with counterparts in the identical calculus, and the relative modules ( and ) are specific to the logic of relatives. The module is the class of all ordered pairs that can be formed with the elements of the domain, that is, 1 = 1². Therefore, 1 is the domain of the relatives. The module 0 is as always the empty class. The module is the identity relation on the first-order domain 11. Finally, is the diversity relation, that is, the class of ordered pairs in 1² whose first component is different from the second.

In my opinion, Schröder thought that the four modules had to be mutually different, as in the algebra of classes. This explains why he required the domain to have more than one element: this condition ensures that one module will never be equal to another.

2.2.4 Relative coefficients

If i and j are elements of the domain and a is a relative, then aij is a relative coefficient. For example, if 1¹ = 2 + 3 (assuming that 2 and3 denote unit classes), the coefficients of the relative are 22, 23, 32; and 33. Relative coefficients can only take two values, which are also denoted by 0 and 1. That is, if aij is a relative coefficient,

where 1 and 0 denote not relatives, but coefficient values. The equalities

are easy examples of formulas in which 1 and 0 occur both as relatives and as coefficient values.¹¹

Relative coefficients admit a propositional interpretation: a_ij expresses that the individual i is in the relation a with the individual j. This interpretation allows us to regard relative coefficients as atomic formulas of a first-order language and the values taken by the coefficients as truth values. The equalities a_ij = 1 and a_ij = 0 are then read as “a_ij is true” and “a_ij = 0” is false, respectively.

Schröder only mentions the propositional interpretation of the coefficients to ease the development of intuitions. Thus, even though a_ij an be propositionally interpreted, in the theory of relatives it should be considered as a term, and not as a formula.¹²

2.2.5 Operations

There are six operations on the set of relatives. Since the relatives are classes, the three operations of the calculus of classes are also applicable to them; these are the identical operations of the calculus:

identical sum (+), identical product (.), and complement (). The relative operations are three operations that are specific to the relatives: relative sum ( ), relative product (;), and inversion The relative sum is not used today; until the moment comes to give the definition, it will suffice to say that it is the dual operation of the relative product.

The symbols corresponding to the identical operations are used ambiguously to refer also to three operations defined on the set {0, 1}. of the coefficient values. For example, (a_ij + b_ij) is a meaningful expression, but + in this case denotes not the identical sum between relatives, but the sum of the Boolean algebra of {0, 1}. Schröder uses the same symbol to denote both sums, because they have the same algebraic properties, since they are Boolean sums. In the same way, . is used to denote both the product of classes and the product of coefficient values, and ‾ denotes both the complement of a class and the complement of a coefficient value. As we will see, Schröder is aware that he uses the same symbols to refer to different operations, and he distinguishes between them when necessary.

In summary, if a and b are relatives, then a+b, a . b (or ab), , a; b, , and are also relatives. Consequently, if i and j are elements of the domain, (a+b)_ij , (a . b)_ij (or (ab)ij ), _ij , (a; b)_ij , (a b)_ij, and _ij are relative coefficients. If A and B denote a coefficient value, so do (A+B), (A.B), and for example, (a_ij + b_ij) (a_ij . b_ij), and ) are meaningful expressions of this sort. Terms that denote a coefficient value admit a propositional reading when the symbols +, . and ^‾ that occur in them are viewed as connectives. Relative operations arenot applicable to relative coefficients; thus, the expressions , (a_ij ; b_ij) and have no meaning.

2.2.6 Nonrelative sums and products generalized

The symbols Σ and II are used to indicate, respectively, nonrelative sums and products which range over all the elements of the first-order domain or over all the relatives (included in 1²). If u is a variable that ranges over relatives and Au is a formula in which u occurs, then

are, respectively, the nonrelative sum and the nonrelative product of all Au that are obtained when u takes values in the set of the relatives included in 1². Specifically, is an identical sum when Au denotes a relative, and a sum of coefficients when Au denotes a coefficient value; analogously, is an identical product or a product of coefficients depending on whether Au denotes a relative or a coefficient value.

These nonrelative operations are the identical ones when Au denotes a relative, but they are the sum and product of coefficients when Au denotes a coefficient value.

When the variable ranges over the elements of the first-order domain, Schröder (but not Löwenheim) writes the variable as a subscript. For example, if i is an index, Ai a formula in which i occurs, and 1¹ = 2 + 3 + 4, then

From the algebraic point of view, the expressions of the form

are terms of the theory, because they denote either a relative or one of the values 1 and 0. When their scopes (Au or Ai) admit a propositional reading, can also be interpreted as the existential quantifier and II as the universal one. For example, can also be read as “there exists i such that for every j; i is in the relation z with j“

It is important to observe that Σ and II cannot be interpreted as quantifiers in all cases. For example, the Σ and II that occur in the equalities

do not admit a reading as quantifiers. Later on we will see a more interesting case in which the same happens.¹³

2.2.7 Subsumption and equality

The canonical terms of theory are the expressions that result when the symbols introduced so far are used in accordance with their meaning. There are two types of terms: those denoting a relative and those denoting a coefficient value. Only the latter terms admit a propositional interpretation.

The formulas of the theory of relatives have one of the forms

where A and B are canonical terms of the same type. The formulas of the form A B are called subsumptions. An equation is a formula of the form A = B.¹⁴

From the algebraic point of view, denotes the ordering of the algebra of relatives (the inclusion relation) when A and B denote relatives, and the usual ordering on {0, 1} when A and B denote coefficient values. If A and B are interpreted propositionally, means that A implies B; and, accordingly, A = B means that A is logically equivalent to B.

2.3 BASIC POSTULATES OF THE THEORY OF RELATIVES

2.3.1 The first group of basic postulates (Schröder's first fifteen stipulations) is the following:

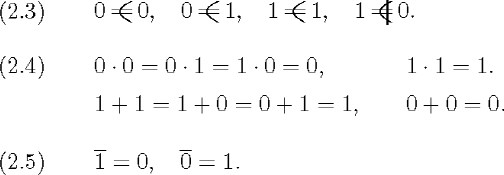
Postulate (2.2) defines the equality in whatever context it occurs. This means that (2.2) is applicable whether the variables stand for relatives or for expressions having a propositional interpretation.

According to Schröder, the postulates above constitute the foundations of a calculus of letters in which the letters take just the values 0 or 1. The formulas of this calculus have the forms A = B or where A and B are Boolean combinations of letters (variables). A formula F is a theorem of this calculus if F holds for every assignment of the values 0 or 1 to the letters that occur in it. These postulates contain all that is needed to verify whether a formula is a theorem. In effect, the four postulates in (2.3) tell us which subsumptions are true between 0 and 1, and the eight in (2.4) together with the two in (2.5) define the operations of product, sum, and complement on {0, 1}.In short, Schröder's calculus of letters is in essence the truth tables method to check validity. He mentions the number of assignments for the case of 2 and 3 letters and, in order to avoid confusion, he points out that these postulates say nothing about identical modules because 0 and 1 do not denote relatives.¹⁵ All the expressions of the theory denoting a coefficient value obey the laws of this calculus.

Obviously, the purpose of this group of postulates is to incorporate propositional logic into the theory of relatives. Schröder explicitly asserts (Vorlesungen III, p. 20) that the formal laws of this calculus are those of the one introduced in volumes I and II of Vorlesungen. He does not prove this claim, but asks the readers to convince themselves of its truth by verifying that the postulates of one calculus characterize the same structure as those of the other (namely, the Boolean algebra of {0, 1}). If we think of propositional calculus not as it was presented in subsection 1.4.3 of chapter 1, but as the restriction of the calculus of classes to the set {0, 1}, then Schröder's remark is enough to show that a formula is a theorem according to the truth tables method if and only if it is a theorem of the propositional calculus.

2.3.2 The first specific postulate of the theory of relatives (Schröder's sixteenth stipulation) is

(2.6)

Schröder points out that the variable a stands for any relative and that, in consequence, (2.6) must be considered as a schema of postulates. Equality (2.6) cannot be understood without specifying, first, which values relative coefficients can take and, second, the rules governing products between coefficient values and individual relatives. The additional stipulations required are (2.1), which asserts that every relative coefficient takes the values 0 or 1; and

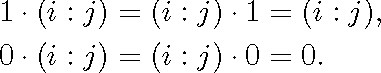
According to Schröder, these additional stipulations must be regarded as a part of the postulate, because they are necessary to understand (2.6). Thus, all the stipulations above count as a single postulate of the theory.¹⁶

An example will help to elucidate the meaning of (2.6). If we suppose that 1¹ = 2 + 3 + 4 and that aij expresses that i has the same parity as j (i.e., aij = 1 if and only if i and j are both odd or both even), then

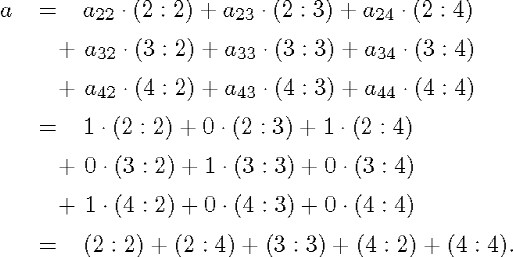
The result is obviously as expected: a is the relative whose elements are the ordered pairs (2 : 2), (2 : 4), (3 : 3), (4 : 2); and (4 : 4).

As this example shows, a relative is an identical sum of individual relatives (ordered pairs) and every relative is determined by its coefficients. If we attribute to the relative coefficients their propositionalinterpretation, (2.6) can be read in this way: a is the set of ordered pairs (i : j) for which aij is true.¹⁷

Relatives and operations on the set of relatives are defined by applying (2.6). Specifically, the equalities

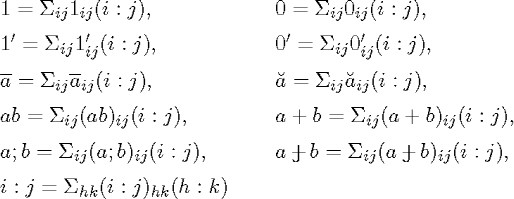
define the four modules, the six operations and the individual relatives in terms of their coefficients.

2.3.3 The following twelve postulates (from seventeenth to twenty-eighth) define the coefficients of the different types of relatives:¹⁸

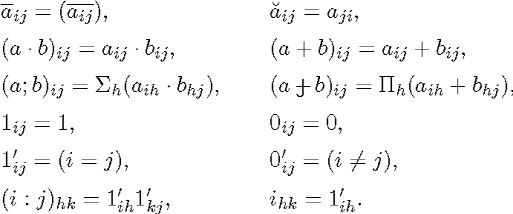
The first four postulates in each column do not require much clarification. The evaluation of a relative product will suffice for an understanding of how these definitions work. Let us suppose that 1¹ = 2 + 3 + 4 and let a and b be the relatives determined by

¹⁹

The first step in order to evaluate the relative product a; b is to obtain all its relative coefficients. For example,

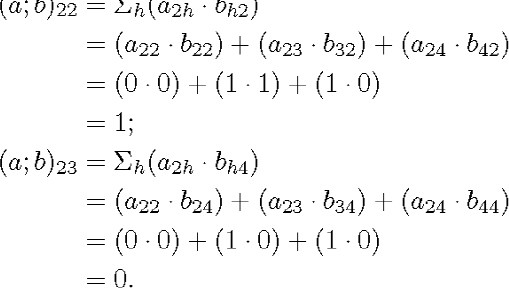
The remaining coefficients of a; b can be calculated in the same way. By applying (2.6), we obtain

The definition of the relative 1 allows us to show that it is the sum of all ordered pairs:

The definitions of and are easily understood. They require no explanation, but the peculiar use of the equality symbol deserves mention. Ordered pairs are relatives; their coefficients are defined by the equality (i : j)hk = ihkj or, expressed more clearly, by

With the aid of this last definition and the principle of extensionality, which we will introduce a little later on, it can be proved that

Thus, a relative determines the values of all its coefficients (Vorlesungen III, p. 416).

In the (not particularly fortunate) words of Schröder, the postulate

shows how to consider and represent the elements of the domain 11 as relatives, which, he says, constitutes the greatest and most ambitious achievement of the theory (I will explain what he means in the next section).²⁰ Schröder warns that it is possible to develop a good part of the theory without the help of this postulate and advises the reader to ignore it initially because it may make the process of learning the theory more difficult.

Schröder's purpose is to define a relative for each element of the first order domain. The reason why (2.7) is hard to understand is that i denotes both the element and the relative: If, for example, we denote by the relative determined by the element i, then (2.7) can be rewritten in this way:

We see that this postulate defines the coefficients of , and its meaning is clear even to a beginner (although he or she cannot initially appreciate the utility of this new relative). The definition of the relative obtained, as always, by applying (2.6):

The relative i is, consequently, the sum of all the ordered pairs (h : k) such that h = i, that is,

In present day terminology, i is the set of ordered pairs of 12 whose first component is i.

An example will help us to understand why Schröder asserts that (2.7) shows how to see the elements of the first-order domain as relatives. The statement

is symbolized in the logic of classes by

where p = {Peter} and s is the class whose elements are the apostles. The same statement can be symbolized in the theory of binary relatives by

where

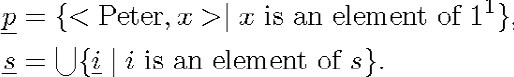
As this example shows, to say that p is an element of s (in Schröder's sense) is equivalent to asserting that , and this equivalence suggests that elements and classes of elements can be represented by binary relatives.

The construction of the logic of predicates within the theory of (binary) relatives is based on the concept of a system.²¹ A relative a is a system if

A system a is called elementary or individual if

Thus, individual systems are the relatives of the form , for some element i of the domain, and every system is an identical sum of individual systems. In the example above, is a system and an elementary system.

If a is a system and i is an element of the domain, then we define the unary coefficient ai by

If a is a system, the formulas and are equivalent.

These definitions make it possible to develop the logic of unary relatives within the theory of relatives. For example, the proof of the following laws now presents no difficulty: if a and b are systems,

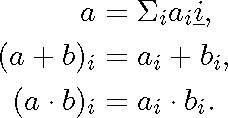
2.3.4 Schröder's twenty-ninth stipulation is the definition of the subsumption relation between relatives:

According to Schröder, the principle of extensionality for relatives,

is obtained by applying (2.2), although in fact it is also necessary to apply certain laws of quantification that he introduces later on. Leaving aside the notational aspects (both formulas are good examples of a noncanonical use of the symbols), there is no need for clarification, as the meanings of the stipulations and the principle are well known.

2.3.5 We know that II and Σ can be used to indicate, respectively, identical products and sums which range over all the relatives. If is an expression that denotes a relative (i.e., an expression formed just with symbols denoting relatives and operations on the set of relatives) and u is a variable ranging over relatives that occur in , then

are relatives. The thirtieth and thirty-first stipulations define the coefficients of these relatives:

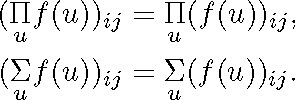
The relatives and are defined by applying (2.6) (Vorlesungen III, pp. 35 and 36).

The translation of the stipulations into statements of set theory is enough to clarify their meaning:

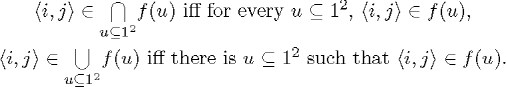
This translation highlights an essential difference between the quantifiers on the left of the equal sign and those on the right. The former denote products and sums of relatives while the latter denote products and sums of coefficient values. Thus, the definitions of II and as operations on the set of relatives depend on the definitions of II and as products and sums of coefficients. I will comment on Schröder's remarks about these definitions in the next subsection.

These two stipulations are necessary to prove the laws met by and II when combined with other operations on the set of relatives. The equations

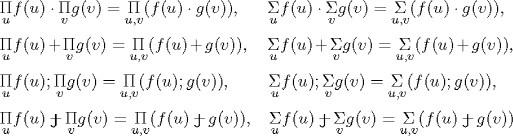
are examples of these kinds of laws.

2.3.6 The two stipulations just introduced are not applicable when II and designate, respectively, products and sums of expressions that denote a coefficient value. In other words, the stipulations above are of no use in proving the laws that and II obey when they admit the interpretation as quantifiers. Schröder considers that these laws canu be proved by merely reflecting on the meaning of the terms every and some. After noting that if Au is a proposition concerning an object u, means that for every u in the range (of the quantifier), Au holds, and means that there is some u in the range such that Au holds, he goes on in this way:

Henceforth, the statement will take the truth value 1 if and only if for each considered u, Au = 1, but will take the truth value 0, if among them there is at least one u, for which Au does not hold, where therefore Au = 0.The statement will take the truth value 1, provided that there is one u in the range for which Au = 1, but it will take the truth value 0 if and only if there is no such u, that is, if for each u in the range, Au does not hold (that is, Au = 0).²²

Schröder warns that these rules for assigning truth values to quantified expressions are not authentic definitions, but explanations of the concepts every and some that he sees as mere applications of the principle dictum de omni et nullo.²³ He seems to think that there is no need to incorporate this principle (or these rules) into the theory, just as there is no need to incorporate all the principles of reasoning that we use when we prove the theorems of the theory. We can summarize Schröder's point of view as follows: in the contexts in which II and can be interpreted as every and some, we can argue according to the meaning of the English terms without the help of any additional stipulation; the rules quoted are just the result of putting this idea into practice.

In the absence of the notions required for a rigorous definition of the concept of truth for formulas of a formal language, we can concede that Schröder's rules are sufficient to determine the truth value taken by a quantified expression (assuming that it is interpreted in a domain) and to prove the basic laws of quantification. However, the rules do not solve the problem because they do not belong to the theory (they are neither stipulations nor theorems). How can we prove, for example, the law if the stipulations introduced so far are not applicable? If the only domains taken into account were the finite ones, we could identify and with strings of products and sums in this way: if a1,...,an are the elements of the quantifiers' range, then

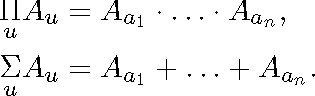
The rules quoted and, therefore, the laws of quantification could then be proved by resorting to the Boolean definition of sum and product on f0; 1g; but the proofs would only show that the laws hold in any finite domain. The only way of proving that they hold in every domain (whether finite or infinite) is by resorting to the rules, but we cannot legitimately use them. Thus, we can accept that the rules allow us to prove the laws of quantification, but the proofs are carried out outside the theory.²⁴

Schröder proceeds in practice as if he had two alternative interpretations of II and (one as products and sums and the other as quantifiers) and he could use whichever he preferred. The majority of the basic laws of quantification are found in the long list that Schröder considers proved.²⁵ I will give only a few as examples:

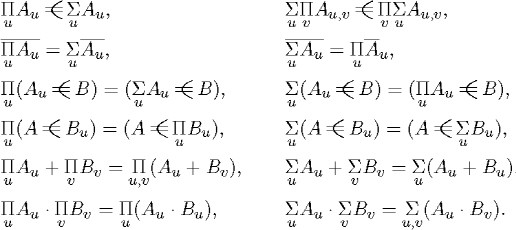
2.4 THEORY OF RELATIVES AND MODEL THEORY

2.4.1 Nowadays, logicians and historians agree that Löwenheim's paper “Über Möglichkeiten” is one of the cornerstones of the history of logic. Its enormous historical interest is due, more than to the acknowledged technical and theoretical importance of the results that it contains, to the fact that it marks the beginning of what we call model theory. For many years this fact was overlooked by historians of logic. The mathematical importance of Löwenheim's results (especially the theorem that bears his name) was recognized at once, but no historian realized that his principal achievement was to have obtained the first results of a clearly metalogical character. As far as we know, nobody before Löwenheim had enquired about the relationship between the formulas of a formal language and their interpretations or models.

Van Heijenoort has been criticized for dismissing the historical interest of the algebraic approach to logic initiated by Boole and developed by Peirce and Schröder (see Anellis and Houser [1991]). However, he was the first scholar to grasp the historical interest of Löwenheim's paper. In “Logic as calculus and logic as language” [1967], “Historical development of modern logic” [1974] and “Set-theoretic semantics” [1977], he emphasized the importance of distinguishing between the algebraic tradition and that of Frege and Russell in order to understand the recent history of logic; he also pointed to the differences between the two traditions, which explained why it was in the former rather than the latter that questions of a semantic or metalogical nature were discussed. The characteristics of the algebraic tradition, according to van Heijenoort ([1977], p. 183), are as follows: a clearer appreciation than in the Frege-Russell tradition of the greater interest of first-order logic as compared to second-order logic; the practice, inherited from Boole, of taking into account different domains of interpretation; the absence of a rigorous concept of proof (something that in the algebraic is not sought); and the fact that results are obtained by means of semantic considerations, even though there is no precise concept of validity or satisfaction. Van Heijenoort attributes these features to the algebraic tradition as a whole, without distinguishing between the works of Löwenheim and Schröder.

Vaught and Goldfarb note some distinctive traits of “Über Möglichkeiten.” In [1974] (p. 154) Vaught observes that an important characteristic of Löwenheim's paper is that it concentrates on first-order logic, “the perfect ‘home' for model theory (and most of the rest of metalogic).” Vaught says that Schröder may have had a more modeltheoretic point of view and a greater interest in first-order logic than Frege and Russell. He also suggests the possibility that Löwenheim inherits these characteristics from Schröder, but he warns that he is making a guess. In [1979] (pp. 354 and 355) Goldfarb states that the question posed by Schröder is in which domains a given equation can be satisfied. Like van Heijenoort, Goldfarb does not differentiate here between Löwenheim and Schröder, although he notes that it was Löwenheim who distinguished quantification over elements of the first-order domain from quantification over relatives (and who thus delimited the first-order fragment of the theory).

In my opinion, Vaught is right to say that an important characteristic of Löwenheim's paper is that it concentrates on first-order logic. Aside from the paper's technical achievements, this focus may well be its most significant aspect. However, I do not think that Löwenheim inherited this interest from Schröder, and it is not true that Schröder had metalogical interests; these characteristics cannot therefore be attributed to the algebraic tradition as a whole. But it cannot be asserted either that Löwenheim was the first in this tradition to concentrate on first-order logic and to direct his investigations towards metalogic, because no thorough investigation of the evolution of the algebraic tradition has been made. It may be that other logicians who worked in the algebraic tradition (Korselt, in particular) took steps in the same direction as Löwenheim, but to my knowledge, the first paper in which these characteristics are to be seen is Löwenheim's, and in this regard, as Vaught says, it is a critical point in the history of mathematics.

In this section I will compare the problems that interested Schröder with the research conducted by Löwenheim in “Über Möglichkeiten,” and I will describe the relationship between the theory of relatives and model theory.²⁶

2.4.2 Schröder had at his disposal almost the same elements as Löwenheim to address questions of a metalogical nature, but he had no interest in them because he was pursuing an objective that in a way was more ambitious than the study of the relations between formulas and their models. I will present a few general ideas about the type of problems that interested Schröder, which will allow us to assess his relationship with model theory.

Schröder was interested above all in structures of a particular type: the algebras of relatives. As Peirce and he himself conceived it, an algebra of relatives consists of a domain (1²), a relation between the classes included in 1² (the relatives), six operations (three identical and three relative), and four distinguished elements (the modules). Schröder's purpose was to study these structures, taking the calculus of classes as his pattern. Indeed, it was in this calculus of relatives that his main interest lay.²⁷ He could have tried to axiomatize it by adding to the calculus of classes the axioms needed to characterize the relative operations, but, following Peirce, he preferred to develop the calculus within the theory of relatives. The main advantage of this approach was that the theory provided a simpler and more intuitive way of obtaining certain results, because the relative operations could then be defined in terms of operations with coefficient values.

Schröder's results were not well received by Peirce, because he had already given up the algebraic approach when the third volume of Vorlesungen was published, and indeed he was highly critical of Schröder. Peirce did not deny the mathematical importance of Schröder's results, but, in general, they were of little interest to him at the time.

Peirce remarked in his review that Schröder's viewpoint was very narrow and that his algebra contained “too many bushels of chaff per grain of wheat” (too much mathematical apparatus for the results of interest to logic that are obtained).²⁸

Neither Peirce nor Schröder thought that the theory of relatives was stronger than the calculus of relatives; perhaps this is one of the reasons why they did not make a terminological distinction between them. Schröder claimed that every formula of the theory can be transformed into an equivalent formula of the calculus. He used the term kondensieren (to condense) to refer to this process (Vorlesungen III, pp. 550 and 551). For example, the formula

can be condensed into either of the formulas

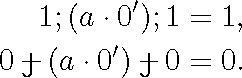
Since the first theorem of “Über Möglichkeiten” states that there exist uncondensable first-order expressions, I will digress a little to clarify this point. Löwenheim proves this theorem by showing that the formula

which expresses that the domain has at least four elements, cannot be condensed.²⁹ He notes in addition that Schröder employed theformula

to carry out the condensation, but when this formula is used, the condensation “becomes such a trivial matter that it does not deserve the name and is utterly worthless.”³⁰

As Löwenheim presents the subject, it seems as if he were speaking of condensation in the same sense as Schröder, and that the difference between the results were due to Schröder's use of (2.8).³¹ However, the answer to the question “is every formula of the theory condensable?” cannot be “it depends on whether or not we use (2.8),” becausethis equation is an elementary theorem.³² The fact is that Schröder does not define condensation in the same way as Löwenheim. According to Schröder, condensing means expressing without relative coefficients; II and Σ can occur in the condensed formula. In contrast, for Löwenheim (or for Korselt), to condense a first-order expression is to transform it into another equivalent expression without quantifiers. Löwenheim does not rule out the possibility that the condensed formula has relative coefficients, and indeed one of his examples (which would not be an example according to Schröder's definition of condensation) is that the result of condensing is (a;b)_ij; if the starting formula is a sentence, the condensed formula will also be a sentence and will have neither quantifiers nor relative coefficients. In summary, Schröder claimed that every formula of the theory of relatives is equivalent to a formula of the calculus, and Korselt proved that not every first-order sentence of the theory is equivalent to a quantifier-free formula of the calculus.³³

The reduction of the whole theory to the calculus only was a part of a reduction program which was comparable to Frege's and Russell's. Schröder was extraordinarily interested in the calculus of relatives (with quantification) because he was convinced that all logical and mathematical problems could be addressed within it. The explicit formulation of this idea can be read in “On pasigraphy”:

Almost everything may be viewed as, or considered under the aspect of, a (dual or) binary relative, and can be represented as such. Even statements submit to be looked at and treated as binary relatives. Classes, assemblages (Mengen, ensembles) or absolute terms may be thus presented. (Schröder [1898], p. 53; his italics)

Equation (2.8) plays an important role in this reduction because it allows us to see atomic formulas (relative coefficients) as relatives, and it is the one that presumably makes it possible to treat any statement of the theory as a relative. The correlate of the concept of set isthat of system.³⁴ Schröder gives a number of definitions which are fundamental for the reduction, but there is no need to go into details, since we only want to sketch Schröder's line of research in order to ascertain its relationship with model theory.

Schröder was chiefly interested in the calculus of relatives, but he did not attempt to axiomatize it. As I already said, he developed the calculus within the theory of relatives, which he did not attempt to axiomatize either. Most of the results of the third volume of Vorlesungen belong to the calculus of relatives or are related in one way or another to his project of reduction. The theory of relatives is developed as far as is necessary for these purposes. Schröder does not address problems of a metalogical nature, in that he does not consider the relation between the formulas of a formal language and their models. Put in algebraic terms which will be easily understood later on, Schröder does not consider the relation between the equations and the domains in which they have a solution. It is not that arguments or considerations of a semantic type are completely absent from Vorlesungen, but they occur only in the proofs of certain equations, and so we cannot view them as properly metalogical. Nor can we say that Schröder was interested in first-order logic or in the theory of relatives with only quantification over individuals, because, among other things, his project required quantification over relatives.

Schröder posed numerous problems regarding the calculus of relations, but very few later logicians showed any interest in them, and the study of the algebras of relatives was largely neglected until Tarski.

In [1941], his first paper on the subject, Tarski claims that hardlyany progress had been made in the previous 45 years and expresses his surprise that this line of research should have had so few followers. ³⁵ In his opinion, Principia Mathematica had made an important contribution to the establishment of the relations between this theory and other parts of logic, but had contributed very little to the theory of relations and specifically to the development of the calculus of relations.

To conclude this subsection, I would like to mention one particular aspect of Tarski's paper that shows the continuity of the line of research. Tarski is centrally interested in the calculus of relatives without quantification. He begins by presenting an axiomatization of the theory of relatives in a first-order language which permits a formulation of the theorems of the calculus (those in which no individual variable occurs). He then observes that the calculus can be developed within this theory, in spite of the fact that no axiom belongs to the calculus because all of them contain quantification over elements.³⁶ (This is in essence the path that Peirce and Schröder had followed.) Next, Tarski gives a list of fifteen theorems of the calculus that can be easily proved in the theory, and proposes to single them out and to take them as an axiomatic system for the calculus. At the end of the paper, Tarski claims that he is “practically sure” that this axiomatization of the calculus allows the proof of the “hundreds of theorems” in the third volume of Vorlesungen.

2.4.3 Although Schröder was not interested in questions of a metalogical nature, the theory of relatives as he conceived it made it possible—in a sense that I will explain—to take them into consideration. When we see the theory of relatives from the perspective of Schröder's investigations we tend to view it exclusively or fundamentally as a theory or as a calculus of relations. This is the correctviewpoint from which to present Schröder's contributions, but it neglects an important aspect: the logical or propositional interpretation of one part of the theory.

As a preliminary appraisal, we can say that in the theory of relatives two interpretations coexist and are occasionally confused: an algebraic interpretation and a propositional interpretation. This means that the same expressions can be seen both as expressions of an algebraic theory (i.e., as sums and products of relatives or coefficients) and as formulas of logic (i.e., as well-formed expressions of a formal language which we may use to symbolize the statements of a theory in order to reflect its logical structure). I do not mean by this that the whole theory admits two interpretations, because not all the expressions can be read in both ways, but the point is that some expressions do.

One way of viewing the theory of relatives that gives a fairly acceptable idea of the situation is as a theory of relations together with a partly algebraic presentation of the logic required to develop it.³⁷ The theory constitutes a whole, but it is important to distinguish the part that deals with the tools needed to construct and evaluate the expressions that denote a coefficient value (i.e., the fragment that concerns logic) from the one that deals specifically with relatives.

The notions and stipulations of a logical character are mainly introduced in subsections 2.3.1 and 2.3.6, but must be taken together with the corresponding clarifications in section 2.2. Subsection 2.3.1 contains a decision procedure for propositional logic, and subsection 2.3.6 contains the rules for evaluating quantified expressions). The rest of section 2.3 deals with the theory of relations in the strict sense. In what follows, I will speak of the logic of relatives to refer to the fragment of the theory that concerns logic. As Löwenheim does implicitly, I consider 10 and 00 to be logical constants, and therefore I assume that their definitions also belong to logic.³⁸ In the next section I will specify as far as possible the syntactic and semantic aspects of the logic of relatives. At the moment I only wish to indicate which part of the theory of relatives we will focus on.

Model theory studies the relation between the formulas of a formal language and their interpretations or models. Thus, model theory requires having a formal language, a concept of satisfaction for the formulas of this language and the distinction between the formallanguage and the metalanguage in which the relation between the formulas and their models is discussed.

Excepting the distinction between object language and metalanguage (a lack that needs emphasizing as it is the cause of many of the problems we will meet), the basic components of model theory are found in one way or another in the theory of relatives. On the one hand, the part of the theory that deals with logic contains more or less implicitly a formal language with quantification over relatives. On the other, the algebraic interpretation supplies a semantics for this language. In this situation, all that remains to be done in order to obtain the first results of model theory is, first, to become aware that the theory does include a formal language and to single it out; second, to focus on this language and, in particular, on its first-order fragment; and third, to investigate the relationship between the formulas of this language and the domains in which they hold. Löwenheim was the first to take these three steps.

2.4.4 We have seen that the theory of relatives contains in a way the basic components of a formal language: a set of logical symbols each with its corresponding propositional interpretation, a syntax borrowed from algebra, and semantic rules which in practice are enough to evaluate the statements of this language. The absence of precise definitions of syntactic and semantic notions is evident, but this limitation is not a reason for denying that the theory includes a formal language. The question now is whether Schröder and Löwenheim were aware of the possibility of isolating the formal language included in the theory and of interest of expressing mathematical theories in that language.

From the fragmentary way in which Schröder presents the components of the logic of relatives we cannot determine to what extent he realized that the theory of relatives included a formal language. In any case, he did not single it out, he had no metalogical interests, and never considered the possibility of formalizing a mathematical theory.³⁹

As “Über Möglichkeiten” shows, Löwenheim saw that the theory of relatives included a formal language. In order to prove the theorems in the paper, he first had to think of logic as a differentiated fragment of the theory of relatives and then to delimit the language at least to the extent required to state and prove the theorems with rigor. His presentation of the language is not as accurate as we require today; he mixes syntactic and semantic aspects, is not as explicit as one might like as to which are the symbols of the language, and gives practically no syntactic rules (probably, because the syntax is borrowed from the algebra and he considers it unnecessary to go into details). Nonetheless, not all his stipulations (as he calls them) are general or imprecise. Löwenheim explicitly clarifies that the equations are obtained by equating two relative expressions and that these expressions are finite sequences constructed from operations, quantifiers, and relatives (or relative coefficients).⁴⁰ He then delimits the first-order fragment of the language and turns his attention to first-order equations (Zählgleichungen). The most significant point about these stipulations is not their degree of accuracy, but that they reveal an interest in the formal aspects of the language that is absent in Schröder.

Löwenheim was also intuitively conscious of some important characteristics of the structure of a formal language. As a part of the proof of his theorem, Löwenheim shows that every first-order equation can be transformed into a logically equivalent equation that has a certain normal form. In my opinion, his proof (which I discuss in chapter 4) shows that Löwenheim was dimly aware of the recursive structure ofthe formulas of the language. This detail has passed unnoticed, for the simple reason that insufficient attention has been paid to this part of the proof of Löwenheim's theorem. As we will see, there are even reasons for thinking that it has not always been understood.

Was Löwenheim aware of the possibility, and the interest, of expressing mathematical theories in a formal language? On several occasions he maintained that every mathematical problem can be reduced to the problem of knowing whether a certain equation is satisfiable or not. At the beginning of “Über Möglichkeiten” he states

All important problems of mathematics and of the calculus of logic can, it seems, be reduced to [[questions about]] such relative equations. (“Über Möglichkeiten,” p. 448 (233); the text in brackets is a clarification presented in From Frege).

Further on, he brings up the idea again:

every theorem of mathematics, or of any calculus that can be invented, can be written as a relative equation; the mathematical theorem then stands or falls according as the equation is satisfied or not. This transformation of arbitrary mathematical theorems into relative equations can be carried out, I believe, by anyone who knows the work of Whitehead and Russell. (Über Möglichkeiten,” p.463 (246))

There are two different ways in which mathematical theorems can be transformed into relative equations, and each is associated to a possible interpretation of Löwenheim's words. The first consists basically of reducing mathematics to the theory of relatives. This reduction transforms mathematical problems into questions about relative equations (under the assumption that any statement of the theory of relatives can be put into the form of a equation). The second consists of symbolizing the mathematical theorems in the formal language that the theory of relatives incorporates. The formalization of a theory immediately gives rise to a system of equations, because if we symbolize a statement without using the symbols = and , we obtain a term of the logic of relatives, and the result of equating it to 1 (or to 0, as the case may be) is a relative equation. The two possible interpretations are, in summary, these: first, any mathematical problem canbe addressed within the framework of the theory of relatives; second, mathematical theories can be symbolized in the language of the theory of relatives, and their symbolization reduces some mathematical problems to questions about the satisfiability of the equations of that language. Unlike the first interpretation, the second one supports the idea that Löwenheim saw or glimpsed the possibility and the interest of viewing mathematical theories as sets of formulas of a formal language.

Goldfarb thinks that the first interpretation is the right one, and relates Löwenheim's claims with his attempt in his [1940] to show that mathematics can be “Schröderized” (see note 34 in this chapter). Goldfarb notices that, on the one hand, the theory of relatives cannot be used as a formal system because (among other things) it does not have rules of inference, and, on the other, Löwenheim does not define the concept of consequence and never considers the satisfiability of infinite sets of formulas. As a result, Goldfarb does not believe that Löwenheim's claims can be related with the formalization of mathematics. His conclusion is that Löwenheim was unable to recognize the importance of first-order languages which he himself had delimited and did not see that formalization made it possible to fully reflect the deductive relations between mathematical sentences; and that, as a result, it cannot be claimed that Löwenheim understood the value of formalizing mathematics (Goldfarb [1979], pp. 355–356).

I do not think that the quotations above can be taken as evidence that Löwenheim grasps the interest of formalizing mathematics, but I also think that Goldfarb's conclusions do not do justice to Löwenheim, and should be qualified. Having his [1940] in mind, it is possible that Löwenheim is primarily thinking of the reduction of mathematics to the theory of relatives, but he is also aware that a mathematical problem can be reduced to a question about a relative equation via formalization.

As an application of his theorem, Löwenheim sets out to show that all decidable questions concerning the dependence or independence of the axioms of class calculus are already decidable in a countable domain (“Über Möglichkeiten,” pp. 456–459 (241–243)).⁴¹ According to Löwenheim's conjecture, what must be shown is that the question of whether or not an axiom follows from the others can be transformed into a question of whether a certain equation is or is not satisfiable in a countable domain. The main step of the proof is the formalization of the axioms of class calculus in a first-order language. Löwenheim explains this step in detail, noting, for example, that formalization requires that classes be considered as elements of a first-order domain and that the cases in which a symbol is used as a connective be carefully distinguished from the cases in which it denotes an operation or a relation between classes.⁴² Once the axioms are formalized, it is easy to convert the question of whether one of them follows from the others into a question of whether a certain equation is or is not satisfiable. Löwenheim does not make the conversion explicit because, I think, he considers it trivial. Assuming that the axioms are formalized and put into the form A = 1, it is obvious that A1 = 1,...,An = 1 implies B = 1 if and only if the equation is not satisfiable. Löwenheim can then apply his theorem to this equation in order to obtain the desired result. In my opinion, this application shows that Löwenheim is aware of the possibility and the interest of expressing mathematical theories in a formal language.

In a sense, there is little to object to in the core of Goldfarb's assertions. It can indeed be said that Löwenheim does not fully recognize the importance of the first-order languages that he himself has delimited; it is also true that he does not have precise definitions of the basic concepts of semantics, that he never considers the satisfiability of infinite sets of formulas, and that he does not have a concept of formal system. These limitations show that Löwenheim's comprehension of the relationship between logic and mathematics is not comparable to that of a modern logician, but these points are beyond doubt. Goldfarb overemphasizes the limitations of Löwenheim's research and underestimates his contribution. If we compare Löwenheim's achievements with those of his contemporaries, we cannot deny that the metalogical theorems included in “Über Möglichkeiten” opened a line of research; to what extent he was interested in it and whether or nothe was in a position to develop it are different matters.

2.4.5 Once the logic of relatives has been separated from the rest of the theory to become the focus of attention, the most natural questions are those of a semantic kind. Due to the algebraic character of the theory, the canonical statements of this logic take the form of equations, and the most immediate response to an equation is to inquire about the systems of values that satisfy it in a given domain.This inquiry has a clear meaning in the context of the theory and no particular clarification is required in order to understand it. The equations of the logic of relatives are composed of expressions that take in a domain a unique value (1 or 0) for each assignment of values to the coefficients generated in that domain by the relatives occurring in the equation. An equation is satisfied in a domain by an assignment of values to the pertinent relative coefficients if the same value is assigned to both members of the equation. There is no essential difference between asking if there are a domain and an assignment of values to the relevant relative coefficients that satisfy the equation A = 1 and asking if the formula A is satisfiable in the modern sense.⁴³ In this way, in the logic of relatives semantic questions arise naturally, propitiated by the algebraic context. I do not mean that questions such as the ones answered by Löwenheim in his paper are suggested by the algebraic context.⁴⁴ The only immediate semantic questions are rather elementary, but they, nevertheless, point the way that leads to Löwenheim's results.

As we have seen, none of the distinctions that today separate syntax from semantics are present in the logic of relatives. There is no precise notion of formal language and, naturally enough, no distinction is made between object language and metalanguage. Nor can there be said to be a precise definition of the concept of satisfaction or of any concepts related to it. Nonetheless, the set of stipulations concerning the expressions that have a propositional interpretation allow us to assert that behind the concepts used in the logic of relatives there is something more than intuitive ideas, although it is difficult to say exactly how much more. But we should at least recognize that these concepts are sufficiently clear and precise to allow the proof of the theorem that is the starting point of what today we call model theory.

2.5 FIRST-ORDER LOGIC OF RELATIVES

2.5.1 Broadly speaking, what I called logic of relatives in subsection 2.4.3 is no more than the logic as it is presented in Schröder's Vorlesungen. This is also the logic assumed by Löwenheim in “Über Möglichkeiten.” In this section I will specify both the syntactic and the semantic concepts of the first-order fragment of the logic of relatives that are necessary for a rigorous discussion of the proof of Löwenheim's theorem.⁴⁵

Since in what follows our attention will be centered on Löwenheim's paper, whenever Schröder's terminology does not coincide with Löwenheim's I will adopt the latter's. I will also introduce some new terminology and use certain conventions that do not belong to the logic of relatives. I will of course warn the reader before using anything that is novel in this respect.

For ease of presentation, I will separate the syntactic and semantic aspects and thus stay as close as possible to the way in which we would present a first-order language today. As I have said, the distinction between syntax and semantics is particularly alien to the logic of relatives and aims only to systematize the exposition. Indeed, this absence of a clear distinction between syntax and semantics will be the cause of most of the problems we will encounter. In consequence, the following presentation should not be used to draw conclusions about the level of precision that we find in Schröder or in Löwenheim.

2.5.2 First of all, I outline the essential syntactic aspects of the logic of relatives, beginning with the list of the symbols of the language. What we would call today logical symbols are the following:

(a) indices: i, j, h, k, l; and m (with subscripts, if necessary);

(b) module symbols: $632$ and ;

(c) operation symbols: +; · and ‾;

(d) quantifiers: Σ and II;

(e) equality symbol: =;

(f) propositional constants: 1 and 0.

The symbols and denote two binary relational constants whose interpretation is already known. The symbols 0 and 1 are used not as modules (relational constants), but as two propositional constants which, stated informally, correspond to the truth values (though our use of them will be more restricted than their syntactical status suggests). The symbol = corresponds to the biconditional, but we will also make only limited use of it. The correspondence between the operation symbols and the modern connectives has already been described above.

Throughout his paper Löwenheim frequently uses the symbol , but he does not consider it to be a primitive symbol of the language. Of course, Löwenheim does not make any distinction between primitive and defined symbols, nor does he present the language in such a way that this kind of detail can be appreciated. For example, he does not mention this symbol in the stipulations concerning the language, but this is not a conclusive reason for considering it as defined, because he does not mention the symbol ^- either. My reason for claiming that for Löwenheim it is not a primitive symbol is that in the first part of the proof of his theorem he explains how to obtain a formula in a certain normal form starting from any given formula and does not take into account the case that the given formula is of the form . In fact, this symbol does not occur anywhere in the proof of Löwenheim's theorem, and therefore we will not need to use it in what follows.

I will ambiguously use the word “relative” to refer both to a symbol of the language and to the object denoted by it. Accordingly, I will also use “element” for the elements of the domain and their canonical names. I will terminologically distinguish between symbols and their denotation whenever the understanding of the exposition requires it.

Löwenheim puts no limitation on the number of places of the relatives (as a special case, they may be unary). As is usual in the logic of relatives, he refers to them with lower case letters other than the ones used for the indices (normally, a, b, c; and z). In the logic of relatives the concept of individual constant per se does not exist, but in practice the canonical names of the elements of the domain are used as individual constants having a fixed interpretation in a given domain.

If x₁,...,x_n are indices or elements, a is a n-place relative and b is a module, ax₁,...,x_n, and bx1x2 are relative coefficients; in other words, the atomic formulas are the relative coefficients. I will use the term formula to refer to the expressions constructed in the usual way from the relative coefficients, the operation symbols and the quantifiers. If A and B are formulas, A = B, A = 0; and A = 1 are equations.⁴⁶ When interpreted, the formulas denote the values 1 or 0, and the equations are true or false.

A product is a formula of type A · B or of type II_i A: The formulas of type A+B or of type are called sums. The formulas A and B are the factors of A · B and the summands of A + B.

A quantifier, either universal or existential, can be simple or multiple. An example will suffice to illustrate the distinction. In

there are n simple (universal) quantifiers; however, in

there is only one multiple (universal) quantifier. Essentially, the difference between these two expressions is the same as the one between “for every a₁, for every a₂,..., for every a_n” and “for every sequence of n elements of the domain.”

Löwenheim uses upper case letters as metalinguistic variables that range over formulas. The free variables that must be taken into account are written as subscripts. For example, A_ijk stands for a formula in which the variables i, j, and k occur free. If the letters do not have subscripts, it is assumed that they stand for sentences or for formulas whose free variables can be ignored in the context. Thus, in the equation

it should be understood that the variable i occurs free in A_i and in B_i, and that j does not occur free either in A_i or in B_i; a variable other than j can occur free in A_i or in B_i.

In the logic of relatives it is assumed that no element occurs in the formulas for which theorems are stated. This means that the relatives are the only nonlogical symbols of what we can call the “basic” formal language. When a formula of this language is interpreted in a domain D, it is implicitly assumed that the canonical names of the elements of D are added to the basic language. Thus, the semantic argumentsare better reproduced when we distinguish between the basic language and the language that results from adding the canonical names of the elements to the basic language. I will adopt this point of view in what follows.

In his presentation of the logic of relatives, Löwenheim uses the terms Zählausdruck (first-order expression) and Zählgleichung (first-order equation) to refer to the formulas and the equations of the basic language, respectively.⁴⁷

In order to avoid the use of subscripts as well as to unify the notation—Löwenheim writes the indices under the quantifiers—I will henceforth write

in place of

respectively (where A_i1...in is, as above, any formula in which the variables i₁,...,i_n occur free). I will not change the original notation in the case of the relative coefficients, but I will add parentheses to the original formulas so that there should be no doubts about their structure. These conventions permit us, for example, to write the equation above in this way:

Nevertheless, I will maintain the original notation in the quotes.

2.5.3. Finally, we should make a number of comments on the semantics of the language. As we know, the set in which the formulas are 2.5.3 interpreted is called the domain. The only condition that the domain must fulfill is to be nonempty. Schröder insists that it must have more than one element, but recall that Löwenheim ignores this restriction.

The sense in which Löwenheim speaks of elements in “Über Möglichkeiten” is not clear. On the one hand, it seems that he cannot think of them in today's sense, because, as I said in subsection 2.3.3 ofthis chapter, in the theory of relatives there is no membership relation. Nonetheless, if Löwenheim considered elements as unit classes, he would express the domain as a sum of elements, but in this paper he denotes it by listing its elements within parentheses. For example, he writes

when he means that the domain has three elements denoted by 1, 2, and 3 (“Über Möglichkeiten,” p. 452 (237)). In any case, the fact that the elements are unit classes has algebraic repercussions, but has no bearing on semantic considerations because the basic notions of the semantics do not depend on whether the elements are or are not unit classes. In what follows I will refer to the domain and its elements as we would do today and I will use the letter D to refer to the domain. Thus, I will write D = {1, 2, 3} in place of 1¹ = (1, 2, 3).

When we present a formal language today, we make a careful distinction between the individual variables of the formal language and the metalinguistic variables that range over the elements of the domain. This distinction does not exist in the logic of relatives. From the moment it is assumed that an equation is interpreted in a domain, the indices simultaneously play the role of variables of the formal language and that of variables of the metalanguage. As we will see, this point is crucial to an understanding of Löwenheim's arguments.

As I said above, the basic formal language has no individual constants. The concept of satisfaction in a domain is assumed to be defined for sentences or equations of an expanded language in which every element of the domain has a canonical name. Thus, there are no atomic sentences in the starting language and the only atomic sentences of the expanded language are the relative coefficients whose subscripts are (canonical names of) elements of the domain.⁴⁸ For example, if 1 and 2 are elements of the domain, a12 is an atomic sentence of the expanded language. In general, when I speak of the relative coefficients in a domain, I am referring to the atomic sentences of the expanded language.

The terminology that Löwenheim uses for the semantic concepts presents a number of problems of interpretation, caused fundamentally by the lack of care with which he handles them. I will not examine this terminology here, because, first of all, it requires a rather long commentary which is both out of place and irrelevant to the discussion of the problems that are dealt with in the next two chapters. Both Löwenheim's terminology and the correspondence between the concepts I introduce next and the ones he uses will be analyzed in chapter 5.

As we have seen, in the theory of relatives interpreting a sentence or an equation means fixing a domain D and an assignment of truth values (1 or 0) to the coefficients in D of the relatives other than and . It is not necessary to assign values to relative coefficients of and because these relatives have a fixed meaning:

Löwenheim does not use any particular name to refer to these assignments. I will call them solutions and will assume that they also assign truth values to the relative coefficients of and preserving their meaning. Thus, a solution in a domain D will be a function that assigns 0 or 1 to the relative coefficients in the domain D.⁴⁹ Since and have a fixed meaning, it is of no importance whether or not a solution assigns truth values to their coefficients, but the assumption that it does permits a more general way of speaking. We can now say, for example, that a solution in a domain D assigns a truth value to each atomic sentence of expanded language.

As we know, if D is any domain, every solution in D can be extended to a unique function which assigns a truth value to each sentence. There is no need to present the definition since, leaving aside the technical details of the case, it is the customary one. I will also call these extended functions solutions. We will say that a sentence is satisfied by a solution in D; or that it is true under a solution in D; when the solution assigns the value 1 to it. A sentence is satisfiable if there exist a domain and a solution in it such that the solution satisfies the sentence. An equation is satisfied in a domain D by a solution in D when the solution assigns the same truth value (1 or 0) to both members of the equation. Specifically, the equation A = 1 is satisfied in a domain by a solution when the solution satisfies A. The remaining semantic concepts are defined as usual.

¹Collected papers (v. III), p. 27; from the Lowell Lectures (1903), quoted by the editor. The laudatory reference to De Morgan is found in Peirce [1885], p. 188. In [1903], p. 367, note 2, Peirce calls De Morgan his “master,” and regrets having introduced the word “relative” in place of “relation,” the term that De Morgan used.

²Peirce ranked himself with Aristotle, Duns Scotus, and Leibniz. This assessment may seem out of proportion, but it was shared by Schröder and by the British mathematician W. K. Clifford (see Brent [1998], pp. 257 and 325).

³See Peirce [1896], 3.447–3.455 (pp. 282–287) and Peirce [1897], 3.499–3.502 (pp. 316–317).

⁴For a short account of Peirce's logic of relatives see Brady [1997].

⁵The problem of axiomatizing the theory in a first-order language was addressedby Tarski in [1941].

⁶Vorlesungen III, p. 4. German text:

Als gegeben, irgendwie begrifflich bestimmt, denken wir uns die “Elemente” oder Individuen

A, B, C, D, E,...

einer “gewöhnlichen” Mannigfaltigkeit (vergl. Bd. 1, S. 342). Dieselben sollen durchweg von einander und vom Nichts (von 0) verschieden geachtet werden. Sie müssen unter sich verträglich (konsistent) sein, sodass nicht etwa die Setzung eines von ihnen der Denkbarkeit eines andern vorbeugt, und sie müssen einander gegenseitig ausschliessen (unter sich disjunkt sein), sodass auch keines der Elemente als eine Klasse gedeutet werden dürfte, die ein andres von ihnen unter sich begreift.

⁷Later in this section I will explain what is in my opinion the reason for this restriction.

⁸This detail is observed by van Heijenoort in From Frege, p. 234, note 2. (From Frege is short for From Frege to Gödel.)

⁹Schröder rigorously defines the concept of ordered pair and proves that they are individuals in Vorlesungen III, §26 (p. 424 ff.).

¹⁰The proof that every relative equation is logically equivalent to a relative equation in which only binary relatives occur is due to Löwenheim (“ Über Möglichkeiten,” theorem 4). In subsection 2.3.3 I will indicate how predicates can be viewed as binary relatives.

¹¹We owe to Peirce the idea of associating a numerical coefficient l_ij to each pair (I : J) of the second-order domain in such a way that l_ij = 1 if and only if (I : J) is an element of the relative l; see Peirce [1882] and Peirce [1883].

¹²Nevertheless, Schröder sees no essential difference between a_ij and a_ij = 1, since, as the relative coefficients admit a propositional interpretation, the laws of propositional calculus can be applied to them, and therefore a_ij = (a_ij = 1) (see subsection 1.4.3.2 in chapter 1 and, in particular, note 46).

¹³In [1883], Mitchell proposed the use of subscripts to denote the expressions “some” and “all.” He used F1 to denote “all U is F” and Fu to denote “some U is F” (U is the universe), and this symbolism allowed him to state some basic laws of quantification (like, for example, , (FG)1 = F1G1, and (F + G)_u = F_u + G_u). Peirce credited Mitchell for being the first in successfully introducing the distinction between some and all in the algebra of classes. Mitchell also made an attempt to extend this symbolism to the algebra of relatives.

The quantifiers in their modern form were introduced in the algebraic approach to logic by Peirce when in his [1883] (p. 464) he noticed, first, that propositions can be represented by sums and products of coefficients, and, second, that Σ and II used to symbolize the sums and products could be read as “some” and “every”:

Any proposition whatever is equivalent to saying that some complexus of aggregates and products of such numerical coefficients is greater than zero. Thus,

means that something is a lover of something; and

means that everything is a lover of something. We shall, however, naturally omit, in writing the inequalities, the > 0 which terminates them all; and the above two propositions will appear as

Peirce abandoned the algebraic point of view between 1883 and 1885. In [1885], p. 180, he interpreted Σ and II exclusively as quantifiers and denied that they could be seen as sums and products:

Here in order to render the notation as iconical as possible we may use Σ for some suggesting a sum, and II for all, suggesting a product.

Thus Σixi means that x is true of someone of the individuals denoted by i or

In the same way, IIixi means that x is true of all these individuals, or

If x is a simple relation II_i II_j x_ij means that every i is in this relation to every j, Σ_i II_j x_ij that [..] It is to be remarked that Σ_ixi and IIixi are only similar to a sum and a product; they are not strictly of that nature, because the individuals of the universe may be innumerable.

(Peirce's italics)

The word “quantifier” was introduced by Peirce in this paper (Peirce [1885], p.183).

¹⁴I have restricted the use of the equality and subsumption symbols in such a way that they cannot occur in the terms. This can be considered the canonical use of these symbols, but Schröder often makes a different use of them. The most frequent exceptions to the rules I have presented in this section consist of using as a connective, indiscriminately writing A and A = 1 by virtue of the axiom A = (A = 1), which eliminates the distinction between terms and formulas, and treating formulas of the theory as terms denoting 0 or 1. We saw some examples of these particular uses of the identity and subsumption symbols in the last section of the previous chapter and we will see more in this chapter.

Schröder uses the word equation to refer to any expression of the form A = B; if the equality and subsumption symbols occur neither in A nor in B (as in the case of my definition), he calls A = B a primary equation. According to Schröder, any equation can be transformed into an equivalent primary equation by applying a number of equivalences (Vorlesungen III, pp. 150 ff.). Since only primary equations can be rigorously defined because of the lack of a clear distinction between terms and formulas, Schröder's assertion can only be evaluated by checking examples of non-primary equations.

¹⁵If 1 and 0 denote the identical modules, the formulas in (2.3), (2.4), and (2.5) are theorems. Schröder proves them in Vorlesungen III, pp. 122 ff.

¹⁶Vorlesungen III, pp. 22–24. Observe that in this case Σ cannot be interpretedas the existential quantifier.

¹⁷The idea of viewing relatives as sums of individual relatives we owe to Peirce ([1870], p. 408). His first attempt to express this idea in symbols was fairly rudimentary: l = Σ(A : B) ([1880], p. 197). In [1882], p. 328, Peirce used numerical coefficients with the same purpose and in [1883], p. 454, he proposed a formulation very close to (2.6):

A general relative may be conceived as a logical aggregate of a number of such individual relatives. Let l denote “lover”; then we may write

where (l)_ij is a numerical coefficient, whose value is 1 in case I is a lover of J, and 0 in the opposite case, and where the sums are to be taken for all individuals in the universe.

As we can observe, the variables I and J denote individuals in the universe, but the range of i and j is not clear. Peirce merely assumes that a unique coefficient should correspond to each ordered pair of elements and that “(l)_ij is the coefficient of the pair (I : J)” (see [1882], pp. 328–329). A few pages later on ([1883], pp. 464–465; see note 13 in this chapter), he makes a propositional reading of the coefficients and the subscripts becomes variables that denote individuals (for example, he reads ()_ijk as “i is an accuser to j of k”), but he does not relate this interpretation of the coefficients to the quoted formula.

¹⁸Vorlesungen III, pp. 25 ff. The first four definitions of each column, with the exception of the definition of relative sum, are in Peirce [1882], pp. 182 and 183 (3.313–315). The definition of relative sum is found in Peirce [1883], p. 197 (3.333).

¹⁹It may seem that in these definitions the indices stand for numbers (not for unit classes), but recall that in the theory of relatives a statement such as, for example, “j is even” is interpreted as j e (where e = 2 + 4).

The relatives a and b are

a = (2 : 3) + (3 : 4) + (2 : 4),

b = (3 : 2) + (3 : 4),

but we cannot describe them in this way, because we do not yet know how to determine the coefficients of a relative which is described as a sum of individual relatives.

²⁰Peirce was the first to observe that the elements of the domain and, therefore, the absolute terms (the unary relatives) can be viewed as binary relatives; see Peirce [1870], p. 373, Peirce [1880], p. 196, and Peirce [1882], p. 329.

²¹Vorlesungen III, §27, pp. 443–467; see in particular pp. 450, 458, and 462–467 (recall that Schröder writes “i” instead of “”).

²²Vorlesungen III, p. 37. German text:

Hienach wird der Aussage der Wahrheitswert 1 immer dann undnur dann zukommen, wenn, für jedes der gedachten u, Au = 1 ist, der Wahrheitswert 0 dagegen, falls es unter jenen mindestens ein u gibt, für welches A_u nicht zutrifft, wo also A_u = 0 ist.

Der Aussage wird der Wahrheitswert 1 schon zukommen, wenn es im Erstreckungsbereiche nur überhaupt ein u gibt, _für welches A_u = 1 ist, dagegen wird ihr der Wahrheitswert 0 dann und nur dann zukommen, wenn es daselbst kein solches u gibt, d. h. wenn für jedes u des Erstreckungsbereiches A_u nicht zutrifft, A_u = 0 ist.

In this case, the variable u can range over relatives or over elements of the first-order domain. The Erstreckungsbereich is the domain (the set) over which the quantified variables range, that is, the first-order domain when the variable is an index, and the set of relations on the first-order domain when the variable ranges over relatives. For lack of a better term, I have translated this word by range.

²³This principle is attributed to Aristotle. Assuming that Y is any part of a collection X; the principle can be stated in this way: what is true of every object of X, is also true of every object of Y ; what is true of no object of X, is true of no object of Y .

²⁴As the reader will recall, this problem had already been envisaged by Peirce (see note 13 in this chapter). In [1911] (p. 72; quoted by Thiel in his [1977], p. 244) Löwenheim pointed out that Schröder was “unable to reach infinite products and sums without a fallacy” and warned that the rules of calculation for infinite sums (and products) of propositions should be proved, because the most important applications depend on them.

²⁵Vorlesungen III, pp. 37–42; see also pp. 110–115.

²⁶For the history of model theory, see Mostowski [1966], Vaught [1974], Chang [1974], the historical sections of Hodges [1993], and Lascar [1998].

²⁷The choice of terminology is a problem because it is not used with any great accuracy, and often it is difficult to know what a particular author is referring to. I call the whole theory such as it has been presented the theory of relatives. The calculus of relatives is a subtheory of the theory of relatives. The essential difference between the calculus and the theory is that the latter allows us to speak of individuals of the first-order domain, whereas the calculus deals only with relatives and operations between them. Both the calculus and the theory permit quantification over relatives (in the theory, naturally enough, quantification is also permitted over individuals).

When Peirce and Schröder speak of the algebra of relatives they appear to be referring above all to what I call “calculus.” The theory of relatives does not seem to receive a specific name, probably because, as I explain later, they consider that it is another form of presenting the calculus of relatives. In his doctoral thesis, N. Wiener uses the expression “algebra of relatives” to refer to what I call “theory.” In “ Über Möglichkeiten” and in [1940] Löwenheim speaks of the calculus of relatives referring, it appears, to the theory of relatives. My terminology corresponds essentially to that used by Lewis, [1918], p. 85, and by Tarski [1941].

²⁸In [1896] (the review of the third volume of Vorlesungen), pp. 267–268 (3.425), Peirce states:

Nevertheless, hereafter, the man who sets up to be a logician without having gone carefully through Schröder's Logic will be tormented by the burning brand of false pretender in his conscience, until he has performed that task;

For the criticisms of Schröder's algebraic approach see Peirce [1896], pp. 284–285 (3.451), Peirce [1897], pp. 320327 (3.510–520) and the draft, dated 7 April 1897, of a letter from Peirce to Schröder (edited by Houser in his [1990], pp. 227–230).

²⁹“Über Möglichkeiten,” pp. 449–450 (233–234); the numbers in parentheses refer to the English translation included in From Frege. As Löwenheim himself says, he was sent the proof of this theorem by Korselt in a letter, and so it is Korselt who should be credited with the result. In [1941], p. 89, Tarski expanded Korselt's result in a number of aspects, and for this reason it is normally attributed to them jointly.

³⁰“ Über Möglichkeiten,” p. 450 (235). Löwenheim does not use the underlining; I have introduced it in subsection 2.3.3 to clarify the meaning of equation (2.7),

which is the key to Schröder's process of condensation.

For a better understanding of (2.8) we observe that, for every h and k, = 1 when akh = 1, and = 0, when akh = 0. Equation (2.8) can be restated in this way:

akh = ,

(see Vorlesungen III, pp. 422–423).

We can now see why Schröder considers definition (2.7) so important, and also why informs the beginner that he may ignore it. This definition is necessary to prove the equalities (2.8) and

which are essential in order to reduce the whole of the theory to the calculus, but this result can be ignored by a beginner (Vorlesungen III, pp. 424 ff.).

I have used underlining to refer to elementary systems. As we have seen, the property of being an elementary system is expressed in the calculus of relatives by the product

Thus, a formula like §khakh can be trivially translated into the calculus of relatives as follows:

Observe that h and k are now variables that range over relatives. This example is very simple, but it suggests why Löwenheim claims that Schröder's condensation is trivial.

³¹Following Löwenheim, this is how Moore explains the difference between Korselt's result and Schröder's in Moore [1988], p. 122.

³²Observe that (2.8) does not depend on any special postulate, because (2.7) is a definition that, in conjunction with (2.8) and the definition of , merely stipulates that relatives of the form Σ_k(i : k) will be denoted by . Probably, Schröder also assumes that (2.7) implicitly defines a function that assigns the relative Σ_k(i : k) to the element i; but this changes nothing.

³³Goldfarb, [1979], p. 354, states that Schröder sought to give the theory the form of a calculus involving just operations on relatives without any type of quantification. Brady, [200], p. 170, is in agreement with him. However, Schröder explicitly asserts that II and Σ can occur in the condensed formula.

³⁴Löwenheim's criticism in “ Über Möglichkeiten” of Schröder's procedure of condensation suggests that he had not yet become interested in the reduction of the whole theory to the calculus when he wrote this paper.

In [1940] Löwenheim claimed that if the theory of sets had been formulated in Schröder's theory of relatives Russell's paradox would never have arisen, because the notion of set of sets is not expressable in this theory. The purpose of the paper is to show that, despite this limitation, any mathematical theorem (whether or not it contains the notion of set of sets) corresponds to a theorem in the theory, and its proof can be transformed into a proof within it.

On p. 2 of this paper, Löwenheim states that the stipulations i_kj = i_k and (i; j) = _{ih kj} are superfluous and lead to confusion; he refuses to consider them.

This confirms that Löwenheim refused to conceive of elements as binary relatives and, therefore, to reduce the entire theory to calculus.

Recall that Löwenheim uses “calculus” to refer to what I am calling “theory.”

Observe in addition that, in Löwenheim's version of the theory, unary relatives must be introduced axiomatically, because he refuses to treat them as binary relatives.

³⁵On Tarski's suggestion, in [1940] J. C. C. McKinsey had given an axiomatization of the theory of atomic algebras of relations. The 45 years that Tarski mentions are the ones that elapsed between the publication of the third volume of Vorlesungen and Mckinsey's paper.

A brief historical summary of the subsequent developments can be found in Jónsson [1986] and Maddux [1991].

³⁶The axioms that Tarski proposes are these: the definitions I presented in subsection 2.3.3, with the exception of the last in each column (the ones corresponding to ordered pairs and to individual systems), the principle of extensionality, and

(the notation is Tarski's).

³⁷It cannot be said to be totally algebraic, given the absence of an algebraic foundation of the sums and products that range over an infinite domain.

³⁸Traditionally, logic of relatives is used to refer to the calculus or, depending on the context, to the theory of relatives. My use of this expression is unorthodox.

³⁹Like Peano and Frege, Schröder claimed that he had achieved Leibniz's ideal of constructing a lingua characteristica and a calculus ratiocinator, but in my opinion this claim is not connected with the question we are considering here. The essential feature of a lingua is that it contains a perfectly determined set of a few primitive notions in terms of which any concept is expressable, but what does “expressable” mean in this case? Schröder thinks of the lingua not as a formal language used to symbolize statements, but as the language of a theory to which every branch of science could be reduced. Schröder was convinced that the language and thepostulates of the calculus of relatives satisfied the Leibnizian ideal, because, to use his own words, almost everything may be viewed as a relative. The discipline (or science) whose purpose was the ultimate establishment of a universal scientific language was called pasigraphy, and according to Schröder's view, the calculus of relatives was an “indispensable base” of it.

Frege and Schröder accused each other of constructing a calculus and not a lingua and thus of only partially fulfilling Leibniz's idea. The details of this controversy are found in Frege [1882], Frege [1895], Schröder [1880], and Schröder [1898]. Peano's viewpoint is in his [1894]. Additional information about Schröder's view on pasigraphy can be found in Peckhaus [1990]. For the algebraic roots of Schröder's reduction project see Peckhaus [1994].

⁴⁰According to Löwenheim's presentation of the language, the canonical statements are the equations that Schröder calls primary, because he (implicitly) excludes the possibility that the equality and subsumption symbols occur in relative expressions. In “ Über Möglichkeiten” we can find relative expressions and equations that do not meet his own definition. This is not a mere inconsistency, because he assumes that any statement of the theory can be put into the form of a primary equation (“ Über Möglichkeiten,” pp. 458–459 (242); see also note 14 in this chapter).

⁴¹I call a set denumerable if it is equinumerous with the set of natural numbers, and countable if it is finite or denumerable. If a set is not countable, then it is uncountable.

⁴²The following examples illustrate Löwenheim's formalization: the axioms

are, respectively, symbolized by

where “s” is a binary predicate symbol that denotes the inclusion relation and “” is a ternary predicate symbol that denotes the product of classes.

⁴³The most usual verb in German is erfüllen, but on occasions the verbs genügen and befriedigen are used.

⁴⁴In “Logic as calculus and logic as language” (p. 444) van Heijenoort offers a possible explanation of how Löwenheim might have come to ask this question.

⁴⁵When I refer to Löwenheim's theorem I mean his version of the theorem that today bears his name (theorem 2 in “ Über Möglichkeiten”).

⁴⁶If we wanted the language to accommodate the processes of simplification that are customary in the logic of relatives (such as, for example, a( + b) = a + ab = 0+ab = ab), we would have to treat 1 and 0 as atomic formulas without any type of limitation. Though Löwenheim resorts to processes of this type in the proof of his theorem, there is no need to account for them, and for this reason I use these symbols in a restricted way.

⁴⁷Skolem slightly modernized the formal language. In Skolem [1920], the only logical symbols of the language are the operation symbols and the quantifiers and the only expression are Löwenheim's Zählausdrücke, which Skolem prefers to call Zählaussagen (first-order formulas). In [1929], pp. 60–61, Gödel erroneously attributes the name Zählaussagen to Löwenheim.

⁴⁸For simplicity, I will omit “canonical name of” and speak merely of elements.

⁴⁹Skolem used the term Lösung (solution) to refer to the assignments of truth values to the relatives coefficients that satisfy a given formula in a domain. See Skolem [1922], p. 145 (294); the number in parentheses refers to the English translation included in From Frege.