Chapter Six

Löwenheim's Theorem

6.1 THE PROBLEM

6.1.1 Today, we use the name Löwenheim-Skolem theorem to refer to all the theorems that guarantee that if a set of formulas has a model of a particular cardinality, it also has a model of some other cardinality. The first theorem in the series (leaving open the question of whether it is also the weakest) is the second of the theorems that Löwenheim proves in “Über Möglichkeiten;” it states:

If the domain is at least denumerably infinite, it is no longer the case that a first-order fleeing equation (Fluchtz ählgleichung) is satisfied for arbitrary values of the relative coefficients. (“Über Möglichkeiten,” p. 450 (235))

If we make explicit the definition of fleeing equation in terms of validity (as explained in the final section of the last chapter), we obtain:

If a first-order equation is not valid but is valid in every finite domain, then it is not valid in any denumerable domain.

For the proof of the theorem, Löwenheim assumes without any loss of generality that every equation is in the form A = 0. As explained at the beginning of chapter 4, this allows us to go from equations to formulas, bearing in mind only that “A = 0 is valid” is equivalent to “A is not satisfiable.” Thus, Löwenheim's argument can also be seen as a proof of

Theorem 6.1 If a first-order sentence is satisfiable but not satisfiable in any finite domain, then it is satisfiable in a denumerable domain.

A first-order sentence is what Löwenheim calls Zählausdruck, an expression without quantifiers over relatives and whose only logical symbols are II, , ·, +, ‾ , , and .

6.1.2 Suppose that A is a sentence not satisfiable in any finite domain, but satisfiable in an infinite domain D. To show that A is satisfiable in a denumerable domain we can use either of the following strategies:

(a) we can construct a solution that satisfies A in some denumerable domain; or

(b) we can use the hypothesis that there exists a solution that satisfies A in an infinite domain D to construct a denumerable subdomain of D in which A is true under the same solution (restricted to the subdomain).

As is well known, these two constructions are associated with two theorems between which we differentiate today. When the proof develops the idea expressed in (a), we usually state Theorem 6.1 (or other equivalent theorem). If we perform the construction indicated in (b), we not only show that A is satisfiable in a denumerable domain, but we also prove that the solution that satisfies A in the subdomain is a restriction of the one that satisfies A in D. In this way, if we construct the subdomain indicated in (b), we actually prove a theorem which is stronger than Theorem 6.1, and which, in addition, has important applications. This theorem can be stated as follows:

Theorem 6.2 If a first-order sentence A is not satisfiable in any finite domain and S is a solution that satisfies A in an infinite domain D, then there is a denumerable subset D' of D such that the restriction of S to D' satisfies A.¹

In what follows I will call Theorem 6.1 the weak version (of Löwenheim's theorem) and Theorem 6.2 the subdomain version.

There is an important technical difference between the two versions. The axiom of choice is required to construct the subdomain indicated in (b) (in fact, it is already required to show that every infinite set has a denumerable subset), but we do not need it to construct the solution referred to in (a). Thus, the axiom of choice is necessary to prove the subdomain version, but not to prove the weak version.

The first question to answer is this: which of the two versions did Löwenheim set out to prove? The way in which he states the theorem is of no help in answering the question, because at the beginning no interesting application of the subdomain version was seen, and, accordingly, no distinction was made between the versions. For a number of years it was normal practice for logicians to state the weakversion and then prove either the weak version or the subdomain version, depending on whether they wanted to avoid the use of the axiom of choice. For example, in [1920] Skolem proves the subdomain version and in [1922] the weak version, but in both cases he states the weak version. The first time that Skolem distinguished between the two versions was in [1929], but even then he did not say what the interest of the subdomain version could be.²

Today it is unanimously accepted, without reserve, that Löwenheim proved the weak version, and that it was Skolem who in [1920] first proved the subdomain version and further generalized it to infinite sets of formulas. The problem is that Skolem thought that the version proved by Löwenheim was the subdomain version. Although Skolem did not then distinguish between the two versions, one finds in [1920] a number of statements on Löwenheim's proof that could be interpreted in that way. However, they are related to a particular aspect of the proof's structure which we have not discussed so far, so I will leave them until the end of the chapter. The explicit attribution is found in [1938]. At the beginning of that paper, we read:

Today it would be said that Löwenheim's considerations and those of Skolem that followed belong to a logic of predicates based on set theory. Löwenheim starts from the hypothesis that the given “Zählausdruck,” which can be assumed to be always in the form (1) [[(x1) ... (x_m) (Ey₁) ...(Ey_n) (z₁) ... (z_p) (Eu₁) ... (Eu_q) ... K(x₁,..., x_m, y₁,..., y_n, z₁,..., z_p, u₁,..., u_q,...; A,B,C,...)]], represents a true proposition in a domain [[champ]] M for a certain choice of the predicates A, B, C,... With this hypothesis, he shows that if the meaning of A, B, C,... is preserved, then proposition (1) is true in a partial denumerable domain M_o of M. (Skolem [1938], p. 455)

The attribution seems clear, but it is not enough to conclude that Skolem thought that Löwenheim had proved the subdomain version, because in the same paper (p. 460) he also asserts that Löwenheim's theorem is one of Herbrand's theorems, a claim that cannot be taken literally.³ The real attribution is found in his later comments on

Löwenheim's proof. The paper concludes with the transcription of a short debate on the application of the theorem to set theory. In this debate (p. 477) M. Mazurkievicz asks Skolem if the use of the axiom of choice was essential to Löwenheim's proof. Skolem says that it was. As we saw in chapter 3, the axiom of choice is necessary to prove the logical equivalence between a formula and its normal form (and, depending on the interpretation of the part we have not yet analyzed, should still be used), but if Skolem had thought that Löwenheim proved the weak version, he would not have said that the use of the axiom of choice was essential because he himself had shown how it could be avoided. In contrast, the axiom of choice must be used to prove the subdomain version. Skolem's affirmative response to Mazurkievicz's question shows that he believed that Löwenheim proved the subdomain version.

The situation, then, is as follows: For Skolem (and, to my knowledge, for him alone) Löwenheim's proof consists essentially in the construction of a subdomain of the infinite domain in which the formula is, by hypothesis, satisfiable; for logicians and historians today, Löwenheim constructs (or sets out to construct) a denumerable domain which need not bear any relation with a previous domain and a solution in it. Evidently, either Skolem is wrong, or today's commentators are wrong. It is hard to accept that Skolem is wrong, as he was a logician trained in the algebraic tradition to which Löwenheim belonged. It is equally hard to accept that the present-day logicians and historians who have examined the proof (though they are relatively few in number) are mistaken. In any case, the fact that Löwenheim's proof allows two interpretations that diverge in an aspect of such importance indicates patently that his argument is far from clear.

The other problem presented by Löwenheim's proof, much less important than the one above, concerns its correctness. I do not know of any contemporary of Löwenheim who asserts that the proof is incorrect or that it has major gaps. The only inconvenience mentioned by Skolem is that the use of fleeing indices unnecessarily complicates the proof (see, e.g., Skolem [1920], p. 103 (254), Skolem [1922], p. 140 (293), and Skolem [1938], pp. 455 and 456). The purpose of Skolem's first version is, he says, to offer a simpler proof that avoids the use of fleeing indices.⁴ Herbrand, to quote another example, thinks that Löwenheim's argument lacks the rigor required by metamathematics, because Löwenheim does not define the semantic notions that he uses; however, Herbrand considers it “sufficient in mathematics.”⁵

The most widely held position today is that the proof has some important gaps, although commentators differ as to precisely how important they are. Without actually stating that the proof is incorrect, van Heijenoort maintains in From Frege that Löwenheim does not account for one of the most important steps.⁶ Largeault agrees with van Heijenoort.⁷ In Gödel [1986] (p. 51), Dreben and van Heijenoort accept that Löwenheim proved the weak version, but state that their reading of the proof is a charitable one. For Vaught ([1974], p. 156), the proof has major gaps, but he does not specify what they are. Wang ([1970], pp. 27 and 29) considers that Löwenheim's argument is “less sophisticated” than Skolem's in [1922], but does not say that it has any important gaps. Eklund ([1996], pp. 147 and 153) says that it was Skolem who first proved the Löwenheim-Skolem theorem for standard first-order logic. According to Brady ([2000], p. 172), there is no gap in the proof, except for an implicit application of the infinity lemma.⁸

Moore's point of view is idiosyncratic. In his opinion, the reason why Löwenheim's argument appears “odd and unnatural” to the scholars I have just mentioned is that they consider it inside standard first-order logic instead of considering it inside an infinitary logic (Moore [1980], p. 101 and Moore [1988], pp. 121 and 122). Moore does not explain why adopting his interpretation (which in fact is difficult to distinguish from van Heijenoort's, as I said in subsection 3.2.2) should dispel the odd and unnatural aspects of Löwenheim's argument.

A highly significant illustration of the difficulty of understanding Löwenheim's argument is that many of the scholars I have mentioned do not appear to be confident that they have fully understood it. Wang and Vaught refuse to go into detail, and instead of explaining Löwenheim's argument offer versions that are held to present its essential ideas. In general, the scholars' opinions tend to be cautious. For example, van Heijenoort ([1982], p. 67) asserts that the text does not allow us to determine whether Löwenheim has an argument behind the step which (in van Heijenoort's opinion) Löwenheim takes without accounting for it. Vaught, for his part, states:

On the other hand, after such a difficulty or gap, Löwenheim always reappears giving exactly the right next step for what would be the right overall argument. The chances that this would happen if he were really making a fundamental error seem to be very small indeed. (Vaught [1974], p. 156)

So the impression we have of these comments is that there may be more to Löwenheim's argument than meets the eye—something we have missed, something that prevents our being sure that we understand it entirely.

The thesis I will defend in this chapter is that Löwenheim aimed to prove the subdomain version. As I said, I coincide with Skolem on this point, but my interpretation is not based on Skolem's opinion (although I take it into account with regard to particular details). On the problem of the correctness of the proof I do not think it is necessary to issue a verdict. My aim is to analyze Löwenheim's argument in detail, so that no doubt should remain regarding its interpretation or whether there is something in it that we have failed to understand. In my opinion, Löwenheim's argument does have gaps (although not the ones that van Heijenoort attributes to it), but the answer to the question of whether the whole proof is acceptable or not, bearing in mind the level of the research in logic at that time, seems to me to be far less important, because it depends above all on one's own level of tolerance.

6.2 AN ANALYSIS OF LÖWENHEIM'S PROOF

6.2.1 The structure of Löwenheim's proof runs as follows. First, he shows that an equation in the form A = 0 is logically equivalent to another in normal form referred to by

where represents a (possibly empty) string of existential quantifiers (either type or ), II represents a (possibly empty) string of universal quantifiers, and F is a quantifier-free formula; he then notes that the existential quantifiers are superfluous to decide whether is logically valid in a domain; and he concludes the proof by showing that IIF = 0 is not logically valid in a denumerable domain (IIF is, of course, the formula that results from removing all the existential quantifiers from ). The structure of proof can be restated thus:

1. Löwenheim shows that any given formula A is logically equivalent to another formula in normal form referred to by

2. he then observes that in this case we can dispense with the existential quantifiers; and

3. assuming that A (and, therefore, ) is satisfiable but not satisfiable in any finite domain, he shows that IIF is satisfiable in a denumerable domain; this concludes the proof, since the same interpretation that satisfies IIF in a denumerable domain, also satisfies and, therefore, A.

The process of obtaining the normal form was analyzed in chapters 3 and 4. I will discuss the step from to IIF in the following subsection (6.2.2). For the sake of clarity, I have divided Löwenheim's proof that IIF is satisfiable in a denumerable domain into three fragments, which I analyze in detail in subsections 6.2.3, 6.2.4, and 6.2.5. Each subsection begins with the quotation of the fragment to be discussed. Some of the quotations repeat paragraphs from other parts that I consider important to an understanding of the fragment as a whole. I have left out part of the development of the example that Löwenheim uses to illustrate the proof, but this is the only omission.

The hypothesis of the theorem comprises two assumptions on A (and, therefore, on ): (1) is satisfiable in an infinite domain, and (2) is not satisfiable in any finite domain. If we construct an interpretation in a countable domain that satisfies IIF, the second assumption is applied to show that the domain has to be infinite. However, the role of the first assumption depends on which version of the theorem we wish to prove. If Löwenheim had only indicated when he is using this assumption it would have been clear which of the two versions he was trying to prove, but, unfortunately, he made no mention of the hypothesis. This omission will oblige us to discuss at all times whether the first assumption is indeed being applied in the fragment of the proof under consideration. For the sake of brevity, I will sometimes use the word “hypothesis” to refer not to the whole hypothesis of the theorem, but to the first assumption.

6.2.2 If we now want to decide whether or not is identically satisfied in some domain, then in our discussion we can omit the and examine the equation

or, in our example,

For, after all, that this equation be identically satisfied means nothing but that it be satisfied for arbitrary values of (z and) l, as well as of the ki (that is, of k_1, k₂,...). But the omitted Σ did not assert anything else, either, and was therefore superfluous, at least for us.⁹

After the explanation in chapter 3 of the semantics of fleeing indices, this part of Löwenheim's argument should present no difficulties of comprehension. In fact, it only seeks to underline the equivalence between the satisfiability in a domain of a formula (or of an equation) in normal form, and the satisfiability in the same domain of the formula that results from removing existential quantifiers. As I have said a number of times, whether or not a formula with fleeing indices is satisfied in a domain depends on the elements assigned to the terms that generate its fleeing indices in the domain. The satisfaction in a domain D of a formula such as IIiA(i, k_i, l) (which is, approximately, the schema of Löwenheim's example) depends on the elements assigned to l and to the terms of the set {k_a|a D}, which are those generated by k_i in D. In essence, the generated indices behave like “normal” indices (i.e., as individual variables), and the effect of removing is the same as that of removing ki. The existential quantifiers can thus be omitted because both IIiA(i, k_i, l) and are satisfiable in a domain D if and only if there are a solution in D and an assignment of values (elements in D) to l and to the terms of {k_a | a D} that satisfies IIiA(i, k_i, l). Löwenheim exemplifies this idea for the case of a denumerable domain, possibly because the purpose of the proof is to construct a domain of this cardinality.

Löwenheim's remark regarding satisfiability is correct, and there is no objection to accepting its complete generality, even though it rests on an example. He cannot avoid the use of examples to make his arguments involving fleeing indices convincing. The intuitive notions that support the reasoning of the logic of relatives are not conceived for formulas with fleeing indices, and there was no conceptual apparatus at that time for defining the syntactic and semantic behavior of this type of index. Examples are, then, the only means with which to show how these intuitive notions are applied to formulas where fleeing indices occur.¹⁰

6.2.3 (i) ... let us denote them [[the constants indices of IIF]], in some order, by the numbers 1, 2,..., n; hence we put l = 1 in our example;

Now of the factors of the II in IIF = 0 we first write down only all those in which no productation index has any value other than the values 1, 2,..., n defined above under (i), or, if constant indices are lacking, we take any element of the domain, denote it by 1, and write down the factor in which all productation indices have the value 1.In this case we put n = 1. But in F there will also occur fleeing indices, say

In each of the factors written down so far, j, l, m,..., being productation indices, have as their values some of the numbers 1, 2,..., n; hence in these factors we shall have as fleeing indices

These are no longer functions of indices but denote quite specific [[bestimmte]] elements, which we shall denote, again in some order, by the numbers n + 1, n + 2,...,, n₁. (Let us remark expressly that two elements denoted by distinct numbers taken among 1,..., n₁ are not assumed to be either equal or distinct.)

The product written down thus far we call P₁. Hence in our example we would have

(Here we were permitted to put ₁₁ = 1; but, if ₁₂ had occurred, we would not have been permitted to set it equal to 0, since it is not being assumed, after all, that 2 denotes an element different from that denoted by 1. Rather, we would have had to let ₁₂ stand.). (“Über Möglichkeiten,” pp. 454 and 455 (238 and 239))

6.2.3.1 Löwenheim begins the proof by constructing a sequence of formulas. In this section I will focus on the construction of the first formula in the sequence (P₁). I will start by giving a version that reflects only the formal aspects of Löwenheim's construction, aspects which would get in the way of our discussion of the fundamental questions if we left them until later. This is a provisional approach, and I will come back to it at the end of the section to discuss the extent to which it is acceptable. So as not to lose sight of Löwenheim's exposition I will mix terminologies, but, naturally enough, I will do my utmost to ensure that the result is intelligible.

Let IIF be a formula in normal form, and let us suppose that 1, 2, 3, ... are new individual constants. We first enumerate the constant indices of IIF and replace them with the corresponding numeral. We now write the product of all the formulas that are obtained when the universal quantifiers of IIF range over the numerals assigned to constant indices. (If the formula does not have constant indices, all the quantified variables will take the value 1.) In the formula thus obtained new indices occur, generated by the fleeing indices. We assign them a number, continuing the enumeration initiated beforehand, and replace them by the corresponding numeral. We will call the resulting formula P₁.

Löwenheim exemplifies the procedure with the formula

Step by step, P₁ is obtained as follows. First, the only constant index, l, is replaced by 1; the result is

next, we let the universally quantified variables take the value 1, thus obtaining

finally, k₁ is replaced by 2, and we get

after simplifying,

6.2.3.2 This form of presenting the construction of P₁ is the first one that comes to mind when we aim to present the general lines of Löwenheim's argument without going into detail. For example, this is essentially the version that Vaught takes as his starting point, his purpose being precisely the one I have mentioned (Vaught [1974], p. 156). The main characteristic of the construction is that it is completely syntactic. Nothing in it refers to a domain, or makes us think of one. In contrast, in Löwenheim's exposition (above all in the part we are dealing with), we see repeated references to a domain. He only uses the word once, but he constantly speaks of elements, and it is understood that they are elements of the domain. Indeed, all the commentaries that seek to explain Löwenheim's proof (i.e., those that do not merely aim to sketch the basic ideas and central steps of the proof) suggest, more or less directly, certain ways of interpreting all these references.¹¹

Although it appears evident that Löwenheim is thinking of a domain, the vagueness of his expression may arouse our doubts. As examples of this I will quote a number of sentences, in the order in which they appear in the proof:

(a)Let us denote them [[the constant indices of IIF]], in some order, by the numbers 1, 2,..., n.

(b) Let us remark expressly that two elements denoted by distinct numbers taken among 1,..., n₁,...

(c) Thus we form from P₁ all those (finitely many) specializations that we obtain when we introduce arbitrarily many or few equations among the elements 1, 2,..., n₁.

(d) Now in P₂ (as before in P₁) the indices used are taken as either equal to or distinct from each other in every conceivable way.¹²

The fact that Löwenheim speaks indiscriminately of either indices or elements, together with the fact that, apparently at least, P1 is constructed merely by replacing particular indices with particular constants, may lead us to think that there is no reason for taking more account of one form of expression than of the other. This ambiguity could be used to challenge the importance that I attribute to the reference to elements (and to challenge my interpretation of the proof as well). The presupposition of a given domain is essential to my reconstruction, and for this reason I am especially keen to put to rest any doubts that may surround it, but it is obvious that, however we interpret Löwenheim's argument, we must account for this ambiguity, even though to date analysts have never paid it any attention.

The problem of explaining why Löwenheim speaks in the way he does was already solved in the previous chapter. It is just the presupposition of a domain that accounts for the ambiguity. Löwenheim does not distinguish between indices and elements of the domain in contexts that we could call “semantic,” that is to say, when he is referring to a domain. Only then do the indices perform the role of variables on elements of the domain, and the ambiguity arises. Thus, the fact that in the same context Löwenheim sees no distinction between speaking of indices or elements is evidence that he is thinking of a domain (which is not the set of indices).

The question whether 1, 2,... denote indices or their values (the elements) is of little importance. Löwenheim is so vague on this point that no reliable conclusion can be drawn. The most sensible step isto leave this detail till last, and give it a reading consistent with the interpretation of the whole proof.

6.2.3.3 If we think that the references to a domain reflect something more than just a careless manner of speaking, we must provide a sensible interpretation of them. There are only two alternatives. Either Löwenheim is referring to a domain that in a certain sense he considers as given, or he is referring to a domain that he is going to construct. In fact, the two alternatives are not incompatible. It could be—and in my opinion is in fact the case—that Löwenheim meant to construct a domain on the basis of another given domain, but there is no need to consider this possibility here; if this is his aim, it will become clear as the proof progresses, as we will not appreciate any attempt to construct a solution. The point I intend to analyze now is whether Löwenheim is referring to an already given domain or to a domain which he will construct, and which need not bear any relation to any previously given domain.

This is where the divergence between my interpretation of Löwenheim's proof and the classical one begins. All traditional discussions of the proof adopt the second alternative, even if only implicitly.¹³ I am not going to comment here on all the problems that this presents (I will do so in the following section), but, naturally, each of the arguments that I will give in favor of the first alternative can be seen as an argument against the traditional position.

First, in my opinion, it is clear that Löwenheim is not referring to a domain that he is going to construct when, for example, he explains how we should proceed when the formula has no constant indices. Second, his use of the term “factor” in this context (in particular, when he says “of the factors of the II in IIF = 0 we first write down only all those in which ...”) necessarily presupposes the existence of a domain.¹⁴ As we saw in the previous chapter, the factors of IIF are theformulas whose product constitutes the expansion of IIF. Therefore, we cannot talk of factors in this sense when there is no previously fixed domain. Even if Löwenheim had never mentioned it, the reference to factors would have indicated that he takes the existence of a given domain for granted.¹⁵

Once we conclude that Löwenheim is referring to a given domain, it is only natural to use the hypothesis of the theorem to ascertain which domain it is. The theorem states that if IIF is satisfiable, but not in any finite domain, then it is satisfiable in a denumerable domain. Therefore, we may suppose the existence of an infinite domain, which from here onwards I will call D, in which IIF is satisfiable. D, then, is the only domain that we can reasonably consider as given, and therefore we should understand that when Löwenheim speaks of elements he is referring to elements of D.¹⁶ This interpretation of Löwenheim's exposition is essentially correct, but, as we will see in the next subsection, the situation is slightly more complicated. For this reason, it is preferable not to resort as yet to the hypothesis, and to continue talking vaguely of a given domain in which IIF is interpreted.

This conjecture, namely that Löwenheim presupposes that IIF is interpreted in a domain, explains the general lines of his argument fairly reliably. As I said above, the indices of an interpreted formula are also variables that range over the elements of the domain of interpretation. If the indices are not quantified, the fact that they are variables ranging over the elements allows us to state, without any additional clarification, that in the formula they stand for elements. When the universally quantified variables in IIF take as values the elements represented by the constant indices, their fleeing indices generate indices that also stand for elements. For example, k_i is an index of a special nature, and does not stand for an element, but k₁ and k₂ behave like any normal (i.e., not fleeing) index, and, since they are not quantified, also stand for (not necessarily distinct) elements. I think that this is what Löwenheim means when he states that the result of replacing the subindices of a fleeing index by elements of the domain is a completely specific element. In summary, both the constant indices of a formula and those generated by its fleeing indices automatically stand for elements of the domain as soon as we consider the formula to be interpreted. Naturally, the role that the indices generated play as representatives of elements of the domain is passed on to the numerals that replace them.¹⁷

An argument that supports this interpretation is that it allows an explanation (with certain limitations which I will mention in a moment) of certain particular points in Löwenheim's exposition of the construction of P₁. For example, it makes sense to say that if IIF has no constant indices, we have to “take any element of the domain and denote it by 1,” because the domain is given by the hypothesis. It is also understandable that Löwenheim should say that only some of the factors of II in IIF should be written: IIF is bound to have more factors than those corresponding to the constant indices, since the domain will have more elements. Finally, it is also understandable that Löwenheim should state that the indices produced by replacing the subindices of the fleeing indices by elements of the domain are specific elements of the domain. If he were talking of the construction of a new domain, it would make sense to say that they should be seen as new elements added to an initial domain formed by the elements corresponding to the constant indices (this is exactly van Heijenoort's reading).

6.2.3.4 This explanation of these points in Löwenheim's exposition only makes complete sense under the assumption that the indices stand for elements that are fixed or, in other words, when we suppose that the elements assigned to the constant indices and to those generated by the fleeing indices are fixed. For example, as I interpret Löwenheim's words, when the formula has constant indices the first step is to write the product of the factors corresponding to the constant indices. Clearly, this description of the beginning of the construction can only be understood supposing that the constant indices stand for specific elements of a given domain.

In principle, this detail appears to be unremarkable. In a context without the concept of assignment, it is natural to assume that the unquantified indices of an interpreted formula stand for elements of the domain to which the interpretation attributes them. The problem is that Löwenheim does not argue as we would expect if the indices stood for those elements. The following example will show what this reasoning would consist of.

If is a sentence and we suppose that it is true under an interpretation in D, we can ignore the assignment because the truth value of under an interpretation depends only on the solution. However, if we assume that IIF is true under an interpretation in a domain D, we cannot ignore the given assignment, because the values used to evaluate the truth value of IIF are just those assigned by it to the constant indices and to the indices generated by the fleeing indices. In essence, the step from to IIF consists in fixing the assignment that is going to be used.

Let us now suppose that IIF is IIiA(i, j, h, k_i), where j and h are constant indices. According to the remark above, if Löwenheim were assuming that IIF is true under an interpretation in D, the argument we would expect nowadays is this: By the hypothesis, there is an interpretation in D that satisfies IIF; let 1 and 2 be the elements assigned to j and h respectively; the assignment in D must also attribute values to k₁ and k₂ so that

is true; let us suppose that 3 and 4 are the elements assigned to k₁ and k₂, respectively; and so on. It is obvious that this argument leads to the proof of the subdomain version. The assignment of values to the constant indices and to those generated by the fleeing indices is considered fixed by the hypothesis, and we are simply enumerating and denoting them in some way. We need not concern ourselves with the values of the relative coefficients, because the solution is also fixed by the hypothesis.

If Löwenheim stated that P₁ is true or indicated in some way that the elements he takes are fixed by the interpretation under which IIF is true, it would be a definitive sign that he is indeed arguing in this way. The problem is that nothing he says at this stage of the proof indicates that he is thinking of those elements. What is more, in the following section we will see that Löwenheim does not use the hypothesis that IIF is true in D in the way I have just explained, and that, to an extent, the structure of his argument corresponds to a proof of the weak version.

The fact that Löwenheim does not proceed as if P1 were true appears to be conclusive evidence that he does not intend to prove the subdomain version. The argument could run as follows. If Löwenheim were thinking of a domain that he considers given, this domain would have to be D. Since it is very hard to believe that Löwenheim is thinking of elements of D but ignores the interpretation that satisfies IIF in that domain, if the indices stood for elements of D, these elements would be those fixed by the given interpretation. However, if this were the case, Löwenheim would doubtless state that P1 is true; as he does not, we must conclude that he is not thinking of elements of D. This means that references to elements are not particularly important, and so the objective of the proof must be the construction of an interpretation in some denumerable domain under which IIF is true. It is most likely an argument of this type that has led all the commentators to conclude that Löwenheim did not prove the subdomain version.

But this argument does not show that Löwenheim intended to prove the weak version. The truth of P₁ does not seem to matter at this point in the proof, and the only conclusion we can draw from this fact is that, if Löwenheim means to prove the subdomain version, then he argues in a way that is far removed from what is now customary. The interest of the above argument is that it shows patently the difficulties that the interpretation of Löwenheim's proof presents. On the one hand, the assumption that he is thinking of elements of a given domain is fundamental to the understanding some of his assertions and, on the other, when we attempt to reconstruct the argument in accordance with this assumption, the result that we obtain is unsatisfactory.

This situation is explained in part by the fact that Löwenheim's argument lies somewhere between syntax and semantics, and in part by the peculiar structure of his proof. The nature of the indices allows a form of reasoning that would not be possible if syntax were sharply separate from semantics. Löwenheim can state, without further explanation, that i is an element simply due to its character as avariable that ranges over the elements of the domain. Nothing obliges him to be more precise. This form of arguing, thinking of elements, has a certain imprecision (and also a kind of generality that we will see later) which becomes apparent, for example, in the difficulty of finding a satisfactory response to the question of which elements correspond to the constant indices. This vagueness is reflected in my explanation of the finer points of Löwenheim's exposition, and cannot be avoided, at least not until we have an overall vision of the whole of the argument. None of the reconstructions of his argument that we might propose at this point, at the beginning of the proof, would satisfy us, because we could always find evidence that Löwenheim does not argue in accordance with the one that we had chosen.

The generality I have just mentioned is related to the peculiarity of the structure of Löwenheim's proof. This aspect will not be completely understood until the following section, but here I will give an indication that explains the sense in which it obscures our understanding of the argument. Essentially, Löwenheim's purpose is to present a procedure for making a particular construction starting from any formula in normal form (IIF), with the sole assumption that it is interpreted in a domain, but is not necessarily true in it. The emphasis in Löwenheim's argument is on the presentation of a general procedure for performing a particular construction. From both the syntactic and the semantic perspectives, the hypothesis of the theorem does not intervene in the construction. The only point of interest, and one that is essential to an understanding of the construction, is the assumption that IIF is interpreted in a domain.

Löwenheim's proof has a syntactic component and a semantic component. Broadly speaking, we can say that it is a construction of a syntactic type hiding a construction of a semantic type. From a syntactic perspective, all Löwenheim does is replace certain indices with certain individual constants, and construct a formula on the basis of another in normal form. This aspect of his argument is the one described in the construction of P₁ which I presented at the beginning, and, from this point of view, there can be no objection to that presentation. Obviously, in order to explain the construction of P₁ we do not need to suppose that IIF is interpreted in a domain, but the construction of a formula is only what we might call the “outward appearance” of the argument.

But we have seen that the construction of P₁ includes, in a way, an argument involving elements of a given domain. One part of this argument of semantic type is contained in P₁ itself, simply because the numerals (i.e., the individual constants) stand for elements. The information that P₁ cannot provide on its own is that the elements belong to a given domain, and for this reason we cannot present this part of the proof as if involved solely the construction of a formula. When I said above that in the construction of P₁ we suppose that IIF is interpreted in a domain, my only intention was to preserve in some way the idea that there is a given domain.

The semantic component of Löwenheim's argument is the main one, but both are important; we must not lose sight of either. As in this subsection, in the one that follows I will initially adopt a syntactic point of view, because it is easier to explain, and then I will reconsider the argument from the semantic perspective.

6.2.4 IIF will certainly vanish identically in every domain if P₁ does, that is, if P₁ vanishes when all elements 1, 2,..., n₁ are mutually distinct as well as when arbitrarily many equations hold among them. In order to see whether this is the case, we go through all these possibilities; thus we form from P₁ all those (finitely many) specializations that we obtain when we introduce arbitrarily many or few equations among the elements 1, 2,..., n₁ (and then in the course of this the relative coefficients of and are evaluated, too).Therefore, if all vanish identically, IIF = 0 is identically satisfied. If not, we now write down, in addition to the factors of IIF already included in P₁ all those that are not yet included in P₁ and in which no productation index has a value other than a number from 1 to n₁. The resulting product (which, therefore, will also contain the old factors of P₁) we call P₂. In P₂ the fleeing indices i_j, k_m,¹⁸... will have the values

of these we denote by the numbers n₁ + 1, n₁ + 2,..., n₂ those that are not already denoted by some number.(We do not assume of these, either, that they represent mutually distinct elements or elements that differ from the old ones.)

Now in P₂ (as before in P₁) the indices used are taken as either equal to or distinct from each other in every conceivable way. The products thus resulting from P₂ we call

If they all vanish, equation IIF = 0 is identically satisfied. If not, we form P₃ by writing down all the factors of IIF in which the productation indices lie between 1 and n₂. We call the new fleeing indices n₂ + 1, n2 + 2,..., n3.

By taking the indices as either equal or distinct we now form

And so forth. Since at this point it is easy to describe how, starting from P_n, we form P_n+1, as well as the denumerably infinite sequence of the P_k, is to be regarded as defined herewith, and likewise the

If for some · (hence also for all succeeding ones) all vanish, the equation is identically satisfied. If they do not all vanish, then the equation is no longer satisfied in the denumerable domain of the first degree just constructed.(“Über Möglichkeiten,” pp. 455 and 456 (239 and 240))

6.2.4.1 In these extracts Löwenheim concludes the construction of the sequence of formulas that begins with P₁ and constructs a sequence of sets of formulas. Both sequences are constructed at the same time. For the sake of simplicity, I will first explain what is required to complete the construction of the sequence P₁, P₂, P₃,...¹⁹

Let us suppose that P_n is constructed and that 1, 2,..., r are the constants that occur in it. We write the product of all the formulas obtained when the universal quantifiers of IIF range over all the constants that occur in P_n. This product contains factors that have not intervened in the construction of P_n. It is assumed that the order of the factors is preserved in each step. The resulting formula willcontain fleeing indices, which did not appear in the construction of P_n. We enumerate these new indices, starting at r + 1. The result of replacing each fleeing index in the said product by its corresponding numeral is P_n+1.

Instead of illustrating the construction with Löwenheim's example, I will use another which will highlight certain details rather better. Let us suppose that IIF is IIiA(i, k_i, h_i). According to the previous subsection, P₁ = A(1, 2, 3), where 2 and 3 substitute for k₁ and h₁, respectively. We now write the product of all the specifications of IIF obtained when its universal quantifier ranges over all the constants that occur in P₁; the result is

This formula contains the indices k₂, h₂, k₃, and h₃, which do not appear in the construction of P₁. If we enumerate them in the order in which they occur, continuing with our enumeration, then

Observe that the order of the factors is preserved. To obtain P₃, we would write the product of all the specifications of IIF when its quantifier ranges over 1, 2,..., 7 and proceed in the same way.²⁰

To illustrate the construction still to be made I will again use Löwenheim's example, which is easier to work with than the one above. The two first formulas of the sequence (which I have left out in the quotation) are

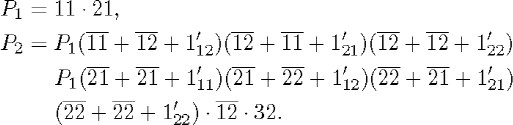
Löwenheim abbreviates, writing nm in place of z_nm.²¹ As in P₁, Löwenheim simplifies P₂ as much as possible. Of course, he only gives the final result of the simplification. Without mentioning the applications of the commutative and associative properties, one way of obtaining Löwenheim's result is as follows. By eliminating the repeated factors with the aid of the symmetry of the equality and the idempotence of conjunction, we obtain

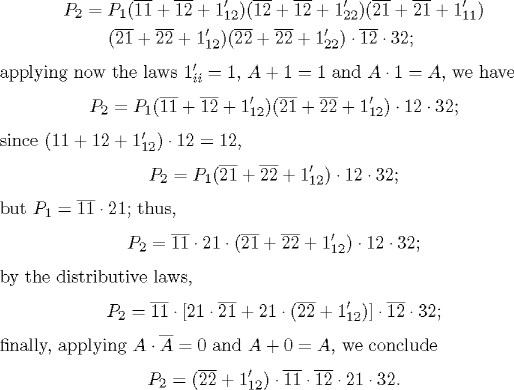
Each formula in the sequence is associated with a set of formulas. I will now explain the construction of this sequence. Let P_n be any formula in the sequence. Let us consider all possible systems of equalities and inequalities between the constants that occur in it (strictly, all possible equivalence relations on the set of constants that occur in P_n). A convenient way of representing these systems of equalities is by means of their associated partitions. Applied to Löwenheim's example, for the two first formulas in the sequence the result would be

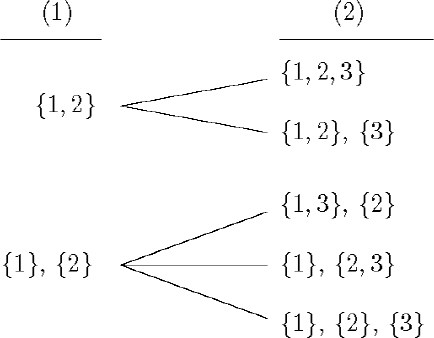
In each case we should understand that the equality holds between the constants that belong to the same set and inequality between the constants belonging to different sets.

Now, we choose a representative of each class of each partition; for example, each class can be represented by the lowest numeral in it.

Then, for each P_n and each system of equalities between its constants, we obtain the formula resulting from

(1) replacing each constant of P_n by the representative of its class; and

(2) evaluating the coefficients of and .

This means that in place of nm we will write 1 or 0, depending on whether n = m or n m, and analogously for the case of _nm. Thus, each system of equalities determines the values of the coefficients of the relatives and and this allows us to eliminate these coefficients.

Returning to Löwenheim's example, if in the above diagram we replace each partition by the formula that results of applying (1) and (2), we obtain the diagram

From each P_n we obtain as many formulas as there are equivalence relations between its constants. The set of all formulas thus obtained can be structured in a natural way in what we will call levels, following Skolem's terminology (Skolem [1922], p. 145 (296)). From here on, I will use the expression “formulas of level n” to refer to the formulas obtained from P_n following the procedure described.

To conclude this subsection, I will emphasize a number of points that will be important in the final part of the proof. Löwenheim mentions the first point explicitly, and the other two are implicit in the construction.

(a) The number of formulas at each level is finite, since Pn has a finite number of constants.

(b) If the order of the factors is preserved in each step, then, for n < m, Pm has the form P_n ·A, and each formula Q of level m is of the form ·A, where is a formula of level n. This last claim implicitly defines a partial order on the set of all satisfiable formulas obtained from P₁, P₂,....²² This kind of partial order is what we today call a tree.²³

(c) All the satisfiable formulas of a given level have constants that do not occur in the formulas of previous levels. Without adequate notation this assertion cannot be stated strictly or proved, but I think the idea is clear. Let us suppose that C_n and C_n+1 are the sets of constants that occur in P_n and P_n+1, respectively. As we have seen, P_n+1 is obtained when the quantified variables of IIF take values on Cn, and the formulas of level n + 1 are obtained by introducing in P_n+1 in the way I have described all the possible systems of equalities between the constants that occur in it. The formulas that result from introducing into P_n+1 a system of equalities in which every constant of C_n+1 – C_n is equated to one in C_n have no constants outside C_n. These systems of equalities thus represent all the possibilities that the fleeing indices do not generate terms outside C_n or, put another way, that the domain closes at this level. Therefore, if one of the formulas that correspond to these systems of equalities were satisfiable, IIF would also be satisfiable on a finite domain, but this contradicts the hypothesis of the theorem.

An example will help to clarify the idea. We have seen that if IIF is IIiA(i, k_i, h_i), then

Let us now consider the system of equalities associated with {{1, 3, 5}, {2, 4, 6}}, which meets what we just have explained. When we introduce in P₂ the corresponding equalities, we obtain

Evidently, if this formula is satisfiable, IIF is also satisfiable in a domain of two elements.

6.2.4.2 Now I turn to a question of terminology. In the part we are discussing, and in the following one, the verb verschwinden (vanish) appears frequently. If we observe how Löwenheim uses it in this proof and in that of Theorem 4, we will see that he only uses this term when referring to relative expressions that are not equations (i.e., to formulas), and that the fact that these expressions do not vanish means that there is a certain interpretation that satisfies them. Thus, the fact that a relative expression vanishes means that it is not satisfiable or, stated explicitly, it takes the value zero for any assignment of values to its relative coefficients (and to its constant indices, if it has any).

On occasion, instead of stating simply that a relative expression vanishes, Löwenheim says that it vanishes identically. As we saw in section 5.4 of chapter 5, “identical” and “identically” are applied to equations. Löwenheim says that A vanishes identically when in the context he is considering it appears as a member of an equation equated to zero. The fact that A vanishes means, in consequence, that the equation A = 0 is identically satisfied, and so Löwenheim modifies the terminology slightly. This happens, for example, in the case of IIF, in the proof that we are discussing. “Vanishing identically” and “vanishing” mean the same, and the choice of term depends exclusively on whether the relative expression is in the form of an equation or not. There is, nevertheless, one case that does not comply with this rule. At the start of the second paragraph of the quotation, Löwenheim says: “if all P₁ vanish identically ....” These relative expressions are never found in the form of an equation of the said type. I think it is a slip on Löwenheim's part, because he never uses this formulation again to refer to these formulas. In any case, the matter is of no importance, as the meaning does not change.

6.2.4.3 When Löwenheim constructs the second sequence of formulas, he states an auxiliary lemma. I will discuss the first paragraph of the quotation, which contains all the relevant material. To makethe references somewhat easier, I will start by presenting the principal statements that intervene in the discussion. Bearing in mind the meaning of “vanishing,” they are the following:

Lemma 6.3 If P₁ is not satisfiable, then IIF is not satisfiable.²⁴

Lemma 6.4 If no formula of level 1 is satisfiable, then P₁ is not satisfiable.

Lemma 6.5 If no formula of level 1 is satisfiable, then IIF is not satisfiable.

The argument that Löwenheim offers in the first paragraph of the quote is not intended to prove Lemma 6.3, because he must consider it to be evident. In my presentation of the construction of P₁, at least one small proof is required to indicate how elements are assigned to the new constants, but we should remember that Löwenheim thinks directly of elements. Let us look at an example. We have seen that if IIF is IIiA(i, k_i, h_i), then

When IIF is interpreted in a domain, 1 automatically stands for an element of that domain; furthermore, Löwenheim sees no essential difference between A(1, 2, 3) and A(1, k₁, h₁).²⁵ In this way, Lemma 6.3 is now an immediate consequence of an evident claim: if an interpretation in a domain satisfies IIF and 1 is an element of the domain, A(1, k₁, h₁) is true (under the same interpretation). Löwenheim, then, thinks of Lemma 6.3 as if it were, stated in our terms, an immediate application of the definition of satisfaction to a universally quantified formula.

Of the three lemmas, the one that interests Löwenheim the most is Lemma 6.5. The role of Lemma 6.4 is purely auxiliary. It may be that Löwenheim considers Lemma 6.5 so obvious as to require noproof, and he merely tells us how to construct the first level formulas; but it may also be the case that he considers the construction itself as essentially a proof of Lemma 6.4 and, since Lemma 6.3 is obvious, as a proof of Lemma 6.5 as well.

Naturally, what I say about P₁ goes for any P_n as well. In conclusion, we can consider the following generalization of Lemma 6.5 as proved:

Lemma 6.6 If there exists n such that no formula of level n is satisfiable, then IIF is not satisfiable.

Initially, then, we can say that the aim of this part of the proof is to show how to construct the formulas of the various levels, and to establish Lemma 6.6. We will now see how Löwenheim interprets this result.

6.2.4.4 The reconstruction I have just offered is not an exact reflection of the structure of Löwenheim's argument. Basically, his exposition of the construction of the formulas of the various levels is as follows: We first construct P₁, and from P₁ the formulas of the first level; we then check whether they all vanish or not (a task which can always be performed, since at each level there are finitely many quantifier-free formulas); if they all vanish, IIF is not satisfiable, and we are done; if not all of them vanish, we construct P₂ and proceed in the same way; if not all the level 2 formulas vanish, we construct P₃; and so on. This way of arguing is slightly surprising since, given the hypothesis of the theorem, it would be more natural to show that at each level there must be satisfiable formulas. Löwenheim, however, reasons as if it were not known that IIF is satisfiable. More specifically, it appears that Löwenheim is describing a procedure which, applied to a formula in normal form, either will prove that it is not satisfiable, or will allow us to determine a sequence of formulas that will show its satisfiability in a finite or denumerable domain.²⁶ Finding an explanation for thisway of presenting the construction of the sequences of formulas is a problem for any interpretation of the proof (although it is never mentioned).

The key to the problem is to be found in the sentence which concludes the quotation (the sentence that is actually the beginning of the last part of the proof). Löwenheim states here that IIF = 0 is not satisfied (and therefore IIF is satisfied) in the denumerable domain that has just been constructed. Strictly speaking, the argument that supposedly determines the domain is the one which he presents next (and which we will deal with in the next section), but this detail is of no importance at present. Significantly, Löwenheim claims that the construction we are analyzing determines a domain. If he did not state this, we would be unlikely to imagine that his aim was the determination of a domain. The assertion is so surprising that we may be tempted to regard it merely as an idiosyncratic manner of speaking, but in fact it is fundamental to an understanding of his conception of the proof; indeed, it is not the only sentence in which he states or suggests the same idea. In the proof of Theorem 3 (“Über Möglichkeiten,” p. 459 (243)), he claims that a domain can be constructed by following the method of the proof we are analyzing, and in the next section we will see that at the end of the proof there is another sentence which can be interpreted along the same lines.²⁷

I will not explain here why Löwenheim believes that he has constructed a domain, nor whether or not he has actually done so. I will leave these considerations for the following section, because by then we will have all the data required for their discussion. My aim at the moment is to analyze Löwenheim's assertion, and to extract from it some of the ideas that are fundamental to an understanding of his argument.

The most pressing question now is: what does Löwenheim mean when he claims here that he has constructed a denumerable domain? It seems clear to me that he can only mean that he believes that he has constructed or presented the necessary steps for constructing a denumerable domain included in the domain on which IIF is interpreted. If he did not believe that he had determined a subdomain, he would have said that he had constructed a domain and a solution in it. If Löwenheim meant this,²⁸ he would be using the word “domain” in an unusual way to refer to what we now call a structure, and there is no reason for thinking that this case is an exception—it would be the only one in the paper.

The problem that this sentence poses is the same as the one we find in the continuous references to elements. It is beyond doubt that when Löwenheim claims that he has constructed a domain it is because he believes that he has fixed (or described the steps for fixing) the assignment of elements to the constant indices of IIF and, in particular, to the indices generated by its fleeing indices. Löwenheim cannot be unaware that if these indices stood for objects of any domain (be it D or not), the main problem would lie in determining the solution, that is, the assignment of truth values to the relative coefficients in the domain. If Löwenheim thought he had constructed a solution, he would say so—above all, if it is the key to the proof.²⁹ Throughout the paper, whenever it is necessary to mention the solution, Löwenheim does so.³⁰ Here, not only does he not mention the solution, he makes no reference to it at any stage of the proof. The only possible explanation for the omission is that he does not consider finding a solution to be the central problem. In other words, stating that he has constructed a domain only makes sense when the solution is considered as given. In my view, this is an important argument against the traditional position which holds that Löwenheim proved or sought to prove the weak version of the theorem. His assertion makes it clear that his aim is to prove the subdomain version. Establishing when and how he uses the solution that, by hypothesis, satisfies IIF in D is undoubtedly a difficult task, but that is no reason for interpreting Löwenheim's assertion in a different way.

In the previous section I said that Löwenheim is thinking of elements of a given domain, and now we will see that the aim of the construction he presents is to determine a domain. More specifically, Löwenheim considers that at this stage of the proof he is presentinga method for determining a domain. This, in his opinion, means that the constants that occur in P₁, P₂,... do not completely determine a domain, because otherwise he would not have needed to construct any further formulas. The determination is made when all the possible systems of equalities are introduced. In a way, it is as if the satisfiable formulas of a level n represented all the possible ways of determining the values of the constants occurring in P_n. Thus, when Löwenheim explains how to construct the formulas, what he thinks he is explaining is how to determine a domain on the basis of an interpreted formula; consequently, when the construction is completed he states that he has constructed it.

The reason for the style that Löwenheim adopts probably lies in his desire to present the construction in as general a form as possible. I think that he intends to make it clear that this type of construction is applicable to any formula in normal form, not only to one that meets the conditions of the hypothesis. If the starting formula is not satisfiable, we will conclude the construction in a finite number of steps because we will reach a level at which none of the formulas is satisfiable; if the starting formula is satisfiable, then, according to Löwenheim, this construction will allows us to determine a finite or denumerable subdomain in which it is satisfiable. As I said in the previous section, in this part of the proof Löwenheim lays emphasis on the construction itself, and does not use the hypothesis of the theorem. Essentially, it is as if the proof were divided into two parts (though no division is shown in his exposition): he first explains how to make a certain type of construction, and then applies the hypothesis of the theorem. The last paragraph in the initial quotation can be seen as the beginning of the second part.

Whether Löwenheim referred to a subdomain or to a domain and a solution in it, it is evident that, if the starting formula meets the hypothesis of the theorem and Löwenheim's construction determines in some way a domain, then it will be denumerable. As we have seen, the constants that occur in the formulas of any level stand for distinct elements.³¹ In addition, supposing that IIF is satisfiable but not satisfiable in any finite domain, at each level there are satisfiable formulas in which new constants occur, that is, constants that do not occur in any formula of a previous level. Thus, the set of formulas of the tree that Löwenheim has constructed is denumerable and theset of constants that occur in any infinite branch of the tree is also denumerable. In consequence, if these constants determine a domain, the domain will be denumerable.

As regards the syntactic version I have presented, there is nothing new to say. It is a reconstruction that reproduces what Löwenheim does accurately enough, but it does not reproduce his interpretation of what he does. By now we have a more concrete idea of the task Löwenheim set himself and we could offer an alternative reconstruction, but it is better to wait until the end of the argument.

6.2.4.5 I have left till the end of the subsection a remark which is related not to the theorem, but to the possible functional interpretation of fleeing indices. As we have seen, the formulas of level n are constructed bearing in mind all the possible ways of considering the constants of P_n as equal or different. But the possible alternatives differ, according to whether the fleeing indices are functional terms or not. More exactly, certain alternatives are only possible when the fleeing indices are not interpreted as functions. For example, let us suppose that IIF = IIiA(i, k_i, l, h). In the first step we would obtain

and after replacing k₁ by 3 and k₂ by 4, we obtain

We may wonder now what equalities are possible between the constants of P₁. If we write, informally, n = m instead of _nm = 1, we may pose the question as follows: can 1 = 2 and 3 4? If we take k_i to be a functional term, then this system of equalities is impossible, since what we are saying is that 1 = 2 but k₁ k₂.

Unfortunately, Löwenheim does not say which formulas are obtained in his example when equalities are introduced; nor does he mention how many there are. If he had, we would have a definitive answer to the question of whether the fleeing indices are functions or not. Nonetheless, I believe there are enough data to suggest that Löwenheim considers these nonfunctional systems of equalities as acceptable. First, he repeatedly insists that two different numerals (or two fleeing indices) can denote the same element. He never places restrictions on this, and his insistence shows that his central concern is with the interpretation of the equalities. Thus, it is reasonable to think that if he places no limitations on the possible systems of equalities it is because there are none to impose (apart from the normalones)—not because he has overlooked them. Second, there is the general idea of the construction. We should recall that the indices generated by the fleeing indices also have the character of variables ranging over the elements of the domain. It is natural to suppose that any consistent system of equalities may hold. It is the same when we see Löwenheim's construction from the syntactic point of view. If we replace the fleeing indices with individual constants, it is normal to suppose that between these constants any system of equalities may hold; I have developed Löwenheim's example in my exposition with this idea in mind.

6.2.5 If for some k (hence also for all succeeding ones) all vanish, the equation is identically satisfied. If they do not all vanish, then the equation is no longer satisfied in the denumerable domain of the first degree just constructed.For then among there is at least one Q₁ that occurs in infinitely many of the nonvanishing as a factor (since, after all, each of the infinitely many nonvanishing contains one of the finitely many 1 as a factor). Furthermore, among there is at least one Q₂ that contains Q₁ as a factor and occurs in infinitely many of the nonvanishing as a factor (since each of the infinitely many nonvanishing that contain Q₁ as a factor contains one of the finitely many 2 as a factor). Likewise, among there is at least one Q₃ that contains Q₂ as a factor and occurs in infinitely many of the nonvanishing as a factor. And so forth.

Every Q_v is = 1; therefore we also have

But now, for those values of the summation indices whose substitution yielded Q₁, Q₂, Q₃,..., IIF is = Q₁Q₁Q₃..., hence = 1. Therefore IIF does not vanish identically. Hence equation (4) is no longer satisfied even in a denumerable domain. Q.e.d. (“Über Möglichkeiten,” p. 456 (240))

6.2.5.1 Rather than discussing the more technical aspects (as I have done in the two previous sections), I will start by giving my interpretation of Löwenheim's argument. The purpose of this initial version is not to present a complete explanation of Löwenheim's reasoning, butto put forward an outline of my interpretation and to draw attention to its more controversial aspects. For this reason I will deliberately leave a number of points unexplained—points which, in my opinion, Löwenheim does not clarify. In the subsequent discussion I will argue for my interpretation and will explain all the details.

To make the exposition easier, we will say that a formula A is an extension of another formula B, if A is of the form B · C. If Q is a level r formula, we will say that Q has infinitely many extensions, if for all n > r, Q has an extension of level n. By construction, all level r+1 formulas are extensions of one and only one level r formula.³² By the hypothesis of the theorem, there is an interpretation in an infinite domain D that satisfies IIF: In consequence, at each level there must be at least one true formula under this interpretation. Among the true formulas of the first level, which, we recall, is finite, there must be at least one which has infinitely many true extensions. Let Q₁ be one of these formulas. At the second level, which is also finite, there are true formulas which are extensions of Q₁ and which also have infinitely many true extensions. Let us suppose that Q₂ is one of these formulas. In the same way, at the third level there must be true formulas which are extensions of Q₂ (and, therefore, of Q₁) and which have infinitely many true extensions. Let Q₃ be one of these formulas. In this way, we can define a sequence of formulas Q₁, Q₂, Q₃,... such that for each n > 0, Q_n+1 is a true extension of Q_n. Consequently,

The values taken by the indices whose substitutions yield the sequence Q₁, Q₂, Q₃,... determine a denumerable subdomain of D on which IIF has the same truth value as Q₁·Q₂·Q₃·.... We therefore concludethat IIF = 1 in a denumerable domain. ³³

6.2.5.2 Before addressing the problems posed by this reconstruction and explaining why it is the one that I have chosen, I will briefly discuss a number of technical aspects.

I think it is beyond doubt that the structure of my argument is the same as that of Löwenheim's. Basically, it is the proof of a specific case of what we know today as infinity lemma proved later with all generality by D. König ([1926] and [1927]). As I said above, the set of satisfiable formulas obtained by introducing all the possible equalities and inequalities in P₁, P₂,... , ordered by the relation of extension between formulas is a tree. Applied to this case, the infinity lemma states that if the tree is infinite (i.e., if the set of formulas in the tree is infinite) but each level is finite, then it has an infinite branch (i.e., there is a sequence of formulas Q₁, Q₂,... such that Q₁ is a formula of the first level, and if n > 1, Q_n is a level n extension of Q_n–1). In general, the proof of the infinity lemma requires the use of some form of the axiom of choice, but when the tree is countable (as in this case) any enumeration of its nodes allows us to choose one of each level without needing to use the axiom of choice. Löwenheim does not specify any enumeration of the formulas of the tree, but it is plain that the natural order of the numerals can be used to easily define a linear ordering on them. So we cannot say whether he is assuming the existence of a enumeration of the nodes or he is implicitly using the axiom of choice. In my opinion, the second option is more probable.

In the previous section we saw that the hypothesis of the infinity lemma is met for the tree whose nodes are the satisfiable formulas obtained from P₁, P₂,.... For my reconstruction of the argument we also need to be sure that this hypothesis is met when the tree isrestricted to the formulas satisfied by the solution assumed to satisfy IIF in D. Slightly more specifically, my reconstruction of Löwenheim's argument presupposes that at each level there are a finite number of formulas that are satisfied by the solution assumed to satisfy IIF in D, and certain assignment of elements of D to the numerals that occur in them. This requirement is certainly met, and so there is no problem. Whether or not Löwenheim considers it proven, though, is another matter; if we believe he does, we must also establish whether he actually proves it or not. All these questions will be answered later on.

6.2.5.3 We have seen that Löwenheim constructs a tree of satisfiable formulas and, at least on a first reading, it looks as if his final argument is intended to show that this tree has an infinite branch. The first impression, then, on reading the argument, is that Q₁, Q₂, Q₃,... is simply a sequence of satisfiable formulas. The most striking aspect of my interpretation is probably that instead of constructing the sequence with satisfiable formulas I do so with formulas that are true under the solution that, by hypothesis, satisfies IIF in D. Obviously, this means that I subscribe to the view that Löwenheim attempted to prove the subdomain version of the theorem.

Immediately after constructing the sequence Q₁, Q₂,..., Löwen-heim surprises us with the following claim:

(6.1) every Q_n is = 1.

Somewhat more explicitly, what Löwenheim asserts is

for every n, Q_n takes the value 1

or, put another way,

for every n, Q_n is true.

On first sight, the difficulty of this sentence is whether Löwenheim means that all formulas are true under the same solution, or that for every Q_n there is a solution that satisfies it. Van Heijenoort believes that the latter interpretation is the correct one, but my opinion (which coincides in part with Wang's) is that Löwenheim would never have asserted (6.1) if he had not thought that all formulas were true under the same solution. Given the terminology that Löwenheim uses in the proof, if he had thought that his construction only guaranteed that the formulas were satisfiable, he would have said:

for every n, Q_n does not vanishor, more explicitly,for every n there is an assignment of values to the relative coefficients for which Qn takes the value 1.

Of course, we can always claim that (6.1) is a careless way of expressing this same idea, but it is hard to believe that Löwenheim would now be using the expression “= 1” in the sense of “does not vanish” when throughout the proof he has used the latter.³⁴ The most natural conjecture is that Löwenheim uses “= 1” because he means that the formulas are true, and in this case his claim only makes sense if he is assuming that the assignment of values to the relative coefficients is the same for every Q_n.

Another detail that supports this interpretation is the fact that Löwenheim does not show that (6.1) implies

If we suppose that all formulas are true under the same solution (whatever this solution may be), it is obvious that (6.1) and (6.2) say essentially the same thing and, therefore, this step requires no proof. Van Heijenoort interprets the step from (6.1) to (6.2) as follows:

for every n, Q_n is satisfiable (nonvanishing); therefore, Q₁ · Q₂ · Q₃ · ... is satisfiable. (From Frege, p. 231)

As we know, this implication is not correct for any arbritary formula, though it is correct in this particular case. To see why, let us suppose that ¡ is any finite subset of {Q₁,Q₂,Q₃,...} and let Q_m be the formula in the subset having the greatest subscript. By construction, for every p < m, Q_m = Q_p ·A, and, since Q_m is satisfiable, the subset is also satisfiable. Thus, any finite subset of {Q₁,Q₂,Q₃,...} is satisfiable; by the compactness theorem, {Q₁,Q₂,Q₃,...} is satisfiable, and therefore Q₁ · Q₂ · Q₃ ·... is satisfiable. In this way, the step from (6.1) to (6.2) is correct even in van Heijenoort's interpretation, but, as the compactness theorem had not been proven in 1915 (it was proved by Gödel in [1930]), the step that I have taken applying this theorem must be accounted for. According to van Heijenoort, the two principal problems in Löwenheim's proof are the use of formulas of infinite length in the proof that all formulas possess normal form, and the lack of an argument for this step.³⁵

Van Heijenoort considers that the two problems have a common characteristic: Löwenheim applies what is valid for the finite case to an infinite case (to formulas of infinite length in one occasion and to infinite sets in another). This suggests that Löwenheim had a tendency to take this type of step unjustifiably and this tendency explains both problems. This interpretation has the reassuring feel of any general explanation, but in my view it is not tenable. First, as Thiel says ([1977], p. 244), it is strange that Löwenheim should make slips of this kind, because in [1911] he himself had warned that the rules for calculating infinite sums and products were still to be proved and that this proof would be necessary in order to achieve the most important applications of these rules. Second, both in the case of the logical equivalence between a formula and its normal form and in this case, we have an alternative interpretation which allows us to take Löwenheim's assertions literally, without there being anything lacking in his argument. The basic problem is that van Heijenoort presupposes that he is trying to prove the weak version, and therefore expects Löwenheim to determine a solution, something that he does not do.

To summarize, I believe that Löwenheim would never have asserted (6.1) nor failed to offer an argument for the step from (6.1) to (6.2), if he had not considered the problem of assigning values to the relative coefficients as completely solved, or, put another way, if he had not believed that he had a solution that satisfied all the formulas of the sequence. The real difficulty posed by (6.1) is not whether Löwenheim means that the formulas are true or satisfiable, but to identify the solution that he alludes to implicitly by asserting that all formulas are true.

One alternative (espoused by Wang and by Brady) is to consider that Löwenheim is thinking not of formulas, but of solutions. According to this interpretation of the proof, the tree that Löwenheim constructs should be seen as if any level n were formed by all thesolutions (restricted to the language of P_n) that satisfy P_n.³⁶ The number of solutions at each level is also finite, although it is not the same as the number of formulas that Löwenheim considers, because each formula may have more than one solution that satisfies it. The ordering relation between the formulas in the tree would become the relation of inclusion between solutions, with the result that each solution would strictly include one from the previous level. Thus, when Löwenheim fixes an infinite branch of the tree, it should be understood that he is fixing a sequence of partial solutions such that each one is an extension of the one at the previous level. The union of all these partial solutions is the solution that satisfies P_n for every n N, and therefore IIF, in a denumerable domain.

As I explained in subsection 6.2.4.4, there is no reason for believing that Löwenheim is thinking of solutions. In my opinion, both the explanation of Wang and that of van Heijenoort are the consequence of the expectations created by a misinterpretation of the objective that Löwenheim sets himself in constructing the tree. Both seek to explain Löwenheim's assertions taking it for granted that his intention is to construct a solution, but in fact he constructs the tree in order to determine not a solution, but a domain.

The paragraph that concludes the argument corroborates this interpretation. Löwenheim claims that “for those values of the summation indices whose substitution yielded Q₁, Q₂, Q₃,...” the following holds:

I will explain later the exact meaning of the sentence in quotation marks. The important point now is not what it says, but what it leaves out. Evidently, the equality above is not a logical equivalence, that is, it does not mean that both formulas always take the same truth value. The idea is that IIF takes the same truth value as the product Q₁·Q₂ ·Q₃ · ... , under a particular solution and a particular assignment of values (i.e., of elements of the domain) to the constant indices of IIF and to those generated by its fleeing indices.³⁷ Themost significant aspect of Löwenheim's assertion is that it does not mention the solution at a moment when it would be particularly appropriate and natural to do so. As I said above, this omission cannot be attributed to an oversight, because Löwenheim does not forget to mention the solution when it is necessary. The proof of theorem 4 is an interesting example, because its conclusion bears similarities to the one we are discussing. There, Löwenheim constructs a formula on the basis of another given formula and states that if the constructed formula does not vanish, then the original does not vanish either (“Über Möglichkeiten,” p. 462 (245)). Immediately after making this assertion, he explains (with the aid of an example) how to find the domain and the solution that will satisfy the original formula if the constructed formula does not vanish.

Löwenheim's statement shows that his objective is to determine (in a sense which we still have to explain) the values (i.e., the elements) that are assigned to the summation indices or, in other words, to determine a denumerable domain. The fact that he makes no mention of the assignment of truth values to the relative coefficients (and, above all, that he does not mention it in the final paragraph) shows that he is not concerned in the slightest with the solution. This can only mean that his intention is to preserve the solution which, by hypothesis, satisfies ΣIIF, and to construct a subdomain. The solution is so obvious that there is no need to mention it.

I am convinced that the construction of the tree is not intended to account for the fact that at each level there is at least one true formula, and I am also convinced that Löwenheim is applying the hypothesis of the theorem when he asserts that all the formulas in the sequence are true. The idea is as follows. Suppose that IIF is true in a domain D under a particular solution; at each level of nonvanishing formulas there must be at least one that is true (under the same solution). For Löwenheim, this application of the hypothesis is trivial and does not require any additional remark or clarification, because both the constant indices and the indices generated by the fleeing indices of IIF stand for elements of D, and the solution in D under which IIF is true fixes the values of all the relative coefficients in D (i.e., if a, b D and z is a relative other than occurring in IIF, the value of zab is fixed by this solution). Thus, by applying the hypothesis, the infinite sequence of formulas automatically becomes a sequence of true formulas.

Löwenheim's global strategy is then as follows: first he presents a procedure of a general nature to construct a tree of a certain type, and then (without any warning, and without differentiating the two ideas) he applies the hypothesis of the theorem to the construction. The precise meaning of this application is easily understood as far as the solution is concerned, but it is not so clear as regards the assignment of elements to the indices. We will discuss this aspect in a moment.

To formulate Löwenheim's argument correctly in accordance with this interpretation we need to choose, at each level, a formula that is true under the solution of the hypothesis. This is why in my reconstruction I use the hypothesis to determine the sequence, and therefore why I talk of true formulas at a point at which Löwenheim speaks of nonvanishing formulas. At first sight, the liberty I am taking here appears similar to the one van Heijenoort takes when he reads “= 1” as “nonvanishing,” but there is an important difference. In Löwenheim's argument there is a significant change which needs to be accounted for: he first speaks of nonvanishing formulas, and later of true formulas. This change is explained, in my opinion, by the application of the hypothesis of the theorem, and all I do in my reconstruction is to apply it before it appears in his exposition. The problem with van Heijenoort's interpretation is that he does not explain this change. One could object to my interpretation on the grounds that Löwenheim would be unlikely to use the hypothesis that IIF is true in D without mentioning it. In my view, however, there is nothing particularly unusual in the fact that he does not bring it to our attention; he does not mention it for the purpose of showing that the domain (or the tree) is infinite. Indeed, if we compare this proof with those of other theorems in the paper, we would hardly expect him to mention it. As I said before, one characteristic of Löwenheim's style is that the details of his proofs can only be understood when the arguments reach their conclusion.

6.2.5.4 We have seen that the aim of the proof was to determine a subdomain. When Löwenheim shows that the tree has an infinite branch, he thinks that he is constructing an infinite subdomain in which IIF is true. What we need to explain is why Löwenheim considers it necessary to construct the tree of satisfiable formulas in order to determine a domain, and whether with this construction he does in fact determine one.

Modern commentators have seen in the construction of the tree an attempt to construct a solution in a denumerable domain. One ofthe reasons for this conclusion is probably that, when Löwenheim's argument is seen as a proof of the subdomain version, the construction of the tree appears to be an unnecessary complication. He could, it seems, have offered a simpler proof which would not have required the construction of the tree and which would have allowed him to reach essentially the same conclusion. Let us imagine that we remove from Löwenheim's proof everything except the explanation of how the sequence P₁, P₂,... is constructed, and add as conclusion:

and since

IIF is = 1 for the countable domain (finite or infinite) constituted by the values taken by all the numerals in the sequence.

From a modern viewpoint, this simplified argument presents no more obstacles than Löwenheim's and does not seem to contain any steps that he would consider unacceptable. In addition, it is such a straightforward and immediate argument that he cannot have been unaware of it. The question is: why did he not use it?

The answer cannot be that Löwenheim was especially interested in proving the weak version and not the subdomain version, since we already saw at the beginning of the chapter that this is not so. In all likelihood, Löwenheim merely offered the simplest proof at his disposal, and for this reason it is interesting to ask why he did not argue in the way that I have just described. Nor is it possible that the construction of the tree is designed to show that the subdomain that is allegedly being constructed is denumerable. In the simplified argument two different numerals can stand for the same element and, therefore, the only conclusion we can draw is that if IIF is true in a domain D, then it is true in a finite or denumerable subdomain of D, but recall that Löwenheim himself states the theorem in this way on occasion (see note 26 in this chapter).

The only way to account for the fact that Löwenheim does not offer the simplified proof is that he considers it to be incorrect or insufficient. It is possible that Löwenheim began by not accepting that the hypothesis of the theorem allows us to claim that for every n, P_n is true, but in any case I am convinced that in his opinion the simplified argument did not prove the theorem. This conclusion is not based only on the fact that the accounts of why Löwenheim does not simplify the proof are not persuasive. Essentially, the simplified argument consistssolely in explaining how to construct a sequence of formulas. However, Löwenheim's aim is to determine a subdomain, and it is reasonable to suppose that he does not consider merely constructing the sequence P₁, P₂,... and assigning numerals to the indices generated in the process of construction as being sufficient for his purpose. It is true that for Löwenheim the indices (and hence the numerals that replace them) stand for elements of the domain on which IIF is interpreted, but even so the construction of the sequence does not appear to be enough to claim that a domain has been constructed.

For Löwenheim, the simplified argument is insufficient because we do not know whether two different numerals stand for the same element or not, and, in his opinion, this implies that the coefficients of the relatives and cannot be evaluated. If we reread the first part of the proof, we will observe that Löwenheim insists time and again that it cannot be assumed that two different numerals (or two different indices) denote different elements. When he explains the construction of the formulas of the first level and says that all the systems of equalities that occur between the numerals of P₁ should be taken into consideration, he states that the evaluation can now be performed. It is highly significant that Löwenheim should assert that a domain has been fixed immediately after constructing the tree (i.e., when it can now be said that each numeral stands for a different element). In conclusion, what the simplified argument lacks is the establishment of a system of equalities between the numerals.³⁸ It may be that Löwenheim thought that even the simplified argument was strictly speaking incorrect—not only insufficient—because he did not consider it acceptable to say that the formulas of the sequence P₁, P₂,... are true (assuming that IIF is) before solving the problem posed bythe relatives and . Once this difficulty is resolved, it would be acceptable to assert (as a consequence of applying the assumption) that at each level there is at least one true formula.

Nowadays we know that determining the system of equalities is unnecessary to the proof of the subdomain version. The hypothesis of the theorem states that there is an interpretation that satisfies IIF in D, and this means that we can suppose the existence of an assignment v that fixes both the elements assigned to the constant indices of IIF and those assigned to the indices generated in D by its fleeing indices. The usual way to prove the subdomain version is, in essence, as follows: Let D₁ be the set of all elements of D that v assigns to the constant indices of IIF, if IIF does not have indices of this type, then D₁ = {a}, where a is any element of D; when the subindices of the fleeing indices take values in D₁, new indices are generated; we call D₂ the set of the elements that v assigns to the new indices; this procedure allows the construction of an infinite sequence of finite subsets of the domain in which IIF is true; the union of all of them will be a countable subdomain (finite or infinite) in which IIF is true. As can be seen, there is no need to determine a system of equalities, because the assignment determines all we need.

When we see that Löwenheim speaks of numerals and indices as if they were elements of a domain that seems to be given, the natural reading is that he is using the hypothesis of the theorem. We assume then that, by hypothesis, both the constant indices of IIF and those generated by its fleeing indices denote fixed elements of the domain, and we conjecture that each numeral stands for the element denoted by the index it replaces. Consequently, we expect an argument that, with its own formal peculiarities, consists basically in constructing a subdomain in the way I have indicated. When we observe divergences from the usual argument in aspects that we consider fundamental (such as, for example, determining the system of equalities), we conclude that our reading was wrong, and that Löwenheim was proving the weak version. If Löwenheim had offered the simplified argument, his approach would have conformed more closely to our expectations, and it is highly likely that all the analysts would have believed that what he was presenting was a slightly imprecise proof of the subdomain version.

Löwenheim's purpose is to construct a subdomain, but he lacks the conceptual distinctions required to formulate the problem accurately. In particular, due to the lack of the distinction between syntax and semantics, he cannot have a precise understanding of the hypothesis when it is applied to formulas with fleeing indices. This explains why he does not use the hypothesis as fully as he might and why he is overdependent on the examples that he uses to develop his intuitions.

The meaning of IIF and the relation between this formula and ΣIIF cannot be fully grasped without the concept of assignment or, at least, without sharply distinguishing between the terms of the language and the elements they denote. For us, the assumption that IIF is satisfied in a domain D means that there exist a solution S and an assignment v in D such that (S, v) satisfies IIF. The assignment fixes the values (elements) taken by all the summation indices, that is, the constant indices of IIF and those generated in D by its fleeing indices. Löwenheim does not have the concept of assignment and, without its aid, cannot appreciate these details. From his point of view, the fact that IIF is interpreted in D does not imply that the values taken by the summation indices are fixed. If this were the case, he would probably have thought that the simplified argument was correct. All Löwenheim manages to intuit is that the problem of showing that ΣIIF is satisfiable is equivalent to the problem of showing that IIF is satisfiable. He proceeds essentially as he would with ΣIIF (but without the inconvenience of having to eliminate the existential quantifiers each time that a formula of the sequence P₁, P₂,... is constructed): he assumes that the nonlogical relatives (i.e., relatives other than and ) of IIF have a fixed meaning in a domain D and proposes fixing the values of summation indices in a denumerable subdomain of D. Put another way, Löwenheim aims to assign elements to the summation indices of IIF without resorting to the assignment which (like the solution) can be considered given by the hypothesis.

As the reader will have noticed, expansions do not actually intervene in the proof of the theorem, but it is beyond doubt that they suggest to Löwenheim a way in which to focus the problem of fixing the values of the summation indices.³⁹ Let us consider, for example, the formula

which, stated vaguely, is the development of IIiA(i, k_i, h_i) in the set of numerals {1, 2, 3}. Let us assume that, for whatever reason, wehave reached the conclusion that each numeral denotes a distinct element of some domain D in which IIiA(i, k_i, h_i) is considered to be interpreted. It is of no importance that we do not know which specific element each numeral denotes; knowing that different numerals denote different elements is enough to consider (6.3) as a part of the expansion of IIiA(i, k_i, h_i) in D. From Löwenheim's perspective, the set of numerals would be seen then as if it were a subdomain of D having three elements, and he reasons as if the numerals were elements of D or, stated more rigorously, as if the elements assigned to the numerals were fixed (although in fact they are not).⁴⁰ In this way, any function that assigns numerals to the indices occurring in (6.3) is seen as an assignment of elements in the subdomain supposedly determined by the numerals. In addition, it is clear that there is a natural correspondence between these functions and certain systems of equalities. Specifically, each function corresponds to the system of equalities which, stated informally, consists in equating each index to the numeral assigned to it.

To focus now more closely on what happens in the proof, let us accept that two different numerals can denote the same element in D. In this case, (6.3) can no longer be seen as a fragment of the expansion of IIiA(i, k_i, h_i) in D, and the numerals cannot be said to determine a subdomain. However, any system of equalities between the numerals of (6.3) together with another system that equates each index to a numeral (i. e:, that assigns numerals to indices) determines, in the sense that I have just explained, a subdomain and also the values that the indices take in it. For example, the system of equalities

determines a subdomain of two different elements that are denoted by 1 and 2, and also indicates which of the two values the indices take. If we introduce this system of equalities in (6.3) (i.e., if we replace each index by the corresponding numeral and replace 3 by 1), we will obtain

This formula is not an expansion (a detail I will look at a little later) nor a fragment of an expansion, but the product

can be seen as an expansion of IIiA(i, k_i, h_i) in a domain of two elements in which the values taken by the indices generated by k_i and hi in the domain have been fixed.

In the two cases above I have argued as if the indices could take values among those taken by the numerals, but this may not necessarily be the case. The indices could denote elements other than those denoted by the numerals. This possibility does not substantially affect the above explanation, but in any case we will take care of it by slightly modifying the last system of equalities.

Löwenheim replaces the indices by numerals, and it is between numerals that the systems of equalities are established. As we have seen, if IIF = IIiA(i, k_i, h_i), then

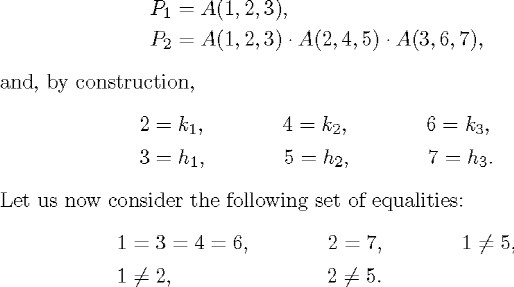
These two systems fix the values taken by the indices generated by k_i and h_i in {1, 2, 3} and determine, in the particular sense that we are now giving to the word, a subdomain of three elements which are assumed to be denoted by 1, 2, and 5. The result of introducing this system of equalities in P₂ is

The formulas (6.4) and (6.5) belong to the second level of the tree that Löwenheim constructs.

In Löwenheim's view, the situation can be described in this way: We begin constructing P₁; the numerals of P₁ determine a subdomain of two elements (since 1 = 3) denoted by 1 and 2, the equalities fixingthe values of h₁ and k₁; we then construct P₂; the equalities fixing the values of h₂, k₂, h₃, k₂; since the value of h₂ is different from that of 1 and 2, the subdomain must be extended; thus, the numerals of P₂ determine a subdomain of three elements denoted by 1, 2, and 5. If we construct P₃, the systems of equalities between its numerals that include the system above will determine the values of k₅ and h₅. Some of these systems will extend the domain (assuming that IIF is not satisfiable in any finite domain), but will leave the values of the indices generated by the new elements indeterminate. These values will be fixed in the next step, and so on. This process of constructing a subdomain is the process that the formulas of the different levels of the tree reflect (or seek to reflect).

Any expansion of IIF has a unique factor for each assignment of values to its quantified variables, but both (6.4) and (6.5) have two factors (the first and the third) for the case in which the variable i takes the value 1. Whether these “unforeseen” factors (as we could call them) occur or not depends on whether or not we consider fleeing indices as functional terms. If we do, then these factors never occur, and the result of introducing a system of equalities is actually either an expansion in a finite domain or a fragment of an expansion. I have the impression that Löwenheim takes for granted that the formulas of the various levels are of one of these two types,⁴¹ but there is no way to prove this because the possible presence of these factors does not affect his proof, since there is nothing in Löwenheim's argument that these factors would render incorrect.

In summary, Löwenheim considers that the problem of determining the system of equalities between numerals is the same (or essentially the same) as that of fixing the values taken by the summation indices of IIF (the constant indices, and the indices generated by the fleeing indices). The formulas of any level n represent, from Löwenheim's perspective, all the possible ways of determining the values taken by the numerals that occur in P_n and, in the last resort, the values taken by the indices replaced by the numerals (i.e., the constant indices in IIF and the indices generated when their fleeing indices vary on theset of numerals occurring in P_n–1). Thus, any assignment of values to these indices is represented by a formula of level n. Now, if IIF is satisfiable, at each level there must be at least one satisfiable formula. In the same way, if IIF is true in a domain D, at each level there must be at least one true formula (in other words, for each n there exists an assignment of elements of D to the numerals of P_n that satisfies Pn, assuming that the relative coefficients are interpreted according to the solution in D that satisfies IIF). The infinite branches of the tree represent the various ways of assigning values to the summation indices of IIF in a denumerable domain. The product of all the formulas of any infinite branch can be seen (leaving aside the repetition of factors due to the fact that P_n always contains the factors of P_n–1) as a possible expansion of IIF in a denumerable domain. This assertion is slightly inexact, but I think this is how Löwenheim sees it, and for this reason he claims without any additional clarification that, for the values of the summation indices that give rise to the sequence Q₁, Q₂, Q₃,... , the formula IIF takes the same truth value as the product Q₁ ·Q₂ ·Q₃ ·....⁴² Clearly, showing that the tree has an infinite branch of true formulas (in the sense I have just described) becomes, from this perspective, the same as constructing a subdomain of D in which IIF is true, and this is what Löwenheim sets out to do.

The only point still to be explained is why Löwenheim talks of satisfiability throughout the construction but at the end uses the fact that at each level there must be a true formula. If instead of stating that

(6.6) if IIF does not vanish, then at each level there must be a nonvanishing formula,

Löwenheim had asserted

(6.7) if IIF takes the value 1, then at each level there must be a formula that takes the value 1,

his argument would have been both easier to understand and easier to relate to the subdomain version. In my opinion, the reason why Löwenheim states (6.6) is that, as I argued in subsection 6.2.4.4, heintends the construction to be also useful to show that IIF is not satisfiable (if it actually is not), and (6.7) will be of no use in this regard. If we check that all the formulas of a level vanish, the first proposition (but not the second) will allow us to conclude that IIF is not satisfiable.

6.3 RECONSTRUCTING THE PROOF

6.3.1 In this section I propose to analyze different ways of reconstructing Löwenheim's proof accurately, regardless of whether the resulting argument is conclusive or not, and in the course of this analysis, to recapitulate the main ideas in my interpretation.

As I have said, Löwenheim's argument is an essentially semantic proof in which a tree of formulas is constructed for the purpose of determining a subdomain. However, this is not its only purpose. Löwenheim also presents the construction of the tree as a procedure designed to show that a formula is not satisfiable. It is not possible to account for both aspects of Löwenheim's argument in a single reconstruction, since, contrary to Löwenheim's belief, the formulas of the tree do not represent the possible forms of fixing the values taken by the summation indices.

The reconstructions that I will take into account give priority to the semantic aspect of Löwenheim's proof. By this I mean that their aim is to analyze different ways of formulating precisely the intuitive ideas behind Löwenheim's procedure to construct a subdomain, without seeking to reflect the way in which he expresses them. As I present the reconstructions, I will indicate what each one takes from Löwenheim's argument and in what ways it differs from it. I will of course say which of them is, in my opinion, the nearest to Löwenheim's proof. At the end of this section I will briefly discuss Löwenheim's construction as a procedure to show that a formula is not satisfiable.

6.3.2 As throughout the previous comments, I will assume that IIF is true in an infinite domain D under an interpretation (S, v), where S is a solution in D and v is an assignment in D which, except in the first reconstruction, we will not use.

The first option is to reconstruct the proof according to the argument which is usually given to prove the subdomain version and which, as I explained in subsection 6.2.5.4, consists in taking an initial set whose elements are those that v assigns to the constant indices in IIF (or any element in D, if IIF has no indices of this type) and, puttingit succinctly, to construct the set generated from this initial set by the fleeing indices. The main problem facing this option is that it makes the construction of the tree unnecessary, because the assignment v fixes the elements assigned to the summation indices (and hence the equalities between them). The only apparently reasonable explanation for Löwenheim's constructing the tree would be that he thought that the hypothesis only fixed the meaning of the relatives other than and and, therefore, he considered it necessary to determine the values of the coefficients of these relatives. The system of equalities, together with S (restricted to the subdomain), will then provide us with the truth value of all atomic sentences and will constitute what we now we could call “the diagram of the interpretation.”

This was the reconstruction that I once preferred, but it now seems to me to be far removed from the spirit of Löwenheim's proof. In fact, I already rejected it in subsection 6.2.5.4, but I will briefly repeat the arguments against it here. First, determining a system of equalities between the numerals is a means to an end, not an end in itself. The last paragraph of the proof makes it clear that Löwenheim's objective is to construct a subdomain or, put another way, to fix the values taken by the summation indices. Second, the explanation that this reconstruction offers for the fact that Löwenheim wishes to determine the system of equalities is less reasonable than it appears. If the values of the summation indices are fixed by hypothesis, then so are the equalities between the numerals. In other words, at each level of the tree there is only one true formula and, consequently, there is no choice of options. It is inconceivable that Löwenheim was not aware of this detail. Third, in order to argue thus, one needs an understanding of the semantics of ΣIIF that Löwenheim does not possess (if he did, he would have not thought of expansions).

In accordance with my interpretation of Löwenheim's proof, in the reconstructions that follow I will not use the fact that the values of the summation indices are fixed by the hypothesis of the theorem. Leaving aside differences of presentation, there is only one way to construct a subdomain without using the assignment v, but we will also examine a number of alternatives that do not allow its construction, because our objective is not so much to offer a correct proof as to reconstruct Löwenheim's argument.

A way of stating precisely the main ideas of Löwenheim's proof is to consider all the functions from the set of numerals of P_n into D, identify the ones that determine the same system of equalities via an equivalence relation, and reproduce Löwenheim's argument for constructing a tree with the equivalence classes instead of formulas.

Let Cn be the set of numerals of P_n. I will call the functions from C_n into D partial assignments of level n. For each n > 0, we will now define a set, V_n, of partial assignments, as follows:

It is easy to see that for every n > 0, V_n . Now, for every n > 0, we can define an equivalence relation between the elements of V_n in this way:

Thus, two partial assignments of level n are related when they determine the same system of equalities. Since C_n is finite, the set of equivalence classes generated by this relation in V_n is finite (although V_n may be uncountable, if D is). The set of equivalence classes of any level ordered by the relation

class X₁ precedes class X₂ iff every function in X₂ extends a function in X₁

constitutes in essence a tree that meets all the necessary conditions for reproducing Löwenheim's argument (such as the condition that for every equivalence class level n+1 there is a unique class at level n that precedes it in the ordering just defined). Thus, to each of the satisfiable formulas of level n in Löwenheim's argument there corresponds in this reconstruction an equivalence class, and vice versa; consequently, to the sequence Q₁, Q₂, Q₃,... there corresponds a finite sequence of equivalence classes which, basically, can be determined in the same way as in Löwenheim's argument.

The problem now is that an infinite sequence of equivalence classes does not determine an assignment. In the union of all the classes of the sequence we can find partial assignments of any level, but no function in it assigns values in D to all the numerals of the sequence P₁, P₂, P₃,..., which is what we need to have in order to prove the theorem.⁴⁴ From the perspective of this reconstruction, then, we should concludethat strictly speaking Löwenheim's argument does not determine any assignments.

I do not think that this reconstruction does justice to Löwenheim's argument. It reproduces the treatment of the equality reliably enough, and also preserves the structure of the last part of the argument (something that the ones we have yet to examine fail to do), but it ignores the intuitive content of Löwenheim's proof, or at least interprets it rather ungenerously. In the following reconstruction we will try to overcome this difficulty, and then my meaning will become clear. I have a more important reason for suggesting that this reconstruction does not do Löwenheim justice, but I will mention this other reason later on, as it also affects the reconstruction I will be presenting next.

One way of approaching the intuitive idea of Löwenheim's argument is to dispense with the equivalence classes and consider the set ordered by the relation of strict inclusion, which is also a tree.⁴⁵ Since now the nodes of the tree are partial assignments, each node of level n is really a possible way of determining of the values of the numerals of P_n, which, in the case n > 1, extends (or includes) one from the previous level. The aim of the proof is to show that the tree has an infinite branch, or stated more precisely, that there exists an infinite sequence f₁, f₂,... of partial assignments such that for every n, f_n V_n and f_n f_n+1. An infinite branch thus actually fixes the values of all the numerals. As a whole, this approach is preferable to the previous one because it reflects Löwenheim's intuitions better (though from this perspective, as we will see, it still leaves something to be desired), but it distances us from his argument in one important aspect. Now, the tree has (or can have) levels with an infinite number of partial assignments, and as a consequence the argument to show that it has an infinite branch cannot be exactly the same as Löwenheim's. The argument should now be as follows: We choose an assignment of the first level with an extension at every higher level, and then concentrate on the partial assignments of the second level which have extensions at every higher level and which include the one we have chosen; we choose one of them and proceed in the same way with the third level assignments, and so on. Obviously, to choose the partial assignments we use the axiom of choice. The question is whether the conditions required for this argument to be correct are met.

The facts that we have established thus far (basically, that and that every partial assignment includes an assignment from the previous level) do not allow us to use the argument I have just outlined, or, more precisely, are not enough to prove that the tree has an infinite branch. The fact that, for every n > 0, does not even ensure that at all levels there are partial assignments that have an extension at every higher level. In addition, the existence at each level of these assignments would not allow us to assert that the tree has an infinite branch. Essentially, the problem is that a partial assignment that has extensions at any higher level might not have an extension with the same property at the next level.⁴⁶

If we could prove that every partial assignment (at whatever level)has an extension at the following level, it would be clear that the tree has an infinite branch, but unfortunately there are partial assignments without any extensions. The point is worth stressing, because this only happens when IIF has fleeing indices that do not depend on all the universally quantified variables. Let us suppose, for example, that IIF = IIijA(i, j, k_ij) and that f is a partial assignment of level n such that (S, f) satisfies P_n. The existence of a partial assignment f1 of level n+1 such that f f₁ and (S, f₁) satisfies P_n+1 is guaranteed, because we suppose that IIF is true in D, this means, stated informally, that for every a and b in D there exists k_ab such that A(a, b, k_ab) is true. The case of IIijA(i, j, k_i) is different. When we assign a value to k_a so that P_n is true we can be sure that for every element b of the subdomain constructed until that moment A(a, b, k_a) is true, but nothing ensures that the same requirements are met when new elements are added (something which may occur when we assign values to the numerals of P_n+1, that is, in the next step of the construction). We can only be sure that a partial assignment has an extension at the following level when values are assigned to the summation indices so that IIjA(a, j, k_a) is true in D. A simple example will help us to better understand the problem.

Let us suppose that and that it is interpreted as follows: D is the set of natural numbers except 1 and 0, and z_ijk signifies that the product of i and j is k. Let us assume also that v is an assignment such that

for all n D; v(k_n) is a prime number.

Since v(k_n) never is the product of two natural numbers of the domain, IIF is true under this interpretation. If we apply Löwenheim's procedure to IIF and, for the sake of simplicity, make the interpretation of IIF partially explicit, then

The partial assignment represented by

satisfies P₂ and therefore belongs to V₂, but has no extension at the next level, since P₃ has as a factor the formula which is false. In this way, if we only require that a partial assignment f of level n meets the condition that (S, f) satisfies P_n, then it is possiblethat f can not have an extension at the level n + 1.⁴⁷ This example shows that the formulas of the sequence P₁, P₂,... do not actually help us to construct a subdomain, since (6.8) does not permit us to construct the tree which interests us.

This difficulty can be solved by modifying (6.8) in such a way that only the partial assignments that have extensions in V_n+1 can belong to V_n. It is not difficult to see the intuitive idea behind this change. The partial assignments that in all probability have an extension at the next level are the ones that assign to each numeral the element assigned to the corresponding summation index by an assignment v such that (S,v) satisfies IIF.⁴⁸ Before taking into account a reconstruction that includes this modification, I would like to make a short remark about the role of numerals in Löwenheim's proof.

The aim of the second and third reconstructions has been to fix the values that the numerals take, but this is not what Löwenheim in fact aims to do; he seeks to determine the values taken by the summation indices. Since we suppose that numerals and summation indices take the same values, there is nothing wrong in regarding the two aims as the same (and I have done so on a number of occasions), but the truth is that an identification of this type is foreign to Löwenheim. Numerals perform a role that is assimilable in many aspects to the role of our individual constants, but Löwenheim does not think of them as symbols of the language whose interpretation must be fixed (i.e., as we think of constants). The relation that exists between a summation index and the corresponding numeral is more similar to the relation between the term of the formal language k_a and the variable n in the expression: let us suppose that the term k_a takes the value n. If it were not for the problem posed by the interpretation of the equality symbol, a numeral would stand for a completely determinate value of the corresponding summation index. Thus, considering numerals as individual constants whose value we have to fix is an unnecessary complication and, above all, totally alien to the spirit of Löwenheim's proof.

The following reconstruction consists basically in constructing a tree whose nodes are partial assignments that assign values to the summation indices instead of to the numerals. As I have just noted, in this way we not only manage to simplify the argument, but come closer to the intuitive content of the aspect of Löwenheim's proof that we are concerned with. The negative side is that we move away from the way in which he expresses it, since the numerals (and hence the formulas in which they occur) do not intervene in the reconstructed argument. Ideally, we would not have to make this choice, but in fact there is no way around it, for the simple reason that Löwenheim does not express his ideas correctly (for which he should be forgiven, as he lacks the resources that would allow him to express them better).

Let V₀ be the set of all the functions that assign elements of D to the constant indices of IIF in such a way that IIF is true under the “interpretations” formed by S and each one of these functions. Stated more rigorously, if J is the set of constant indices of IIF; the elements of V₀ are those of the form v J (the restriction of v to the set J), where v is an assignment such that (S, v) satisfies IIF. We will call functions in V₀ “partial assignments of level zero.” Each subset of D determines a set of terms: the set of the indices generated by the fleeing indices of IIF when the universally quantified variables range over (canonical names of) the elements of the subset. If g is a partial assignment, by G_ran(g) I refer to the set of indices generated by the range of g. As I explained at the end of subsection 6.2.5.4, if IIF is not satisfiable in any finite domain, then no partial assignment will assign values to all the indices generated by its range. Each partial assignment of any level greater than 0 fixes appropriately the values taken by all the indices generated by the range of one of the partial assignments of the previous level. The set of partial assignments of level n + 1, V_n+1, is then recursively defined by

The set of all the partial assignments ordered by the inclusion relation constitutes is a tree. Now, every partial assignment g has at least one extension at the next level, since g is the restriction of some assignment v such that (S, v) satisfies IIF and v assigns values to all the indices generated by the range of g. The selection of an infinite branch of the three (i.e., of a sequence f₀, f₁, f₂,... of partial assignments such that for every and ) is a trivial application of the axiom of choice: we choose a partial assignment of level zero and at each of the following levels we choose an assignment that already includes the one we chose at the previous level. The union, f, of all the partial assignments of the sequence is a function whose range, D₀, is a denumerable subdomain of D (assuming that IIF is not satisfiable in any finite domain) and whose domain is the set of all the indices generated by the fleeing indices of IIF in D₀. If S₀ is the restriction of S to D₀, it is evident that the interpretation (S₀, f) satisfies IIF in D₀.⁴⁹

There is no need to insist on the differences between this reconstruction and Löwenheim's proof, as I already mentioned them beforehand. They are so patent that at first sight it seems that the two proofs are totally unrelated, but in fact they only differ in the way in which the ideas are expressed. I am convinced that this reconstruction offers a relatively faithful reflection of the intuitive content of Löwenheim's argument (at least as far as the determination of the subdomain is concerned). In this regard, I think we can assert that the above argument is essentially the one that Löwenheim offered (or, at least, the one that he wanted to offer). As a consequence, this reconstruction is the one that I prove in the appendix, under the name Löwenheim's theorem.

6.3.3 Throughout this commentary I have avoided quoting Skolem to support my interpretation, in the belief that it should stand on its own, but now that the commentary has concluded and the argument has been reconstructed I would like to show that some of Skolem's assertions indicate that he interpreted Löwenheim's proof essentially as I have just done. Before quoting Skolem, I will recapitulate several ideas that will show why it was necessary to offer another version of the proof and will make it patent that the conclusions we can reach on the basis of my reconstruction are not very different from the ones that Skolem appears to have reached.

In the logic of relatives it is not possible to characterize accurately the concept of fleeing index. All we can say about them is that they have the capacity to generate indices that, like any non-fleeing index, stand for elements of the domain. The only possible way of explaining the meaning of the formulas with fleeing indices is with the help of expansions. Given this situation, it is only natural that it should have been expansions that suggested to Löwenheim a way of approaching the problem of constructing a subdomain, and that Skolem should say that the proof was based on developments of infinite sums and products. Probably, Skolem thought that the arguments based on fleeing indices were not only unnecessarily complicated (the only problem with Löwenheim's argument that he mentions), but also rather imprecise and, as a consequence, he considered it necessary (or, at leastconvenient) to offer a proof in which these indices played no part.

Judging from my reconstruction it is clear that, as far as the assignment of the values to the summation indices is concerned, Löwenheim proceeded essentially as if instead of the fleeing indices the formula had the corresponding existential quantifiers (which indeed is the most natural way to conceive the problem of fixing the values taken by the summation indices when no sharp distinction can be made between the semantics of and the semantics of IIF). Now, considered from this point of view, the use of fleeing indices is of little interest. The advantage that they offer lies in their ability to generate terms when their subindices take values; we can therefore dispense (at least in this proof) with the existential quantifiers, and the construction of the sequence of formulas becomes simpler. The problem is that in Löwenheim's proof we cannot take advantage of this special ability that the fleeing indices possess. For Löwenheim, the process of constructing the sequence Q₁, Q₂, Q₃,... in a way represents the process of constructing a subdomain. Naturally, this form of representing the construction of a subdomain is imprecise and, strictly speaking, incorrect, but when the fleeing indices depend on all the universally quantified variables the construction of the sequence P₁, P₂, P₃,... bears a certain resemblance to the construction of a subdomain. In addition, Löwenheim realizes that to be able to assert that the values taken by the summation indices have been fixed one needs to do more than simply construct that sequence (whether or not he solved the problem is another matter). However, when the fleeing indices do not depend on all the universally quantified variables, the formulas of the sequence do not represent at all the construction of the subdomain, since to take the values of the summation indices in such a way that P_n is true (for each n) will not suffice for the proof to be correct.⁵⁰ As we cannot use the formulas of the sequence in this way, the advantage of using fleeing indices is lost, and they become an unnecessary complication, since Löwenheim reasons in practice as if the existential quantifiers were present. An example will suffice to understand thisidea. Let us suppose that IIijA(i, j, k_ij) and ) are true in a domain, when i takes the value a and j the value b. Löwenheim considers that kij generates the term k_ab; he does not assume that the value of kab is fixed (since the problem of the proof is to determine the values of the summation indices); what he actually supposes is that k_ab denotes an element that can be chosen in such a way that A(a, b, k_ab) is true. In the case of the formula ), we say that A(a, b, k) is true, for some values of k; thus we can choose one of these values, assign it to k, and refer to it as k_ab. In summary, if the starting formula were in prenex form with each existential quantifier within the scope of all the universal quantifiers, we could proceed in the same way as Löwenheim does (and even preserve the notation), with the advantage that the argument would be simpler, because then we could dispense with the fleeing indices. In essence, this is precisely how Skolem avoided using fleeing indices.

Skolem's first proof of Löwenheim's theorem is in his [1920]. At the beginning of this paper (Skolem [1920], pp. 103 (254)), Skolem asserts explicitly that his aim is to present a simpler proof without the use of fleeing indices. He then defines a notion of normal form suitable for his purpose. This normal form, today known as the Skolem normal form for satisfiability, is just the one I have described above: a formula is in this new normal form if it is in prenex form and the universal quantifiers precede the existential ones. Skolem then shows that the subdomain version of the theorem can be proven without loss of generality for formulas in normal form for satisfiability.⁵¹

After stating the main theorem Skolem immediately says:

It would be extremely easy to prove this theorem in Löwenheim's way, but without the use of symbols for individuals as subindices. However, I would rather carry out the proof in another way, one in which we do not reason with successive choices but proceed more directly according to the customary methods of mathematical logic.*

*[[Footnote by Skolem]] For the more general theorems that appear later in this section I shall carry out the proofs in a way closer to Löwenheim's. (Skolem [1920], pp. 106– 107 (256); the boldface is mine, the italics are Skolem's)

It would be difficult to understand the beginning of the quotation if Skolem had not interpreted Löwenheim's proof in accordance with my reconstruction. The reference to successive choices may be misleading. Skolem means that if, for example, the starting formula is ), he will begin by supposing that for every a we can choose a unique j(a) (his notation) such that A(a, j(a)) is true. The alternative is to construct a sequence of formulas, as Löwenheim does—namely P₁, P₂,...—and then consider all the possible forms of determining the numerals that occur in them.⁵² This is the schema of the proof which, according to Skolem, Löwenheim had presented. The first generalization that Skolem proves (the only one that interests us, as the others are practically corollaries of this one) consists in showing that the theorem also holds for infinite sets of formulas. Basically, Skolem proves his generalization in the same way as the theorem (i.e., reasoning “directly”), but with the difference that in this case he introduces numerals and constructs a sequence of formulas much as Löwenheim had done. So Skolem cannot say that the proof is the same as Löwenheim's, but he can say that it is rather closer, since it also constructs a sequence of formulas.

As we can see, the structure that Skolem attributes to Löwenheim's proof (without saying so explicitly) is that of our third reconstruction (the one that drew our attention to the difficulty posed by reasoning with formulas), and the intuitive idea of the argument is the same as the idea of the reconstruction that we finally selected. I think that these details show that in essence my interpretation of Löwenheim's proof coincides with Skolem's.

6.3.4 The reconstruction that I present is faithful to what Löwenheim wants to express, though not to the way in which he expresses it. His main purpose is to show that, if IIF is true in a domain, then it is possible to assign values to the summation indices so that it remains true in a numerable subdomain. The problem is that the process that Löwenheim seeks to describe (the construction of a subdomain) cannot be described as he does. This explains why the sequence P₁, P₂,... does not really play a role in my reconstruction, in spite of being an important aspect of Löwenheim's proof. However, the construction of a subdomain is not the only aim of his proof.

When Löwenheim explains the construction of the sequence P₁, P₂,... , he does so without assuming that IIF is satisfiable. As we saw in subsection 6.2.4.4, the scheme of his argument is the following: We construct P₁, we verify whether P₁ vanishes or not; if it vanishes, we have finished: IIF is not satisfiable; if it does not vanish, we construct P₂ and verify whether it is satisfiable or not; if it vanishes we have finished: IIF is not satisfiable; and so on. Thus, the procedure for constructing the sequence P₁, P₂,... has a double objective: if IIF is not satisfiable, we will prove this in a finite number of steps; if IIF is true in some domain, this sequence allows us to show that IIF is true in a numerable subdomain.

The way in which Löwenheim would decide whether a formula vanishes or not is of little importance for the analysis of the proof, but this aspect deserves a short remark. In order to check whether any P_n vanishes (identically) or not, Löwenheim introduces in P_n all the possible equalities between the terms of P_n. If all the resulting formulas vanish, then P_n vanishes. Löwenheim does not explain how to decide whether or not these formulas vanish, because he thinks it is a trivial matter. The formulas obtained from any P_n by means of this procedure are essentially propositional formulas (since the identity symbol and the quantifiers do not occur in them) and the method to decide whether or not a propositional formula vanishes was well known at that time. Probably, Löwenheim would first apply laws in order to simplify the formula and then, if necessary, would argue in terms of truth values. We can say that in a sense Löwenheim possesses an informal procedure for showing that any quantifier-free formula of a first-order language with identity vanishes: first, he takes into account all the possible equalities between the terms of the formula in the way explained in the proof, and then, by applying propositional methods, he checks whether all of the resulting formulas vanish. This procedure, together with the one used in order to construct the sequence P₁, P₂,..., can be seen as an informal way of showing that a formula in normal form vanishes. An additional definition is also necessary: if IIF is a formula in normal form and P₁, P₂,... the associated sequence, then IIF vanishes if and only if there exists n such that Pnvanishes. Löwenheim is not interested in this procedure, but it seems clear to me that it is not alien to his proof.⁵³

When we see Löwenheim's proof from the point of view of the informal procedure just described, we distinguish between saying that a formula is not satisfiable and saying that the same formula does not vanish under the informal procedure. The lemmas I am going to state are completely alien to Löwenheim because he does not make this distinction, but they are worth taking into account.

With the help of this distinction, Lemma 6.6 can be restated in this way:

Lemma 6.7 If IIF vanishes under the informal procedure, then IIF is not satisfiable.

Now, this lemma asserts the correctness of the informal procedure with respect to nonsatisfiability.

The reciprocal of Lemma 6.6 is

Lemma 6.8 If for every n, P_n is satisfiable, then IIF is satisfiable.

Assuming that Löwenheim's proof is correct, did he prove this lemma? The answer to this question will depend on the reading of last part of the proof. I have maintained that Löwenheim claims that the formulas of the sequence Q₁, Q₂,... are true under the solution whose existence guarantees the hypothesis of theorem and, accordingly, I maintain that he did not prove Lemma 6.8. If we think, as van Heijenoort does, that Löwenheim is merely claiming that the formulas of the sequence Q₁, Q₂,... are satisfiable, then we are reading Löwenheim's argument as a proof of Lemma 6.8. In summary, if we think that Löwenheim proved the weak version of the theorem, we are accepting that he proved (or sought to prove) Lemma 6.8.

If we introduce the distinction between vanishing under the informal procedure and being nonsatisfiable in the reciprocal of Lemma 6.8, we obtain

Lemma 6.9 If IIF is not satisfiable, then IIF vanishes under the informal procedure.

This lemma asserts the completeness of the informal procedure with respect to nonsatisfiability. In my opinion, this lemma is alien to Löwenheim, not only because he lacks the necessary distinctions to state it, but also because he does not prove Lemma 6.8.

Gödel asserted on several occasions that the completeness theorem for first-order logic had been proved implicitly by Skolem in [1922], although he had not read Skolem's paper when he proved the theorem. ⁵⁴ Gödel refers to the proof of the weak version of Löwenheim's theorem that Skolem proved for the first time in 1922 for a first-order language without identity. Assuming that A is any first-order formula without equality and is a formula logically equivalent to A in normal form for satisfiability, Skolem proceeds as follows: (1) he constructs a sequence of formulas which is, in essence, Löwenheim's sequence P1, P2,..., (2) he defines a linear ordering on the set Sn of (partial) solutions that satisfy and (3) after observing that the extension relation on is an infinite tree whose levels are finite, he fixes an infinite branch of this tree; this branch determinesan interpretation that satisfies A in the set of natural numbers.

As we see, the core of Skolem's argument is the proof of

Lemma 6.10 If for every n, P_n is satisfiable, then is satisfiable.

What Gödel means is that, when the appropriate distinctions are introduced, this lemma states the completeness of the informal refutation procedure employed by Skolem in his proof.

Löwenheim normal form is very different from Skolem normal form for satisfiability, but we have seen (subsection 6.3.3) that Löwenheim does not take advantage of the fleeing indices and that he reasons in practice as if the universal quantifiers preceded the existential ones. Thus, there is no essential difference between the proof of Lemma 6.8 and that of Lemma 6.10. In fact, Skolem's proof of this lemma is the one that, according to the traditional reconstructions, Löwenheim set out to offer. So, if one accepts that Löwenheim proved the weak version of the theorem, then, assuming that his proof of Lemma 6.8 is correct, one should accept that Gödel's remark applies to Löwenheim as well (at least when the completeness theorem is restricted to formulas in normal form). This aspect of Löwenheim's proof is never mentioned by commentators who hold that he proved the weak version.

Löwenheim's argument bears some similarities to Skolem's proof in [1922], but the degree of similarity depends on how we interpret what Löwenheim did. If we see him as proving the weak version of the theorem, then the arguments differ in the normal form used to construct the sequence P₁, P₂,..., but they have a common core: the proof of Lemma 6.8 (which in Löwenheim's case has some gaps). However, if Löwenheim was attempting to prove the subdomain version, the arguments are very different: each one uses a distinct notion of normal form, fleeing indices do not intervene in Skolem's proof, and, more important, the trees constructed in each case have different purposes and involve different objects (in Löwenheim's proof the nodes represent partial assignments of values to the summation indices, while in Skolem's the nodes are partial solutions; as a consequence, Skolem, but not Löwenheim, proved Lemma 6.8).

Skolem did not relate his [1922] proof to Löwenheim's. This is only surprising if we make the traditional reading of Löwenheim's argument, but if he argued in the way that I propose, Skolem had no reason for relating the two proofs. So, this detail confirms that Skolem did not see in Löwenheim's argument a proof of the weak version of the theorem, and supports my interpretation of it.

¹I state the theorems for sentences instead of formulas in order to avoid assignments as far as possible, but Löwenheim's proof does not depend on this detail.

²The fact that Skolem distinguishes between the two does not mean that he states the strong version accurately. As we will see in the following quotation, he simply notes that the interpretation of the relational symbols is the same in the subdomain as in the domain in which the formula is assumed to be satisfiable.

³Van Heijenoort does not seem to feel that this attribution is important, because he does not mention it in his commentary on Skolem [1920] (From Frege, p. 253), in which he explains that in [1938] Skolem compares different proofs of the two versions. Vaught, [1974], p. 157, in contrast, takes it more seriously, and is surprised that Skolem attributes the subdomain version to Löwenheim.

⁴He probably intended not only to simplify the proof, but also to make it rather more rigorous. Skolem thought that Löwenheim's proof was based on developmentsof sums and products (i.e., on expansions of formulas), and I do not think that from this perspective Löwenheim's argument struck him as being completely rigorous (although he did not doubt its correctness).

⁵Herbrand [1968], pp. 28, 143, and 144. As van Heijenoort notes ([1982], pp. 67–68), Herbrand must have thought not only that it was necessary to define the semantic notions, but also that they should be dispensed with, but this is another problem.

⁶From Frege, p. 231. He also criticizes him (unjustly, in my opinion) for using formulas of infinite length instead of applying the axiom of choice, but this aspect seems to be linked more to the proof's precision than with its correctness.

⁷In fact, Largeault's commentary on Löwenheim's theorem ([1972], pp. 111– 115) follows closely that of van Heijenoort in From Frege without contributing new ideas. In what follows, I will not take it into account.

⁸Since I only had access to Brady [2000] when this book was already going to the press, I don't discuss her views in any detail. Nevertheless, her reconstruction of the proof agrees in the essentials with that of Wang (as she herself observes, p. 193), which is taken into account in this book.

⁹“ Über Möglichkeiten,” pp. 453 and 454 (238). The second equation in the quotation is the result of removing the existential quantifiers (Σl and k_i) in the normal form of the equation that Löwenheim uses as example.

¹⁰This may explain why Skolem related the use of fleeing indices in Löwenheim's proof with expansions of formulas (see subsection 3.3.5 in chapter 3). The truth value of a formula with fleeing indices depends on terms (those generated by its fleeing indices) that do not occur in the formula itself, but in its expansion in the domain. Without a conceptual apparatus which allows a different perspective on Löwenheim's arguments, it is only natural that they should be interpreted in terms of expansions.

¹¹For example, in [1970], p. 27, Wang understands that Löwenheim is thinking of natural numbers. In From Frege (p. 231), van Heijenoort claims: “If IIF contains individual constants or free variables, an initial domain [...] is assumed to consist of individuals corresponding to them.”

¹²The first two quotes are from the part we are currently discussing (one at the beginning, and the other at the end); the other two are from the following part. The italics are mine.

In order to understand the relation between (d) and the other three quotations, we should clear up one point. As we will see later, (c) and (d) refer to the same transformation (one on P₁ and the other on P₂); in addition, among what are called “indices” in P₂ we find 1, 2,..., n1, called “elements” in (c).

¹³The traditional analysis does not go into such depth; but recall that in order to prove the weak version traditionally attributed to Löwenheim we need to construct a domain (and a solution in it), which need not bear any relation to the one in which the formula by hypothesis is satisfied.

¹⁴In [1988], p. 122, Moore does not analyze Löwenheim's proof, but he grasps this idea in a short remark about the theorem:

he regarded this formula [[]] (for the given domain M) as expandable to an infinitary formula with a first-order existential quantifier for each individual of M.

(In essence, is Löwenheim's ΣIIF and M is the infinite domain in which, according the hypothesis of the theorem, ΣIIF is satisfied.)

¹⁵Strictly, we may only speak of factors when each numeral denotes a different element in the domain, and in this case the numerals that replace the various indices can stand for the same element. This detail does not detract from my argument, first because only distinguishing sharply between syntax and semantics could the construction of P₁ be described in a different way, and second because it is still true that Löwenheim would not use the term “factor” in this context if he were not thinking of elements in a given domain. Indeed, Löwenheim is aware of this difficulty (his objective is to be able to claim, by the end of the proof, that each numeral denotes a different element).

¹⁶It may be that Löwenheim is referring to domains which, like the set of natural numbers or the set of indices (I cannot see any other alternatives in this case), could be considered as given in some sense. As I said above, Wang states that Löwenheim constructs an interpretation of IIF in the set of natural numbers, but it is obvious that in this case the numerals do not denote numbers. I do not know of anyone who has thought that the domain Löwenheim speaks of is the set of indices, and indeed this interpretation is so unlikely that it is hardly worth mentioning. I will give two reasons for rejecting it nonetheless. First, the domains that we could call “syntactic” were totally inconceivable in Löwenheim's time; further, as I explained in sections 5.1 and 5.3 of the previous chapter, Löwenheim lacked the distinctions necessary to use the set of indices as a domain. Second, if the indices were elements of the domain, there would be no point in Löwenheim's taking into consideration the possible equalities and inequalities between them, since considered as elements of a set they are all different. We will see this in the following section.

Of course, once we understand the idea of the proof, none of the above prevents us from reconstructing it taking natural numbers or the set of indices as our domain.

¹⁷Numerals are inserted in order to avoid subindices. For example, the fleeing index k_i generates the index k₁ when i takes the value 1, but as this procedure must be repeated, and we do not want to write k_k1 , we must give k₁ a name. The numerals thus figure in the place of indices that stand for elements of the domain in which IIF is interpreted, and therefore automatically acquire this characteristic.

¹⁸[[The k_m should be k_lm. This erratum is in the German version and it ispreserved in the English version.]]

¹⁹The progressive procedure that Löwenheim follows in order to construct sequence P₁, P₂,... was used by Herbrand in the proof of the theorem that today bears his name.

²⁰Observe that P₁, P₂,... cannot in the strict sense be considered expansionsin a domain.

²¹There is an erratum in the English version: appears as a factorof P₂ in place of .

²²The above diagram represents the ordering relation implicitly defined. As we will see in the following section, Löwenheim asserts that every formula of a given level contains as a factor another from the previous level. If we interpret Löwenheim's statement literally, the relation on which his argument is based is not exactly the same as mine. It is easy to see that a formula can contain as a factor more than one formula from the previous level and therefore may have more than one immediate predecessor. In any case, this detail is of no importance.

²³A tree is a partially ordered set such that for every x T the set P_x = {y T | y < x} of strict predecessors of x is well-ordered by < (i.e., every nonempty subset of P_x has a least member). A chain in a tree is a linearly ordered subset of T. A chain is maximal, or is a branch, if for no x T — A is a chain.

²⁴Literally, Löwenheim says:

IIF will certainly vanish identically in every domain if P₁ does,which is equivalent to my statement. Perhaps by adding “in every domain” Löwenheim intends to stress the fact that IIF can vanish in domains in which P₁ does not.

²⁵Indeed, he refers to them in the same way. For example, in the second paragraph of the quote, he uses P₂ to refer to the second level formula corresponding to A(1,k₁,h₁), and in the third paragraph he uses it to refer to the formula that results from introducing the constants.

²⁶Löwenheim himself states the theorem in this way when he applies it to calculus of classes and in the proof of the Theorem 3 (“ Über Möglichkeiten,” p. 458 and 459 (242 and 243)). Moreover, I do not believe that it is a coincidence that Skolem frequently adopted this type of statement. For instance, in [1920], p. 106 (256), Skolem states the theorem as follows:

Every proposition in normal form [[sensu Skolem]] either is a contradiction [[Widerspruch]] or is already satisfiable in a finite or denumerably infinite domain.

²⁷On p. 458 (242) Löwenheim says that if a first-order equation is not identically satisfied, his theorem allows the construction of a counterexample in a finite or denumerable domain. I think that the word “counterexample” in this case could be interpreted either as being a domain or as including both a domain and a solution in it.

²⁸As we will see in the next section, this is the interpretation implicitly adopted by Wang, since in his opinion Löwenheim argues thinking of solutions rather than elements.

²⁹In theory, it could be that Löwenheim were thinking of constructing the solution later on, but here this is impossible. As I said, Löwenheim has constructed a tree, and the point under discussion is whether he believes that this construction allows the determination of a domain and a solution, or only of a domain. There are no other constructions to appeal to, because in order to conclude the proof it only remains to determine a branch of the tree.

³⁰See, for instance, “ Über Möglichkeiten,” p. 469 (251) and, less explicitly, p.462 (245).

³¹Depending on the interpretation we adopt, we will say that the elements belong to the domain on which IIF is interpreted, or simply that the constants denote different objects, but at present this detail is of no importance.

³²Recall that P_r+1 is constructed as an extension of P_r. Observe also that, in Löwenheim's terms, a level r + 1 formula can contain as factors more than one formula from the previous level, though it will only be an extension of one of them. For example, we have seen that if IIF = IIiA(i, h_i, k_i), then

P₁ = A(1, 2, 3),

P₂ = A(1, 2, 3) · A(2, 4, 5) · A(3, 6, 7).

One of the formulas obtained from P2 is

A(1, 1, 3) · A(1, 1, 1) · A(3, 3, 3),

which has as factors the level 1 formulas A(1, 1, 1) and A(1, 1, 3), but is only an extension of the latter.

³³Note that strictly speaking the equality

Q₁Q₂Q₃ ... = 1

cannot be interpreted as “the infinite product Q₁ · Q₂ · Q₃ ·... takes the value 1,” because the product Q₁ · Q₂ · Q₃ · ... contravenes Löwenheim's stipulation on language. (Recall in addition that in 1911 he had warned that the rules of calculation for infinite sums and products had not yet been proved.) To do justice to Löwenheim, we must consider the equality above as an abbreviated way of saying: for every n, Q_n = 1. Accordingly,

IIF = Q₁Q₂Q₃ ...

cannot be read as “IIF takes the same value as the product Q₁ ·Q₂ ·Q₃ · ...,” but as “IIF = 1 iff for every n, Q_n = 1:”

³⁴It could also be said that Löwenheim does not distinguish clearly between saying that a formula is true and saying that it does not vanish, but this would be going too far, and indeed I do not know of anyone who accuses him of confusing the concept of satisfiability with that of truth. If Löwenheim had been confused on this point he would not have proved the theorem.

³⁵From Frege, p. 231. As I have said, in [1982], p. 67, van Heijenoort is more cautious than in From Frege and warns that Löwenheim's text does not allow us to say whether “he passes unjustifiably from the finite to the infinite, or whether he has a real argument in mind.”

³⁶Recall that a solution interprets the identity as such.

³⁷Van Heijenoort says (From Frege, p. 240, note 4) that the summation indices are the ones quantified existentially in ΣIIF and adds “in fact, they are the free variables of IIF.” This assertion is slightly ambiguous. In ΣIIF both individual variables and fleeing indices occur existentially quantified. These last quantifiers can be seen (with the clarifications I have presented) as a string of existential quantifiers each one of which has the form Σk_a1..._an, where k_a1..._an is an index generated by the fleeing indices in the domain under consideration. Thus, the summation indices are not just the constant indices of IIF, but all the ones that generate their fleeing indices. Furthermore, if the summation indices were only the constant indices, Löwenheim's assertion would not make sense.

³⁸Essentially, this is how van Heijenoort interprets the proof: as an argument that aims to determine a system of equalities. In [1970], p. 29, Wang seems to reply to van Heijenoort when he says:

The alternative interpretation of accusing him of using one fixed assignment for all except those atomic formulas containing the equality sign seems to me to involve too many difficulties.

On this point I agree with van Heijenoort's interpretation. The fundamental difference is that, as I have said, he believes that Löwenheim aims to determine a solution, and therefore he finds the argument unsatisfactory. In my opinion, Löwenheim is only concerned with the problem of determining the values of the coefficients of (and ) because he is assuming that the values of the other coefficients (the nonlogical coefficients of the formula) are determined by the hypothesis of the theorem. Wang's comment would be right if Löwenheim sought to prove the subdomain version, as both he and van Heijenoort think.

³⁹It is not surprising that Löwenheim should think of this type of problem in terms of expansions (the fact that he considers incorrect to use them in the proof is a different matter). As explained in chapter 3, Löwenheim does not have the conceptual apparatus needed to accurately state the semantics of formulas with fleeing indices and, therefore, he can not make a complete abstraction of the examples that support his intuitions.

⁴⁰Depending on the requirements of the argument, this set of numerals may not represent all subdomains of three elements, but only those that meet certain conditions. For example, {1, 2, 3} could represent only the subdomains of D in which (6.3) is true (under a given solution).

⁴¹I do not think that this detail suggests that Löwenheim treated fleeing indices as terms of a functional character. Löwenheim put no limitation on the systems of equalities and, in all likelihood, he did not see that these unforeseen factors might occur. There is nothing particularly noteworthy about this. When the construction is exemplified for a specific formula and when those constructed from it (P₁, P₂, etc.) are simplified as much as possible, the general form taken by the developments of IIF cannot be appreciated, and so it is highly likely that these unforeseen factors would pass completely unnoticed.

⁴²If one of the formulas in the branch had one of the factors that I called “unforeseen,” the product could not be seen as an expansion. However, it would still be true that it contains all the factors of an expansion, and this ensures that if the product takes the value 1, IIF takes the value 1 (which is the basis of the argument).

⁴³The partial assignments are not assignments, since they do not assign values to all the terms of the language and therefore the use of the notation “(S, f)” is not particularly rigorous, but it does not raise any difficulties. All we need to know in order to decide whether P_n is true or false is, apart from the solution, the elements that are assigned to the constants of P_n; this is the information that the partial assignments provide.

⁴⁴Observe that taking a partial assignment as representative of its class and considering that it is these assignments that form the levels would not allow usto determine an assignment of values to all the numerals either. Even inside the same equivalence class, some partial assignments would be expected to have an infinite number of extensions, and others not. Given that we only know which partial assignments have an infinite number of extensions once the construction is finished, it may be that none of the assignments chosen as representatives have an infinite number of extensions (even though others in the same class might have them) and in this case we would reach a level at which none of the partial assignments admits an extension of a higher level.

⁴⁵To be more faithful to Löwenheim's argument we should consider the set of all the partial assignments, but as we are only interested in the ones that belong to V_n (for some n > 0) and this detail is of little importance, I will ignore it. From here on, whenever I speak of partial assignments it should be understood that I mean the functions that belong to some V_n (and not any assignments of elements of D to the numerals of some C_n).

⁴⁶The following schema represents a situation of this type:

We can see that f has successors (extensions, in our case) in any level, but none of its successors has this property. Thus, a tree may have at each level an assignment that branches in the same way as f but have no infinite branches. (Naturally, we know that in fact in our case this is not so, and the tree has an infinite branch, but the question is how to prove it preserving the structure of Löwenheim's argument; it would not make sense to show it by arguing here in the way we did in the first reconstruction, for example.)

⁴⁷This problem does not affect Lemma 6.6 (if IIF is satisfiable, then for every n, Pn is satisfiable).

⁴⁸Observe that the partial assignment of the previous example does not meet this requirement and that it can be stated without referring to the formulas of the sequence P₁, P₂,....

⁴⁹It is not difficult to prove now that if IIF is satisfiable, then for every n, P_n is satisfiable: the function h that assigns to each numeral the value that the function f assigns to the corresponding summation index is such that (S, h) satisfies P_n for every n.

⁵⁰Most probably, Löwenheim was not aware of this difficulty, but there is no way of knowing, because he might also have thought that the summation indices took, in a manner of speaking, the correct value. In any case, he should have pointed out this limitation of the use of formulas (even if he had gone on using them due to the lack of any other way to express the idea of the construction); since he does not, we can only conclude that it is an important gap in his argument.

We cannot know whether Skolem saw this gap. It may be that he did not realize it, but perhaps he simply omits to mention it, so as not to detract from Löwenheim's achievement.

⁵¹Incidentally, Skolem does not properly state the lemma (his Theorem 1). He wishes to show that the subdomain version of Löwenheim's theorem can be proven without loss of generality for formulas in normal form. Assuming that A is any sentence and B its normal form, the lemma that Skolem states is

A is satisfiable in any domain D, iff B is.

However, what he actually proves is

for every domain D and every solution S in D, S satisfies A iff there exists a solution in D such that and S agree on the relative coefficients that occur in A and satisfies B.

This proposition (but not the first) shows that the theorem can be proven only for formulas in normal form.

⁵²Of course, the axiom of choice is used in both cases, but there is a difference in the structure of the argument, which Skolem wants to stress.

⁵³This procedure is essentially the same as the one Quine calls “a method of proving inconsistency by functional normal forms” (see Quine [1955] and Quine [1972], pp. 185 ff.). If the existential quantifiers of a formula in Löwenheim's normal form are removed, we obtain a formula in what Quine denominates functional normal form. Quine, though, associates the method not with Löwenheim but with Skolem (who also used the method).

⁵⁴On 7 October 1963 Gödel wrote to van Heijenoort:

As far as Skolem's paper is concerned, I think I first read it about the time when I published my completeness paper. That I did not quote it must be due to the fact that either the quotations were taken over from my dissertation or that I did not see the paper before the publication of my work. At any rate I am practically sure that I did not know it when I wrote my dissertation. Otherwise I would have quoted it, since it is much closer to my work than the paper of 1920, which I did quote. (Dreben and van Heijenoort [1986], p. 51)

On 14 August 1964 Gödel wrote to van Heijenoort:

As for Skolem, what he could justly claim, but apparently does not claim, is that, in his 1922 paper, he implicitly proved: “Either A is provable or ¬A is satisfiable” (“provable” taken in an informal sense). However, since he did not clearly formulate this result (nor, apparently, had he made it clear to himself), it seems to have remained completely unknown, as follows from the fact that Hilbert and Ackermann in 1928 do not mention it in connection with their completeness problem. (Dreben and van Heijenoort [1986], p. 52)

On 7 December 1967 Gödel wrote to Wang:

The completeness theorem, mathematically, is indeed an almost trivial consequence of Skolem 1922. However, the fact is that, at that time, nobody (including Skolem himself) drew this conclusion (neither from Skolem 1922 nor, as I did, from similar considerations of his own). (Wang [1974], p. 8)