Chapter One
Algebra of Classes and Propositional Calculus
1.1.1 George Boole (1815–1864) is justly considered the founder of mathematical logic in the sense that he was the first to develop logic using mathematical techniques. Leibniz (1646–1716) had been aware of this possibility, and De Morgan (1806–1878) worked in the same direction, but Boole was the first to present logic as a mathematical theory, which he developed following the algebraic model. His most important contributions are found in The mathematical analysis of logic [1847], his first work on logic, and An investigation of the laws of thought [1854], which contains the fullest presentation of his ideas on the subject. In what follows I will focus solely on the latter work, to which I will refer as Laws.1
Boole's aim is to examine the fundamental laws (i.e., the most basic truths from which all the other laws are deduced) of the mental processes that underlie reasoning. Boole does not challenge the validity of the basic laws of traditional logic, but he is convinced that they are reducible to other more basic laws of a mathematical nature; it is these basic laws that he sets out to find.
In Boole's opinion, the mental processes that underlie reasoning are made manifest in the way in which we use signs. Algebra and natural language are systems of signs, and so the study of the laws that the signs of these systems meet should allow us to arrive at the laws of reasoning. The question of whether or not two different systems of signs obey the same laws can only be answered a posteriori. Applied to natural language—the commonest system of signs—Boole's idea implies that the laws by means of which certain terms combine to form statements or other more complex terms are the same as those observed by the mental processes that these combinations reveal. Thus, Boole believes that it is possible to establish a theory of reasoning by examining the laws by means of which the terms and statements of language are combined.
Boole classifies the propositions of interest to logic into primary and secondary (Laws, pp. 53 and 160). Primary propositions are the ones that express a relation between things. Secondary propositions express relations between propositions, or judgments on the truth or falsity of a proposition. For example, “men are mortal” is a primary proposition (because it expresses a relation between men and mortal beings), but “it is true that men are mortal” is secondary. Propositions that result from combining propositions with the aid of connectives are also secondary. Boole begins his study of the laws of reasoning with the analysis of primary propositions and of the reasonings in which they alone intervene.
1.1.2 According to Boole (Laws, p. 27), in order to formulate the laws of reasoning, the following signs or symbols are sufficient:
(a) literal signs: x, y, z, ...;
(b) signs of operations of the mind: ×, +, and —;
(c) the sign of identity: =.
This claim, however, does not have the meaning it would have today. As we will see, Boole uses other signs and operations as well to present and develop his theory.
A literal symbol represents “the class of individuals to which a particular name or description is applicable.”2Strictly speaking, literal signs stand for classes, but Boole frequently speaks (the definition of product that I will quote later on is an example of this) as if they denoted expressions of the natural language that determine classes (nouns, adjectives, descriptions or even proper names). The reason for this ambiguity is that both literal signs and expressions determining classes are signs of the same conceptions of the mind. For example, the use of the word “tree” indicates that we have performed a mental operation that consists of selecting a class (the class of all trees) that we represent by that word. Now, since the same class can also be represented by a literal sign, Boole sees no substantial difference between saying that x stands for the class of trees and saying that it stands for the word “tree.”
Boole defines the product in the following way: “by the combination xy shall be represented that class of things to which the names ordescriptions represented by x and y are simultaneously applicable.”3 For example, if x stands for “white” and y for “horse,” xy stands for “white horse” or for the class of white horses.
If x and y represent classes that do not have elements in common, x + y represents the class resulting from adding the elements of x to those of y (Laws, pp. 32–33). The sum corresponds to the mental operation of aggregating two disjoint classes into a whole. This operation is performed when we combine two terms by means of “and” as in “men and women,” or by “or” as in “rational or irrational.” Boole argues for the restriction of the sum to disjoint classes by stating that the rigorous use of these particles presupposes that the terms are mutually exclusive, but, as Jevons observed, Boole himself on occasion analyzes examples with disjunctions whose terms do not exclude each other.4
It has been said on occasion that Boole interprets the sum x + y as an excluding disjunction, but, as Corcoran notes, this assertion is incorrect.5 It is important to distinguish between the definition of sum that Boole adopts and the following one: x + y is the class of objects that belong either to x or to y (but not to x and to y). If Boole had adopted this definition (i.e., if he really had defined the sum as an excluding disjunction), then the sum x+y would be meaningful both if x and y have elements in common and if they do not. However, with Boole's definition, x + y lacks logical significance when x and y have elements in common. In short, Boole's sum is the usual union, but defined only for disjoint classes.
The difference is the inverse operation of the sum, and it consists of separating a part from a totality. Thus, Boole says, if class y is a part of class x, x—y is the class of things that are elements of x and not of y. This mental operation is the one that is expressed by the word “except” when it occurs in expressions such as, for example,“politicians except for conservatives.”
The only sign that allows us to form statements is the sign of identity. The equality x = y means that the classes x and y have the sameelements; this identification is expressed in language using the verb “to be.”
Boole also introduces the symbols 0 and 1, which represent, respectively, the empty class and the class of all the things to which the discourse is limited. As is well known, the idea of limiting the universe to things that are talked about was introduced by De Morgan in [1846]. Boole adopted this idea in Laws, but did not mention its origin.6
To be able to refer to a nondetermined part of a class, Boole introduces the symbol v which, he says, represents an indefinite class (Laws, p. 61). The linguistic term that corresponds to this symbol is “some.” Now, the expression “some men” is symbolized by vx (where x represents the class of all men). Boole claims that v meets the same laws that the literal symbols meet, but in fact this is not so. Indeed, the interpretation of the symbol v presents numerous problems, whose analysis is beyond the scope of this introduction.
The restrictions on the sum and the difference place limits not on the use of the operation symbols, but on the logical interpretability of the expressions where the symbols occur. An expression is logically interpretable if all the sums and differences that occur in it meet their respective restrictions no matter what classes the literal symbols denote. Thus, both v and literal symbols are logically interpretable, but the sum x + y is not, because it only denotes a class when x and y are disjoint classes. The union of any two classes can be symbolized by the sum
which is logically interpretable, since both the difference and the sum obey their respective restrictions whatever classes x and y denote.
Boole symbolizes the four basic types of categorical propositions as follows (Laws, p. 228):
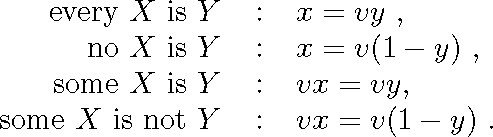
These are the symbolizations he prefers, but he thinks that “every X is Y ” can be symbolized in an equivalent way by x(1 – y) = 0 (anccordingly, “no X is Y ” by xy = 0) (Laws, pp. 123 and 230).7
When Boole comments on the sEymbolization of “every X is Y ” he warns that in x = vy it should be supposed that v and y have elements in common, and when he comments on the symbolization
of “some X is not Y ” he notes that this can only be considered acceptable if we suppose that 
(Laws, pp. 61 and 63). As we will see later, Boole does not always interpret the products of the form vx in this way, but it seems
that at least in this context it is necessary to suppose that v is a nonempty set that has elements in common with the class
x. Now, if this supposition holds, the two symbolizations of “every X is Y ” cannot be equivalent, in spite of what Boole thinks, because if x = 0, then x(1 – y) = 0 is true and x = vy is false. The
same can be said of two symbolizations of “no X is Y.” Boole accepts all the traditional laws of syllogism and, specifically, he accepts that the universal propositions imply
the corresponding particular propositions, but these two implications can only be proved if the universal propositions are
symbolized with the aid of the sign of indefinite class (Laws, p. 229).
1.1.3 Boole obtains the basic laws of his system by reflecting on the meaning of the signs. The following list of the main basic laws allows us to compare Boole's system with what today we know as Boolean algebra:
As can be seen, 0+x is the only sum logically interpretable in these laws, but I have already pointed out that the restrictions of the sum and the difference only affect the logical interpretability of the expressions. 8 The law x2 = x is only applicable to logically meaningful terms; the remaining laws hold in general, that is, the literal symbols that occur in them can be replaced by any term, be it logically interpretable or not. In Boole's system the sum is not distributive overthe product. Nor are
laws of the system; indeed, neither of these sums is logically interpretable.
Boole attributes special importance to the law x2 = x (that is, xx = x)because from it the principle of noncontradiction 
is deduced, but above all because he considers it to be characteristic of the operations of the mind, as it is the only one
of the basic laws that does not hold in the algebra of numbers. Boole observes that from the arithmetical point of view the
only roots of x2 = x are 0 and 1; this fact is enough for him to conclude that the axioms and processes of the algebra of logic are the same
as those of the arithmetic of numbers 0 and 1; and that it is only the interpretation that differentiates one from the other
(Laws, p. 37). This identification ignores the existence of laws that hold in the arithmetic of numbers 0 and 1, but not in
the algebra of logic.9
The consequence that Boole extracts from the identification of the algebra of logic with the arithmetic of the numbers 0 and 1 can be read in the following quotation:
It has been seen, that any system of propositions may be expressed by equations involving symbols x, y; z; which, whenever interpretation is possible, are subject to laws identical in form with the laws of a system of quantitative symbols, susceptible only of the values 0 and 1 (II.15). But as the formal processes of reasoning depend only upon the laws of symbols, and not upon the nature of their interpretation, we are permitted to treat the above symbols x, y; z; as if they were quantitative symbols of the kind above described. We may in fact lay aside the logical interpretation of the symbols in the given equation; convert them into quantitative symbols, susceptible only of the values 0 and 1; perform upon them as such all the requisite processes of solution; and finally restore to them their logical interpretation. (Laws, pp. 69–70; Boole's italics)
The conclusion that Boole reaches is, as we see, that logical problems can be solved by applying techniques of an algebraic nature. Since the result of symbolizing a set of statements is always a system of equations, the problem of extracting consequences from a set of premises (which is the type of logical problem that Boole considers) is merely an algebraic problem which consists essentially of solving a system of equations. When Boole says that we can lay aside the logical interpretation, he means not merely that we can ignore the restrictions on the sum and the difference, but also that we are allowed to use any algebraic procedure (including those that contain operations such as, for example, the quotient, that do not belong to logic). This is what Boole means by “all the requisite processes of solution.”10
The usual algebraic techniques lead, or can lead, to results that are impossible to interpret logically. To solve this difficulty,
Boole introduced a highly complex algebraic procedure of reduction of systems of equations which supposedly makes it possible
to obtain logically interpretable results. The transformations required to obtain these results only rarely have a logical
interpretation; Boole sees nothing wrong in this. In his opinion, the essential issue in the resolution of a problem of a
logical nature is that both the initial equations and the conclusion should be logically interpretable, but it is not necessary
that either the intermediate expressions or the transformations required to obtain the result should be so (as, he says, in
trigonometry, when p¡
1 intervenes in a proof) (Laws, p. 69). Nor is Boole concerned that, on occasion, in order to interpret logically the results that he obtains using his
technique it is necessary to interpret ad hoc quotients that are not even interpretable algebraically.11
1.1.4 The logic of secondary propositions is the same as the logic of primary propositions. The only difference between them concerns the way in which the laws are interpreted. The solution that Boole proposes in Laws to the problem of relating secondary with primary propositions consists in associating each primary proposition with the portion of time in which it is true (Laws, pp. 162 ff.).12 Specifically, the universe 1 is now the whole time to which the discourse is limited
(which may be an hour, a day, or eternity), and if X is one of the elementary propositions that intervene in the discourse, then x is the time in which X is true. The equality 
expresses that the proposition X is true (during all the time to which the discourse is limited). The difference 1 – x is the time in which X is false, and x = 0 means that X is false throughout the temporal universe. The operations are interpreted as in the case
of the logic of primary propositions with the sole difference that now they operate between temporal intervals.
The product xy is the time (limited to the discourse) during which X and Y are both true. The equality xy = 1 means that “X and Y” is true. The nonexclusive disjunction of the propositions X and Y is symbolized by
and the exclusive disjunction by
The conditional “if X, then Y ” (or, more precisely, the proposition “it is true that if X, then Y ”) is symbolized in the same way as an affirmative universal proposition, that is, by 
or 
). If we interpreted vy as in the case of the primary propositions, then 
, and so every conditional with a false antecedent would also be false. To avoid this difficulty, Boole warns that in this
case it may be that there is no temporal instant that is common to v and y (Laws, p 170). We see then that Boole admits or rejects the possibility that vy is equal to 0 as it suits him.
The only aim of the temporal interpretation is to show that a secondary proposition can be symbolized by means of equations. Once this relation is established, the temporal interpretation plays no further role.
William Stanley Jevons (1835–1882) thought that Boole's logic was excessively complicated because it mixed two distinct perspectives: the extensional and the intensional. In the former, a statement expresses a relation between the classes determined by the terms that occur in it; in the latter, it expresses a relation between the meanings of the terms. In Jevons' view, to establish the laws of the operations between classes, Boole had been obliged to restrict the applicability of the operations and to use algebraic techniques that did not have a logical interpretation. The result of introducing these restrictions and techniques had been a system that was excessively complex and did not reflect well the processes of reasoning. Jevons believed that the way to overcome these problems and to obtain a pure logic was to adopt the intensional perspective and to ignore the extensional one. This is what he set out to do in Pure logic or the logic of quality apart from quantity.14
Like Boole, Jevons believed that language is a tool of reasoning, that correct thought is manifested in the correct use of language, and that the laws by which the terms (or their meanings) combine are the laws of reasoning, but, unlike Boole, he did not speak of classes or of operations of the mind, but of terms (or meanings) and of the form in which they combine or are related to each other. Thus, when in Pure logic he introduces languages, he only says that he will use capital letters as variables for terms and that any two terms A and B cancombine to form the term AB or the term A + B, which he calls plural (Pure logic, chap. VI). Jevons considers the existential quantifier “some” as a term whose meaning remains unknown throughout any argument and denotes it by U. The categorical propositions can then be symbolized as in Boole's logic.
I will now summarize the most significant discrepancies between Boole's and Jevons' systems of logic.
Jevons does without the operation of difference, but admits contrary terms, which is essentially equivalent to replacing the difference by the complementation. If A is a simple term, a is the term contrary to A and signifies the absence of the quality signified by A.15 In this way, instead of speaking of the difference between A and B, Jevons speaks of the combination Ab. When it is necessary to negate a composite term, it is assigned a new variable. For example, to express that the negation of A + B is equal to ab two equations are used: C = A + B and c = ab.
As I said, Jevons observed that the restriction imposed by Boole on the sum was not justified, and therefore considered that the plural term A+B was always meaningful even if A and B did not represent excluding terms (Pure logic, pp. 67–75). The most significant consequence of this change was that the equation A+A = A became a law of logic. As far as the basic laws are concerned, the only difference between Jevons' system of logic and the modern calculus of classes is that Jevons does not accept the distributivity of sum over product as a law of logic.
In place of Boole's algebraic proofs, Jevons introduced others that had the advantage of being simpler and logically interpretable. In general, Jevons' proofs were based on the examination of what we could call “logical possibilities.” These possibilities depend on the simple terms that we wish to consider. For example, if the simple terms are A, B, and C, the logical possibilities are
In this way, the universe (for which Jevons did not use a symbol) is given in each case by the sum of all these possibilities. This conception of the universe allows Jevons to replace Boole's proofs with others that bear similarities to the proofs based on diagrams.16
1.3.1 Charles Sanders Peirce (1839–1914) published his first papers on logic in 1867 (Peirce [1867a] and [1867b]. His initial objective was to complete and expand on Boole's calculus. He distinguished between arithmetical and logical operations, and added new operations to Boole's calculus so that each operation had both a logical and an arithmetical version. Peirce thought that the arithmetical operations were useful for applying calculus to the study of probabilities, but were of no logical interest. The logical product was the same as Boole's, but the logical sum was the union of classes as we understand it today (the arithmetical sum was Boole's sum). Initially, Peirce took credit for being the first to eliminate the restriction on the sum, but when he read the works of Jevons and De Morgan he acknowledged that they had beaten him to it.17
From the algebraic point of view, Peirce's most important papers are [1870] (“Description of a notation for the logic of relatives”) and [1880] (“On the algebra of logic”). In the former Peirce lays the foundations of the theory of binary relations that we will discuss in the next chapter, and in [1880] he puts forward a logical calculus which will give rise to the first axiomatization of the algebra of classes—the subject that concerns us in this section and in this chapter as a whole.
Guided by the analogy between arithmetical and logical calculus, in [1870] Peirce introduced the inclusion relation, which
he symbolized by
,a variant of 
. Peirce did not want to use the symbol · because, he said, it could not “be written rapidly enough” and because it mistakenly suggested that inclusion was obtained
on the basis of identity. Peirce observed ([1870], p. 360) that identity could be defined in terms of the inclusion relation
and concluded that the simplest logical relation was not identity, as was generally accepted at the time, but inclusion. An
important consequence of this conclusion was that Peirce abandoned the search for an equational basis for calculus, although
this is not yet patent in [1870].
With the exception of his first papers, Peirce does not speak of classes, but of terms, and distinguishes between absolute and relative terms ([1870], p. 365). The relative terms are those that are used to express relations between objects. Thus, logic of relatives is merely an abbreviation of “logic of relative terms.” The absolute terms are the nonrelative terms (as Peirce frequently calls them).
In [1880] Peirce aimed to show that it was possible to ground the algebra of logic in the inclusion relation, which there
he preferred to call copula. Peirce began the paper with a series of general considerations on the notion of correct argument
and on the different types of 
propositions. In this context, he showed that when the symbol was interpreted as the copula, it allowed a satisfactory symbolization
of the categorical propositions that surmounts the problems created by the Boolean treatment of the expression “some.” The
symbolizations that Peirce proposed for the categorical propositions were
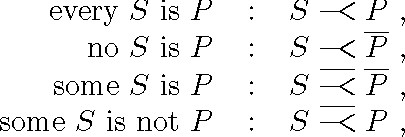
where S
P is the negation of 
. Peirce noted that, according to this interpretation, the universal propositions did not have existential import; that is,
they were true when the extension of the subject term was empty.18
In his attempt to develop a logical calculus on the basis of the new relation, Peirce made a number of vitally important contributions
to the algebraic development of logic: he stated the basic properties of this relation (reflexivity, antisymmetry, and transitivity);
he characterized 0 and 1 as the only objects of the algebra that satisfy 0 
a and a 
;19 he defined the operations of sum and product; he characterized the operation of complementation and, with the aid of these
characterizations, demonstrated most of the basic properties of the logical operations which until that time were considered
as nondemonstrable fundamental laws (i.e., as axioms of the theory, although that name was not used). Among the laws that
Peirce proved in [1880] are the associative properties of the sum and the product, whose proof Schröder considered to be one
of the most beautiful results of the paper.20
Peirce was in a position to axiomatize the theory that we know today as Boolean algebra, but he did not do so, possibly due to a rather loose conception of the axiomatic method together with an unfortunate identification:
To say, “if A, then B” is obviously the same as to say that from A, B follows, logically or extralogically. By thus identifying the relation expressed by the copula with the illation, we identify the proposition with the inference, and the term with the proposition. This identification, by means of which all that is found true of term, proposition, or inference is at once known to be true of all three, is a most important engine of reasoning, which we have gained by beginning with a consideration of the genesis of logic.*
*[[Footnote by Peirce]] In consequence of the identification in question, in S P, I speak of S indifferently as subject, antecedent, or premiss, and of P as predicate, consequent, or conclusion. (Peirce [1880], p. 170; Peirce's italics.)
One of the advantages that Peirce saw in this identification was that it helped to obtain certain basic principles of the
particular calculus of terms that he aimed to develop. On the one hand, the identification allowed him to interpret as the relation of consequence whenever he considered it convenient, with the guarantee that the results that were obtained
would also hold when were interpreted as the copula. On the other, Peirce believed it was legitimate to use in his arguments the characterization
of the intuitive concept of consequence which he had presented in the consideration on the genesis of the logic that precedes
the quotation. This belief, together with the identification, explains why Peirce saw nothing wrong in accepting as proofs
of the calculus arguments based on the characterization of the concept of consequence, which, strictly speaking, is a definition
that is foreign to the calculus. Consequently, certain laws such as
were considered by Peirce as theorems of the calculus when they should have the status of axioms ([1880], pp. 173 and 186). The proof of the distributive laws, which present a problem of the same type, gave rise to an interesting controversy between Peirce and Schröder which I will discuss in the next section.
1.3.2 Peirce [1880] is beyond doubt a key paper in the history of the algebraic development of logic, as Schröder himself recognized.21 Peirce, however, always had a very low opinion of this paper, because he thought that it contained numerous blunders, and because shortly after writing it he became convinced that the approach he had adopted in the early sections was mistaken.22
By 1885, when Peirce had developed his theory of quantification, the analysis of categorical propositions he had proposed in [1880] appeared to him to be totally unsatisfactory. One of the mistakes that he acknowledged was the formal identification of the conditional with the relation of logical consequence. Peirce distinguished between the two notions in [1885] (“On the algebra of logic: A contribution to the philosophy of notation”), but the idea is presented more fully in [1896] (“The regenerated logic”).23 Peirce notes that the difference lies in the fact that “A implies B” means
for every possible state of things i, not Ai or Bi,
whereas “if A then B” is true in a certain state of things i if
not Ai or Bi,
where Ai and Bi mean that A and B, respectively, are true in the state of things i. Peirce then observes that the affirmative universal proposition “every S is P” can be stated in the following way:
for every individual object i, not Si or Pi,
where Si (or Pi) now means that i has the property S (or the property P). From this analysis he concludes that the difference between an implication and a conditional resides in the universal quantifier of the former, and that there is no formal difference between the relation of logical consequence and the relation that exists between the subject and the predicate in an affirmative universal proposition. At the end of the paper Peirce explains that in [1880] he “contented” himselfwith considering only conditionals (consequences de inesse) because he did not have the “algebra of quantifiers” at his disposal (Peirce [1896], 3.448, p. 283).
As I said, another of the reasons for Peirce's low opinion of [1880] was the approach he had used in the early work. He particularly regretted following too closely the steps of the algebra of numbers. This self-criticism has its roots in his evolution after writing this paper. Between 1883 and 1885 Peirce became convinced that the algebra of logic was not arithmetical in nature, or, put another way, that the algebraic point of view he had adopted in [1880] was ill suited to the treatment of the problems of logic. From 1885 onwards his criticisms of the algebraic approach to logic were constant, and frequently aimed at Schröder, in whose investigations Peirce saw an example of the drawbacks of applying algebraic methods to logic.24 Though he recognizes the value of the algebraic approach in the solution of certain problems, one of his most frequent criticisms is that it diverts the attention towards results that are of no logical interest, even though they may be of mathematical interest (in fact, Peirce disputes this as well).
1.3.3 Peirce [1885] is the first paper in which Peirce's renunciation of the Boolean algebraic approach is clearly discernible, and like [1880], it is a landmark in the history of logic. Peirce's contributions to propositional logic in [1885] and later papers are beyond the scope of this brief introduction, for the very reason that they are not algebraic in nature. Nonetheless, I will mention some important contributions that can be found in [1885].
In this paper Peirce uses the term non-relative logic to refer to propositional logic, which he does not identify with the
logic of classes or absolute terms (as he had done in [1880]); this allows him to interpret the variables unequivocally as
propositions and the symbol 
as the conditional. Categorical propositions are analyzed within the logic of relatives and, consequently, the logic of absolute
terms is included in that logic. His presentation of propositional logic bears certain similarities to modern nonalgebraic
presentations. Peirce begins by observing that the fundamental principle of logic is that every proposition is true or false,
which, applied to the case of propositional logic, means that the variables can take only two values. He denotes them by v
and f, and states, in order to distance himself from a possible algebraic interpretation, that he does not identify them with
0 and 1. According to Church ([1956], p. 25, note 67), this is the first explicit use of truth values in logic. Peirce completely
ignores the calculus he had presented in [1880] and proposes in its place a system of logic which can be considered as a partially
successful attempt to construct an axiomatic calculus of deduction for propositional logic. The logical operations now do
not have an algebraic interpretation, and the expressions x + y and xy are introduced as abbreviations for 
and 
, respectively. Peirce concludes the section on propositional logic by showing how to decide the validity of a formula or
the correction of an argument by substituting the variables with truth values (Peirce [1885], p. 175). So in this paper we
find the first explicit declaration that the replacement of propositional variables by truth values can be used as a decision
procedure for validity.
1.4.1 Ernst Schröder (1841–1902) was one of the most prominent logicians of the end of the nineteenth century.25 His most important work is the monumental Vorlesungen über die Algebra der Logik (henceforth Vorlesungen), an exhaustive logical treatise from an algebraic perspective, in which all the results known at that time in algebraic logic are systematically and painstakingly compiled. It is sometimes said that Vorlesungen is a mere work of systematization, but it is more than this, as we will see. Moreover, the lengths to which Schröder goes to quote the origin of the results of other logicians and the discussions that frequently accompany their presentation make the Vorlesungen a valuable source for the historian of logic.
Vorlesungen is divided into three volumes. The first focuses on the calculus of classes, the second on the propositional calculus and the third on the algebra of relatives.26 In this chapter I will present the calculus of classes and the propositional calculus, and I will discuss certain aspects to be borne in mind in order to understand the algebra of relatives, which I will present in detail in the following chapter.
1.4.2 The calculus of classes
1.4.2.1 Schröder's calculus of classes is in essence the result of accurately axiomatizing the calculus whose bases had been laid down by
Peirce in [1880]. As the structure of Vorlesungen indicates, Schröder separated the logic of terms from the propositional logic and distinguished between the calculus of classes and propositional calculus. In the first volume of Vorlesungen Schröder stated a number of principles, postulates and definitions which, taken together, constitute the first complete axiomatization of the algebra of classes or, in other words, of the theory of Boolean algebras. Schröder called this theory identischer Kalkul in order to differentiate it from the arithmetical calculus and from the calculus of relatives.27 His presentation has some slight inaccuracies, but none important enough to cast doubt upon his achievement of axiomatizing the algebra of classes.
The symbols I will use to present the axioms of the calculus of classes are the ones that Schröder finally adopted: 
, and 1.28 The symbol 
denotes the inclusion relation that Schröder termed subsumption. When Schröder refers to 0; 1; and the operations of the
calculus of classes he usually adds the adjective “identical” to the noun to distinguish them terminologically from their
relative counterparts.
Unlike his predecessors, Schröder maintains that the universe must be restricted to certain kinds of classes or manifolds. Specifically, Schröder claims that a manifold (Mannigfaltigkeit) is acceptable as universe if and only if (1) its elements are compatible with each other, and (2) no element of it is a class one of whose members is some other element of the manifold.29 I will now comment on this definition.
Schröder indiscriminately uses the terms element and individual (and on occasion point as well) to refer to the same concept. In the second volume of Vorlesungen, he offers a number of equivalent definitions of it; one of them is
that is, an individual is a class a other than 0 (the empty class) and such that for every class x, a is included in x or x is included in the complement of a. As we can see, unit classes are the only ones that satisfy the requirements of the definition. The elements of a class are its unit subclasses.30
ALGEBRA OF CLASSES AND PROPOSITIONAL CALCULUS 19
Schröder thinks of manifolds as aggregates of conceptually determined elements that are given in advance. More precisely, a manifold is an (identical) sum of elements. A manifold that meets condition (1) is a consistent manifold. According to Schröder, only a manifold of this kind is conceivable as a whole. Schröder says that inconsistent manifolds can only be found in the field of opinions and assertions.He offers this example: the propositions “f(x; y) is symmetric” and “f(x; y) is not symmetric” cannot belong to a consistent manifold (Vorlesungen I, p. 213).
I do not see the point of this condition. Possibly, Schröder is trying to prevent an argument such as the following: let P be a proposition; if P and not-P are elements of a manifold, we can assert P and not P, and this is a contradiction; so, the manifold does not exist (and, therefore, no theory can be based on it). This argument is clearly unacceptable, because both propositions are being regarded as assertions that retain their original meaning. If they were treated as mere objects, “P and not-P” would not be meaningful. If this interpretation of condition (1) is right, it adds nothing to the notion of manifold and, therefore, can be ignored. Interestingly, Frege, Bernays, and Church do not mention this condition when discussing Schröder's notion of universe.31
A manifold that meets condition (2) is a pure manifold (reine Mannigfaltigkeit) (Vorlesungen I, p. 248). The purpose of this requirement is to prevent the possibility that a variable be interpreted as a class having as an element the class denoted by another variable that occurs in the same formula. Schröder thought that a contradiction can be deduced from the assumption that any non-pure manifold is acceptable as a universe, and he consequently restricted the notion of universe.32 Pure manifolds are hierarchically structured. If M is a pure manifold and we sum the elements associated to the subclasses of M (i.e., the unit classes whose sole member is a subclass of M), we obtain a “derived” pure manifold to which the calculus is equally applicable. This process can be iterated, thus giving rise to an infinite sequence of pure manifolds that can be used as universes.33
An immediate consequence of condition (2) is that it is not admissible to interpret 1 as the universal class (the class of all existing things) since this class is not a pure manifold. Schröder misinterpreted Boole and thought that the universe of discourse (Universum des Diskussionsfähigen) was the universal class, and in order to distinguish terminologically between his point of view and Boole's, he used the expression Denkbereich to refer to the universe (the manifold denoted by 1) (Vorlesungen I, pp. 245–246).
The axioms of Schröder's calculus of classes are the following:
1. a 
a.
2. If a b and b c, then a c:
3. a b and b a iff34 a = b.
4. 0 a.
5. a 1.
6. c ab iff c a and c b.
7. a + b c iff a c and b c.
8. If bc = 0, then a(b + c) ab + ac.
9. 1 a + 
and a 0.
10. 1 
0 0.35
1.4.2.2 Axiom 9 and the distributive laws have the status of theorems in Peirce [1880]. Neither Peirce nor Schröder mentions their differences of opinion regarding axiom 9, but they maintained an interesting dispute about the distributive laws. What follows is a reconstruction of the main aspects of this dispute.36
We saw in subsection 1.1.3 that
was one of the basic laws of Boole's system. The distributivity of the sum over the product, that is, the law
was established for the first time by Peirce in [1867a]. Peirce not only stated the law, but also, in the same paper, proved both distributive laws by showing in each case that the formula on the left of the equal symbol refers to the same region of the universe as the formula on the right.37 Peirce does not use diagrams to show the laws, but he reasons as we do when we prove them using diagrams.
We have also seen that in [1880] Peirce aimed to develop a calculus on the basis of the inclusion relation which he then identified with the consequence relation (the illation) and with the copula. Peirce showed that the most important basic laws of logic could be proved starting from the principles of his new calculus. He did not include the proofs of the distributive laws in the paper because, according to him, they were straightforward and “too tedious to give” (Peirce [1880], p. 184).
When Schröder read Peirce's paper, he tried to prove the distributive laws, but he was unable to show
Schröder doubted that these inclusions could be proven in Peirce's calculus and wrote him asking for the omitted proofs. Peirce was unable to reproduce the proofs he had prepared for [1880] and he then concluded that they were probably incorrect. Peirce considered this supposed error to be one of the many blunders that, in his opinion, the paper contained due to the bout of flu that afflicted him during its writing.
In 1883 Schröder presented a paper to the British Association for the Advancement of Science in which he showed that (1.1) was independent of axioms 1–7 (and 10, which is implicit). Schröder constructed two models in which (1.1) was false and in contrast the first seven axioms were true.38 I conjecture that this is the first independence proof in the field of logic (results of this kind had already been obtained in geometry), because in his review of Vorlesungen Peano described it as “very remarkable” (Peano [1891], p. 116), and I suppose it would not have deserved this accolade if it had not been the first. Schröder sent this proof to Peirce, who accepted it without examining it in detail, taking it as confirmation that the proofs he had prepared for [1880] must have been wrong. In order to solve the problem, Schröder decided to take as axiom the weakest version of (1.1) that would allow him to prove the two distributive laws. This version is axiom 8.
Peirce's first reference to Schröder's result is found in [1885] (p. 173, footnote), where he states: “I had myself independently discovered and virtually stated the same thing.” Peirce refers to [1883], a paper on the logic of relatives in which this problem is not mentioned, and all Peirce does is to include (1.1) among “the main formulas of aggregation and composition” (Peirce [1883], p. 455). Schröder's reply to Peirce is found in the first volume of Vorlesungen:
For the other theorem, 26) [[26×) is (1.1) and 26+) is (1.2)]], I was quite unable to obtain the missing proof.I was instead able to demonstrate the unprovability of the theorem—as discussed above in connection with the appendices mentioned—and correspondence with Mr. Peirce on the subject suggested the explanation that he himself was aware of his error—see for this the footnote on p. 190
in the continuation of his mentioned paper, in the seventh volume of the American Journal [[the footnote is in Peirce [1885] and contains the claim quoted above]].
Although I coincided with Mr. Peirce regarding this rectification, I believe that I go further than he does, as I prove the unobtainability of what he in principle believed that he had obtained.
It will be interesting to see now in what form Peirce's scientific construction will proceed after this rectification.39
Some years later, Peirce found the proofs he had prepared for [1880] and they appeared to him to be correct. Peirce sent the proof of (1.1) to Huntington, who was in the process of writing [1904]. I do not think that Schröder ever saw this proof, as he died midway through 1902 and Peirce must have found it slightly later (he sent it to Huntington in December 1903; this cannot have been long after he found it). In February 1904 Peirce wrote to Huntington again to ask him to publish the proof, thus freeing himself from a task which he had been putting off but which, given the situation, was obviously a necessary one.40 Peirce now notes that Schröder thought that he had proved the indemonstrability of (1.1), and admits that he had not in fact examined Schröder's independence proof in detail. Peirce does not mention in this letter that in [1885] he claimed that he had reached the same conclusion as Schröder (although this detail did not escape Huntington, because he refers to Peirce's assertion).
As we will see, the problems derived to a large extent from Peirce's formal identification of the inclusion relation with the consequence relation. Both Peirce's and Schröder's proofs were correct, but, naturally, they proceeded from different assumptions. For the proof of (1.1), in addition to other principles of his calculus (those corresponding to the seven first axioms in Schröder's axiomatization), Peirce used this assumption:
(1.3) If a c is false, then there exists an x 
0 such that 
a and 
In the 1903 letter, Peirce told Huntington that (1.3) followed from the definition of 
in [1880]. The definition to which Peirce refers is this:
The form implies
both, 1, that a premise of the class Pi is possible
and, 2, that among the possible cases of the truth of a Pi there is one in which the corresponding Ci is not true.(Peirce [1880], p. 166; Peirce's italics)
For our concerns, we can think of Pi and Ci as single statements.41
Now, it is clear that Peirce is speaking of the concept of consequence and says that Ci is not a consequence of Pi. It thus emerges that Peirce accounted for (1.3) by interpreting as the consequence relation and, therefore, “a c is false” as “c is not a consequence of a” and x 0 as “x is possible” (recall that Peirce interprets 1 as “the possible”).
This case is thus analogous to that of axiom 9, which, as I said above, Peirce obtained starting from considerations on the validity of certain arguments. Peirce showed (1.1) with the help of (1.3) and proved this principle using his definition of the notion of consequence. Furthermore, this definition had to play an essential role in the proof of (1.3), as can be inferred from the independent proofs of Schröder and Huntington. It is not necessary to know Peirce's proof of (1.3)
in order to assert that it cannot be reproduced in the calculus of classes due to his dependence on the concept of consequence (and therefore his essential dependence on a particular interpretation of the calculus). Thus, even if Peirce had included both proofs in [1880], Schröder would not have been able to do anything different from what he did: to add an axiom. Knowing Peirce's proof of (1.1), Huntington preferred for simplicity's sake to replace Schröder's axiom 8 by (1.3). In his paper Huntington reproduces Peirce's proof of (1.1), and tedious it is.42
1.4.3 The algebra of propositions
1.4.3.1 We have seen that Boole and Peirce in [1880] thought that the logic of classes and propositional logic were the result of two different interpretations of the same calculus. In [1885] Peirce observed that propositions were characterized by being true or false, and showed how to use the assumption that propositional variables can take only two values to determine whether or not a formula is a theorem of propositional logic. Peirce made no attempt to relate his new considerations on propositional logic with the class calculus that he had introduced in [1880], because in 1885 he had already abandoned the algebraic point of view. It was Schröder who tried to obtain a propositional calculus starting from the calculus of classes.
According to Schröder, the propositional calculus (Aussagenkalkul) is obtained by adding a new axiom to the calculus of classes. The purpose of this axiom is to allow the proof of the theorem that states that a variable can take only the values 0 or 1. Thus, what Schröder ultimately claims is that the algebra of the propositional logic is the Boolean algebra of 0 and 1 and that the purpose of the new axiom is to characterize this algebra.
In the second volume of Vorlesungen Schröder presents the axioms in this way:
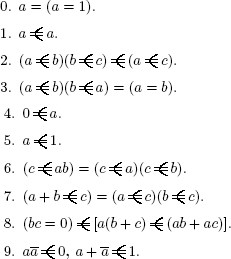
10. 1 0.43
Axiom 0 is the specific principle of the propositional calculus (as Schröder calls it). The remaining axioms are symbolized versions of the corresponding axioms in the calculus of classes.
The fact that the axioms are presented as formulas of a propositional language (or, more exactly, as schemata of formulas,
since this is how they are understood), does not mean that Schröder's calculus can be viewed as an axiomatic calculus for
propositional logic in the modern sense. Strictly speaking, the axioms are not formulas of propositional logic, and what makes
it possible to use them in proofs is that when necessary they are read in accordance with the formulation that they had in
the calculus of classes. This is, for example, the way in which N. Wiener uses them in his doctoral thesis. His proof in propositional
logic of 
illustrates quite well what I mean: “by axiom 1, 
; by axiom 7 and the verbal definition of 
”44 The way in which axiom 7 is applied becomes clear when we make explicit the steps of the proof: by axiom 7,
and bearing in mind the interpretation of the product as a conjunction, 
.
We see that Wiener uses axiom 7 in the same way that he would use the following formulation of it:
This is in fact the appropriate formulation if, as Schröder says, the propositional calculus must be seen as the result of adding an axiom to the calculus of classes.
When the calculus of classes is interpreted propositionally, 
stands for the consequence relation, = stands for the logical equivalence, and 1 and 0 must be regarded as propositional
constants that denote the values “true” and “false,” respectively. Schröder reads 
as “ifa holds, b holds” (wenn a gilt, gilt auch b) or as “from a follows b” (aus a folgt b) and he asserts that a = 1 and
a = 0 mean that a always holds (a gilt stets) and that a never holds, respectively.45 As we see, Schröder gives the right meanings that a = 1 and a = 0 have when the calculus of classes is propositionally reinterpreted,
but the two readings of 
show that he does not clearly distinguish between the conditional and implication (or between biconditional and logical equivalence).
1.4.3.2 The interpretation of the axiom a = (a = 1) presents a difficulty. We cannot interpret both occurrences of the equality as the relation of logical equivalence, nor as the biconditional of the metalanguage, because the result does not make sense in either case. There remains the possibility of interpreting them as the biconditional of the formal language, but this interpretation is not consistent with the one we have attributed to the remaining axioms. It is therefore clear that in this axiom the equality symbol is used in two different senses. The occurrence outside the parentheses must be interpreted as the equivalence relation, and the one inside the parentheses as the biconditional of the formal language, that is, as a connective. This axiom could thus be rigorously stated in this way:
As we can see, this axiom introduces another possible interpretation of the equality symbol. Depending on the context, the equalitysymbol must be interpreted as the relation of logical equivalence, the biconditional of the object language, or the biconditional of the metalanguage. 46
If my interpretation of axiom 0 is right, we can be sure that the addition of this axiom to the calculus of classes will not
permit the proof of a theorem T such that T holds if and only if the algebra of propositions consists of only two classes,
because all the axioms (including axiom 0) are true in any algebra of propositions. So when different uses of the equality
and subsumption symbols are accurately distinguished, it becomes plain that the proofs of some basic theorems are incorrect.
For example, Schröder proves 
as follows:
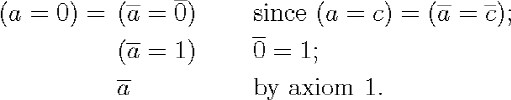
I do not think that this proof can be accepted. The auxiliary theorem 
) (proved within the calculus of classes) cannot be applied to a = 0, because the equality symbol does not have the samemeaning
in a = 0 as in a = c. Explicitly, the theorem to be proven must be interpreted as 
and the auxiliary theorem as
The same type of difficulty is found in, for example, the proof of (a b) = (a + b).
47
Schröder claimed that the theorems of propositional calculus were the same as those of an algebra of classes with only two classes. The theorem in which he seems to base his claim is
which he reads as “every proposition is always true or always false” (Vorlesungen II, pp. 64–65). The status of this equation is under suspicion, because its proof depends on 
(it is an immediate consequence of this equality, axiom 0, and 
), but let us suppose for the sake of argument that (1.4) is really a theorem. Does (1.4) justify Schröder's claim?
The answer to this question depends on whether or not Schröder's reading of (1.4) is correct. There are two possible interpretations of (1.4):
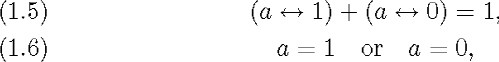
(where + denotes the disjunction of the formal language and the equality symbol the relation of logical equivalence). Observe in addition that Schröder's use of the symbols does not permit us to differentiate between (1.5) and (1.6), because both can be symbolized by (1.4).
Equation (1.5) expresses in essence that any proposition is true or false and, in my opinion, this is what (1.4) really means.
Schröder's claim cannot be concluded from (1.5), because 
is a tautology and, in consequence, is true in any Lindenbaum algebra no matter how many elements it has.48
Schröder identifies “a is true” with “a is always true” and his reading of (1.4) is the one that corresponds to (1.6). From an algebraic point of view, (1.6) means that the Lindenbaum algebra consists of only two equivalence classes. Thus, (1.6) justifies Schröder's claim, but it cannot be proved within the calculus, because all the axioms are true in any algebra of propositions and (1.6) is false when the algebra has more than two equivalence classes. It is plain that an easy way of achieving Schröder's goal is to take (1.6) as an axiom in place of a = (a = 1), but I suppose that this is not an option for someone who uses (1.4) to express (1.6).
1To a more detailed exposition of Boole's work on logic see, for example, Hailperin [1986]. There is a clear introduction to all the subjects treated in this chapter in Lewis [1918].
The secondary bibliography on Boole and, in general, on algebraic logic published until 1995 has been compiled by I. H. Anellis [1995].
2Laws, p. 28. In The mathematical analysis of logic (p. 61) these signs represent mental operations that consist of selecting classes, and for this reason Boole calls them elective.
3Laws, p. 28. As is customary in algebra, the sign of product is usually omitted, and ab is written instead of a × b.
4In Pure logic, pp. 68–70, Jevons denies that the rigorous use of the disjunction presupposes that the terms are mutually exclusive and notes that Boole himself accepts that the terms of the disjunction “either productive of pleasure or preventive of pain” (Laws, pp. 56 and 59–60) are not mutually exclusive
5Claims of this type regarding Boole's sum can be seen, for example, in Smith [1982], p. 23, Houser [1991], p. 12, and Brady [1997] p. 175. Corcoran's criticism is found in the review of Smith's book (Corcoran [1986], p. 71).
6In The mathematical analysis of logic, p. 60, 1 denotes the class of all conceivable objects whether actually existing or not.
7Boole's symbolizations coincide essentially with those proposed by Leibniz in Generales inquisitiones (a work that Boole could not have known, because it was published for the first time in 1903, by Couturat).
8Boole does not explicitly state the associative laws, but he uses them implicitly when he writes sequences of sums and products without brackets.
9Examples of these laws are
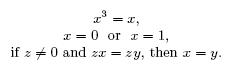
It is slightly surprising that Boole ignores the law x3 = x; because in Laws, p. 50, he explicitly denies that it is a logical law, arguing that neither of its factorizations,
has a logical interpretation. (Observe that the terms –1 and 1 + x lack logical significance in Boole's system.) In The mathematical analysis of logic, p. 62, Boole had included xn = x among the laws of logic.
10The situation is in fact even more complicated. When Boole applies algebraic techniques he does so following the principles
of symbolic algebra which allow the manipulation of expressions devoid of algebraic interpretation. Due to this, his working
frequently contains quotients such as 
which are not interpretableeither logically or algebraically.
The distinction between arithmetic and symbolic algebra was introduced by G. Peacock in [1833] and language, or the biconditional
of the nineteenth—century algebraists such as D. F. Gregory, De Morgan, and Boole himself. Peacock conceived symbolic algebra
as a theory of symbols and their combinations. It was accepted that the laws of symbolic algebra were those of arithmetic,
except that the symbols of the theory lacked interpretation and the operations were applied without restrictions. Symbolic
algebra, for example, allows the operation 
to be always possible, since if b > a, then 
where all that is supposed of is that it is merely a symbol that was necessary in order to generalize the operation of extraction of the square roots.
Since the symbols are not interpreted, it is not considered necessary to examine the nature of
The ideas on which symbolic algebra was based were in general rather obscure, but they had the merit of suggesting the possibility of building a formal system that could be interpreted in various forms. This innovatory idea is expressed clearly in the introduction to The mathematical analysis of logic:
They who are acquainted with the present state of Symbolical Algebra, are aware, that the validity of the processes of analysis does not depend upon the interpretation of the symbols which are employed, but solely upon the laws of their combination. Every system of interpretation which does not affect the truth of the relations supposed, is equally admissible, and thus the same process may, under one scheme of interpretation, represent the solution of a question on the properties of numbers, under another, that of a geometrical problem, and under a third, that of a problem of dynamics or optics.
11On pp. 89–92 of Laws, Boole identifies the indefinite class v with the “indefinite number” 
, but, contrary to his previous comment on the meaning of vx, he now asserts that 
indicates that all, some, or none of the class x must be taken. Boole makes this reading of because he has shown that
and this conditional would be false if 
could not take the value 0. Boole does not maintain this interpretation of 
along Laws. On pp. 232–233, he implicitly assumes that 
cannot be equal to 0 when he identifies with vz and reads 
as “all X's are Z's.”
12In The mathematical analysis of logic Boole had adopted a different (andmore interesting) interpretation: x represented the class of all the conceivable circumstances in which the proposition X was true. Boole had even come close to a truthfunctional concept when he observed (p. 88) that if we limit ourselves to a proposition only two cases are conceivable: that the proposition is true and that the proposition is false. Boole then lists the four possible cases when two propositions intervene and the eight possible cases arising with three propositions. None of this is mentioned in Laws.
13Boole erroneously claims that the proposition thus symbolized is “X is true or Y is true.” The difference between this proposition and “X or Y ” (which in Boole's system cannot be distinguished from “X or Y is true”) becomes patent if we compare “X or not-X ” with “X is true or not-X is true.” The former cannot be false and is symbolized by an identity. x+(1 – x) = 1. The latter cannot be fully symbolized since it is not a secondary proposition, and it can be false because it means that x = 1 or x = 0 (i.e., that X is true throughout the time delimited by 1 or false during the same period). Similar remarks can be made about conjunctions and conditionals.
14The title reflects the point I have just made. The logic of quality is intensional, and the logic of quantity extensional. Jevons' objections to Boole can be found in chapter XV of this book.
Jevons' assessment of Boole's system changed over time. While in Pure logic (p. 67) he states that it is “consistent and perfect within itself” and “perhaps, one of the most marvellous and admirable pieces of reasoning ever put together,” in The principles of science (p. 113) he qualifies it as “quasimathematical” and considers it to lack demonstrative force due to the use of unintelligible symbols which only acquire significance through analogy. However, Jevons believes that Boole's achievement is comparable only to Aristotle's, because, though his system was defective, “Boole discovered the true and general form of logic, and put the science into the form which it must hold for evermore” (The principles of science, p. 113).
15Both the terminology and the symbolism were introduced by De Morgan (see, e.g., “On the syllogism I,” p. 3).
16Jevons' proofs are simpler than Boole's and all the steps in Jevon's proofs arelogically meaningful.
17See Peirce [1870], p. 368, Peirce [1880], p. 182, note, and De Morgan's definition of aggregationin [1860], pp. 180–181.
18This interpretation of universal propositions was first defended by Brentano in [1874] (Psychologie vom empirischen Standpunkte, book II, chap. VII), Peirce in [1880], and J. Venn in [1881] (Symbolic logic, chap. v). For a historical overview of the subject of the existential range of categorical propositions, see Church [1965] and Prior [1976].
19Peirce [1880], p. 182. Peirce uses 
instead of 1 and he interprets the symbols and 0 as “the possible” and “the impossible,” respectively. (Observe that when the variables stand for propositions, 
not means “a is false,” but “a is impossible.”)
20Vorlesungen über die Algebra der Logik I, p. 256.
21Schröder, Vorlesungen über die Algebra der Logik I, p. 290.
22Peirce [1933], p. 104 (note 1) and p. 128 (editors' note reproducing a letter that Peirce wrote to Huntington on February 14, 1904; the same letter is reproduced by Huntington in his [1904], p. 300, footnote).
23Peirce [1885], pp. 166 and 170; Peirce [1896], 3.441 ff. (pp. 279 ff.).
24See, for example, Peirce [1896], 3.431 (pp. 272–273) and 3.451 (p. 284), Peirce [1897], 3.510–3.519 (pp. 320–326), and Peirce [1911], 3.619 (p. 394) and 3.643 (p. 409).
25For the reception and influence of Schröder's works see Dipert [1990a].
26The second part of volume II was published after Schröder's death by K. E. Müller. On Müller's edition of Schröder's works, see Peckhaus [1987].
27By a Gebiet Schröder understands a set of elements of a Mannifaltigkeit. The Gebietekalkul is what today we call theory of lattices (applied to classes).
28In the two first volumes of Vorlesungen Schröder writes 
in place of 
.
29Vorlesungen I, p. 213, pp. 243–248 and p. 342, and Vorlesungen III, p. 4. For the origins of the concept of Mannigfaltigkeit, see Ferreirós [1999], ch. 2.
30Vorlesungen II, §47 (pp. 318 ff.); the above definition is on p. 325. The concept of individual was defined by Peirce in his [1880], p. 194, although the idea is already present in [1870]. The philosophical implications of this extensional notion of individual are analyzed by Dipert in his [1990b].
Observe that Schröder's individuals are what in presentday terminology we call atoms of a Boolean algebra.
31See Frege [1895], Bernays [1975], and Church [1976].
32Schröder's proof of this claim cannot be accepted, because he concludes 0 = 1 from a = {1} and 0 a. Both Frege and Bernays discuss the proof in their respective reviews of the first volume of Vorlesungen (Frege [1895], p. 97 and Bernays [1975], p. 611), and they agree that Schröder confuses membership with inclusion.
Peano ([1899], p. 299) and Padoa ([1911], p. 853) also accuse Schröder of confusing the two relations, but they seem to base
their conclusion on the fact that he would symbolize “Peter is an apostle” as p s. This criticism ignores
that in this symbolization p denotes the class whose only element is Peter and that, in Schröder's sense, p is an element of s.
For a short account of the dispute concerning the distinction between membership and inclusion, see Grattan-Guinness [1975].
33Vorlesungen I, pp. 246–251. In [1976] Church noticed that Schröder's hierarchy of manifolds anticipates Russell's simple theory of types. (Church presented this paper at the Fifth International Congress for the Unity of Science in 1939, but the volume of Erkenntnis in which it should have been published never appeared.)
34“Iff” is short for “if and only if.”
35Axiom 1: Principle I (or of identity) in Vorlesungen I, p. 168; it had been stated by Peirce in [1880], p. 173. Axiom 2: Principle II (or of syllogism) in Vorlesungen I, p. 170; it had been stated by Peirce in [1870], p. 360. Axiom 3: Peirce [1870], p. 360; Schröder, Vorlesungen I, p. 184. Axioms 4 and 5: Peirce [1880], p. 182; Schröder, Vorlesungen I, p. 188. Axioms 6 and 7: Peirce [1880], p.183; Schröder, Vorlesungen I, p. 196. Axiom 8: Principle III in Vorlesungen I, p.293. Axiom 9: Peirce [1880], p. 186; Schröder, Vorlesungen I, p. 302. Schröder does not explicitly state axiom 10 in Vorlesungen I, but he asserts that its negation is false (Vorlesungen I, p. 445) and he explicitly mentions it in Vorlesungen II, p.64.
36For a different view of this dispute, see Houser [1991].
37Peirce [1867a], pp. 13 and 14. Recall that in this paper Peirce proposes to improve Boole's calculus and, therefore, he attributes to the symbols their standard interpretation in the calculus of classes.
38These models are described in appendices 5 and 6 of Vorlesungen I. The model in appendix 5 is described by Peckhaus in [1994], and the one in appendix 6 together with other simpler ones are expound by Thiel in [1994].
Schröder left undecided the question whether (1.1) was independent of axioms 1–7 plus axioms 9–10; Huntington proved that it was in [1904].
39Vorlesungen I, p. 291. German text:
Für den andern Teilsatz 26) aber wollte es mir zunächst durchaus nicht gelingen, den fehlenden Beweis zu erbringen. Statt dessen glückte es mir vielmehr, die Unbeweisbarkeit des Satzes—wie oben (in Verbindung mit den citirten Anhängen) auseinandergesetzt—darzutun, und eine dieserhalb mit Herrn Peirce geführte Korrespondenz lieferte die Aufklärung, dass derselbe seines diesbezüglichen Irrtums ebenfalls schon inne geworden war—vergleich hiezu die Fussnote auf p. 190 im dessen inzwischen erfolgter Fortsetzung seines citirten Aufsatzes, im siebten Bande die American Journal.
Wenn ich auch in dieser Berichtigung mit Herrn Peirce zusammentraf, so glaube ich doch darin über ihn hinauszugehen, dass ich eben die Unerreichbarkeit des zuerst von ihm erreicht Geglaubten nachweise. Interessant wir es nunmehr sein, zu sehen, in welcher Gestalt das von Peirce errichtete wissenschaftliche Gebäude nach jener Berichtigung weiterzuführen ist.
40This letter is reproduced by Huntington in [1904], p. 300, footnote.
41In this definition Peirce makes an implicit appeal to what he calls the leading principle of an argument (or class of arguments).
If an argument 
is valid, its leading principle is the proposition which states that any argument of the same logical structure is valid. Thus, if the argument is valid and i is any argument of the same logical structure as , then for every state of things in which Pi (the premise of i) is true, the corresponding conclusion Ci is also true. According to Peirce, a leading principle is the expression of a habit of inference.
42In Huntington's paper, the characterization of the complement of a class (Schröder's axiom 9) is axiom 8, and (1.3) is axiom 9. Peirce's proof can also be found in Lewis [1918], pp. 128–129.
43The specific principle of propositional calculus, which I introduce as axiom 0, is found in Vorlesungen II, p. 52; the remaining ones, together with a recapitulation of the theorems of the calculus of classes, are found in Vorlesungen II, p. 28. My numeration bears no relation to Schröder's:
Schröder's uses capitals for the variables and writes 
instead of 1 (
is only used on pp. 345–347). Neither in the third volume of Vorlesungen nor in Abriss der Algebra der Logik are or used.
44Wiener [1913], p. 52. Wiener studied Schröder's calculus to compare it with Russell's. I take Wiener's example because it is interesting to see how other logicians understood and used the calculus.
45Vorlesungen II, pp. 13 and 63. In Abriss der Algebra der Logik (Vorlesungen III, p. 719) Schröder reads a = 1 as “a is a theorem.”
46When I encountered the difficulties that the interpretation of axiom a = (a = 1) poses, I was surprised by the fact that logicians as L. Couturat and C. I. Lewis did not notice them (Couturat [1905], p 84 and Lewis [1918], p. 224). I have recently read a text of Tarski and Givant that corroborates my view:
The idea of abolishing the distinction between terms and formulas can be traced back, in an inceptive form, to some earlier work in mathematical logic. We recall a curious postulate which appears in Schröder, Couturat and Lewis: A = (A = 1): Schröder seemed to believe that what is now called the two-valued logic could be treated as a specialized form of the theory of Boolean Algebras, and that specialization would simply consists in adding A = (A = 1) to an ordinary set of postulates for that theory.
For a contemporary logician the problem of clarifying the connection between Boolean algebras and sentential logic is not as simple as it seemed to Schröder. In Schröder's work the theory of Boolean algebras is presented as a nonformalized mathematical theory developed in the common language. In this presentation A = (A = 1) appears to be a meaningless expression which cannot influence in any way the development of the theory. (Tarski and Givant [1987], p. 164)
What follows can be read as an explanation that, according to Tarski-Givant's remark, the axiom A = (A = 1) is of no use to characterize the Boolean algebra of {0, 1}, even if we adopt a meaningful interpretation of it like
. Tarski and Givant ignore this interpretation, because it is alien to Schröder's system. I take it into account because it
allows us a better evaluation of the relation between the calculus of classes and that of propositions.
47The proof of 
is in Vorlesungen II, p. 66, and that of 
on p. 68. Observe that in the latter equality the subsumption symbol should be interpreted as the conditional of the formal
language.
48A Lindenbaum algebra is the Boolean algebra of sentences of a formal language modulo equivalence in a given theory. More precisely,
given a possibly empty set of sentences 
of a formal language L, the elements of the Lindenbaum algebra corresponding to are the equivalence classes of sentences of L modulo the relation
defined by 
. The Boolean operations on the equivalence classes are defined from the logical operations on their members.