Chapter 7:

Big O Analysis of Algorithms

This chapter covers the most popular metric for analyzing the efficiency and scalability of algorithms—Big O notation—in the context of a technical interview.

There are plenty of articles dedicated to this topic. Some of them are purely mathematical (academic), while others try to explain it with a more friendly approach. The pure mathematical approach is quite hard to digest and not very useful during an interview, so we will go for a more friendly approach that will be much more familiar to interviewers and developers.

Even so, this is not an easy mission because besides being the most popular metric for measuring the efficiency and scalability of algorithms, Big O notation can often also be the thing that you've never been motivated enough to learn about, despite knowing that it's going to show up in every single interview. From juniors to senior warriors, Big O notation is probably the biggest Achilles heel for everyone. However, let's make an effort to turn this Achilles heel into a strong point for our interviews.

We will quickly go over Big O notation and highlight the things that matter the most. Next, we'll jump into examples that have been carefully crafted to cover a wide range of problems, and so by the end of this chapter, you'll be able to determine and express Big O for almost any given snippet of code. Our agenda includes the following:

• Analogy
• Big O complexity time
• The best case, worst case, and expected case
• Big O examples

So, let's start our Big O journey!

Analogy

Imagine a scenario where you've found one of your favorite movies on the internet. You can order it or download it. Since you want to see it as soon as possible, which is the best way to proceed? If you order it, then it will take a day to arrive. If you download it, then it will take half a day to download. So, it is faster to download it. That's the way to go!

But wait! Just when you get ready to download it, you spot the Lord of the Rings Master Collection at a great price, and so you think about downloading it as well. Only this time, the download will take 2 days. However, if you place an order, then it will still only take a single day. So, placing an order is faster!

Now, we can conclude that no matters how many items we order, the shipping time remains constant. We call this O(1). This is a constant runtime.

Moreover, we conclude that the download time is directly proportional to the file sizes. We call this O(n). This is an asymptotic runtime.

From day-to-day observations, we can also conclude that online ordering scales better than online downloading.

This is exactly what Big O time means: an asymptotic runtime measurement or an asymptotic function.

As an asymptotic measurement, we are talking about Big O complexity time (this can be complexity space as well).

Big O complexity time

The following diagram reveals that, at some moment in time, O(n) surpasses O(1). So, until O(n) surpasses O(1), we can say that O(n) performs better than O(1):

Figure 7.1 – The asymptotic runtime (Big O time)

Besides the O(1)—constant time—and O(n)—linear time runtimes—we have many other runtimes, such as O(log n), O(n log n)—logarithmic time—O(n2)—quadratic time, O(2n)— exponential time, and O(n!)—factorial time. These are the most common runtimes, but many more also exist.

The following diagram represents the Big O complexity chart:

Figure 7.2 – Big O complexity chart

As you can see, not all O times perform the same. O(n!), O(2n), and O(n2) are considered horrible and we should strive to write algorithms that perform outside this area. O(n log n) is better than O(n!) but is still bad. O(n) is considered fair, while O(log n) and O(1) are good.

Sometimes, we need multiple variables to express the runtime performance. For example, the time for mowing the grass on a soccer field can be expressed as O(wl), where w is the width of the soccer field and l is the length of the soccer field. Or, if you have to mow p soccer fields, then you can express it as O(wlp).

However, it is not all about time. We care about space as well. For example, building an array of n elements needs O(n) space. Building a matrix of n x n elements needs O(n2) space.

The best case, worst case, and expected case

If we simplify things, then we can think of the efficiency of our algorithms in terms of best case, worst case, and expected case. The best case is when the input of our algorithms meets some extraordinary conditions that allow it to perform the best. The worst case is at the other extreme, where the input is in an unfavorable shape that makes our algorithm reveal its worst performances. Commonly, however, these amazing or terrible situations won't happen. So, we introduce the expected performance.

Most of the time, we care about the worst and expected cases, which, in the case of most algorithms, are usually the same. The best case is an idealistic performance, and so it remains idealistic. Mainly, for almost any algorithm, we can find a special input that will lead to the O(1) best-case performance.

For more details about Big O, I strongly recommended you read the Big O cheat sheet (https://www.bigocheatsheet.com/).

Now, let's tackle a bunch of examples.

Big O examples

We will try to determine Big O for different snippets of code exactly as you will see at interviews, and we will go through several relevant lessons that need to be learned. In other words, let's adopt a learning-by-example approach.

The first six examples will highlight the fundamental rules of Big O, listed as follows:

• Drop constants
• Drop non-dominant terms
• Different input means different variables
• Different steps are summed or multiplied

Let us begin with trying out the examples.

Example 1 – O(1)

Consider the following three snippets of code and compute Big O for each of them:

// snippet 1

return 23;

Since this code returns a constant, Big O is O(1). Regardless of what the rest of the code does, this line of code will execute at a constant rate:

// snippet 2 - 'cars' is an array

int thirdCar = cars[3];

Accessing an array by index is accomplished with O(1). Regardless of how many elements are in the array, getting an element from a specific index is a constant operation:

// snippet 3 - 'cars' is a 'java.util.Queue'

Car car = cars.peek();

The Queue#peek() method retrieves but does not remove, the head (first element) of this queue. It doesn't matter how many elements follows the head, the time to retrieve the head via the peek() method is O(1).

So, all three snippets in the preceding code block have the O(1) complexity time. Similarly, inserting and removing from a queue, pushing and popping from a stack, inserting a node in a linked list, and retrieving the left/right child of a node of a tree stored in an array are also cases of O(1) time.

Example 2 – O(n), linear time algorithms

Consider the following snippet of code and compute Big O:

// snippet 1 - 'a' is an array

for (int i = 0; i < a.length; i++) {

    System.out.println(a[i]);

}

In order to determine the Big O value for this snippet of code, we have to answer the following question: how many times does this for loop iterate? The answer is a.length times. We cannot say exactly how much time this means, but we can say that the time will grow linearly with the size of the given array (which represents the input). So, this snippet of code will have an O(a.length) time and is known as linear time. It is denoted as O(n). 

Example 3 – O(n), dropping the constants

Consider the following snippet of code and compute Big O:

// snippet 1 - 'a' is an array

for (int i = 0; i < a.length; i++) {

    System.out.println("Current element:");

    System.out.println(a[i]);

    System.out.println("Current element + 1:");

    System.out.println(a[i] + 1);

}

Even if we added more instructions to the loop, we would still have the same runtime as in Example 2. The runtime will still be linear in the size of its input, a.length. As in Example 2 we had a single line of code in a loop, while here we have four lines of code in a loop, you might expect Big O to be O(n + 4) or something like that. However, this kind of reasoning is not precise or accurate—it's just wrong! Big O here is still O(n).

Important note

Keep in mind that Big O doesn't depend on the number of code lines. It depends on the runtime rate of increase, which is not modified by constant-time operations.

Just to reinforce this scenario, let's consider the following two snippets of code, which compute the minimum and maximum of the given array, a:

7.3 – Code Comparison

Now, which one of these two code snippets runs faster?

The first code snippet uses a single loop, but it has two if statements, while the second code snippet uses two loops, but it has one if statement per loop.

Thinking like this opens the door to insanity! Counting the statements can continue at a deeper level. For example, we can continue to count the statements (operations) at the compiler level, or we might want to take into consideration the compiler optimizations. Well, that's not what Big O is about!

Important note

Big O is not about counting the code statements. Its goal is to express the runtime growth for input sizes and express how the runtime scales. In short, Big O just describes the runtime rate of increase.

Moreover, don't fall into the trap of thinking that because the first snippet has one loop, Big O is O(n), while in the case of the second snippet, because it has two loops, Big O is O(2n). Simply remove 2 from 2n since 2 is a constant!

Important note

As a rule of thumb, when you express Big O, drop the constants in runtime.

So, both of the preceding snippets have a Big O value of O(n).

Example 4 – dropping the non-dominant terms

Consider the following snippet of code and compute Big O (a is an array):

7.4 – Code snippet executed in O(n)

The first for loop is executed in O(n), while the second for loop is executed in O(n2). So, we may think that the answer to this problem is O(n) + O(n2) = O(n + n2). But this is not true! The rate of increase is given by n2, while n is a non-dominant term. If the size of the array is increased, then n2 affects the rate of increase much more than n, and so n is not relevant. Consider a few more examples:

• O(2n + 2n) -> drop constants and non-dominant terms -> O(2n).
• O(n + log n) -> drop non-dominant terms -> O(n).
• O(3*n2 + n + 2*n) -> drop constants and non-dominant terms -> O(n2).

  Important note

  As a rule of thumb, when you express Big O, drop the non-dominant terms.

Next, let's focus on two examples that are a common source of confusion for candidates.

Example 5 – different input means different variables

Consider the following two snippets of code (a and b are arrays). How many variables should be used to express Big O?

7.5 – Code snippets 1 and 2

In the first snippet, we have two for loops that loop the same array, a (we have the same input for both loops), and so Big O can be expressed as O(n), where n refers to a. In the second code snippet, we also have two for loops, but they loop different arrays (we have two inputs, a and b). This time, Big O is not O(n)! What does n refer to – a or b? Let's say that n refers to a. If we increase the size of b, then O(n) doesn't reflect the runtime rate of increase. Therefore, Big O is the sum of these two runtimes (the runtime of a plus the runtime of b). This means that Big O must refer to both runtimes. For this, we can use two variables that refer to a and to b. So, Big O is expressed as O(a + b). This time, if we increase the size of a and/or b, then O(a + b) captures the runtime rate increase.

Important note

As a rule of thumb, different inputs mean different variables.

Next, let's see what happens when we add and multiply the algorithm steps.

Example 6 – different steps are summed or multiplied

Consider the following two snippets of code (a and b are arrays). How do you express Big O for each of these snippets?

7.6 – Code snippet a and b

We already know from the previous example that, in the case of the first snippet, Big O is O(a + b). We sum up the runtimes since their work is not interweaved as in the case of the second snippet. So, in the second snippet, we cannot sum up the runtimes since, for each case of a[i], the code loops the b array, and so Big O is O(a * b).

Think twice before deciding between summing and multiplying the runtimes. This is a common mistake made in interviews. Also, it is quite common to not notice that there is more than one input (here, there are two) and to mistakenly express Big O using a single variable. That would be wrong! Always pay attention to how many inputs are present. For each input that affects the runtime rate of increase, you should have a separate variable (see Example 5).

Important note

As a rule of thumb, different steps can be summed or multiplied. The runtimes should be summed or multiplied based on the following two statements:

If you describe your algorithm as it foos and when it's done, it buzzes, then sum the runtimes.

If you describe your algorithm as for each time it foos, it buzzes, then multiply the runtimes.

Now, let's discuss log n runtimes.

Example 7 – log n runtimes

Write a snippet of pseudo-code that has Big O as O(log n).

In order to understand the O(log n) runtimes, let's start with the Binary Search algorithm. The Binary Search algorithm details and implementation is available in Chapter 14, Sorting and Searching. This algorithm describes the steps for looking for element x in an array, a. Consider a sorted array, a, of 16 elements, such as the following:

Figure 7.7 – Ordered array of 16 elements

First, we compare x with the midpoint of the array, p. If they are equal, then we return the corresponding array index as the final result. If x > p, then we search on the right side of the array. If x < p, then we search on the left side of the array. The following is a graphical representation of the binary search algorithm for finding the number 17:

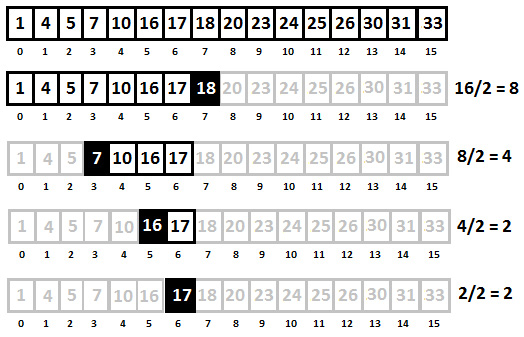
Figure 7.8 – The binary search algorithm

Notice that we start with 16 elements and end with 1. After the first step, we are down to 16/2 = 8 elements. At the second step, we are down to 8/2 = 4 elements. At the third step, we are down to 4/2 = 2 elements. Then, at the last step, we find the searched number, 17. If we translate this algorithm into pseudo-code, then we obtain something as follows:

search 17 in {1, 4, 5, 7, 10, 16, 17, 18, 20,

              23, 24, 25, 26, 30, 31, 33}

    compare 17 to 18 -> 17 < 18

    search 17 in {1, 4, 5, 7, 10, 16, 17, 18}

        compare 17 to 7 -> 17 > 7

        search 17 in {7, 10, 16, 17}

            compare 17 to 16 -> 17 > 16

            search 17 in {16, 17}

                compare 17 to 17

                return

Now, let's express Big O for this pseudo-code. We can observe that the algorithm consists of a continuous half-life of the array until only one element remains. So, the total runtime is dependent on how many steps we need in order to find a certain number in the array.

In our example, we had four steps (we halved the array 4 times) that can be expressed as following:

Or, if we condense it then we get:

One step further, and we can express it for general case as (n is the size of the array, k is the number of steps to reach the solution):

But, 2k = n is exactly what logarithm means - A quantity representing the power to which a fixed number (the base) must be raised to produce a given number. So, we can write the follows:

In our case, 2k = n means 24 = 16, which is log216 = 4.

So, Big O for the Binary Search algorithm is O(log n). However, where is the logarithm base? The short answer is that the logarithm base is not needed for expressing Big O because logs of different bases are only different by a constant factor.

Important note

As a rule of thumb, when you have to express Big O for an algorithm that halves its input at each step/iteration, there are big chances of it being a case of O(log n).

Next, let's talk about evaluating Big O for recursive runtimes.

Example 8 – recursive runtimes

What is Big O for the following snippet of code?

int fibonacci(int k) {

    if (k <= 1) {

        return k;

    }

    return fibonacci(k - 2) + fibonacci(k - 1);

}

On our first impression, we may express Big O as O(n2). Most likely, we will reach this result because we are misled by the two calls of the fibonacci() method from return. However, let's give value to k and quickly sketch the runtime. For example, if we call fibonacci(7) and we represent the recursive calls as a tree, then we obtain the following diagram:

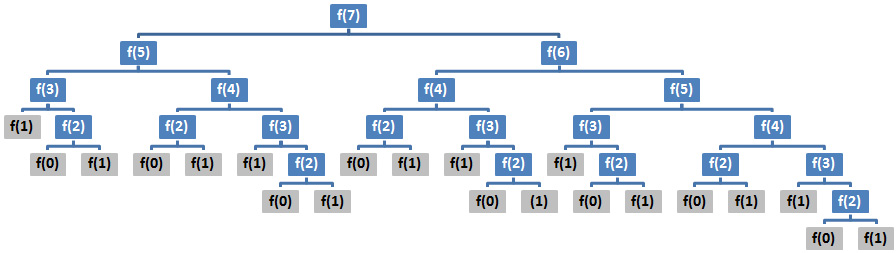
Figure 7.9 – Tree of calls

We almost immediately notice that the depth of this tree is equal to 7, and so the depth of the general tree is equal to k. Moreover, with the exception of the terminal levels, each node has two children, and so almost every level has twice the number of calls as the one above it.This means that we can express Big O as O(branches depth). In our case, this is O(2k), denoted O(2n).

In an interview, just saying O(2n) should be an acceptable answer. If we want to be more accurate, then we should take into account the terminal levels, especially the last level (or the bottom of the call stack), which can sometimes contain a single call. This means that we don't always have two branches. A more accurate answer would be O(1.6n). Mentioning that the real value is less than 2 should be enough for any interviewer.

If we want to express Big O in terms of space complexity, then we obtain O(n). Do not be fooled by the fact that the runtime complexity is O(2n). At any moment, we cannot have more than k numbers. If we look in the preceding tree, we can only see numbers from 1 to 7.

Example 9 – in-order traversal of a binary tree

Consider a given perfect binary search tree. If you need a quick remainder of binary trees then consider the Nutshell section of Chapter 13, Trees and Graphs.What is Big O for the following snippet of code?

void printInOrder(Node node) {

    if (node != null) {

       printInOrder(node.left);

       System.out.print(" " + node.element);

       printInOrder(node.right);

    }

}

A perfect binary search tree is a binary search tree whose internal nodes have exactly two children and all the leaf nodes are on the same level or depth. In the following diagram, we have a typical perfect binary search tree (again, visualizing the runtime input is very useful):

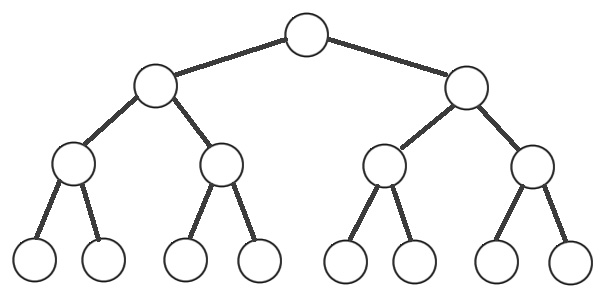
Figure 7.10 – Height-balanced binary search tree

We know from experience (more precisely, from the previous example) that when we face a recursive problem with branches, we can have an O(branches depth) case. In our case, we have two branches (each node has two children), and so we have O(2 depth). Having an exponential time looks weird, but let's see what the relationship between the number of nodes and the depth is. In the preceding diagram, we have 15 nodes and the depth is 4. If we had 7 nodes, then the depth would be 3, and if we had 31 nodes, then the depth would be 5. Now, if we don't already know from the theory that the depth of a perfect binary tree is logarithmic, then maybe we can observe the following:

• For 15 nodes, we have a depth of 4; therefore, we have 24 = 16, equivalent to log216 = 4.
• For 7 nodes, we have a depth of 3; therefore, we have 23 = 8, equivalent to log28 = 3.
• For 31 nodes, we have a depth of 5; therefore, we have 25 = 32, equivalent to log232 = 5.

Based on the preceding observations, we can conclude that we can express Big O as O(2log n) since the depth is roughly log n. So, we can write the following:

Figure 7.11 – Big O expression

So, Big O in this case is O(n). We could reach the same conclusion if we recognized that this code is in fact the In-Order traversal of a binary tree, and in this traversal (exactly as in case of Pre-Order and Post-Order traversals), each node is visited a single time. Moreover, for each traversed node, there is a constant amount of work, and so Big O is O(n).

Example 10 – n may vary

What is Big O for the following snippet of code?

void printFibonacci(int k) {

    for (int i = 0; i < k; i++) {

        System.out.println(i + ": " + fibonacci(i));

    }

}

int fibonacci(int k) {

    if (k <= 1) {

        return k;

    }

    return fibonacci(k - 2) + fibonacci(k - 1);

}

From Example 8, we already know that the Big O value of the fibonacci() method is O(2n). printFibonacci() calls fibonacci() n times, so it is very tempting to express the total Big O value as O(n)*O(2n) = O(n2n). However, is this true or have we rushed to give an apparently easy answer?

Well, the trick here is that n varies. For example, let's visualize the runtime:

We cannot say that we execute the same code n times, so this is O(2n).

Example 11 – memoization

What is Big O for the following snippet of code?

void printFibonacci(int k) {

    int[] cache = new int[k];

    for (int i = 0; i < k; i++) {

        System.out.println(i + ": " + fibonacci(i, cache));

    }

}

int fibonacci(int k, int[] cache) {

    if (k <= 1) {

        return k;

    } else if (cache[k] > 0) {

        return cache[k];

    }

    cache[k] = fibonacci(k - 2, cache)

        + fibonacci(k - 1, cache);

    return cache[k];

}

This code computes the Fibonacci number via recursion. However, this code uses a technique known as Memoization. Mainly, the idea is to cache the return value and use it to reduce recursive calls. We already know from Example 8 that Big O of the fibonacci() method is O(2n). Since Memoization should reduce recursive calls (it introduces an optimization), we can guess that Big O of this code should do better than O(2n). However, this is just an intuition, so let's visualize the runtime for k = 7:

Calling fibonacci(0):

Result of fibonacci(0) is 0

Calling fibonacci(1):

Result of fibonacci(1) is 1

Calling fibonacci(2):

fibonacci(0)

fibonacci(1)

fibonacci(2) is computed and cached at cache[2]

Result of fibonacci(2) is 1

Calling fibonacci(3):

fibonacci(1)

fibonacci(2) is fetched from cache[2] as: 1

fibonacci(3) is computed and cached at cache[3]

Result of fibonacci(3) is 2

Calling fibonacci(4):

fibonacci(2) is fetched from cache[2] as: 1

fibonacci(3) is fetched from cache[3] as: 2

fibonacci(4) is computed and cached at cache[4]

Result of fibonacci(4) is 3

Calling fibonacci(5):

fibonacci(3) is fetched from cache[3] as: 2

fibonacci(4) is fetched from cache[4] as: 3

fibonacci(5) is computed and cached at cache[5]

Result of fibonacci(5) is 5

Calling fibonacci(6):

fibonacci(4) is fetched from cache[4] as: 3

fibonacci(5) is fetched from cache[5] as: 5

fibonacci(6) is computed and cached at cache[6]

Result of fibonacci(6) is 8

Each fibonacci(k) method is computed from the cached fibonacci(k-1) and fibonacci(k-2) methods. Fetching the computed values from the cache and summing them is a constant time work. Since we do this work k times, this means that Big O can be expressed as O(n).

Besides Memoization, we can use another approach, known as Tabulation. More details are available in Chapter 8, Recursion and Dynamic Programming.

Example 12 – looping half of the matrix

What is Big O for the following two snippets of code (a is an array)?

7.12 – Code snippets for Big O

These snippets of code are almost identical, except that in the first snippet, j starts from 0, while in the second snippet, it starts from i+1.

We can easily give value to the array size and visualize the runtime of these two snippets of code. For example, let's consider that the array size is 5. The left-hand matrix is the runtime of the first snippet of code, while the right-hand matrix corresponds to the runtime of the second snippet of code:

Figure 7.13 – Visualizing the runtime

The matrix corresponding to the first snippet of code reveals an n*n size, while the matrix corresponding to the second snippet of code roughly reveals an n*n/2 size. So, we can write the following:

• Snippet 1 runtime is: .
• Snippet 2 runtime is: since we eliminate constants.

So, both snippets of code have O(n2).

Alternatively, you can think of it like this:

• For the first snippet, the inner loop doesn't work and it is run n times by the outer loop, and so n*n = n2, results in O(n2).
• For the second snippet, the inner loop does roughly n/2 work and it is run n times by the outer loop, so n*n/2 = n2/2 = n2 * 1/2, which results in (after removing the constants) O(n2).

Example 13 – identifying O(1) loops

What is Big O for the following snippet of code (a is an array)?

for (int i = 0; i < a.length; i++) {

    for (int j = 0; j < a.length; j++) {

        for (int q = 0; q < 1_000_000; q++) {

            System.out.println(a[i] + a[j]);

        }

    }

}

If we ignore the third loop (the q loop), then we already know that Big O is O(n2). So, how does the third loop influence the total Big O value? The third loop iterates from 0 to 1 million, independent of the array size, and so Big O for this loop is O(1), which is a constant. Since the third loop doesn't depend on how the input size varies, we can write it as follows:

for (int i = 0; i < a.length; i++) {

    for (int j = 0; j < a.length; j++) {

        // O(1)  

    }

}

Now, it is clear that Big O for this example is O(n2).

Example 14 – looping half of the array

What is Big O for the following snippet of code (a is an array)?

for (int i = 0; i < a.length / 2; i++) {

    System.out.println(a[i]);

}

Confusion here can be caused by the fact that this snippet loops only half of the array. Don't make the common mistake of expressing Big O as O(n/2). Remember that constants should be removed, and so Big O is O(n). Iterating only half of the array doesn't impact the Big O time.

Example 15 – reducing Big O expressions

Which of the following can be expressed as O(n)?

• O(n + p)
• O(n + log n)

The answer is that O(n + log n) can be reduced to O(n) because log n is a non-dominant term and it can be removed. On the other hand, O(n + p) cannot be reduced to O(n) because we don't know anything about p. Until we establish what p is and what the relationship between n and p is, we have to keep both of them.

Example 16 – looping with O(log n)

What is Big O for the following snippet of code (a is an array)?

for (int i = 0; i < a.length; i++) {

    for (int j = a.length; j > 0; j /= 2) {

        System.out.println(a[i] + ", " + j);

    }

}

Let's just focus on the outer loop. Based on the experiences from the previous examples, we can quickly express Big O as O(n).

How about the inner loop? We can notice that j starts from the array length and, at each iteration, it is halved. Remember the important note from Example 7 that say: When you have to express Big O for an algorithm that halves its input at each step, there are big chances to be in a O(log n) case.

Important note

Whenever you think that there are big chances of it being a case of O(log n), it is advised that you use test numbers that are powers of the divisor. If the input is divided by 2 (it is halved), then use numbers that are a power of 2 (for example, 23 = 8, 24 = 16, 25 = 32, and so on). If the input is divided by 3, then use numbers that are a power of 3 (for example, 32 = 9, 33 = 27, and so on). This way, it is easy to count the number of divisions.

So, let's give value to a.length and visualize the runtime. Let's say that a.length is 16. This means that j will take the 12, 8, 4, 2, and 1 values. We have divided j by 2 exactly four times, so we have the following:

Figure 7.14 – Loop with O (log n)

So, Big O for the inner loop is O(log n). To compute the total Big O, we consider that the outer loop is executed n times, and within that loop, another loop is executed log n times. So, the total Big O result is O(n)* O (log n) = O(n log n).

As a tip, a lot of sorting algorithms (for example, Merge Sort and Heap Sort) have the O(n log n) runtime. Moreover, a lot of O(n log n) algorithms are recursive. Generally speaking, algorithms that are classified under the Divide and Conquer (D&C) category of algorithms are O(n log n). Hopefully, keeping these tips in mind will be very handy in interviews.

Example 17 – string comparison

What is Big O for the following snippet of code? (note that a is an array, and be sure to carefully read the comments):

String[] sortArrayOfString(String[] a) {

    for (int i = 0; i < a.length; i++) {

        // sort each string via O(n log n) algorithm          

    }

    // sort the array itself via O(n log n) algorithm              

    return a;

}

sortArrayOfString() receives an array of String and performs two major actions. It sorts each string from this array and the array itself. Both sorts are accomplished via algorithms whose runtime is expressed as O(n log n).

Now, let's focus on the for loop and see the wrong answer that is commonly given by candidates. We already know that sorting a single string gives us O(n log n). Doing this for each string means O(n) * (n log n) = O(n*n log n) = O(n2 log n). Next, we sort the array itself, which is also given as O(n log n). Putting all of the results together, the total Big O value is O(n2 log n) + O(n log n) = O(n2 log n + n log n), which is O(n2 log n) since n log n is a non-dominant term. However, is this correct? The short answer is no! But why not?! There are two major mistakes that we've done: we've used n to represent two things (the size of the array and the length of the string) and we assumed that comparing String requires a constant time as is the case for fixed-width integers.

Let's detail the first problem. So, sorting a single string gives us O(n log n), where n represents the length of that string. We sort a.length strings, so n now represents the size of the array. This is where the confusion comes from, because when we say that the for loop is O(n2 log n), to which n are we referring to? Since we are working with two variables, we need to denote them differently. For example, we can consider the following:

• s: The length of the longest String.
• p: The size of the array of String.

In these terms, sorting a single string is O(s log s), and doing this p times results in O(p)*O(s log s) = O(p*s log s).

Now, let's tackle the second problem. In our new terms, sorting the array is O(p log p) – I've just replaced n with p. However, does the comparison of String require a constant time as is the case of fixed-width integers? The answer is no! String sorting changes O(p log p) because the String comparison itself has a variable cost. The length of String varies, and so the comparison time varies as well. So, in our case, each String comparison takes O(s), and since we have O(p log p) comparisons, it results that sorting the array of strings is O(s) * O(p log p) = O(s*p log p).

Finally, we have to add O(p*s log s) to O(s*p log p) = O(s*p(log s + log p)). Done!

Example 18 – factorial Big O

What is Big O for the following snippet of code?

long factorial(int num) {

    if (num >= 1) {

        return num * factorial(num - 1);

    } else {

        return 1;

    }

}

It is obvious that this snippet of code is a recursive implementation of computing factorials. Don't do the common mistake of thinking that Big O is O(n!). This is not true! Always analyze the code carefully without prior assumption.

The recursive process traverses the sequence n–1, n–2, ... 1 times; therefore, this is O(n).

Example 19 – using n notation with caution

What is Big O for the following two snippets of code?

7.15 – Code snippets

The first snippet (on the left-side hand) does constant work for y times. The x input doesn't affect the runtime rate of increase, and so Big O can be expressed as O(y). Pay attention to the fact that we don't say O(n) since n can be confused with x as well.

The second snippet (on the right-side hand) recursively traverses y-1, y-2, ..., 0. Each y input is traversed a single time, so Big O can be expressed as O(y). Again, the x input doesn't affect the runtime rate of increase. Moreover, we avoid saying O(n) since there is more than one input and O(n) will create confusion.

Example 20 – the sum and count

What is Big O for the following snippet of code (x and y are positive)?

int div(int x, int y) {

    int count = 0;

    int sum = y;

    while (sum <= x) {

       sum += y;

       count++;

    }

    return count;

}

Let's give values to x and y and watch the count variable, which counts the number of iterations. Consider that x=10 and y=2. For this scenario, count will be 5 (10/2 = 5). Following the same logic, we have x=14, y=4, count=3 (14/4 = 3.5), or x=22, y=3, or count=7 (22/3 = 7.3). We can notice that in the worst-case scenario, count is x/y, and so Big O can be expressed as O(x/y).

Example 21 – the number of iteration counts in Big O

The following snippet of code tries to guess the square root of a number. What is Big O?

int sqrt(int n) {

    for (int guess = 1; guess * guess <= n; guess++) {

        if (guess * guess == n) {

            return guess;

        }

    }

    return -1;

}

Let's consider that the number (n) is a perfect square root, such as 144, and we already know that sqrt(144) = 12. Since the guess variable starts from 1 and stops at guess*guess <= n with step 1, it is quite simple to compute that guess will take the values 1, 2, 3, ... , 12. When guess is 12, we have 12*12 = 144, and the loop stops. So, we had 12 iterations, which is exactly sqrt(144).

We follow the same logic for a non-perfect square root. Let's consider that n is 15. This time, guess will take the 1, 2, and 3 values. When guess=4, we have 4*4 > 15 and the loop stops. The returned value is -1. So, we had 3 iterations.

In conclusion, we have sqrt(n) iterations, so Big O can be expressed as O(sqrt(n)).

Example 22 – digits

The following snippet of code sum up the digits of an integer. What is Big O?

int sumDigits(int n) {

    int result = 0;

    while (n > 0) {

        result += n % 10;

        n /= 10;

    }

    return result;

}

At each iteration, n is divided by 10. This way, the code isolates a digit in the right-side of the number (for example, 56643/10 = 5664.3). To traverse all the digits, the while loop needs a number of iterations equal to the number of digits (for example, for 56,643 it needs 5 iterations to isolate 3, 4, 6, 6, and 5).

However, a number with 5 digits can be up to 105 = 100,000, which means 99,999 iterations. Generally speaking, this means a number (n) with d digits can be up to 10d. So, we can say the following:

Figure 7.16 – Digits relationship

Example 23 – sorting

What is Big O for the following snippet of code?

boolean matching(int[] x, int[] y) {

    mergesort(y);

    for (int i : x) {

        if (binarySearch(y, i) >= 0) {

            return true;

        }

    }

    return false;

}

In Example 16, we said that a lot of sorting algorithms (including Merge Sort) have a runtime of O(n log n). This means that mergesort(y) has a runtime of O(y log y).

In Example 7, we said that the Binary Search algorithm has a runtime of O(log n). This means that binarySearch(y, i) has a runtime of O(log y). In the worst-case scenario, the for loop will iterate the whole x array, and so the binary search algorithm will be executed x.length times. The for loop will have a runtime of O(x log y).

So, the total Big O value can be expressed as O(y log y) + O(x log y) = O(y log y + x log y).

Done! This was the last example presented here. Next, let's try to extract several key hints that can help you in interviews to determine and express Big O.

Key hints to look for in an interview

During an interview, time and stress are serious factors that can affect concentration. Having the capacity to identify templates, recognize certain cases, guess the correct answer, and so on gives you a major advantage. As we stated in Chapter 5, How to Approach a Coding Challenge, in figure 5.2, building an example (or a use case) is the second step to tackling a coding challenge. Even if the code is given by the interviewer, building an example is still quite useful for determining Big O.

As you probably noticed, in almost every non-trivial example that we covered, we preferred to visualize the runtime for one or several concrete cases. That way, you can really understand the details of the code, identify the inputs, determine the static (constant) and dynamic (variable) parts of the code, and get a general view of how the code works.

The following is a non-exhaustive list of key hints that can help you in an interview:

• If the algorithm does constant work, then the Big O is O(1): This kind of example uses the inputs to perform constant work (for example, take three integers, x, y, and w, and do some computations, such as x-y and y*w). In some cases, to create confusion, it adds repetitive statement as well (for example, the computations are done in for(int i=0; i<10; i++)). So, it is very important to settle right from the start whether the inputs of the algorithm affect its runtime or not.
• If the algorithm loops the entire array or list, then O(n) may be involved in the total Big O value: Commonly, the code snippets contain one or more repetitive statements that loop the whole input, which is usually an array or list (for example, for(int i=0; i<a.length; i++), where a is an array). Typically, these structures have a runtime of O(n). In some cases, to create confusion, the repetitive structure adds a condition that validates a break statement. Remember that Big O is about the worst-case scenario, so you should evaluate the runtime keeping in mind that the condition that validates the break statement may never happen and Big O is still O(n).
• If, at each iteration, the algorithm halves the input data, then O(log n) may be involved in the total Big O value: As you saw in Example 7, the Binary Search algorithm is a famous case of O(log n). Typically, you can identify similar cases by trying to visualize the runtime.
• A recursive problem of having branches is a good signal that O(branches depth) might be part of the total Big O value: The most common case where O(2depth) is encountered is in snippets of code that manipulate binary trees. Pay attention to how you determine the depth as well. As you saw in Example 9, the depth can influence the final result. In that case, O(2log n) was reduced to O(n).
• Recursive algorithms that use Memoization or Tabulation are good candidates for having O(n) as their total Big O value: Typically, recursive algorithms expose exponential runtimes (for example, O(2n)) but optimizations such as Memoization and Tabulation may reduce the runtime to O(n).
• Sort algorithms commonly introduce O(n log n) in the total Big O value: Keep in mind that a lot of sorting algorithms (for example, Heap Sort, Merge Sort, and so on) have a runtime of O(n log n).

I hope these hints help you as we have covered some very tried and tested examples.

Summary

In this chapter, we covered one of the most predominant topics in an interview, Big O. Sometimes, you'll have to determine Big O for a given code, while other times, you'll have to determine it for your own code. In other words, there is little chance of bypassing Big O in an interview. No matter how hard you train, Big O always remains a hard topic that can put even the best developers in trouble. Fortunately, the cases covered here are the most popular in interviews and they represent perfect templates for a lot of derived problems.

In the next chapter, we will tackle other favored topics in interviews: recursion and Dynamic Programming.