Chapter 9:

Bit Manipulation

This chapter covers the most important aspects of bit manipulation that you should know about when it forms part of a technical interview. Such problems are often encountered in interviews and they are not easy. The human mind was not designed to manipulate bits; computers were designed for that. This means that manipulating bits is quite hard and extremely prone to mistakes. Hence, it is advisable to always double-check every bit operation.

Two things are extremely important for mastering these kinds of problems, as follows:

• You must understand the theory of bits very well (for example, bit operators)
• You must practice bit manipulation as much as possible

We need to keep these two statements in mind as we tackle the following topics:

• Understanding bit manipulation
• Coding challenges

Let's start with the theoretical part. It is strongly recommended that you extract the diagrams from this section. They will be your best friends in the second part of this chapter.

Technical requirements

All the code present in this chapter can be found on GitHub at https://github.com/PacktPublishing/The-Complete-Coding-Interview-Guide-in-Java/tree/master/Chapter09.

Bit manipulation in a nutshell

In Java, we can manipulate bits of the following data types: byte (8-bit), short (16-bit), int (32-bit), long (64-bit), and char (16-bit).

For example, let's use the positive number, 51. In this situation, we have the following statements:

• The binary representation of 51 is 110011.
• Because 51 is an int, it is represented as a 32-bit value; that is, 32 values of 1 or 0 (from 0 to 31).
• All the positions to the left of 110011 are actually filled with zeros, up to 32 bits in total.
• This means that 51 is 00000000 00000000 00000000 00110011 (we render it as 110011 since the additional zeros are usually not needed for displaying the binary representation).

Obtaining the binary representation of a Java integer

How do we know that 110011 is the binary representation of 51? How can we compute the binary representation of 112 or any other Java integer? A simple approach consists of successively dividing the number by 2 until the quotient is less than 1 and interpret the remainder as 0 or 1. A remainder of 0 is interpreted as 0, while a remainder greater than 0 is interpreted as 1. For example, let's apply this to 51:

1. 51/2 = 25.5 has a quotient of 25 and a remainder of 5 -> store 1
2. 25/2 = 12.5 has a quotient of 12 and a remainder of 5 -> store 1
3. 12/2 = 6 has a quotient of 6 and a remainder of 0 -> store 0
4. 6/2 = 3 has a quotient of 3 and a remainder of 0 -> store 0
5. 3/2 = 1.5 has a quotient of 1 and a remainder of 5 -> store 1
6. 1/2 = 0.5 has a quotient of 0 and a remainder of 5 -> store 1

So, we stored 110011, which is the binary representation of 51. The rest of the 26 bits are zeros (00000000 00000000 00000000 00110011). The reverse process starts from right to left and involves adding powers of 2 where the bits are equal to 1. So here, 51 = 20+21+24+25. The following diagram can help us understand this:

Figure 9.1 – Binary to decimal (32-bit integer)

In Java, we can quickly see the binary representation of a number via Integer#toString(int i, int radix) or Integer#toBinaryString(int i). For example, a radix of 2 means binary:

// 110011

System.out.println("Binary: " + Integer.toString(51, 2));

System.out.println("Binary: " + Integer.toBinaryString(51));

The reverse process (from binary to decimal) can be obtained via Integer#parseInt(String nr, int radix):

System.out.println("Decimal: "

  + Integer.parseInt("110011", 2));  //51

Next, let's tackle bitwise operators. These operators allow us to manipulate bits, so it is very important to understand them.

Bitwise operators

Manipulating bits involves several operators. These operators are as follows:

• Unary bitwise complement operator [~]: Being unary, this operator needs a single operand that is placed before the number. This operator takes every bit of the number and flips its value, so 1 becomes 0 and vice versa; for example, 5 = 101, ~5 = 010.
• Bitwise AND [&]: This operator needs two operands and is placed between two numbers. This operator compares the bits of both numbers one by one. It acts as the logical AND (&&), meaning that it returns 1 only if the compared bits are equal to 1; for example, 5 = 101, 7 = 111, 5 & 7 = 101 & 111 = 101 = 5.
• Bitwise OR [|]: This operator needs two operands and is placed between two numbers. This operator compares the bits of both numbers one by one. It acts as the logical OR (||), meaning that it returns 1 if at least one of the compared bits is 1 (or both). Otherwise, it returns 0; for example, 5 = 101, 7 = 111, 5 | 7 = 101 | 111 = 111 = 7.
• Bitwise Exclusive OR (XOR) [^]: This operator needs two operands and is placed between two numbers. This operator compares the bits of both numbers one by one. It returns 1 only if the compared bits have a different value. Otherwise, it returns 0; for example, 5 = 101, 7 = 111, 5 ^ 7 = 101 | 111 = 010 = 2.

The following diagram is a handy tool that you should keep close when you need to deal with bits. Basically, it summarizes how bit operators work (I suggest you keep this table close when you read through the Coding challenges section):

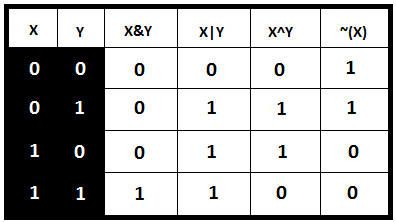
Figure 9.2 – Bitwise operators

Moreover, the following diagram represents several tips that are quite useful for manipulating bits. The 0s notation represents a sequence of zeros, while the 1s notation represents a sequence of ones:

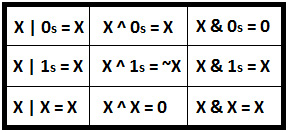
Figure 9.3 – Bitwise tips

Take your time and explore each of these tips. Take a paper and a pen and go through each of them. Moreover, try to discover other tips as well.

Bit shift operators

Shifting is a common operation when working on bits. Here, we have Signed Left Shift [<<], Signed Right Shift [>>], and Unsigned Right Shift [>>>]. Shifting works for byte (8-bit), short (16-bit), int (32-bit), long (64-bit), and char (16-bit); bit shift operators don't throw exceptions.

Signed Left Shift [<<]

Signed Left Shift, or shortly Left Shift , takes two operands. Left Shift gets the bit pattern of the first operand (left-hand side operand) and shifts it to the left by the number of positions given by the second operand (right-hand operand).

For example, the following is the result of left shifting 23 by 3 positions, 23 << 3:

Figure 9.4 – Signed Left Shift

As we can see, every bit of the integer 12 (10111) is shifted 3 positions to the left, while all the positions to the right are automatically padded with zeros.

Important note

Here are two hints that can be quite useful in certain scenarios:

1. Left shifting a number by n positions is equivalent to multiplying by 2n (for example, 23 << 3 is equal to 184, which is equivalent to 184 = 23 * 23).

2. The number of positions to shift is automatically reduced to modulo 32; that is, 23 << 35 is equivalent to 23 << (35 % 32), which is equivalent to 23 << 3.

Negative integers in Java

First of all, it is important to keep in mind that the binary representation itself doesn't tell us whether a number is negative. This means that computers need some rules for representing negative numbers. Commonly, computers store integers in what is known as the two's complement representation. Java uses this representation as well.

In short, the two's complement representation takes the binary representation of a negative number and flips (negates) all its bits. After that, it adds 1 and appends it to the left of the bit sign. If the leftmost bit is 1, then the number is negative. Otherwise, it is positive.

Let's look at the 4-bit integer, -5, as an example. We have one bit for the sign and three bits for the value. We know that 5 (positive number) is represented as 101, while -5 (negative number) is represented as 1011. This is obtained by flipping 101 so that it becomes 010, adding 1 to obtain 011 and appending it to the left of the sign bit (1) to obtain 1011. The 1 in bold is the sign bit. So, we have one bit for sign and three bits for value.

Another way to do this is to know that the binary representation of -Q (negative Q) as an n-bit number is obtained by concatenating 1 with 2n - 1 – Q.

Signed Right Shift [>>]

Signed Right Shift, or Arithmetic Right Shift [>>], takes two operands. Signed Right Shift gets the bit pattern of the first operand (left-hand side operand) and shifts it to the right by the number of positions given by the second operand (right-hand operand) by preserving the sign.

For example, the following is the result of -75 >> 1 (-75 is an 8-bit integer where the sign bit is the Most Significant Bit (MSB)):

Figure 9.5 – Signed Right Shift

As we can see, every bit of -75 (10110101) is shifted by 1 position to the right (notice that the Least Significant Bit (LSB) has changed) and the bit sign is preserved.

Important note

Here are three hints that can be quite useful in certain scenarios:

Right shifting a number by n positions is equivalent to dividing by 2n (for example, 24 >> 3 is equal to 3, which is equivalent to 3 = 24/23).

The number of positions to shift is automatically reduced to modulo 32; that is, 23 >> 35 is equivalent to 23 >> (35 % 32), which is equivalent to 23 >> 3.

A sequence of all 1s in (signed) binary terms represents -1 in decimal form.

Unsigned Right Shift [>>>]

Unsigned Right Shift, or Logical Right Shift [>>>], takes two operands. Unsigned Right Shift gets the bit pattern of the first operand (left-hand side operand) and shifts it to the right by the number of positions given by the second operand (right-hand operand). The MSB is set to 0. That means that, for positive numbers, the Signed and Unsigned Right Shift return the same result, while negative numbers always become positives.

For example, the following is the result of -75 >>> 1 (-75 is an 8-bit integer where the sign bit is the MSB):

Figure 9.6 – Unsigned Right Shift

Important note

The number of positions to shift is automatically reduced to modulo 32; that is, 23 >>> 35 is equivalent to 23 >>> (35 % 32), which is equivalent to 23 >>> 3.

Now that you have an idea of what bit shift operators are, it's time to tackle more tips and tricks.

Tips and tricks

Manipulating bits involves great skill when working with bits operators and knowing some tips and tricks. You already saw several tips earlier in this chapter. Now, let's add some more as a bullet point list:

• If we XOR[^] a number with itself for an even number of times, then the result is 0 (x ^ x = 0; x ^ x ^ x^ x = (x ^ x) ^ (x ^ x) = 0 ^ 0 = 0).
• If we XOR[^] a number with itself for an odd number of times, then the result is that number (x ^ x ^ x = (x ^ (x ^ x)) = (x ^ 0) = x; x ^ x ^ x ^ x ^ x = (x ^ (x ^ x) ^ (x ^ x)) = (x ^ 0 ^ 0) = x).
• We can compute the value of the expression p % q with p > 0, q > 0, where q is a power of 2; that is, p & (q - 1). A simple application where you can see this is ComputeModuloDivision.
• For a given positive integer p, we say that it is odd if ((p & 1) != 0) and even if ((p & 1) == 0). A simple application where you can see this is OddEven.
• For two given numbers p and q, we can say that p is equal to q if ((p ^ q) == 0). A simple application where you can see this is CheckEquality.
• For two given integers p and q, we can swap them via p = p ^ q ^ (q = p). A simple application where you can see this is SwapTwoIntegers.

Ok, it is time to tackle some coding challenges.

Coding challenges

In the next 25 coding challenges, we will exploit different aspects of bit manipulations. Since these kinds of problems are really brain-teasing, they are preferred in interviews. Understanding a snippet of code that manipulates bits is not an easy task, so take your time and dissect each problem and snippet of code. This is the only way to obtain some patterns and templates in order to solve these kinds of problems.

The following figure contains a set of four bit-mask that are important to have in your toolbelt:

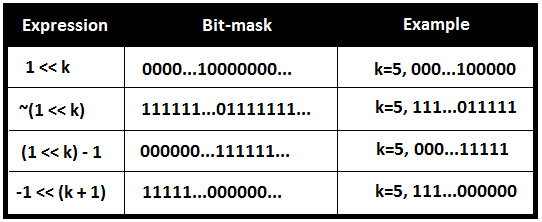
Figure 9.7 – Bit-masks

They can be useful for solving a variety of problems where you need to manipulate bits.

Coding challenge 1 – Getting the bit value

Problem: Consider a 32-bit integer, n. Write a snippet of code that returns the bit value of n at the given position, k.

Solution: Let's consider that n=423. Its binary representation is 110100111. How can we say what the value of the bit at position k=7 is (the bold bit at position 7 has a value of 1)? A solution will consist of right shifting the given number by k positions (n >> k). This way, the kth bit becomes the bit at position 0 (110100111 >> 7 = 000000011). Next, we can apply the AND [&] operator as 1 & (n >> k):

Figure 9.8 – Binary representation

If the value of the bit at position 0 is 1, then the AND[&] operator will return 1; otherwise, it will return 0. In terms of code, we have the following:

public static char getValue(int n, int k) {

  int result = n & (1 << k);

  if (result == 0) {

    return '0';

  }

  return '1';

}

Another approach consists of replacing the expression 1 & (n >> k) with the expression n & (1 << k). Take your time and try to dissect it. The complete application is called GetBitValue.

Coding challenge 2 – Setting the bit value

Amazon, Google, Adobe, Microsoft, Flipkart

Problem: Consider a 32-bit integer, n. Write a snippet of code that sets the bit value of n at the given position, k to 0 or 1.

Solution: Let's consider that n=423. Its binary representation is 110100111. How can we set the bit from position k=7, which is now 1, to 0? Having the bitwise operators table in front of us helps us see that the AND[&] operator is the only operator with two operands that allows us to write that 1 & 0 = 0 or the 7th bit & 0 = 0. Moreover, we have 1 & 1 = 1, 0 & 1 = 0 and 0 & 0 = 0, so we can take a bit-mask as 1...101111111 and write the following:

Figure 9.9 – Binary representation

This is exactly what we want. We want to turn the 7th bit from 1 into 0 and leave the rest untouched. But how do we obtain the 1...101111... mask? Well, there are two bit-masks that you need to know about. First, a bit-mask, that has a 1 and the rest are 0s (10000...). This can be obtained by left shifting 1 by k positions (for example, the bit mask 1000 can be obtained as 1 << 3, though if we represent it as a 32-bit mask, we get 00000000 00000000 00000000 0001000). The other bit-mask contains a 0, while the remainder are 1s (01111...). This can be obtained by applying the unary bitwise complement operator [~] to the bit-mask 10000.... (for example, ~(1000) = 0111, though if we represent it as a 32-bit mask, we get 11111111 11111111 11111111 1110111). So, we can obtain the 1...101111... bit-mask as ~(1 << k). Finally, all we have to do is use the AND[&] operator, as shown in the following code:

public static int setValueTo0(int n, int k) {      

  return n & ~(1 << k);

}

If we take k=3, 4, or 6, then we get 0 & 0 = 0.

Let's consider that n=295. Its binary representation is 100100111. How can we set the bit from position k=7, which is now 0, to 1? Having the bitwise operators table in front of us helps us see that the OR[|] and XOR[^] operators are the operators with two operands that allow us to write that 0 | 1 = 1 or 0 ^ 1 = 1, respectively.

Or, we can write that 7th | 1 = 1 and 7th ^ 1 = 1.

By going one step further, we can see that in the case of the OR[|] operator, we can write the following:

1 | 1 = 1, while in the case of the XOR[^] operator, we write 1 ^ 1 = 0.

Since we want to turn the 7th bit value from 0 to 1, we can use either of these two operators. However, if k indicates a bit with an initial value of 1, then 1 ^ 1 = 0 doesn't help us anymore, while 1 | 1 = 1 is exactly what we want. So here, we should use the 10000... bit-mask, as shown here:

Figure 9.10 – Binary representation

In terms of code, we have the following:

public static int setValueTo1(int n, int k) {      

  return n | (1 << k);

}

If we take k=0, 1, 2, 5, or 8, then we get 1 | 1 = 1.

The complete application is called SetBitValue.

Coding challenge 3 – Clearing bits

Amazon, Google, Adobe

Problem: Consider a 32-bit integer, n. Write a snippet of code that clears the bits of n (sets their value to 0) between the MSB and the given k.

Solution: Let's consider that n=423. Its binary representation is 110100111. How can we clear the bits between MSB and position k=6 so that there are 110 bits? Having the bitwise operators table in front of us helps us see that we need a bit-mask of type 00011111. Let's see what happens if we apply the AND[&] operator between n and this bit-mask:

Figure 9.11 – Binary representation

So, we cleared the bits between MSB and k=6. Generally speaking, we need a bit-mask that contains 0s between the MSB and k (inclusive) and 1s between k (exclusive) and LSB. We can do this by left shifting the bits of 1 with k positions (for example, for k=6, we obtain 1000000) and subtracting 1. This way, we obtain the needed bit-mask, 0111111. So, in terms of code, we have the following:

public static int clearFromMsb(int n, int k) {        

  return n & ((1 << k) - 1);

}

How about clearing the bits between the given k and the LSB? Let me show you the code:

public static int clearFromPosition(int n, int k) {        

  return n & ~((1 << k) - 1);

}

Now, take your time and dissect this solution. Moreover, we can replace this solution with this one: n & (-1 << (k + 1)).

Again, use a paper and a pen and take it step by step. The complete application is called ClearBits.

Coding challenge 4 – Summing binaries on paper

Problem: Consider several positive 32-bit integers. Take a pen and some paper and show me how you sum up their binary representation.

Note: This is not quite a coding challenge, but it is important to know about.

Solution: Summing binary numbers can be done in several ways. A simple approach is to do the following:

1. Sum all the bits of the current column (the first column is the column of LSB).
2. Convert the result into binary (for example, via successive divisions by 2).
3. Keep the rightmost bit as the result.
4. Carry the remains bits into the remaining columns (one bit per column).
5. Go to the next column and repeat from step 1.

An example will clarify things. Let's add 1 (1) + 9 (1001) + 29 (011101) + 124 (1111100) = 163 (10100011).

The following diagram represents the result of summing these numbers:

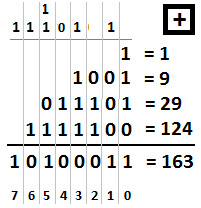
Figure 9.12 – Summing binary numbers

Now, let's see this step by step (the bold sections are carried):

• Sum bits on column 0: 1 + 1 + 1 + 0 = 3 = 11 1
• Sum bits on column 1: 1 + 0 + 0 + 0 = 1 = 1 1
• Sum bits on column 2: 0 + 1 + 1 = 2 = 10 0
• Sum bits on column 3: 1 + 1 + 1 + 1 = 4 = 100 0
• Sum bits on column 4: 0 + 1 + 1 = 2 = 10 0
• Sum bits on column 5: 1 + 1 + 0+1 = 3 = 11 1
• Sum bits on column 6: 1 + 1 = 2 = 10 0
• Sum bits on column 7: 1 = 1 = 1 1

So, the result is 10100011.

Coding challenge 5 – Summing binaries in code

Problem: Consider two 32-bit integers, q and p. Write a snippet of code that computes q + p using their binary representation.

Solution: We can try an implementation of the algorithm presented in the previous coding challenge, or we can try another approach. This approach introduces an equation that is useful to know:

Notice the presence of the AND[&] and XOR[^] bitwise operators. If we denote p & q with and, and p ^ q with xor, then we can write that as follows:

If p and q have no common bits, then we can reduce this to the following:

For example, if p = 1010 and q = 0101, then p & q = 0000. Since 2*0000 = 0, we remain with p + q = xor, or p + q = 1111.

However, if p and q have common bits, then we must deal with the addition of and and xor. So, and + xor can be solved if we force the and expression to return 0. This can be done via recursion.

Through recursion, we can write the first step of recursion as:

Alternatively, if we denote and{1} = 2 * and & xor, and xor{1} = 2 * and ^ xor where {1} means one step of recursion, then we can write this:

But when does this recursion stop? Well, it should stop when the intersection between the two bit sequences (p and q) in the and{n} expression returns 0. So, here, we forced the and expression to return 0.

In terms of code, we have the following:

public static int sum(int q, int p) {

  int xor;

  int and;

  int t;

  and = q & p;

  xor = q ^ p;

  // force 'and' to return 0

  while (and != 0) {

    and = and << 1; // this is multiplication by 2

    // prepare the next step of recursion

    t = xor ^ and;

    and = and & xor;

    xor = t;

  }

  return xor;

}

The complete application is called SummingBinaries.

Coding challenge 6 – Multiplying binaries on paper

Problem: Consider two positive 32-bit integers, q and p. Take some paper and a pen and show me how you multiply the binary representation of these two numbers (q*p).

Note: This is not quite a coding challenge, but it is important to know about.

Solution: When we multiply binary numbers, we must keep in mind that multiplying a binary number by 1 gives us back exactly the same binary number, while multiplying a binary number by 0 gives us back 0. The steps for multiplying two binary numbers are as follows:

1. Multiply every bit of the second binary number by every bit of the first binary number, starting from the rightmost column (column 0).
2. Sum up the results.

Let's do 124 (1111100) * 29 (011101) = 3596 (111000001100).

The following diagram represents the result of our computation:

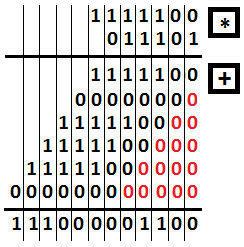
Figure 9.13 – Multiplying binary numbers

So, we multiply every bit of 29 with every bit of 124. Next, we sum up those binaries, as you saw earlier in the Coding challenge 4 – Summing binaries on paper section.

Coding challenge 7 – Multiplying binaries in code

Amazon, Google, Adobe

Problem: Consider two 32-bit integers, q and p. Write a snippet of code that computes q * p using their binary representation.

Solution: We can try an implementation of the algorithm presented in the previous coding challenge, or we can try another approach. This approach starts by assuming that p=1, so here, we have q*1=q. We know that any q multiplied by 1 is q, so we can say that q*1 follows the next sum (we go from 0 to 30, so we ignore the signed bit on position 31):

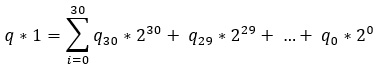
Figure 9.14 – Multiplying binaries in a code

For example, if q=5 (101), then 5 * 1 = 0*230 + 0*229 + ...1*22 + 0*21 + 1*20 = 5.

So, 5 * 1 = 5.

So far, this is not such a big deal, but let's continue with 5 * 2; that is, with 101 * 10. If we think that 5 * 2 = 5 * 0 + 10 * 1, then this means that 101 * 10 = 101 * 0 + 1010 * 1. So, we left shifted 5 by one position and we right shifted 2 by one position.

Let's continue with 5 * 3. This is 101 * 011. However, 5 * 3 = 5 * 1 + 10 * 1. Hence it is like 101 * 1 + 1010 * 1.

Let's continue with 5 * 4. This is 101 * 100. However, 5 * 4 = 5 * 0 + 10 * 0 + 20 * 1. Thus, it is like 101 * 0 + 1010 * 0 + 10100 * 1.

Now, we can start to see a pattern that follows these steps (initially, result=0):

1. If the LSB of p is 1, then we write the following:
   

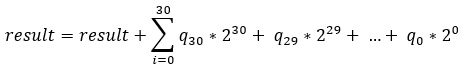
   Figure 9.15 – LSB of p is 1

2. We left shift q by one position and logical right shift p by one position.
3. We repeat from step 1 until p is 0.

If we put these three steps into code, then we obtain the following output:

public static int multiply(int q, int p) {

  int result = 0;

  while (p != 0) {

    // we compute the value of q only when the LSB of p is 1            

    if ((p & 1) != 0) {

      result = result + q;

    }

    q = q << 1;  // q is left shifted with 1 position

    p = p >>> 1; // p is logical right shifted with 1 position

  }

  return result;

}

The complete application is called MultiplyingBinaries.

Coding challenge 8 – Subtracting binaries on paper

Problem: Consider two positive 32-bit integers, q, and p. Take some paper and a pen and show me how you subtract the binary representation of these two numbers (q-p).

Note: This is not quite a coding challenge, but it is important to know about.

Solution: Subtracting binary numbers can be reduced in order to compute 0 minus 1. Mainly, we know that 1 minus 1 is 0, 0 minus 0 is 0, and 1 minus 0 is 1. To compute 0 minus 1, we must follow these steps:

1. From the current column, we search the left column(s) until we find a bit of 1.
2. We borrow this bit and put it in the preceding column as two values of 1.
3. We then borrow one of these two values of 1 from the preceding column as other two of 1.
4. Repeat step 3 for each column until we reach the current column.
5. Now, we can perform the computation.
6. If we encounter another 0 minus 1, then we repeat this process from step 1.

Let's do 124 (1111100) - 29 (011101) = 95 (1011111).

The following diagram represents the result of our computation:

Figure 9.16 – Subtracting binary numbers

Now, let's see this step by step:

1. Start from column 0, so from 0 minus 1. We search in the left column(s) until we find a bit of 1. We find it at column 2 (this bit corresponds to 22=4). We borrow this bit in column 1 and use it as two values of 1 (in other words, two of 2 is 21+21). We borrow one of these two values of 1 (this is 21=2) in column 0 and use them as two other two values of 1 (in other words, two of 1 is 20+20). Now, we can do the computation as 2 minus 1 equals 1. We write down 1 and move on to column 1.
2. We continue with column 1, so with 1 minus 0 equals 1. We write down 1 and we move to column 2.
3. We then continue with column 2, so with 0 minus 1. We search in the left column(s) until we find a bit of 1. We find it at column 3 (this bit corresponds to 23=8). We borrow this bit from column 2 and use it as two values of 1 (in other words, two of 2 is 22+22). Now, we can do the computation as 2 minus 1 equals 1. We write down 1 and we move to column 3.
4. We continue with column 3, so with 0 minus 1. We search in the left column(s) until we find a bit of 1. We find it at column 4 (this bit corresponds to 24=16). We borrow this bit in column 3 and use it as two values of 1 (in other words, two of 2 is 23+23). Now, we can do the computation as 2 minus 1 equals 1. We write down 1 and we move to column 4.
5. We continue with column 4, so with 0 minus 1. We search in the left column(s) until we find a bit of 1. We find it at column 5 (this bit corresponds to 25=32). We borrow this bit in column 4 and use it as two values of 1 (in other words, two of 2 is 24+24). Now, we can do the computation as 2 minus 1 equals 1. We write down 1 and we move to column 5.
6. We continue with column 5, so with 0 minus 0. We write down 0 and we move to column 6.
7. We continue with column 6, so with 1 minus 0. We write down 1 and then we're done.

So, the result is 1011111.

Coding challenge 9 – Subtracting binaries in code

Problem: Consider two 32-bit integers, q and p. Write a snippet of code that computes q - p using their binary representation.

Solution: We already know from the previous coding challenge that subtracting binary numbers can be reduced to compute 0 minus 1. Moreover, we know how to solve 0 minus 1 by using the borrowing technique. Besides the borrowing technique, it is important to notice that |q - p| = q ^ p; for example:

|1 - 1| = 1 ^ 1 = 0, |1 - 0| = 1 ^ 0 = 1, |0 - 1| = 0 ^ 1 = 1 and |0 - 0| = 0 ^ 0 = 0.

Based on these two statements, we can implement the subtraction of two binaries, as follows:

public static int subtract(int q, int p) {

  while (p != 0) {

    // borrow the unset bits of q AND set bits of p

    int borrow = (~q) & p;

    // subtraction of bits of q and p

    // where at least one of the bits is not set

    q = q ^ p;

    // left shift borrow by one position            

    p = borrow << 1;

  }

  return q;

}

The complete application is called SubtractingBinaries.

Coding challenge 10 – Dividing binaries on paper

Problem: Consider two positive 32-bit integers, q and p. Take some paper and a pen and show me how you divide the binary representation of these two numbers (q/p).

Note: This is not quite a coding challenge, but it is important to know about.

Solution: In binary division, there are only two possibilities: either 0 or 1. Division involves the dividend (q), the divisor (p), the quotient, and the remainder. For example, we know that 11(dividend) / 2(divisor) = 5(quotient) 1(remainder). Or, in binary representation, we have 1011(dividend) / 10 (divisor) = 101(quotient) 1(remainder)

We start by comparing the divisor with the MSB of the dividend (let's call this the sub-dividend) and do the following:

a. If the divisor doesn't fit into the sub-dividend (divisor > sub-dividend), then we append 0 to the quotient.

a.a) We append the next bit of the dividend to the sub-dividend and continue from step a).

b. If the divisor fits into the sub-dividend (divisor <= sub-dividend), then we append 1 to the quotient.

b.a) We subtract the divisor from the current sub-dividend.

b.b) We append the next bit of the dividend to the result of the subtraction (this is the new sub-dividend) and we repeat from step a).

c. When we've processed all the bits of the dividend, we should have the quotient and the remainder, which is the result of the division.

c.a) We can stop here and express the result in terms of the obtained quotient and the remainder.

c.b) We can append a dot (".") to the quotient and a 0 to the current remainder (this is the new sub-dividend) and continue from step a until the remainder is 0 or we are satisfied by the result.

The following diagram represents the 11/2 division:

Figure 9.17 – Dividing binary numbers

Now, let's see this step by step (focus on the left-hand side of the preceding diagram):

• Sub-dividend = 1, 10 > 1 since 2 > 1, therefore we append 0 to the quotient.
• Sub-dividend = 10, 10 = 10 since 2 = 2, therefore we append 1 to the quotient.
• Do subtraction, 10 - 10 = 0.
• Sub-dividend = 01, 10 > 01 since 2 > 1, therefore we append 0 to the quotient.
• Sub-dividend = 011, 10 < 011 since 2 < 3, therefore we append 1 to the quotient.
• Do subtraction, 011 - 10 = 1.
• There are no more bits to process from the dividend, so we can say that 11/2 has the quotient 101 (which is 5) and that the remainder is 1.

If you look at the right-hand side of the preceding diagram, then you will see that we can continue the computation until the remainder is 0 by applying the step c.b given.

Coding challenge 11 – Dividing binaries in code

Amazon, Google, Adobe

Problem: Consider two 32-bit integers, q and p. Write a snippet of code that computes q/p using their binary representation.

Solution: There are several approaches we can use to divide two binaries. Let's focus on implementing a solution that computes only the quotient, which means we skip the remainder.

This approach is quite straightforward. We know that a 32-bit integer contains the bits that count for us between 31 and 0. All we have to do is left shift the divisor (p) by i positions (i=31, 30, 29, ..., 2, 1, 0) and check if the result is less than the dividend (q). Each time we find such a bit, we update the ith bit position. We accumulate the result and pass it to the next position. The following code speaks for itself:

private static final int MAX_BIT = 31;

...

public static long divideWithoutRemainder(long q, long p) {

  // obtain the sign of the division

  long sign = ((q < 0) ^ (p < 0)) ? -1 : 1;

  // ensure that q and p are positive

  q = Math.abs(q);

  p = Math.abs(p);

  long t = 0;

  long quotient = 0;

  for (int i = MAX_BIT; i >= 0; --i) {

    long halfdown = t + (p << i);

    if (halfdown <= q) {

      t = t + p << i;

      quotient = quotient | 1L << i;

    }

  }

  return sign * quotient;

}

The complete application is called DividingBinaries. It also contains the implementation that computes the remainder.

Coding challenge 12 – Replacing bits

Amazon, Google, Adobe

Problem: Consider two positive 32-bit integers, q and p, and two bit positions, i and j. Write a snippet of code that replaces the bits from q between positions i and j with the bits of p. You can assume that, between i and j, there is enough space to fit all bits of p.

Solution: Let's consider that q=4914 (in binary, 1001100110010), p=63 (in binary, 111111), i=4, and j=9. The following diagram shows what we have and what we want to obtain:

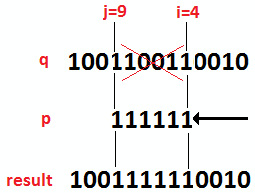
Figure 9.18 – Replacing the bits between i and j

As we can see, the solution should accomplish three main steps. First, we need to clear the bits of q between i and j. Second, we need to left shift p by i positions (this way, we place p in the right position). Finally, we merge p and q in the final result.

In order to clear the bits of q between i and j (set those bits to 0, no matter their initial value), we can use the AND[&] operator. We know that only 1 & 1 return 1, so if we have a bit-mask that contains 0s between i and j, then q & bit mask will result in a sequence of bits containing only 0s between i and j since 1 & 0 and 0 & 0 are 0. Moreover, between the MSB and j (exclusive), and i (exclusive) and the LSB of the bit mask, we should have only values of 1. This way, q & bit mask will preserve the q bits since 1 & 1 = 1 and 0 & 1 = 0. So, our bit mask should be 1110000001111. Let's see it at work:

Figure 9.19 – Bit-mask (a)

But how can we obtain this mask? We can obtain it via the OR[|] operator, as follows:

Figure 9.20 – Bit-mask (b)

The 1110000000000 bit mask can be obtained by left shifting -1 by j+1 positions, while the 0000000001111 bit mask can be obtained by left shifting 1 by i positions and subtracting 1.

Here, we solved the first two steps. Finally, we need to put p in the right position. This is easy: we just left shift p by i positions. Finally, we apply the OR[|] operator between q with cleared bits between i and j, and the shifted p:

Figure 9.21 – Binary representation

We're done! Now, let's put this into code:

public static int replace(int q, int p, int i, int j) {

  int ones = ~0; // 11111111 11111111 11111111 11111111          

  int leftShiftJ = ones << (j + 1);

  int leftShiftI = ((1 << i) - 1);

  int mask = leftShiftJ | leftShiftI;

  int applyMaskToQ = q & mask;

  int bringPInPlace = p << i;

  return applyMaskToQ | bringPInPlace;

}

The complete application is called ReplaceBits.

Coding challenge 13 – Longest sequence of 1

Amazon, Adobe, Microsoft, Flipkart

Problem: Consider a 32-bit integer, n. A sequence of 101 can be considered 111. Write a snippet of code that computes the length of the longest sequence of 1.

Solution: We will look at several examples (the following three columns represent the integer number, its binary representation, and the length of the longest sequence of 1):

Figure 9.22 – Three examples

The solution to this problem is quite easy to implement if we know that n & 1 = 1 if the LSB of n is 1 and n & 0 = 0 if the LSB of n is 0. Let's focus on the first example, 67534 (10000011111001110). Here, we do the following:

• Initialize the longest sequence = 0.
• Apply AND[&]:10000011111001110 & 1 = 0, longest sequence = 0.
• Right shift and apply AND[&]:1000001111100111 & 1 = 1, longest sequence = 1.
• Right shift and apply AND[&]:100000111110011 & 1 = 1, longest sequence = 2.
• Right shift and apply AND[&]:10000011111001 & 1 = 1, longest sequence = 3.
• Right shift and apply AND[&]:1000001111100 & 1 = 0, longest sequence = 0
• Right shift and apply AND[&]:100000111110 & 1 = 0, longest sequence = 0.
• Right shift and apply AND[&]:10000011111 & 1 = 1, longest sequence = 1.
• Right shift and apply AND[&]:1000001111 & 1 = 1, longest sequence = 2.
• Right shift and apply AND[&]:100000111 & 1 = 1, longest sequence = 3.
• Right shift and apply AND[&]:10000011 & 1 = 1, longest sequence = 4.
• Right shift and apply AND[&]:1000001 & 1 = 1, longest sequence = 5.
• Right shift and apply AND[&]:100000 & 1 = 0, longest sequence = 0.

So, as long as we don't have any 0s interleaved in the longest sequence of 1, we can implement the preceding approach. However, this approach does not work for the third case, 339809 (1010010111101100001). Here, we need to do some additional checks; otherwise, the longest sequence will have a length equal to 4. But since 101 can be treated as 111, the correct answer is 9. This means that when we have n & 1 = 0, we must perform the following checks (mainly, we check that the current bit of 0 is guarded by two bits of 1 as 101):

• Check that the next bit is 1 or 0, (n & 2) == 1 or 0
• If the next bit is 1, then check whether the previous bit was 1

We can put this into code as follows:

public static int sequence(int n) {

  if (~n == 0) {

    return Integer.SIZE; // 32

  }

  int currentSequence = 0;

  int longestSequence = 0;

  boolean flag = true;

  while (n != 0) {

    if ((n & 1) == 1) {

      currentSequence++;

      flag = false;

    } else if ((n & 1) == 0) {

      currentSequence = ((n & 0b10) == 0) // 0b10 = 2

        ? 0 : flag

        ? 0 : ++currentSequence;

      flag = true;

    }

    longestSequence = Math.max(

      currentSequence, longestSequence);

    n >>>= 1;

  }

  return longestSequence;

}

The complete application is called LongestSequence.

Coding challenge 14 – Next and previous numbers

Adobe, Microsoft

Problem: Consider a 32-bit integer, n. Write a snippet of code that returns the next largest number that contains exactly the same number of 1 bits.

Solution: Let's consider that n=124344 (11110010110111000). To obtain another number with the same number of 1 bits, we have to flip a bit of 1 to turn it into 0 and another bit of 0 to turn it into 1. The resulting number will be different from the given one and will contain the same number of 1 bits. Now, if we want this number to be bigger than the given one, then the bit that was flipped from 0 to 1 should be at the left of the bit that was flipped from 1 to 0. In other words, having two bit positions, i and j, and flipping the bit at position i from 1 to 0 and the bit at position j from 0 to 1, this will result in the new number being smaller than the given number if i > j, while bigger if i < j, respectively.

This means that we must find the first bit of 0 that doesn't contain only zeros on its right (in other words, the first bit of non-trailing zero). This way, if we flip this bit from 0 to 1, then we know that there is at least one bit of 1 in the right of this bit that can be flipped from 1 to 0. This means that we obtain a bigger number with the same number of 1 bits. The following diagram shows these numbers in pictorial form:

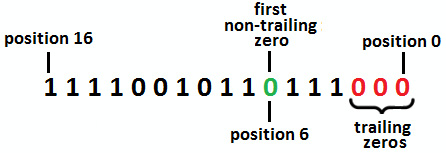
Figure 9.23 – The non-trailing zero

So, for our number, the first non-trailing zero is at bit 6. If we flip this bit from 0 to 1, then the resulting number is bigger than the given number. But now, we must choose a bit, from the right of this bit, that will flip from 1 to 0. Basically, we must choose between the bits from positions 3, 4, and 5. However, is this the proper logic? Remember that we must return the next largest number, NOT any number larger than the given one. Flipping the bit at position 5 is better than flipping the bit from position 3 or 4, but this is not the next largest number. Check out the following relationships (the subscript is the decimal value corresponding to the binary representation):

Figure 9.24 – Several relationships

So far, we can conclude that 11110010111011000124376 looks like the proper choice. However, we should also take note of the following:

11110010111011000124376 > 11110010111000011124355

So, the next largest number is obtained if we count the number of bits of 1 between positions 6 (exclusive) and 0 (let's denote it with k=3), clear all the bits between positions 6 (exclusive) and 0 (set them to 0), and set k-1 bits to 1 between positions k-1 and 0.

OK; so far, so good! Now, let's put this algorithm into code. First, we need to find the position of the first bit of non-trailing zero. This means we need to sum the count of trailing zeros with the count of 1s until we get the first 0. Counting the trailing zeros can be done as follows (we are working on a copy of n since we don't want to shift the bits of the given number):

int copyn = n;

int zeros = 0;

while ((copyn != 0) && ((copyn & 1) == 0)) {

  zeros++;

  copyn = copyn >> 1;

}

Counting the 1s until the first 0 can be done like so:

int ones=0;

while ((copyn & 1) == 1) {

  ones++;

  copyn = copyn >> 1;

}

Now, marker = zeros + ones gives us the searched position. Next, we flip the bit from this position from 0 to 1 and clear all the bits between this position (exclusive) and 0:

n = n | (1 << marker);

In our case, marker=6. The effect of this line produces the following output:

Figure 9.25 – Output (1)

n = n & (-1 << marker);

Figure 9.26 – Output (2)

Finally, we set the bits between (ones - 1) and 0 to 1:

n = n | (1 << (ones - 1)) - 1;

In our case, ones=3. The effect of this line produces the following output:

Figure 9.27 – Output (3)

So, the final result is 11110010111000011, which is 124355. So, the final method looks as follows:

public static int next(int n) {

  int copyn = n;

  int zeros = 0;

  int ones = 0;

  // count trailing 0s

  while ((copyn != 0) && ((copyn & 1) == 0)) {

    zeros++;

    copyn = copyn >> 1;

  }

  // count all 1s until first 0

  while ((copyn & 1) == 1) {

    ones++;

    copyn = copyn >> 1;

  }

  // the 1111...000... is the biggest number

  // without adding more 1

  if (zeros + ones == 0 || zeros + ones == 31) {

    return -1;

  }

  int marker = zeros + ones;

  n = n | (1 << marker);

  n = n & (-1 << marker);

  n = n | (1 << (ones - 1)) - 1;

  return n;

}

The complete application is called NextNumber. It also contains a method that returns the next smallest number that contains exactly the same number of 1 bits. Take up the challenge and try to provide a solution by yourself. When you're done, just confront your solution with the one from the bundled code. As a hint, you will need the number of trailing 1s (let's denote this with k) and the number of 0s immediately to the left of the trailing 1s until you reach the first 1. Summing up these values will give you the position of the bit that should be flipped from 1 to 0. Next, clear up all the bits to the right of this position and set (k + 1) bits to 1 immediately to the right of this position.

Coding challenge 15 – Conversion

Amazon, Google, Adobe

Problem: Consider two positive 32-bit integers, q and p. Write a snippet of code that counts the number of bits that we should flip in q in order to convert it into p.

Solution: The solution to this problem becomes clear if we observe that the XOR[^] operator only returns 1 when the operands are different. Let's consider q = 290932 (1000111000001110100) and p = 352345 (1010110000001011001). Let's apply the XOR[^] operator:

Figure 9.28 – Conversion

In other words, if we denote q ^ p with xor (xor = q ^ p), then all we have to do is count the number of bits of 1 in xor (in our example, we have six of 1). This can be done using the AND[&] operator, which only returns 1 for 1 & 1 = 1, so we can count xor & 1 for each bit in xor. After each comparison, we right shift xor by one position. The code speaks for itself:

public static int count(int q, int p) {

  int count = 0;

  // each 1 represents a bit that is

  // different between q and p

  int xor = q ^ p;

  while (xor != 0) {

    count += xor & 1; // only 1 & 1 = 1

    xor = xor >> 1;

  }

  return count;

}

The complete application is called Conversion.

Coding challenge 16 – Maximizing expressions

Problem: Consider two positive 32-bit integers, q and p, where q≠ p. What is the relationship between q and p that maximizes the expression (q AND s) * (p AND s), where AND is the logical operator [&]?

Solution: This is the kind of problem that sounds hard but is extremely simple. Let's start with a simple a * b. When is a * b at its maximum? Well, let's consider that b = 4. When is a * 4 at its maximum? Let's write some test cases:

a = 1, 1 * 4 = 4

a = 2, 2 * 4 = 8

a = 3, 3 * 4 = 12

a = 4, 4 * 4 = 16

So, when a = b, we have reached the maximum value, 16. However, a can be 5 and 5 * 4 = 20 > 16. This is correct, but this means that b can be 5 as well, so 5 * 5 =, 25 > 20. This is far away from a mathematical demonstration, but we can notice that a * b is at its maximum if a = b.

For those interested in the mathematical demonstration, let's say that we have the following:

Figure 9.29 – Maximizing expressions (1)

This means that we have the following:

Figure 9.30 – Maximizing expressions (2)

Furthermore, this means that we have the following:

Figure 9.31 – Maximizing expressions (3)

Now, if we say that a * b is the maximum when a = b, then let's denote a = (q AND s) and b = (p AND s). So, (q AND s) * (p AND s) is at its maximum when (q AND s) = (p AND s).

Let's consider that q = 822 (1100110110) and p = 663 (1010010111). The LSB of q is 0, while the LSB of p is 1, so we can write the following:

(1 AND s) = (0 AND s) → s = 0 → (1 & 0) = (0 & 0) = 0

If we right shift q and p by 1 position, then we find that the LSB of q is 1 and that the LSB of p is 1:

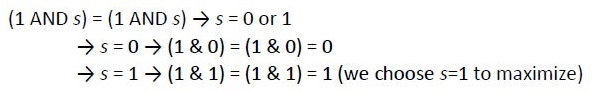
Figure 9.32 – Right shifting q and p by 1 position

Here, we have two more cases that can be intuited as follows:

Figure 9.33 – Two cases

Here, we can see that the answer to our problem is q & p = s. Let's see this at work:

Figure 9.34 – Answer

The answer is 1000010110, which is 534. This means that (822 AND 534) = (663 AND 534).

Coding challenge 17 – Swapping odd and even bits

Adobe, Microsoft, Flipkart

Problem: Consider a positive 32-bit integer, n. Write a snippet of code that swaps the odd and even bits of this integer.

Solution: Let's consider that n = 663 (1010010111). If we perform the swap manually, then we should obtain 0101101011. We can do this in two steps:

1. We take the odd bits and shift them to the right by one position.
2. We take the even bits and shift them to the left by one position.

But how we can do this?

We can take the odd bits via the AND[&] operator and a bit-mask that contains bits of 1 in the odd positions: 10101010101010101010101010101010. Let's see this in action:

Figure 9.35 – Swapping odd and even bits (1)

The result reveals that 1010010111 contains the odd bits of 1 at positions 1, 7, and 9. Next, we shift the result, 1010000010, to the right by one position. This results in 0101000001.

We can take the even bits via the AND[&] operator and a bit-mask that contains bits of 1 in the even positions: 1010101010101010101010101010101. Let's see this in action:

Figure 9.36 – Swapping odd and even bits (2)

The result reveals that 1010010111 contains the even bits of 1 at positions 0, 2, and 4. Next, we shift the result, 0000010101, to the left by one position. This results in 0000101010.

To obtain the final result, we just need to apply the OR[|] operator to these two results:

Figure 9.37 – Final result

The final result is 0101101011. The implementation follows these steps ad litteram, so this is straightforward:

public static int swap(int n) {

  int moveToEvenPositions

    = (n & 0b10101010101010101010101010101010) >>> 1;

  int moveToOddPositions

    = (n & 0b1010101010101010101010101010101) << 1;

  return moveToEvenPositions | moveToOddPositions;

}

The complete application is called SwapOddEven.

Coding challenge 18 – Rotating bits

Amazon, Google, Adobe, Microsoft, Flipkart

Problem: Consider a positive 32-bit integer, n. Write a snippet of code that rotates k bits to the left or the right. By rotation, we understand that the bits that fall off at one end of the binary representations are sent to the other end. So, in the left rotation, the bits that fall off the left end are sent to the right end, while in the right rotation, the bits that fall off the right end are sent to the left end.

Solution: Let's focus on the left rotation (typically, the right rotation solution is a mirrored left rotation solution). We already know that by shifting k bits to the left, we move the bits to the left and the empty spots are padded with zeros. However, in place of these zeros, we have to put the bits that fell off the left end.

Let's consider that n= 423099897 (00011001001101111111110111111001) and k=10, so we rotate 10 bits to the left. The following diagram highlights the falling bits and the final result:

Figure 9.38 – Left rotating bits

The preceding diagram gives us the solution. If we look carefully at points b) and c), we will see that the fallen bits appear in the final result. This result can be obtained by right shifting the fallen bits by 32-10 = 22 positions.

So, if we left shift n by 10 positions, we obtain a binary representation padded with zeros on the right-hand side (as in point b) of the preceding diagram or the dividend of the next division). If we right shift n by 22 positions, we obtain a binary representation padded with zeros on the left-hand side (as the divisor of the next division). At this point, the OR[|] operator enters the scene, as shown in the following example:

Figure 9.39 – Applying the OR[|] operator

The final result of the left rotation is 11011111111101111110010001100100. Now, we can easily put this into code, as follows:

public static int leftRotate(int n, int bits) {

  int fallBits = n << bits;

  int fallBitsShiftToRight = n >> (MAX_INT_BITS - bits);

  return fallBits | fallBitsShiftToRight;

}

Now, challenge yourself by implementing the right rotation.

For the right rotation, the code will look as follows (you should be able to follow this solution with no issues):

public static int rightRotate(int n, int bits) {

  int fallBits = n >> bits;

  int fallBitsShiftToLeft = n << (MAX_INT_BITS - bits);

  return fallBits | fallBitsShiftToLeft;

}

The complete application is called RotateBits.

Coding challenge 19 – Calculating numbers

Problem: Consider two positions, i and j (j > i), representing the positions of two bits in a binary representation. Write a snippet of code that returns a 32-bit integer containing 1s (set) between i (inclusive) and j (inclusive) and where the rest of the bits are 0s (unset).

Solution: Let's consider that i=3 and j=7. We know that the required 32-bit integer is 248, or, in binary representation, 11111000 (or with all 0s, 00000000000000000000000011111000).

If you paid attention to Coding challenge 8 – Subtracting binaries on paper, then you should know that 0 minus 1 is an operation that can be accomplished by borrowing a bit from the left of the current bit. The borrowing technique is propagated to the left until a bit of 1 is found. Moreover, if we remember that 1 minus 0 is 1, then we can write the following subtraction:

Figure 9.40 – Subtraction

Look at the result of this subtraction. The 1s are exactly between positions i=3 (inclusive) and j=7 (inclusive). This is exactly the number that we are looking for: 248. The dividend and the divisor are obtained by left shifting 1 by (j+1) positions and by i positions, respectively.

With these statements in place, it is very easy to put them into code:

public static int setBetween(int left, int right) {

  return (1 << (right + 1)) - (1 << left);

}

The complete application is called NumberWithOneInLR.

Coding challenge 20 – Unique elements

Amazon, Google, Adobe, Microsoft, Flipkart

Problem: Consider a given array of integers, arr. Every element from this array occurs exactly three times, except for one element, which occurs only once. This makes it unique. Write a snippet of code that finds this unique element in O(n) complexity time and O(1) extra space.

Solution: Let's consider that the given array is arr={4, 4, 3, 1, 7, 7, 7, 1, 1, 4}, so 3 is the unique element. If we write the binary representation of these numbers, we obtain the following: 100, 100, 011, 001, 111, 111, 111, 001, 001, 100. Now, let's sum up the bits at the same positions and check whether the resulting sums are multiples of 3, as follows:

• Sum of first bits % 3 = 0+0+1+1+1+1+1+1+1+0 = 7 % 3 = 1
• Sum of second bits % 3 = 0+0+1+0+1+1+1+0+0+0 = 4 % 3 = 1
• Sum of third bits % 3 = 1+1+0+0+1+1+1+0+0+1 = 6 % 3 = 0

The unique number is 011 = 3.

Let's take a look at another example. This time, arr={51, 14, 14, 51, 98, 7, 14, 98, 51, 98}, so 7 is the unique element. Let's apply the same logic we used previously to the binary representation: 110011, 1110, 1110, 110011, 1100010, 111, 1110, 1100010, 110011, 1100010. This time, let's use a diagram since this makes things clearer:

Figure 9.41 – Finding the unique element in the given array

So, based on these two examples, we can elaborate the following algorithm:

1. Sum up the bits on the same positions.
2. For each sum, compute the modulus 3.
3. If sum % 3 = 0 (sum is a multiple of 3), this means that the bit is set in the elements that appear thrice among the given elements.
4. If sum % 3 ! = 0 (sum is not a multiple of 3), this means that the bit is set in the element that appears once (but it is not sure if that bit is unset or set in the elements that appear thrice).
5. We have to repeat steps 1, 2, and 3 for all the given elements and for all the positions of the bits. By doing this, we will get the element that appears only once, exactly as you saw in the preceding diagram.

The code for this is as follows:

private static final int INT_SIZE = 32;

public static int unique(int arr[]) {

  int n = arr.length;

  int result = 0;

  int nr;

  int sumBits;

  // iterate through every bit

  for (int i = 0; i < INT_SIZE; i++) {

    // compute the sum of set bits at

    // ith position in all array

    sumBits = 0;

    nr = (1 << i);

    for (int j = 0; j < n; j++) {

      if ((arr[j] & nr) == 0) {

        sumBits++;

      }

    }

    // the sum not multiple of 3 are the

    // bits of the unique number

    if ((sumBits % 3) == 0) {                

      result = result | nr;

    }

  }

  return result;

}

This was one approach to solving this problem. Another approach starts from the fact that the XOR[^] operator, when applied to the same number twice, returns 0. Moreover, the XOR[^] operator is associative (gives the same result, regardless of grouping: 1 ^ 1 ^ 2 ^ 2 = 1 ^ 2 ^ 1 ^ 2 = 0) and commutative (independent of order: 1 ^ 2 = 2 ^ 1). However, if we XOR[^] the same number three times, then the result will be the same number, so using XOR[^] on all the numbers will not be helpful here. However, we can employ the following algorithm:

Use a variable to note that the variable appeared for the first time.

1. For each new element, put the XOR[^] of it in a variable, oneAppearance.
2. If the element appears a second time, then it will be removed from oneAppearance and we put the XOR[^] of it in another variable, twoAppearances.
3. If the element appears a third time, then it will be removed from oneAppearance and twoAppearances . The oneAppearance and twoAppearances variables become 0 and we start looking for a new element.
4. For all the elements that appear three times, the oneAppearance and twoAppearances variables will be 0. On the other hand, for the element that appears only once, the oneAppearance variable will be set with that value.

In terms of code, this looks as follows:

public static int unique(int arr[]) {

  int oneAppearance = 0;

  int twoAppearances = 0;

  for (int i = 0; i < arr.length; i++) {

    twoAppearances = twoAppearances

        | (oneAppearance & arr[i]);

    oneAppearance = oneAppearance ^ arr[i];

    int neutraliser = ~(oneAppearance & twoAppearances);

    oneAppearance = oneAppearance & neutraliser;

    twoAppearances = twoAppearances & neutraliser;

  }

  return oneAppearance;

}

The runtime of this code is O(n) with O(1) extra time. The complete application is called OnceTwiceThrice.

Coding challenge 21 – Finding duplicates

Amazon, Google, Adobe, Microsoft, Flipkart

Problem: Consider that you're given an array of integers ranging from 1 to n, where n can be, at most, 32,000. The array may contain duplicates and you don't know the value of n. Write a snippet of code that prints all the duplicates from the given array using only 4 kilobytes (KB) of memory.

Solution: The solution should start from the fact that 4 KB of memory is the equivalent to 4 * 8 * 210 bits. Since 4 * 8 * 210 is greater than 32,000, we can create a vector of 32,000 bits and represent each integer as 1 bit. There is no need to write our own implementation for a vector of bits; we can simply use Java's built-in BitSet class (this class implements a vector of bits that grows as needed).

With a BitSet, we can iterate the given array and, for each traversed element, flip the bit from the corresponding index from 0 to 1. If we attempt to flip a bit that is already 1, then we find and print a duplicate. The code for this is quite simple:

  private static final int MAX_N = 32000;

  public static void printDuplicates(int[] arr) {

    BitSet bitArr = new BitSet(MAX_N);

    for (int i = 0; i < arr.length; i++) {

      int nr = arr[i];

      if (bitArr.get(nr)) {                

        System.out.println("Duplicate: " + nr);

      } else {

        bitArr.set(nr);

      }

    }

  }

The complete application is called FindDuplicates.

Coding challenge 22 – Two non-repeating elements

Amazon, Google, Adobe

Problem: Consider that you're given an array of integers containing 2n+2 elements. The 2n elements are n elements repeated once. So, each element in 2n appears twice in the given array. The remaining two elements appear only once. Write a snippet of code that finds these two elements.

Solution: Let's consider that the given array is arr={2, 7, 1, 5, 9, 4, 1, 2, 5, 4}. The two numbers that we are looking for are 7 and 9. These two numbers appear only once in the array, while 2, 1, 5, and 4 appear twice.

If we consider the brute-force approach, then it is quite intuitive to iterate the array and check the number of occurrences for each element. But the interviewer will not be impressed by this solution since its runtime is O(n2).

Another approach consists of sorting the given array. This way, the repeated elements are grouped together so that we can count the number of occurrences for each group. The group of size 1 represents a non-repeated value. It is good to mention this approach during the process of finding a better solution.

A better solution relies on hashing. Create a Map<Element, Count> and fill it with elements and the number of occurrences (for example, for our data, we will have the following pairs: (2, 2), (7, 1), (1, 2), (5, 2), (9, 1), and (4, 2)). Now, traverse the map and locate the elements whose count is 1. It is good to mention this approach during the process of finding a better solution.

In this chapter, we are dealing with bits, so the best solution should rely on bit manipulation. This solution relies on the XOR[^] operator and a tip that we mentioned in the Tips and tricks section:

• If we XOR[^] a number with itself for an even number of times, then the result is as follows 0 (x ^ x = 0; x ^ x ^ x^ x = (x ^ x) ^ (x ^ x) = 0 ^ 0 = 0)

On the other hand, if we apply the XOR[^] operator to two different numbers, p and q, then the result is a number that contains the set of bits (bits of 1) at the places where p and q differ. This means that if we apply XOR[^] to all the elements in the array (xor = arr[0]^arr[1]^arr[2] ^ ... ^ arr[arr.length-1]), then all the repeating elements would nullify each other.

So, if we take any set bit (for example, the rightmost bit) of the result of XOR[^] and divide the elements of the array into two sets, then one set will contain elements with the same bit set and the other set will contain elements with the same bit not set. In other words, we divide the elements into two sets by comparing the rightmost set bit of XOR[^] with the bit at the same position in each element. By doing so, we will get p in one set and q in the other set.

Now, if we apply the XOR[^] operator to all the elements in the first set, then we will get the first non-repeating element. Doing the same in the other set will get the second non-repeating element.

Let's apply this flow to our data, arr={2, 7, 1, 5, 9, 4, 1, 2, 5, 4}. So, 7 and 9 are the non-repeating values. First, we apply the XOR[^] operator to all the numbers:

xor = 2 ^ 7 ^ 1 ^ 5 ^ 9 ^ 4 ^ 1 ^ 2 ^ 5 ^ 4 = 0010 (2) ^ 0111 (7) ^ 0001 (1) ^ 0101 (5) ^ 1001 (9) ^ 0100 (4) ^ 0001 (1) ^ 0010 (2) ^ 0101 (5) ^ 0100 (4) = 1110 = 7 ^ 9 = 0111 & 1001 = 1110 = 14.

So, 7 ^ 9 ! = 0 if 7 ! = 9. Hence, there will be at least one set bit (at least one bit of 1). We can take any set bit, but it is quite simple to take the rightmost bit as xor & ~(xor-1). So, we have 1110 & ~(1101) = 1110 & 0010 = 0010. Feel free to take any other set bit.

So far, we found this set bit (0010) in XOR[^] of these two numbers (7 and 9), so this bit must be present in 7 or 9 (in this case, it is present in 7). Next, let's divide the elements into two sets by comparing the rightmost set bit of XOR[^] with the bit at the same position in each element. We obtain the first set, containing the elements {2, 7, 2}, and the second set, containing the elements {1, 5, 9, 4, 1, 5, 4}. Since 2, 7, and 2 contain the set bit, they are in the first set, while 1, 5, 9, 4, 1, 5, and 4 don't contain the set bit, which means they are part of the second set.

With that, we've isolated the first non-repeated element (7) in a set and put the second non-repeated element (9) in the other set. Moreover, each repeated element will be in the same set of bit representations (for example, {2, 2} will always be in the same set).

Finally, we apply XOR[^] to each set. So, we have xor_first_set = 2 ^ 7 ^ 2 = 010 ^ 111 ^ 010 = 111 = 7 (the first non-repeated element).

For the second set, we have:

xor_second_set = 1 ^ 5 ^ 9 ^ 4 ^ 1 ^ 5 ^ 4 = 0001 ^ 0101 ^ 1001 ^ 0100 ^ 0001 ^ 0101 ^ 0100 = 1001 = 9 (the second non-repeated element).

Done!

In terms of code, we have the following:

public static void findNonRepeatable(int arr[]) {

  // get the XOR[^] of all elements in the given array

  int xor = arr[0];

  for (int i = 1; i < arr.length; i++) {

    xor ^= arr[i];

  }

  // get the rightmost set bit (you can use any other set bit)

  int setBitNo = xor & ~(xor - 1);

  // divide the elements in two sets by comparing the

  // rightmost set bit of XOR[^] with the bit at the same

  // position in each element

  int p = 0;

  int q = 0;

  for (int i = 0; i < arr.length; i++) {

    if ((arr[i] & setBitNo) != 0) {

      // xor of the first set

      p = p ^ arr[i];

    } else {

      // xor of the second set

      q = q ^ arr[i];

    }

  }

  System.out.println("The numbers are: " + p + " and " + q);

}

The runtime of this code is O(n) with an O(1) auxiliary space (n is the number of elements from the given array). The complete application is called TwoNonRepeating.

Coding challenge 23 – Power set of a set

Amazon, Google, Adobe

Problem: Consider a given set, S. Write a snippet of code that returns the Power Set of S. A Power Set, P(S), of a set, S, is the set of all possible subsets of S, including the empty set and S itself.

Solution: Consider that the given S is {a, b, c}. If so, the Power Set includes {}, {a}, {b}, {c}, {a, b}, {a, c}, {a, c} and {a, b, c}. Notice that for a set containing three elements, the Power Set contains 23=8 elements. For a set containing four elements, the Power Set contains 24=16 elements. Generally speaking, for a set of n elements, the Power Set contains 2n elements.

Now, if we generate all the binary numbers from 0 to 2n-1, then we obtain something similar to the following (this example is for 23-1):

20=000, 21=001, 22=010, 23=011, 24=100, 25=101, 26=110, 27=111

Next, if we list these binaries and we consider that the first set bit (rightmost bit) is associated with a, the second set bit is associated with b, and the third set bit (the leftmost bit) is associated with c, then we obtain the following:

20 = 000 = {}

21 = 001 = {a}

22 = 010 = {b}

23 = 011 = {a, b}

24 = 100 = {c}

25 = 101 = {a, c}

26 = 110 = {b, c}

27 = 111 = {a, b, c}

Notice that if we replace the bits of 1 with a, b, and c, then we obtain the Power Set of the given set. Based on these statements, we can create the following pseudo-code for the given set, S:

Compute the Power Set size as 2 size of S

Iterate via i from 0 to Power Set size

     Iterate via j from 0 to size of S

          If jth bit in i is set then

               Add jth element from set to current subset

     Add the resulted subset to subsets

Return all subsets

So, a solution to this problem can be written as follows:

public static Set<Set<Character>> powerSet(char[] set) {

  // total number of subsets (2^n)

  long subsetsNo = (long) Math.pow(2, set.length);

  // store subsets

  Set<Set<Character>> subsets = new HashSet<>();

  // generate each subset one by one

  for (int i = 0; i < subsetsNo; i++) {

    Set<Character> subset = new HashSet<>();

    // check every bit of i

    for (int j = 0; j < set.length; j++) {

      // if j'th bit of i is set,

      // add set[j] to the current subset

      if ((i & (1 << j)) != 0) {                    

        subset.add(set[j]);

      }

    }

    subsets.add(subset);

  }

  return subsets;

}

The complete code is called PowerSetOfSet.

Coding challenge 24 – Finding the position of the only set bit

Adobe, Microsoft

Problem: Consider a positive integer, n. The binary representation of this number has a single bit set (a single bit of 1). Write a snippet of code that returns the position of this bit.

Solution: The problem itself give us an important detail or constraint: the given number contains a single bit of 1. This means that the given number must be a power of 2. Only 20, 21, 22, 23, 24, 25, ..., 2n have binary representations containing a single bit of 1. All other numbers contain 0 or multiple values of 1.

An n & (n-1) formula can tell us whether the given number is a power of two. Check out the following diagram:

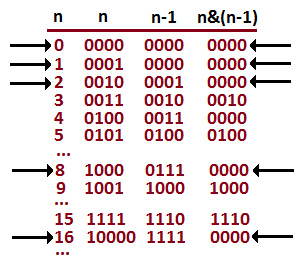
Figure 9.42 – The n & (n-1) formula gives us the powers of two

So, the numbers 0, 1, 2, 8, 16, ... have their binary representation of n & (n-1) as 0000. So far, we can say that the given number is a power of two. If it is not, then we can return -1 since there is no bit of 1 or there are multiple bits of 1.

Next, we can shift n to the right as long as n is not 0 while tracking the number of shifts. When n is 0, this means we've shifted the single bit of 1, so we can stop and return the counted shifts. Based on these statements, the code for this is quite simple:

public static int findPosition(int n) {

  int count = 0;

  if (!isPowerOfTwo(n)) {

    return -1;

  }

  while (n != 0) {

    n = n >> 1;

    ++count;

  }

  return count;

}

private static boolean isPowerOfTwo(int n) {

  return (n > 0) && ((n & (n - 1)) == 0);

}

The complete code is called PositionOfFirstBitOfOne.

Coding challenge 25 – Converting a float into binary and vice versa

Problem: Consider a Java float number, n. Write a snippet of code that converts this float into an IEEE 754 single-precision binary floating-point (binary-32) and vice versa.

Solution: To solve this problem, it is important to know that Java uses IEEE 754 single-precision binary floating-point representation for float numbers. The IEEE 754 standard specifies a binary-32 as having the sign bit (1 bit), exponent width (8 bits that can represent 256 values), and significant precision (24 bits (23 explicitly stored)), also known as the mantissa.

The following diagram represents a binary-32 in the IEEE 754 standard:

Figure 9.43 – IEEE 754 single-precision binary floating-point (binary 32)

The float value, when represented by the 32-bit binary data with a given sign, biased exponent, e, (the 8-bit unsigned integer), and a 23-bit fraction, is as follows:

Figure 9.44 – Float value

The exponent stored on 8 bits uses values from 0 to 127 to represent negative exponents (for example, 2-3) and uses the values from 128-255 for positive exponents. A negative exponent of 10-7 would have a value of -7+127=120. The 127 value is known as the exponent bias.

With this information, you should be able to convert a float number into the IEEE 754 binary-32 representation and vice versa. Before checking the source code for this, called FloatToBinaryAndBack, try using your own implementation.

This was the last coding challenge of this chapter. Let's quickly summarize it!

Summary

Since this chapter is a comprehensive resource for bit manipulation, then if you got this far, you've seriously boosted your bit manipulation skills. We covered the main theoretical aspects and solved 25 coding challenges in order to help you learn patterns and templates for solving bit manipulation problems.

In the next chapter, we'll continue our journey with arrays and strings.