Recursion and Dynamic Programming
This chapter covers one of the favorite topics of interviewers: Recursion and Dynamic Programming. Both work hand in hand, so you must be able to cover both. Commonly, the interviewer expects to see a plain recursive solution. However, they may ask you to provide some optimization hints or even to code an optimized version of your code. In other words, your interviewer will want to see Dynamic Programming at work.
In this chapter, we will cover the following topics:
- Recursion in a nutshell
- Dynamic Programming in a nutshell
- Coding challenges
By the end of this chapter, you will be able to implement a wide range of recursive algorithms. You'll have a significant number of recursive patterns and approaches you can use to recognize and implement recursive algorithms in minutes in your toolbelt. Let's start with the first topic of our agenda: recursion.
Technical requirements
You will find all the code presented in this chapter on GitHub at https://github.com/PacktPublishing/The-Complete-Coding-Interview-Guide-in-Java/tree/master/Chapter08.
Recursion in a nutshell
A method that calls itself directly/indirectly is called recursion. This method is known as a recursive method. The famous Fibonacci numbers problem can be implemented recursively, as follows:
int fibonacci(int k) {
// base case
if (k <= 1) {
return k;
}
// recursive call
return fibonacci(k - 2) + fibonacci(k - 1);
}
There are two important parts in this code:
- Base case: Returns a value without subsequent recursive calls. For special input(s), the function can be evaluated without recursion.
- Recursive call: Since the fibonacci() method calls itself, we have a recursive method.
Recognizing a recursive problem
Before we try to solve a problem via a recursive algorithm, we must recognize it as a good candidate for such an algorithm. Most of the recursive problems used in interviews are famous, so we recognize them by name. For example, problems such as Fibonacci numbers, summing a list of numbers, greatest common divisor, the factorial of a number, recursive Binary Search, reversing a string, and so on are well-known recursive problems.
But what do all these problems have in common? Once we know the answer to this question, we will be able to recognize other recursive problems as well. The answer is quite simple: all these problems can be built off of sub-problems. In other words, we say that we can express the value returned by a method in terms of other values returned by that method.
Important Note
When a problem can be built off sub-problems, it is a good candidate for being solved recursively. Typically, such problems include the words list top/last n ..., compute the nth or all..., count/find all solutions that ..., generate all cases that ..., and so on. In order to compute the nth..., we must compute nth-1, nth-2, and so on so that we can divide the problem into sub-problems. In other words, computing f(n) requires computing f(n-1), f(n-2), and so on.Practice is the keyword in recognizing and solving recursive problems. Solving a lot of recursive problems will help you recognize them just as easily as you blink.
Next, we'll highlight the main aspects of Dynamic Programming and learn how to optimize plain recursion via Dynamic Programming.
Dynamic Programming in a nutshell
When we talk about optimizing recursion, we talk about Dynamic Programming. This means that solving recursive problems can be done using plain recursive algorithms or Dynamic Programming.
Now, let's apply Dynamic Programming to the Fibonacci numbers, starting with the plain recursive algorithm:
int fibonacci(int k) {
if (k <= 1) {
return k;
}
return fibonacci(k - 2) + fibonacci(k - 1);
}
The plain recursive algorithm for the Fibonacci numbers has a runtime of O(2n) and a space complexity of O(n) – you can find the explanation in Chapter 7, Big O Analysis of Algorithms. If we set k=7 and represent the call stack as a tree of calls, then we obtain the following diagram:
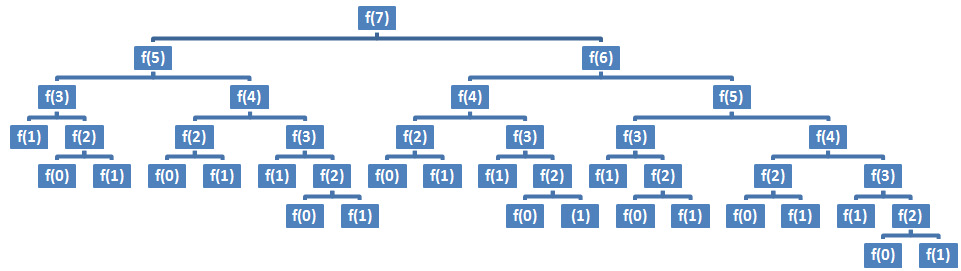
Figure 8.1 – Tree of calls (plain recursion)
If we check the Big O chart from Chapter 7, Big O Analysis of Algorithms, then we'll notice that O(2n) is far from being efficient. Exponential runtimes fit the Horrible area of the Big O chart. Can we do this better? Yes, via the Memoization approach.
Memoization (or Top-Down Dynamic Programming)
When a recursive algorithm has repeated calls for the same inputs, this indicates that it performs duplicate work. In other words, a recursive problem may have overlapping sub-problems, so the road to the solution involves solving the same sub-problem multiple times. For example, if we redraw the tree of calls for Fibonacci numbers and we highlight the overlapping problems, then we obtain the following diagram:
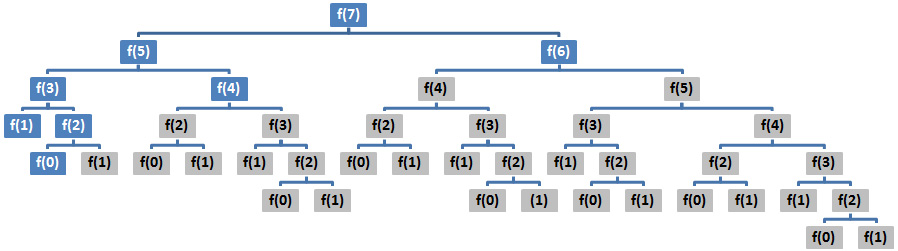
Figure 8.2 – Tree of calls (duplicate work)
It is obvious that more than half of the calls are duplicate calls.
Memoization is a technique that's used to remove duplicate work in a method. It guarantees that a method is called for the same input only once. To achieve this, Memoization caches the results of the given inputs. This means that, when the method should be called to compute an input that has already been computed, Memoization will avoid this call by returning the result from the cache.
The following code uses Memoization to optimize the plain recursive algorithm for the Fibonacci numbers (the cache is represented by the cache array):
int fibonacci(int k) {
return fibonacci(k, new int[k + 1]);
}
int fibonacci(int k, int[] cache) {
if (k <= 1) {
return k;
} else if (cache[k] > 0) {
return cache[k];
}
cache[k] = fibonacci(k - 2, cache)
+ fibonacci(k - 1, cache);
return cache[k];
}
If we redraw the tree of calls from the preceding code, then we obtain the following diagram:
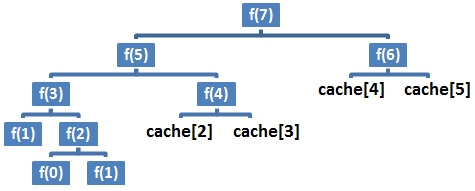
Figure 8.3 – Tree of calls (Memoization)
Here, it is obvious that Memoization has drastically reduced the number of recursive calls. This time, the fibonacci() method take advantage of cached results. The runtime was reduced from O(2n) to O(n), so from exponential to polynomial.
Important note
Memoization is also referred to as a Top-Down approach. The Top-Down approach is not very intuitive because we start developing the final solution immediately by explaining how we develop it from smaller solutions. This is like saying the following:
I wrote a book. How? I wrote its chapters. How? I wrote the sections of each chapter. How? I wrote the paragraphs of each section.
The space complexity remains O(n). Can we improve it? Yes, via the Tabulation approach.
Tabulation (or Bottom-Up Dynamic Programming)
Tabulation, or the Bottom-Up approach, is more intuitive than Top-Down. Essentially, a recursive algorithm (often) starts from the end and works backward, while a Bottom-Up algorithm starts right from the beginning. The Bottom-Up approach avoids recursion and improves space complexity.
Important note
Tabulation is commonly referred to as a Bottom-Up approach. Going bottom-up is an approach that avoids recursion and is quite natural. It's like saying the following:
I wrote the paragraphs of each section. And? And I wrote the sections of each chapter. And? And I wrote all the chapters. And? And I wrote a book.
Bottom-Up reduces the memory cost imposed by recursion when it builds up the call stack, which means that Bottom-Up eliminates the vulnerability of getting stack overflow errors. This may happen if the call stack gets too large and runs out of space.
For example, when we compute fibonacci(k) via the recursive approach, we start with k and continue with k-1, k-2, and so on until 0. With the Bottom-Up approach, we start with 0 and continue with 1, 2, and so on until k. As shown in the following code, this is an iterative approach:
int fibonacci(int k) {
if (k <= 1) {
return k;
}
int first = 1;
int second = 0;
int result = 0;
for (int i = 1; i < k; i++) {
result = first + second;
second = first;
first = result;
}
return result;
}
The runtime of this algorithm is still O(n), but the space complexity was brought down from O(n) to O(1). So, to recap the Fibonacci numbers algorithms, we have that the following:
- The plain recursion algorithm has a runtime of O(2n) and a space complexity of O(n).
- The Memoization recursion algorithm has a runtime of O(n) and a space complexity of O(n).
- The Tabulation algorithm has a runtime of O(n) and a space complexity of O(1).
Now, it's time to practice some coding challenges.
Coding challenges
In the following 15 coding challenges, we will exploit recursion and Dynamic Programming. These problems have been carefully crafted to help you understand and cover a wide range of problems from this category. By the end of this coding challenge session, you should be able to recognize and solve recursive problems in the context of an interview.
Coding challenge 1 – Robot grid (I)
Adobe, Microsoft
Problem: We have an m x n grid. A robot is placed at the top-left corner of this grid. The robot can only move either right or down at any point in time, but it is not allowed to move in certain cells. The robot's goal is to find a path from the top-left corner to the bottom-right corner of the grid.
Solution: First, we need to set some conventions of the m x n grid. Let's assume that the bottom-right corner has the coordinates (0, 0), while the top-left corner has the coordinates (m, n), where m is the row and n is the column of the grid. So, the robot starts from (m, n) and must find a path to (0, 0). If we try to sketch an example for a 6x6 grid, then we can obtain something like the following:
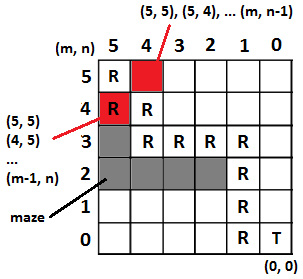
Figure 8.4 – Determining the moving pattern
Here, we can see that the robot can go from one cell (m, n) to an adjacent cell, which can be (m-1, n) or (m, n-1). For example, if the robot is placed at (5, 5), then it can go to (4, 5) or (5, 4). Furthermore, from (4, 5), it can go to (3, 5) or (4, 4), while from (5, 4), it can go to (5, 3) or (4, 4).
So, we have a problem that can be divided into sub-problems. We must find the final path for the cells (the problem), which we can do if we are able to find the path to an adjacent cell (sub-problem). This sounds like a recursive algorithm. In recursion, we approach the problem from top to down, so we start from (m, n) and move back to the origin (0, 0), as shown in the preceding diagram. This means that from cell (m, n), we try to go into (m, n-1) or (m-1, n).
Putting this into code can be done as follows (the maze[][] matrix is a boolean matrix that has values of true for cells that we are not allowed to go in – for example, maze[3][1] = true means that we are not allowed in cell (3,1)):
public static boolean computePath(int m, int n,
boolean[][] maze, Set<Point> path) {
// we fell off the grid so we return
if (m < 0 || n < 0) {
return false;
}
// we cannot step at this cell
if (maze[m][n]) {
return false;
}
// we reached the target
// (this is the bottom-right corner)
if (((m == 0) && (n == 0))
// or, try to go to the right
|| computePath(m, n - 1, maze, path)
// or, try to go to down
|| computePath(m - 1, n, maze, path)) {
// we add the cell to the path
path.add(new Point(m, n));
return true;
}
return false;
}
The returned path is stored as a LinkedHashSet<Point>. Each path contains m+n steps and there are only two valid choices we can make at each step; therefore, the runtime is O(2m+n). But we can reduce this runtime to O(mn) if we cache the cells that failed (returned false). This way, the Memoization approach saves the robot from trying to go in a failed cell multiple times. The complete application is called RobotGridMaze. It also contains the Memoization code.
Another popular problem of using a robot is as follows. Let's say we have an m x n grid. A robot is placed at the top-left corner of this grid. The robot can only move either right or down at any point in time. The robot's goal is to find all the unique paths from the top-left corner to the bottom-right corner of the grid.
The plain recursive solution and Bottom-Up approach are available in the RobotGridAllPaths application.
Coding challenge 2 – Tower of Hanoi
Problem: This is a classical problem that can occur in an interview at any time. The Tower of Hanoi is a problem with three rods (A, B, and C) and n disks. Initially, all the disks are placed in ascending order on a single rod (the largest disk is on the bottom (disk n), a smaller one sitting on it (n-1), and so on (n-2, n-3, ...) until the smallest disk is on the top (disk 1). The aim is to move all the disks from this rod to another rod while respecting the following rules:
- Only one disk can be moved at a time.
- A move means to slide the upper disk from one rod to another rod.
- A disk cannot be placed on top of a smaller disk.
Solution: Trying to solve such problems means that we need to visualize some cases. Let's consider that we want to move the disks from rod A to rod C. Now, let's put n disks on rod A:
For n=1: Having a single disk, we need to move one disk from rod A to C.
For n=2: We know how to move a single disk. To move two, we need to complete the following steps:
- Move disk 1 from A to B (rod B acts as an intermediate for disk 1).
- Move disk 2 from A to C (disk 2 goes directly in its final place).
- Move disk 1 from B to C (disk 1 can be moved on top of disk 2 on rod C).
For n=3: Let's get some help from the following diagram:
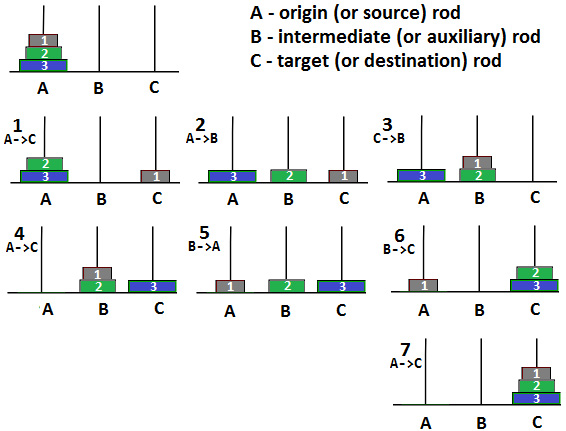
Figure 8.5 – Tower of Hanoi (three disks)
Due to n=2, we know how to move the top two disks from A (origin) to C (target). In other words, we know how to move the top two disks from one rod to another rod. Let's move them from A to B, as follows:
- Move disk 1 from A to C (this time, we use C as the intermediate).
- Move disk 2 from A to B.
- Move disk 1 from C to B.
OK, so this is something that we've done before. Next, we can move disks 2 and 3 onto C, as follows:
- Move disk 3 from A to C.
- Move disk 1 from B to A (we use A as the intermediate).
- Move disk 2 from B to C.
- Finally, move disk 3 from A to C.
Continuing with this logic, we can intuit that we can move four disks because we know how to move three, we can move five disks because we know how to move four, and so on. With rod A as the origin, rod B as the intermediate, and rod C as the target, we can conclude that we can move n disks by doing the following:
- Move the top n - 1 disks from the origin to the intermediate, using the target as an intermediate.
- Move the top n - 1 disks from the intermediate to the target, using the origin as an intermediate.
At this point, it is clear that we have a problem that can be divided into sub-problems. Based on the preceding two bullets, we can code this as follows:
public static void moveDisks(int n, char origin,
char target, char intermediate) {
if (n <= 0) {
return;
}
if (n == 1) {
System.out.println("Move disk 1 from rod "
+ origin + " to rod " + target);
return;
}
// move top n - 1 disks from origin to intermediate,
// using target as a intermediate
moveDisks(n - 1, origin, intermediate, target);
System.out.println("Move disk " + n + " from rod "
+ origin + " to rod " + target);
// move top n - 1 disks from intermediate to target,
// using origin as an intermediate
moveDisks(n - 1, intermediate, target, origin);
}
The complete application is called HanoiTowers.
Coding challenge 3 – Josephus
Amazon, Google, Adobe, Microsoft, Flipkart
Problem: Consider a group of n men arranged in a circle (1, 2, 3, ..., n). Every kth man will be killed around the circle until only one survivor remains. Write an algorithm that finds the k position of this survivor. This is known as the Josephus problem.
Solution: Remember that we had a note previously saying that when a problem contains the words compute the nth and similar expressions, then it is possibly a good candidate for being solved via recursion. Here, we have find the k position, which is a problem that can be divided into sub-problems and be solved via recursion.
Let's consider n=15 and k=3. So, there are 15 men and every third man will be eliminated from the circle until only one remains. Let's visualize this via the following diagram (this is very useful for figuring out the pattern of killings):

Figure 8.6 – Josephus for n=15 and k=3
So, we have five rounds until we find the survivor, as follows:
- Round 1: The first elimination is position 3; next, 6, 9, 12, and 15 are eliminated.
- Round 2: The first elimination is position 4 (1 and 2 are skipped, since position 15 was the last eliminated in round 1); next, 8 and 13 are eliminated.
- Round 3: The first elimination is position 2 (14 and 1 are skipped, since position 13 was the last eliminated in round 2); next, 10 and 1 are eliminated.
- Round 4: The first elimination position is 11, followed by position 7.
- Round 5: 14 is eliminated and 5 is the survivor.
Trying to identify a pattern or a recursive call can be done based on the following observations. After the first man (kth) is eliminated, n-1 men are left. This means that we call josephus(n – 1, k) to get the position of the n-1th man. However, notice that the position returned by josephus(n – 1, k) will take into account the position starting from k%n + 1. In other words, we have to adjust the position returned by josephus(n – 1, k) to obtain (josephus(n - 1, k) + k - 1) % n + 1. The recursive method is shown here:
public static int josephus(int n, int k) {
if (n == 1) {
return 1;
} else {
return (josephus(n - 1, k) + k - 1) % n + 1;
}
}
If you find this approach quite tricky, then you can try an iterative approach based on a queue. First, fill up the queue with n men. Next, loop the queue and, for each man, retrieve and remove the head of this queue (poll()). If the retrieved man is not the kth, then insert this man back in the queue (add()). If this is the kth man, then break the loop and repeat this process until the queue's size is 1. The code for this is as follows:
public static void printJosephus(int n, int k) {
Queue<Integer> circle = new ArrayDeque<>();
for (int i = 1; i <= n; i++) {
circle.add(i);
}
while (circle.size() != 1) {
for (int i = 1; i <= k; i++) {
int eliminated = circle.poll();
if (i == k) {
System.out.println("Eliminated: "
+ eliminated);
break;
}
circle.add(eliminated);
}
}
System.out.println("Using queue! Survivor: "
+ circle.peek());
}
The complete application is called Josephus.
Coding challenge 4 – Color spots
Amazon, Google, Adobe, Microsoft, Flipkart
Problem: Consider an r x c grid where r stands for rows and c stands for columns. Each cell has a color represented by a number k (for example, for three colors, k=3). We define the connected set of a cell (or a color spot) as the total cells in which we can go from the respective cell by successive displacements on the row or the column, thus keeping the color. The goal is to determine the color and the number of cells of the maximum connected set. In other words, we need to determine the biggest color spot.
Solution: Let's consider a 5x5 grid and three colors, where we have r=c=5 and k=3. Next, let's represent the grid as shown in the following diagrams:
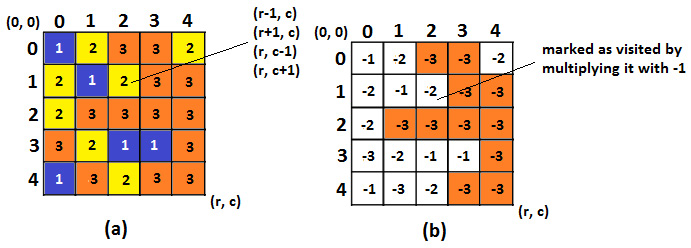
Figure 8.7 – Biggest color spot ((a) – initial grid, (b) – solved grid)
Let's focus on image (a). Here, we can see that moving from a cell to another cell can be done in a maximum of four directions (up, down, left, and right). This means that, from a cell (r,c), we can try to go to (r-1, c), (r+1, c), (r, c-1), and (r, c+1). We cannot perform a move if we risk falling from the grid or the targeted cell has another color than the current cell. So, by iterating each cell ((0, 0), (0, 1), ... (r, c)), we can determine the size of the connected set of that cell (the size of the color spot) by visiting each allowed cell and counting it. In image (a), we have four spots that are color 1 whose sizes are 1, 1, 1, and 2. We also have six spots that are color 2 whose sizes are 1, 1, 2, 1, 1, and 1. Finally, we have three spots that are color 3 whose sizes are 11, 1, and 1.
From this, we can conclude that the biggest color spot has a size of 11 and a color of 3. Mainly, we can consider that the color spot of the first cell is the maximum spot and that each time we find a color spot bigger than this one, we replace this one with the one we found.
Now, let's focus on image (b). Why do we have negative values? Because when we visit a cell, we switch its color value to -color. This is a convenient convention that's used to avoid computing the same connected set of a cell multiple times. It is like saying that we mark this cell as visited. By convention, we cannot move in a cell that has a negative value for a color, so we will not compute the size of the same color spot twice.
Now, gluing these observations together to make a recursive method leads to the following code:
public class BiggestColorSpot {
private int currentColorSpot;
void determineBiggestColorSpot(int cols,
int rows, int a[][]) {
...
}
private void computeColorSpot(int i, int j,
int cols, int rows, int a[][], int color) {
a[i][j] = -a[i][j];
currentColorSpot++;
if (i > 1 && a[i - 1][j] == color) {
computeColorSpot(i - 1, j, cols,
rows, a, color);
}
if ((i + 1) < rows && a[i + 1][j] == color) {
computeColorSpot(i + 1, j, cols, rows, a, color);
}
if (j > 1 && a[i][j - 1] == color) {
computeColorSpot(i, j - 1, cols,
rows, a, color);
}
if ((j + 1) < cols && a[i][j + 1] == color) {
computeColorSpot(i, j + 1, cols,
rows, a, color);
}
}
}
While the preceding recursive method, computeColorSpot(), can compute the size of a color spot, starting from the given cell, the following method determines the biggest color spot:
void determineBiggestColorSpot(int cols,
int rows, int a[][]) {
int biggestColorSpot = 0;
int color = 0;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
if (a[i][j] > 0) {
currentColorSpot = 0;
computeColorSpot(i, j, cols,
rows, a, a[i][j]);
if (currentColorSpot > biggestColorSpot) {
biggestColorSpot = currentColorSpot;
color = a[i][j] * (-1);
}
}
}
}
System.out.println(" Color: " + color
+ " Biggest spot: " + biggestColorSpot);
}
The complete application is called BiggestColorSpot.
Coding challenge 5 – Coins
Google, Adobe, Microsoft
Problem: Consider an amount of n cents. Count the ways you can change this amount using any number of quarters (25 cents), dimes (10 cents), nickels (5 cents), and pennies (1 cent).
Solution: Let's imagine that we have to change 50 cents. Right from the start, we can see that changing 50 cents is a problem that can be solved via sub-problems. For example, we can change 50 cents using 0, 1, or 2 quarters. Or we can do it using 0, 1, 2, 3, 4, or 5 dimes. We can also do it using 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, or 10 nickels. Finally, we can do it using 0, 1, 2, 3, ..., 50 pennies. Let's assume that we have 1 quarter, 1 dime, 2 nickels, and 5 pennies. We can use our quarter to say the following:
calculateChange(50) = 1 quarters + ...
But this is like saying the following:
calculateChange(25) = 0 quarters + ...
We don't have more quarters; therefore, we add a dime:
calculateChange(25) = 0 quarters + 1 dimes + ...
This can be reduced, as follows:
calculateChange(15) = 0 quarters + 0 dimes + ...
We don't have any more dimes. We add the nickels:
calculateChange(15) = 0 quarters + 0 dimes + 2 nickel + ...
This can be reduced to the following:
calculateChange(5) = 0 quarters + 0 dimes + 0 nickel + ...
Finally, since we don't have more nickels, we add the pennies:
calculateChange(5) = 0 quarters + 0 dimes + 0 nickel + 5 pennies
This can be reduced to the following:
calculateChange(0) = 0 quarters + 0 dimes + 0 nickel + 0 pennies
If we try to represent all the possible reductions, we obtain the following diagram:

Figure 8.8 – Changing n cents into quarters, dimes, nickels, and pennies
Implementing this reducible algorithm can be done via recursion, as shown in the following code. Notice that we are using Memoization to avoid changing the same amount multiple times:
public static int calculateChangeMemoization(int n) {
int[] coins = {25, 10, 5, 1};
int[][] cache = new int[n + 1][coins.length];
return calculateChangeMemoization(n, coins, 0, cache);
}
private static int calculateChangeMemoization(int amount,
int[] coins, int position, int[][] cache) {
if (cache[amount][position] > 0) {
return cache[amount][position];
}
if (position >= coins.length - 1) {
return 1;
}
int coin = coins[position];
int count = 0;
for (int i = 0; i * coin <= amount; i++) {
int remaining = amount - i * coin;
count += calculateChangeMemoization(remaining,
coins, position + 1, cache);
}
cache[amount][position] = count;
return count;
}
The complete application is called Coins. It also contains the plain recursive approach (without Memoization).
Coding challenge 6 – Five towers
Problem: Consider a 5x5 grid with five defensive towers spread across the grid. To provide an optimal defense for the grid, we have to build a tower on each row of the grid. Find all the solutions for building these towers so that none of them share the same column and diagonal.
Solution: We know that, on each row, we must build a tower and that it is not important in what order we build them on the grid. Let's sketch a solution and a failure, as follows:
_B15403.jpg)
Figure 8.9(a) – Failure and solution
Let's focus on the solution and start from the first row: row 0. We can build a tower on this row in any column; therefore, we can say the following:
_B15403.jpg)
Figure 8.9(b): Part 1 of the logic to build the towers
If we continue with the same logic, then we can say the following:
_B15403.jpg)
Figure 8.9(c): Part 2 of the logic to build the towers
So, we start from the first row and build the first tower on (0,0). We go to the second row and try to build the second tower so that we don't share the column or diagonal with the first tower. We go to the third row and try to build the third tower so that we don't share the column or diagonal with the first two towers. We follow the same logic for the fourth and fifth towers. This is our solution. Now, we repeat this logic – we build the first tower at (0,1) and continue building until we find the second solution. Next, we build the first tower at (0, 2), (0, 3) and finally at (0,4) while we repeat the process. We can write this recursive algorithm as follows:
protected static final int GRID_SIZE = 5; // (5x5)
public static void buildTowers(int row, Integer[] columns,
Set<Integer[]> solutions) {
if (row == GRID_SIZE) {
solutions.add(columns.clone());
} else {
for (int col = 0; col < GRID_SIZE; col++) {
if (canBuild(columns, row, col)) {
// build this tower
columns[row] = col;
// go to the next row
buildTowers(row + 1, columns, solutions);
}
}
}
}
private static boolean canBuild(Integer[] columns,
int nextRow, int nextColumn) {
for (int currentRow=0; currentRow<nextRow;
currentRow++) {
int currentColumn = columns[currentRow];
// cannot build on the same column
if (currentColumn == nextColumn) {
return false;
}
int columnsDistance
= Math.abs(currentColumn - nextColumn);
int rowsDistance = nextRow - currentRow;
// cannot build on the same diagonal
if (columnsDistance == rowsDistance) {
return false;
}
}
return true;
}
The complete application is called FiveTowers.
Coding challenge 7 – Magic index
Adobe, Microsoft
Problem: Consider a sorted array of n elements that allows duplicates. An index k is magic if array[k] = k. Write a recursive algorithm that finds the first magic index.
Solution: First, let's quickly draw two sorted arrays containing 18 elements, as shown in the following diagram. The array at the top of the image contains no duplicates, while the array at the bottom contains duplicates. This way, we can observe the influence of these duplicates:

Figure 8.10 – Sorted array of 18 elements
If we halve the array with no duplicates, then we can conclude that the magic index must be on the right-hand side because array[8] < 8. This is true since the magic index is 11, so array[11] = 11.
If we halve the array with duplicates, we cannot get the same conclusion we received previously. The magic index can be on both sides. Here, we have array[5] = 5 and array[12] = 12. We must find the first magic index, so we should search the left-hand side first.
But how do we find it? The most obvious approach consists of looping the array and checking if array[i] = i. While this works for any ordered array, it will not impress the interviewer since it is not recursive, so we need another approach.
In Chapter 7, Big O Analysis of Algorithms, you saw an example of searching in a sorted array via the Binary Search algorithm. This algorithm can be implemented via recursion since, at each step, we halve the previous array and create a sub-problem. Since the indexes of an array are ordered, we can adapt the Binary Search algorithm. The main issue that we face is that duplicated elements complicate the search. When we halve the array, we cannot say that the magic index is on the left or the right, so we have to search in both directions, as shown in the following code (first, we search the left-hand side):
public static int find(int[] arr) {
return find(arr, 0, arr.length - 1);
}
private static int find(int[] arr,
int startIndex, int endIndex) {
if (startIndex > endIndex) {
return -1; // return an invalid index
}
// halved the indexes
int middleIndex = (startIndex + endIndex) / 2;
// value (element) of middle index
int value = arr[middleIndex];
// check if this is a magic index
if (value == middleIndex) {
return middleIndex;
}
// search from middle of the array to the left
int leftIndex = find(arr, startIndex,
Math.min(middleIndex - 1, value));
if (leftIndex >= 0) {
return leftIndex;
}
// search from middle of the array to the right
return find(arr, Math.max(middleIndex + 1,
value), endIndex);
}
}
The complete application is called MagicIndex.
Coding challenge 8 – The falling ball
Problem: Consider an m x n grid where each (m, n) cell has an elevation represented by a number between 1 and 5 (5 is the highest elevation). A ball is placed in a cell of the grid. This ball can fall into another cell, as long as that cell has a smaller elevation than the ball cell. The ball can fall in four directions: north, west, east, and south. Display the initial grid, as well as the grid after the ball falls on all possible paths. Mark the paths with 0.
Solution: Always pay attention to the problem requests. Notice that we must display the solved grid, not list the paths or count them. The easiest way to display a grid is to use two loops, as shown in the following code:
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.format("%2s", elevations[i][j]);
}
System.out.println();
}
Now, let's sketch a 5x5 grid and view an input and its output. The following image shows the initial grid in the form of a 3D model, along with a possible path and the solved grid:

Figure 8.11 – The falling ball
I think we have enough experience to intuit that this problem can be solved via recursion. Mainly, we move the ball in all acceptable directions and mark each visited cell with 0. When we have the ball in the (i, j) cell, we can go in (i-1, j), (i+1, j), (i, j-1), and (i, j+1) directions, as long those cells have smaller elevations. In terms of code, we have the following:
public static void computePath(
int prevElevation, int i, int j,
int rows, int cols, int[][] elevations) {
// ensure the ball is still on the grid
if (i >= 0 && i <= (rows-1) && j >= 0 && j <= (cols-1)) {
int currentElevation = elevations[i][j];
// check if the ball can fall
if (prevElevation >= currentElevation
&& currentElevation > 0) {
// store the current elevation
prevElevation = currentElevation;
// mark this cell as visited
elevations[i][j] = 0;
// try to move the ball
computePath(prevElevation,i,j-1,
rows,cols,elevations);
computePath(prevElevation,i-1,
j,rows,cols,elevations);
computePath(prevElevation,i,j+1,
rows,cols,elevations);
computePath(prevElevation,i+1,j,
rows,cols,elevations);
}
}
}
The complete application is called TheFallingBall.
Coding challenge 9 – The highest colored tower
Adobe, Microsoft, Flipkart
Problem: Consider n boxes of different widths (w1...n), heights (h1...n), and colors (c1...n). Find the highest tower of boxes that respects the following conditions:
- You cannot rotate the boxes.
- You cannot place two successive boxes of the same color.
- Each box is strictly larger than the box above it in terms of their width and height.
Solution: Let's try to visualize this, as follows:

Figure 8.12(a) – The highest colored tower
We have seven boxes of different sizes and colors. We can imagine that the highest tower will contain all these boxes, b1...b7. But we have several constraints that don't allow us to simply stack the boxes. We can choose one of the boxes as the base box and place another allowed box on top of it, as follows:
_The_logic_to_select_the_boxes_to_build_the_highest_tower.jpg)
Figure 8.12(b) The logic to select the boxes to build the highest tower
So, we identified a pattern. We choose a box as the base, and we try to see which of the remaining boxes can go on top as the second level. We do the same for the third level and so on. When we are done (we cannot add more boxes or no boxes are left), we store the size of the highest tower. Next, we repeat this scenario with another base box.
Since every box must be larger in terms of width and height than the box above it, we can sort the boxes by width or height in descending order (it is not important which one we choose). This way, for any tower of b0,...bk, k < n boxes, we can find the next valid box by searching the bk+1...n interval.
Moreover, we can avoid recalculating the best solution for the same base box by caching the best solutions via Memoization:
// Memoization
public static int buildViaMemoization(List<Box> boxes) {
// sorting boxes by width (you can do it by height as well)
Collections.sort(boxes, new Comparator<Box>() {
@Override
public int compare(Box b1, Box b2) {
return Integer.compare(b2.getWidth(),
b1.getWidth());
}
});
// place each box as the base (bottom box) and
// try to arrange the rest of the boxes
int highest = 0;
int[] cache = new int[boxes.size()];
for (int i = 0; i < boxes.size(); i++) {
int height = buildMemoization(boxes, i, cache);
highest = Math.max(highest, height);
}
return highest;
}
// Memoization
private static int buildMemoization(List<Box> boxes,
int base, int[] cache) {
if (base < boxes.size() && cache[base] > 0) {
return cache[base];
}
Box current = boxes.get(base);
int highest = 0;
// since the boxes are sorted we don’t
// look in [0, base + 1)
for (int i = base + 1; i < boxes.size(); i++) {
if (boxes.get(i).canBeNext(current)) {
int height = buildMemoization(boxes, i, cache);
highest = Math.max(height, highest);
}
}
highest = highest + current.getHeight();
cache[base] = highest;
return highest;
}
The complete application is called HighestColoredTower. The code also contains the plain recursion approach to this problem (without Memoization).
Coding challenge 10 – String permutations
Amazon, Google, Adobe, Microsoft, Flipkart
Problem: Write an algorithm that computes all the permutations of a string and accommodates the following two conditions:
- The given string can contain duplicates.
- The returned list of permutations should not contain duplicates.
Solution: Like in any recursive problem, the key consists of recognizing the relationship and patterns between the different sub-problems. Right away, we can intuit that permuting a string with duplicates should be more complicated than permuting a string with unique characters. This means that we must understand the permutations of a string with unique characters first.
The most natural way of permuting the characters of a string can follow a simple pattern: each character of the string will become the first character of the string (swap their positions) and then permute all the remaining letters using a recursive call. Let's delve into the general case. For a string containing a single character, we have a single permutation:
P(c1) = c1
If we add another character, then we can express the permutations as follows:
P(c1c2) = c1c2 and c2c1
If we add another character, then we must express the permutations using c1c2. Each permutation of c1c2c3 represents an ordering of c1c2, as follows:
c1c2 -> c1c2c3,c1c3c2,c3c1c2
c2c1 -> c2c1c3,c2c3c1,c3c2c1
Let's replace c1c2c3 with ABC. Next, we represent P(ABC) as a diagram:

Figure 8.13 – Permuting ABC
If we add another character, then we must express the permutations using c1c2c3c4. Each permutation of c1c2c3c4 represents an ordering of c1c2c3, as follows:
c1c2c3 -> c1c2c3c4,c1c2c4c3,c1c4c2c3,c4c1c2c3
c1c3c2 -> c1c3c2c4,c1c3c4c2,c1c4c3c2,c4c1c3c2
c3c1c2 -> c3c1c2c4,c3c1c4c2,c3c4c1c2,c4c3c1c2
c2c1c3 -> c2c1c3c4,c2c1c4c3,c2c4c1c3,c4c2c1c3
c2c3c1 -> c2c3c1c4,c2c3c4c1,c2c4c3c1,c4c2c3c1
c3c2c1 -> c3c2c1c4,c3c2c4c1,c3c4c2c1,c4c3c2c1
We can continue like this forever, but I think it is quite clear what pattern can be used for generating P(c1, c2, ..., cn).
So, this is the right moment to take our logic a step further. Now, it is time to ask the following questions: if we know how to compute all the permutations for strings of k-1 characters (c1c2...ck-1), then how we can use this information to compute all the permutations for strings of k characters (c1c2...ck-1ck)? For example, if we know how to compute all the permutations for the c1c2c3 string, then how we can express all the permutations of the c1c2c3c4 string using c1c2c3 permutations? The answer is to take each character from the c1c2...ck string and append the c1c2...ck-1 permutation to it, as follows:
P(c1c2c3c4) = [c1 + P(c2c3c4)] + [c2 + P(c1c3c4)] + [c3 + P(c1c2c4)] + [c4 + P(c1c2c3)]
[c1 + P(c2c3c4)] -> c1c2c3c4,c1c2c4c3,c1c3c2c4,c1c3c4c2,c1c4c2c3,c1c4c3c2
[c2 + P(c1c3c4)] -> c2c1c3c4,c2c1c4c3,c2c3c1c4,c2c3c4c1,c2c4c1c3,c2c4c3c1
[c3 + P(c1c2c4)] -> c3c1c2c4,c3c1c4c2,c3c2c1c4,c3c2c4c1,c3c4c1c2,c3c4c2c1
[c4 + P(c1c2c3)] -> c4c1c2c3,c4c1c3c2,c4c2c1c3,c4c2c3c1,c4c3c1c2,c4c3c2c1
We can continue to add another character and repeat this logic so that we have a recursive pattern that can be expressed in terms of code as follows:
public static Set<String> permute(String str) {
return permute("", str);
}
private static Set<String> permute(String prefix, String str) {
Set<String> permutations = new HashSet<>();
int n = str.length();
if (n == 0) {
permutations.add(prefix);
} else {
for (int i = 0; i < n; i++) {
permutations.addAll(permute(prefix + str.charAt(i),
str.substring(i + 1, n) + str.substring(0, i)));
}
}
return permutations;
}
This code will work fine. Because we use a Set (not a List), we respect the requirement stating that the returned list of permutations should not contain duplicates. However, we do generate duplicates. For example, if the given string is aaa, then we generate six identical permutations, even if there is only one. The only difference is that they are not added to the result since a Set doesn't accept duplicates. This is far from being efficient.
We can avoid generating duplicates in several ways. One approach starts by counting the characters of a string and storing them in a map. For example, for the given string abcabcaa, the key-value map can be a=4, b=2, and c=2. We can do this via a simple helper method, as follows:
private static Map<Character, Integer> charactersMap(
String str) {
Map<Character, Integer> characters = new HashMap<>();
BiFunction<Character, Integer, Integer> count = (k, v)
-> ((v == null) ? 1 : ++v);
for (char c : str.toCharArray()) {
characters.compute(c, count);
}
return characters;
}
Next, we choose one of these characters as the first character and find all the permutations of the remaining characters. We can express this as follows:
P(a=4,b=2,c=2) = [a + P(a=3,b=2,c=2)] + [b + P(a=4,b=1,c=1)] + [c + P(a=4,b=2,c=1)]
P(a=3,b=2,c=2) = [a + P(a=2,b=2,c=2)] + [b + P(a=3,b=1,c=1)] + [c + P(a=3,b=2,c=1)]
P(a=4,b=1,c=1) = [a + P(a=3,b=1,c=1)] + [b + P(a=4,b=0,c=1)] + [c + P(a=4,b=1,c=0)]
P(a=4,b=2,c=1) = [a + P(a=3,b=2,c=1)] + [b + P(a=4,b=1,c=1)] + [c + P(a=4,b=2,c=0)]
P(a=2,b=2,c=2) = [a + P(a=1,b=2,c=2)] + [b + P(a=2,b=1,c=2)] + [c + P(a=2,b=2,c=1)]
P(a=3,b=1,c=1) = ...
We can continue writing until there are no remaining characters. Now, it should be quite simple to put this into lines of code:
public static List<String> permute(String str) {
return permute("", str.length(), charactersMap(str));
}
private static List<String> permute(String prefix,
int strlength, Map<Character, Integer> characters) {
List<String> permutations = new ArrayList<>();
if (strlength == 0) {
permutations.add(prefix);
} else {
// fetch next char and generate remaining permutations
for (Character c : characters.keySet()) {
int count = characters.get(c);
if (count > 0) {
characters.put(c, count - 1);
permutations.addAll(permute(prefix + c,
strlength - 1, characters));
characters.put(c, count);
}
}
}
return permutations;
}
The complete application is called Permutations.
Coding challenge 11 – Knight tour
Amazon, Google
Problem: Consider a chessboard (an 8x8 grid). Place a knight on this board and print all its unique movements.
Solution: As you've already seen, the best way to tackle such problems is to take a piece of paper and a pen and sketch the scenario. A picture is worth a thousand words:
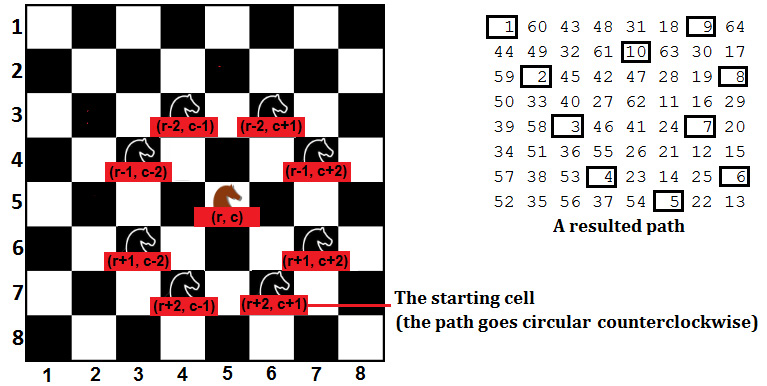
Figure 8.14 – Knight tour
As we can see, a knight can move from a (r, c) cell into a maximum of eight other valid cells; that is, (r+2, c+1), (r+1, c+2), (r-1,c+2), (r-2, c+1), (r-2, c-1), (r-1, c-2), (r+1, c-2), and (r+2, c-1). So, in order to obtain the path from 1 to 64 (as shown in the right-hand side of the preceding diagram), we can start from a given location and recursively try to visit each valid movement. If the current path doesn't represent a solution or we've tried all eight cells, then we backtrack.
To be as efficient as possible, we consider the following aspects:
- We start from a corner of the chessboard: This way, the knight can initially go in only two directions instead of eight.
- We check for valid cells in a fixed sequence: Maintaining a circular path will help us find a new move faster than picking one randomly. The counterclockwise circular path from (r, c) is (r+2, c+1), (r+1, c+2), (r-1, c+2), (r-2, c+1), (r-2, c-1), (r-1, c-2), (r+1, c-2), and (r+2, c-1).
- We compute the circular path using two arrays: We can move from (r, c) to (r + ROW[i],c + COL[i]) with i in [0, 7]:
COL[] = {1,2,2,1,-1,-2,-2,-1,1};
ROW[] = {2,1,-1,-2,-2,-1,1,2,2};
- We avoid cycles in paths and duplicate work (for example, visiting the same cell multiple times) by storing the visited cells in an r x c matrix.
By gluing everything together in terms of code, we obtain the following recursive approach:
public class KnightTour {
private final int n;
// constructor omitted for brevity
// all 8 possible movements for a knight
public static final int COL[]
= {1,2,2,1,-1,-2,-2,-1,1};
public static final int ROW[]
= {2,1,-1,-2,-2,-1,1,2,2};
public void knightTour(int r, int c,
int cell, int visited[][]) {
// mark current cell as visited
visited[r][c] = cell;
// we have a solution
if (cell >= n * n) {
print(visited);
// backtrack before returning
visited[r][c] = 0;
return;
}
// check for all possible movements (8)
// and recur for each valid movement
for (int i = 0; i < (ROW.length - 1); i++) {
int newR = r + ROW[i];
int newC = c + COL[i];
// check if the new position is valid un-visited
if (isValid(newR, newC)
&& visited[newR][newC] == 0) {
knightTour(newR, newC, cell + 1, visited);
}
}
// backtrack from current cell
// and remove it from current path
visited[r][c] = 0;
}
// check if (r, c) is valid chess board coordinates
private boolean isValid(int r, int c) {
return !(r < 0 || c < 0 || r >= n || c >= n);
}
// print the solution as a board
private void print(int[][] visited) {
...
}
}
The complete application is called KnightTour.
Coding challenge 12 – Curly braces
Amazon, Google, Adobe, Microsoft, Flipkart
Problem: Print all the valid combinations of n pairs of curly braces. A valid combination is when the curly braces are properly opened and closed. For n=3, the valid combinations are as follows:
{{{}}},{{}{}},{{}}{},{}{{}},{}{}{}
Solution: The valid combination for n=1 is {}.
For n=2, we immediately see the combination as {}{}. However, another combination consists of adding a pair of curly braces to the previous combination; that is, {{}}.
Going one step further, for n=3, we have the trivial combination {}{}{}. Following the same logic, we can add a pair of curly braces to combinations for n=2, so we obtain {{{}}}, {{}}{}, {}{{}}, {{}{}}.
Actually, this is what we obtain after we remove or ignore duplicates. Let's sketch the case for the n=3 build based on n=2, as follows:

Figure 8.15 – Curly braces duplicate pairs
So, if we add a pair of curly braces inside each existing pair of curly braces and we add the trivial case ({}{}...{}) as well, then we obtain a pattern that can be implemented via recursion. However, we have to deal with a significant number of duplicate pairs, so we need additional checks to avoid having duplicates in the final result.
So, let's consider another approach, starting with a simple observation. For any given n, a combination will have 2*n curly braces (not pairs!). For example, for n=3, we have six curly braces (three left curly braces ({{{) and three right curly braces (}}})) arranged in different, valid combinations. This means that we can try to build the solution by starting with zero curly braces and add left/right curly braces to it, as long as we have a valid expression. Of course, we keep track of the number of added curly braces so that we don't exceed the maximum number, 2*n. The rules that we must follow are as follows:
- We add all left curly braces in a recursive manner.
- We add the right curly braces in a recursive manner, as long as the number of right curly braces doesn't exceed the number of left curly braces.
In other words, the key to this approach is to track the number of left and right curly braces that are allowed. As long as we have left curly braces, we insert a left curly brace and call the method again (recursion). If there are more right curly braces remaining than there are left curly braces, then we insert a right curly brace and call the method (recursion). So, let's get coding:
public static List<String> embrace(int nr) {
List<String> results = new ArrayList<>();
embrace(nr, nr, new char[nr * 2], 0, results);
return results;
}
private static void embrace(int leftHand, int rightHand,
char[] str, int index, List<String> results) {
if (rightHand < leftHand || leftHand < 0) {
return;
}
if (leftHand == 0 && rightHand == 0) {
// result found, so store it
results.add(String.valueOf(str));
} else {
// add left brace
str[index] = '{';
embrace(leftHand - 1, rightHand, str, index + 1,
results);
// add right brace
str[index] = '}';
embrace(leftHand, rightHand - 1, str, index + 1,
results);
}
}
The complete application is called Braces.
Coding challenge 13 – Staircase
Amazon, Adobe, Microsoft
Problem: A person walks up a staircase. They can hop either one step, two steps, or three steps at a time. Count the number of possible ways they can reach the top of the staircase.
Solution: First, let's set what hopping one, two, or three steps means. Consider that hopping one step means to go up the staircase step by step (we land on each step). To hop two steps means to jump over a step and land on the next one. Finally, to hop three steps means to jump over two steps and land on the third one.
For example, if we consider a staircase with three steps, then we can go from step 0 (or, no step) to step 3 in four ways: step by step (we land on each step), we jump over step 1 and land on step 2 and walk on step 3, we walk on step 1 and jump over step 2, thereby landing on step 3, or we jump directly on step 3, as shown in the following diagram:
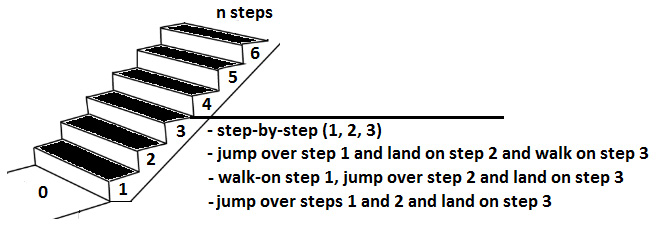
Figure 8.16 – Staircase (how to reach step 3)
By going one step further in our logic, we may ask ourselves how to reach step n. Mainly, the nth step can be reached if we do the following:
- n-1 step and hop 1 step
- n-2 step and hop 2 steps
- n-3 step and hop 3 steps
However, reaching any of these steps – n-1, n-2, or n-3 – is possible if we follow the preceding bullets. For example, we can reach the n-1 step if we are on n-2 and hop 1 step, we are on n-3 step and hop 2 steps, or we are on n-4 step and hop 3 steps.
So, to reach the nth step, we have three possible paths. To reach step n-1th, we also have three possible paths. So, to reach both steps, we must have 3+3=6 paths. Do not say 3*3=9 paths! This is wrong!
Now, we can conclude that adding all the paths in a recursive manner should give us the expected answers. Moreover, we can use our experience to add Memoization as well. This way, we avoid calling the method with the same inputs many times (exactly as in the case of the Fibonacci numbers):
public static int countViaMemoization(int n) {
int[] cache = new int[n + 1];
return count(n, cache);
}
private static int count(int n, int[] cache) {
if (n == 0) {
return 1;
} else if (n < 0) {
return 0;
} else if (cache[n] > 0) {
return cache[n];
}
cache[n] = count(n - 1, cache)
+ count(n - 2, cache) + count(n - 3, cache);
return cache[n];
}
The complete application is called Staircase. It also contains the plain recursion approach (without Memoization).
Coding challenge 14 – Subset sum
Amazon, Adobe, Microsoft, Flipkart
Problem: Consider a given set (arr) of positive integers and a value, s. Write a snippet of code that finds out if there is a subset in this array whose sum is equal to the given s.
Solution: Let's consider the array, arr = {3, 2, 7, 4, 5, 1, 6, 7, 9}. If s=7, then a subset can contain the elements 2, 4, and 1, as shown in the following diagram:

Figure 8.17 – Subset of sum 7
The subset containing the elements 2, 4, and 1 is just one of the possible subsets. All possible subsets include (3, 4), (2, 4, 1), (2, 5), (7), (1, 6), and (7).
Recursive approach
Let's try to find a solution via recursion. If we add the subset arr[0]=3, then we have to find the subset for s = s-arr[0] = 7-3 = 4. Finding a subset for s=4 is a sub-problem that can be solved based on the same logic, which means we can add arr[1]=2 in the subset, and the next sub-problem will consist of finding the subset for s = s-arr[1] = 4-2 = 2.
Alternatively, we can think like this: start with sum=0. We add arr[0]=3 to this sum as sum=sum+arr[0] = 3. Next, we check if sum = s (for example, if 3 = 7). If so, we found a subset. If not, we add the next element, arr[1]=2, to the sum as sum = sum+arr[1] = 3+2 =5. We recursively continue to repeat this process until there are no more elements to add. At this point, we recursively remove elements from sum and check if sum = s upon each removal. In other words, we build every possible subset and check if its sum is equal to s. When we have this equality, we print the current subset.
So far, it is clear that if we recursively solve each and every sub-problem, then it will lead us to the result. For each element from arr we must make a decision. Mainly, we have two options: include the current element in the subset or not include it. Starting from these statements, we can create the following algorithm:
- Define a subset as an array of the same length as the given arr. This array takes only values of 1 and 0.
- Recursively add each element from arr to the subset by setting a value of 1 at that particular index. Check for the solution (current sum = given sum).
- Recursively remove each element from the subset by setting a value of 0 at that particular index. Check for the solution (current sum = given sum).
Let's see the code:
/* Recursive approach */
public static void findSumRecursive(int[] arr, int index,
int currentSum, int givenSum, int[] subset) {
if (currentSum == givenSum) {
System.out.print(" Subset found: ");
for (int i = 0; i < subset.length; i++) {
if (subset[i] == 1) {
System.out.print(arr[i] + " ");
}
}
} else if (index != arr.length) {
subset[index] = 1;
currentSum += arr[index];
findSumRecursive(arr, index + 1,
currentSum, givenSum, subset);
currentSum -= arr[index];
subset[index] = 0;
findSumRecursive(arr, index + 1,
currentSum, givenSum, subset);
}
}
The time complexity of this code is O(n2n), so it's far from being efficient. Now, let's try an iterative approach via Dynamic Programming. This way, we avoid solving the same problem repeatedly.
Dynamic Programming approach
Via Dynamic Programming, we can solve this problem in O(s*n). More precisely, we can rely on the Bottom-Up approach and a boolean bidimensional matrix of dimension (n+1) x (s+1), where n is the size of the set (arr).
To understand this implementation, you have to understand how this matrix is filled up and how it is read. If we consider that the given arr is {5, 1, 6, 10, 7, 11, 2} and s=9, then this boolean matrix starts from an initial state, as shown in the following diagram:
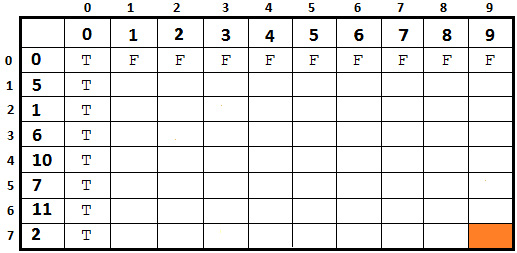
Figure 8.18 – Initial matrix
So, we have s+1 = 9+1 = 10 columns and n+1 = 7+1 = 8 rows. As you can see, we have filled up row and column 0. These are the base cases and can be interpreted as follows:
- Initialize the first row (row 0) of the matrix (matrix[0][]) with 0 (or false, F) except matrix[0][0], which is initialized with 1 (or true, T). In other words, if the given sum is not 0, then there is no subset to satisfy this sum. However, if the given sum is 0, then there is a subset containing only 0. So, the subset containing a 0 can form a single sum equal to 0.
- Initialize the first column (column 0) of matrix (matrix[][0]) with 1 (or true, T) because, for any set, a subset is possible with 0 sum.
Next, we take each row (5, 1, 6, ...) and we try to fill it up with F or T. Let's consider the second row, which contains the element 5. Now, for each column, let's answer the following question: can we form a sum of column number with a 5? Let's see the output:
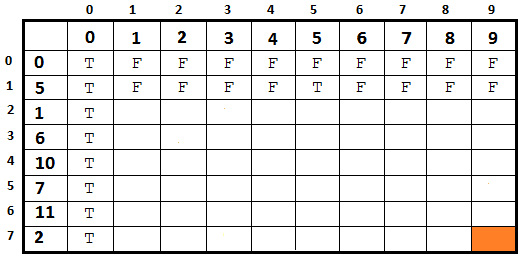
Figure 8.19 – Filling up the second row
- Can we form a sum of 1 with a 5? No, so false (F).
- Can we form a sum of 2 with a 5? No, so false (F).
...
- Can we form a sum of 5 with a 5? Yes, so true (T).
- Can we form a sum of 6 with a 5? No, so false (F).
...
- Can we form a sum of 9 with a 5? No, so false (F).
We can try to apply this question to each of the remaining rows, but the more we advance, the harder it will be. Moreover, we cannot implement this question in code without an algorithm. Fortunately, we can employ an algorithm that can be applied to each (row, column) cell. This algorithm contains the following steps:
- While the element of the current row (i) is greater than the value of the current column (j), we just copy the preceding value (i-1, j), in the current (i, j) cell.
- If the element of the current row (i) is smaller than or equal to the value of the current column (j), then we look to the (i-1, j) cell and do the following:
a. If cell (i-1, j) is T, then we fill up the (i, j) cell with T as well.
b. If cell (i-1, j) is F, then we fill up the (i, j) cell with the value at (i-1, j-element_at_this_row).
If we apply this algorithm to the second row (containing the element 5), then we obtain the same result shown in the following diagram:

Figure 8.20 – Applying the algorithm to the second row
Conforming to step 1, for 5 < 1, 5 < 2, 5 < 3, and 5 < 4, we copy the value from the preceding cell. When we reach cell (1, 5), we have 5=5, so we need to apply step 2. More precisely, we apply step 2b. The cell (1-1, 5-5) is the cell (0, 0) that has the value T. So, the cell (1, 5) is filled up with T. The same logic applies to the remaining cells. For example, cell (1, 6) is filled up with F since F is the value at (0, 5); the cell at (1, 7) is filled up with F since F is the value at (0, 6), and so on.
If we apply this algorithm to all the rows, then we obtain the following filled matrix:

Figure 8.21 – Complete matrix
Notice that we highlighted the last cell at (7, 9). If the right-bottom cell has the value T, then we say that there is at least a subset that satisfies the given sum. If it is F, then there is no such subset.
So, in this case, there is a subset whose sum is equal to 9. Can we identify it? Yes, we can, via the following algorithm:
- Start from the right-bottom cell, which is T (let's say that this cell is at (i, j)).
a. If the cell above this one, (i-1, j), is F, then write down the element at this row (this element is part of the subset) and go to cell (i-1, j-element_at_this_row).
b. While the cell above this one, (i-1, j), is T, we go up the cell (i-1, j).
c. Repeat this from step 1a until the entire subset is written down.
Let' s draw the path of the subset in our case:

Figure 8.22 – Subset solution path
So, we start from the bottom-right cell, which is at (7, 9) and has the value T. Because this cell is T, we can attempt to find the subset that has the sum 9. Next, we apply step 1a, so we write down the element at row 7 (which is 2) and go to cell (7-1, 9-2) = (6, 7). So far, the subset is {2}.
Next, we apply step 1b, so we land in cell (3, 7). The cell above (3, 7) has the value F, so we apply step 1a. First, we write down the element at row 3, which is 6. Then, we go to cell (3-1, 7-6) = (2, 1). So far, the subset is {2, 6}.
The cell above (2, 1) has the value F, so we apply step 1a. First, we write down the element at row 2, which is 1. Then, we go to cell (2-1, 1-1) = (1, 0). Above cell (1,0), we have only T, so we stop. The current and final subset is {2, 6, 1}. Obviously, 2+6+1 = 9.
The following code will clarify any other details (this code can tell if the given sum at least has a corresponding subset):
/* Dynamic Programming (Bottom-Up) */
public static boolean findSumDP(int[] arr, int givenSum) {
boolean[][] matrix
= new boolean[arr.length + 1][givenSum + 1];
// prepare the first row
for (int i = 1; i <= givenSum; i++) {
matrix[0][i] = false;
}
// prepare the first column
for (int i = 0; i <= arr.length; i++) {
matrix[i][0] = true;
}
for (int i = 1; i <= arr.length; i++) {
for (int j = 1; j <= givenSum; j++) {
// first, copy the data from the above row
matrix[i][j] = matrix[i - 1][j];
// if matrix[i][j] = false compute
// if the value should be F or T
if (matrix[i][j] == false && j >= arr[i – 1]) {
matrix[i][j] = matrix[i][j]
|| matrix[i - 1][j - arr[i - 1]];
}
}
}
printSubsetMatrix(arr, givenSum, matrix);
printOneSubset(matrix, arr, arr.length, givenSum);
return matrix[arr.length][givenSum];
}
The printSubsetMatrix() and printOneSubset() methods can be found in the complete code named SubsetSum.
Coding challenge 15 – Word break (this is a famous Google problem)
Amazon, Google, Adobe, Microsoft, Flipkart
Problem: Consider that you're given a dictionary of words and a string, str. Write a snippet of code that returns true if the given string (str) can be segmented into a space-separated sequence of dictionary words.
Solution: This problem is common to Google and Amazon and at the time of writing, it is adopted by a lot of medium-large companies. If we type a string that doesn't make sense into Google, then Google attempts to break it down into words and asks us if that is what we actually tried to type. For example, if we type "thisisafamousproblem", then Google will ask us if we wanted to type "this is a famous problem".
Plain recursion-based solution
So, if we assume that the given string is str="thisisafamousproblem" and the given dictionary is {"this" "is" "a" "famous" "problem"}, then we can form the result; that is, "this is a famous problem".
So, how can we obtain this? How can we check if the given string can be segmented into a space-separated sequence of dictionary words?
Let's start with an observation. If we start from the first character of the given string, then we notice that "t" is not a word in the given dictionary. We can continue by appending the second character to "t", so we get "th". Since "th" is not a word in the given dictionary, we can append the third character, "i". Obviously, "thi" is not a word in the dictionary, so we append the fourth character, "s". This time, we found a word because "this" is a word in the dictionary. This word becomes part of the result.
Taking this logic further, if we found "this", then the initial problem is reduced to a smaller problem that consists of finding the remaining words. So, by appending every character, the problem reduces to a smaller problem but essentially remains the same. This sounds like an ideal case for a recursive implementation.
If we elaborate on the recursive algorithm, then we have the following steps that we must perform:
- Iterate the given string, str, from the first character (index 0).
- Take each substring from the given string (by substring, we understand substring from index to 1, substring from index to 2, ...substring from index to str.length). In other words, as long as the current substring is not a word in the given dictionary, we continue to add a character from the given string, str.
- If the current substring is a word in the given dictionary, then we update the index so that it's the length of this substring and rely on recursion by checking the remaining string from index to str.length.
- If index reaches the length of the string, we return true; otherwise, we return false.
The code for this is as follows:
private static boolean breakItPlainRecursive(
Set<String> dictionary, String str, int index) {
if (index == str.length()) {
return true;
}
boolean canBreak = false;
for (int i = index; i < str.length(); i++) {
canBreak = canBreak
|| dictionary.contains(str.substring(index, i + 1))
&& breakItPlainRecursive(dictionary, str, i + 1);
}
return canBreak;
}
There is no surprise that the runtime of this code is exponential. Now, it is time to deploy Dynamic Programming.
Bottom-up solution
We can avoid recursion and deploy Dynamic Programming instead. More precisely, we can use the Bottom-Up solution shown here:
public static boolean breakItBottomUp(
Set<String> dictionary, String str) {
boolean[] table = new boolean[str.length() + 1];
table[0] = true;
for (int i = 0; i < str.length(); i++) {
for (int j = i + 1; table[i] && j <= str.length(); j++) {
if (dictionary.contains(str.substring(i, j))) {
table[j] = true;
}
}
}
return table[str.length()];
}
This code still runs in exponential time O(n2).
Trie-based solution
The most efficient solution to solve this problem relies on Dynamic Programming and the Trie data structure since it provides the best time complexity. You can find a detailed implementation of the Trie data structure in the book Java Coding Problems: (https://www.amazon.com/gp/product/B07Y9BPV4W/).
Let's consider the problem of breaking a given string into a set of components representing its words. If p is a prefix of str and q is the suffix of str (the remaining characters), then pq is str (the concatenation of p with q is str). And, if we can break p and q into words via recursion, then we can break pq = str by merging the two sets of words.
Now, let's continue this logic in the context of a Trie representing the given dictionary of words. We can assume that p is a word from the dictionary, and we must find a way to construct it. This is exactly where the Trie comes in. Because p is considered a word from the dictionary and p is a prefix of str, we can say that p must be found in the Trie via a path consisting of the first few letters of str. To accomplish this via Dynamic Programming, we use an array, let's denote it as table. Every time we find an appropriate q, we signal it in the table array by setting a solution at |p| + 1, where |p| is the length of the prefix, p. This means that we can continue by checking the last entry to determine if the whole string can be broken up. Let's see the code for this:
public class Trie {
// characters 'a'-'z'
private static final int CHAR_SIZE = 26;
private final Node head;
public Trie() {
this.head = new Node();
}
// Trie node
private static class Node {
private boolean leaf;
private final Node[] next;
private Node() {
this.leaf = false;
this.next = new Node[CHAR_SIZE];
}
};
// insert a string in Trie
public void insertTrie(String str) {
Node node = head;
for (int i = 0; i < str.length(); i++) {
if (node.next[str.charAt(i) - 'a'] == null) {
node.next[str.charAt(i) - 'a'] = new Node();
}
node = node.next[str.charAt(i) - 'a'];
}
node.leaf = true;
}
// Method to determine if the given string can be
// segmented into a space-separated sequence of one or
// more dictionary words
public boolean breakIt(String str) {
// table[i] is true if the first i
// characters of str can be segmented
boolean[] table = new boolean[str.length() + 1];
table[0] = true;
for (int i = 0; i < str.length(); i++) {
if (table[i]) {
Node node = head;
for (int j = i; j < str.length(); j++) {
if (node == null) {
break;
}
node = node.next[str.charAt(j) - 'a'];
// [0, i]: use our known decomposition
// [i+1, j]: use this String in the Trie
if (node != null && node.leaf) {
table[j + 1] = true;
}
}
}
}
// table[n] would be true if
// all characters of str can be segmented
return table[str.length()];
}
}
Apparently, because we have two nested loops, the runtime of this solution is O(n2). Actually, the inner loop breaks if the node is null. And, in the worst-case scenario, this happens after k steps, where k is the deepest path in the Trie. So, for a dictionary that contains the longest word of size z, we have k=z+1. This means that the time complexity of the inner loop is O(z) and that the total time complexity is O(nz). The extra space is O(space of the Trie + str.length).
The complete application is called WordBreak. This application also contains a method that prints all the strings that can be generated for the given string. For example, if the given string is "thisisafamousproblem" and the dictionary is {"this", "th", "is", "a", "famous", "f", "a", "m", "o", "u", "s", "problem"}, then the output will contain four sequences:
- th is is a f a m o u s problem
- th is is a famous problem
- this is a f a m o u s problem
- this is a famous problem
Done! Now, it's time to summarize this chapter.
Summary
In this chapter, we covered one of the most popular topics in interviews: recursion and Dynamic Programming. Mastering this topic requires a lot of practice. Fortunately, this chapter provided a comprehensive set of problems that covered the most common recursive patterns. From permutations to grid-based problems, from classical problems such as Tower of Hanoi to tricky problems such as generating curly braces, this chapter has covered a wide range of recursive cases.
Don't forget that the key to solving recursive problems consists of drawing a meaningful sketch and practicing several cases. This way, you can identify patterns and recursive calls.
In the next chapter, we will discuss problems that require bit manipulation.
