1.5
Proofs in Predicate Logic
1.5.1 Introduction
Most theorems in mathematics begin with quantifiers such as “for all” or “there exists,” or some variation of these such as “for all x, there exists a y,” although often not stated explicitly inasmuch the quantification is understood. Euclid's famous theorem about prime numbers is often stated simply as “there are an infinite number of prime numbers,” which begs the question, where is the “if” in the theorem? The answer is that the assumption is the definition of a prime number. In this section, we always include the all‐important quantifiers and prove theorems stated in the language of predicate logic.
1.5.2 Proofs Involving Quantifiers
Since many theorems in mathematics are stated in the form (∀x ∈ U)P(x) or (∃x ∈ U)P(x), the question we ask is how do we go about proving them. We begin by proving theorems that include a single universal quantifier.
Note: We could also prove Theorem 1 by writing the theorem in a contrapositive form as
where 6∤ n means 6 does not divide n.
Proofs involving the existential quantifier ∃ are often easier than ones involving the universal quantifier ∀ since it is only necessary to find one element in the universe that satisfies the given proposition.
Simply because we only have to find one object that satisfies the given condition, does not automatically mean the theorem is easy to prove. There are many unsolved conjectures related to finding just one thing. For example, a perfect number is a natural number that is equal to the sum of its proper divisors,1 such as 6 = 1 + 2 + 3, 28 = 1 + 2 + 4 + 7 + 14, …. Currently, it is unknown if there are any odd perfect numbers. The largest perfect number currently known is
and contains 44 677 235 digits.
Note that we have not determined which of the two powers

is rational, but we have shown one of them is rational.
1.5.3 Proofs by Contradiction for Quantifiers
Proofs by contradiction are important tools in a mathematician's toolkit.
Some theorems contain both universal and existential quantifiers. The following theorem is an example.
1.5.4 Unending Interesting Properties of Numbers
Is the number 10 008 036 000 540 a multiple of 9? The answer is yes, and if you know a certain theorem, you can answer the question in about five seconds. To prove this result, one must make the observation that 10 = 9 + 1. Here is the theorem stated in the language of predicate logic.
In general, to determine if a large number is a multiple of 9, one sums the digits to get a new number. If it is not immediately known if the new number is a multiple of 9, sum the digits again, and again. If the end product of all this is 9, then the original number is divisible by 9, otherwise no. Try a few numbers yourself.
It is also possible to prove theorems involving the existential quantifier by contradiction.
Proof of (∃x) P(x) by Contradiction
To prove a proposition of the form (∃x)P(x) by contradiction, assume the proposition false, or
and then reach some kind of contradiction.
Another proposition involving the existential quantifier ∃ is of the form (∼ ∃ x)P(x). To prove a proposition of this form by contradiction, assume the contrary, i.e.(∃x) P(x) and then reach a contradiction.
Theorem 6 No Largest Even Integer
There is no largest even integer.
Proof
Assume there is a largest even integer we call N, which we can write N = 2k for some k ∈ ℤ. Now consider N + 2, which we can write as
But this says N + 2 is an even integer greater than N, which contradicts the assumption that N is the largest even integer. Hence, we cannot claim there is a largest even integer.▌
Historical Note
There are theorems and then there are theorems. In the Classification Theorem for Simple Groups (known lovingly at the enormous theorem). The proof required the work of hundreds of mathematicians and consists of an aggregate of hundreds of papers. If the theorem were to be written out, it is estimated it would take between 10 000 and 15 000 pages.
1.5.5 Unique Existential Quantification ∃!
A special type of existential quantifier is the unique existential quantification
Proving Unique Existential Theorems
A theorem of the form
with an exclamation point ! after the existential quantifier ∃ states there exists a unique element x such that P(x) is true, the emphases being on the word “unique.” To prove a theorem of this form, we must show P(x) is true for exactly one element of the given universe U. A common strategy is to first show P(x) is true for some x ∈ U, and then if P(x) is true for another element y ∈ U, then x = y.
The concept of uniqueness is important in mathematics. For many problems, the first step is to first show existence, and the second step is to show uniqueness.
Theorem 7 Uniqueness: Diophantine Equation
There exist unique natural numbers m and n that satisfy
or (∃ ! m ∈ ℕ)(∃ ! n ∈ ℕ)(m2 − n2 = 12).
Proof
An equation that allows only integer solutions is called a Diophantine equation. We begin by factoring
and note that the difference between the two factors (m + n)(m − n) is 2n, which means that both factors must be even or both must be odd. But the only factor of 12 that meets this requirement is 12 = 2 × 6. Hence, we are left with
which only has the solution m = 4, n = 2.▌
Historical Note
In the late 1800s and early 1900s, there was a shift in the philosophy of mathematics, from thinking that logic was simply the tool for mathematics to thinking that logic was the foundation or precursor of mathematical thought. This thesis, called the “logistic thesis” (or “Frege–Russell thesis”), contends that mathematics is an extension of logic, as described in Russell and Whitehead's seminal work, Principia Mathematica. For others, like Giuseppe Peano, symbolic logic is only a tool for mathematics, which is the philosophy of many mathematicians today.
Historical Note
The American logician Charles Saunders Pierce (pronounced “purse”) introduced second‐order logic, which in addition to quantifying variables like x, y, … also quantifies functions and entire sets of variables. For most mathematics, first‐order logic is adequate. Pierce also developed first‐order logic, but Frege carried out his research earlier and is generally given credit for its development. However, it was Pierce who coined the term “first‐order” logic.
Theorem 8 Proof by Pictures
Does the drawing in Figure 1.11 constitute a “legitimate” proof of the Pythagorean theorem a2 + b2 = c2, with legs having lengths a, b and a hypotenuse having length c? Some people say yes, others say no, but the best way to think about “visual” proofs is that they provide an idea that can be turned into a valid logical proofs.
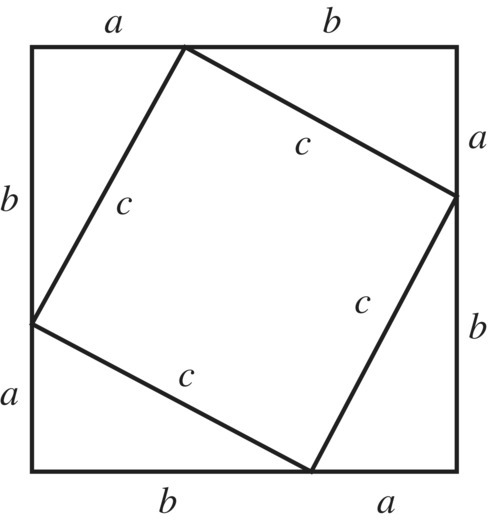
Figure 1.11 Visual proof of the Pythagorean theorem.
Proof by Picture
Setting the area of the large square equal to the sum of the areas of the four triangles plus the area of the smaller square yields.
Important Note
A great mathematical proof is one that is distinguished by beauty and economy. There are some proofs that get the job done but do not lift ones' intellectual spirit. On the other hand, some proofs overwhelm one with creative and novel insights. You might grade the proofs in this section according to those principles.
Problems
- True or False
Which of the following are true?
- (∀x ∈ ℝ)(x2 + x + 1 > 0)
- (∀x ∈ ℝ)[x2 > 0 ∨ x2 < 0 ]
- (∀x ∈ ℤ)(x2 > x)
- (∀x ∈ ℝ)(∃y ∈ ℝ)(y = sin x)
- (∀x ∈ ℝ)(∃y ∈ ℝ)(y = tan x)
- (∃x ∈ ℝ)(∃y ∈ ℝ)(y = sin x)
- (∃x, y ∈ ℕ)(∃n > 2)(xn + yn = 1)
- (∃x ∈ ℝ)(∀a, b, c ∈ ℝ)(ax2 + bx + c = 0)
- (∃x ∈ ℂ)(∀a, b, c ∈ ℝ)(ax2 + bx + c = 0)
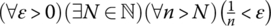
- (∀ε > 0)(∃δ > 0)(|x − 2| < δ ⇒ |x2 − 4| < ε)
- Predicate Logic Form
Write the following theorems in the language of predicate logic.
- A number is divisible by 4 if and only if its last two digits are divisible by four.
- A natural number is divisible by 2n if and only if its last n digits are divisible by 2n.
- There exists irrational numbers a, b such that ab is rational.
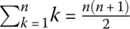
- For positive real numbers a, b, we have
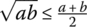 .
. - If a, b are integers and b ≠ 0, then there exists unique integers q, r such that a = qb + r where 0 ≤ r < |b|.
- If p is a prime number that does not divide an integer a, then p divides ap − a.
- The square of any natural number has each of its prime factor occurring an even number of times in its prime factorization.
- All prime numbers p greater than 2 are of the form either p = 2n + 1 or p = 2n + 3 for some natural number n.
- Every even number greater than 4 can be expressed as the sum of two prime numbers.
- Euler's Conjecture: There are no natural numbers a, b, c, d that satisfy a4 + b4 + c4 = d4.
- Negation
Negate the following propositions and tell whether the original statement or the negation is true. Let x and y be real variables.
- (∃x)(∀y)(xy < 1)
- (∀x)(∀y)(∃z)(xyz = 1)
- (∀x)(∀y)(∀z)(∃w)(x2 + y2 + z2 + w2 = 0)
- ∼(∃x)(∀y)(x < y)
- (∀x)(∃y)(xy < 1 ∧ xy > 1)
- (∃x)(∃y)(xy = 0 ∨ xy ≠ 0)
- Counterexamples
All the following statements are wrong. Prove them wrong by finding a counterexample.4
- All mathematicians make tons of money writing textbooks.
- For all positive integers n, n2 + n + 41 is prime.5
- Every continuous function defined on the interval (0,1) has a maximum and minimum value.
- Every continuous function is differentiable.
- If the terms of an infinite series approach zero, then the series converges.
- The perimeter of a rectangle can never be an odd integer.
- (∀x ∈ ℝ)(∃y ∈ ℝ)(x = y2)
- Every even natural number is the sum of two primes.
- If m and n are positive integers such that m divides n2 − 1, then m divides n − 1 or m divides n + 1.
- If {fn : n = 1, 2, …} is a sequence of continuous functions defined on (0, 1) that converge to a function f, then f is continuous.
- If and Only If Theorems
State each of the following theorems in the language of predicate logic. Take the function f as a real‐valued function of a real variable.
- A function f is even if and only if for every real number x we have f(x) = f(−x).
- A function f is odd if and only if for every real number x we have f(x) = − f(−x).
- A function f is periodic if and only if there exists a real number p such that f(x) = f(x + p) for all real numbers x.
- A function is increasing if and only if for every real numbers x and y we have x ≤ y ⇒ f(x) ≤ f(y).
- A function f is continuous at x0 if and only if for any ε > 0 there exists a δ > 0 such that |x − x0| < δ ⇒ |f(x) − f(x0)| < ε.
- A function f is uniformly continuous on a set E if and only if for any ε > 0 there exists a δ > 0 such that |f(x) − f(y)| < ε for any x, y in E that satisfy |x − y| < δ.
- Hard or Easy?
Prove that if there is a real number a ∈ ℝ that satisfies a3 + a + 1 = 0, then there is a real number b ∈ ℝ that satisfies b3 + b − 1 = 0. This problem is either very hard or very easy, depending how it is approached. It is your job to determine which is true.
- Predicate Logic in Analysis
The so‐called ε − δ proofs in analysis were originated by the German mathematician Karl Weierstrass in the 1800s and involve inequalities and universal and existential quantifiers. They often start with (∀ε > 0) followed by (∃δ > 0). The idea is that your adversary can pick ε > 0 as small as one pleases, but you have the advantage of picking the δ second. Of course, your choice of δ will most likely depend on ε.
- Show that for every real number ε > 0 there exists a real number δ > 0 such that 2δ < ε. In the language of predicate logic, prove (∀ε > 0)(∃δ > 0)(2δ < ε).
- For every real number ε > 0, there exists an integer N > 0 such that for n > N one has 1/n < ε. In the language of predicate logic, prove (∀ε > 0)(∃N > 0)(∀n > N)(1/n < ε).
- Show that for every real number ε > 0, there exists a real number δ > 0 such that if |x| < δ then x2 < ε. In the language of predicate logic, prove (∀ε > 0)(∃δ > 0)(∀x ∈ ℝ)(|x| < δ ⇒ x2 < ε)
- Show that for every positive integer M there is a positive integer N such that
 .
.
In the language of predicate logic, this says

- Doing Mathematics
Textbooks sometimes lead one to believe that theorems appear out of thin air for mathematicians to prove. If this were so, mathematics would be a purely deductive science, but in fact “doing mathematics” and mathematical research is as much an inductive science as deductive. Table 1.35 below lists the number of divisors τ(n) of n for the first 24 natural numbers. Looking at the table, can you think of any question to ask about the number of divisors of a natural number? A couple of candidates are
- Theorem 1: τ(n) is odd if and only if n is a square, like 4, 9, 16, …
- Theorem 2: If m and n have no common factor, then τ(m)τ(n) = τ(mn).
Table 1.35 Divisors of a few natural numbers.
n τ(n) n τ(n) 1 1 13 2 2 2 14 4 3 2 15 4 4 3 16 5 5 2 17 2 6 4 18 6 7 2 19 2 8 4 20 6 9 3 21 4 10 4 22 4 11 2 23 2 12 6 24 8 - Casting Out 9s
Show that a number d1d2d3 is a multiple of 9 if and only if d1 + d2 + d3 is a multiple of 9.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your search engine toward philosophy of intuitionism, Gottlob Frege, casting out nines, proofs in predicate logic, and proofs by pictures.
