Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

2.3
Counting: The Art of Enumeration

2.3.1 Introduction

Although counting is one of the first things we learn at a tender age, be assured there are counting problems that test the mental agility of the brightest minds among us. In this section, we will learn to count, although we refer to it as combinatorics. We will answer such counting questions as

how many ways can 10 people choose sides and play a game 5 against 5?

Counting problems often require almost no technical background and are often characterized by being easy to understand and hard to solve. Finding the number of ways to cover an 8 x 8 checkerboard with dominoes is a good example. The problem is easy to understand, but the number of coverings was not determined until 1961 by a M. E. Fischer, who found the number to be 2⁴ × (901)² = 12 988 816.

To assist you in perfecting counting skills, we introduce one of the basic tools of the trade, the multiplication principle.

2.3.2 Multiplication Principle

One of the basic principles of counting is the multiplication principle, although the principle is simple, it has far‐reaching consequences. For example, how many dots are there in Figure 2.11?

Diagram of counting exercise displaying three rows of ten solid circles. — **Figure 2.11** Counting exercise.

We suspect you said 30 after about three seconds, and you did not even bother to count all the dots. You simply counted the number of columns in the first row and then multiplied by 3. If so, you used the multiplication principle.

As a small step up the counting ladder, count the number of paths in Figure 2.12 going from A to C. No doubt this problem did not stump you either, getting 4 ⋅ 5 = 20 paths. Again, you used the multiplication principle.

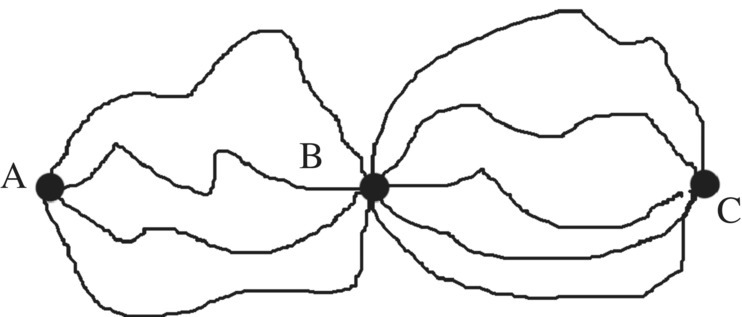
Diagram displaying four curve lines connecting solid circles labeled A and B and five curve lines connecting solid circles labeled B and C. — **Figure 2.12** How many paths from A to C?

This leads us to the formal statement of the multiplication principle.

We now let you test your counting skills using the multiplication rule with something a little harder.

2.3.3 Permutations

One of the important uses of the multiplication principle is counting permutations. A permutation is simply an arrangement of things. For example, there are six permutations of the three letters abc, which are

The number of permutations increases dramatically as the size of the set increases. The number of permutations of the letters of the alphabet is

To determine the number of permutations of these letters, we begin by selecting one member of the alphabet as the left‐most member in the permutation (or arrangement), which can be done in 26 ways. Once this is done, there are 25 remaining letters for the second member, the third member 24 ways, and so on, down to the last member. Using the principle of multiplication, the number of permutations of 26 objects is 26!.

2.3.4 Permutations of Racers

Suppose four individuals a, b, c, d are in a foot race, and we wish to find the number of ways four runners can finish first and second. Since each of the four runners can finish first, and for each winner, there are three possible second‐place finishers, there are 4 ⋅ 3 = 12 possible ways the runners can go 1–2. The tree diagram in Figure 2.14 illustrates these finishes.

Diagram of permutations of two elements from a set of four elements labeled a, b, c, and d (solid circles) with dotdash line indicating levels from first place to second place leading to permutation. — **Figure 2.14** Permutations of two elements from a set of four elements.

This leads to the general definition of permutations of different sizes.

Using the multiplication principle, we can find the number of permutations of r elements taken from a set of n elements.

Example 3 Permutations of a Set with Three Elements

Find the permutations of size r = 1, 2, 3 selected from {a, b, c}.

Solution

The permutations of size r = 1, 2, 3 taken from the set {a, b, c} with n = 3 elements are listed in Table 2.6.

Table 2.6 Permutations P(n, r)_.

r = 1	r = 2	r = 3
a	ab	abc
b	ac	acb
c	ba	bac
	bc	bca
	ca	cab
	cb	cba

We do not use set notation for writing permutations² since order is important. The permutation ab is not the same as ba.

2.3.5 Distinguishable Permutations

The number of permutations of elements in a set of the three letters is 3! = 6, however, for the three letters in the word “too” we cannot distinguish one “o” from the other, hence, we only have three distinguishable permutations that we can distinguish with our eyes, which are too, oto, oot.

Example 4 Distinguishable Permutations

How many distinguishable permutations are there of the letters of the word SYSTEM?

Solution

Since the two S's in SYSTEM are indistinguishable,³ we must modify our counting strategy. If we momentarily denote the two S's as S₁ and S₂, we have S₁YS₂TEM, which has 6! permutations. But the two letters S₁ and S₂ have two permutations, so we must divide 6! by 2!, getting the number of distinguishable

A few more distinguishable permutations are given in Table 2.7.

Table 2.7 Distinguishable permutations.

Word	Indistinguishable permutations
Too
Error
Toot
Mississippi

2.3.6 Combinations

Now that we have mastered permutations, we turn to combinations. A combination of things is simply a subset of things selected from larger collection of things. For the set {a, b, c} of three elements, a typical combination of two elements is {a, c}. We write combinations in set notation { } since the order of the members in the combination does not matter. The combination {a, c} is the same as the combination {c, a}. Just remember, order counts in permutations but not in combinations.

Example 5 Combinations

Find the combinations of size r = 1, 2, 3 selected from the set {a, b, c}.

Solution

The combinations are listed in Table 2.8, which are the eight subsets of {a, b, c}with the exception of the empty set Ø.

Table 2.8 Nonempty subsets of {a, b, c}_.

r = 1	r = 2	r = 3
{a}	{a, b}	{a, b, c}
{b}	{a, c}
{c}	{b, c}

We denote combinations by either notation

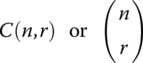
The second notation is possibly familiar to the reader since it is often the notation for the coefficients in binomial expansion formulas:

It helps in thinking about combinations to read C(n, r) as “n choose r” since it represents the number of ways one can choose r things from a set of n things. For example C(4, 2) = 6 is read “4 choose 2” meaning there are six ways you can choose two things from four things. Can you visualize in your mind the six subsets of size two from the set {a, b, c, d}?

Example 7 Number of Seven‐Game‐Series

How many ways can two teams play a best‐of‐seven game series, like the World Series⁴ in the United States? By “ways” we do not distinguish the two teams. For example, Team A or Team B can sweep the series in four games, but we call this the single outcome WWWW, not two outcomes as AAAA when Team A sweeps or BBBB when Team B sweeps.

Solution

Since the number of games played will be four, five, six, or seven, we begin by finding the number of each of those series. Since the winner of the series wins a total of four games and always wins the last game, we ask how many ways can the series be played before the last game. For example, for a six‐game series, we find the number of ways the winner can win three games in the first five games, which is “5 choose 3” or C(5, 3) = 10. For all four, five, six, and seven game series, the number of each of those series is

images .

Adding these series gives 35 possible outcomes for a best‐of‐seven game series. If we distinguish between the teams A and B, the total is 70.

Example 9 How Many Ways Home?

How many ways can Mary go home from school in the road system in Figure 2.15 when she always moves to the right or down?

Figure 2.15 Counting paths.

Solution

Since all paths pass through the one‐point gap, we find the number of paths before the gap and the number of paths after the gap, then multiply the results. From start to the gap, we travel a total of eight blocks, four blocks to the right and four blocks down. Labeling each block as R or D, depending whether the move is to the right or down, all paths can be written {x, x, x, x, x, x, x, x}, where four xs are R and four x's are D. Hence, the total number of paths is the number of ways one can select four D's (or four R's) from a set of size 8, which is “8 choose 4” or C(8, 4) = 70. Similarly, the number of paths from the “gap” to end is C(7, 3) = 35 Hence, the total number is

2.3.7 The Pigeonhole Principle

The pigeonhole principle (or Dirichlet Principle) illustrated in Figure 2.16 is based on the observation that if n items are placed in m containers, where n > m, then at least one container will contain more than one item. Although the principle seems almost too trivial to yield useful ideas, nothing is further from the truth. Its applications are far‐reaching and deep and widely used in many fields, including computer science, mathematical analysis, probability, number theory, geometry, and statistics.

Diagram of pigeonhole principle displaying a rectangle enclosing a pigeon with a call-out symbol (left) and nine pigeons inside individual square (right). — **Figure 2.16** Pigeonhole principle.

Should the pigeonhole principle be taken as an axiom or should it be proven from more fundamental principles? The word “obvious” is a loaded word in mathematics, since many famous “obvious” claims of the past have turned out not only nonobvious but nontrue.⁵ Although the pigeonhole principle seems obvious, it can be proven from more “basic principles” of set theory, although one wonders what could be more basic than the pigeonhole principle. Interested readers can find references on the Internet.

Problems

Compute the following
1. P(5, 3)
2. P(30, 2)
3. C(4, 1)
4. C(10, 8)
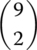
7. (a + b)⁶
Distinguishable Permutations
Find the number of distinguishable permutations in the following words.
1. SNOOT
2. DALLAS
3. TENNESSEE
4. ILLINOIS
Going to the Movies
Find the numbers of ways in which four boys and four girls can be seated in a row of eight seats if they sit alternately as boy and girl.
Movies Again
Three couples go to the movies and sit together in six seats. How many ways can they be arranged so that each couple sits together?
Counting Softball Teams
A college softball team is taking 25 players on a road trip. The traveling squad consists of three catchers, six pitchers, eight infielders, and eight outfielders. Assuming each player can only play her own position, how many different teams can the coach put on the field?
Counting Functions
How many functions are there from A = {a, b, c} to B = {0, 1, 2}?
Interesting Problem
How many three‐digit numbers d₁d₂d₃ are there whose digits add up to eight? That is, d₁ + d₂ + d₃ = 8, Note: 063 is not a three‐digit number, it is the two‐digit number 63.
World Series Time
Two teams compete in a best‐of‐five game series. In other words, the team that wins three games wins the series. How many possible ways are there to play a five-game series when we do not distinguish between the two teams?
Bell Numbers
A partition of a set A is defined as a collection of nonempty subsets of A that are pairwise disjoint and whose union is A. The number of such partitions of a set A of size n is called the Bell number B_n of the set. For example when n = 3, the Bell number B₃ = 5 since there are five partitions of a set of size three. For example, if A = {a, b, c}, then the five partitions are

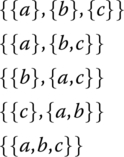
Enumerate the partitions of the set {a, b, c, d} to find the Bell number B₄.
Two Committees
What is the total number of ways the Snail Darter Society, which consists of 25 members, can elect an executive committee of 2 members and an entertainment committee of 4 members, if no member can serve on both committees?
Serving on More than One Committee
How many different ways can the Snail Darter Society, which has 25 members, elect an executive committee of 2 members, an entertainment committee of 3 members, and a welcoming committee of 2 members, if members can serve on more than one committee?
Single‐Elimination Tournaments
In a 64‐team single elimination tournament, what is the total number of possible outcomes of the tournament?
Counting Handshakes
There are 20 people in a room and each person shakes hands with everyone else. How many handshakes are there?
Not Serving on More than One Committee
How many ways can the Snail Darter Society, who has 25 members, elect an executive committee of 2 members, an entertainment committee of 3 members, and a welcoming committee of 2 members if members can not serve on more than one committee?
Counting Softball Teams
A college softball team is taking 25 players on a road trip. The traveling squad consists of three catchers, six pitchers, eight infielders, and eight outfielders. Assuming each player can only play her own position, how many different teams can the coach put on the field?
Catalan Numbers
The Catalan numbers C_n, n = 1, 2, 3, … are the number of ways a convex polygon with n + 2 sides can be subdivided into triangles. The following Figure 2.18 illustrates the Catalan numbers C₁, C₂, and C₃. Can you find the Catalan number C₄ which is the number of ways to triangulate a convex hexagon which has six sides?

Figure 2.18 First three Catalan numbers.
Famous Apple Problem
We wish to distribute eight identical apples to four children. How many ways is this possible if each child gets at least one apple?
Basic Pizza Cutting
You are given a circular pizza and ask to cut it into as many pieces as possible, where a cut means any line that passes all the way through the pizza although not necessarily through the center.
1. How many different pieces can you obtain with three slices?
2. How many different pieces can you obtain with four slices?
Pizza Cutter's Formula
A pizza cutter wants to cut a pizza in such a way that it has the maximum number of pieces, not necessarily the same size or shape. The only restriction on how the pizza is cut is that each cut much pass all the way through the pizza, not necessary through the center. See Figure 2.19.
1. If P(n) is the maximum number of pieces from n cuts, then
2. Show the pizza cutter's formula is given by
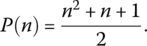
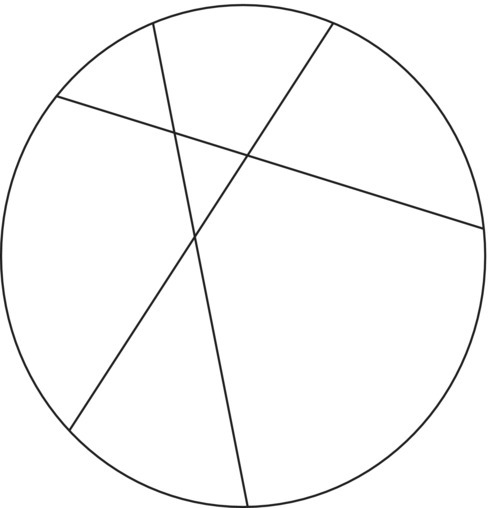
Figure 2.19 Typical pizza after three cuts with seven pieces.
Round Robin Tournaments
In a round robin tournament, every team plays every other team exactly once. Normally, an even number n teams compete and the tournament goes n − 1 rounds, where each team competes on each round. Find the total number of games played in a round robin tournament of n teams, assuming n is an even number.
Lottery Problem
A lottery works as follows. A container is filled with 36 marbles numbered 1, 2, …, 36 whereupon six marbles are selected at random by the lottery organizers. You buy a ticket and fill in six blanks with numbers between 1 and 36. You win if you choose the same six numbers selected by the organizers, regardless of order. How many different choices of six numbers can you select and since only one choice is a winner, the probability you win is 1 over that number. How many ways can you pick your six numbers and what are your chances of winning?
Relatively Prime Light
How many positive integers ≤32 are relatively prime to 32? Two numbers are relatively prime if their greatest common divisor is 1. For example, the positive integers relatively prime to 10 are 1, 3, 7, and 9.
Relatively Prime Medium
How many positive integers ≤35 are relatively prime to 35? Two numbers are relatively prime if their greatest common divisor is 1. For example the positive integers relatively prime to 10 are 1, 3, 7, and 9.
Relatively Prime Hard
How many positive integers ≤70 are relatively prime to 70? Two numbers are relatively prime if their greatest common divisor is 1. For example the positive integers relatively prime to 10 are 1, 3, 7, and 9.
Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward problems in combinatorics, applications of combinatorics, and pigeonhole principle.

Notes

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 2.3 Counting: The Art of Enumeration

Create new playlist

Sign In

Sign Up

2.3.1 Introduction

2.3.2 Multiplication Principle

2.3.3 Permutations

2.3.4 Permutations of Racers

2.3.5 Distinguishable Permutations

2.3.6 Combinations

2.3.7 The Pigeonhole Principle

Problems

Notes

Table of Contents for
2.3 Counting: The Art of Enumeration