2.4
Cardinality of Sets
2.4.1 Introduction
No one knows exactly when people first started counting, but a good guess might be when people started accumulating things. However, long before number systems were invented, two people might have determined whether they had the same number of goats and sheep as illustrated in Figure 2.20 by simply placing them in a one‐to‐one correspondence with each other.

Figure 2.20 Counting sheep.
Another person might have designated a stone for each goat, thus obtaining a one‐to‐one correspondence between the goats and a pile of stones. Today, we no longer use stones to enumerate things since we have symbolic stones in the form of 1, 2, …. To determine the number of goats, we simply “count,” 1, 2, … and envision the rocks R = {1, 2, 3, 4, 5} in our mind as illustrated in Figure 2.21.
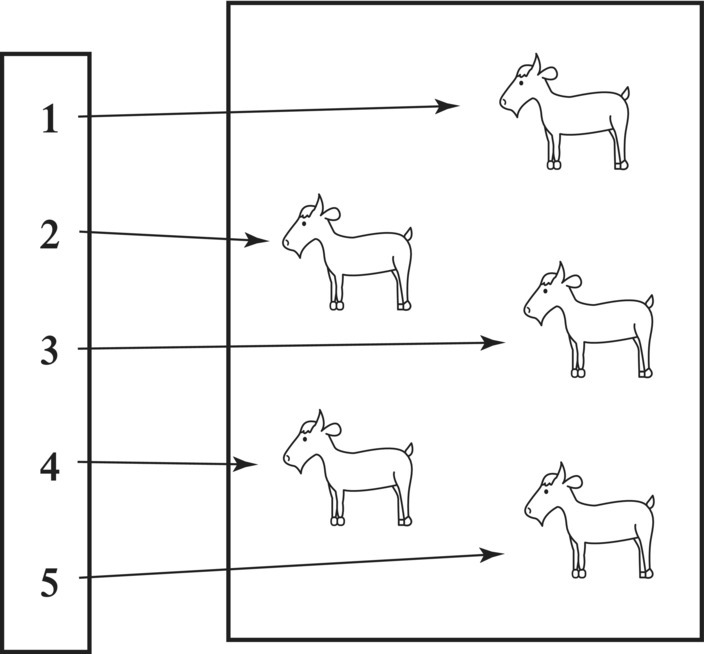
Figure 2.21 Modern way to count.
Throughout the history of mathematics, the subject of infinity has been mostly taboo, more apt to be included in discussions on religion or philosophy. The Greek philosopher Aristotle (c. 384–322 BCE), was one of the first mathematicians to think seriously about the subject, said there were two kinds of infinity, the potential and actual. He said the natural numbers 1, 2, 3, … are potentially infinite since they can never be completed. The philosopher and theologian Thomas Aquinas (1225−1275) argued that with the exception of God, nothing is actual infinite.
In the seventeenth century, the Italian astronomer Galileo made an observation concerning the perfect squares 1, 4, 9, 16, 25, …. He said since they constitute a subset of the natural numbers, there should be “fewer” of them than the natural numbers, and Table 2.9 would seem to bear this out.
Table 2.9 More natural numbers than perfect squares.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 4 | 9 | 16 |
However, he also observed that when one lines up the perfect squares as in Table 2.10, it appears that both sets contain the same number of members.
Table 2.10 Equal number of perfect squares as natural numbers.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ⋯ | n |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | |
| 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | ⋯ | n2 |
His argument was that for every perfect square n2, there is exactly one natural number n, and conversely for every natural number n, there is exactly one square n2. Using this reasoning, he concluded terms like less than, equal, and greater than apply to the size of finite sets but not infinite sets.
2.4.1.1 Early Bouts with Infinity
To get an idea how difficult it is to think about infinity, the ancient Greek philosopher Zeno of Elea (fifth century BCE) argued that motion is an illusion since a person who wishes to travel a fixed distance must first travel half the distance, then half the remaining distance, and then half that remaining distance and so on. So how could a person travel an infinite number of distances in a finite amount of time? Surprisingly, the paradox was not satisfactorily resolved until the tools of calculus were rigorously developed in the nineteenth century. Today, we understand that an infinite number of objects can add ad infinitum and still yield a finite result, much like the one‐foot square in Figure 2.22, whose area is the union of an unending series of areas of smaller and smaller and smaller squares and rectangles, but yielding a total area of
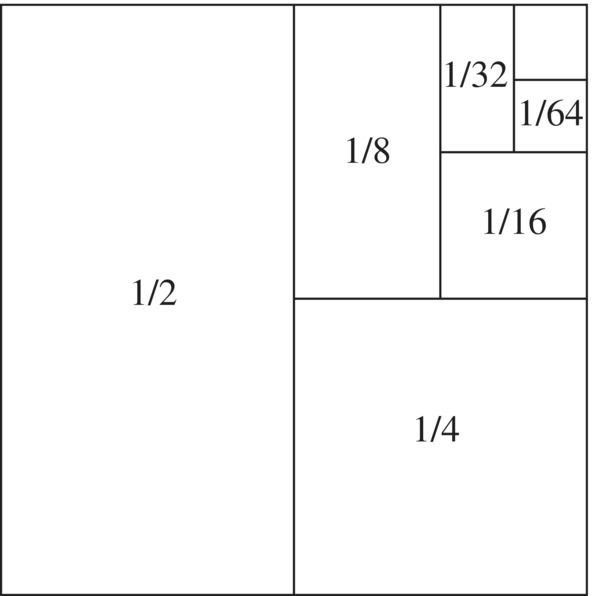
Figure 2.22 Visual response to Zeno's paradox.
The above discussion motivates the formal definitions related to Cantor's fundamental ideas.
2.4.2 Cardinality, Equivalence, Finite, and Infinite
We begin with several important definitions.
We now know there are two kinds of sets when it comes to size, finite and infinite. We know that some finite sets are larger, smaller, or equal in size to other sets. The cardinality of A = {a, b, c} is |A| = 3 and the cardinality of B = {a, b, c, d} is |B| = 4, and so we have |A| < |B|. But what about the cardinality of infinite sets, such as ℕ, ℤ, and ℚ? We know these sets have infinite cardinalities, but are the cardinalities the same, or is one cardinality larger than the others? And if that is so, exactly how many different cardinalities are there? Is there more than one infinity?
When it comes to comparing sizes of sets, finite or infinite, we have a good friend, and a friend the reader is no doubt familiar. It is the concept of a function, and although we do not formally introduce functions until the next chapter, the reader no doubt will have an adequate understanding of functions to understand the ideas presented here. We begin by introducing three important types of functions f : A → B that map a domain A into a set B; the one‐to‐one function, the onto function, and the one‐to‐one correspondence function.
The second type of function is onto function.
The third type of function we introduce is the one‐to‐one correspondence.
2.4.3 Major Result Comparing Sizes of Finite Sets
For finite sets A, B we know what is means when we say |A| < |B|, but this meaning breaks down for infinite sets when sets cannot be counted. However, the language of sets helps us overcome this difficulty. For finite sets, it is intuitively clear that |A| ≤ |B| when there is an injection (1–1) from A to B. We now use this motivation do define what it means by |A| ≤ |B| for infinite sets.
2.4.4 Countably Infinite Sets
We defined an infinite set as a set that is not finite. We now define a countably infinite (or denumerable) set.
Infinity can be tricky. If we add a new member to a finite set, we increase its cardinality by one, but things behave much differently for infinite sets. If we add “0” to the natural numbers ℕ = {1, 2, 3, …} getting ℕ ∪ {0}, do we increase the “size” of the set? The answer is no since we can relate the two sets with the one‐to‐one correspondence shown in Table 2.11.
Table 2.11 ℕ ∪ {0} ≈ ℕ.
| ℕ ∪ {0} | 0 | 1 | 2 | 3 | 4 | 5 | ⋯ | n |
| ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ | ↕ |
| ℕ | 1 | 2 | 3 | 4 | 5 | 6 | ⋯ | n + 1 |
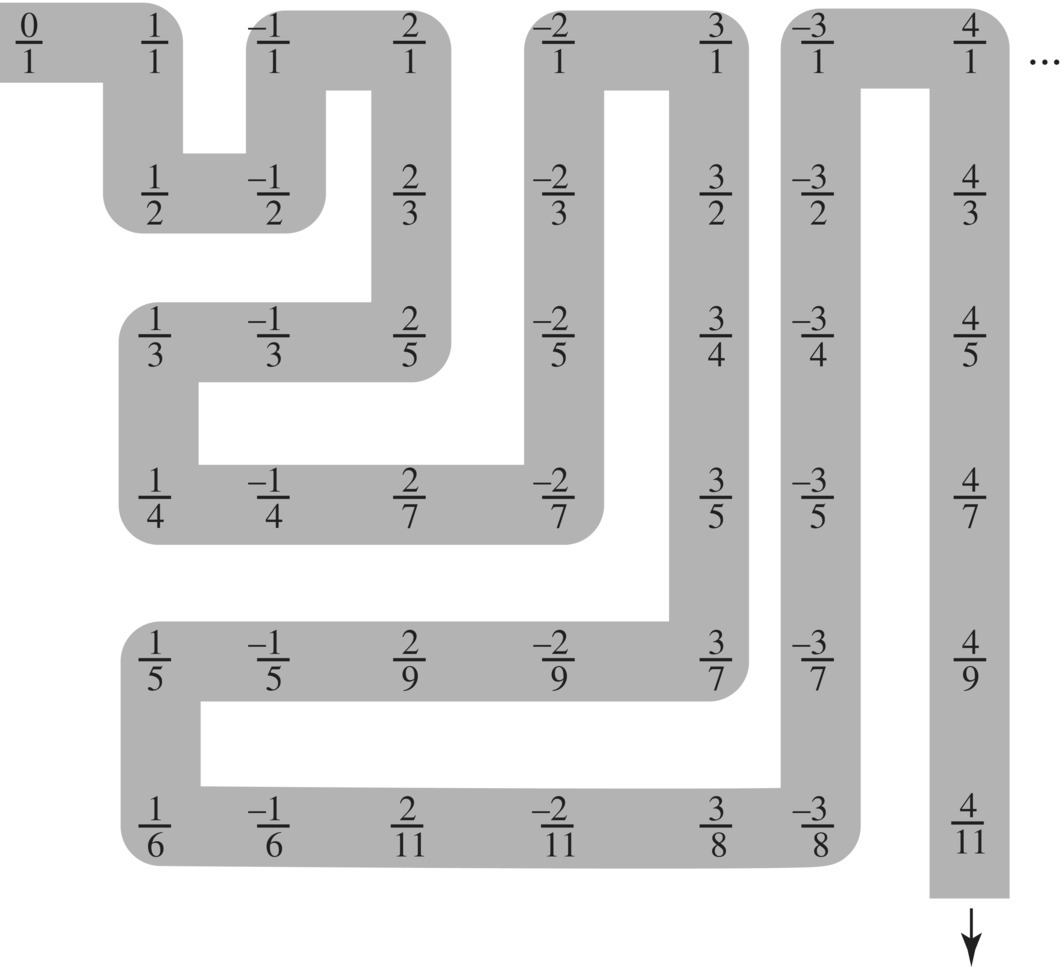
Figure 2.28 Graphical illustration of ℚ ≈ ℕ.
Cantor was initially convinced that all infinite sets were countably infinite as suggested from |ℕ| = |ℤ| = |ℚ|. The next obvious question was what about the cardinality of the real numbers? What is |ℝ|? Cantor tried and tried to prove the real numbers are countably infinite by proving they could be put in a one‐to‐one correspondence with the natural numbers, but in the process discovered something amazing. What did he discover? Wait until the next section.
Problems
- Countable Sets
Show that the union of two countable sets is countable.
- Equivalent Sets
For the following sets, find an explicit one‐to‐one correspondence that shows the intervals are equivalent.
- {a, b, c} ≈ {1, 2, 3}
- [0, 1) ≈ [0, ∞)
- (0, 1) ≈ ℝ
- [0, 1] ≈ [3, 5]
- Even and Odd Natural Numbers
Let E be the set of even positive integers and O be the set of odd positive integers. Given is an explicit function to show the following equivalences:
- E ≈ O
- ℕ ≈ O
- ℕ ≈ E
- ℕ × ℕ ≈ ℕ
- Infinite Sets
A set is infinite if and only if it is equivalent to a proper subset of itself. Use this definition of an infinite set to show the following sets are infinite:
- ℕ
- ℝ
- Bijection from the Prime Numbers
The following sets are equivalent. Find a bijection f : A → B.
- A = ℕ, B = prime numbers
- A = ℕ, B = {10, 12, 14, …}
- A = ℝ, B = (0, ∞)
- Cardinality Test
Use the results of Theorem 1 to show the following.
- Prove the cardinality of A = {a, b} is less than or equal to the cardinality of B = {1, 2, 3} by finding a 1–1 function f : A → B.
- Prove the cardinality of A = {a, b} is strictly less than the cardinality of B = {1, 2, 3} by finding a 1–1 function f : A → B that is not onto.
- Prove that the cardinality of A = {a, b, c} is greater than or equal to the cardinality of B = {1, 2} by finding an onto function f : A → B.
- Prove the cardinality of A = {a, b, c} is strictly greater than that of B = {1, 2} by finding an onto function f : A → B that is not 1–1.
- Prove that the cardinality of A = {a, b, c} is equal to the cardinality of B = {1, 2, 3} by finding a one‐to‐one correspondence between the sets.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward countably infinite, Georg Cantor, Zeno of Elea, and cardinality of a set.
