6.1
Symmetries and Algebraic Systems
6.1.1 Abstraction and Abstract Algebra
The ability to think abstractly is a unique feature of human thought, a capacity not shared by “lower forms” of living creatures.1 The power to capture the essence of what we experience is so engrained in our mental processes that we never give it a second thought. If the human mind did not have the capability to abstract commonalities in daily living, we would be living in a different world. Imagine lacking the capacity to grasp the “essence” of what makes up a chair. We would be forced to call every chair by a different name in order to communicate to others what we are referring to. The statement “the chair in the living room” would have no meaning unless we knew exactly what chair was being mentioned. Parents point to a picture of a dog in a picture book and tell their one‐year‐old infant, “dog,” and it is a proud moment for the parent when the child sees a strange dog in the yard and says, “dog!”
The concept of number is a crowning achievement of human's ability to abstract the essence of size of sets. It is not necessary to talk about “three people,” “three days,” “three dogs,” and so on. We have abstracted among those things the commonality of threeness, so there is no need to say “three goats plus five goats is eight goats,” or “three cats plus five cats is eight cats,” we simply say three plus five equals eight.
The current chapter is a glimpse into some ideas of what is called abstract algebra. Before defining what we mean by an abstract algebra, you should realize you have already studied some abstract algebras whether you know it or not. The integers are an example of an abstract algebra, although you probably have never called them abstract or even an algebra. The integers are a set of objects, supplied with binary operations of addition, subtraction, multiplication, and a collection of rules the operations must obey. Abstract algebra abstracts the essence of the integers and other mathematical structures, and says, “let's not study just this or that, let's study all things which have certain properties of interest.” Not all that different from when the infant first says “dog,” realizing there are more dogs than just the one in the picture book. Abstract mathematics allows one to think about attributes and relationships, and not focus on specific objects that possess those attributes and relationships.
The benefits of abstraction are many; it uncovers relationships between different areas of mathematics by allowing one to “rise up” above the nuances of a particular area of study and see things from a broader viewpoint, like seeing the forest and not simply the trees, like the saying goes. A disadvantage of abstraction, if there is one, is that abstract concepts are more difficult to grasp and require more “mathematical maturity” before they can be appreciated. It also might be argued that by seeing things from afar, we are unable to get into the nitty‐gritty of a discipline. In summary, abstract algebra studies general mathematical structures with given properties, important structures being groups, rings, and fields.
However, before we start a formal discussion of algebraic groups in the next section, we motivate their study with the introduction of symmetries.
6.1.2 Symmetries
We are all familiar with symmetrical objects, which we generally think of as objects of beauty, and although you may not be prepared to give a mathematical definition of symmetry, you know one when you see one. Most people would say a square is more symmetrical than a rectangle, and a hexagon more symmetrical than a square, and a circle is the most symmetrical object of all.
Regular patterns and symmetries are known to all cultures and societies. Although we generally think of symmetry in terms of geometric objects, we can also include physical objects as well, like a molecule, the crystalline structure of a mineral, a plant, an animal, the solar system, or even the universe. The concept of symmetry embodies processes like chemical reactions, the scattering of elementary particles, a musical score, the evolution of the solar system, and even mathematical equations. In physics, symmetry has to do with the invariance (i.e. unchanging) of natural laws under space and time transformations. A physical law that has space/time symmetries establishes that the law is independent of translating, rotating, or reflecting the coordinates of the system. The symmetries of a physical system are fundamental to how the system acts and behaves. The equation
is symmetric in the three variables x, y, z, since after interchanging any two the equation is unchanged.
Symmetry also plays an important role in calculus. The graph of a real valued function f of a real variable that satisfies f(x) = f(−x) is symmetric about the y‐axis, and when f(x) = − f(−x) the graph of the function is symmetric through the origin and unchanged when the graph is rotated 180° about the origin.
6.1.3 Symmetries in Two Dimensions
For a single (bounded) figure in two dimensions, there are two types of symmetries.2 There is symmetry across a line in which one side of the object is the mirror image of its other half. This bilateral symmetry, or the symmetry of left and right, and is common in the structure of many animals, especially humans. This type of symmetry is called line symmetry (or reflective or mirror symmetry). Figure 6.1 shows an isosceles triangle with a line symmetry through its vertical median.

Figure 6.1 Line symmetry.
We measure the extent to which an object is “symmetric” by counting the number of its symmetries. The parallelogram, rectangle, and square in Figure 6.2 have zero, two, and four lines of symmetry. You can envision yourself other objects that have various lines of symmetry. Chemists are well aware of lines of symmetry of molecules since they relate to how chemical compounds behave.

Figure 6.2 Degrees of symmetry.
A second type of symmetry is rotational (or radial) symmetry. An object has a rotational symmetry if the object appears exactly the same when rotated a certain number of times around a central point. The triangle in Figure 6.1 has no rotational symmetry, whereas the three figures in Figure 6.3 have various levels of rotational symmetry. The letter “Z” has no line symmetries, but repeats itself when rotated 0 and 180°,3 so we say it has rotational symmetry of degree two. The object the middle, again has no line symmetries, but repeats itself when rotated 0, 120, and 240°, so it has rotational symmetries of degree three. Finally, we have the most symmetric planar object of all, the circle which has both an infinite number of rotational and line symmetries.

Figure 6.3 Rotational symmetries.
Some objects have both reflective and rotational symmetries as illustrated by the regular polygons4 in Figure 6.4 which have the same number of reflective and rotational symmetries. The equilateral triangle has three rotational symmetries (rotations of 0°, 120°, and 240° about a center point) and three reflective symmetries through median lines passing through the vertices. A regular polygon with n vertices has n rotation symmetries (each rotation 360/n degrees) and n lines of symmetry.
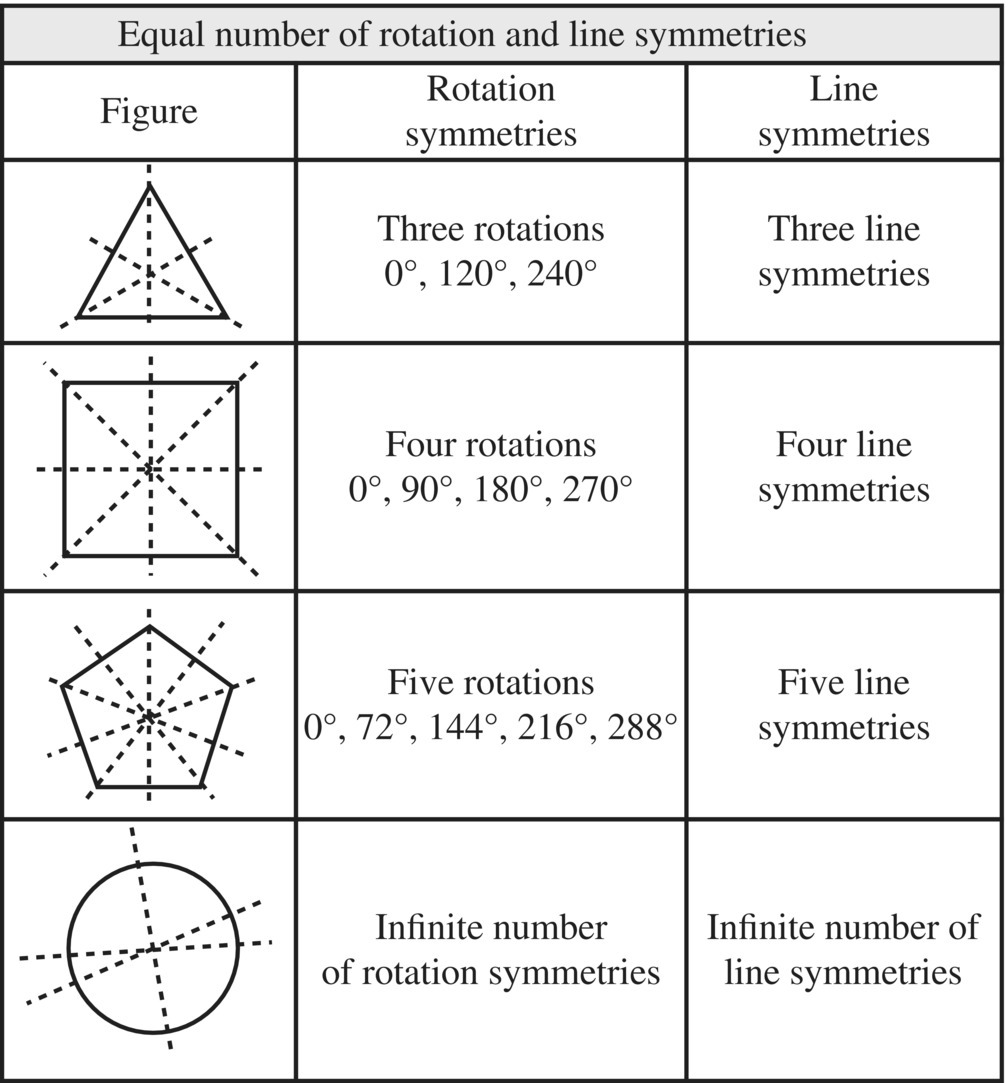
Figure 6.4 Figures having both rotational and reflective symmetries.
6.1.4 Symmetry Transformations
Although you can think of symmetries as a property of an object, there is another interpretation of symmetries that is more beneficial for our purposes. A symmetry is a function or mapping or transformation.
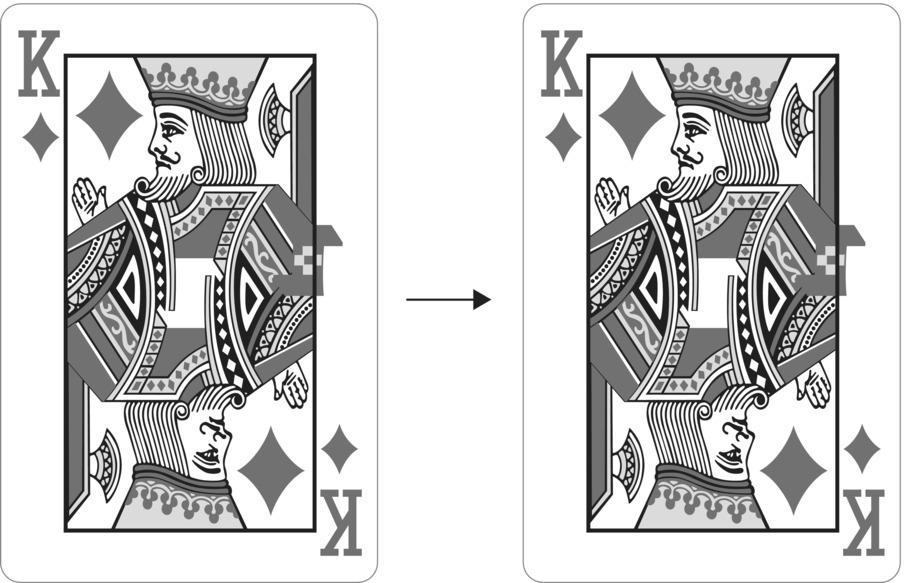
Figure 6.5 Rotation symmetry of 180°.
6.1.5 Symmetries of a Rectangle
Figure 6.6 shows a rectangle where the length and width are different and the corners are labeled A, B, C, D,
Figure 6.6 Four symmetries of a rectangle.
The rectangle has two rotational symmetries of 0°, 180° and two line (or flip) symmetries, where the lines of symmetry are the horizontal and vertical midlines. These four symmetries5 are illustrated in Figure 6.7.
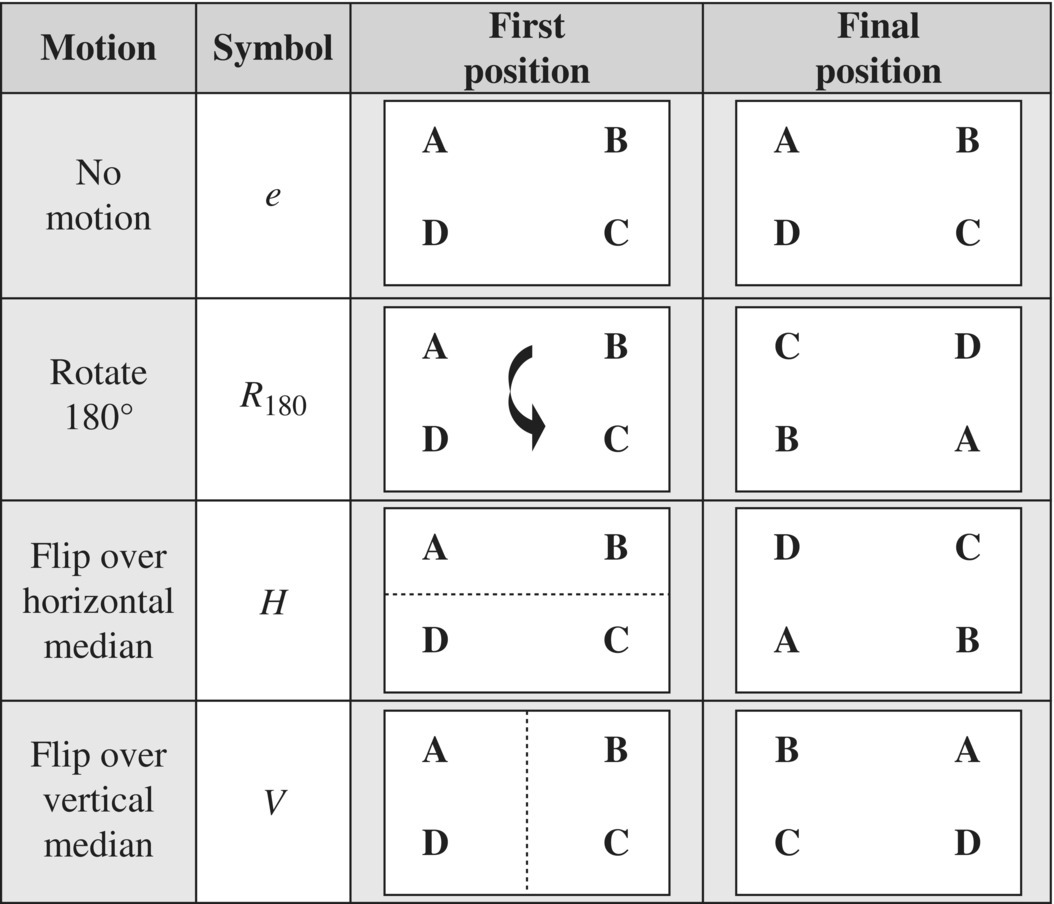
Figure 6.7 Four symmetries of a rectangle.
So what do these symmetries have to do with algebraic structures, which is the focus of this chapter? Since a symmetry is a transformation that maps the points of an object back onto itself, we can define the product of two symmetries as the composition of two symmetries and the result will be a new symmetry. If each symmetry leaves the object unchanged so does the composition of two symmetries. Hence, the composition of symmetries defines a product of two symmetries, just like the product of two numbers 2 × 3 = 6 getting a new number.
If we perform a 180° rotation,6 denoted by R180, followed by H, a flip through the horizontal midline, we denote this composition or product by R180 H reading left to right. The net result (product) of these two symmetry operations is illustrated in Figure 6.8, and is the same as performing the single symmetry V, a flip through the vertical midline. Hence, we write the product R180 H = V. It is important to note that symmetry operations are carried out from “left‐to‐right” in the product notation.
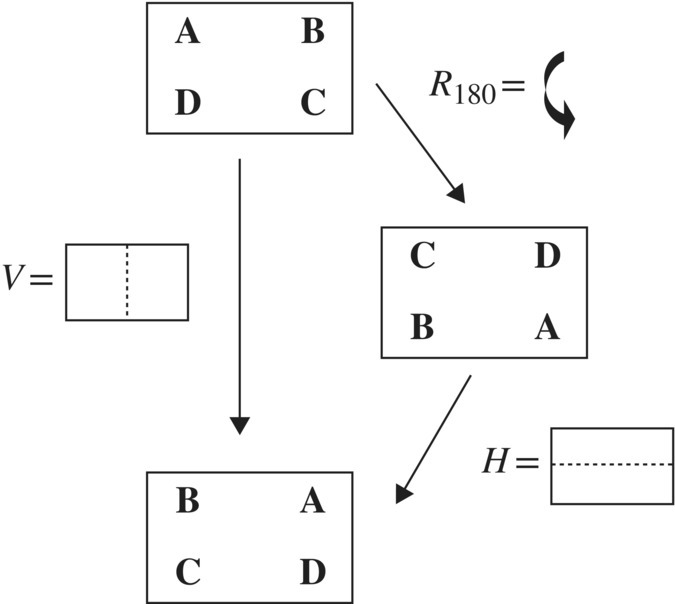
Figure 6.8 Product of symmetries R180H = V.
Note that the “do nothing” symmetry e (rotation of zero degrees), called the identity symmetry, is analogous to the number one in the multiplication of integers. Note that some operations like e, R180, V, H return the figure to its original position after operating two times. For that reason, we say these symmetries are equal to their inverse, which we illustrate by the equations in Table 6.1.
Table 6.1 Typical symmetry products.
| Symmetry | Symmetry products |
| e | ee = e ⇒ e = e−1 |
| H | HH = e ⇒ H = H−1 |
| V | VV = e ⇒ V = V−1 |
| R180 |
Since the composition of symmetries, which we call products, yields a new symmetry, we can construct multiplication tables for symmetries, much like we did in grade school for multiplication tables of numbers. The multiplication table for symmetries of a rectangle is shown in Figure 6.9. The product of two symmetries lies at the intersection of the row and column symmetries, where the row symmetry is carried out first. For example, the intersection of the row labeled R180 and column labeled H is V, which means R180H = V. The borders of the cells containing the identity symmetry e are darkened as an aid in reading the table.

Figure 6.9 Multiplication table for symmetries of a rectangle.
6.1.6 Observations
- Every row and column of the multiplication table contains one and exactly one of the four symmetries. It is a Latin square.
- The main diagonal contains the identity symmetry e, which means every symmetry is its own inverse.
- The table is symmetric about the main diagonal which means the multiplication of symmetries is commutative. In other words, AB = BA, just like multiplication of numbers. We call this a commutative algebraic system.
- The four symmetries e, R180, V, H along with their product as defined by the table, forms what is called an algebraic group. Observe how this system is analogous to the integers with the operation of addition, with some similarities and some differences.
6.1.7 Symmetries of an Equilateral Triangle
We now examine the equilateral triangle drawn in Figure 6.10. It is “more symmetric” than the triangle drawn in Figure 6.1 that had one line symmetry. The equilateral triangle has three rotational symmetries where the triangle is rotated 0°, 120°, 240° about its center, and three line symmetries where the triangle is reflected through lines passing through vertices as drawn as dotted line segments.
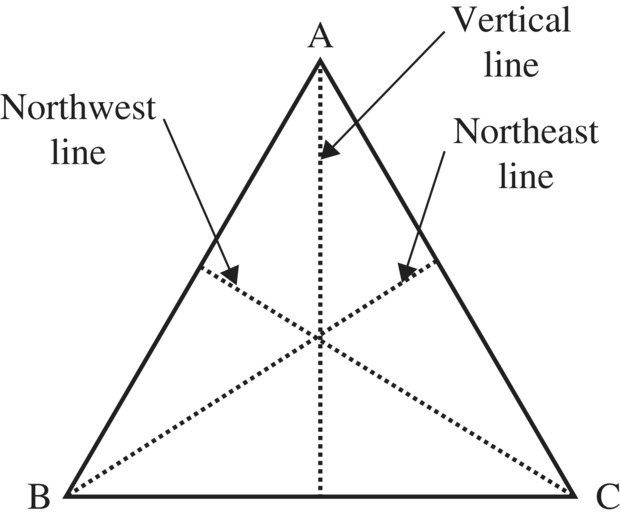
Figure 6.10 Six symmetries of an equilateral triangle.
We denote these symmetry mappings by
where
- e = R0 is the identity (rotation by 0°) symmetry
- R120 = counterclockwise rotation of 120°
- R240 = counterclockwise rotation of 240°
- Fv = flip through the vertical median
- Fnw = flip through the northwest median
- Fne = flip through the northeast median
These symmetries are illustrated in Figure 6.11.
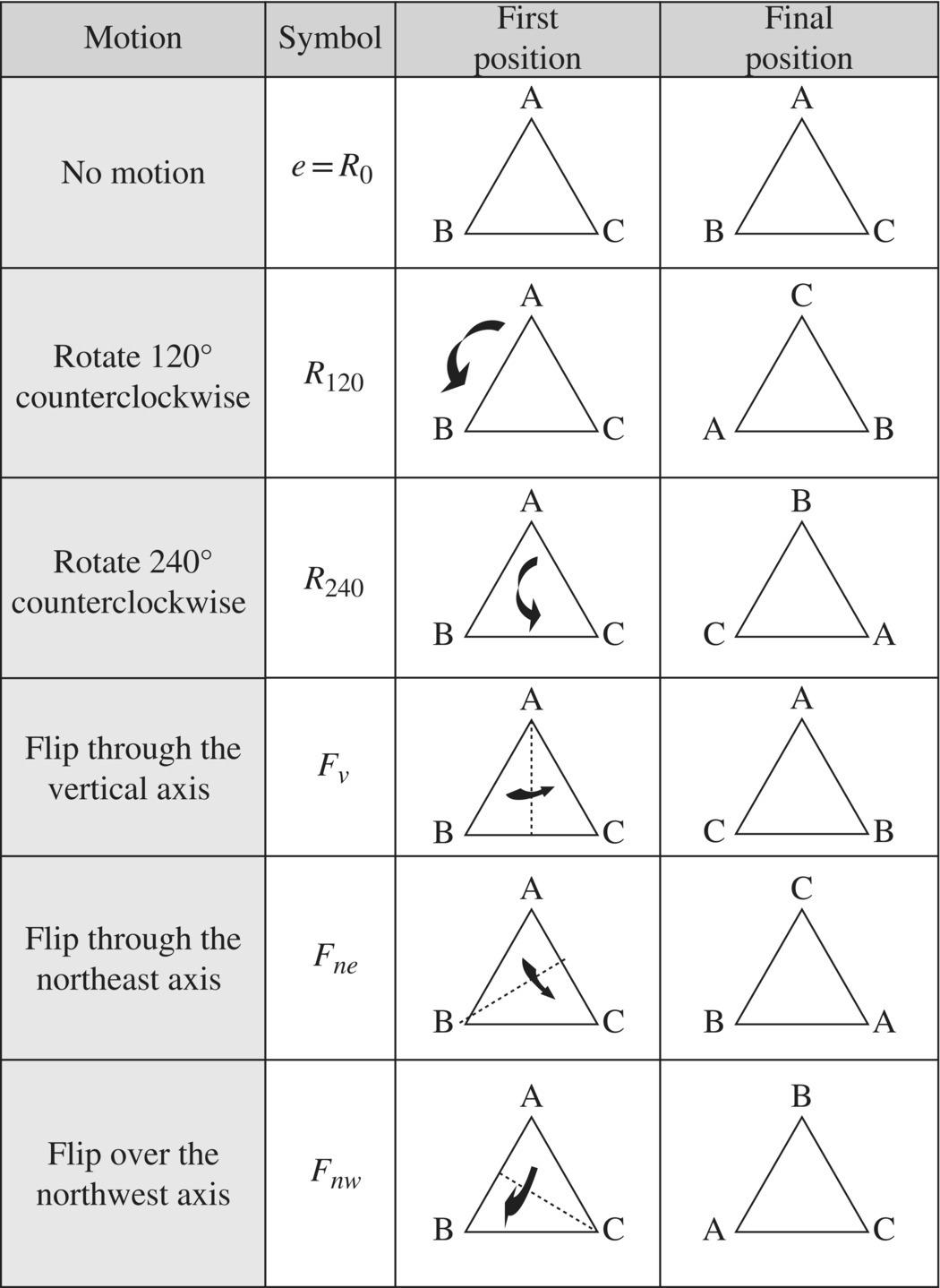
Figure 6.11 Six symmetries of an equilateral triangle.
As we did for the rectangle, we can construct a multiplication table for the symmetries called a Cayley table shown in Figure 6.12.
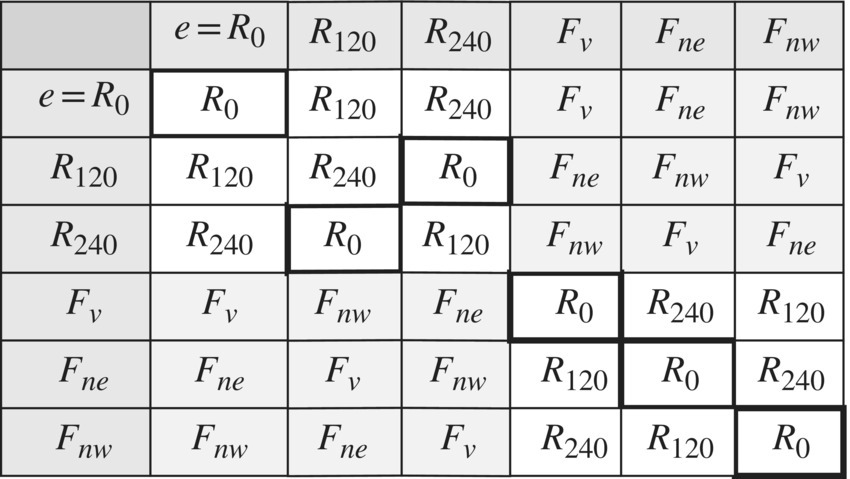
Figure 6.12 Cayley table for symmetries of an equilateral triangle.
Again, we have drawn darker around the identity symmetry e = R0 as an aid in understanding and interpreting its results. We have also shaded the “northeast” and “southwest” blocks in the table as an aid in reading the table.
6.1.8 Rotation Symmetries of Polyhedra
In addition to symmetries in the plane, there are symmetries in higher dimensions that play an important role in many areas of science. For instance in crystallography, which shows how atoms and molecules can be arranged within crystals, chemists are interested in the symmetry axes of various polyhedra. Since polyhedra have vertices (v), edges (e), and faces ( f ), the symmetry axes can be one of six types vv, ee, ff, ve, vf, ef. A vv symmetry means the axis of symmetry passes through two vertices (vv), whereas a vf symmetry means the axis of symmetry passes through a vertex and an opposite face, and so on.
6.1.9 Rotation Symmetries of a Cube
Table 6.2 shows the 24 rotational symmetries of the cube of the form ff, ee, vv, meaning the axis or rotation always passes through opposite faces, edges, and vertices.
Table 6.2 Rotational symmetries of a cube.
| Rotation symmetries of a cube | Symmetry angles | Total symmetries |
| 3 ff symmetry axes | 90°, 180°, 270° | 9 |
| 4 vv symmetry axes | 120°, 240° | 8 |
| 6 ee symmetry axes | 180° | 6 |
| Identity map | 0° | 1 |
These 24 symmetries are visualized in Figure 6.13. The reader can try to visualize these symmetries or obtain a child's block to simulate them.

Figure 6.13 Rotational symmetries of a cube.
Problems
- Finding Symmetries
Determine the symmetries of the letters of the alphabet. The more the symmetries, the more symmetric the letter. Which letter is the most/least symmetric?
- Drawing Symmetries
Draw a figure that has the following symmetries. We do not allow the identity symmetry to be a symmetry in these classifications.
- 0 rotational and 0 line symmetries
- 1 rotational and 0 line symmetries
- 0 rotational and 1 line symmetry
- 2 rotational and 0 line symmetries
- 1 rotational and 0 line symmetries
- 3 rotational and 0 line symmetries
- Symmetries of a Parallelogram
Describe the symmetries of a parallelogram that is neither a rhombus nor a rectangle.
- Symmetries of an Ellipse
Describe the symmetries of an ellipse
- Representation of D2 with Matrices
Show that the matrices

with operation of matrix multiplication obey the multiplication table in Figure 6.14. This is called the dihedral group D2.

Figure 6.14 Dihedral multiplication table.
- Symmetries of a Square
The following matrices define the six symmetries of a square. Find the multiplication table for these symmetries.

- Symmetry Groups
Find the symmetries of the following letters and make a multiplication table for the symmetries of each letter.
- S
- T
- J
- Symmetries of a Tetrahedron
Can you find the seven axes of symmetries of the regular tetrahedron with four identical triangular sides as illustrated in Figure 6.15.
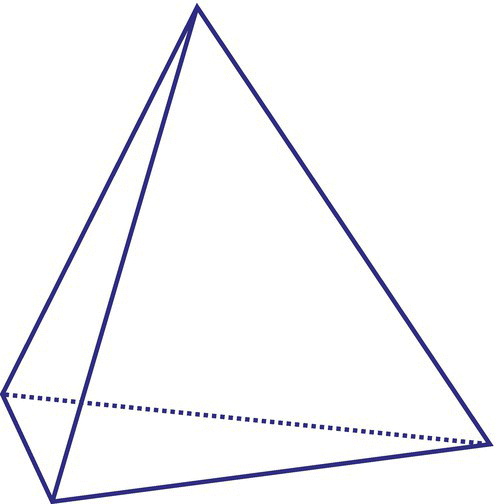
Figure 6.15 Tetrahedron.
- Cayley Table for D3
Note that the Cayley table for the symmetries of an equilateral triangle bunched together into four distinct blocks, two blocks consisting of rotations, and two consisting of blocks of flips. From this table, tell if the following statements are true or false.
- rotation followed by a rotation is the rotation, i.e. RR = R
- rotation followed by a flip is a rotation, i.e. RF = R
- rotation followed by a rotation is a flip, i.e. RR = F
- rotation followed by a flip is a flip, i.e. RF = F
- flip followed by a flip is a rotation, i.e. FF = R
- flip followed by a rotation is a rotation, i.e. FR = R
- flip followed by a flip is a flip, i.e. FF = F
- flip followed by a rotation is a flip, i.e. FR = F
- Symmetries of Solutions of Differential Equations
The solutions of the differential equation dy/dx = y are the functions of the form y = cex, where c is an arbitrary constant. Show that the transformation x′ = x + h, y′ = y, where h is an arbitrary real number that maps the set of solutions back into the set of solutions, and hence is a symmetry transformation of the solutions of the differential equation.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward lines of symmetry (look under the image tab), rotational symmetry, symmetry in theoretical physics, and history of symmetry.
