6.4
Subgroups: Groups Inside a Group
6.4.1 Introduction
Recall the six symmetries of an equilateral triangle: the identity map, three flips about the midlines, and two (counterclockwise) rotations of 120° and 240° illustrated in Figure 6.47.

Figure 6.47 Symmetries of an equilateral triangle.
Although we have seen that these symmetries, along with the operation of compositions forms an algebraic group, what is also true is that the group is made up of several smaller groups, In the given case of the six symmetries of an equilateral triangle, the subset of three rotational symmetries {e, R120, R240} whose multiplication table is shown in Figure 6.48, can easily be verified to form a group.

Figure 6.48 Subgroup of rotations of symmetries of an equilateral triangle.
The above discussion motivates the following definition of “groups within groups,” or subgroups.
6.4.1.1 At Least Two Subgroups
Although all groups have two subgroups, the group itself and the trivial group consist of only the identity {e}, and we are mainly interested in the other subgroups, called proper subgroups, although we often refer to them simply as subgroups.

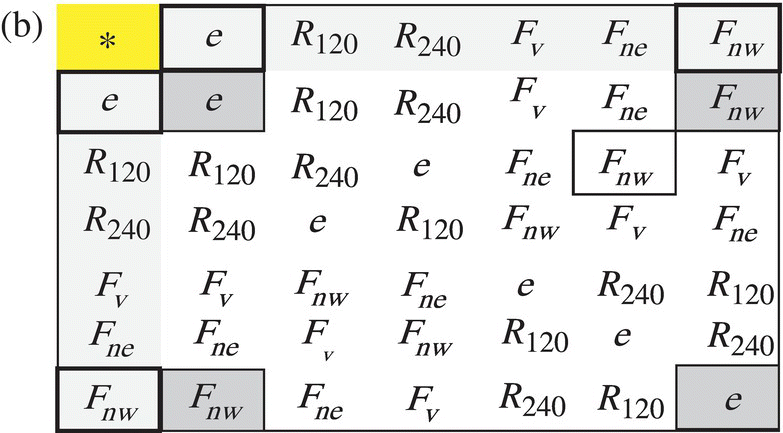
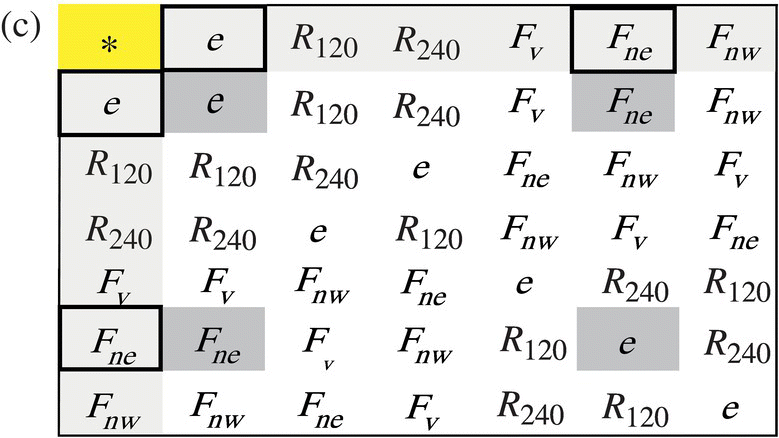

Figure 6.49 (a) H1 = {e, Fv} flip around vertical axis. (b) H2 = {e, Fnw} flip around the northwest axis. (c) H3 = {e, Fne} flip around the northeast axis. (d) Three rotations of a rectangle.
We let the reader verify each of these subgroups satisfy the required conditions to be a group.
6.4.2 Subgroups of the Klein Four‐Group
Recall that the group of symmetries of a rectangle forms the Klein four‐group with elements
Figure 6.50 shows the Cayley table of these symmetries and three subgroups of order 2.

Figure 6.50 Symmetry group of a rectangle and three subgroups.
Note that the order of a subgroup divides the order of the group. This fundamental property of subgroups is called Lagrange's Theorem after the French/Italian mathematician Joseph‐Louis Lagrange (1736–1813).
6.4.3 Test of Subgroups
Although a subset H of a group G is a group only if it satisfies the requirements for a group, it is only necessary to verify that the group operation * is closed in H and that every element of H has an inverse in H. There is no need to show the associative property or the existence of an identity since the identity in G is also an identity in H. This result is summarized in the following theorem.

Figure 6.51 Eight symmetries of a square.
The subgroups of the symmetry group of a square form a partially ordered set, ordered by set inclusion, illustrated in Figure 6.52. The octic group D4 is itself a subgroup of the group S4 of 24 permutations of four elements.
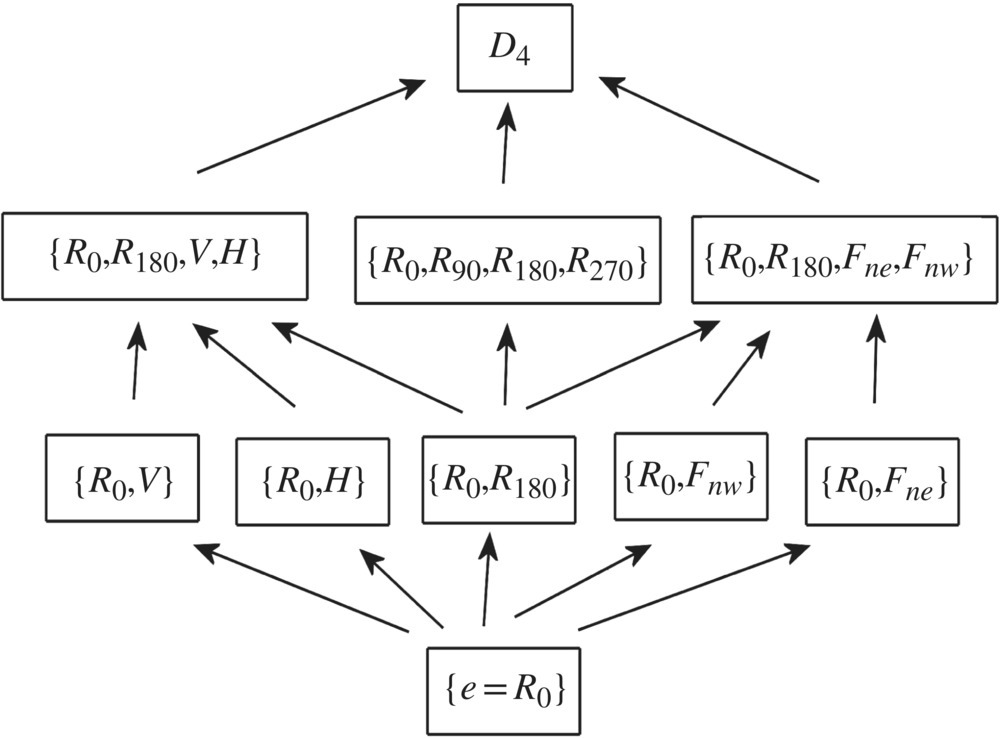
Figure 6.52 Hasse diagram for the subgroups of the octic group D4.
6.4.4 Subgroups of Cyclic Groups
We have seen that the cyclic group Zn is generated by an element in the group. That is, there exists a g ∈ Zn such that
To find the subgroups of Zn, we begin with an arbitrary element h ∈ Zn and compute the set 〈h〉 generated by h. The elements generated by h may or may not be all of Zn, but they will always create a subgroup of Zn. We then pick a second member h′ ∈ Zn which is not in the first generated set 〈h〉 and compute 〈h′〉. This will yield another subset of Zn. Continuing this process will eventually yield all subgroups of Zn.
Let us apply this technique to find all the subsets of the cyclic group
where the group operation is addition modulo 12. Starting with 1, we generate powers of g = 1, remembering that powers of one in this group are really adding 1. Hence, we have
which generates the entire group ℤ12. We now select the element g = 2, which generates the subgroup
Figure 6.53 shows the subgroups generated by g = 1, 2, 3, 4. Do you see why 〈5〉 = ℤ12 and 〈6〉 = {0, 6}.

Figure 6.53 Four typical subgroups generated by elements of the group.
You might notice that the numbers 1, 5, 7, 11 are relative prime to 12 to generate the entire group ℤ12. Do you also see a pattern between the orders of those subgroups generated by numbers not relatively prime with 12? That is, the orders of the subgroups 〈2〉, 〈3〉, 〈4〉, 〈6〉, 〈8〉, 〈9〉, 〈10〉?
Table 6.5 shows the subgroups generated by each element of the group and the order of the subgroup generated by the generator.
Table 6.5 Generators of subsets of ℤ12.
| Generator | Order of the generator |
| 〈1〉 = ℤ12 | 12(112 = 0) |
| 〈2〉 = {0, 2, 4, 6, 8, 10} | 6(26 = 0) |
| 〈3〉 = {0, 3, 6, 9} | 4(34 = 0) |
| 〈4〉 = {0, 4, 8} | 3(43 = 0) |
| 〈5〉 = ℤ12 | 12(512 = 0) |
| 〈6〉 = {0, 6} | 2(62 = 0) |
| 〈7〉 = ℤ12 | 12(712 = 0) |
| 〈8〉 = {0, 4, 8} | 3(83 = 0) |
| 〈9〉 = {0, 3, 6, 9} | 4(94 = 0) |
| 〈10〉 = {0, 2, 4, 6, 8, 10} | 6(106 = 0) |
| 〈11〉 = ℤ12 | 12(1112 = 0) |
6.4.5 Cosets and the Quotient Group
If G is a group with group operation “+” and subgroup H, then for any g ∈ G the “g‐translation” of H
is called the left coset3 of H with respect to g. Similarly, the right cosets are defined by
If the left and right coset coincide,4 as they do for commutative groups or for certain subgroups called normal subgroups, we simply refer to them as cosets without specifying left or right. You can think of the cosets of a subgroup as what you get when you “shift” the subgroup to the left or right with members g ∈ G, that is “translated” subgroups. The subgroup H itself is a coset when the “shifting factor” g ∈ G is the identity element in G. By selecting various g ∈ G, one can create a partition of the group G into equivalence classes of cosets. This is useful since subdividing a group into disjoint parts allows one to identify parts of the group that are similar from some point of view.
For example, the (commutative) group G = ℤ6 of integers mod 6 has a subgroup H = {0, 3} of two elements 0 and 3. Translating the subgroup with the six elements g ∈ ℤ6, we arrive at three cosets of the form
which are
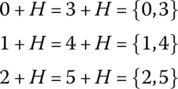
Note that the subgroup H = {0, 3} itself is a coset when g = 0 ∈ ℤ6.
The question now arises, is it possible to do “arithmetic” with the cosets, and the answer if yes, when the left and right cosets coincide. Without verification, it is not difficult to show that the binary operation

acting on the cosets forms a group. This group is called the quotient (or factor) group of G modulo H, and are written
pronounced G mod H.
The following example illustrates how an infinite (commutative) group can be “factored” into just three equivalence classes, each having a common property.
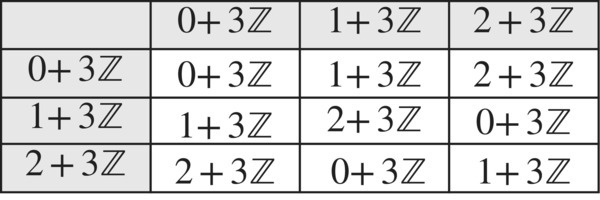
Figure 6.54 Quotient Group of Z/3Z.
Problems
- True or False
- The order of any subgroup divides the order of the group.
- Every subgroup of a group contains an identity element.
- Some groups do not have any subgroups.
- ℤ is a subgroup of ℝ under the operation of addition.
- The symmetric group S2 has two subgroups.
- There are some groups where every subset is a subgroup.
- The set {e, h} is a subgroup of the group of symmetries of a square, where e denotes the identity map, and h is the horizontal flip.
- There are five subgroups of order 2 of the group of symmetries of a square.
- Subgroups of ℤ6
List the subgroups of ℤ6 = {0, 1, 2, 3, 4, 5} generated by the different elements of the group. What is the order of each of these generated groups?
- Cayley Table
Find the Cayley table for the subgroup {e, R180, v, h} of symmetries of a square.
- Cayley Table
Show that the group defined by the following Cayley table in Figure 6.55 is a subgroup of S3.
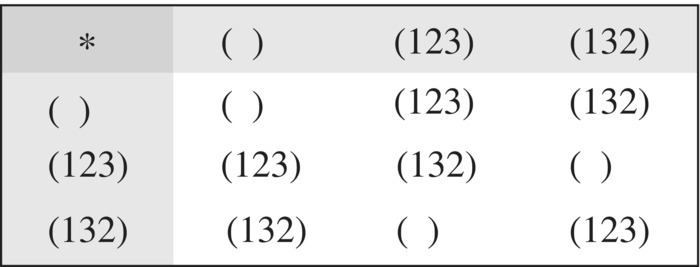
Figure 6.55 Subgroup S3.
- Subgroup Generated by R240
Find the subgroup of the dihedral group D3 of symmetries of an equilateral triangle generated by R240.
- Generated Groups of Symmetries of a Rectangle
In the Klein Four‐group {e, R180, v, h} of symmetries of a rectangle, find the subgroups generated by each element in the group. What is the order of each member?
- Center of a Group
The center Z(G) of a group G consists of all elements of the group that commute with all elements of the group. That is
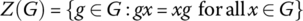
It can be shown that the center of any group is a subgroup of the group. Find the center of the group of symmetries of a rectangle. Note: The center of a group is never empty since the identity element of a group always commutes with every element of the group. The question is, are there other elements that commute with every element of the group?
- Hasse Diagram
Draw the Hasse diagram for the subgroups of symmetries of a rectangle.
- Subgroups of ℤ8
Find the subgroups of the cyclic group ℤ8.
- Subgroups of ℤ11
Find the subgroups of ℤ11.
- Matrix Subgroup
The set G of all 2 × 2 invertible matrices with real entries forms a group under matrix multiplication. Show that the subset of matrices of the form

is a subgroup of G.
- Cosets
The set 4ℤ = {…, − 12, − 8, − 4, 0, 4, 8, 12, …} is a subgroup of the integers ℤ with the addition operation. What are the cosets of 4ℤ and show them along with 4ℤ partition ℤ into disjoint sets.
- Cosets in the Plane
The Cartesian plane
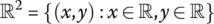
with the usual operation pointwise addition is a group and the line H = {(x, y) : y = x} passing through the origin is a subgroup.
- What are the cosets of this subgroup?
- What is the sum of the two cosets

- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward why are subgroups important, number of subgroups, and groups with no proper list of small groups.
