5.4
Point‐Set Topology on the Real Line
5.4.1 Introduction
There are several areas of topology, such as graph theory and network topology, geometric topology, algebraic topology, differential topology, combinatorial topology, and point‐set (or general) topology. Some areas of topology are sufficiently diverse that practicing researchers in one area may have only a passing knowledge of other areas. While graph theory is interested in connections between objects, and geometric topology was interested in shapes of objects, point‐set topology is about “closeness.” By closeness, we mean closeness of numbers, points, functions, matrices, operators, and other mathematical objects. The interest in closeness lies in the fact it gives rise to limits, infinite series, convergence, continuity, and mathematical concepts associated with calculus, differential equations, real and complex analysis, as well as areas of science and engineering.
Point‐set topology can be studied in any dimension, even infinite, but in this section, we restrict our attention to the one‐dimensional real line, mostly because it is easier to visualize than in two and three dimensions, and a whole lot simpler than dimensions larger than three.1 The basic concepts of point‐set topology begin with open intervals and the concept of neighborhoods.
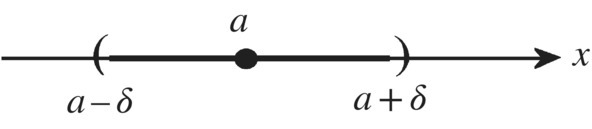
Figure 5.65 δ‐neighborhood.
This brings us to the unifying concept of this section, and in much of point‐set topology, the open set.

Figure 5.66 Open set.
In the definition of an open set, when we say “there exists a δ greater than zero,” we normally are thinking of a small δ, not a large one. In plain language, a set is open if you can “wiggle” any point in the set around, and if you do not wiggle it around too much it will still be in the set. Still another way of thinking about open sets is that every point in an open set is surrounded by other points in the set, i.e. every point in the set is insulated from the outside.
In other words, a set is not open if there exists at least one point a ∈ A right on the boundary of A and not insulated from the outside by other points of A. The interval (a, b] is not open since the point x = b cannot be “wiggled” any amount without finding itself outside (a, b].
The most important properties of open sets relate to their union and intersection.
5.4.2 Interior, Exterior, and Boundary of a Set
Three important concepts of topology are the concepts of interior, exterior, and boundary of a set.5
5.4.3 Interiors, Boundaries, and Exteriors of Common Sets
Table 5.5 shows the interiors, boundaries, and exteriors of some common sets. Note that the interior and exterior of a set are always open. Also, note that the exterior is the complement of the union of the interior and boundary, and is always closed. Note too that the union of the interior, boundary, and exterior of a set is everything. In other words, the real numbers ℝ.
Table 5.5 Interiors, boundaries, and exteriors of sets.
| A ⊆ ℝ | Int(A) ⊆ A | Bdy(A) | Ext(A) |
| Ø | Ø | Ø | ℝ |
| (a, b) | (a, b) | {a, b} | (− ∞ , a) ∪ (b, ∞) |
| [a, b] | (a, b) | {a, b} | (− ∞ , a) ∪ (b, ∞) |
| (a, b] | (a, b) | {a, b} | (− ∞ , a) ∪ (b, ∞) |
| {a} | Ø | {a} | (− ∞ , a) ∪ (a, ∞) |
| {a, b, c} | Ø | {a, b, c} | ℝ − {a, b, c} |
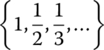 |
Ø | 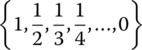 |
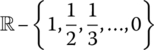 |
| (0, 1) ∪ {2} | (0, 1) | {0, 1, 2} | (− ∞ , 0) ∪ (1, 2) ∪ (2, ∞) |
| (−1, 0) ∪ (0, 1) | (−1, 0) ∪ (0.1) | {−1, 0, 1} | (− ∞ , − 1) ∪ (1, ∞) |
| ℕ | Ø | ℕ | ℝ − ℕ |
| ℤ | Ø | ℤ | ℝ − ℤ |
| ℚ | Ø | ℝ | Ø |
| ℝ | ℝ | Ø | Ø |
5.4.4 Limit Points
The concept of a limit is fundamental in calculus and analysis. The reader will recall that the two fundamental operations of the calculus, the derivative and integral, are both limits. We can thank the French mathematician Augustin‐Louis Cauchy (1789–1857) and German mathematician Karl Weierstrass (1815–1897) for providing rigorous definition of the limit, the so‐called epsilon, delta (ε, δ) definition, which allows mathematicians to reason with precision the ideas of calculus and avoid the imprecise reasoning of the past.

Figure 5.71 Limit point.
5.4.5 Closed Sets Contain Their Limit Points
We have seen that a good way to determine if a set is closed is to show that its complement is open. Although this indirect procedure is useful, there is a direct way to determine if a set is closed. The following theorem makes this precise.
Table 5.6 gives the limit points of some common sets of real numbers.
Table 5.6 Limit points of some common sets.
| A ⊆ ℝ | Limit points(A) | Limit points(A) ⊆ A? |
| Ø | Ø | Closed |
| (a, b) | [a, b] | Open |
| [a, b] | [a, b] | Closed |
| (a, b] | [a, b] | Neither open or closed |
| {a} | Ø | Closed |
| {a, b, c} | Ø | Closed |
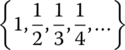 |
{0} | Neither open or closed |
| (0, 1) ∪ {2} | [0, 1] | Neither open or closed |
| [0, 1] ∪ {2} | [0, 1] | Closed |
| ℕ | Ø | Closed |
| ℤ | Ø | Closed |
| ℚ | ℝ | Neither open or closed |
| ℝ | ℝ | Closed |
5.4.6 Topological Spaces
We saw in Chapter 4 how relations (ordering, equivalence, function, …) can be defined on a set so that the elements of the set can be compared, ordered, and classified. We now introduce a different structure on a set, a topology, which places a general “distance” structure on a set, allowing one to make precise concepts like closeness, limits, and all those concepts used in calculus, like continuous functions, derivatives, and integrals.
We now show how open sets are the foundation of a topological structure on a set, in our case the real numbers ℝ.
5.4.7 Calculus Without Topology Is No Calculus
Recall that functions f : ℝ → ℝ are the basis of many areas of mathematics, like calculus, which the reader no doubt has some familiarity. If there is no topological structure on ℝ, there are no limits, continuity, differentiable and integral functions, and so on. When a student of calculus thinks about the real numbers, the student most likely is thinking about the topological structure of the real numbers and the distance between points, and so on.7
Topology allows one to make precise many of the important concepts of mathematics, one of the most important being continuous functions. We now give the topological definition of continuity.
Problems
- Tell if the following sets subsets of ℝ are open, closed, both, or neither.
- (−1, 0) ∪ (0, 1)
- [0, ∞)
- (0, ∞)
- ℕ
- ℤ
- ℚ
- A = {0, 1, 2, … , 100}
- {x : |x − 1| < 3}
- Ø
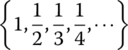

- {x : x2 > 0}
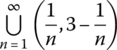
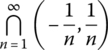
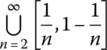
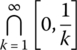
- Interiors, Boundaries, and Exteriors
Fill the blanks in Table 5.7.
Table 5.7 Interiors, boundaries, and exteriors.
A Int(A) Bdy(A) Ext(A) a) ℤ b) {sin x : 0 < x < 2π} c) (0, ∞) d) (0, 1) ∪ {2} e) {1, 2} f) {sin x : 0 ≤ x ≤ π} g) (−1, 0) ∪ (0, 1) h) 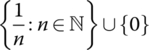
- True or False
Answer true or false about the following sets of real numbers.
- A nonempty set can be both open and closed.
- A point can lie both in the interior and on the boundary.
- Finite sets are always closed.
- Infinite sets are always open.
- The boundary of a set is always finite.
- Mystery Sets
Find two sets, which are not equal, but have the same interior, boundary, and exterior.
- Finding Examples
Find the following sets of real numbers.
- Set with two boundary points in the set, one not in the set.
- Set with four boundary points in the set, three not in the set.
- A set with three boundary points, none in the set.
- A set with three boundary points, all in the set.
- Finite Sets Closed
Show that the finite set A = {1, 2} is closed by finding its complement and showing the complement is an open set.
- Limit Points
If they exist, find the limit points of the following sets.
- ℕ
- ℚ
- ℝ
- (2, 4) ∪ (4, 5)
- {(−1)n : n ∈ ℕ}
- Ø
- ℚ ∩ (0, 1)

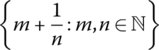
- Closed Sets
A set is closed if and only if it contains its limit points. Find the limit points of the following sets and determine if the sets are closed.
- ℤ Ans: Limits (ℤ) = Ø, hence, ℤ is closed.
- ℚ
- ℝ
- (2, 4) ∪ (4, 5)
- {(−1)n : n ∈ ℕ}
- Ø
- ℚ ∩ (0, 1)
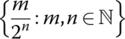
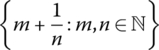
- Examples
Give examples of the following.
- A bounded set with no limit points.
- An unbounded set with one limit point.
- A set with two limit points.
- An unbounded set whose limit points have cardinality ℵ0.
- An unbounded with one limit point.
- An open set with no limit points.
- Sets and Limits
Find examples of a set A of real numbers with the following properties:
- A set that is equal to its limit points.
- A set that is a subset of its limit points.
- A set that contains all its limit points.
- A set that is not a subset of its limit points and its limit points are not a subset of the set.
- Intersections and Unions of Closed Sets
Show the following properties for collections of closed sets.
- The intersection of any family (finite or infinite) of closed sets is closed.
- The union of a finite number of closed sets is closed.
Hint: Use the properties of open sets and DeMorgan's laws.
- Cantor Set
Let I = [0, 1]. Remove the open middle third

and call A1 the set that remains; that is

Now remove the open third intervals from each of these two parts of A1, and call the remaining part A2. Thus
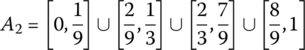
Continuing in this manner, remove the open middle third of each segment in Ak and call the remaining set Ak + 1. Note that we will get
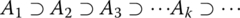
Continue this process indefinitely, always removing the middle third of existing segments (see Figure 5.72). The limiting set of this infinite process is called the Cantor set, and is defined as
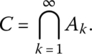

Figure 5.72 Cantor set.
- Are there any points left in the Cantor set?
- Show the Cantor set is closed.8
- Intersection of Open Sets
Find an example of a family of open sets whose intersection is not open.
- Union of Closed Sets
Find an example of a family of closed sets whose union is not closed.
- Topologies on {a, b, c}
A topology on a set X is a family of subsets of X that is closed under unions and finite intersections. Show whether the families T1, T2 ⊆ P(X) are or are not topologies on X = {a, b, c}.
- T1 = {Ø, {a}, {a, b}, {a, b, c}}
- T2 = {Ø, {a}, {c}, {a, b}, {a, b, c}}
- Continuous Image of an Open Set
We saw that for a continuous function, the inverse image of an open set is open in their respective sets, but that does not mean the image of an open set is open under a continuous mapping. Give an example of an open set in U ⊆ ℝ and a continuous function f : ℝ → ℝ whose image f(U) ⊆ ℝ is not open.
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward history of point‐set topology, what is point‐set topology, types of topology, interior, and boundary and exterior of a set.
