12
Homotopy Perturbation Method
12.1 Introduction
Homotopy perturbation method (HPM) is a semi‐analytical technique for solving linear as well as nonlinear ordinary/partial differential equations. The method may also be used to solve a system of coupled linear and nonlinear differential equations. The HPM was proposed by J. He in 1999 [1]. This method was developed by making use of artificial parameters [2]. Interested readers may go through Refs. [3–6] for further details.
Almost all traditional perturbation methods are based on small parameter assumption. But, a majority of nonlinear problems have no small parameters at all and the determination of small parameters seems to be a special art requiring special techniques. These small parameters are so sensitive, such that a small change in small parameters will affect the results. An appropriate choice of small parameters leads to ideal results. However, an unsuitable choice of small parameters results in bad effects, sometimes seriously. Liu [2] proposed artificial parameter method and Liao [7,8] contributed homotopy analysis method to eliminate small parameter assumption. Further, He [ 1 ,9] developed two effective techniques viz. variational iteration method (VIM) and HPM in which no small parameter assumptions are required, where details of the VIM are given in Chapter 13.
12.2 Basic Idea of HPM
In this section we illustrate the basic idea of the HPM. For this we consider the following differential equation:
subject to the boundary condition
where A represents a general differential operator, B is a boundary operator, Γ is the boundary of the domain Ω, and f(r) is known analytic function.
The operator A can be decomposed into two parts viz. linear (L) and nonlinear (N). Therefore, Eq. (12.1) may be written in the following form:
An artificial parameter p can be embedded in Eq. (12.3) as follows:
where p ∈ [0, 1] is the embedding parameter (also called as an artificial parameter).
Using homotopy technique, proposed by He [1] and Liao [ 7 , 8 ], we construct a homotopy v(r, p) : Ω × [0, 1] → R to Eq. ( 12.3 ) which satisfies
and
Here, u0 is an initial approximation of Eq. (12.6) which satisfies the given conditions.
By substituting p = 0 and p = 1 in Eq. ( 12.6 ), we may get the following equations, respectively.
and
As p changes from zero to unity, v(r, p) changes from u0(r) to u(r). In topology, this is called deformation and L(v) − L(u0) and A(v) − f(r) are homotopic to each other. Due to the fact that p ∈ [0, 1] is a small parameter, we consider the solution of Eq. (12.5) as a power series in p as below
The approximate solution of Eq. ( 12.1 ) may then be obtained as
The convergence of the series solution (12.8) has been given in Ref. [1] .
12.3 Numerical Examples
Here, we use the present method to solve a nonlinear ordinary differential equation in Example 12.1 and a nonlinear partial differential equation in Example 12.2. Finally, a coupled nonlinear system of partial differential equations has been solved in Example 12.3. It is worth mentioning that the HPM can also be used for handling linear ordinary and partial differential equations.
Exercise
- 1
Apply the HPM to find the solution differential equation
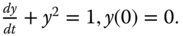
- 2 Solve the homogenous KdV equation ut − 6uux + uxxx = 0 subject to initial condition u(x, 0) = 6x using the HPM.
References
- 1 He, J.H. (1999). Homotopy perturbation technique. Computer Methods in Applied Mechanics and Engineering 178 (3): 257–262.
- 2 Liu, G.L., (1997). New research directions in singular perturbation theory: artificial parameter approach and inverse‐perturbation technique. Proceedings of the 7th Conference of modern Mathematics and Mechanics, Shanghai (September 1997), pp. 47–53.
- 3 Karunakar, P. and Chakraverty, S. (2017). Comparison of solutions of linear and non‐linear shallow water wave equations using homotopy perturbation method. International Journal of Numerical Methods for Heat and Fluid Flow 27 (9): 2015–2029.
- 4 Karunakar, P. and Chakraverty, S. (2018). Solution of interval shallow water wave equations using homotopy perturbation method. Engineering Computations 35 (4): 1610–1624.
- 5 He, J.H. (2003). Homotopy perturbation method: a new nonlinear analytical technique. Applied Mathematics and Computation 135 (1): 73–79.
- 6 He, J.H. (2004). The homotopy perturbation method for nonlinear oscillators with discontinuities. Applied Mathematics and Computation 151 (1): 287–292.
- 7 Liao, S.J. (1995). An approximate solution technique not depending on small parameters: a special example. International Journal of Non‐Linear Mechanics 30 (3): 371–380.
- 8 Liao, S.J. (1997). Boundary element method for general nonlinear differential operators. Engineering Analysis with Boundary Elements 20 (2): 91–99.
- 9 He, J.‐H. (1999). Variational iteration method–a kind of non‐linear analytical technique: some examples. International Journal of Non‐Linear Mechanics 34 (4): 699–708.
- 10 Wazwaz, A.M. (2010). Partial Differential Equations and Solitary Waves Theory. Beijing: Springer Science & Business Media, Higher Education Press.
- 11 Sweilam, N.H. and Khader, M.M. (2009). Exact solutions of some coupled nonlinear partial differential equations using the homotopy perturbation method. Computers and Mathematics with Applications 58 (11): 2134–2141.
