10 Sequences, Series, and Probability
In This Chapter
10.3 Convergence of Sequences and Series
10.7 Introduction to Probability
In rolling a pair of dice, what is the probability of obtaining a 7? See Example 4 in Section 10.7.
A Bit of History This chapter could have been titled Discrete Mathematics, since each of the topics that we will consider–sequences, series, induction, the Binomial Theorem, counting, and probability–depends in a special way only on a set of integers. For example, we will see in Section 10.1 that a sequence is a function whose domain is the set of positive integers. When we study probability in Section 10.7, we leave the world of certitude. In life an event may or may not happen. When tossing, or flipping, an unbiased coin, a head or a tail is equally likely to appear. If we were asked, “Will a head appear when the coin is tossed?” our best reply would be “There is a 50–50 chance of obtaining a head.” In more precise mathematical terminology, the probability of a head appearing is 1/2 (one head out of two possible outcomes).
The year 1654 marks the beginning of probability theory. It was then that the Chevalier de Mere, a member of the French nobility, sent some questions that had occurred to him during gambling to the mathematician, physicist, and philosopher Blaise Pascal (1623-1662). Pascal's interest was aroused and he, in turn, corresponded with Pierre de Fermat (1601-1665), the leading French mathematician of the day. The resulting exchange of letters contained the basic results on which the subject was founded.
10.1 Sequences
Introduction Most people have heard the phrases “sequence of cards,” “sequence of events,” and “sequence of car payments.” Intuitively, we can describe a sequence as a list of objects, events, or numbers that come one after the other, that is, a list of things given in some definite order. The months of the year listed in the order in which they occur,
are two examples of sequences. Each object in the list is called a term of the sequence. The lists in (1) and (2) are finite sequences: The sequence in (1) has 12 terms and the sequence in (2) has 10 terms. A sequence such as
where no last term is indicated, is understood to be an infinite sequence. The three dots in (1), (2), and (3) is called an ellipsis and indicates that succeeding terms follow the same pattern as that set by the terms given.
Note 
In this chapter, unless otherwise specified, we will use the word sequence to mean infinite sequence.
The terms of a sequence can be put into a one-to-one correspondence with the set N of positive integers. For example, a natural correspondence for the sequence in (3) is
Because of this correspondence property, we can give a precise mathematical definition of a sequence.
You should be aware that in some instances it is convenient to take the domain of a sequence to be the set of nonnegative integers {0, 1, 2, 3,…}. A finite sequence is also a function and its domain is some subset {1, 2, 3,…, n} of N.
Terminology The elements in the range of a sequence are simply the terms of the sequence. We will assume hereafter that the range of a sequence is some set of real numbers. The number f (1) is taken to be the first term of the sequence, the second term is f (2), and, in general, the n th term is f (n). Rather than using function notation, we commonly represent the terms of a sequence using subscripts: f (1) = a1, f (2) = a2,…, and so on. The n th term f(n) = an is also called the general term of the sequence. We denote a sequence
a1, a2, a3,…, an,…
by the notation {an}. If we identify the general term in (3) as 1/n, the sequence 1, 1/2, 1/3,…, can then be written compactly as {1/n}.
EXAMPLE 1 Three Sequences
List the first five terms of the given sequence.
(a) 
(b) 
(c) 
Solution Letting n take on the values 1, 2, 3, 4, and 5, the first five terms of the (infinite) sequences are
Sequences Defined Recursively Instead of giving the general term of a sequence a1, a2, a3,…, an, an + 1,…, sequences are often defined using a rule or formula in which an+1 is expressed using the preceding terms. For example, if we set a1 = 1 and define successive terms by an+1 + = an + 2 for n = 1, 2,…, then
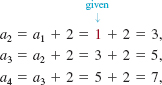
and so on. Sequences such as this are said to be defined recursively. In this example, the rule that an+1 = an + 2 is called a recursion formula.
EXAMPLE 2 Sequence Defined Recursively
List the first five terms of the sequence defined by a1 = 2 and an+1 = (n + 2)an.
Solution We are given a1 = 2. From the recursion formula we have, respectively, for n = 1, 2, 3, 4,…
and so on. Including a1 = 2 the first five terms of the sequence are
2, 6, 24, 120, 720,….
Of course, if we choose a different value for a1 in Example 2 we would obtain an entirely different sequence.
For the remainder of this section we will examine two special types of recursively defined sequences.
Arithmetic Sequence In the sequence 1, 3, 5, 7,…, note that each term after the first is obtained by adding the number 2 to the term preceding it. In other words, successive terms in the sequence differ by 2. A sequence of this type is known as an arithmetic sequence.
From an+1 - an = d, we obtain the recursion formula
for an arithmetic sequence with common difference d.
EXAMPLE 3 An Arithmetic Sequence
The first several terms of the recursive sequence defined by a1 = 3 and an +1 = an + 4 are
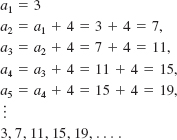
or 3, 7, 11, 15, 19,….
This is an arithmetic sequence with common difference 4.
If we let a1 be the first term of an arithmetic sequence having common difference d, we find from the recursion formula (4) that
and so on. In general, an arithmetic sequence with first term a1 and common difference d is given by
EXAMPLE 4 Arithmetic Sequence Using (5)
A woman decides to jog a particular distance each week according to the following schedule. The first week she will jog 1000 m per day. Each succeeding week she will jog 250 m per day further than she did the preceding week.
(a) How far will she jog per day in the 26th week?
(b) In which week will she jog 10,000 m per day?
Solution The example describes an arithmetic sequence with a1 = 1000 and d = 250.
(a) To find the distance the woman jogs per day in the 26th week, we set n and compute a26 using (5):
a26 = 1000 + (26 - 1) (250) = 1000 + 6250 = 7250.
Thus she will jog 7250 m per day in the 26th week.
(b) Here we are given an and we need to find n. From (5) we have 10,000 = 1000 + (n - 1) (250) or 9000 = (n - 1) (250) or Solving for n gives
Therefore, she will jog 10,000 m per day in the 37th week.
EXAMPLE 5 Find the First Term
The common difference in an arithmetic sequence is -2 and the sixth term is 3. Find the first term of the sequence.
Solution From (5) the sixth term of the sequence is
a6 = a1 + (6 – 1) d.
Setting a6 = 3 and d = –2, we have 3 = a1 + 5(– 2), or a1 = 3 + 10. Thus the first term is a1 = 13.
Check: The sequence with a1 = 13 and d = –2 is 13, 11, 9, 7, 5, 3,…. The sixth term of this sequence is 3.
Geometric Sequence In the sequence 1, 2, 4, 8,…, each term after the first is obtained by multiplying the term preceding it by the number 2. In this case, we observe that the ratio of a term to the term preceding it is a constant, namely, 2. A sequence of this type is said to be a geometric sequence.
From an+1 an = r, we see that a geometric sequence with a common ratio r is defined recursively by the formula
EXAMPLE 6 Geometric Sequence Using (6)
The sequence defined recursively by a1 = 2 and an+1 = -3an is
2, -6, 18, -54,….
This is a geometric sequence with common ratio r = -3.
If we let a1 = a be the first term of a geometric sequence with common ratio r, we find from the recursion formula (6) that
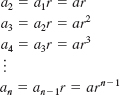
and so on. In general, a geometric sequence with first term a and common ratio r is
EXAMPLE 7 Find the Third Term
Find the third term of a geometric sequence with common ratio 
and sixth term 
.
Solution We first find a. Since a6 = and r = , we have from (7) that
Solving for a, we find
Applying (7) again with n = 3, we have
The third term of the sequence is a3 =16/3
Compound Interest An initial amount of money deposited in a savings account is called the principal and is denoted by P. Suppose that the annual rate of interest for the account is r. If interest is compounded annually, then at the end of the first year the interest on P is Pr and the amount A1 accumulated in the account at the end of the first year is principal plus interest:
The interest earned on this amount at the end of the second year is P(1 + r)r. If this amount is deposited, then at the end of the second year the account contains
Continuing in this fashion, we can construct the following table.
The amounts in the second column of the table form a geometric sequence with first term P(1 + r) and common ratio 1 + r. Thus from (7) we conclude that the amount in the savings account at the end of the n th year is An = [P(1 + r)](1 + r)n-1 or
EXAMPLE 8 Compound Interest
On January 1, 2010, a principal of $500 was deposited in an account drawing 4% interest compounded annually. Find the amount in the account on January 1, 2024.
Solution We make the identification P = 500 and r = 0.04. As of January 1, 2024, the principal will have drawn interest for 14 years. Using (8) and a calculator, we find
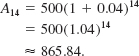
To the nearest dollar amount, the account will contain $866 at the end of 14 years.
10.1 Exercises Answers to selected odd-numbered problems begin on page ANS-23.
In Problems 1-8, list the first five terms of the given sequence.
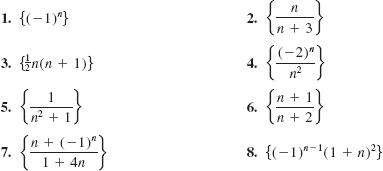
In Problems 9 and 10, list the first six terms of a sequence whose general term is given.
In Problems 11 and 12, discern a pattern for the given sequence and determine the next three terms.
11. 1, 2, 1/9, 4, 1/25, 6,…
12. 2, 3, 5, 8, 12, 17,…
In Problems 13-20, list the first five terms of the sequence defined recursively.
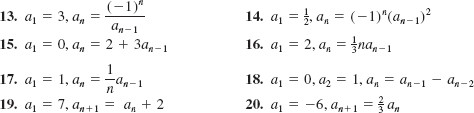
In Problems 21-30, the given sequence is either an arithmetic or a geometric sequence. Find either the common difference or the common ratio. Write the general term and the recursion formula of the sequence.
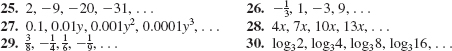
31. Find the twentieth term of the sequence – 1, 5, 11, 17,….
32. Find the fifteenth term of the sequence 2, 6, 10, 14,….
33. Find the fifth term of a geometric sequence with first term 8 and common ratio r = –
.
34. Find the eighth term of the sequence 
35. Find the first term of a geometric sequence with third and fourth terms 2 and 8, respectively.
36. Find the first term of an arithmetic sequence with fourth and fifth terms 5 and –3, respectively.
37. Find the seventh term of an arithmetic sequence with first and third terms 357 and 323, respectively.
38. Find the tenth term of a geometric sequence with fifth and sixth terms 2 and 3, respectively.
39. Find an arithmetic sequence whose first term is 4 such that the sum of the second and third terms is 17.
40. Find a geometric sequence whose second term is 1 such that a5/a3 = 64.
41. If $1000 is invested at 7% interest compounded annually, find the amount in the account after 20 years.
42. Find the amount that must be deposited in an account drawing 5% interest compounded annually in order to have $10,000 in the account 30 years later.
43. At what rate of interest compounded annually should $450 be deposited in order to have $750 in 8 years?
44. At 6% interest compounded annually, how long will it take an initial investment to double?
Miscellaneous Applications
45. Cookie-Jar Savings A couple decides to set aside $5 each month the first year of their marriage, $15 each month the second year, $25 each month the third year, and so on, increasing the monthly amount by $10 each year. Find the amount they will set aside each month of the fifteenth year.
46. Cookie-Jar Savings–Continued In Problem 47, find a formula for the amount the couple will set aside each month of the n th year.
47. Population Growth The population of a certain community is observed to grow geometrically by a factor of 
each year. If the population at the beginning of the first year is 1000, find the population at the beginning of the eleventh year.
48. Profit A small company expects its profits to increase at a rate of $10,000 per year. If its profit after the first year is $6000, how much profit can the company expect after 15 years of operation?
49. Family Tree Everyone has two parents. Determine how many great-great-great- grandparents a person will have.
Statue of Fibonacci in Pisa, Italy
50. How Many Rabbits? Besides its famous leaning bell tower, the city of Pisa, Italy, is also noted as the birthplace of Leonardo Pisano, aka Leonardo Fibonacci (1170-1250). Fibonacci was the first in Europe to introduce the Hindu-Arabic place-valued decimal system and the use of Arabic numerals. His book Liber Abacci, published in 1202, is basically a text on how to do arithmetic in this decimal system. But in Chapter 009 of Liber Abacci, Fibonacci poses and solves the following problem on the reproduction of rabbits:
How many pairs of rabbits will be produced in a year beginning with a single pair, if in every month each pair bears a new pair that become productive from the second month on?
Discern the pattern of the solution of this problem and complete the following table.
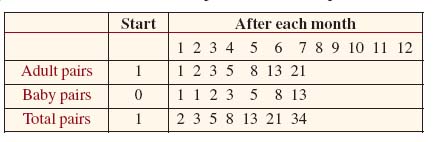
51. Write out five terms, after the initial two, of the sequence defined recursively by Fn+1 = Fn + Fn-1, = F1 = 1, F2 = 1.The elements in the range of this sequence are called Fibonacci numbers. Reexamine Problem 50.
For Discussion
52. Verify that the general term of the sequence defined in Problem 51 is
by showing that this result satisfies the recursion formula.
53. Find two different values of x such that -
, x, -
,…is a geometric sequence.
10.2 Series
Introduction In the following discussion, we will be concerned with the sum of the terms of a sequence. Of special interest are the sums of the first n terms of arithmetic and geometric sequences. We begin by considering a special notation that is used as a convenient shorthand for an indicated sum of terms.
Summation Notation Suppose we are interested in the sum of the first n terms of a sequence {an}. Rather than writing
a1 + a2 +…+ an,
mathematicians have invented a notation for representing such sums in a compact manner:
Because Σ a is the capital Greek letter sigma, the notation 
is referred to as summation or sigma notation and is read “the sum from k = 1to k = n of a sub k.” The subscript k is called the index of summation and takes on the successive values 1, 2,…, n:
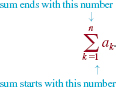
EXAMPLE 1 Summation Notation
Write out each sum.
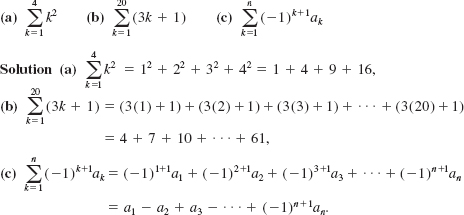
The choice of the letter used as the index of summation is arbitrary. Although we will consistently use the letter k, we note that
and so on. Also, as we see in the next example, we may sometimes allow the index of summation to start at a value other than k = 1.
EXAMPLE 2 Using Summation Notation
Write 
using summation notation.
Solution We observe that the k th term of the sequence 1, -
, 
, -
,…can be written as 
, where k = 0, 1, 2,…. We note too that 
. Therefore,
Properties Some properties of summation notation are listed in the theorem that follows next.
Property (i) of Theorem 10.2.1 is simply factoring a common term from a sum:
To understand property (ii), consider the following simple examples:
Thus, if ak = c is a real constant for k = 1, 2,…, n, then
a1, = c, a2 = c,…, an = c.
Consequently,
For example, 
Arithmetic Series Recall, we saw in (5) of Section 10.1 that an arithmetic sequence could be written as {a1 + (n – 1)d}. The addition of the first n terms of an arithmetic sequence,
is called an arithmetic series. If we denote the last term of the series in (1) by an, then Sn can be written as
Reversing the terms in (1), we have
Adding (2) and (3) gives
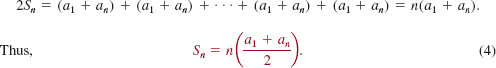
In other words, the sum of the first n terms of an arithmetic sequence is the number of terms n times the average of the first term a1 and the n th term an of the sequence.
EXAMPLE 3 Arithmetic Series
Find the sum of the first seven terms of the arithmetic sequence {5 – 4(n – 1)}.
Solution The first term of the sequence is 5 and the seventh term is –19. By identifying a1 = 5, a7 = –19, and n = 7 it follows from (4) that the sum of the seven terms in the arithmetic series
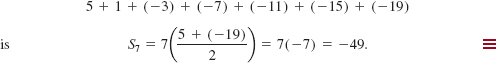
EXAMPLE 4 Sum of the First 100 Positive Integers
Find the sum of the first 100 positive integers.
Solution The sequence of positive integers {k},
1, 2, 3,…,
is an arithmetic sequence with common difference 1. Thus, from (4) the value of S100 = 1 + 2 + 3 +…+ 100 is given by
An alternative form for the sum of an arithmetic series can be obtained by substituting a1 + (n – 1 1)d for an in (4). We then have
which expresses the sum of an arithmetic series in terms of the first term, the number of terms, and the common difference.
EXAMPLE 5 Paying Off a Loan
A woman wishes to pay off an interest-free loan of $1300 by paying $10 the first month and increasing her payments by $15 each succeeding month. How many months will it take to pay off the entire loan? Find the amount of the final payment.
Solution The monthly payments form an arithmetic sequence with first term a1 = 10 and common difference d = 15. Since the sum of the arithmetic series formed by the sequence of payments is $1300, we let Sn = 1300 in (5) and solve for n:
By dividing by 5 the last equation simplifies to 3n2 + n - 520 = 0 or (3n + 40) (n - 13) = Thus, n = -
or n = 13. Since n must be a positive integer, we conclude that it will take 13 months to pay off the loan. The final payment will be
a13 = 10 + (13 - 1)15 = 10 + 180 = 190 dollars.
Geometric Series The addition of the first n terms of a geometric sequence {arn-1} is
and is called a finite geometric series. Multiplying (6) by the common ratio r gives
Subtracting (7) from (6) and simplifying gives
or (1 - r)Sn = a(1 - rn).
Solving this equation for Sn, we obtain a formula for the sum of a geometric series containing n terms:
EXAMPLE 6 Sum of a Geometric Series
Compute the sum 
Solution This geometric series is the sum of the first six terms of the geometric sequence 
Identifying the first term a = 3, the common ratio r = , and n = 6 in (8), we have
EXAMPLE 7 Sum of a Geometric Series
A developer constructed one house in 2002. With his profits, he was able to build two houses in 2003. With the profits from these, he constructed four houses in 2004. Assuming that he is able to continue doubling the number of houses he builds each year, find the total number of houses he will have constructed by the end of 2012.
Solution The total number of houses he constructs in the 11 years from 2002 through 2012 is the sum of the geometric series with first term a = 1 and common ratio r = 2. From (8) the total number of houses is
We will return to the subject of geometric series in Section 10.3.
10.2 Exercises Answers to selected odd-numbered problems begin on page ANS-24.
In Problems 1-6, compute the given sum.
In Problems 7-10, write out the terms of the given sum.
In Problems 11-16, write the given series in summation notation.
In Problems 17-22, find the sum of the given arithmetic series.
In Problems 23-28, find the sum of the given geometric series.
29. If {an} is an arithmetic sequence with d = 2 such that S10 = 135, find a1 and a10.
30. If {an} is an arithmetic sequence with a1 = 4 such that S8 = 86, find a8 and d.
31. Suppose that a1 = 5 and an = 45 are the first and nth terms, respectively, of an arithmetic series for which Sn = 2000. Find n.
32. If {an} is a geometric sequence with r = such that S6 = 
, find the first term a.
33. The sum of the first n terms of the geometric sequence {2n} is Sn = 8190. Find n.
34. Find the sum of the first 10 terms of the arithmetic sequence
35. Find the sum of the first 15 terms of the geometric sequence
36. (a) Find a formula for the sum of the first n positive integers:
1 + 2 + 3 +…+ n.
(b) Reexamine the photo on the opening page for Chapter 001. Assume that the numerator of the fraction is the sum of the first 100 positive integers. Find the value of the fraction.
37. Find a formula for the sum of the first n even integers.
38. Find a formula for the sum of the first n odd integers.
39. Use the result obtained in part (a) of Problem 36 to find the sum of the first 1000 positive integers.
40. Use the result obtained in Problem 38 to find the sum of the first 50 odd integers.
Miscellaneous Applications
41. Cookie-Jar Savings A couple decides to set aside $5 each month the first year of their marriage, $15 each month the second year, $25 each month the third year, and so on, increasing the monthly amount by $10 each year. Find the total amount that they will have set aside by the end of the fifteenth year.
42. Cookie-Jar Savings–Continued In Problem 41, find a formula for the total amount that the couple will have set aside by the end of the n th year.
43. Distance Traveled An automobile accelerating at a constant rate travels 2 m the first second, 6 m the second second, 10 m the third second, and so on, traveling an additional 4 m each second. Find the total distance that the automobile has traveled after 6 seconds.
44. Total Distance Find a formula for the total distance traveled by the automobile in Problem 43 after n seconds.
45. Annuity If the same amount of money P is invested each year for n years at a rate of interest r compounded annually, then the amount accumulated after the n th payment is given by
S = P(1 + r)n-1 + P(1 + r)n - 2 +…+ P(1 + r) + P.
Such a savings plan is called an annuity. Show that the value of the annuity after the n th payment is
46. Watch the Bouncing Ball A ball is dropped from an initial height of 15 ft onto a concrete slab. Each time it bounces, it reaches a height of its preceding height. What height does it reach on its third bounce? On its nth bounce? How many times does the ball have to hit the concrete before its height is less than ft? See FIGURE 10.2.1.
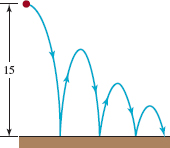
FIGURE 10.2.1 Bouncing ball in Problem 46
47. Total Distance In Problem 46, find the total distance the ball has traveled up to the time when it hits the concrete slab for the seventh time.
48. Desalinization A solution of salt water containing 10 kg of salt is passed through a filter that removes 20% of the salt. The resulting solution is then filtered again, removing 20% of the remaining salt. If 20% of the salt is removed during each filtration, find the amount of salt removed from the solution after 10 filtrations.
49. Drug Accumulation A patient takes 50 mg of a drug each day and of the amount accumulated, 90% is excreted each day by bodily functions. Determine how much of the drug has accumulated in the body immediately after the eighth dosage.
50. Pyramid Display A grocer wants to display canned soup in a pyramid with 20 cans on the bottom row, 19 cans on the next row, 18 on the next row, and so on, with a single can at the top. How many cans of soup are required for the display?
Display of soup cans
For Discussion
51. A Chess Master According to legend, the king of a middle eastern country was so taken with the new game of chess that he queried its peasant inventor on how he might reward him. The inventor's modest request was for the sum of the grains of wheat that would fill the chess board according to the rule: 1 grain on the first square, 2 grains on the second square, 4 on the third square, 8 on the fourth square, and so on, for the entire 64 squares. The king immediately acceded to this request. If an average bushel contains 106 grains of wheat, how many bushels did the king owe the inventor? Do you think the peasant lived to see his reward?
Chess board
10.3 Convergence of Sequences and Series
Introduction Sequences and series are important and are studied in depth in a typical course in calculus. In that study, we distinguish between sequences that are convergent or are divergent. In the discussion that follows we examine these concepts from an intuitive point of view.
Convergence The sequence 
f is an example of a convergent sequence.
Although it is apparent that the terms of the sequence,
are increasing as n increases, the values 
do not increase without bound. This is because n < n + 1 and so
for all values of n. For example, for n = 100, a100 = 100/101 < 1. Moreover, it appears that the terms of the sequence can be made closer and closer to 1 by letting the values of n become progressively larger. Using the → symbol for the word approach as we did in earlier chapters, this is written
We can see the foregoing a little better by dividing the numerator and the denominator of the general term n/(n + 1) by n:
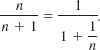
As n → ∞ the term 1/n in the denominator gets closer and closer to 0 and so
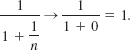
We write 
and we say that sequence converges to 1.
Notation In general, if the n th term an of a sequence {an} can be made arbitrarily close to a number L for n sufficiently large we say that the sequence {an} converges to L. We indicate that a sequence is convergent to a number L by writing either
The notions of “arbitrarily close” and “for n sufficiently large” are made precise in a course in calculus. For our purposes, in determining whether a sequence {an} converges, we will work directly with 
. The symbol “lim” is an abbreviation for the word limit.
We summarize the discussion.
EXAMPLE 2 Using Summation Notation
Write using summation notation.
Solution We observe that the k th term of the sequence 1, -, , -,…can be written as , where k = 0, 1, 2,…. We note too that . Therefore,
Properties Some properties of summation notation are listed in the theorem that follows next.
Property (i) of Theorem 10.2.1 is simply factoring a common term from a sum:
To understand property (ii), consider the following simple examples:
Thus, if ak = c is a real constant for k = 1, 2,…, n, then
a1, = c, a2 = c,…, an = c.
Consequently,
For example,
Arithmetic Series Recall, we saw in (5) of Section 10.1 that an arithmetic sequence could be written as {a1 + (n – 1)d}. The addition of the first n terms of an arithmetic sequence,
is called an arithmetic series. If we denote the last term of the series in (1) by an, then Sn can be written as
Reversing the terms in (1), we have
Adding (2) and (3) gives
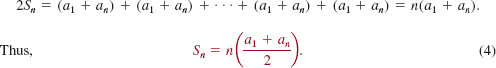
In other words, the sum of the first n terms of an arithmetic sequence is the number of terms n times the average of the first term a1 and the n th term an of the sequence.
EXAMPLE 3 Arithmetic Series
Find the sum of the first seven terms of the arithmetic sequence {5 – 4(n – 1)}.
Solution The first term of the sequence is 5 and the seventh term is –19. By identifying a1 = 5, a7 = –19, and n = 7 it follows from (4) that the sum of the seven terms in the arithmetic series
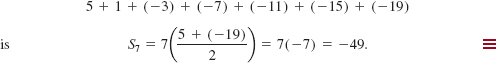
EXAMPLE 4 Sum of the First 100 Positive Integers
Find the sum of the first 100 positive integers.
Solution The sequence of positive integers {k},
1, 2, 3,…,
is an arithmetic sequence with common difference 1. Thus, from (4) the value of S100 = 1 + 2 + 3 +…+ 100 is given by
An alternative form for the sum of an arithmetic series can be obtained by substituting a1 + (n – 1 1)d for an in (4). We then have
which expresses the sum of an arithmetic series in terms of the first term, the number of terms, and the common difference.
EXAMPLE 5 Paying Off a Loan
A woman wishes to pay off an interest-free loan of $1300 by paying $10 the first month and increasing her payments by $15 each succeeding month. How many months will it take to pay off the entire loan? Find the amount of the final payment.
Solution The monthly payments form an arithmetic sequence with first term a1 = 10 and common difference d = 15. Since the sum of the arithmetic series formed by the sequence of payments is $1300, we let Sn = 1300 in (5) and solve for n:
By dividing by 5 the last equation simplifies to 3n2 + n - 520 = 0 or (3n + 40) (n - 13) = Thus, n = - or n = 13. Since n must be a positive integer, we conclude that it will take 13 months to pay off the loan. The final payment will be
a13 = 10 + (13 - 1)15 = 10 + 180 = 190 dollars.
Geometric Series The addition of the first n terms of a geometric sequence {arn-1} is
and is called a finite geometric series. Multiplying (6) by the common ratio r gives
Subtracting (7) from (6) and simplifying gives
If a sequence {an} converges, then its limit L is a unique number.
If an either increases or decreases without bound as n → ∞, then {an} is necessarily divergent and we write, respectively,
In each case, the limits do not exist.
In the first case we say that {an} diverges to infinity and in the second, {an} diverges to negative infinity. For example, the sequence 1, 2, 3,…, n,…diverges to infinity.
To determine whether a sequence converges or diverges we often have to rely on analytic procedures (such as algebra) or on previously proven theorems. So in this brief discussion we will accept without proof the following three results:
EXAMPLE 1 Three Convergent Sequences
(a) The constant sequence {π},
π, π, π, π,…
converges to π because of (2), 
π = π.
(b) The sequence 
When n = 1,000,000, the laws of exponents shows that 
= 0.001.
converges to 0. With the identification r = in (3), we have
(c) The sequence {(1/2n)},
The 20th term of the sequence is approximately a20 ~ 0.00000095.
converges to 0. With the identifications r = and |r| = < 1 in (4), we see 
. = 0
EXAMPLE 2 Divergent Sequences
(a) The sequence {(-1)n - 1},
1, -1, 1, -1,…
is divergent. As n → ∞, the terms of the sequence oscillate between 1 and -1. Thus 
does not exist because an = (- 1)n does not approach a single constant L for large values of n.
(b) The first four terms of the sequence {(5/2)n} are
The 20th term of the sequence is approximately a20 ≈ 90,949,470.2.
Because the general term an = (
)n increases without bound as n → ∞, we conclude tha 
in other words, the sequence diverges to infinity.
Expanding on (4) and part (b) of Example 2, it can be proved that
It is often necessary to manipulate the general term of a sequence to demonstrate convergence of the sequence.
EXAMPLE 3 Convergent Sequence
Determine whether the sequence 
converges.
Solution By dividing the numerator and denominator by n it follows that
as n → ∞. Thus, we can write
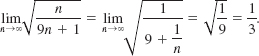
The sequence converges to 
.
EXAMPLE 4 Convergent Sequence
Determine whether the sequence 
converges.
Solution Since e > 1, a fast inspection of the general term may lead you to the false conclusion that the sequence is divergent because 12en - 5 → ∞ and 3en + 2 → ∞ as n → ∞. But if we divide the numerator and denominator by en and then use 12 - 5e-n → 12 and 3 + 2e-n → 3 as n → ∞, we can write
Note that e-n = (1/e)n. Since 1/e < 1, it follows from (4) that (1/e)n → 0 as n → ∞.
The sequence converges to 4.
Infinite Series Under certain conditions it is possible to assign a numerical value to an infinite series. In Section 10.2 we saw that we could add terms of a sequence using sigma notation. Associated with every sequence {an} is another sequence called the sequence of partial sums {Sn}, where S1 is the first term, S2 is the sum of the first two terms, S3 is the sum of the first three terms, and so on. In symbols:
sequence: a1, a2, a3,…, an,…
sequence of partial sums: a1, a1 + a2, a1 + a2 + a3,…, a1 + a2 + a3 +…+ an,….
In other words, the sequence of partial sums for {an} is the sequence {Sn}, where the general term can be written Sn = 
Just as we can ask whether a sequence {an}converges, we now ask whether a sequence of partial sums can converge.
This question is answered in the next definition.
Although the proper place for digging deeper into the above concepts is a course in calculus, we can readily illustrate the notion of convergence of an infinite series using geometric series.
Every student of mathematics knows that
Suspend, for the sake of illustration, that you know this rational number.
is the decimal representation of a well-known rational number. The decimal in (6) is the same as the infinite series
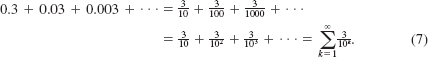
If we consider the geometric sequence
it is possible to find a formula for the general term of the associated sequence of partial sums:
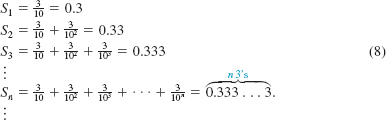
In view (8) of Section 10.2 with the identifications a = 3/10 and r = 1/10 we can write the general term Sn of the sequence (8):
We now let n increase without bound, that is, n → ∞. From (4) and (5) we know that (1/10)n → 0 as n → ∞ and so the limit of (9) is
Thus, 1/3 is the sum of the infinite series in (7):
Geometric Series In general, the sum of an infinite geometric series
is defined whenever |r| < 1.To see why this is so, recall
By letting n → ∞ and using rn → 0 whenever | r | < 1, we see that
Therefore for | r | < 1 we define the sum of the infinite geometric series in (10) to be a/(1 - r).
A divergent geometric series 
has no sum.
Formula (12) gives a method for converting a repeating decimal to a quotient of integers. We use the fact that
Every repeating decimal is the sum of an infinite geometric series.
Before giving another example of this, let's be clear that a repeating decimal is a decimal number that after a finite number of decimal places has a sequence of one or more digits that repeats endlessly.
Recall from Section 1.1, a rational number is one that is either a terminating decimal or a repeating decimal. An irrational number is one that is neither a terminating nor a repeating decimal.
EXAMPLE 5 Repeating Decimal
Write 0.232323…as a quotient of integers.
Solution Written as an infinite geometric series, the repeating decimal is the same as
With the identifications 
< 1 it follows from (12) that
EXAMPLE 6 Repeating Decimal
Write 0.72555…as a quotient of integers.
Solution The repeating digit 5 does not appear until the third decimal place so we write the number as the sum of a terminating decimal and a repeating decimal:
Combining the last two rational numbers by a common denominator we find
Every repeating decimal number (rational number) is a geometric series, but do not get the impression that the sum of every convergent geometric series need be a quotient of integers.
EXAMPLE 7 Sum of a Geometric Series
The infinite series 
is a convergent geometric series because | r | + |-1/e | = 1/e < 1. By (12) the sum of the series is the number
EXAMPLE 8 A Divergent Geometric Series
The infinite series
is a divergent geometric series because 
.
NOTES FROM THE CLASSROOM
(i) When written in terms of summation notation, a geometric series may not be immediately recognizable, or if it is, the values of a and r may not be apparent. For example, to see whether 
is a geometric series it is a good idea to write out two or three terms:
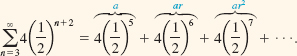
From the right side of the last equality, we can make the identifications a = 4(1/2)5
and | r | = 1/2 < 1. Consequently, the sum of the series is 
If desired, although there is no real need to do this, we can express 
in the more familiar form 
by letting k = n – 2. The result is
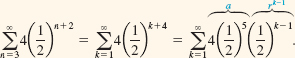
(ii) In general, it is very difficult to find the sum of a convergent infinite series using the sequence of partial sums. In most cases it is impossible to find a formula for the general term Sn = 
of this sequence. The geometric series is, of course, an important exception. But there is another type of infinite series whose sum can be found by finding the limit of the sequence {Sn}. If interested, see Problems 35 and 36 in Exercises 10.3.
In Problems 1-18, determine whether the given sequence converges.
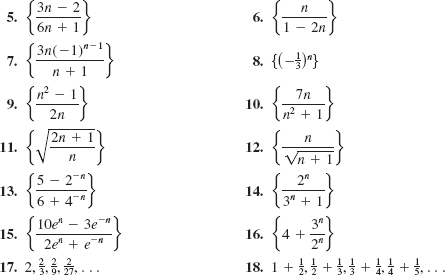
In Problems 19-24, write the given repeating decimal as a quotient of integers.
19. 0.222…
20. 0.555…
21. 0.616161…
22. 0.393939…
23. 1.314314…
24. 0.5262626…
In Problems 25-34, determine whether the given infinite geometric series converges. If convergent, find its sum.
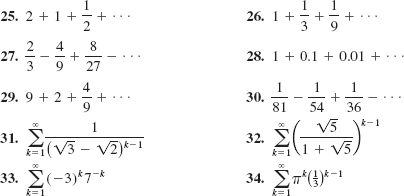
35. The infinite series 
is an example of a telescoping series. For such series it is possible to find a formula for the general term Sn of the sequence of partial sums.
(a) Use the partial fraction decomposition
as an aid in finding a formula for Sn. This will also explain the meaning of the word telescoping.
(b) Use part (a) to find the sum of the infinite series.
36. Use the procedure in part (a) of Problem 35 to find the sum of the infinite series 
Miscellaneous Applications
37. Distance Traveled A ball is dropped from an initial height of 15 ft onto a concrete slab. Each time the ball bounces, it reaches a height of f its preceding height. Use an infinite geometric series to determine the distance the ball travels before it comes to rest.
38. Drug Accumulation A patient takes 15 mg of a drug at the same time each day. If 80% of the drug accumulated is excreted each day by bodily functions, how much of the drug will accumulate in the patient's body after a long period of time, that is, as n → ∞? (Assume that the measurement of the accumulation is made immediately after each dose.)
Calculator/Computer Problems
39. It can be proved that the terms of the sequence {an} defined recursively by the formula
converges when a1 = 1 and r = 3. Use a calculator to find the first 10 terms of the sequence. Conjecture the limit of the sequence.
40. The sequence
is known to converge to a number γ called Euler's constant. Calculate at least the first 10 terms of the sequence. Conjecture the limit of the sequence.
For Discussion
41. Use algebra to show that the sequence 
converges.
42. Determine whether the sequence
converges or diverges.
43. The infinite series 
is known to be convergent. Discuss how the sum of the series can be found. State any assumptions that you make.
44. Find the values of x for which the infinite series 
converges.
45. The infinite series 1 + 1 + 1 +…is a divergent geometric series with r = 1. Note that formula (5) does not yield the general term for the sequence of partial sums. Find a formula for Sn and use that formula to argue that the infinite series is divergent.
46. Consider the rational function f(x) = 1/(1 - x).Show that
For what values of x is the equality true?
47. Discuss whether the equality 1 = 0.999…is true or false.
48. The Trains and the Fly At a specified time two trains T1 and T2, 20 miles apart on the same track, start on a collision course at a rate of 10 mi/h. Suppose that at the precise instant the trains start a fly leaves the front of train T1, flies at a rate of 20 mi/h in a straight line to the front of the engine of train T2, then flies back to T1 at 20 mi/h, then back to T2, and so on. Use geometric series to find the total distance traversed by the fly when the trains collide (and the fly is squashed). Then use common sense to find the total distance the fly flies. See FIGURE 10.3.1.
Trains and fly in Problem 50
49. Embedded Squares In FIGURE 10.3.2 the square shown in red is 1 unit on a side. A second blue square is constructed inside the first square by connecting the midpoints of the first one. A third green square is constructed by connecting the midpoints of the sides of the second square, and so on.
(a) Find a formula for the area An of the n th inscribed square.
(b) Make a conjecture about the convergence of the sequence {An}.
(c) Consider the sequence {Sn}, where Sn = A1 + A2 +…+ An. Calculate the numerical values of the first 10 terms of this sequence.
(d) Make a conjecture about the convergence of the sequence {Sn}.
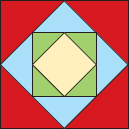
Embedded squares in Problem 51
50. Golden Ratio In Problem 51 of Exercises 10.1 we saw that the Fibonacci numbers were defined recursively by Fn+1 = Fn + Fn-1 F1 = 1, F2. Dividing the recursion formula by Fn, gives
If we define an = Fn+1/Fn, then the sequence {an} is defined recursively by
The sequence {an} is known to converge to the golden ratio 
(a) Find ø [Hint: ø = 
(b) Write a short report on the significance of the number ø.
Polygonal path in Problem 52
10.4 Mathematical Induction
Introduction Frequently, a mathematical statement or proposition that depends on the natural numbers or positive integers N = {1,2,3,…} can be proved using a technique known as mathematical induction. Suppose we can show two things:
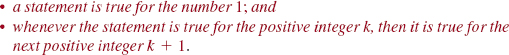
In other words, suppose we can demonstrate that the
and that the
What can we conclude from this? From (1) we have that
the statement is true for the number 1,
and by (2) the statement is true for the number 1 + 1 = 2.
In addition, it now follows from (2) that
It seems clear that the statement must be true for all positive integers n. This is precisely the assertion of the following principle.
Falling dominoes
Although we have stated the Principle of Mathematical Induction as a theorem, it is actually considered to be an axiom of the natural numbers.
By way of a physical analogy to the foregoing principle, imagine that we have an endless row of correctly spaced dominoes each standing on its end. Suppose we can demonstrate that whenever a domino (give it a name, say, the kth domino) falls over that its neighboring domino (the (k + 1)st domino) also falls over. Then we conclude that all the dominoes must fall over provided we can show one more thing, namely, that the first domino falls over.
We now illustrate the use of induction with several examples. We begin with an example from arithmetic.
EXAMPLE 1 Using Mathematical Induction
Prove that the sum of the first n positive integers is given by
Solution Here the statement S(n) is the formula in (3). The first step is to show that S(1) is true, where S(1) is the statement
Since this is clearly true, condition (i) is satisfied.
The next step is to verify condition (ii). This requires that from the hypothesis “S(k) is true,” we prove that” S(k + 1) is true” Thus we assume that the statement S(k),
is true. From this assumption we wish to demonstrate that S(k + 1),
is also true. Now we can obtain a formula for the sum of the first k + 1 positive integers by using the equality (4) and some algebra:
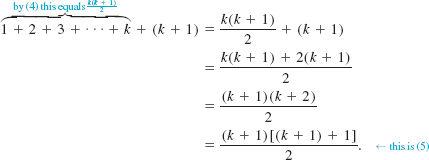
Thus we have shown that the statement S(k + 1) is true. It follows from the Principle of Mathematical Induction that S(n) is true for every positive integer n.
In basic algebra we learned how to factor. In particular, from the factorizations
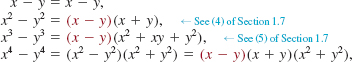
a reasonable conjecture is that x - y is always a factor xn - yn for any positive integer n. We now prove that this is so.
EXAMPLE 2 Using Mathematical Induction
Prove that x - y is a factor of xn - yn for any positive integer n.
Solution For the statement S(n),
x - y is a factor of xn + yn,
we must show that the two conditions (i) and (ii) are satisfied. For n = 1 we have the true statement S(1),
x - y is a factor of x1 - y1.
Now assume that S(k),
x - y is a factor of xk - yk.
is true. Using this assumption, we must show that S(k + 1) is true; that is, x - y is a factor of xk+1 - yk+1. To this end we perform a bit of cleverness, namely, let's subtract. and add to xyk to xk+1 - yk+1:
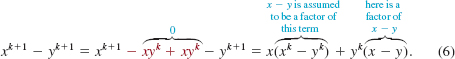
But by hypothesis, x - y is a factor of xk - yk. Therefore, x - y is a factor of both terms on the right-hand side of (6). It follows that x - y is a factor of the right-hand side, and thus we have shown that the statement S(k + 1),
x - y is a factor of xk+1 - yk+1,
is true. It follows by the Principle of Mathematical Induction that x - y is a factor of xn - yn for any positive integer n.
EXAMPLE 3 Using Mathematical Induction
Prove that 8n - 1 is divisible by 7 for all positive integers n.
Solution We let S(n)be the statement “8n - 1 is divisible by 7 for all positive integers n.” With n = 1 we see that 81 - 1 = 7 is obviously divisible by 7.
Therefore S(1) is true. Now let us assume that S(k) is true; that is, 8k – 1 is divisible by 7 for some positive integer k. Using that assumption we must show that 8k + 1 – 1 is divisible by 7. Consider
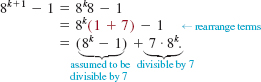
The last equality proves S(k + 1) is true because both 8k – 1 and 7.8k are divisible by 7. It follows from the Principle of Mathematical Induction that S(n) is true for every positive integer n.
In Problems 1-20, use the Principle of Mathematical Induction to prove that the given statement is true for every positive integer n.
For Discussion
21. If we assume that
2 + 4 + 6 +…+ 2n = n2 + n + 1
is true for n = k show that the formula is true for n = k + 1 Show, however, that the formula itself is false. Explain why this does not violate the Principle Mathematical Induction.
Introduction When (a + b)n is expanded for an arbitrary positive integer n, the exponents of a and b follow a definite pattern. For example, from the expansions
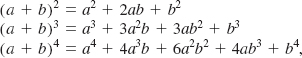
we see that the exponents of a decrease by 1, starting with the first term, whereas the exponents of b increase by 1, starting with the second term. In the case of (a + b)4, we have
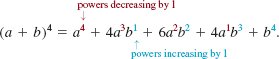
To extend this pattern, we consider the first and last terms to be multiplied by b0 and a0, respectively; that is,
We also note that the sum of the exponents in each of the five terms of the expansion (a + b)4 is 4. For example, in the second term we have 
.
EXAMPLE 1 Using (1)
Expand (y2 - 1)4.
Solution With the identifications a = y2 and b = -1 it follows from (1) and the laws of exponents that
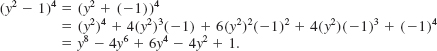
The Coefficients The coefficients in the expansion of (a + b)n also follow a pattern. To illustrate, we display the coefficients in the expansions of (a + b)0 (a + b)1, (a + b)2, (a + b)3, and (a + b)4 in a triangular array
Observe that each number in the interior of this array is the sum of the two numbers directly above it. Thus the next line in the array can be obtained as follows:
As you might expect, these numbers are the coefficients of the powers of a and b in the expansion of (a + b)5; that is,
The array obtained by continuing in this manner is called Pascal's triangle after the French philosopher and mathematician Blaise Pascal (1623-1662).
EXAMPLE 2 Using (1)
Expand (3 - x)5.
Solution From (3), with a = 3 and b = -x, we can write
Factorial Notation Before we give a general formula for the expansion of (a + b)n, it will be helpful to introduce factorial notation. The symbol r! is defined for any positive integer r as the product
See Problem 57 in Exercises 4.1.
and is read “r factorial.” For example, 1! = 1 and 4! = 4.3.2.1 = 24. Also, it is convenient to define
0! = 1.
EXAMPLE 3 A Simplification
Simplify 
where r is a positive integer.
Solution Using the definition of r! in (4) we can write the numerator as
Thus, 
The Binomial Theorem The general formula for the expansion of (a + b)n is given in the following result, known as the Binomial Theorem.
By paying attention to the increasing powers on b in (5) we see that the expression
is the (r + 1)stterm in the expansion of (a + b)n.For r = 0, 1,…, n, the numbers
are called binomial coefficients and are, of course, the same as those obtained from Pascal's triangle. Before proving the Binomial Theorem by mathematical induction, we consider some examples.
EXAMPLE 4 Using (5)
Expand (a + b)4.
Solution We use the Binomial Theorem (5) with coefficients given by (7). With n = 4 we obtain:
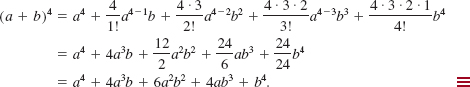
EXAMPLE 5 Finding the Sixth Term
Find the sixth term in the expansion of (x2-2y)7.
Solution Since (6) gives the (r + 1)st term in the expansion of (a + b)n, the sixth term in the expansion of (x2 - 2y)7 corresponds to r = 5 (that is, r + 1 = 5 + 1 = 6). With the identifications n = 7, r = 5, a = x2, and b = –2y, it follows from (6) that the sixth term is
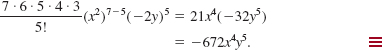
An Alternative Form The binomial coefficients can be written in a more compact manner using factorial notation. If r is any integer such that 0 ≤ r ≤ n, then
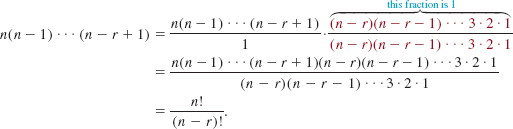
Thus the binomial coefficients of an - rbr for r = 0, 1,…, n given in (7) are the same as n!/r!(n – r)!.This latter quotient is usually denoted by the symbol 
. That is, the binomial coefficients are
Hence the Binomial Theorem (5) can be written in the alternative form
It is this form that we will use to prove (5).
Summation Notation The Binomial Theorem can be expressed in a compact manner by using summation notation. Using (6) and (8), the sums in (5) and (9) can be written as
or
respectively. From these forms it is apparent that since the index of summation starts at 0 and ends at n, a binomial expansion contains n + 1 terms.
The following property of the binomial coefficient will play a pivotal role in the proof of the Binomial Theorem. For any integer r, 0 < r ≤ n, we have
We leave the verification of (10) as an exercise (see Problem 63 in Exercises 10.5).
Proof of Theorem 10.5.1 We now prove the Binomial Theorem by mathematical induction. Substituting n = 1 into (9) gives a true statement,
since
This completes the verification of the first condition of the Principle of Mathematical Induction.
For the second condition, we assume that (9) is true for some positive integer n = k:
Using this assumption we then must show that (9) is also true for n = k + 1.To do this we multiply both sides of (11) by (a + b):
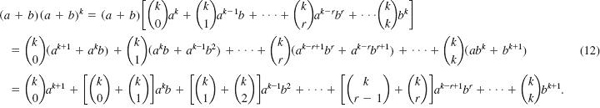
Using (10) to rewrite the coefficient of the (r + 1)st term in (12) as
and the facts that (a + b)(a + b)k = (a + b)k+1,
the last line in (12) becomes
Because this is (9) with n replaced by k + 1, the proof is complete by the Principle of Mathematical Induction.
In Problems 1-12, evaluate the given expression.
3!
5!
3!4!
0!5!
In Problems 13-16, simplify the given expression.
In Problems 17-26, use factorial notation to rewrite the given product.
5 · 4 · 3 · 2 · 1
7 · 6 · 5 · 4 · 3 · 2 · 1
100 · 99 · 98…3 · 2 · 1
t(t – 1)(t – 2)…3 · 2 · 1
(4 · 3 · 2 · 1 ·) (5 · 4 · 3 · 2 · 1)
(6 · 5 · 4 · 3 · 2 · 1)/ (3 · 2 ·)
4 · 3
10 · 9 · 8
n(n–1), n ≥ 2
n(n–1) (n–2)…(n –r + 1),n ≥ r
In Problems 27–32, answer true or false.
5! = 5 · 4!
3! + 3! = 6!
n!(n + 1) = (n + 1)!
In Problems 33–42, use the Binomial Theorem to expand the given expression.
(x2 – 5y4)2
(x–1 + y–1)3
(x2 – y2)3
(x–2 + 1)4
(x½ + y½)4
(3 – y2)4
(x2 + y2)5
(a – b – c)3
(x + y + z)4
By referring to Pascal's triangle, determine the coefficients in the expansion of (a + b)n for n = 6 and n = 7.
If f(x) = xn, where n is a positive integer, use the Binomial Theorem to simplify the difference quotient:
In Problems 45–54, find the indicated term in the expansion of the given expression.
Sixth term of (a + b)6
Second term of (x – y)5
Fourth term of (x2 – y2)6
Third term of (x – 5)5
Fifth term of (4 + x)7
Seventh term of (a – b)7
Tenth term of (x + y)14
Fifth term of (t + 1)4
Eighth term of (2 – y)9
Ninth term of (3 – z)10
Find the coefficient of the constant term in (x + 1/x)10.
Find the first five terms in the expansion of (x2 – y)11.
Use the first four terms in the expansion of (1 – 0.01)5 to find an approximation to (0.99)5. Compare with the answer obtained from a calculator.
Use the first four terms in the expansion of (1 + 0.01)10 to find an approximation to (1.01)10. Compare with the answer obtained from a calculator.
For Discussion
Without adding the terms, determine the value of 
If 
, what is x?
Use the Binomial Theorem to show that
Use the Binomial Theorem to show that
Prove that
Prove that
ch0010_s1_6.10 Principles of Counting
Introduction A wide variety of practical problems involve counting the number of ways in which something can occur. For example, the telephone prefix at a certain university is 642. If the prefix is followed by four digits, how many telephone numbers are possible before a second prefix is needed? We will be able to solve this problem (see Example 2) and others using the counting techniques discussed in this section.
Tree Diagrams We begin by considering a more abstract problem. How many different arrangements can be made of the three letters a, b, and c using two letters at a time? One way to solve this problem is to list all the possible arrangements. As shown in FIGURE 10.6.1, a tree diagram can be used to illustrate all the possibilities. From the point labeled “Start,” line segments lead to each of the three possible choices for a first letter. From each of these, a line segment leads to each of the possible choices for a second letter. Each possible arrangement corresponds to a path, or branch of the tree, beginning at the “Start” and traveling to the right through the tree. We see that there are 6 different arrangements of the three letters:
ab, ac, ba, bc, ca, cb.
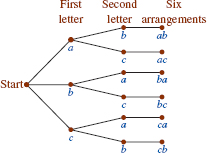
Tree diagram for number of arrangements of a, b, c taken two at a time
Another way to solve the foregoing problem is to recognize that each arrangement consists of a selection of letters to fill the two blank positions indicated by the red lines:
Any one of the three letters a, b, or c can be chosen for the first position. Once this choice is made, any one of the two remaining letters can be chosen for the second position. Since each of the three letters for the first position can be associated with either of the remaining two letters, the total number of arrangements is given by the product
This simple example illustrates the Fundamental Counting Principle.
This Fundamental Counting Principle can be extended to three or more events in an obvious way:
Simply multiply the number of ways each event can occur.
EXAMPLE 1 Number of Outfits
A college student has 5 shirts, 3 pairs of slacks, and 2 pairs of shoes. How many different outfits can he wear consisting of a shirt, a pair of slacks, and a pair of shoes?
Solution Three selections or events are to occur, with 5 choices for the first event (choosing a shirt), 3 choices for the second event (choosing a pair of slacks), and 2 choices for the third event (choosing a pair of shoes). By the Fundamental Counting Principle, the number of different outfits is the product 5 · 3 · 2 = 30.
We now return to the problem given in the introduction.
EXAMPLE 2 Telephone Numbers
The telephone prefix at a certain university is 642. If the prefix is followed by four digits, how many different telephone numbers are possible before a second prefix is needed?
Solution Four events are to occur: selecting the first digit after the prefix, selecting the second digit after the prefix, and so on. Since repeated digits are allowed in telephone numbers, any one of the 10 digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 can be selected for each position. Hence there are 10 · 10 · 10 · 10 = 10,000 possible different phone numbers with the single prefix 642.
EXAMPLE 3 Arrangements of Letters
How many different ways are there to arrange the letters in the word RANDOM?
Solution Since RANDOM has 6 distinct letters, there are 6 events: choosing the first letter, choosing the second letter, and so on. Any one of the 6 letters can be chosen for the first position, then any of the remaining 5 letters can be chosen for the second position, then any of the remaining 4 letters can be chosen for the third position, and so on. The total number of arrangements is 6 · 5 · 4 · 3 · 2 · 1 = 720.
Permutations A permutation is an arrangement that is made by using some or all of the elements of a set without repetition. This means that no element of the set appears more than once in the arrangement. For example, 312 is a permutation of the digits in the set {1, 2, 3}, but 112 is not. In Example 3, each of the rearrangements of the six letters in the word RANDOM (for instance, MODRAN) is a permutation. More generally, we have the following definition.
An ordered arrangement of r elements selected from a set of n distinct elements is called a permutation of n elements taken r at a time (n ≥ r).
Notation We will use the symbol P(n, r) to denote the number of permutations of n distinct objects taken r at a time. Using the notation P(n, r), we write the number of permutations of 5 objects taken 3 at a time as P(5, 3).
It is possible to find an explicit formula for P(n, r), that is, the number of permutations of n distinct objects taken r at a time for 0 ≤ r ≤ n. For r ≥ 1, we can think of the process of forming a permutation of n objects taken r at a time as r events: choose the first object, choose the second object, and so on. When we make the first choice, there are n objects available; when we make the second choice, there are n – 1 objects; for the third choice, there are n – 2 objects; and so on. When we choose the r th object, there are n – (r – 1) objects to choose from. Thus from Theorem 10.6.1,
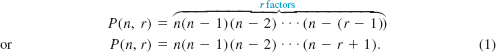
An alternative expression for P(n, r) involving factorial notation can be found by multiplying the right–hand side of (1) by
The result is
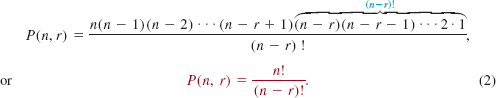
When r = n, formula (2) reduces to
because 0! is defined to be 1. This result is the same as that obtained by using the counting principle in Theorem 10.6.1:
since any one of the n objects can be chosen first, any one of the remaining objects can be chosen second, and so on. In Example 3, the number of 6–letter arrangements of the words RANDOM is the number of permutations of the 6 letters taken 6 at a time, that is, P(6, 6) = 6! = 720.
If r = 0, we define P(n, 0) = 1, which is consistent with (2).
EXAMPLE 4 Using (2) and (3)
Evaluate (a) P(5, 3), (b) P(5, 1), and (c) P(5, 5).
Solution In (a) and (b) we use formula (2):
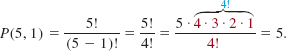
From formula (3) we find that
EXAMPLE 5 Awarding Medals
At a track meet 6 athletes are entered in the 100 m dash. In how many ways can gold, silver, and bronze metals be awarded?
Solution We wish to count the number of ways of arranging 3 of the 6 athletes in the winning positions. The solution is given by the number of permutations of 6 things (athletes) taken 3 at a time:
This problem can also be solved using the Fundamental Counting Principle. Since there are 3 choices to be made, with 6 athletes available for the gold medal, 5 for the silver, and 4 for the bronze, we find 6 · 5 · 4 = 120.
EXAMPLE 6 Arrangements of Books
How many arrangements are possible for 10 different books on a bookshelf?
Solution We wish to find the number of permutations of 10 objects taken 10 at a time, or P(10, 10) = 10! = 3,628,800.
Ten books on a shelf
Combinations In the preceding discussion we were concerned with the number of ways of arranging or choosing r elements from a set of n elements, where the order in which they were arranged or chosen was considered. However, in certain applications the order of the elements is not important. For example, if a committee of two is to be chosen from the four students Angie, Brandon, Cecilia, and David, the committee formed by choosing Angie and Brandon is the same as the committee formed by choosing Brandon and Angie. A selection of objects in which the order does not make any difference is called a combination.
Notation We use the symbol C(n, r) to denote the number of combinations of n distinct objects taken r at a time. By using (2) it is possible to derive a formula for C(n, r). At the beginning of this section we saw that there are 6 arrangements (permutations) of the 3 letters a, b, and c taken 2 at a time:
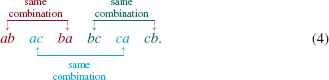
In (4) we see that if we disregard the order in which the letters are listed, then there are only 3 combinations of the letters: ab, ac, and bc. Thus, C(3, 2) = 3. We see that each of these combinations can be arranged in 2! ways to yield the list of permutations in (4). By the Fundamental Counting Principle,
In general, for 0 < r ≤ n, each of the C(n, r) combinations can be rearranged in r! different ways, so that
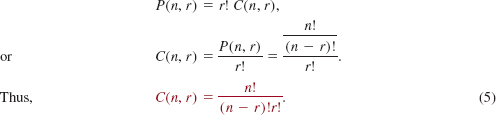
For r = 0, we define C(n, 0) = 1, which is consistent with formula (5).
Note that C(n, r) is identical to the binomial coefficient in the expansion of (a + b)n, where n is a nonnegative integer. See (7) and (8) of Section 10.5.
EXAMPLE 7 Using Formula (5)
Evaluate (a) C(5, 3), (b) C(5, 1), and (c) C(5, 5).
Solution Using formula (5), we have the following:
(a) 
(b) 
(c)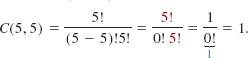 
EXAMPLE 8 Number of Card Hands
How many different 5–card hands can be dealt from a deck of 52 cards?
Solution Since a hand is the same regardless of the order of the cards, we are talking about the number of combinations of 52 cards taken 5 at a time. Using (5), the solution is
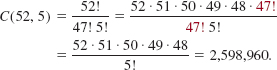
Note that we cancelled the larger of the two factorials 47! and 5! to simplify the calculations of C(52, 5).
EXAMPLE 9 Organizing a Club
A card club has 8 members.
(a) In how many ways can 3 members be chosen to be president, secretary, and treasurer?
(b) In how many ways can a committee of 3 members be chosen?
Solution In choosing officers, order does matter, whereas in choosing a committee, the order of the selection does not affect the resulting committee. Thus in (a) we are counting permutations and in (b) we are counting combinations. We find
(a) 
(b) 
In deciding whether to use the formula for P(n, r) or C(n, r), consider the following two informal rules.
Note of Caution
• Permutations are involved if you are considering arrangements in which different orderings of the same objects are to be counted.
• Combinations are involved if you are considering ways of choosing objects in which the order of the chosen objects makes no difference.
EXAMPLE 10 Choosing Reporters
A college newspaper staff has 6 junior reporters and 8 senior reporters. In how many ways can 2 junior and 3 senior reporters be chosen for a special assignment?
Solution Two events are to occur: the selection of 2 junior reporters and the selection of 3 senior reporters. Because the order in which the 2 junior reporters are chosen makes no difference, we count combinations. Therefore, the number of ways of choosing 2 junior reporters is
Likewise in selecting the 3 senior reporters order does not matter, so we again count combinations:
Thus we choose the junior reporters in 15 ways and, for each of these selections, there are 56 ways of selecting the senior reporters. Applying the Fundamental Counting Principle gives
ways to make the choices for the special assignment.
EXAMPLE 11 Selecting a Display
A cheese store has 10 varieties of domestic cheese and 8 varieties of imported cheese. In how many ways can a selection of 6 cheeses, consisting of 2 domestic and 4 imported varieties, be placed on a display shelf?
Solution The domestic varieties can be chosen in C(10, 2) ways and the imported varieties in C(8, 4) ways. Thus by the Fundamental Counting Principle the 6 cheeses can be selected in C(10, 2) · C(8, 4) ways. Up to this point in the solution, order has not been important in making the selection of the cheeses. Now we observe that each selection of 6 cheeses can be placed or arranged on the shelf in P(6, 6) ways. Thus the total number of ways the cheese can be displayed is
In Problems 1–4, use a tree diagram.
List all possible arrangements of the letters a, b, and c.
If a coin is tossed 4 times, list all possible sequences of heads (H) and tails (T).
If a red die and a black die are rolled, list all possible results.
If a coin is tossed and then a die is rolled, list all possible results.
In Problems 5–8, use the Fundamental Counting Principle.
Number of Meals A cafeteria offers 8 salads, 6 entrees, 4 vegetables, and 3 desserts. How many different meals are possible if one item is selected from each category?
Number of Systems How many different stereo systems consisting of speakers, receiver, and CD player can be purchased if a store carries 6 models of speakers, 4 of receivers, and 2 of compact disc players?
Number of Prefixes How many different 3–digit telephone prefixes are possible if neither 0 nor 1 can occupy the first position?
Number of License Plates If a license plate consists of 3 letters followed by 3 digits, how many license plates are possible if the first letter cannot be O or I?
In Problems 9–16, evaluate P(n, r).
P(6, 3)
P(6, 4)
P(6, 1)
P(4, 0)
P(100, 2)
P(4, 4)
P(8, 6)
P(7, 6)
In Problems 17–24, evaluate C(n, r).
C(4, 2)
C(4, 1)
C(50, 2)
C(2, 2)
C(13, 11)
C(8, 2)
C(2, 0)
C(7, 4)
Miscellaneous Applications
In Problems 25–28, use permutations to solve the given problem.
Family Portrait In how many ways can a family of four line up in a row to have their family portrait taken?
Volunteer Work As part of a fund–raising drive, a volunteer is given 5 names to contact. In how many different orders can the volunteer complete the task?
Scrabble A Scrabble game player has the following 7 letters: A, T, E, L, M, Q, F.
(a) How many different 7–letter “words” can be considered?
(b) How many different 5–letter “words”?
Politics From a class of 24, elections are held for president, vice president, secretary, and treasurer. In how many ways can the offices be filled?
A family of four
The game Scrabble®
In Problems 29–32, use combinations to solve the given problem.
Good Luck! A student must answer any 10 questions on a 12–question exam. In how many different ways can the student select the questions?
Chem Lab For a chemistry lab class, a student must correctly identify 3 “unknown” samples. In how many ways can the 3 samples be chosen from 10 chemicals?
Volunteers In how many ways can 5 subjects be chosen from a group of 10 volunteers for a psychology experiment?
Potpourri In how many ways can 4 herbs be chosen from 8 available herbs to make a potpourri?
In Problems 33–44, use one or more of the techniques discussed in this section to solve the given counting problem.
Spelling Bee If 10 students enter a spelling bee, in how many different ways can first– and second–place awards be made?
Show Business A theater company has a repertoire consisting of 8 dramatic skits, 6 comedies, and 4 musical numbers. In how many ways can a program be selected consisting of a dramatic skit followed by either a comedy or a musical number?
Take Your Pick A pediatrician allows a well–behaved child to select any 2 of 5 small plastic toys to take home. How many different selections of toys are possible?
Tournament Rankings If 8 teams enter a soccer tournament, in how many different ways can first, second, and third place be decided, assuming ties are not allowed?
Another Jackson Pollock If 8 colors are available to make an abstract spatter–paint picture, how many different color combinations are possible if only 3 colors are chosen?
Seating Arrangements Three couples have reserved seats in a row at the theater. In how many different ways can they be seated
if there are no restrictions?
if each couple wishes to sit together?
if the 3 women and 3 men wish to sit together in 2 groups?
Mastermind In a popular board game that originated in England called Mastermind, one player creates a secret “code” by filling 4 slots with any one of 6 colors. How many codes are possible
if repetitions are not allowed?
if repetitions are allowed?
if repetitions and blank slots are allowed?
Super Mastermind Some advertisements for the game Super Mastermind(a more difficult version of the Mastermind game described in Problem 39) claim that up to 59,000 codes are possible. If Super Mastermind involves filling 5 slots with any one of 8 colors and if blanks and repetitions are allowed, is the claim correct?
Playing with Letters From 5 different consonants and 3 different vowels, how many 5–letter “words” can be made consisting of 3 different consonants and 2 different vowels?
The game Mastermind®
Defective Lights A box contains 24 Christmas tree bulbs, 4 of which are defective. In how many ways can 4 bulbs be chosen so that
all 4 are defective?
all 4 are good?
2 are good and 2 are defective?
3 are good and 1 is defective?
More Playing with Letters How many 3–letter “words” can be made from 4 different consonants and 2 different vowels
if the middle letter must be a vowel?
if the first letter cannot be a vowel? Assume that repeated letters are not allowed.
Store Display A wine store has 12 different California wines and 8 different French wines. In how many ways can a group of 6 wines consisting of 4 California and 2 French wines
be selected for display?
be placed in a row on a display shelf?
ch0010_s1_7.10 Introduction to Probability
Introduction As we mentioned in the chapter introduction, the development of the mathematical theory of probability was initially motivated by questions arising in the seventeenth century about games of chance. Today, applications of probability are found in medicine, sports, law, business, and many other areas. In this section we present a brief introduction to this fascinating subject.
Terminology Consider an experiment that has a finite number of possible results or outcomes. The set S of all possible outcomes of a particular experiment is called the sample space of the experiment. For our purposes we will assume that each outcome is equally likely to occur. Thus, if the experiment consists of tossing, or flipping, a fair coin, there are two possible equally likely outcomes: obtaining a head or obtaining a tail. If the outcome of obtaining a head is denoted by H and the outcome of obtaining a tail is denoted by T, then the sample space of the experiment can be written in set notation as
Any subset E of a sample space S is called an event. Generally, an event E is one or more outcomes of an experiment. For example,
is the event of obtaining a head when a coin is tossed.
There are two outcomes in tossing a coin
EXAMPLE 1 Sample Space and Two Events
On a single roll of a fair die, there is an equal chance of obtaining a 1, 2, 3, 4, 5, or 6. Thus the sample space of the experiment of rolling a fair die is the set
The event E1 of obtaining a 4 on a roll of the die is the subset E1 = {4} of S.
The event E2, consisting of obtaining an odd number on a roll of the die, is the subset E2 = {1, 3, 5} of S.
A die showing 4 is one of six possible outcomes
We shall use the notation n(S) to denote the number of outcomes in a sample space S and n(E) to denote the number of outcomes associated with an event E. Thus, in Example 1 we have n(S) = 6; in parts (a) and (b) of the example we have n(E1) = 1 and n(E2) = 3, respectively.
The definition of the probability P(E) of an event E is expressed in terms of n(S) and n(E).
Let S be the sample space of an experiment and let E be an event. If each outcome of the experiment is equally likely, then the probability of the event E is given by
where n(E) and n(S) denote the number of outcomes in the sets E and S, respectively.
EXAMPLE 2 The Probability of Tossing a Head
Find the probability of obtaining a head if a coin is tossed.
Solution From (1) and (2),E = {H}, S = {H, T}, and so n(E) = 1 and n(S) = 2. From (4) of Definition 10.7.1 the probability of obtaining a head is
EXAMPLE 3 Three Probabilities
On a single roll of a fair die, find the probability
(a) of obtaining a 4, (b) of obtaining an odd number, (c) of obtaining a number that is not a 4.
Solution Let the symbols E1, E2, and E3 denote, respectively, the events in parts (a), (b), and (c) of this example. Also, in each part we have S = {1, 2, 3, 4, 5, 6}.
From part (a) of Example 1, E1 = {4}, and so n(E1) = 1 and n(S) = 6. From (4), the probability of obtaining a 4 when a die is rolled is then
From part (b) of Example 1, E2 = {1, 3, 5}, so n(E2) = 3 and n(S) = 6. Again from (4), the probability of rolling an odd number is
The event of obtaining a number that is not a 4 on a roll of a die is the subset E3 = {1, 2, 3, 5, 6} of S. Using n(E3) = 5 and n(S) = 6 the probability of obtaining a number that is not a 4 is
EXAMPLE 4 Probability of 7
Find the probability of obtaining a total of 7 when two dice are rolled.
One of six possible ways of throwing a 7 on a pair of dice
Solution Since there are 6 numbers on each die, we conclude from the Fundamental Counting Principle of Section 10.6 that there are 6 · 6 = 36 possible outcomes in the sample space S; that is, n(S) = 36. In the accompanying table, we have listed the possible ways of obtaining a total of 7.
E = two dice showing a total of 7
First die
1
2
3
4
5
6
Second die
6
5
4
3
2
1
From the table we see that n(E) = 6. Hence from (4) the probability of throwing a 7 with two dice is
EXAMPLE 5 Using Combinations
A bag contains 5 white marbles and 3 red marbles. A person reaches into the bag and randomly withdraws 3 marbles. What is the probability that all the marbles will be white?
Solution The sample space S of the experiment is the set of all possible combinations of 3 marbles drawn from the 8 marbles in the bag. The number of ways of choosing 3 marbles from a bag of 8 marbles is the number of combinations of 8 objects taken 3 at a time; that is, n(S) = C(8, 3). Similarly, the number of ways of choosing 3 white marbles from 5 white marbles is the number of combinations n(E) = C(5, 3). Since the event E is “all marbles are white,” we have
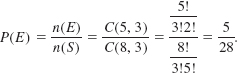
Bounds on the Probability of an Event Since any event E is a subset of a sample space S, it follows that 0 ≤ n(E) ≤ n(S). By dividing the last inequality by n(S) we see that
If E = S, then n(E) = n(S) and P(E) = n(S)/n(S) = 1; whereas if E has no elements, we take E = Ø, n(Ø) = 0, and P(E) = n(Ø)/n(S) = 0/n(S) = 0. If P(E) = 1, then E always happens and E is called a certain event. On the other hand, if P(E) = 0, then E is an impossible event, that is, E never happens.
EXAMPLE 6 Rolling a Die
Suppose a fair die is rolled once.
What is the probability of obtaining a 7?
What is the probability of obtaining a number less than 7?
Solution (a) Because the number 7 is not in the set S of all possible outcomes (3) the event E of “obtaining a 7” is an impossible event; that is, E = Ø, n(Ø) = 0. Therefore,
(b) Because the outcomes of rolling a fair die are all positive integers less than 7 we have E = {1, 2, 3, 4, 5, 6 } = S. Thus E is a certain event and
Complement of an Event The set of all outcomes in the sample space S that do not belong to an event E is called the complement of E and is denoted by the symbol E'. For example, in rolling a die, if E is the event of “obtaining a 4,” then E' is the event of “obtaining any number except 4.” Because events are sets, we can describe the relationship between an event E and its complement E' using the operations of union and intersection:
In view of the foregoing properties we can write n(E) + n(E’) =n(S). Dividing both sides of the last equality by n(S) we see that the probabilities of E and E' are related by
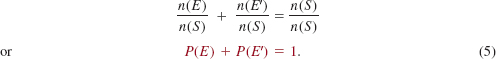
For instance, the complement of the event E1 = {4} in part (a) of Example 3 is the set E'1 = E3 = {1, 2, 3, 5, 6} in part (c). Observe in accordance with (5), we have 
.
The relationship (5) is useful in either of the two forms:
The second of the two formulas in (6) allows us to find the probability of an event if we know the probability of its complement. Sometimes it is easier to calculate P(E’) than it is to calculate P(E). Also, it is interesting to note that the equation P(E) + P(E’) = 1 can be interpreted as saying that something must happen.
EXAMPLE 7 Probability of an Ace
If 5 cards are drawn from a well–shuffled 52–card deck without replacement, find the probability of obtaining at least one ace.
Solution We let E be the event of obtaining at least one ace. Since E consists of all 5–card hands that contain 1, 2, 3, or 4 aces, it is actually easier to consider E'; that is, all 5–card hands that contain no aces. The sample space S consists of all possible 5–card hands. From Section 10.6 we have that n(S) = C(52, 5). Since 48 of the 52 cards are not aces we find n(E’) = C(48, 5). By (4) the probability of drawing 5 cards where none of the cards are aces is given by
From the first formula in (5) the probability of drawing 5 cards where at least one of them is an ace is
Up to this point we have considered the probability of a single event. In the discussion that follows, we examine the probability of two or more events.
Review the notions of the union and intersection of two sets in Section 1.1
Union of Two Events Two events E1 and E2 are said to be mutually exclusive if they have no outcomes, or elements, in common. In other words the events E1 and E2 cannot occur at the same time. In terms of sets, E1 and E2 are disjoint sets; that is, E1 ∩ E2 = Ø. Recall, the set E1 U E2 consists of the elements that are in E1 or in E2. In this case of mutually exclusive events the number of outcomes in the set E1 U E2 is given by
By dividing (7) by n(S) we obtain
In view of (4), the foregoing expression is the same as
In the next example we return to the results in Example 3.
EXAMPLE 8 Mutually Exclusive Events
On a single roll of a fair die, find the probability of obtaining a 4 or an odd number.
Solution From Example 3 the two events are E1 = {4}, E2 = {1, 3, 5}, and the sample space is again S = {1, 2, 3, 4, 5, 6}. The events of rolling a 4 and rolling an odd number are mutually exclusive: E1 ∩ E2 = {4} ∩ {1, 3, 5} = Ø.Thus by (8) the probability P(E1 or E2) of rolling a 4 or an odd number is given by
Alternative Solution From E1 U E2 = {1, 3, 4, 5}, n(E1 U E2) = 4, and so (4) of Definition 10.7.1 yields
The additive property in (8) extends to the probability of three or more mutually exclusive events. See Problems 31 and 32 in Exercises 10.7.
Addition Rule Formula (8) is just a special case of a more general rule. In (8) there were no outcomes in common in the events E1 and E2. Of course, this need not be the case. For example, in the experiment of rolling a single fair die, the events E1 = {1} and E2 = {1, 3, 5 } are not mutually exclusive because the number 1 is an element in both sets. When two sets E1 and E2 have a nonempty intersection, the number of outcomes in n(E1 U E2) is not given by (7) but rather by the formula
See Problem 76 in Exercises 1.1.
Dividing (9) by n(S) yields
The result in (10) is called the addition rule of probability.
EXAMPLE 9 Probability of a Union of Two Events
On a single roll of a fair die, find the probability of obtaining a 1 or an odd number.
Solution The sets are E1 = {1}, E2 = {1, 3, 5}, and S = {1, 2, 3, 4, 5, 6}. Now {1} ∩ {1, 3, 5} = {1} so that n(E1 ∩ E2) = 1.Thus by (10) the probability of rolling a 1 or an odd number is given by
Alternative Solution Since E1 is a subset of E2, E1 U E2 = E2 = {1, 3, 5}, and n(E1 U E2) = 3. From (4) of Definition 10.7.1,
It might help if you think of the symbols P(E1 U E2) and P(E1 ∩ E2) in (10) as P(E1 or E2) and P(E1 and E2), respectively.
Note
EXAMPLE 10 Probability of a Union of Two Events
A single card is drawn from a well–shuffled standard deck. Find the probability of obtaining either an ace or a heart.
Solution As shown in the photo to the left, a standard deck contains 52 cards divided into 4 suits with 13 cards in each suit. Thus the sample space S of this experiment consists of the 52 cards. The event E1 of drawing an ace consists of the 4 aces and so the probability of drawing an ace is 
. The event E2 of drawing a card that is a heart consists of the 13 hearts in that suit and so the probability of drawing a heart is 
. Since one of the hearts is an ace 
Therefore, from (10)
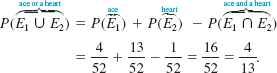
52–card deck in Example 10
In Problems 1–4, use set notation to write the sample space S of the given experiment.
Two coins are tossed.
Three coins are tossed.
A die is rolled and then a coin is tossed.
Two dice are rolled.
In Problems 5–12, find the probability of the given event.
Drawing a face card (jack, queen, or king) from a deck of 52 cards
Drawing a heart from a deck of 52 cards
Rolling a 2 with a single die
Rolling a number less than 3 with a single die
Rolling snake eyes (a total of 2) with two dice
Rolling a total of 7 or 11 with two dice
Obtaining all heads when 3 coins are tossed
Obtaining exactly 1 head when 3 coins are tossed
In Problems 13–16, find the probability of obtaining the indicated hand by drawing 5 cards without replacement from a well–shuffled 52–card deck.
Four of a kind (such as 4 aces)
A straight (5 cards in sequence, such as 4, 5, 6, 7, 8, where an ace can count as a 1 or an ace)
A flush (5 cards, all of the same suit)
A royal flush (10, jack, queen, king, and ace, all of the same suit)
In Problems 17–20, use the first formula in (5) to find the probability of the given event.
Obtaining at least 1 heart if 5 cards are drawn without replacement from a 52–card deck
Obtaining at least 1 face card if 5 cards are drawn without replacement from a 52–card deck
Obtaining at least 1 head in 10 tosses of a coin
Obtaining at least one 6 when 3 dice are rolled
Miscellaneous Applications
Family Planning Assume that the probability of having a girl equals the probability of having a boy. Find the probability that a family with 4 children has at least 1 girl.
Thank You! OOPS! After Joshua writes personalized thank–you notes to each of his 3 aunts for their birthday gifts, his sister randomly inserts them into pread– dressed envelopes. Find the probability that (a) each aunt receives the correct thank–you note,(b) at least one aunt receives the correct thank–you note.
Now Hiring Five male and eight female applicants are found to be qualified for 3 identical positions as bank tellers. If 3 of the applicants are selected at random, find the probability that
(a) only women are hired, (b) at least one woman is hired.
Forming a Committee A committee of 6 people is to be chosen at random from a group of 4 administrators, 7 faculty members, and 8 staff members. Find the probability that all 4 administrators and no faculty members are on the committee.
Just Guessing On a 10–question true–false examination, find the probability of scoring 100% if a student guesses the answer for each question.
Got Caramel? In a box of 20 chocolates of the same shape and appearance, 10 are known to have caramel centers. Four chocolates are selected at random from the box. Find the probability that all four will have caramel centers.
In Problems 27–30, proceed as in Example 8 to find the indicated probability.
A Natural In the dice game of “craps,” a player rolls 2 dice and wins on the first roll if a total of 7 or 11 is obtained. Find the probability of winning on the first roll.
Black or Red A drawer contains 8 black socks, 4 white socks, and 2 red socks. If 1 sock is drawn at random, find the probability that it is either black or red.
You Want to Bet? At the beginning of the baseball season, an oddsmaker estimates that the probability of the Dodgers winning the World Series is 
, and the probability of the Mets winning is 
. On the basis of these probabilities determine the probability that either the Dodgers or the Mets will win the World Series.
Trying for a Good Grade A student estimates that his probability of earning an A in a certain math course is 
. What is the probability that he earns either an A or a B?
Rolling Dice Two dice are rolled. Find the probability that the total showing on the dice is at most 4.
Tossing a Coin A coin is tossed 5 times. Let E1 be the event of obtaining 3 tails, E2 be the event of obtaining 4 tails, and E3 be the event of obtaining 5 tails. Intuitively, which of the following probabilities
(a) P(E1 or E2) (b) P(E2 or E3) (c) P(E1 or E2or E3)
is the least number? Now compute each probability in parts (a)–(c).
Raindrops Keep Falling According to the newspaper there is a 40% probability of rain tomorrow. What is the probability that it will not rain tomorrow?
Will She Lose? A tennis player believes that she has a 75% chance of winning a tournament. Assuming ties are played off, what does she think the probability of losing is?
In Problems 35 and 36, proceed as in Example 10 to find the indicated probability.
More Rolling Dice Two dice are rolled. Find the probability that the total showing on the dice is either an even number or a multiple of 3.
Choosing at Random At ABC Plumbing and Heating Company, 30% of the workers are female, 70% are plumbers, and 40% of the workers are female plumbers. If a worker is chosen at random, find the probability that the worker is either female or a plumber.
For DiscussionA 12–sided die can be constructed in the form of a regular dodecahedron; each face of the die is a regular pentagon. See FIGURE 10.7.1. When rolled, one of the pentagonal faces will be horizontal to a table top. If each of the numbers from 1 to 6 appears twice on the die, show that the probability of each outcome is the same as that for an ordinary 6–sided die.
Suppose a die is a 12–sided regular dodecahedron as in Problem 37, where each face of the die is a regular pentagon. But in this case, suppose that each face bears one of the numbers 1, 2,…, 12 as shown in FIGURE 10.7.2.
If two such dice are rolled, what is the probability of obtaining a total of 13?
A total of 8?
A total of 23?
What number total is least likely to appear?
FIGURE 10.7.1 12–sided die in Problem 37
FIGURE 10.7.2 12–sided die in Problem 38
For the spinner shown in FIGURE 10.7.3, let S be the sample space for a single spin of the spinner. Let B and R be the events that the pointer lands on blue and red, respectively, so that S = {B, R}. What, if anything, is wrong with the computation 
for the probability of the pointer landing on blue?
Project
The Birthday Problem Find the probability that in a group of n people at least 2 people have the same birthday. Assume that a year has 365 days. Consider the three cases (a) n = 10, (b) n = 25, (c) n = 90.
FIGURE 10.7.3 Spinner in Problem 39
Same birthday
A. True/False__________________________________________________
In Problems 1–12, answer true or false.
2(8!) = 16! ____
= 10____
(n – 1)!n = n!
210 < 10! ____
There is no constant term in the expansion of 
There are exactly 100 terms in the expansion of (a + b)100.____
A sequence that is defined recursively by is a geometric an+1 = (–1)an is a geometric sequence. ____
{In 5n}is an arithmetic sequence.____
= In 120____
1 = 0.999…____
0! = 1 ____
P(n, n) = n! ____
B. Fill in the Blanks_____________________________________________
In Problems 1–12, fill in the blanks.
The next three terms in the arithmetic sequence 2x + 1, 2x + 4, are…are ________
The fifth term of the sequence 
is________
The twentieth term of the arithmetic sequence –2, 3, 8,…is _________.
The common ratio r of the geometric sequence 
If E1 and E2 are mutually exclusive events such that 
then P(E1 U E2) = _________.
_________
C. Review Exercises
In Problems 1–4, list the first five terms of the given sequence.
{6 – 3(n – 1)}
{ – 5 + 4n}
{(–1)n n}
List the first five terms of the sequence defined by a1 = 1, a2 = 3, and an = (n + 1)an–1 + 2.
Find the seventeenth term of the arithmetic sequence with first term 3 and third term 11.
Find the first term of the geometric sequence with third term 
and fourth term 1.
Find the sum of the first 30 terms of the sequence defined by a1 = 4 and an + 1 = an + 3.
Find the sum of the first 10 terms of the geometric series with first term 2 and common ratio
Write 2.515151…as an infinite geometric series and express the sum as a quotient of integers.
Best Gift Determine the best gift from the following choices:
A: $10 each month for 10 years.
B: 10¢ the first month, 20¢ the second month, 30¢ the third month, and so on, receiving an increase of 10¢ each month for 10 years.
C: 1¢ the first month, 2¢ the second month, 4¢ the third month, and so on, doubling the amount received each month for 2 years.
Distance Traveled The Italian astronomer and physicist Galileo Galilei (1564–1642) discovered that the distance a mass moves down an inclined plane in consecutive time intervals is proportional to an odd integer. Therefore, the total distance D that a mass will move down the inclined plane in n seconds is proportional to 1 + 3 + 5 +…+ (2n – 1).Show that D is proportional to n2.
Annuity If an annual rate of interest r is compounded continuously, then the amount S accrued in an annuity immediately after the n th deposit of P dollars is given by
Show that
Number of Sales In 2009 a new high–tech firm projects that its sales will double each year for the next 5 years. If its sales in 2009 are $1,000,000, what does it expect its sales to be in 2014?
In Problems 15–20, use the Principle of Mathematical Induction to prove that the given statement is true for every positive integer n.
n2(n + 1)2 is divisible by 4
9 is a factor of 10n + 1 – 9n – 10
In Problems 21–26, evaluate the given expression.
C(7,2)
P(9,6)
In Problems 27–30, use the Binomial Theorem to expand the given expression.
(a + 4b)4
(2y – 1)6
(x2 – y)5
(4 – (a + b))3
In Problems 31–34, find the indicated term in the expansion of the given expression.
Fourth term of (5a – b3)8
Tenth term of (8y2 – 2x)11
Fifth term of (xy2 + z3)10
A multiple of x2 occurs as which term in the expansion of 
Solve for x:
If the first term of an infinite geometric series is 10 and the sum of the series is 
then what is the value of the common ratio r?
Consider the sequence {an} whose first four terms are
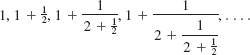
(a) With a1 = 1, find a recursion formula that defines the sequence.
(b) What are the fifth and sixth terms of the sequence?
In Problems 39 and 40, conjecture whether the given sequence converges.
If a coin is tossed 3 times, use a tree diagram to find all possible sequences of heads (H) and tails (T).
List all possible 3–digit numbers using only the digits 2, 4, 6, and 8.
Ice Cream If 32 different flavors of ice cream are available, in how many ways can a double scoop cone be ordered
(a) if both scoops must be different flavors?
(b) if both scoops must be the same flavor?
[Hint: Assume that the order in which the scoops are placed on the cone does not matter.]
More Ice Cream At a dessert bar there are 3 flavors of ice cream, 6 different toppings, 2 kinds of nuts, and whipped cream. How many different sundaes can be made consisting of 1 flavor of ice cream with 1 topping
if nuts and whipped cream are required?
if nuts are optional, but whipped cream is required?
if both nuts and whipped cream are optional?
Build Your Own Domingo's Pizza offers 10 extra toppings. How many different pizzas can be made using just 3 of the toppings?
Arrangements In how many ways can 8 books be arranged on a shelf?
Rearrangements In making up a scrambled word puzzle, how many rearrangements of the letters in the word shower are possible?
Time to Plant Burtee's seed catalog offers 9 varieties of tomatoes. In how many ways can a gardener choose 3 to order?
Modeling There are 10 casual and 12 formal outfits to be modeled one at a time in a fashion show. In how many different orders can they be shown
(a) if all the casual outfits are grouped together and all the formal outfits are grouped together?
(b) if there are no restrictions on the order?
At the Races In how many ways can win, place, and show (that is, first-, second-, and third-place finish, respectively) be decided if 10 horses are entered in a race? Assume that there are no ties.
In Problems 51 and 52, use set notation to write the sample space of the given experiment.
The spinner in FIGURE IO.R.I is spun twice.
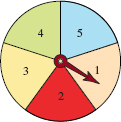
FIGURE 10.R.1 Spinner in Problems 51 and 52
The spinner in Figure 10.R.1 is spun once and then a coin is tossed.
Drawing Cards If 2 cards are drawn from a well–shuffled 52–card deck, what is the probability that both are black?
Choosing a Pen Five pens are selected at random from a batch of 100 Pic pens. If 90% of this batch of Pic pens will write the first time, what is the probability that
all 5 of the pens selected will write the first time?
none of them will write the first time?
at least 1 of them will write the first time?
Family Planning Assume that the probability of giving birth to a female baby equals the probability of giving birth to a male baby. In a family of 4 children, which is more likely: (i) all the same sex, (ii) 2 of each sex, (iii) 3 of one sex and 1 of the other?
Average Young Woman Statistics indicate that the probability of death in the next year for a 20-year-old female is 0.0006. What is the probability that an “average” 20-year-old female will live through the next year?
Feeling Lucky? A drawer contains 8 black socks and 4 white socks. If 2 socks are drawn at random, what is the probability that
(a) a black pair is obtained?
(b) a white pair is obtained?
(c) a matching pair is obtained?
Bingo A Bingo card has 5 rows and 5 columns. See Figure 10.R.2. Any five of the numbers 1 through 15 appear in the first column (designated B); any five of the numbers 16 through 30 appear in the second column (I); any four of 31 through 45 appear in the third column (N), where the center square marked “FREE” is found; any five of 46 through 60 appear in the fourth column (G); and any five of 61 through 75 appear in the last column (O). How many different Bingo cards are possible? (Consider 2 cards to be different if any 2 corresponding entries are different.)
FIGURE 10.R.2 Bingo card in Problem 58
More Bingo One version of Bingo requires a player to cover all the numbers on the card as numbers are called out at random. See Problem 58.
(a) What is the minimum number of calls before there can be a winner in this version?
(b) Assume that there is a winner at the minimum number of calls obtained in part (a). What is the probability that the card being played is a winning card at that point?
Areas Let {An} be the sequence of areas of the isosceles triangles shown in Figure 10.R.3. Find the sum of the infinite series A1 + A2 + A3 +….
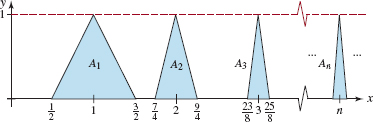
FIGURE 10.R.3 Isosceles triangles in Problem 60