1 Review of Basic Algebra

In This Chapter

1.1 The Real Number System

2.1 The Real Number Line

3.1 Integer Exponents

4.1 Radicals

5.1 Rational Exponents

6.1 Polynomials and Special Products

8.1 Factoring Polynomials

9.1 Rational Expressions

Chapter 1 Review Exercises

If you wish, you can wait until Chapter 10 to find the value of this fraction.

A Bit of History Most students do not realize that much of the algebraic notation used in algebra textbooks is less than 400 years old.

The greatest French mathematician of the sixteenth century was François Viète (1540-1603), a lawyer and a member of Parliament, who devoted most of his leisure time to mathematics. He wrote a number of works on algebra, geometry, and trigonometry, most of which were printed and distributed at his own expense. Viète's most famous work, In Artem, significantly advanced algebraic notation. Before Viète's work, it was common practice to use different symbols to represent various powers such as x, x², x³, and so on. Viète, writing in Latin, used the same letter properly qualified for these powers: x, x quadratum, x cubum, and so on. In addition, Viète expanded the use of letters of the alphabet to denote not only variables but also constant coefficients. Viète's new notation clarified the operations that went into building up a complex series of terms.

Chapter 1 provides a review of fundamental concepts such as set theory, the real number system, and algebraic notation. This material forms the foundation for the remainder of the text and for any further study of mathematics.

1.1 The Real Number System

Introduction The theory of sets enables us to describe in a very precise way collections of numbers that share a common property. This can be very useful in stating the solutions to certain types of problems. You are no doubt already familiar with most of the following concepts from basic set theory. In this review section we focus on the set of real numbers.

Set Terminology A set is a collection of distinct objects. An object in a set is called an element of the set. We usually designate a set by a capital letter, such as A or B, and an element of the set by a lowercase letter, such as x. To indicate that x is an element of a set A, we write x A.

A set can be specified in two ways: by listing the elements in the set or by stating a property that determines the elements in the set. In each case, braces { } are used. For example, the set consisting of the numbers 5, 10, and 15 can be denoted by either

The first notation in (1), where the elements of the set are listed, is called the roster method. The second notation in (1) is called set-builder notation, and in this case, is read “the set of all numbers x such that x = 5n, where n = 1, 2, 3.”

If every element of a set B is also an element of set A, we say that B is a subset of A and write

It follows that every set is a subset of itself.

A set containing no elements is said to be empty and is denoted by the symbol .

The union of two sets A and B is the set of elements belonging to at least one of the sets A or B. In set notation, we write

The intersection of two sets A and B is the set of elements common to both sets A and B and is written as

If A and B have no common elements, that is, if A ∩ B = , then the sets are said to disjoint.

EXAMPLE 1 Union and Intersection

If A = {1, 2, 3, 4, 5}, B = {1, 3, 5}, C = {2, 4, 6}, then we have B A because the numbers 1, 3, and 5 are elements in A. Also,

and

Numbers Recall that the set of natural numbers, or positive integers, consists of

The set N is a subset of the set of integers:

The three dots (…) in the sets N and Z are called an ellipsis and indicate that the elements follow indefinitely the same pattern as that set by the elements given. The set Z includes both the positive and the negative integers and the number 0, which is neither positive nor negative. The set Z of integers is, in turn, a subset of the set of rational numbers:

The set Q consists of all numbers that are quotients of two integers, provided that the denominator is nonzero; for example,

The quotient p/q is said to be undefined whenever q = 0. For example, 8/0 and 0/0 are undefined.

FIGURE 1.1 Unit square

The set of rational numbers is not sufficient to solve certain elementary algebraic and geometric problems. For example, there is no rational number p/q for which

See Problem 69 in Exercises 1.1. Thus we cannot use rational numbers to describe the length of a diagonal of a unit square. See FIGURE 1.1.1. By the Pythagorean theorem, we know that the length of the diagonal d must satisfy

We write d = √2and call d “the square root of 2.” As we have just indicated,√2is not a rational number. It belongs instead to the set of irrational numbers, that is, the set of numbers that cannot be expressed as a quotient of two integers. Other examples of irrational numbers are

If we denote the set of irrational numbers by the symbol H, then the set of real numbers R can be written as the union of two disjoint sets:

We also note that the set of real numbers R can be written as the union of three disjoint sets:R = R ^-{O}R ⁺, where R ^-is the set of negative real numbers and R⁺ is the set of positive real numbers. Elements of the set{0} R⁺ are called nonnegative real numbers.

The chart in FIGURE 1.1.2 summarizes the relationship between some principal sets of real numbers.

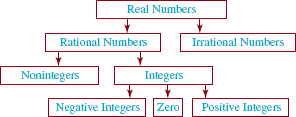
FIGURE 1.1.2 Real numbers are either rational or irrational

Decimals Every real number can be written in decimal form. For example,

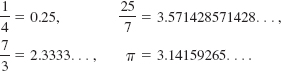
Numbers such as 0.25 and 1.6 are said to be terminating decimals, whereas numbers such as

The number π is a nonterminating and nonrepeating decimal

are called repeating decimals. A repeating decimal, such as 1.323232., is often written as , where the bar indicates the number or numbers that repeat. It can be shown that every rational number has either a repeating or a terminating decimal representation. Conversely, every repeating or terminating decimal is a rational number. Thus the two numbers in (2) are rational. It is also a basic fact that every decimal number is a real number. It follows, then, that the set of irrational numbers consists of all decimals that neither terminate nor repeat. Thus π and √2 have nonrepeating and nonterminating decimal representations.

The Real Number System The set R ofreal numbers together with the operations of addition and multiplication is called the real number system. The basic rules of algebra for this system enable us to express mathematical facts in simple, concise forms and to solve equations to find answers to mathematical questions. The basic properties of the real number system with respect to the operations of addition (denoted by +) and multiplication (denoted by • or ×) are given next. In each list the letters a, b, and c denote real numbers.

In property 4(i) the number 0 is called the additive identity of the real number system; in property 4(ii) the number 1 is called the multiplicative identity of the real number system. In property 5(i), the number -a is called the additive inverse, or the negative, of the number a. Every real number has an additive inverse, but in property 5(ii) every nonzero number a has a multiplicative inverse 1/a, a ≠ 0. The multiplicative inverse of the nonzero number a is also called the reciprocal of a.

EXAMPLE 2 Inverses

The distributive property of real numbers combines the two operations of addition and multiplication. As a matter of course, the product a • b of two real numbers a and b is usually written without the multiplication dot, that is, as ab.

The distributive property can be extended to include more than two numbers in the sum. For example,

and

EXAMPLE 3 Recognizing the Properties

State one basic algebraic property of the real number system to justify each of the following statements, where x, y, and z represent real numbers.

Solution

It is possible to define the operations of subtraction and division in terms of addition and multiplication, respectively.

In the quotient a/b, a is called the numerator and b is called the denominator. Frequently, the quotient of two real numbers a/b is called a fraction. Note that a ÷ b or a/b is not defined when b = 0. Thus a/0 is not defined for any real number a. As the following example shows, not all the properties that hold for addition and multiplication are valid for subtraction and division.

EXAMPLE 4 Subtraction is Not Associative

Since 1 - (2 - 3) = 2 and (1 - 2) - 3 = -4, we see that

1 - (2 - 3) ≠ (1 - 2) - 3.

Thus the operation of subtraction is not associative.

Many additional properties of the real numbers can be derived from the basic properties. The following properties will also be used throughout this text.

As we will see in Chapter 1, property 8(ii) is extremely important in solving certain kinds of equations. For example, if x(x + 1) = 0, then we can conclude that either x = 0 or x + 1 = 0.

EXAMPLE 5 Cancellation

EXAMPLE 6 Simplify

Simplify-(4+x-y)

Solution In view of property 10(iii) we can write

-(4 + x - y) = (-1)(4 + x - y).

Then by the distributive law, property 6(i),

You should already be familiar with the following list of properties of fractions a/b and c/d, where b ≠ 0 and d ≠ 0.

EXAMPLE 7 Example 2(a) Revisited

The multiplicative inverse, or reciprocal, ofsince

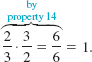
EXAMPLE 8 Products and Quotients

Evaluate each of the following expressions.

(a)(-x)(-y)

(b)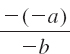

(c)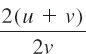

(d)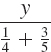

(e)

(f)

Solution

(a)

(b)

(c)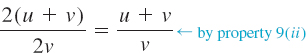

(d) To evaluate y/(1/4 + 3/5), we first evaluate the denominator:

Then we have

(e)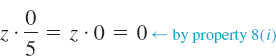

(f) The expression w/[2 - (5 - 3)] is undefined, because its denominator is zero; that is, 2 - (5 - 3) = 2 - 2 = 0. See property 16(ii).

NOTES FROM THE CLASSROOM

In the solution of part (c) of Example 8, a common mistake (seen too often on students' homework and tests) is to cancel the v's in the numerator and denominator:

No further cancellation can be performed in the simplification of, since v is not a multiplicative factor of both the numerator and the denominator as required by the cancellation property 9(ii).

1.1 Exercises Answers to selected odd-numbered problems begin on page ANS-1.

In Problems 1-8, find the indicated set if A = {1, 4, 6, 8, 10, 15}, B = {3, 9, 11, 12, 14}, and C = {1, 2, 5, 7, 8, 13, 14}.

1. A B

2. A C

3. B C

4. A ∩ B

5. A ∩ C

6. B ∩ C

7. (A ∩ B) B

8. A (B C)

In Problems 9-12, list the elements of the given set.

9. {r|r = p|q, p = 1, 2,q = -1, 1}

10. {t|t = 4 + z, z = -1,-3,-5}

11.

12. {yy - 5 = 2}

In Problems 13-16, use set notation to express the given set.

13. The set of negative integers greater than -3

14. The set of real numbers whose square is 9

15. The set of even integers

16. The set of odd integers

In Problems 17-32, state one of the basic properties of the real number system (properties 1-6) to justify each of the given statements.

17. (2 + 3) + 5 = 2 + (3 + 5)

18. [(1)(2)](3) = [(2)(1)](3)

19. (x + y) + 3 = (y + x) + 3

20. (a + 2) + π = π + (a+ 2)

21.

22. (1 + 2)(-3) = 1(-3) + 2(-3)

23. 1 √ (√2) = √2

24. (3 + 4)(5 + 2) = (3 + 4)5 + (3 + 4)2

25.

26.

27. x(y + 0) + z = xy + z

28. {3 + [(-5)(1)]} + 4 = {3 + (-5)} +4

29. [(w + 3)2]z = [2(w + 3)]z

30. (-13 + z)(2) 17 = [z + (-13)](2) + 7

31. (a - b) + [-(a - b)] = 0

32.

In Problems 33-44, state one of the additional properties of the real number system (properties 7-16) to justify each of the given statements.

33. (-5)(-x) = 5x

34. -(-17) = 17

35. If x + 3 = y + 3, then x = y.

36. If y +z = 5 + z, then y = 5.

37. If (x + 2)(3) = 4(3), then x + 2 = 4.

38. If z² = 0, then z = 0.

39. If (x + 1)(x - 2) = 0, then x + 1 = 0 or x - 2 = 0.

40. (a +b +c) · 0 = 0

41.

42.

43.

44.

In Problems 45-50, simplify the given expression.

45. -(-a)[2 - 3]

46.

47.

48.

49.

50. (π - π)(x + y - 3)

The Rhind papyrus

Miscellaneous Applications

51. Old Math The Rhind papyrus (c. 1650 BCE), purchased by the Scottish Egyptologist Alexander Henry Rhind in 1858, is considered one of the best examples of Egyptian mathematics. In it the Egyptians used as the value of π.

(a) Is this approximation greater than or less than π?

(b) Show that the error in using this pproximation is less than 1% of π.

52. Bible Study Using the fact that the circumference of a circle is π times the diameter, determine what value of π is implied from the following biblical quotation. “Also he made the molten sea of ten cubits from brim to brim, round in compass, and the height thereof was five cubits; and a line of thirty cubits did compass it round about.” (This is taken from II Chronicles 4:2 and I Kings 7:23, which date from the tenth century BCE)

For Discussion

For Problems 53-68, answer true or false.

53. is an element of Z.___

54. is an element of Q.___

55. √3 is an element of R.___

56. √2 is a rational number.___

57. 0.1333…is an irrational number.___

58. 1.5 is a rational number.___

59. 0.121212…is a rational number.___

60. is an element of Q.___

61. -4 is an element of Z, but -4 is not an element of N.___

62. π is an element of R, but π is not an element of Q.___

63. Every irrational number is a real number.___

64. Every integer is a rational number.___

65. Every decimal number is a real number.___

66. The intersection of the set of rational numbers and the set of irrational numbers is the empty set.___

67. If c ≠ 0, then (a + b) ÷ c = (a ÷ c) + (b ÷ c).___

68. If a≠ 0,b ≠ 0, and a + b ≠ 0, then c ÷ (a + b) = (c ÷a) + (c ÷ b).___

69. Show that √2 cannot be written as a quotient of integers.[Hint: Assume that there is a fraction p/q, reduced to lowest terms, such that (p/q)² = 2. This simplifies to p² = 2q², which implies that p², hence p is an even integer, say p = 2r. Make this substitution and consider (2r/q)² = 2. You should arrive at a contradiction to the fact that p/q was reduced to lowest terms.]

70. Discuss: The sum of an irrational number and a rational number must be irrational. [Hint: If the sum of the two numbers were rational, then it could be written as a quotient of integers p/q. Why does this lead to a contradiction?]

71. Discuss: Is the sum of two irrational numbers necessarily irrational?

72. Discuss: Is the product of two irrational numbers necessarily irrational?

73. Discuss: Is the quotient of two irrational numbers necessarily irrational?

74. In general,a + (-b) ≠ b + (-a). What does this say about the operation of subtraction?

75. Some secret codes work by shifting letters of the alphabet. FIGURE 1.1.3 shows a shift of 2. Each letter in a message can be represented by the digits in a decimal number. For example, the decimal number 0.12121212…codes the message STUDY MATH into TVVFZ OBVI. If using 9/37 produces the coded message RCWJEJQVDU PLXIV, what was the original message?

76. Suppose that the sets A and B have a finite number of elements. Let n(A) and n(A) denote the number of elements in sets A and B, respectively. Discuss why the formula n(A B) =n(A) +n(B) - n(A ∩B) gives the number of elements in the union A B.

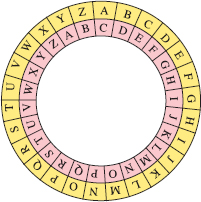
FIGURE 1.1.3 Code wheel in Problem 75

1.2 The Real Number Line

Introduction For any two distinct real numbers a and b, there is always a third real number between them; for example, their average (a + b)/2 is midway between them. Similarly, for any two distinct points A and B on a straight line, there is always a third point between them; for example, the midpoint M of the line segment AB. There are many such similarities between the set R of real numbers and the set of points on a straight line that suggest using a line to “picture” the set of real numbers R = R^- {0} R⁺.This can be done as follows.

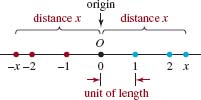
Real Number Line Given any straight line, we choose a point O on the line to represent the number 0. This particular point is called the origin. If we now select a line segment of unit length as shown in FIGURE 1.2.1, each positive real number x can be represented by the point at a distance x to the right of the origin. Similarly, each negative real number -x can be represented by the point at a distance x to the left of the origin. This association results in a one-to-one correspondence between the set R of real numbers and the set of points on a straight line, called the real number line. For any given point P on the number line, the number p, which corresponds to this point, is called the coordinate of P. Thus the set R^- of negative real numbers consists of the coordinates of points to the left of the origin, the set R⁺ of negative real numbers consists of the coordinates of points to the right of the origin; the number 0 is the coordinate of the origin O. See FIGURE 1.2.2.

Number line

FIGURE 1.2.2 Positive and negative directions on the number line

In general, we will not distinguish between a point on the number line and its coordinate. Thus, for example, we will sometimes refer to the point on the real number line with coordinate 5 as “the point 5.”

Less Than and Greater Than Two real numbers a and b,a ≠ b, can be compared by the order relation less than. We have the following definition.

If a is less than b, then equivalently we can say that b is greater thana and write b > a. For example, -7 < 5, because 5 - (- 7) = 12 is positive. Alternatively, we can write 5 > - 7.

EXAMPLE 1 An Inequality

Using the order relation greater than, compare the real numbers π and

Solution From π = 3.1415…and = 3.1428…, we find that - π = (3.1428…) - (3.1415…) = 0.001….

Since this difference is positive, we conclude that > π.

FIGURE 1.2.3 The number a is to the left of the number b

Inequalities The number line is useful in demonstrating order relations between two real numbers a and b. As shown in FIGURE 1.2.3, we say that the number a is less than the number b, and write a < b, whenever the number a lies to the left of the number b on the number line. Equivalently, because the number b lies to the right of a on the number line we say that b is greater thana and write b > a. For example, 4 < 9 is the same as 9 > 4. We also use the notation a ≤ b if the number a is less than or equal to the number b. Similarly,b ≥ a means b is greater than or equal toa. For example, 2 ≤ 5 since 2 < 5. Also, 4 ≥ 4 because 4 = 4.

For any two real numbers a and b, exactly one of the following is true:

The property given in (1) is called the trichotomy law.

Terminology The symbols <,>, ≤, and ≥ are called inequality symbols and expressions such as a <b or b ≥a are called inequalities. An inequality a < b is often called a strict inequality, whereas an inequality such as b ≥ a is called a non- strict inequality. The inequality a > 0 means the number a lies to the right of the number 0 on the number line and so a is positive. We signify that a number a is negative by the inequality a < 0. Because the inequality a ≥ 0 means a is either greater than 0 (positive) or equal to 0 (which is neither positive nor negative), we say that a is non- negative. Similarly, if a ≤ 0, we say that a is nonpositive.

Inequalities also have the following transitivity property.

For example, if x < 12 and 12 < y, we conclude from the transitivity property that x < y. Theorem 1.2.1 can easily be visualized on the number line by placing a anywhere on the line,b to the right of a, and the number c to the right of b.

FIGURE 1.2.4 Distance on the number line

FIGURE 1.2.5 The distance from 0 to x is x; the distance from 0 to y is -y

Absolute Value We can also use the real number line to picture distance. As shown in FIGURE 1.2.4, the distance from the point 3 to the origin is 3 units, and the distance from the point - 3 to the origin is 3, or - (-3), units. It follows from our discussion of the number line that, in general, the distance from any number to the origin is the “unsigned value” of that number.

More precisely, as shown in FIGURE 1.2.5, for any positive real number x, the distance from the point x to the origin is x, but for any negative number y, the distance from the point y to the origin is -y. Of course, for x = 0, the distance to the origin is 0. The concept of the distance from a point on the number line to the origin is described by the notion of the absolute value of a real number.

EXAMPLE 2 Absolute Values

Since 3 and √2 are positive numbers,

|3| = 3 and | √2| = √2.

But since -3and -√2are negative numbers; that is, -3 < 0 and -√2 < 0, we see from (2) that

|-3| = -(-3) = 3 |-√2| = - (-√2) = √2.

EXAMPLE 3 Absolute Values

EXAMPLE 4 Absolute Value

Find | √2 - 3|.

Solution To find | √2 - 3|, we must determine first whether the number √2 - 3 is positive or negative. Since √2 ≈ 1.4, we see that √2 - 3 is a negative number.

Thus,

It is a common mistake to think that -y represents a negative number because the symbol y is preceded by a minus sign. We emphasize that if y represents a negative number, then the negative of y, that is, -y, is a positive number. Hence, if y is negative, then |y| = -y.

EXAMPLE 5 Value of an Absolute Value Expression

Find |x - 6| if (a)x> 6, (b)x = 6, and (c)x < 6.

Solution

(a) If x> 6, then x - 6 is positive. Then from the definition of absolute value in (2), we conclude that|x - 6| =x - 6.

(b) If x = 6, then x - 6 = 0;hence |x - 6| = |0| = 0.

(c) If x < 6, then x - 6 is negative and we have that |x - 6| = - (x - 6) = 6 - x.

For any real number x and its negative, -x, the distance to the origin is the same. That is,|x| = |-x|. This is one of several special properties of the absolute value, which we list in the following theorem.

Restating these properties in words is one way of increasing your understanding of them. For example, property (i) states that the absolute value of a quantity is always non- negative. Property (iv) says that the absolute value of a product equals the product of the absolute values of the two factors. Part (vi) of Theorem 1.2.2 is an important property and is called the triangle inequality.

FIGURE 1.2.6 Distance on the number line

Distance Between Points The concept of absolute value not only describes the distance from a point to the origin. It is also useful in finding the distance between two points on the number line. Since we want to describe distance as a positive quantity, we subtract one coordinate from the other and then take the absolute value of the difference. See FIGURE 1.2.6.

EXAMPLE 6 Distances

(a) The distance from -5 to 2 is

d(-5, 2) = 2 - (-5) = 7 = 7.

(b) The distance from 3 to √2 is

d(3, √2) = |√2 -3| = 3 - √2. ← see Example⁴

We see that the distance from a to b is the same as the distance from b to a, since by (iii) of Theorem 1.2.2,

d(a, b) = |b - a| = |-(b - a)| = |a - b| = d(b, a). ← b aplays the part of x in (iii) of Theorem 1.2.2.

Thus,d(a, b) = d(b, a).

Coordinate of the Midpoint Definition 1.2.3 can be used to find an expression for the midpoint of a line segment. The midpoint m of the line segment joining a and b is the average of the two endpoints:

FIGURE 1.2.7 Distance from a to m equals the distance from m to b

See FIGURE 1.2.7.

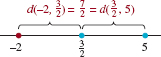
FIGURE 1.2.8 Midpoint in Example 7

EXAMPLE 7 Midpoint

From (4), the midpoint of the line segment joining the points 5 and -2 is

See FIGURE 1.2.8.

EXAMPLE 8 Given the Midpoint

The line segment joining a to b has midpoint m = 4. If the distance from a to b is 7, find a and b.

Solution As we can see in FIGURE 1.2.9, since m is the midpoint,

i = d(a, m) = d(m, b).

Thus, 2j = 7 or j = We now have a = 4 - = and b = 4 + = .

FIGURE 1.2.9 Distances are equal in Example 8

1.2 Exercises Answers to selected odd-numbered problems begin on page ANS-1.

In Problems 1 and 2, construct a number line and locate the given points on it.

1.

2.

In Problems 3-10, write the statement as an inequality.

3. x is positive

4. y is negative

5. x +y is nonnegative

6. a is less than -3

7. b is greater than or equal to 100

8. c- 1 is less than or equal to 5

9. |t- 1| is less than 50

10. | s + 4 | is greater than or equal to 7

In Problems 11-16, compare the pair of numbers using the order relation “less than.”

11. 15, -3

12. -9, 0

13.

14.

15. π, 3.14

16. 1.732, √3

In Problems 17-22, compare the pair of numbers using the order relation “greater than or equal to.”

17. -2, -7

18.

19.

20.

21.

22. √2, 1.414

In Problems 23-44, find the absolute value.

23. |7|

24. |-7|

25. |22|

26.

27.

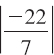
28. |√5|

29. |-√5|

30. |0.13|

31. |π-4|

32. |2-6|

33. |6-2|

34. ||2|-|-6||

35. |-6|-|-2|

36. |√5-3|

37. |3-√5|

38. |8-√7|

39. |√7-8|

40. |-(√7-8)|

41. |√5-2.3|

42.

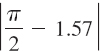
43. |6.28-2π|

44. |√7-4.123|

In Problems 45-56, write the expression without using absolute value symbols.

45. |h|, if h is negative

46. |-h|, if h is negative

47. |x-2|, if x< 2

48. |x-2|, if x = 2

49. |x-2|, if x>2

50. |5-x|, if x < 5

51. |5-x|, if x=5

52. |5-x|, if x>5

53. |x-y|-|y-x|

54.

55.

56.

In Problems 57-64, (a) find the distance between the given points and (b) find the coordinate of the midpoint of the line segment joining the given points.

57. 7,3

58. 2,5

59. 0.6, 0.8

60. -100, 255

61. -5, -8

62. 6, -4.5

63.

64.

In Problems 65-72,m is the midpoint of the line segment joining a (the left endpoint) and b (the right endpoint). Use the given conditions to find the indicated values.

65. m = 5,d(a, m) = 3;a, b

66. m = - 1,d(m, b) = 2;a, b

67. m = 2,d(a, b) = 7;a, b

68. m = √2,d(a, b) = 1;a, b

69. a = 4, d(a, m) = π; b,m

70. a = 10,d(b, m) = 5;b, m

71. b = -3,d(a, b) = √2;a, m

72.

In Problems 73-80, determine which statement from the trichotomy law (a <b, a = b, or a > b) is true for the given pair of numbers a, b.

73. (10)(10), 100

74. √3 - 3, 0

75. π, 3.14

76. |-15 |, 15

77.

78.

79. √2, 1.4

80. - √2, -1.4

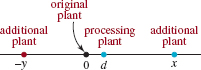
FIGURE 1.2.10 Plants in Problem 82

Miscellaneous Applications

81. How Far? Greg, Tricia, Ethan, and Natalie live on Real Street. Tricia lives a mile from Greg, and Ethan lives one-half mile from Tricia. Natalie lives halfway between Ethan and Tricia. How far does Natalie live from Greg?[Hint: There are two solutions.]

82. Shipping Distance A company that owned one manufacturing plant next to a river bought two additional manufacturing plants, one x miles upstream and the other y miles downstream. Now the company wants to build a processing plant located so that the total shipping distance from the processing plant should be built at the same location as the original manufacturing plant. [Hint: Think of the plants as being located at 0, x, and -y on a number line.] See FIGURE 1.2.10. Using absolute values, find an expression for the total shipping distance if the processing plant is located at point d.

For Discussion

For Problems 83-90, answer true or false for any real number a.

83. a

84. |a| > -1_

85. -|a| ≤ |a|_

86. -a ≤ a_

87. a ≤ |a|_

88. - |a| ≤ a_

89. If x < a and a <z, then x < z_

90. |a + 1| ≤ |a| + 1_

91. For what values of x is it true that x ≤ |x|?

92. For what values of x is it true that x =|x|?

93. Use Definition 1.2.2 to prove that |xy | = |x ||y | for any real numbers x and y.

94. Use Definition 1.2.2 to prove that |x/y| = |x|/|y | for any real number x and any nonzero real number y.

95. Under what conditions does equality hold in the triangle inequality; that is, when is it true that |a + b|= |a| + |b|?

96. Use the triangle inequality to prove |a - b| ≤ |a| + |b|.

97. Use the triangle inequality to prove |a - b| ≥ |a| - |b|.[Hint: a = (a - b) + b.]

98. Prove the midpoint formula (4).

1.3 Integer Exponents

Introduction We find it more convenient to write a repeated sum such as x + x + x + x as 4x. Similarly, we can write a repeated product such as x · x · x more efficiently using exponents. In this section we review the laws of integer exponents. We begin with a definition of “x to the n th power.”

For example, x · x · x = x³. In the case when n= 1 we have x¹ = x.

In the expression xⁿ, n is called the exponent or power of x, and x is called the base.

EXAMPLE 1 Using (1)

(a) 5² = 5 · 5 = 25 ← by (1) of Definition 1.3.1 with x = 5

(b) y³ = y · y · y ←by (1) of Definition 1.3.1 with x replaced by y

(c) (2x)³ = 2x · 2x · 2x = 8x³ ←by (1) of Definition 1.3.1 with xreplaced by 2x

(d) (—3)⁴ = (—3) · (— 3) · (—3) · (— 3) = 81 ←by (1) of Definition 1.3.1 with x = —3

The exponential statement in part (a) of Example 1 is read “5 squared,” whereas in part (b) we say “ y cubed.”

Negative powers of x are defined next.

EXAMPLE 2 Using (2)

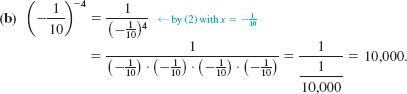
Finally, for any nonzero base x, we define

Thus,

2⁰ = 1 and = 1.

See Problem 93 in Exercises 1.3 for a rationale for the special definition (3). Note that 0⁰ is not defined.

Laws of Exponents Several rules for combining powers, called the laws of exponents, have been established. As an example, consider the product 3² • 3⁴. By counting factors we see that

that is

In general, if x is any number and m and n are positive integers, then

When both m and n are negative, the factors are counted in the same way, although they are in the denominator of the resulting fraction. If m ≥ 0 and n is negative, we let n = -q, where q > 0. Then

After all possible factors have been cancelled, either m – q factors remain in the numerator or q – m factors remain in the denominator. In the first case,

and in the second case,

By a similar argument, x^mxⁿ = x^{m + n} can be verified if m is negative and n ≥ 0.

This and several other formulas involving exponents are listed next.

In the statement of these laws, whenever x or y occurs in a denominator or with a negative exponent, x or y must be nonzero. Also, (iii) of Theorem 1.3.1 extends to more than two variables; for example

(xyzw)ⁿ = xⁿyⁿzⁿwⁿ.

In the following examples, we illustrate each of the laws of exponents.

EXAMPLE 3 Using the Laws of Exponents

(a)

(b)

(c)

(d)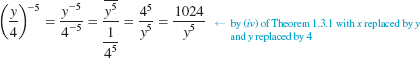

(e)

The laws of exponents are useful in simplifying algebraic expressions, as we see in the following example.

EXAMPLE 4 Using the Laws of Exponents

Simplify

Solution By the laws of exponents, we have

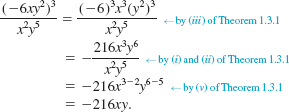
Scientific Notation Integer exponents are frequently used to write very large or very small numbers in a convenient way. Any positive real number can be written in the form

a × 10ⁿ,

where 1 ≤ a < 10 and n is an integer. We say that a number written in this form is in scientific notation. For example,

1,000,000 = 1 × 10⁶ = 10⁶ and 0.0000000537 = 5.37 × 10^-8

Scientific notation is most useful in chemistry and physics, where numbers such as

92,900,000 = 9.29 × 10⁷ and 0.000000000251 = 2.51 X 10^-10

frequently occur. These numbers are the average distance from the Earth to the Sun in miles and the average lifetime of a lambda particle in seconds, respectively. Numbers such as these are certainly easier to write and to remember when given in scientific notation and are easily simplified. This is illustrated in the following example.

EXAMPLE 5 Using Scientific Notation

Find the value of

Solution We write the numbers in scientific notation and use the laws of rational exponents:

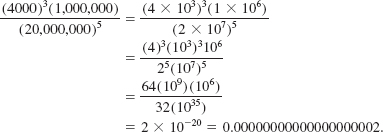
Most calculators automatically convert a number to scientific notation whenever it is too large or too small to be displayed in decimal form. For example, the number 1.234 × 10¹⁵ requires 16 digits for its decimal form, but since few calculators can display more than 10 digits, the multiplication sign and the base 10 are not shown. Therefore the number 1.234 × 10¹⁵ may appear as . On many calculators it is possible to use scientific notation when entering a number. Consult your calculator manual for details.

Significant Digits Most real-world applications of mathematics involve measurements that are subject to error and therefore are considered to be approximations. We can describe the accuracy of an approximation by stating how many significant digits it has.

Suppose that the result of a measurement is expressed in scientific notation

x = a × 10ⁿ, wher 1 ≤ a < 10,

and the digits in a are known to be accurate (except possibly for the last digit, which may be off by one if the number was rounded.) If a contains k decimal places (that is, k digits to the right of the decimal point), then x is said to have k + 1 significant digits. According to this convention, 2.0285 × 10²³ has five significant digits and 9.30 ×10^-20 has three significant digits.

EXAMPLE 6 Length of a Light Year

A light year is the distance traveled by light in one Earth year (365.25 days). The speed of light is 3.00 × 10⁵ kilometers per second (accurate to three significant digits). Find the length of one light year in kilometers. In miles.

Solution To determine the length of one light year in kilometers, we multiply the speed of light in kilometers per second by the number of seconds in an Earth year. We first set up the conversion of one Earth year to seconds:

Then the length of one light year in kilometers is given by

Now 1 km = 6.21 × 10^-1 mi and so the length of a light year in miles is

NOTES FROM THE CLASSROOM

You should get in the habit of taking a little extra time in reading a mathematical expression containing powers of x. For example, the distinction between the quantities 5x³ and (5x)³ is often overlooked in the rush to complete homework or a test. The parentheses indicate that the exponent 3 applies to 5x and not just to x. In other words,

5x³ = 5 × x × x × x

whereas (5x³) 5 5x × 5x × 5x 5 125x³.

Similarly, -3⁴ = -(3 × 3 × 3 × 3) = -81

whereas (-3)⁴ = (-3)(-3)(-3)(-3) = 81.

1.3 Exercises Answers to selected odd-numbered problems begin on page ANS-1.

Assume in Problems 1-86 that all variables are nonzero.

In Problems 1-4, write the expression with positive exponents.

1.

2. 3 × 3 × 3

3. 2y × 2y × 2y × 2y

4.

In Problems 5–8, write the expression with negative exponents.

5.

6.

7.

8.

In Problems 9–14, find the indicated numbers.

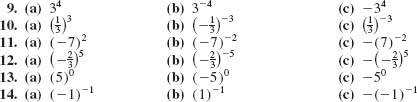
In Problems 15-20, evaluate the expression.

15. 2^-1 - 2¹

16.

17.

18.

19.

20.

In Problems 21–26, find the value of the expression if a = 2, b = -3, and c = -1.

21. -2ab + c²

22. ^{ab2 - c3}

23. ab² + bc² + ca²

24. a^-1 b^-1 c^-1

25. ab^-1 + ca^-1

26. a^-1 + b^-1 + c^-1

In Problems 27–50, simplify and eliminate any negative exponents.

27. x⁶x^-2

28. 2¹⁰2¹²

29. (7x⁴)(-3x²)

30. (-5x²y³)(3xy^-2)

31.

32.

33.

34.

35. (5x)²

36. (-4x)³

37. (5²)³

38. (x⁴)-5

39. (4x²y^-1)³

40. (3x²y⁴)^-2

41. x²x³x^-4

42.

43.

44.

45. (-3xy⁵)²(x³y)^-1

46.

47.

48. (-x²y⁴)³(x³y^-1)²

49.

50.

In Problems 51-56, determine whether the given number is positive or negative.

51. (—4)^—3(2^—4)

52. (—1)^—1(—1)⁰(—1)

53. [10^—5(—10)⁵(—10)^—5]²

54. [(—1)^—2]^—3

55. [— 10 — 10]^—10+10

56. [π²π³π^—4]^—1

In Problems 57-62, write a formula for the given quantity using exponents.

57. The area A of a square is the square of the length s of a side.

58. The volume V of a cube is the cube of the length s of a side.

59. The area A of a circle is π times the square of the radius r.

60. The volume V of a sphere is times the cube of the radius r.

61. The volume V of a right circular cylinder is π times the square of the radius r times the height h.

62. The area A of an equilateral triangle is times the square of the length s of a side.

In Problems 63-66, write the given numbers in scientific notation.

In Problems 67-70, write the given numbers in decimal form.

In Problems 71-76, use a calculator to perform the computation. Write your answer in scientific notation using five significant digits

71. (0.90324)(0.0005432)

72.

73.

74.

75. (2.75 X 10³)(3.0 X 10¹⁰)

76.

In Problems 77-80, find the value of the given expression without the aid of a calculator. Write your answer (a) in decimal form and (b) in scientific notation.

77. (3000)²(200,000)³(0.0000000001)

78. [(1,000,000)^-1(0.00001)]^-1

79.

80.

Miscellaneous Applications

81. Population The estimated population of China for 2009 was 1,335,000,000. Write this number in scientific notation.

82. Population If the average annual growth rate for the population of China is 1.4%, use the information given in Problem 81 to compute the population of China (a) in 2010 and (b) in 2020. Write your answers in scientific notation.

83. GDP The gross domestic product is a basic measure of a country's overall economic output. In October 2009 it was predicted that the GDP for the United States would be 14.261 trillion dollars. Write this number (a) in decimal form and (b) in scientific notation.

84. Of Things to Come Future computers may be photonic (that is, operating on light signals rather than electronic. The speed of light (3 × 10¹⁰ cm/s) will be a limiting factor on the size and speed of such computers. Suppose that a signal must get from one component of a photonic computer to another within 1 nanosecond (1 × 10^-9 s). What is the maximum possible distance between these two components? [Hint. How far does light travel in 1 nanosecond?] State your answer (a) in centimeters and (b) in inches (1 in. ≈ 2.5 cm).

85. Galactic Distance The distance to the Andromeda galaxy (Messier 31), located in the direction of the constellation Andromeda, is 2,500,000 light years from our own Milky Way galaxy. As we have seen in Example 6, a light year is a measure of distance. If a light year is (approximately) 6 million million miles, write the approximate distance (in miles) to the Andromeda galaxy in scientific notation.

Andromeda galaxy

86. Average Speed Pioneer 10, a deep-space probe, took 21 months to travel from Mars to Jupiter. If the distance from Mars to Jupiter is 998 million kilometers, find the average speed of Pioneer 10 in kilometers per hour. (Assume that there are 30.4 days in a month.)

For Discussion

In Problems 87-92, answer true or false.

87. 0⁰ = 0___

88.

89. If n is even, xⁿ ≥ 0 for all real numbers x.___

90. x-ⁿ ≥ 0, for all real numbers x___

91. (x + y)² = x² + y²___

92. (xⁿ)^-1 = x^—n, for x ≠ 0___

93. By (v) of the laws of exponents, if x ≠ 0, then what does xⁿ/xⁿ equal? However, what does any nonzero number divided by itself equal? Use the answer to these two questions to explain the rationale behind the definition x⁰ = 1, for any nonzero base x.

1.4 Radicals

Introduction Many problems in science, business, or engineering lead to statements such as s² = 25 or x³ = 64. The numbers that satisfy these simple exponential equations are called roots. In particular, a number s that satisfies s² = 25 is said to be a square root of 25 and a number x satisfying x³ = 64 is a cube root of 64.

There are two real number square roots of the number 25 because

(—5)² = 25 and 5² = 25.

By convention the symbol √ denotes the principal square root, which is a non- negative real number. Thus, √25 = 5.

In this section we review the definition and the properties of the principal rath roots of a real number x, where n is a positive integer.

To summarize (i), (ii), and (iv) of Definition 1.4.1, the statement

= r means x = rⁿ.

Terminology The symbol “Vx that denotes the principal nth root of x is called a radical, the integer n is the index of the radical, and the real number x is called the radicand. If the index n is 2, it is usually omitted from the radical; that is, is written . When n = 2 we say is the square root of x and when n = 3 we say is the cube root of x. If the index n is an odd positive integer, it can be shown that for any real number x, there is exactly one real nth root of x. For example,

and

If the index n is an even positive integer and x is positive, then there are two real nth roots of x. The symbol , however, is reserved for the positive (principal) nth root; we denote the negative nth root by - . Thus, for example,

and

and

If n is even and x is negative, there is no real n th root of x.^*

EXAMPLE 1 Roots

Find

(a).

(b).

(c).

Solution There will be a single answer in each case since we are finding, in turn, the principal square root, the principal cube root, and the principal fourth root.

(a).

(b).

(c).

The Laws of Radicals The following properties can often be used to simplify expressions involving radicals.

PARTIAL PROOF: The laws of radicals (iii)-(v) can be verified using the laws of exponents discussed in Section 1.3. For example, to prove (iii) we let

Then, by definition

x = aⁿ and y = bⁿ.

Thus, xy = aⁿbⁿ = (ab)ⁿ,

which can be written in radical form as

Combining (1) and (2), we obtain

Each of the foregoing laws is illustrated in the next example. Probably the most familiar property of radicals, the square root of a product is the product of the square roots,

for x ≥ 0, y ≤ 0, is just a special case of (iii) of Theorem 1.4.1 when For example,

EXAMPLE 2 Simplifying Using the Laws of Radicals

Simplify each of the following expressions.

(a).

(b).

(c).

(d).

(e).

Solution In each case we use one or more laws of radicals.

(a).

(b).

(c).

(d).

(e).

EXAMPLE 3 Using the Laws of Radicals

Simplify each of the following expressions.

(a).

(b).

Solution In parts (a) and (b), supply a reason on the colored line above the correspondingly colored equality sign.

(a).

(b).

As we have just seen in Example 2, the laws of radicals in Theorem 1.4.1 allow us to simplify products and quotients of radicals with the same index. We can frequently simplify sums and differences of radicals with the same index by using the distributive laws, as shown in the following example.

EXAMPLE 4 Simplifying

Simplify each of the following expressions.

(a).

(b).

Solution We again use the laws of radicals given in Theorem 1.4.1.

(a).

(b).

Rationalizing When we remove radicals from the numerator or the denominator of a fraction, we say that we are rationalizing. In algebra, we usually rationalize the denominator, but in calculus it is sometimes important to rationalize the numerator. The procedure of rationalizing involves multiplying the fraction by 1 written in a special way. For example,

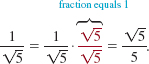
EXAMPLE 5 Rationalizing a Denominator

Rationalize the denominator of each of the following expressions.

(a).

(b).

Solution

(a).

(b). Since we multiply the numerator and the denominator by :

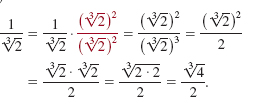
Using a Conjugate Factor If a fraction contains an expression such as we make use of the fact that the product of and its conjugate contains no radicals:

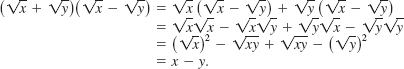
The conjugates of the expressions are, respectively, , and . You should verify that the product of each of these expressions with its conjugate contains no radicals.

EXAMPLE 6 Rationalizing a Denominator

Rationalize the denominator of the expression.

Solution The conjugate of the denominator is . To eliminate radicals from the denominator, we multiply the given expression by

Thus,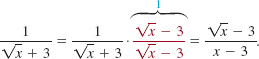

EXAMPLE 7 Rationalizing a Numerator

Eliminate the radicals in the numerator of

Solution Since the conjugate of the numerator is , we proceed as follows:

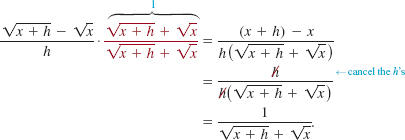
The rationalization of a numerator, as illustrated in Example 7, occurs often in calculus.

Early design of a space station with artificial gravity

EXAMPLE 8 Artificial Gravity

An artificial gravity can be created in a space station (or interplanetary spaceship) by rotating the station like a giant centrifuge. The rotation will produce a force against the astronauts on board that cannot be distinguished from gravity. The rate of rotation N, measured in rotations per second, required to produce an acceleration of a m/s² at a point r meters from the center of rotation is given by

If the radius of the station is 150 m, calculate the rotation rate necessary to produce the equivalent of Earth's gravity.

Solution The acceleration due to gravity on Earth is 9.8 m/s². Therefore, we identify a = 9.8 and r = 150 and obtain

Using the square root and keys on a calculator, we find that N ≈ 0.04. Therefore, approximately 0.04 rotations per second (or, equivalently, 2.4 rotations per minute) are required to produce the equivalent of Earth's gravity.

NOTES FROM THE CLASSROOM

In this note we discuss some common mistakes using radicals and the laws of radicals.

(i) It is a common mistake to simplify as x. This is valid only for nonnegative x. For example, if x = -3, we see that

The correct result is given by (ii) of the laws of radicals:

(ii) In part (b) of Example 5, it would be incorrect to try to rationalize by multiplying the numerator and the denominator by :

1.4 Exercises Answers to selected odd-numbered problems begin on page ANS-1.

Assume in Problems 1-62 that all variables are positive.

In Problems 1-32, evaluate the radical(s).

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

In Problems 33–44, rationalize the denominator of the expression.

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

43.

44.

In Problems 45–48, rationalize the numerator of the expression.

45.

46.

47.

48. [Hint: First combine terms in the numerator.]

In Problems 49–56, combine the radicals and simplify.

49.

50.

51.

52.

53.

54.

55.

56.

In Problems 57–60, write a formula for the given quantity using radical notation.

57. The length s of the side of a square is the square root of the area A.

58. The length s of the side of a cube is the cube root of the volume V.

59. The length c of the hypotenuse of a right triangle is equal to the square root of the sum of the squares of the lengths a and b of the other two sides.

60. The velocity v of a satellite in a circular orbit around the Earth is equal to the square root of the product of the radius r of the orbit and the acceleration due to gravity g_r at the orbit.

Miscellaneous Applications

61. Earth Satellite If a satellite revolves around the Earth in a circular orbit of radius r = 6.70×10⁶ m, find its velocity v if v = , where R is the radius of the Earth and g is the acceleration due to gravity at the Earth's surface. Use the values R = 6.40 × 10⁶ mand g = 9.80 m/s².

62. Relativity According to Einstein's theory of relativity, the mass m of an object moving at velocity v is given by

where m₀ is the mass of the object at rest and c is the speed of light. Find the mass of an electron traveling with velocity 0.6c if its rest mass is 9.1 × 10^-31 kg.

For Discussion

In Problems 63-70, answer true or false.

63.

64.

65. for any real number a ___

66. , for any real number a ___

67. If n is odd, is defined for any real number x. ___

68. If n is even, is defined for any real number x. ___

69. , for any real number x ___

70. , for any real numbers a and b ≠ 0 ___

1.5 Rational Exponents

Introduction The concept of the nth root of a number enables us to extend the definition of xⁿ from integer exponents to rational exponents. And, as we will see, it is often easier to work with rational exponents than with radicals.

In part (i) of Definition 1.5.1, x^1/n is simply another way of designating the principal n th root of x. In part (ii) of Definition 1.5.1, keep in mind that n is a positive integer greater than or equal to 2 and m can be any integer (positive, zero, or negative) and that the rational number m/n is reduced to lowest terms. Finally, x^m/n can be computed by using either but as a matter of practicality, it is usually easier to take the n th root of the number x first and then raise it to the m th power; in other words, use .

EXAMPLE 1 Using Definition 1.5.1(i)

We evaluate each of the following rational powers using part (i) of Definition 1.5.1.

(a).

(b).

EXAMPLE 2 Using Definition 1.5.1(ii)

We evaluate each of the following rational powers using part (ii) of Definition 1.5.1.

(a).

(b).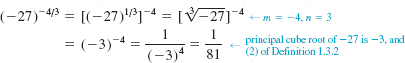

EXAMPLE 3 A Comparison

Although part (ii) of Definition 1.5.1 stipulates the equality

the computation

can be done mentally, whereas

may require the use of a calculator.

The following example illustrates a case in which x^m/n, (x^m)^1/n), and (x^1/n)^m are not equivalent. This example illustrates why m/n must be in lowest terms in part (ii) of Definition 1.5.1.

EXAMPLE 4 Comparison of Three Results

Compare (a) x^m/n, (b) (x^m)^1/n, and (c) (x^1/n)^m for x = -9, m = 2, and n = 2.

Solution Substituting x = -9, m = 2, and n = 2, we find:

(a).

(b).

(c). , which is not a real number, since it involves the square root of a negative number.

Laws of Exponents The laws of exponents given for integer exponents in Theorem 1.3.1 of Section 1.3 also hold true for rational exponents.

As shown in the following examples, these laws enables us to simplify algebraic expressions. For the remainder of this section we will assume that all variable bases x, y, a, b, and so on represent positive numbers so that all rational powers are defined.

EXAMPLE 5 Using the Laws of Exponents

(a).

(b).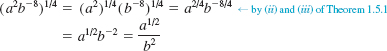

(c).

(d).

EXAMPLE 6 Simplifying

Simplify

Solution You should supply the parts of the laws of rational exponents (Theorem 1.5.1) used in the following simplification:

As we will see in the next two examples, certain radical expressions can be simplified more easily if they are rewritten using rational exponents.

EXAMPLE 7 Write as One Radical

Write as a single radical.

Solution We rewrite using rational exponents and then simplify using the laws of rational exponents:

From (ii) of Definition 1.5.1, we can write x^5/8 as .

EXAMPLE 8 Write as One Radical

Write as a single radical.

Solution We write the numbers in scientific notation and use the laws of rational exponents:

Next we must find a common base so that we can use the properties of rational exponents to simplify the expression. Since 16 = 2⁴ we have,

From (ii) of Definition 1.5.1, the last term 2^5/6 is the same as .

EXAMPLE 9 Simplifying

Simplify

Solution We write the numbers in scientific notation and use the laws of rational exponents:

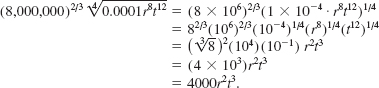
EXAMPLE 10 Inflation

Suppose that a piece of property cost p dollars n years ago. If it is now worth q dollars, then the average annual inflation rate for the property r is given by

Find the average annual inflation rate for a home now worth $500,000 if it was purchased 12 years ago for $80,000.

Solution We first identify p = 80,000, q = 500,000, and n = 12. Substituting, we then obtain

Using the key on a calculator with y = 6.25 and , we find r ≈ 0.165. Therefore, the average annual inflation rate for this property has been 16.5%.

In Section 5.1 we shall indicate how expressions with irrational exponents such as or x^π can be defined. The laws of exponents also hold for irrational exponents.

1.5 Exercises “Answers to selected odd-numbered problems begin on page ANS-2”.

Assume throughout this exercise set that all variables are positive.

In Problems 1-8, rewrite the expression using rational exponents.

1.

2.

3.

4.

5.

6.

7.

8.

In Problems 9-16, rewrite the expression using radical notation.

9.

10.

11.

12.

13.

14.

15.

16.

In Problems 17-22, find the indicated numbers.

In Problems 23-48, simplify and eliminate any negative exponents.

23. (4x^1/2)(3x^1/3)

24. (3w^3/2)(7w^5/2)

25. a^3/2(4a^2/3)

26. (-5x³)x^5/3

27. x^1/2x^1/4x^1/8

28. (2a^1/2)(2a^1/3)(2a1/6)

29. (a²b⁴)^1/4

30. (100x⁴)^-3/2

31. (25x^1/3y)^3/2

32. (4x⁴y^-6)^1/2

33.

34.

35.

36.

37. ((-27a³b^-6)^1/3)²

38. ^{a1/3(a2/3(ab)5/3b}-1/3)^-1/2

39. (x^1/2)(x^-1/2)2x^1/2

40. y^1/4(y^1/4(y^1/2)24)^-1/2

41. (5x^2/3(x^4/3)^1/4)³

42. (2z^1/2(2z1/2)^-1/2)^1/2

43.

44.

45.

46.

47.

48.

In Problems 49–56, rewrite the expression as a single radical.

49.

50.

51.

52.

53.

54.

55.

56.

In Problems 57-60, use scientific notation to simplify the expression.

57.

58.

59.

60.

Miscellaneous Applications

61. Pendulum Motion For a simple pendulum the period of time required for one complete oscillation is approximately T ≈ 2π (L/g)^1/2, where L is the length of the pendulum string and g is the gravitational constant. Use a calculator to approximate the period of a pendulum with a 10-in. string if the value of g is 32 ft/s². [Hint: Use consistent units.]

62. Sphere The radius r of a sphere with volume V is given by r = (3V/4π)^1/3. Use a calculator to find the radius of a sphere of volume 100 cm³.

63. Speed of Sound The speed of sound v measured in feet per second through air of temperature t degrees Celsius is given by

Use a calculator to find the speed of sound through air when the temperature is 20°C.

64. Flowing Water A fast-running stream can carry along larger particles than a slow-moving one. Laboratory studies have shown that the critical velocity v_t of the water needed to start a particle in a stream bed moving is given by the formula

where v_t is measured in meters per second, d is the diameter of the particle in millimeters, and G is the specific gravity of the particle. Find the critical velocity needed to begin moving a grain of feldspar that has a specific gravity of 2.56 and a diameter of 3 mm.

For Discussion

In Problems 65-74, answer true or false.

65. (z² + 25)^1/2 = z + 5_____

66.

67. ((-4)²)^1/2 = 4_____

68. [(-4)^1/2]² = -4_____

69. ((-1)^-1)^-1 = -1_____

70. (-1)^-1)(-1)^-1 = 1_____

71.

72.

73.

74.

1.6 Polynomials and Special Products

Introduction We have already found it convenient to use letters such as x or y to represent numbers. Such a symbol is called a variable. An algebraic expression is the result of performing a finite number of additions, subtractions, multiplications, divisions, or roots on a collection of variables and real numbers. The followi ng are examples of algebraic expressions:

, and

Sometimes an algebraic expression represents a real number only for certain values of a variable. In considering the expression , we find that we must have in order for to represent a real number. When we work with algebraic expressions, we assume that the variables are restricted so that the expression represents a real number. The set of permissible values for the variable is called the domain of the variable. Thus the domain of the variable in is the set of all nonnegative real numbers and for 3/(x + 1) the domain is the set of all real numbers except x = -1, that is,

If specific numbers are substituted for the variables in an algebraic expression, the resulting real number is called the value of the expression. For example, the value of x² + 2y when x = 1 and y = 2 is (1)² 1 2(2) = 5.

Polynomials Certain algebraic expressions have special names. A monomial in one variable is any algebraic expression of the form

axⁿ,

where a is a real number, x is a variable, and n is a nonnegative integer. The number a is called the coefficient of the monomial and n is called the degree. For example, 17x⁵ is a monomial of degree 5 with coefficient 17 and the constant - 5 is a monomial of degree 0. The sum of two monomials is called a binomial. The sum of three monomials is called a trinomial. For example,

3x - 2 and x³ 1 6x

are binomials, whereas

4x² - 2x - 1 and 8x⁴ + x² - 4x

are trinomials.

A polynomial is any finite sum of monomials. More formally, we have the following definition.

The expression (1) is called the standard form of a polynomial; that is, the polynomial is written in descending powers of x. Of course, not all powers need be present in a polynomial; some of the coefficients a_i, i = 0, 1, ., n could be 0.

Since a polynomial in x represents a real number for any real number x, the domain of a polynomial is the set of all real numbers R. The monomials a_ixⁱ in the polynomial are called terms of the polynomial, and the coefficient a_n of the highest power of x is called the leading coefficient. For example, 6x⁵ - 7x³ + 3x² - 1 is a polynomial of degree 5 with leading coefficient 6. The terms of this polynomial are 6x⁵, -7x³, 3x², and -1. The number a₀ is called the constant term of the polynomial. It may be 0, as in the polynomial 6x² - x. If all the coefficients of a polynomial are zero, then the polynomial is called the zero polynomial and is denoted by 0.

Polynomials can be classified by their degrees, although the zero polynomial is not assigned a degree. Special names are used to describe the lower-degree polynomials, as listed in the following table.

In each term in a polynomial, the exponent of the variable must be a nonnegative integer. For example,

and

are not polynomials. However,

and

are polynomials, since the coefficients can be any real numbers.

EXAMPLE 1 Recognition of a Polynomial

Determine which of the following algebraic expressions are polynomials. If the expression is a polynomial, give its degree and its leading coefficient.

(a).

(b).

(c).

(d).x⁴ - x²

Solution Since the variable in each term must be raised to a nonnegative integer power, (a) and (c) are not polynomials. The polynomials in (b) and (d) are of degree 8 and degree 4, respectively. Writing (b) in the standard form (1), , we see that the leading coefficient is -17. Since (d) is already written in standard form, the leading coefficient is 1.

Algebra of Polynomials Since each symbol in a polynomial represents a real number, we can use the properties of the real number system discussed in Section 1.1 to add, subtract, and multiply polynomials. In other words, the sum, difference, and product of two polynomials is a polynomial.

EXAMPLE 2 Sum of Two Polynomials

Find the sum of the polynomials x⁴ - 3x² + 7x - 8 and 2x⁴ + x² + 3x.

Solution Rearranging terms and using the distributive properties, we have

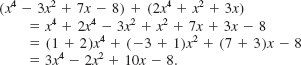
Example 2 indicates that we can add two polynomials in x by adding the coefficients of like powers. Some students find it easier to add polynomials by lining up terms with like powers of x in a vertical format, as shown below:

The choice of which format to use is simply a matter of personal preference. Generally, the vertical format requires more space, so after this section of the text we will use the horizontal format.

As the next example shows, subtraction of polynomials is performed in a manner similar to addition.

EXAMPLE 3 Difference of Two Polynomials

Subtract 2x³ - 3x - 4 from x³ + 5x² - 10x + 6.

Solution Subtracting terms with like powers of x, we have

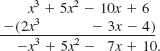
To perform this subtraction using a horizontal format, we proceed as follows:

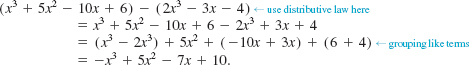
In order to find the product of two polynomials, we use the distributive properties and the laws of exponents, as the following example shows.

EXAMPLE 4 Product of Two Polynomials

Multiply x³ + 3x - 1 and 2x² - 4x + 5.

Solution We begin by using the distributive law several times:

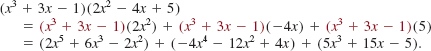
Combining like terms, we find the product to be

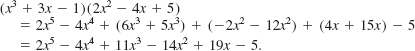
As in Example 4, when multiplying two polynomials, we must multiply each term of the first polynomial by each term of the second. A vertical format can be used (provided we keep like terms aligned), as follows:

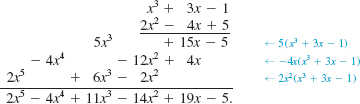
Special Products Certain products of binomials occur so frequently that you should learn to recognize them. We begin with the product of two binomials ax + b and cx + d:

Some polynomials can be expressed as a positive integer power of a binomial. The square and cube of a binomial x + a are, in turn,

and

It is readily shown that the product of a binomial x + a and its conjugate x - a results in the difference of two squares:

A classic mnemonic for carrying out the multiplication in (2) is the so-called FOIL method. The idea is outlined schematically in FIGURE 1.6.1; the letters F, O, I, and L, are, respectively, the first letter in the words f irst, o uter, i nner, and l ast.

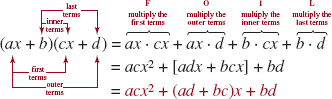
The FOIL method of multiplying two binomials

EXAMPLE 5 Using the FOIL Method

Find the product .

Solution We identify , b = —2, c = 1, and . Using the FOIL method we get

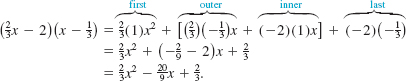
At first glance some products may not appear to be in the form (2) when, in fact, they are. With practice, however, you will become adept at recognizing them.

EXAMPLE 6 Using the FOIL Method

Find the product (5x² + 3)(4x² — 6).

Solution In (2) we simply replace ax by 5x² and cx by 4x²:

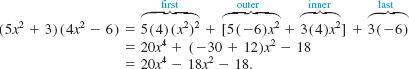
So too in each of the special products (3), (4), and (5) bear in mind that the symbols x and a can be replaced by another variable, a number, or a more complicated expression.

EXAMPLE 7 Squares

Find each of the following products.

(a).(3x + 7)²

(b).(5x - 4)²

Solution (a).From (3) with x replaced by 3x and a replaced by 7, we have

(b).From (3) with x replaced by 5x and a replaced by we have

EXAMPLE 8 Cubes

Find each of the following products.

(a).

(b).

Solution (a) With x replaced by 1/2x, a replaced by 2, and using the laws of exponents, (4) yields

(b) Before proceeding, we note that the answer we obtain will not be a polynomial because the two-term expression 4x - 1/x² is, strictly speaking, not a binomial. Nevertheless, (4) can be used with the symbol x replaced by 4x and the symbol a replaced by -1/x²:

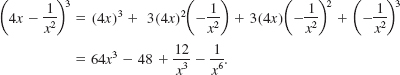
EXAMPLE 9 Difference of Two Squares

Find the product .

Solution With x replaced by 6y and a replaced by √2, the product formula (5) gives

Polynomials in Two Variables So far we have primarily considered polynomials in one variable. We may have polynomials in x or in other variables, such as , or we may have polynomials in two or more variables. A polynomial in two variables x and y is a sum of monomials (or terms) of the form axⁿy^m, where a is a real number, x and y are variables, and n and m are nonnegative integers. Examples are

, and

Similarly, a polynomial in three variables x, y, and z is a sum of monomials of the form axⁿy^mz^k, where n, m, and k are nonnegative integers. For example, xy²z³ - 2xy + z - 1 is a polynomial in three variables. Polynomials of four or more variables are defined in a similar manner. For example, xy + 5y - 3yz³ + 6xy²z³w⁴ is a polynomial in four variables.

We add, subtract, and multiply polynomials of several variables using the properties of real numbers just as we did for polynomials in one variable.

EXAMPLE 10 Sum of Two Polynomials in x and y

Find the sum of xy³ + x³y - 3 and x³ - y³ + 3xy³ - x³y.

Solution We simply add like terms that are indicated by the same color:

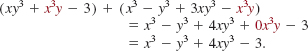
EXAMPLE 11 Product of Two Polynomials in x and y

Multiply x + y and x² - xy + y².

Solution As in Example 4 we use the distributive law several times and then combine like terms:

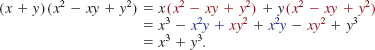
In Example 11 we have verified one of our last two special products formulas. The difference of two cubes is

whereas the sum of two cubes is

Formulas (6) and (7) are probably more important in factoring polynomials than they are as formulas to remember for carrying out a multiplication.

Division by a monomial uses the properties of fractions and the laws of exponents, as shown in Example 12. Division of two polynomials is more complicated and is discussed in Chapter 005.

EXAMPLE 12 Dividing Two Polynomials

Divide 15xy³ + 25x²y² - 5xy² by 5xy².

Solution We use the common denominator property

reading it right to left. With the identification d = 5xy² and the laws of exponents we get

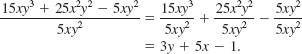
EXAMPLE 13 Using a Product Formula Twice

Find the product (2x + y)(2x - y)(4x² + y²).

Solution We use (5) twice in succession:

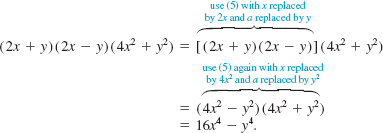
The more familiar you are with these special products (2)-(5) the easier it will be to understand factoring, which is reviewed in the next section.

NOTES FROM THE CLASSROOM

A very common mistake when subtracting polynomials in the horizontal format is to fail to apply the distributive property. The sign of each term of the polynomial being subtracted must be changed:

1.6 Exercises Answers to selected odd-numbered problems begin on page ANS-2.

In Problems 1-8, find the value of the polynomial for (a)x = -3, (b)x = 1/2 and (c)x = 0.

1. x² - 5x + 6

2.

3. x 2 3x² 1 6x³

4. x⁴ 2 x³ 1 x² 2 x + 1

5.

6. (x - 1)² + (x - 1)

7. 0.1x² - 0.5x + 0.2

8. (2x + 1)³

In Problems 9-16, determine whether the algebraic expression is a polynomial in one variable. If it is, give its degree and its leading coefficient.

9.

10. 0.5x¹⁰ - 1.7x³ + 3.4x- 7.2

11. y³ + y² 1 y^1/3 - 7

12. t⁴ - t³ 1 t^-1 - 1

13. 7x¹⁰⁰ - 4x⁹⁹ + 26x¹⁰¹ - 5

14.

15.

16. z²(5z³ - 4z + 18)

In Problems 17-30, perform the indicated operation and express the result as a polynomial in standard form.

17. (3x⁵ - 5x² + 4x - 7) + (x³ - 3x² 1 2x + 1)

18. (4x¹⁰ - 7x⁵ + 1) + (3x⁵ + 2x² - 7x + 1)

19. (y³ – 3y² + 7y – 8) + (5y³ + 4y² – 9y + 1)

20.

21. (x² + 2x – 1) – (3x⁴ – 4x² + 2x)

22. (3y⁴ – 2y² + 8y – 16) – (6y⁴ + 5y² + 10y – 11)

23. (3x⁷ – 7x⁶ + x⁵ – 14) – (x⁴ – 2x² + 8x)

24.

25. 3(t³ – 4t² + 6t – 3) + 5(-t³ + 2t² – 9t + 11)

26. 6(2x⁴ – 5x³ – 10x² + 4x – 8) – 4(-5x⁴ + 7x³ + 9x² – 3x – 13)

27. (2v + 4)(v² – 6v)

28. (w² – w + 1)(w⁴ – w²)

29. (y² + 2y – 4)(y² – y + 5)

30. (z³ + 4z – 3)(2z³ – 7z + 1)

In Problems 31-38, perform the indicated operations and simplify.

31. (8a⁴ + 7a²b² + 6b⁴) + (7a⁴ – a³b + a²b² – 8ab³ + 5b⁴)

32.

33. (2a – b)(3a² – ab + b²)

34. (x² – xy + y)(5x – 3y²)

35.

36.

37.

38.

In Problems 39-80, find the given product.

39. (x – 1)(x + 2)

40. (4x – 5)(x + 3)

41. (2r³ + 1)(r³ 2 7)

42. (v² + 3)(v² 2 5)

43. (5t – 7)(2t + 8)

44. (3z – 5)(7z + 1)

45.

46.

47. (0.3x + 0.7) (10x + 2.1)

48. (1.2x + 0.4) (2x – 1.3)

49.

50.

51. 1 + 5b)2

52. (2c – 4)2

53. (5x + 2)(10x + 4)

54. (–3x2 + 9)(x2 – 3)

55.

56. [4(x + 1) + 3][4(x + 1) – 3]

57. (y^-1 – 2x)(y^-1 + 2x)

58. (2z² + z)(2z² – z)

59. (2x – 3)³

60. (x + 5)³

61. (x²y³ – 2)³

62.

63. (x + y)(x² + 2xy + y²)

64. (2a² – 1)(4a⁴ – 4a² + 1)

65. (a – 3)(a² + 3a + 9)

66. (2 – y)(4 + 2y + y2)

67. (9 + y)(81 – 9y + y2)

68. (x + z²)(x² – xz² + z⁴)

69. (5x – y)(5x + y)(25x² + y²)

70. (2 – x + y)(2 – x – y)

71. (x + y + 1)²

72. (x + x² + x³)²

73. (x + y + 1)³

74. (x + x² + x³)³

75. (x^2/3 – x^1/3)(x_2/3 + x^1/3)

76.

77.

78.

79. (x⁵ – x²)(x – 1)

80. (2x^1/2– x)(x + 5)

81. Write polynomials in standard form for (a) the volume and (b) the surface area of the solid object shown in FIGURE 1.6.2. 82.

82. Write a polynomial in the variables r and s for the area of the region (a rectangle with semicircular ends) shown in FIGURE 1.6.3.

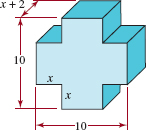
FIGURE 1.6.2 Solid object in Problem 81

FIGURE 1.6.3 Region in Problem 82

For Discussion

In Problems 83-88, answer true or false.

83. (t + l)² = t² + 1_____

84. The degree of the polynomial is x⁴ – 3x² + x⁵ is 4. _____

85. The leading coefficient of 2y³ — y¹² + 4 is — 1._____

86. The expression is a polynomial in the variable r._____

87. 4t³ + 3t — (2t³ + t + 7) = 2t³ + 4t + 7_____

88. The value of z⁴ — 3z + 1 when z =._____

In Problems 89 and 90, the polynomials are of a single variable x.

89. If a polynomial of degree 2 and a polynomial of degree 3 are added, what is the degree of the resulting polynomial? What is the degree of their product?

90. For two polynomials of degree n, what can be said about the degree of their sum? Their product? Their difference?

1.7 Factoring Polynomials

Introduction In the preceding section we multiplied polynomials. Now we reverse the procedure and try to write a polynomial as a product of other polynomials. This process is called factoring, and each polynomial in the product is called a factor of the original polynomial. For example, 3x²and x² + 2 are factors of 3x⁴ + 6X² because

3x⁴ + 6x² = 3x²(x² + 2).

Generally, we seek polynomial factors of degree 1 or higher.

By factoring, we can sometimes replace a complicated expression by a product of linear factors. An example is

5x³ + 6x² – 29x — 6 = (5x + 1)(x – 2)(x + 3).

Thus factoring can be very useful in simplifying expressions. As we will see in Chapter 002, it is particularly useful in solving equations. We will study factoring of polynomials in greater depth in Section 5.3.

In general, the first step in factoring any algebraic expression is to determine whether the terms have a common factor.

EXAMPLE 1 Factoring

Factor .

Solution Since 2xy2 is a common factor of the terms, we have

When the terms of an expression do not have a common factor, it may still be possible to factor by grouping the terms in an appropriate manner.

EXAMPLE 2 Grouping

Factor x² + 2xy – x – 2y.

Solution Grouping the first two terms and the last two terms gives

We observe the common factor x + 2y and complete the factorization as

Factoring Quadratic Polynomials It is sometimes possible to factor the quadratic polynomial ax² + bx + c, where a, b, and c are integers, as

(Ax + B)(Cx + D),

where the symbols A, B, C, and D also represent integers.

Initially, to simplify our discussion we assume that the quadratic polynomial has as its leading coefficient a = 1. If x² + bx + c has a factorization using integer coefficients, then it will be of the form

(x + B)(x + D),

where B and D are integers. Carrying out the multiplication and comparing coefficients,

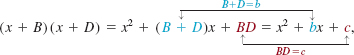
we see that

B + D = b and BD = c.

Thus to factor with integer coefficients, we list all possible factorizations of c as a product of two integers B and D. We then check which, if any, of the sums equals b.

EXAMPLE 3 Factoring a Polynomial

Factor x² – 9x + 18.

Solution With and, b = -19 and c = 18, we look for integers B and D such that

B + D= -9 and BD = 18.

We can write 18 as a product BD in the following ways:

1(18), 2(9), 3(6), (-1)(-18), (-2)(-9), (-3)(-6).

Since – 9 is the sum B + D when B = —3 and D = —6, the factorization is

x² – 9x + 18 = (x – 3)(x – 6).

Note that it is always possible to check a factorization by multiplying the factors.

EXAMPLE 4 Factoring a Polynomial

Factor x² + 3x – 1.

Solution The number – 1 can be written as a product of two integers BD in only one way, namely, (—1)(1). With B = – 1 and D = 1 we conclude from

B + D = – 1 + 1 ≠ 3

that x² + 3x – 1 cannot be factored using integer coefficients.

It is more complicated to factor the general quadratic polynomial ax² + bx + c, with a ≠ 1, since we must consider factors of a as well as of c. Finding the product and comparing coefficients

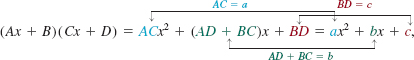
we see that ax² + bx + c factors as (Ax + b)(Cx + D) if we can find integers A, B, and C that satisfy

EXAMPLE 5 Factoring a Polynomial

Factor 2x² + 11x - 6.

Solution The factors will be

(2x 1 ___) (1x 1 ___),

where the blanks are to be filled with a pair of integers B and D whose product BD equals - 6. Possible pairs are:

1 and -6, -1 and 6, 3 and -2, -3 and 2.

Now we must check to see if one of the pairs gives 11 as the value of AD + BC (the coefficient of the middle term), where A = 2 and C = 1. We find

2(6) + 1(-1) = 11;

therefore,

2x² + 11x - 6 = (2x - 1)(x + 6). =

This general method can be applied to polynomials in two variables x and y of the form

ax² + bxy + cy²,

where a, b, and c are integers.

EXAMPLE 6 Factoring

Factor 15x² + 17xy + 4y².

Solution The factors could have the form

There is no need to consider the cases

(Why?) The blanks in (1) must be filled with a pair of integers whose product is 4. Possible pairs are

1 and 4, -1 and -4, 2 and 2. -2 and -2

We check each pair with the possible forms in (1) to see which combination, if any, gives a coefficient of 17 for the middle term. We find

15x² + 17xy 1 4y² 5 (5x + 4y)(3x + y).

EXAMPLE 7 Factoring a Polynomial

Factor 2t⁴ + l1t² + 12.

Solution If we let x = t², then we can regard this expression as a quadratic polynomial in the variable x,

2x² + 11 x + 12.

We then factor this quadratic polynomial. The factors will have the form

where the blanks are to be filled with a pair of integers whose product is 12. Possible pairs are

1 and 12, -1 and -12, 2 and 6, -2 and -6, 3 and 4, -3 and -4.

We check each pair with (2) to see which combination, if any, gives a coefficient of 11 for the middle term. We find

2X² + 11x + 12 = (x + 4) (2x + 3).

Substituting t² for x gives us the desired factorization

2t⁴ + 11t² + 12 = (t² + 4)(2t² + 3)

In the preceding example you should verify that neither t² + 4 nor 2t² + 3 will factor using integer coefficients, or for that matter, using real numbers.

Factorization Formulas By reversing the special product formulas from Section 1.6, we have the following important factorization formulas. These formulas are simply (3), (5), (6), and (7) of Section 1.6 written in reverse manner.

Perfect square:

Difference of two squares:

Difference of two cubes:

Sum of two cubes:

As noted in Section 1.6 the symbols x and a can be replaced by another variable, a number, or a more complicated expression.

EXAMPLE 8 Perfect Square

Factor y² - 6y + 9.

Solution With the symbol y playing the part of x and with a = -3 we see from (3) that

y² - 6y + 9 = y² + 2(-3)y + (-3)² = (y - 3)².

EXAMPLE 9 Difference of Two Squares

Factor 16x⁴y² - 25.

Solution By rewriting the expression as

16x⁴y² - 25 = (4xy²)² - 5²

we recognize the difference of two squares. Thus from formula (4) with the symbol x replaced by 4x²y and a = 5, we have

EXAMPLE 10 Sum of Two Cubes

Factor 8a³ + 27b⁶.

Solution Because we can write the given expression as the sum of two cubes,

8a³ + 21b⁶ = (2a)³ + (3b¹⁵)³,

it can be factored using formula (6). If we replace x by 2a and a by 3b², then it follows from formula (6) that

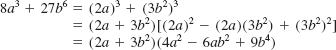
Observe that formulas (4)-(6) indicate that the difference of two squares and the sum and difference of two cubes always factor, provided that we do not restrict the coefficients to integers. For example, using formula (4) to factor x² - 5, we identify so that

We now consider an example in which a first factorization yields expressions that can be factored again. In general, we require that an expression be factored completely, that is, factored until none of the factors can themselves be factored into polynomials of degree 1 or higher with integer coefficients.

EXAMPLE 11 Two Different Methods

Factor completely x⁶ - y⁶.

Solution We can view the expression x⁶ - y⁶ in two ways: as a difference of two squares or as a difference of two cubes. Using the difference of two cubes, formula (5), we write

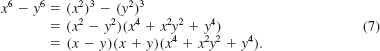
From this foregoing result we might conclude that the factorization is complete. However, treating the expression x⁶ - y⁶ as a difference of two squares is more revealing, since

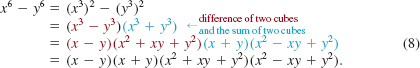
In Example 11, if we compare the results in the last lines of the factorizations in (7) and (8), we discover the additional factorization:

x⁴ + x²y² + y⁴ 5 (x² + xy + y²)(x² - xy + y²).

We leave it to you to check that neither of the expressions on the right-hand side of the equality will factor further.

1.7 Exercises Answers to selected odd-numbered problems begin on page ANS-2.

In Problems 1-10, factor the polynomial by finding a common factor or by grouping.

1. 12x³ + 2x² + 6x

2. 6x³y⁴ - 3 √3x²y² - 3x²y + 3xy

3. 2y² - yz + 6y - 3z

4. 6x⁵y⁵ + √2x²y³ + 14xy³

5. 15at +3bt + 5as + bs

6. 3a²b³ - 3√2a⁴b² + 9a²b

7. xyz³ - xy³z + x³yz

8. x³ + 2x + x² + 2

9. 2p³ - p² +2p - 1

10. 2uv - 5wz +2uz - 5wv

In Problems 11-22, use the factorization formulas (3)-(6) to factor the given polynomial.

11. 36x² - 25

12. a²- 4b²

13. 4x²y² - 1

14. 49x² - 64y²

15. x⁴-y⁴

16. x⁶ +y⁶

17. x⁸ -y⁸

18. a³- 64b³

19. 8x³y³ + 27

20. y³ + 125

21. y⁶-1

22. 1 -x³

In Problems 23-42, use techniques for factoring quadratic polynomials to factor the given polynomial, if possible.

23. x² - 5x + 6

24. x² - 10x + 24

25. y² + 7y + 10

26. y⁴ + 10y² + 21

27. x⁴ - 3x² - 4

28. x² + 4x - 12

29. r² +2r + 1

30. s² + 5s - 14

31. x² -xy - 2y²

32. x² - 4xy + 3y²

33. x² + 10x + 25

34. 4x² + 12x + 9

35. s² - 8st + 16t²

36. 9m² -6mv + v²

37. 2p² +7p + 5

38. 6a⁴ + 13a² - 15

39. 8q² +2q - 3

40. 10b⁴ - 23b² + 12

41. 2x² -7xy + 3y²

42. - 3x² - 5xy + 12y²

In Problems 43-60, use any method to factor the given polynomial.

43. (x² + 1)³ + (y² - 1)³

44. (4 - x²)³ - (4 - y²)³

45. x(x - y) +y (y - x)

46. x (x - y) -y (y - x)

47. (1 - x²)³ - (1 - y²)³

48. (x² - 4)³ + (4 - y²)³

49. 1 - 256v⁸

50. s⁸ - 6561

51. x⁶ + 7x³ - 8

52. z¹⁰ - 5z⁵ - 6

53. r³s³ - 8t³

54. 25c²d² - x²y²

55. a³ +a²b -b³ -ab²

56. p³ -pq² +p²q -q³

57. 4z² + 7zy - 2y²

58. 36x² + 12xy + y²

59. 16a² - 24ab + 9b²

60. 4m² + 2mm - 12n²

In Problems 61-70, use the factorization formulas (3) and (4) to factor the expression into linear factors. [Hint: Some coefficients will not be integers.]

61. x² - 3

62. 2r² - 10000

63. 5y² - 1

64.

65.

66.

67. a² - 2b²

68. 3u² - 4v²

69. 24 -x²

70. x² - 2 √2xy + 2y²

For Discussion

In Problems 71-74, answer true or false.

71. x² + y² = (x + y)(x + y)__

72. a³ + b³ = (a + b)³__

73. (r - 1)(r - 1) = r² + 1__

74. r³ - s³ = (r - s)(r² +rs + s²)__

In Problems 75-77, several of the factorization formulas are discussed in geometric terms.

In Book II of Euclid's Elements (c. 300 BCE), algebraic problems are discussed and solved in geometric terms, because the Greeks lacked algebraic notation. For example, the product of two positive numbers a and b is represented as the area of a rectangle whose sides have lengths a and b, respectively.

75. Explain howFIGURE 1.7.1 justifies the factorization formula a² +2ab + b² = (a + b)²for positive numbers a and b.

76. Explain howFIGURE 1.7.2 justifies the factorization formula a² - b² = (a - b) (a + b), where a > b > 0.

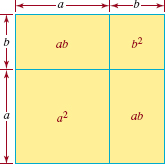
FIGURE 1.7.1 Rectangles in Problem 75

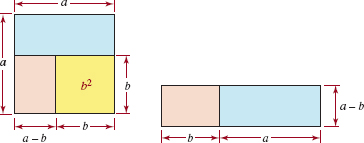
FIGURE 1.7.2 Rectangles in Problem 76

FIGURE 1.7.3 Cube in Problem 77

77. FIGURE 1.7.3 suggests that the factorization formula for the difference of two cubes, a³ - b³ = (a - b)(a² +ab + b²) for a > b > 0, can be justified geometrically. Complete the proof.[Hint: Label the four boxes inside the cube and compute the volume of each.]

1.8 Rational Expressions

Introduction When one polynomial is divided by another, the result need not be a polynomial. A quotient of two polynomials is called a rational expression. For example,

are rational expressions. The domain of the variable in a rational expression consists of all real numbers for which the value of the denominator is nonzero. For example, in (2x² + 5)/(x + 1)the domain of the variable is {x|x ≠ -1}.

In solving problems, we often must combine rational expressions and then simplify the results. Since a rational expression represents a real number, we can apply the properties of the real number system to combine and simplify rational expressions. The properties of fractions from Section 1.1 are particularly helpful. We repeat the most frequently used ones here for convenience.

EXAMPLE 1 Simplifying

Simplify the rational expression

Solution We factor the numerator and the denominator and cancel common factors using the cancellation property (i):

Note that in Example 1 the cancellation of the common factor x -1 is valid only for those values of x such that x- 1 is nonzero; that is, for x ≠ 1. However, since the expression (2x² -x-1)/(x² - 1) is not defined for x = 1, our simplification is valid for all real numbers in the domain of the variable x in the original expression. We emphasize that the equality

is not valid for X = 1, even though the right-hand side, (2X + 1)/(X + 1), is defined for x = 1. Considerations of this sort will be important in the next chapter when we solve equations involving rational expressions.

For the remainder of this chapter we will assume without further comment that variables are restricted to values for which all denominators in an equation are nonzero.

EXAMPLE 2 Simplifying

Simplify the rational expression

Solution

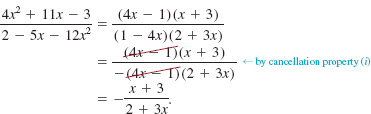
Least Common Denominator In order to add or subtract rational expressions, we proceed just as we do when adding or subtracting fractions. We first find a common denominator and then apply property (ii). Although any common denominator will do, less work is involved if we use the least common denominator (LCD). This is found by factoring each denominator completely and forming a product of the distinct factors, using each factor with the highest exponent with which it occurs in any single denominator.

EXAMPLE 3 Least Common Denominator

Find the LCD of

Solution Factoring the denominators in the rational expressions, we obtain

The distinct factors of the denominators are x, x - 1, and x + 1. We use each factor with the highest exponent with which it occurs in any single denominator. Thus the LCD is x²(x-1)(x+1)²

EXAMPLE 4 Combining Terms

Combine

and simplify the resulting rational expression.

Solution In factored form, the denominators are(x - 2)(x + 2)and(x + 2)².Thus the LCD is (x - 2)(x + 2)².We use property (i) in reverse to rewrite each of the rational expressions with the LCD as denominator:

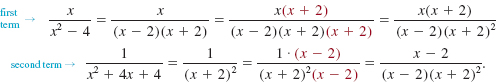
Then using property (ii) we add and simplify:

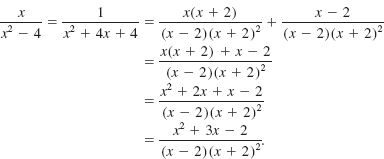
To multiply or divide rational expressions, we apply property (iii) or property (iv) and then simplify.

EXAMPLE 5 Combining Terms

Combine

and simplify the resulting rational expression.

Solution We begin by using property (iii):

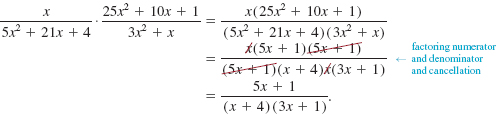
EXAMPLE 6 Combining Terms

Combine

and simplify the resulting rational expression.

Solution We begin by writing the given expression as a product:

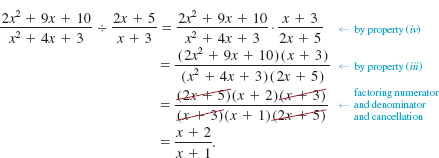
Fractional Expressions A quotient of two algebraic expressions that are not polynomials, such as(√x-l)/(³√x + l), is called a fractional expression. The techniques used to simplify fractional expressions are similar to those used for rational expressions.

EXAMPLE 7 Simplifying

Simplify

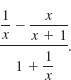
Solution First we obtain single rational expressions for the numerator,

and the denominator,

Hence the given expression is the same as

Next we apply property (iv) to this quotient to obtain

An alternative method of simplifying a complex fraction is to multiply both the numerator and the denominator by the LCD of all the fractions that occur in the complex fraction. Using this approach here, we multiply the numerator and the denominator by x(x + 1) and simplify as follows:

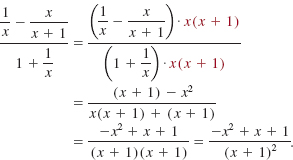
The techniques discussed in this section can often be applied to expressions containing negative exponents, as we see in the following example.

EXAMPLE 8 Simplifying

Simplify(a^-1+b^-1)^-1

Solution We first replace all negative exponents by the equivalent quotients and then use the properties of fractions to simplify the resulting algebraic expression:

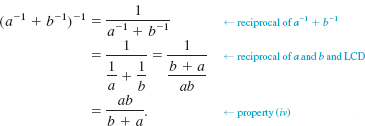
EXAMPLE 9 Combining Terms

Combine

and simplify the resulting fractional expression.

Solution First we find a common denominator and then add:

If we desire to rationalize the denominator, the final result would be

Examples 10 and 11 illustrate how to simplify certain types of fractional expressions that occur in calculus.

EXAMPLE 10 Simplifying

Simplify

Solution We begin by combining the terms in the numerator:

Then by properties (i) and (iv),

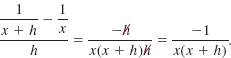
EXAMPLE 11 Simplifying

Combine

and simplify the resulting fractional expression.

Solution In the second term we use and then use as the LCD:

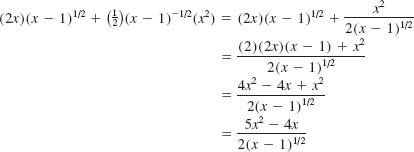
1.8 Exercises Answers to selected odd-numbered problems begin on page ANS-2.

In Problems 1–8, simplify the rational expression.

1.

2.

3.

4.

5.

6.

7.

8.

In Problems 9–16, find the least common denominator (LCD) of the rational expressions.

9.

10.

11.

12.

13.

14.

15.

16.

In Problems 17–42, combine terms and simplify the rational expression.

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

39.

40.

41.

42.

In Problems 43–64, simplify the given fractional expression.

43.

44.

45.

46.

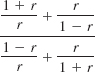
47.

48.

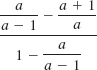
49.

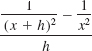
50.

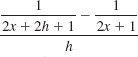
51.

52.

53.

54.

55.

56.

57.

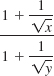
58.

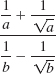
59.

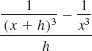
60.

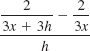
61.

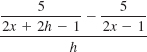
62.

63.

64.

Miscellaneous Applications

65. Resistance in a Circuit If three resistors in an electrical circuit with resistances R₁, R₂, and R₃ ohms, respectively, are connected in parallel, then the resistance (in ohms) of the combination is given by

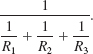
Simplify this fractional expression.

66. Optics In the field of optics, if p is the distance from the object to the lens and q is the distance from the image to the lens, then the focal length of the lens is given by

Simplify this fractional expression.

CHAPTER 1 Review Exercises Answers to selected odd-numbered problems begin on page ANS-3.

A. True/False__________________________________________________

In Problems 1–26, answer true or false.

1. -3.3 is greater than -3.___

2. Every real number has a reciprocal.___

3. 0/0 is a real number.___

4. π is a rational number.___

5. Every real number can be written as a quotient of two integers.___

6. No irrational number can be written as a fraction.___

7. = –10___

8. = ±10___

9. For .___

10. If x^1/n = r, then rⁿ = x.___

11. The LCD of ___

12. For a > 0, m ≥ 2 and n ≥ 2 positive integers, .___

13. For all t, = –1.___

14. (u^–2 + v^–2)^–1 = u² + v² ___

15.

16. |–6x| = 6|x|___

17. If a and b are real numbers such that a < b, then a² < b².___

18. Every real number x possesses a multiplicative inverse.___

19. The algebraic expression 6x^–2 + is not a polynomial.___

20. The cube root of a negative number is undefined. ___

21.

22. (a + b + c)(a + b – c) = (a + b)² – c²

23.

24. (–1)(–a + b – c) = a + b – c ___

25. The sum of two rational numbers is rational.___

26. The sum of two irrational numbers is irrational.___

B. Fill in the Blanks_____________________________________________

In Problems 1–22, fill in the blanks.

1. The first three nonnegative integers are___________.

2. –10(x – y) = –10x + 10y is an example of the ___________law.

3. The quotient C/d of a circle's circumference C and its diameter d is a ___________(rational or irrational) number.

4. On the number line, the ___________of the segment joining –1 and 5 is 2.

5. Geometrically, a < b means that the point corresponding to a on the number line lies to the ___________of the point corresponding to b.

6. If x is a negative, then |x| = ___________.

7. The ___________ of x ≠ 0 can be written as 1/x or as x^–1.

8. For x ≠ 0, x⁰ = ___________.

9. Using rational exponents, .

10. The domain of the variable x in (3x + 1)/(x² – 1) is___________.

11. The expression 3x⁴ – x² + 5x is a___________of degree___________with leading coefficient___________and constant term___________.

12. In simplifying x(x + 2)/((x – 2)(x + 2)) to x/(x – 2), we used the___________property.

13. The distance from a to b is given by___________.

14. On the number line, the absolute value of a number measures its distance to the___________.

15. The number 4.2 × 10^–5 is written in___________.

16. The real numbers a and b for which are ___________.

17. The sets {1, 3, 5} and {2, 4} with no common elements are said to be___________.

18. On the number line, if the distance between x and 7 is 3, then x is___________.

19. In the expression x³, x is called the___________and 3 is called the ___________.

20. The expression is called a ___________ of index___________.

21. For real numbers x and y, xy = yx is an example of the ___________law of multiplication.

22. If a < b, then ___________is positive.

C. Review Exercises_____________________________________________

In Problems 1–6, find the indicated set if A = {1, 3, 5, 7, 9}, B = {1, 2, 3, 4, 5}, and C = {2, 4, 6, 8}.

1. A ∪ B

2. A ∩ B

3. (A ∪ B) ∩ C

4. (A ∩ C) ∪ B

5. (A ∪ B) ∪ C

6. (A ∩ B) ∩ C

In Problems 7 and 8, write the given statement as an inequality.

7. x – y is greater than or equal to 10.

8. z is nonnegative.

In Problems 9–12, insert the appropriate symbol: <, >, or =.

9. –1.4, –

10. 0.50,

11. , 0.67

12. –0.9, –0.8

In Problems 13–18, find the indicated absolute value.

13.

14.

15. |x² + 5 |

16.

17. |t + 5 |, if t < –5

18. |r – s|, if r > s

In Problems 19 and 20, find (a) the distance between the given points and (b) the coordinate of the midpoint of the line segment joining the given points.

19. –3.5, 5.8

20. ,

In Problems 21–38, eliminate negative and zero exponents and simplify. Assume that all variables are positive.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37.

38.

In Problems 39 and 40, write the given number in scientific notation.

39. 0.0000007023

40. 158,000,000,000

In Problems 41 and 42, use scientific notation to evaluate the given expression.

41.

42.

43. In 2009 it is estimated that American taxpayers spent $52.67 billion on the war on drugs. Write this number (a) in decimal form and (b) in scientific notation.

44. One nanosecond is 0.000000001 second.

(a) Write 0.000000001second in scientific notation.

(b) One second equals how many nanoseconds?

In Problems 45–52, perform the indicated operations and simplify.

45. (4x³ – 3x² + 6x – 2) – (x² – 3x + 4)

46.

47. (a + 1)(a – 2)(a + 3)

48.

49. (3z⁴ – 2z)²

50. (x² + 2y)³

51. (3x² + 5y)(3x² – 5y)

52. (u – v)(u² + uv + v²)

In Problems 53–60, factor the given polynomials using integer coefficients.

53. 12x² – 19x – 18

54. 16a⁴ – 81b⁴

55. 2xy + 3y – 6x – 9

56. 4w² + 40wz + 100z²

57. 8x³ + 125y⁶

58. 2x³ + 3x² – 18x – 27

59. 4t⁴ – 4t²s + s²

60. 125 + 75uv + 15u²v² + u³v³

In Problems 61–72, perform the indicated operations and simplify.

61.

62.

63.

64.

65.

66.

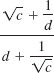
67.

68.

69.

70.

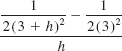
71.

72.

In Problems 73 and 74, rationalize the denominator and simplify.

73.

74.

In Problems 75 and 76, rationalize the numerator and simplify.

75.

76.

---

^*An even root of a negative number, for example, , is called a complex number. Complex numbers are discussed in Section 1.4.