2 Equations and Inequalities
In This Chapter
2.2 Building an Equation from Words
2.6 Absolute-Value Equations and Inequalities
2.7 Polynomial and Rational Inequalities

The 1911 Oldsmobile Limited Touring Car plays a part in Problem 82 of the Chapter 002 Review Exercises.
A Bit of History Little is known of the personal life of the Greek mathematician Diophantus, who lived in Alexandria, Egypt, in the third century CE. His work, however, was of tremendous importance to the development of algebra and greatly influenced seventh-century European mathematicians. He wrote several treatises, the most famous of which are the 13 books of his Arithmetica. This series of texts deals primarily with special types of equations now called diophantine equations. Legend has it that the following epitaph marked Diophantus' grave:
Diophantus passed one-sixth of his life in childhood, onetwelfth in youth, and one-seventh as a bachelor. Five years after his marriage was born a son who died four years before his father at one-half his father's (final) age.
If the symbol x represents Diophantus' age at death, then the information above can be interpreted as the equation
![]()
In this chapter we will examine techniques for solving various types of equations (including the one above) and inequalities. We will also discuss how to apply these methods to obtain solutions to practical problems.
ch002_s1_1.2 Equations
![]() Introduction An equation is a statement that two expressions are equal, whereas an inequality states that one expression is less than another. A wide variety of real- world problems can be expressed as either equations or inequalities. We begin this section with some terminology describing equations and their solutions.
Introduction An equation is a statement that two expressions are equal, whereas an inequality states that one expression is less than another. A wide variety of real- world problems can be expressed as either equations or inequalities. We begin this section with some terminology describing equations and their solutions.
![]() Terminology When two expressions, and at least one of the expressions contains a variable, are set equal to each other we say that the mathematical statement is an equation in one variable. For example,
Terminology When two expressions, and at least one of the expressions contains a variable, are set equal to each other we say that the mathematical statement is an equation in one variable. For example,
![]()
are equations in the variable x. A solution, or root, of an equation is a number that, when substituted into the equation, makes it a true statement. A number is said to satisfy an equation if it is a solution of the equation. To solve an equation means to find all its solutions.
EXAMPLE 1 Verifying a Solution
The number 2 is a solution of the equation 3x – 2 = x + 2, because when substituted into the equation we get the true statement:
![]()
As we will see later, there are no other values of x that satisfy this equation.
See Section 1.6 for a review of the concept domain of a variable. ![]()
An equation is called an identity if it is satisfied by all numbers in the domain of the variable. If there is at least one number in the domain of the variable for which the equation is not satisfied, then it is said to be a conditional equation.
EXAMPLE 2 An Identity and a Conditional Equation
The equation
![]()
is satisfied by the set of all real numbers except x = 1. Because the number 1 is not in the domain of the variable, the equation is an identity.
The number 3 is in the domain of the variable in the equation 4x – 1 = 2, but it does not satisfy this equation since 4(3) – 1 ≠ 2. Thus, 4x - 1 = 2 is a conditional equation.
The set of all solutions of an equation is called its solution set. In Example 1 the solution set of 3x – 2 = x + 2 is written {2}. You are encouraged to verify that the solution set of the equation |x + 1| = 5 is {–6, 4}.
![]() Equivalent Equations We say that two equations are equivalent if they have the same solutions, that is, their solution sets are exactly the same. For example,
Equivalent Equations We say that two equations are equivalent if they have the same solutions, that is, their solution sets are exactly the same. For example,
![]()
are equivalent equations. Generally, we solve an equation by finding an equivalent equation with solutions that are determined easily. The following operations yield equivalent equations.

EXAMPLE 3 A Simple Equation
Solve 3x – 18 = 0.
Solution We obtain the following list of equivalent equations:
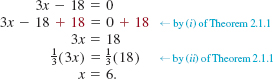
The solution set of the equation is {6}.
Since it is not unusual to make arithmetic or algebraic errors when solving an equation, it is always good practice to verify each solution by substituting it into the original equation. To verify the solution in Example 3, we substitute 6 for x in 3x – 18 = 0:
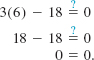
![]() Note of Caution
Note of Caution
![]() Linear Equations An equation of the form
Linear Equations An equation of the form
![]()
where b is a real number, is called a linear equation. The equation in Example 3 is a linear equation. To solve (1), we proceed in a manner similar to Example 3:
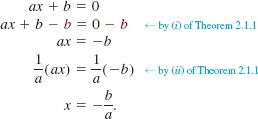
Thus the linear equation ax + b = 0, a ≠ 0, has exactly one solution, {–b/a}.
EXAMPLE 4 A Linear Equation
Solve 2x – 7 = 5x + 6.
Solution You should supply reasons why the following equations are equivalent.
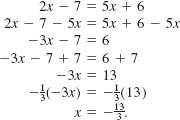
Thus the solution set of the original equation is ![]()
![]() Extraneous Solutions When both sides of an equation are multiplied by an expression containing a variable, the resulting equation may not be equivalent to the original, since we have excluded multiplication by 0 in operation (ii) of Theorem 2.1.1. For example, multiplication of the equation 2x = 4 by x yields 2x2 = 4x. The two equations are not equivalent, since obviously 0 is a solution of the latter equation but is not a solution of the former equation. We say that 0 is an extraneous solution of the original equation.
Extraneous Solutions When both sides of an equation are multiplied by an expression containing a variable, the resulting equation may not be equivalent to the original, since we have excluded multiplication by 0 in operation (ii) of Theorem 2.1.1. For example, multiplication of the equation 2x = 4 by x yields 2x2 = 4x. The two equations are not equivalent, since obviously 0 is a solution of the latter equation but is not a solution of the former equation. We say that 0 is an extraneous solution of the original equation.
EXAMPLE 5 Multiplying an Equation by a Variable
Solve
![]()
Solution Multiplying both sides of the given equation by z + 1 yields a linear equation:
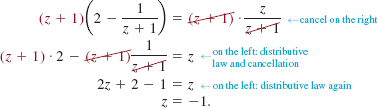
Because we have multiplied by an expression containing a variable, we must check z = – 1 by substituting it into the original equation (2). We obtain
![]()
or
![]()
Since division by 0 is not defined, z = – 1 is not a solution of the original equation. Thus, – 1 is an extraneous solution, and so we conclude that equation (2) has no solutions. That is, the solution set is the empty set ![]() .
.
Note of Caution ![]()
As Example 5 shows, it is essential to check a “solution” that has been obtained as a result of multiplying both sides of an equation by an expression that may be 0 for some values of the variable.
EXAMPLE 6 Multiplying an Equation by a Variable
Solution
![]()
Solution To clear the denominators in (3), we multiply both sides of the equation by the LCD x(x – 4) of the fractions in the equation

Substituting x = 3 into (3), we find that this value satisfies the original equation:
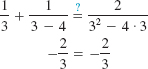
and so the solution set is {3}.
![]() Solving for a Variable In other courses, especially physics, you will often encounter equations that contain several variables. It is often necessary to solve for a particular variable in terms of the remaining variables. The next example illustrates the idea.
Solving for a Variable In other courses, especially physics, you will often encounter equations that contain several variables. It is often necessary to solve for a particular variable in terms of the remaining variables. The next example illustrates the idea.
EXAMPLE 7 Solving for Another Variable
The total resistance R of an electric circuit containing two resistors, of resistance R1 and R2, connected in parallel is given by
![]()
See FIGURE 2.1.1. Solve for R2 in terms of R and R1.

Electric circuit in Example 7
Solution First we clear the equation of fractions by multiplying both sides by the quantity RR1R2, which is the least common denominator of the fractions in the equation
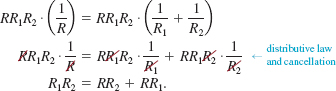
To obtain an equivalent equation with all terms containing R2 on the left-hand side, we subtract RR2 from both sides:
![]()
Since R2 is a common factor of each term on the left-hand side, we can write
![]()
Dividing both sides by R1 – R gives us the desired result
![]()
2.1 Exercises Answers to selected odd-numbered problems begin on page ANS-3.
In Problems 1–6, determine whether the given pairs of equations are equivalent.
1.x = 8; x – 8 = 0
2.x2 = x; x = 1
3.4y – (y – 1) = 2; 3y = 1
4.–2z – 4 = 6z + 10; –4z = 7
5.t + 1 = 1; ![]()
6.x2 = (x + 1)2; 2x + 1 = 0
In Problems 7–48, solve the given equation.
7.2x + 14 = 0
8.3x – 5 = 0
9.–5w + 1 = 2
10.7z + 8 = –6
11.7(y + 1) – 2 = 5(y + 1) + 2
12.3y – 2 = y + 6
13.x – (2 - x) = 3(x + 1) + x
14.![]()
15.![]()
16.![]()
17.–5t + 3 = 4(t - 6)
18.![]()
19.![]()
20.![]()
21.0.2x + 1.2 = 0.5
22.2.1x – 3 = 0.5x + 0.2
23.–3.6z + 1.3 = 0.2(z – 3)
24.4.5x – 1.5x = 0.3(2 - x)
25.![]()
26.![]()
27.p2 + 6p – 1 = p2 – p + 6
28.r2 + 5 = – (10r – r2)
29.(2t – 1)2 = 4t2 + 1
30.(w – 1)(w + 1) = w(w – 4)
31.(x – 1)3 = x2(x – 3) + x
32.(x + 3)2 + (x + 2)3 = x3 + 7x2 + 9
33.![]()
34.![]()
35.![]()
36.![]()
37.![]()
38.![]()
39.![]()
40.![]()
41.![]()
42.![]()
43.![]()
44.![]()
45.![]()
46.![]()
47.![]()
48.![]()
49.Find a so that the solution of 3x + 3a = 6x – a is 4.
50.Find d so that the equation
![]()
has no solutions.
51.Find c so that 3(y – c) = 3y + 7 is an identity.
52.Find a so that (x – 1)(x + a) = x2 – 2x – a is an identity.
53.Find a so that 5 – z = 1 and 3z + 2a = 10 are equivalent equations.
54.Find the relationship between a and b if ax + b = 0 has the solution x = 5.
In Problems 55–66, solve for the indicated variable in terms of the remaining variables.
55.Circumference of a circle
C xs = 2πr, for r
56.Perimeter of a rectangle
P = 2w + 2l, for l
57.Simple interest
I = Prt, for t
58.Lateral surface area of a cylinder
S = 2πrh, for h
59.Amount accrued by simple interest
A = P + Prt, for P
60.Volume of a rectangular parallelepiped
V = lwh, for h
61n th term of an arithmetic sequence
an = a + (n – 1)d, for n
62.Sum of a geometric series
![]() for r
for r
63.Newton's universal gravitation law
![]() for m1
for m1
64.Free-falling body
![]() for v0
for v0
65.Resistance in a parallel circuit
![]() for R2
for R2
66.Surface area of a cylinder
A = 2πr(r + h), for h
Miscellaneous Applications
67.Temperature The relationship between temperature measured in degrees Celsius (TC) and in degrees Fahrenheit (TF) is given by ![]()
(a)Solve the last equation for TF.
(b)Use the result in part (a) to convert the Celsius temperatures –5°C, 0°C, 16°C, 35°C, and 100°C to degrees Fahrenheit.
68.Tennis Anyone? The velocity v in ft/s of a tennis ball t seconds after it has been thrown upward with an initial velocity of 8 ft/s is given by v = – 32t + 8. How many seconds have elapsed when (a)v = 4 ft/s and (b)v = 0 ft/s?
69.Diophantus'Age In the chapter opening, we saw that the equation
![]()
described the age x of Diophantus when he died. Determine how long Diophantus lived.
70.Heart Rate As reported in Science and Sport by Thomas Vaughan (Boston: Little, Brown & Co., 1970), a series of 4200 readings taken on 136 world-class athletes resulted in the formula for the maximum heart rate rmax in heartbeats per minute during exercise:
![]()
where r5 is the heart rate taken within 5 seconds after ceasing to exercise.
(a)If a walking champion has a maximum heart rate of 215, find the heart rate immediately after exercising.
(b)If a world-class cyclist has a maximum heart rate of 180, find the heart rate immediately after exercising.
71.Ideal Gas For an ideal gas at low pressure, the volume V at T degrees Celsius is given by
![]()
76.where V0 is the volume at 0°C. At what temperature does ![]() for an ideal gas at low pressure?
for an ideal gas at low pressure?
72.Snow Cover Empirical studies of snowfall on the island of Great Britain found that the number of days D in a year on which the ground is covered with snow increases linearly with elevation:
![]()
where H is the elevation measured in meters.
(a)According to this formula, how many days of snow cover are there at sea level?
(b)At what elevation does this formula predict year-round (365-day) snow cover?
For Discussion
73.Point out the error in the following reasoning:
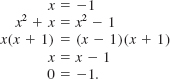
74.Consider the following sequence of equations:
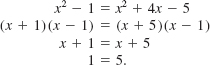
(a)What is the solution to the first equation in the sequence?
(b)Find an equation in the sequence that is not equivalent to the equation that precedes it.
2.2 Building an Equation from Words
![]() Introduction Algebra is useful in solving many practical problems involving rates, mixtures, money, and so on. Because these problems are often stated in words, the basic idea is to translate the words and build or construct an appropriate algebraic equation. Since there is no single procedure for making this translation, work, practice, and patience are required to become proficient in solving problems of this sort. The following suggestions may be helpful.
Introduction Algebra is useful in solving many practical problems involving rates, mixtures, money, and so on. Because these problems are often stated in words, the basic idea is to translate the words and build or construct an appropriate algebraic equation. Since there is no single procedure for making this translation, work, practice, and patience are required to become proficient in solving problems of this sort. The following suggestions may be helpful.

![]() Age Problems As our first example, consider the following age problem.
Age Problems As our first example, consider the following age problem.
EXAMPLE 1 An Age Problem
Two years ago John was five times as old as Bill. Now he is 8 years older than Bill. Find John's present age.
Solution The unknown quantity to be determined is John's present age, so we let
x = John's present age.
Then we can represent the other quantities in the problem in terms of x:
x – 8 = Bill's present age,
x – 2 = John's age 2 years ago,
(x – 8) – 2 = x – 10 = Bill's age 2 years ago.
You may find it helpful to list this information in tabular form, as shown below.
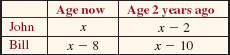
An equation that expresses the relationship of their ages 2 years ago is
![]()
We solve this equation:
![]()
Thus John's present age is 12.
Check: If John is now 12, Bill must be 4. Two years ago John was 10 and Bill was 2. Since 10 = 5(2), the answer checks.
![]() Investment Problems Many investment problems utilize the simple-interest formula
Investment Problems Many investment problems utilize the simple-interest formula
![]()
where I is the amount of interest earned on a sum of money P (called the principal) invested at a simple interest rate of r percent for t years. As the following example shows, it can be helpful to organize the data in tabular form.
EXAMPLE 2 Simple Interest
A businesswoman plans to invest a total of $30,000. Part of it will be put into a certificate of deposit (CD) paying 3% simple interest and the remainder into an investment fund yielding 5.5% simple interest. How much should she invest in each in order to obtain a 4% return on her money after 1 year?
Solution In (1) we identify r = 0.03 and t = 1. Now if x represents the amount (in dollars) invested in the CD, then
30,000 – x = the amount in dollars put into the investment fund.
The following table summarizes the given information.
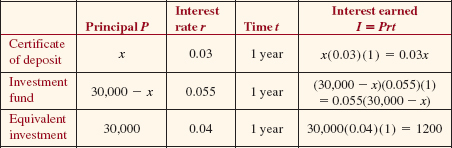
Since the combined interest from the CD and the investment fund is to equal that of an equivalent total investment made at 4% simple interest, we have
![]()
We begin our solution of the foregoing equation by multiplying it by 100:
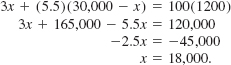
Thus, $18,000 should be invested in the CD, and $30,000 – $18,000 = $12,000 should be put into the investment fund.
Check: The sum of $18,000 and $12,000 is $30,000. The interest earned on the CD is ($18,000)(0.03)(1) = $540. The interest earned on the investment fund is ($12,000)(0.055)(1) = $660. If the $30,000 were invested at 4%, the interest earned would be ($30,000)(0.04)(1) = $1200. Since $540 + $660 = $1200, the answer checks.
![]() Rate Problems If an object moves at a constant rate r, then the distance d it travels in t units of time is given by distance = rate × time, or in symbols:
Rate Problems If an object moves at a constant rate r, then the distance d it travels in t units of time is given by distance = rate × time, or in symbols:
![]()
Other forms of (2) that may be useful in solving certain rate problems are
![]()
Usually the most difficult part of solving a distance problem is determining what relationship to express as an equation. It can be helpful to consider the following questions:
![]() Are there two distances (or times or rates) that are equal?
Are there two distances (or times or rates) that are equal?
![]() Is the sum of two distances (or times or rates) a constant?
Is the sum of two distances (or times or rates) a constant?
![]() Is the difference of two distances (or times or rates) a constant?
Is the difference of two distances (or times or rates) a constant?
The second equation in (3) is used in the next problem.
EXAMPLE 3 A Rate Problem
It takes a motorist 1 hour and 30 minutes longer to travel between two cities at night than it does during the day. At night she averages 40 mi/h while during the day she can average 55 mi/h. Find the distance between the two cities.
Solution Let the symbol d represent the distance between the two cities. The following table displays the distance, rate, and time for each trip.

Since it takes 1.5 h longer to travel the distance between the two cities at night, we have
![]()
We multiply both sides of this equation by (40)(55) = 2200 and solve:
![]()
The distance between the two cities is 220 mi.
Check: Her time at night is 220/40 = 5.5 h, and her time during the day is 220/55 = 4 h. Since 5.5 – 4 = 1.5, the answer checks.
![]() Mixture Problems occur frequently in chemistry, pharmacology, manufacturing, and everyday situations. When solving mixture problems, we focus on the amount of one element in each of the different mixtures. Again, it can be helpful to organize the information in tabular form, as we see in the following example.
Mixture Problems occur frequently in chemistry, pharmacology, manufacturing, and everyday situations. When solving mixture problems, we focus on the amount of one element in each of the different mixtures. Again, it can be helpful to organize the information in tabular form, as we see in the following example.
EXAMPLE 4 A Mixture Problem
Find how many liters of pure alcohol must be added to a 15-liter solution containing 20% alcohol so that the resulting mixture is 30% alcohol.
Solution If x represents the amount of pure alcohol added, then
15 + x = the amount in liters in the new solution.
The following table summarizes the given information.
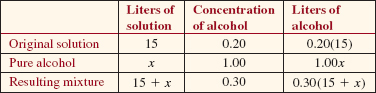
Since the amount of alcohol in the original solution plus the amount of pure alcohol added equals the amount of alcohol in the resulting mixture, we have
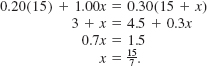
The amount of pure alcohol added is ![]()
Check: If ![]() L of alcohol is added, the new solution totaling
L of alcohol is added, the new solution totaling ![]() contains
contains ![]() of alcohol. Since
of alcohol. Since ![]() the new solution is 30% alcohol and the answer checks.
the new solution is 30% alcohol and the answer checks.
![]() Work Problems Several people (or machines) doing the same job, each working at a constant rate, can complete the job faster than any one of them working alone. Therefore, when solving work problems, we use the following basic principle:
Work Problems Several people (or machines) doing the same job, each working at a constant rate, can complete the job faster than any one of them working alone. Therefore, when solving work problems, we use the following basic principle:
![]()
For example, if one person can do an entire job in 5 h, then in 3 h, ![]() of the job can be done.
of the job can be done.
EXAMPLE 5 A Work Problem
Working alone, pump A can fill a tank in 2 h and pump B can fill the same tank in 3 h. Determine how fast the pumps can fill the tank working together.
Solution If we let x be the number of hours required for both pumps working together to fill the tank, then
![]() = the fractional part of the entire job completed in x hours by pump A
= the fractional part of the entire job completed in x hours by pump A
and
![]() = the fractional part of the entire job completed in x hours by pump B.
= the fractional part of the entire job completed in x hours by pump B.
This information is summarized in the following table.
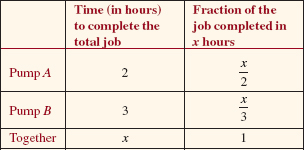
The sum of the fractional parts done by each pump in x hours is 1, since the two pumps working together complete the entire job in x hours. Thus we have
![]()
We begin by multiplying the equation by the least common denominator of the fractions in the equation. Then solving for x, we find
![]()
Together it takes the pumps ![]() (or 1 h and 12 min.) to fill the tank.
(or 1 h and 12 min.) to fill the tank.
Check: In ![]() h pump A fills
h pump A fills ![]() of the tank, and pump B fills
of the tank, and pump B fills ![]() of the tank. Because
of the tank. Because ![]() the solution checks.
the solution checks.
![]() Miscellaneous Problems In addition to the age, investment, rate, mixture, and work problems that we have just considered, there is a wide variety of word problems. We end this section with two additional examples.
Miscellaneous Problems In addition to the age, investment, rate, mixture, and work problems that we have just considered, there is a wide variety of word problems. We end this section with two additional examples.
EXAMPLE 6 A Fence Problem
A rectangular field that is 20 m longer than it is wide is enclosed with exactly 100 m of fencing. What are the dimensions of the field?
Solution The geometric description of this problem compels us to draw a diagram. See FIGURE 2.2.1. If we let w be the width of the field in meters, then
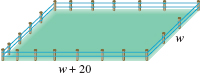
Field in Example 6
w + 20 = the length of the field in meters.
Since the perimeter of the field is 100 m, we have
![]()
or
![]()
Solving for w, we find
![]()
Thus the width is w = 15 m and the length is w + 20 = 35 m.
Check: The length is 20 m longer than the width since 35 – 15 = 20, and the amount of fencing required is 2(35) + 2(15) = 70 + 30 = 100. Thus the answers check.
EXAMPLE 7 Improving an Exam Grade Average
A student scores 75 and 82 on his first two exams. What score on the next exam will raise the student's average to 85?
Solution We begin by letting x denote the score on the future third exam. Then the average of the three exam scores is
![]()
Since this average must equal 85, we want
![]()
We multiply each side of the last equation by 3 and solve for x:
![]()
Therefore, a score of 98 on the third exam will raise the student's average score to 85.
Check: If the three exam scores are 75, 82, and 98, the student's average score will be
![]()
Hence the answer checks.

2.2 Exercises:Answers to selected odd-numbered problems begin on page ANS-3.
In Problems 1–46, build and solve an equation from the given words.
Number Problems
1.Find two integers whose sum is 50 and whose difference is 26.
2.The quotient of two numbers is 4. If one number is 39 less than the other, find the two numbers.
3.Find three consecutive integers whose sum is 48.
4.The difference of the squares of two consecutive even integers is 92. Find the two numbers.
Age Problems
5.In 5 years Bryan will be three times as old as he was 7 years ago. How old is Bryan?
6.The plumbing firm Papik and Son advertises a total of “30 years of experience” in plumbing. If the father has 16 years more plumbing experience than his son, how long has each been a plumber?
Investment Problems
7.A couple has $40,000 to invest. If they invest $16,000 at 12% and $14,000 at 8%, at what rate should they invest the remainder in order to have a yearly income of $4000 from their investments?
8.Mr. Janette has three investments from which he receives an annual income of $2780. One investment of $7000 is at an annual rate of 8%. Another investment of $10,000 is at an annual rate of 9%. What is the annual rate of interest he receives on the third investment of $12,000?
9.Ms. Beecham invested part of $10,000 in a savings certificate at 7% simple interest. She invested the remainder in a bond fund yielding 12%. If she received a total of $900 in interest for the first year, how much money was invested in the bond fund?
10.The Wilsons have $30,000 invested at 12% and another sum invested at 8.5%. If the yearly income on the total amount invested is equivalent to a rate of 10% on the total, how much do they have invested at 8.5%?
Rate Problems
11.A car travels from point A to point B at an average speed of 55 mi/h and returns at an average of 50 mi/h. If the round trip takes 7 h, find the distance between A and B.
12.A jet airplane flies with the wind between Los Angeles and Chicago in 3.5 h and flies against the wind from Chicago to Los Angeles in 4 h. If the speed of the plane in still air is 600 mi/h, find the speed of the wind. What is the distance between Los Angeles and Chicago?
13.A woman can walk to work at a rate of 3 mi/h, or she can bicycle to work at a rate of 12 mi/h. If it takes her 1 h longer to walk than to ride, find the time it takes her to walk to work.
14.A boy leaves point P on a bicycle and rides at a speed of 15 km/h. Thirty minutes later another boy leaves point P on a bicycle and rides at a different speed. He overtakes the first rider 2½ h later. Find the speed of the second rider.
15.A man drove a car 280 km and then rode a bicycle an additional 50 km. If the total time for the trip was 12 h and the speed on the bicycle was ¼ of the speed driving, find each rate.
16.An instrument capsule was carried into the atmosphere by a rocket. The capsule landed 72 min later, after making a controlled descent with an average vertical speed of 420 km/h. If the rocket had an average vertical speed of 1010 km/h from liftoff to release of the capsule, at what height was the capsule released?
Mixture Problems
17.An automobile radiator contains 10 qt of a mixture of water and antifreeze that is 20% antifreeze. How much of this mixture must be drained out and replaced with pure antifreeze in order to obtain a 50% mixture in the radiator?
18.A lawn mower uses a fuel mixture of 23 parts gasoline to 1 part oil. How much gasoline should be added to a liter of a mixture that is 5 parts gasoline and 1 part oil in order to obtain the right mixture?
19.A certain brand of potting soil contains 10% peat and another brand contains 30% peat. How much of each soil should be mixed in order to produce 2 ft3 (cubic feet) of potting soil that is 25% peat?
20.The manager of a service station bought a total of 15,000 gallons of regular and premium gasoline for $37,000. If the wholesale price was $2.40 per gallon for the regular gas and $2.60 per gallon for the premium gas, determine how many gallons of each type of gasoline were purchased.
21.A grocer sells one grade of ground beef at $3.95 per pound and another grade at $4.20 per pound. He wants to mix the two grades in order to obtain a mixture that sells for $4.15 per pound. What percentage of each grade should be used?
Work Problems
22.If Meagan can complete a task in 50 min working alone and Colleen can do it alone in 25 min, how long will it take them working together?
23.If Karen can pick a raspberry patch in 6 h and Stan can pick it in 8 h, find how fast they can harvest the patch together.
24.Using two hoses of different diameters, a homeowner can fill a hot tub in 40 min. If one hose alone can fill the tub in 90 min, find how fast the other hose would fill the tub by itself.
25.Margot can clean her room alone in 50 min. If Jeremy helps her, it takes 30 min. How long would it take Jeremy alone to clean the room?
26.An outlet pipe can empty a tank in 4 h. The pipe was opened for 1.5 h and then closed. At that time a second outlet pipe was opened and it took 2 h to finish emptying the tank. How long would it have taken the second pipe alone to empty the tank?
Dimension Problems
27.The perimeter of a rectangle is 50 cm and the width is ![]() of the length. Find the dimensions of the rectangle.
of the length. Find the dimensions of the rectangle.
28.The area of a trapezoid is 250 ft2 and the height is 10 ft. What is the length of the long base if the short base is 20 ft?
29.The longest side of a triangle is 2 cm longer than the shortest side. The third side is 5 cm less than twice the length of the shortest side. If the perimeter is 21 cm, how long is each side?
30.A farmer wishes to enclose a rectangular field and to divide it into three equal parts with fencing. See FIGURE 2.2.2. If the length of the field is three times the width and 1000 m of fencing is required, what are the dimensions of the field?
![]()
Fenced field in Problem 30
31.The area of a circle is 80π cm2 less than the area of a circle whose radius is 4 cm larger. Find the radius of the smaller circle.
Miscellaneous Problems
32.Dose of a Medicine Friend's rule for converting an adult dose of a drug to a child's dose assumes a relationship between age and dosage and is used for children under 2 years of age:
![]()
At what age is the adult dosage 10 times that of the child's dosage?
33.Joshua Battles for a Passing Grade Joshua has taken one exam. If he must score 99 on a second exam in order to have an average of 73 for both exams, what did he score on the first exam?
34.Trying for a B Going into the final exam a student has test scores of 72 and 86. If the final exam counts as one half of the final grade, what exam score must the student make in order to finish the course with an average of 80?
35.Class Politics Judy defeated John in a close election for senior class president in which 211 votes were cast. If five students had voted for John instead of Judy, then John would have won by one vote. How many students voted for Judy?
36.How Many? At Cayley Avenue School, 40 more than half the students are boys. If the number of girls at the school is two less than half the number of boys, how many students attend the school?
37.A Coin Problem Kurt has four more dimes than nickels. If the total value of these coins is $2.35, find how many nickels and dimes Kurt has.
38.Another Coin Problem Heidi has $4.65 in nickels, dimes, and quarters. She has four more quarters than dimes and five more nickels than quarters. How many coins of each type does Heidi have?
39.Playing with Numbers The units digit of a 2-digit number is five more than the 10's digit. If the original number is divided by the number with its digits reversed, the result is ![]() . Find the original number.
. Find the original number.
40.More Playing with Numbers The denominator of a fraction is two more than the numerator. If both the numerator and the denominator are increased by one, the resulting fraction equals ![]() . Find the original number.
. Find the original number.
41.Bribery? Mr. Chaney and his son Ryan agreed that Mr. Chaney would give Ryan $5 for each word problem Ryan solved correctly but Ryan would pay his father $2 for each incorrect solution. After Ryan had completed 70 problems, neither owed the other any money. How many word problems had Ryan solved correctly?
42.Got a Raise A worker gets a 6% raise, which is $480. What was the old salary? What is the new salary?
43.Pay for Itself? A local gas company sells an insulating blanket for a hot water heater for $20. It claims that the blanket will reduce fuel costs by 10%. If the average monthly fuel cost for heating water is $20, how soon will the insulation “pay for itself”?
44.Paying Taxes A restaurant manager provides a no-host bar at a banquet with drinks priced at round dollar amounts to simplify the transactions. The 5% sales tax is included in the rounded prices. At the end of the banquet, the manager finds exactly $200 in the register. He is smart enough to know that $10 is too much to take out for the tax, but he is unable to figure out the proper amount of tax to pay.
(a).Explain why $10 is too much tax.
(b).Find the correct amount of sales tax (to the nearest penny).
45.Clerk in Need of More Training During 25%-off sales one store clerk always computes the discount first and then adds on the 6% sales tax. Another clerk in the same store always adds the sales tax first and then applies the discount.
(a).Does it make a difference?
(b).Can you show that this is always the case for any discount d% and any sales tax t%?
46.Competing Plants Two industrial plants that manufacture identical engine components are located 100 mi apart on the Watchacallit River. See FIGURE 2.2.3. Both plants sell components at the same price, $150. However, because one plant is upstream, its shipping costs are lower for customers located between the two plants: 30 cents per mile per component rather than 75 cents per mile.
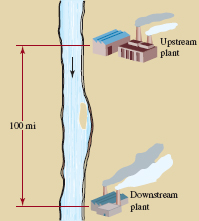
Industrial plants in Problem 46
(a).Assuming that a customer will buy from the plant offering the lowest total cost, how far up the river will the downstream plant have customers?
(b).How does your answer to part (a) change if both plants raise the price of their components from $150 to $160?
(c).How does your answer to part (a) change if shipping costs double?
(d).What selling price would the downstream plant have to offer in order to capture half of the territory between the two industrial plants?
2.3 Quadratic Equations
![]() Introduction In Section 2.1 we saw that a linear equation is an equation that can be put into the standard form ax + b = 0, a ≠ 0. The equation ax + b = 0, a ≠ 0, is a special type of polynomial equation. A polynomial equation of degree n is an equation of the form
Introduction In Section 2.1 we saw that a linear equation is an equation that can be put into the standard form ax + b = 0, a ≠ 0. The equation ax + b = 0, a ≠ 0, is a special type of polynomial equation. A polynomial equation of degree n is an equation of the form
![]()
where n is a nonnegative integer and ai, i = 0, 1,…, n, are real numbers. A linear equation corresponds to the degree n = 1 in equation (1). Except for different symbols, ax + b is the same as a1x + a0.
A solution of a polynomial equation is also called a root of the equation. For example, we know that ![]() is the only root of the linear or first-degree polynomial equation ax + b = 0.
is the only root of the linear or first-degree polynomial equation ax + b = 0.
In this section we examine polynomial equations of degree 2 or quadratic equations. A quadratic equation is a polynomial equation that can be written in the standard form:
![]()
Polynomial equations of higher degrees will be studied in Chapter 005.
Many problems about moving objects involve quadratic equations. For example, if a water balloon is thrown with an initial velocity of 48 ft/s, straight down from a dormitory window 64 ft above the ground, then the height s (in feet) above the ground after t seconds can be shown to be
![]()
When the balloon hits the ground, its height 5 equals 0, so we can determine the elapsed time by solving
![]()
By dividing by – 16 the foregoing equation is equivalent to
![]()
![]() Method of Factoring As we will see, equation (3) is easily solved by the method of factoring. This method is based on the zero factor property, which was introduced in Section 1.1. Recall, if a and b represent real numbers and a · b = 0, then either a = 0 or b = 0. The technique is illustrated in the following example.
Method of Factoring As we will see, equation (3) is easily solved by the method of factoring. This method is based on the zero factor property, which was introduced in Section 1.1. Recall, if a and b represent real numbers and a · b = 0, then either a = 0 or b = 0. The technique is illustrated in the following example.
EXAMPLE 1 Solution by Factoring
Solve 2x2 + 5x – 3 = 0.
Solution The equation is already in standard form. By factoring the left-hand side of the given equation, we obtain the equivalent equation
![]()
If we apply the zero factor property, we conclude that either
![]()
The solutions of these linear equations are x = –3 and x = ½, respectively. The fact that these are roots of the given equation can be verified by substitution. The solution set is ![]()
We can now readily solve equation (3) to find the time it takes the water balloon to strike the ground. We first write t2 + 3t – 4 = 0 in the factored form:
![]()
From the zero factor property we find that we must solve t + 4 = 0 and t – 1 = 0. The solutions of these equations are t = –4 and t = 1. By substitution we can verify that both t = –4 and t = 1 satisfy the original quadratic equation – 16t2 – 48t + 64 = 0. Because t = 1 second is the only positive solution, it is the only meaningful answer to the physical problem.
EXAMPLE 2 Solution by Factoring
Solve 12x2 + 15x = 18.
Solution Since we plan to try the method of factoring, we must begin by writing the equation in the standard form ax2 + bx + c = 0:
![]()
Eliminating the common factor 3 by division simplifies the equation
![]()
to
Factoring then gives
![]()
Using the zero factor property, we set each factor equal to zero to obtain 4x – 3 = 0 and x + 2 = 0. Solving each of these equations gives x = ¾ and x = –2. The roots of the quadratic equation are ¾ and –2; the solution set is {–2, ¾}.
EXAMPLE 3 Solution by Factoring
Solve 4x2 + 4x + 1 = 0.
Solution The left-hand side of the equation readily factors as
![]()
and so x = –½ or x = –½. The solution set is {–½}.
In Example 3, we say that x = –½ is a repeated root or a root of multiplicity 2. When counting roots we count such roots twice.
![]() Square Root Method If a quadratic equation has the special form
Square Root Method If a quadratic equation has the special form
![]()
we can solve it by factoring:
![]()
which yields ![]() or
or ![]() An alternative approach to solving Equation (4) is to take the square root of both sides of the equation. This is summarized as the square root method:
An alternative approach to solving Equation (4) is to take the square root of both sides of the equation. This is summarized as the square root method:
![]()
EXAMPLE 4 Solution by Square Root Method
Use the square root method to solve (a) 2x2 = 6 (b) (y – 3)2 = 5.
Solution (a) We multiply both sides of 2x2 = 6 by ½ to obtain the special form (4):
![]()
From the last line we see that the solution set is ![]()
(b) We note that for x = y – 3 and d = 5, the equation (y – 3)2 = 5 has the special form (4). Therefore, we take the square root of both sides of the equation:
![]()
This yields two linear equations y – 3 = – ![]() and y – 3 =
and y – 3 = ![]() . Solving each of these, we find y = 3 –
. Solving each of these, we find y = 3 – ![]() and y = 3 +
and y = 3 + ![]() , respectively. Therefore, the solution set is
, respectively. Therefore, the solution set is ![]()
![]() Completing the Square When a quadratic expression cannot be factored easily and the equation does not have the special form (4), we can find the roots by completing the square. This technique is applied to quadratic expressions of the form x2 + Bx + C; that is, the quadratic expression must have 1 as its leading coefficient. We rewrite the equation
Completing the Square When a quadratic expression cannot be factored easily and the equation does not have the special form (4), we can find the roots by completing the square. This technique is applied to quadratic expressions of the form x2 + Bx + C; that is, the quadratic expression must have 1 as its leading coefficient. We rewrite the equation
![]()
so that only the terms containing the variable x are on the left-hand side of the equation:
![]()
By adding (B/2)2 to both sides of the last equation,
![]()
the left-hand side of the resulting equation is a perfect square:
![]()
It is now easy to solve for x using the square root method. This procedure is illustrated in the following example.
EXAMPLE 5 Solution by Completing the Square
Solve 2x2 + 2x – 1 = 0 by completing the square.
Solution We begin by dividing both sides of the equation by the leading coefficient 2 to obtain the form (5):
![]()
Now we write this equation as
![]()
and add the square of half the coefficient of x (in this case it is 1) to both sides of the equation:
![]()
Thus we have
![]()
Taking the square root of both sides of the equation gives
![]()
The two solutions, or roots, then are ![]() and –
and –![]() respectively. The solution set of the equation is
respectively. The solution set of the equation is ![]()
![]() The Quadratic Formula The technique of completing the square on a quadratic expression is very useful in other situations. We will encounter it again in Chapters 3, 4, and 7. For now its value is to help us derive a formula that expresses the roots of ax2 + bx + c = 0, a ≠ 0, in terms of the coefficients a, b, and c. First we rewrite the equation so that it has leading coefficient 1:
The Quadratic Formula The technique of completing the square on a quadratic expression is very useful in other situations. We will encounter it again in Chapters 3, 4, and 7. For now its value is to help us derive a formula that expresses the roots of ax2 + bx + c = 0, a ≠ 0, in terms of the coefficients a, b, and c. First we rewrite the equation so that it has leading coefficient 1:
![]()
Then we complete the square and solve for x:

If a > 0, then ![]() and we have
and we have
![]()
This result is known as the quadratic formula. If a < 0, then ![]() and, after simplification, we see that the result in (6) is still valid.
and, after simplification, we see that the result in (6) is still valid.

![]() The Discriminant The nature of the roots x1 and x2 of a quadratic equation ax2 + bx + c = 0 is determined by the radicand b2 – 4ac in the quadratic formula (6). The quantity b2 – 4ac is called the discriminant of the quadratic equation. The discriminant must be positive, zero, or negative. These three possible cases are summarized next.
The Discriminant The nature of the roots x1 and x2 of a quadratic equation ax2 + bx + c = 0 is determined by the radicand b2 – 4ac in the quadratic formula (6). The quantity b2 – 4ac is called the discriminant of the quadratic equation. The discriminant must be positive, zero, or negative. These three possible cases are summarized next.
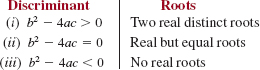
EXAMPLE 6 Solution by the Quadratic Formula
Solve 3x2 – 2x – 4 = 0.
Solution Here we identify a = 3, b = –2, and c = –4. The positive discriminant b2 – 4ac = 13 implies that the given equation has two real distinct roots. From the quadratic formula (6) we find
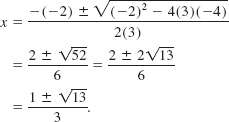
Therefore, the roots are ![]() and
and ![]()
EXAMPLE 7 Repeated Roots
Solve 9x2 + 16 = 24x
Solution To use the quadratic formula, we must first write the equation in the form 9x2 – 24x + 16 = 0. The quadratic formula
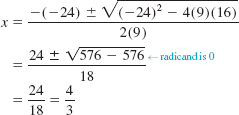
shows that ![]() is a repeated root or a root of multiplicity 2.
is a repeated root or a root of multiplicity 2.
EXAMPLE 8 No Real Roots
Solve 3x2 – x + 2 = 0.
Solution Since the discriminant
![]()
is negative, we conclude that the given equation has no real roots.
![]() Quadratic Forms Certain polynomial equations of degree greater than 2 can be solved using the quadratic formula. This demands that we recognize that the equation can be put into the standard quadratic form at2 + bt + c = 0, where the symbol t represents some positive integer power of x. The next example illustrates this idea.
Quadratic Forms Certain polynomial equations of degree greater than 2 can be solved using the quadratic formula. This demands that we recognize that the equation can be put into the standard quadratic form at2 + bt + c = 0, where the symbol t represents some positive integer power of x. The next example illustrates this idea.
EXAMPLE 9 A Fourth-Degree Polynomial Equation
Solve x4 – 2x2 – 2 = 0.
Solution This polynomial equation can be considered as a quadratic equation in the variable x2, that is,
![]()
Using the quadratic formula to solve for the symbol x2 we have
![]()
Thus, either
![]()
Now, the quadratic equation x2 = 1 – ![]() has no real roots since 1 –
has no real roots since 1 – ![]() < 0. But from x2 = 1 +
< 0. But from x2 = 1 + ![]() we obtain two real roots,
we obtain two real roots,![]() and
and ![]() of the original equation.
of the original equation.
![]() The square of any real number is nonnegative.
The square of any real number is nonnegative.
We conclude this section with several applications that involve quadratic equations.
EXAMPLE 10 A Rectangle Problem
The area of a rectangle is 138 in2. If the length is 5 in. more than 3 times the width, find the dimensions of the rectangle.
Solution We begin by drawing and labeling a rectangle, as shown in FIGURE 2.3.1. We let

Rectangle in Example 10
w = the width of the rectangle in inches. |
|
Then |
3w + 5 = the length of the rectangle in centimeters |
and |
w(3w + 5) = 138. |
In order to use the quadratic formula we rewrite this equation in standard form:
![]()
From the quadratic formula, we find that either ![]() or w = 6. Since the width of a rectangle must be positive, we discard the solution
or w = 6. Since the width of a rectangle must be positive, we discard the solution ![]() . Therefore, we take w = 6. Then the length is 3(6) + 5 = 23, and the dimensions ofthe rectangle are 6 in. by 23 in.
. Therefore, we take w = 6. Then the length is 3(6) + 5 = 23, and the dimensions ofthe rectangle are 6 in. by 23 in.
Check: Since 23 = 3(6) + 5 and 6(23) = 138, the answer checks.
![]() Pythagorean Theorem The Pythagorean theorem is one of the most widely used theorems from geometry. Many of its applications involve quadratic equations. Although it is named after the Greek mathematician Pythagoras, (c. 540 BCE), the result was known prior to his time. The theorem states that in a right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. For a right triangle as shown in FIGURE 2.3.2, we have the following formula:
Pythagorean Theorem The Pythagorean theorem is one of the most widely used theorems from geometry. Many of its applications involve quadratic equations. Although it is named after the Greek mathematician Pythagoras, (c. 540 BCE), the result was known prior to his time. The theorem states that in a right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides. For a right triangle as shown in FIGURE 2.3.2, we have the following formula:
![]()
There are a wide variety of algebraic and geometric proofs of this theorem. See Problems 91 and 92 in Exercises 2.3.
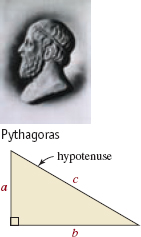
Right triangle
EXAMPLE 11 A Sidewalk Problem
In a park two sidewalks at right angles join the playground P, the refreshment stand R, and the parking lot L, as shown in FIGURE 2.3.3. The total length of the sidewalks is 700 m. By walking diagonally across the grass (dashed red line) directly from the parking lot L to the playground P, children can shorten the distance by 200 m. What are the lengths of the sidewalks?

Sidewalks and diagonal shortcut in Example 11
Solution If we let
x = the length of the sidewalk from P to R, |
|
then |
700 –xs x = the length of the sidewalk from R to L. |
Since the distance from P to L is 200 m less than the total length of the two sidewalks, we have
700 – 200 = 500 = the distance from P to L.
From the Pythagorean theorem, we obtain the following relationship:
![]()
We rewrite this equation and solve by factoring:
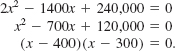
From the last form of the equation we see immediately that x = 400 or x = 300. Referring to FIGURE 2.3.3, if we use x = 400, we find that the length of the sidewalk from the playground to the refreshment stand is 400 m and the length of the sidewalk from the refreshment stand to the parking lot is 700 – 400 = 300 m. From >x = 300, we find that these distances are reversed. Thus there are two possible solutions to this problem.
Check: The solution checks because
![]()
EXAMPLE 12 Bottles of Wine
A wine broker spent $800 for some bottles of reserve California cabernet sauvignon wine. If each bottle had cost $4 more, the broker would have obtained 10 fewer bottles for the $800. How many bottles were purchased?
Solution The solution of this problem is based on the following relationship:
![]()
For the actual purchase, if we let
x = the number of bottles purchased,
then ![]() = the cost per bottle.
= the cost per bottle.
At the more expensive price,
x – 10 = the number of bottles purchased
and ![]() = the cost per bottle.
= the cost per bottle.
Using this information in the relationship (8), we obtain the equation
![]()
which we solve for x as follows:
![]()
The quadratic formula gives
![]()
and so x = 50 or x = –40. Since we must have a positive number of bottles purchased, we find that 50 bottles of wine were purchased.
Check: If 50 bottles were purchased for $800, the cost per bottle was $800/50 = $16. If each bottle cost $4 more, then the price per bottle would have been $20. At this more expensive price, only 800/20 = 40 bottles could have been purchased for $800. Since 50 – 10 = 40, the answer checks.

2.3 Exercises:Answers to selected odd-numbered problems begin on page ANS-3.
In Problems 1–16, solve the equation by factoring.
1. x2 – 16 = 0
2. y2 – 17y + 16 = 0
3. 2x2 + x – 1 = 0
4. 8t2 – 22t + 15 = 0
5. 1 + 4x + 4x2 = 0
6. 4 + 5z – 6z2 = 0
7. u2 + 12 =7u
8. v2 + 5v = –4
9. 25y2 + 15y = –2
10. 2a2 = a + 1
11. 16b2 – 1 = 0
12. 25 – c2 = 0
13. x3 – 9x = 0
14. 16p4 – p2 = 0
15. 4q5 – 25q3 = 0
16. x4 – 18x2 + 32 = 0
In Problems 17–22, solve using the square root method.
17. x2 = 17
18. 2y2 = 100
19. (v + 5)2 = 5
20. 5(w – 1)2 = 4
21. 3(t + 1)2 = 9
22. 4(s – 3)2 = 5
In Problems 23–26, solve for x. Assume a, b, c, and d represent positive real numbers.
23. x2 – b2 = 0
24. x2 + 2dx + d2 = 0
25. (x – a)2 = b2
26. (x + c)2 = d2
In Problems 27–34, solve by completing the square.
27. u2 + 2u – 1 = 0
28. v2 + 3v – 2 = 0
29. 2k2 + 5k + 3 = 0
30. 4b2 – 4b – 35 = 0
31. 10x2 – 20x + 1 = 0
32. 36 – 16w – w2 = 0
33. 9t2 = 36t – 1
34. r = 4r2 – 1
In Problems 35–46, solve using the quadratic formula.
35. 3x2 – 7x + 2 = 0
36. 4x2 – 12x + 9 = 0
37. 9z2 + 30z + 25 = 0
38. 1 + 2w – 6w2 = 0
39. 2 + 5r – 10r2 = 0
40. 8t = –(16t2 + 1)
41. 3s – 2s2 = ![]()
42. ½x2 + x = 5
43. 2c(c – 1) = 1
44. 4x2 = 2(x + 1)
45. x4 – 6x2 + 7 = 0
46. y4 – 2y2 = 4
In Exercises 47–56, solve the equation using any method.
47. 3s2 – 13s + 4 = 0
48. 4x2 + 8x + 4 = 0
49. s2 – 4s – 4 = 0
50. 2.4 + 1.0y + 0.1y2 = 0
51. 8t2 + 10t + 5 = 0
52. r2 + 2r = 35
53. 24t3 – 3t = 0
54. 9u2 + 25 = 30u
55. 4p2 = 60
56. 5(c + 1)2 = 25
In Problems 57–62, the given formula occurs frequently in applications. Solve for the indicated variables in terms of the remaining variables. Assume that all variables represent positive real numbers.
57. Volume of a cylinder
![]()
58. Area of a circle
![]()
59. Surface area of a cylinder
![]()
60. Equation of an ellipse
![]()
61. Free-falling body
![]()
62. Newton's universal gravitation law
![]()
63. Determine all values of d so that x2 + (d + 6)x + 8d = 0 has two equal roots.
64. Determine all values of d so that 3dx2 – 4dx + d + 1 = 0 has two equal roots.
65. Determine the other root of (k – 2)x2 – x – 4k = 0, given that one root is –3.
66. If x1 and x2 are two real roots of the quadratic equation ax2 + bx + c = 0, then show that x1 + x2 = – b/a and x1 · x2 = c/a.
Miscellaneous Applications
67. Playing with Numbers The sum of two numbers is 22, and the sum of their squares is 274. Find the numbers.
68. Playing with Numbers The product of two numbers is 1 more than 3 times their sum. Find the numbers if their difference is 9.
69. Area of a Triangle The base of a triangle is 3 cm longer than the altitude. If the area of the triangle is 119 cm2, find the base and the altitude.
70. How Long? On a 35-km hike one boy walks ½ km/h faster than another boy. If he makes the trip in 1 h and 40 min less time than the other boy, find how long it takes each boy to make the hike.
71. Planting a Garden Barbara has planned a rectangular vegetable garden with a perimeter of 76 m and an area of 360 m2. Find the dimensions of her garden.
72. Distance A baseball diamond is a square that is 90 ft on a side. Find the distance from third base to first base.
73. Area If a square playing field has a diagonal length of 100 ft, find the area of the field.
74. Garden Trim A flower garden is in the shape of an isosceles right triangle with a hypotenuse of 50 ft. How many feet of redwood bender board are required to edge it?
75. Length of Sides Suppose that the hypotenuse of a right triangle is 10 cm longer than one of the sides and that side is 10 cm longer than the other side. Find the lengths of the three sides of this right triangle.
76. How Far? A 17-ft ladder is positioned against the side of a house so that its base is 8 ft from the house. If it slips so that the base of the ladder is 10 ft from the house, how far does the top of the ladder slide down the side of the house?
77. Distance Two motorboats leave a dock at the same time. One travels north at a speed of 18 mi/h and the other travels west at 24 mi/h. Find the distance between them after 3 h.
78. Speed A motorcyclist travels at a constant speed for 60 mi. If he had gone 10 mi/h faster, he would have shortened his traveling time by 1 h. Find the speed of the motorcyclist.
79. How Fast? James took 1 h more than John to drive a 432-mi trip at an average speed of 6 mi/h less than John. How fast did they each drive?
80. How Many? A group of women plan to share equally in the $14,000 cost of a boat. At the last minute three of the women drop out, which raises the share for each of the remaining women by $1500. How many women were in the original group?
81. How Many? Mr. Arthur buys some stock for $720. If he had bought the stock the day before when the price per share was $15 less, he could have purchased four additional shares. How many shares did Mr. Arthur buy?
82. Find the Dimensions A rectangular garden is surrounded by a gravel path that is 2 ft wide. The area covered by the garden is 80 ft2, and the area covered by the sidewalk is 108 ft2. Find the dimensions of the garden.
83. Width A 50-m by 24-m rectangular grassy area has a sidewalk surrounding it. If the area covered by the sidewalk is 480 m2, what is its width?
84. Building an Open Container A container is made from a square piece of tin by cutting a 3 in. square piece from each corner and bending up the sides. See FIGURE 2.3.4. If the container is to have a volume of 48 in3, find the length of a side of the original piece of tin.
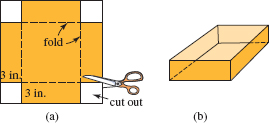
Container in Problem 84
85. Building an Open Box Maria has a piece of cardboard that is twice as long as it is wide. If she cuts out 2-in. squares from the corner and bends up the sides to form a box with no top, she will have a box with a volume of 140 in3. Find the dimensions of the original piece of cardboard.
86. Length A wire that is 32 cm long is cut into two pieces, and each piece is bent to form a square. The total area enclosed is 34 cm2. Find the length of each piece of wire.
87. How Far? If an object is projected upward from the ground at an angle of 45° with an initial velocity of v0 meters per second, then the height y in meters above the ground at a horizontal distance of x meters from the point of projection is given by the formula
![]()
See FIGURE 2.3.5. If a projectile is launched at a 45° angle with an initial velocity of 12 m/s, how far from the projection point will it land?
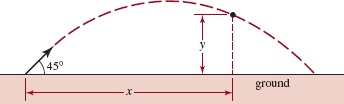
Projectile in Problem 87
88. How Far? If a fountain spouts water at an angle of 45° with a velocity of 7 m/s, how far from the spout will the water splash into the pool? See FIGURE 2.3.6 and Problem 87.

Fountain in Problem 88
For Discussion
In Problems 89 and 90, use the notion of a quadratic equation to solve the given equation. [Hint: Review Section 1.5.]
89. ![]()
90. ![]()
91. One of the shortest proofs of the Pythagorean theorem was given by the Hindu scholar Bhaskara (c. 1150 CE). He offered the diagram shown in FIGURE 2.3.7 without the labeling to assist the reader. His only “explanation” was the word “Behold!” Assume that a square of side c can be divided into four congruent right triangles and a square of length b – a as shown. Prove that a2 + b2 = c2.
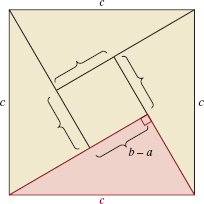
Square in Problem 91
92. Assuming that a square of side a + b can be divided in two ways, as in FIGURE 2.3.8, prove the Pythagorean theorem.
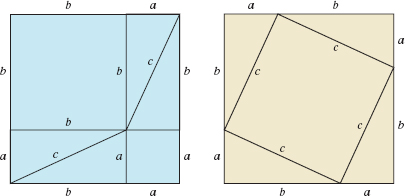
Squares in Problem 92
2.4 Complex Numbers
![]() Introduction In the preceding section we saw that some quadratic equations have no real solutions. For example, x2 + 1 = 0 has no real roots because there is no real number x such that x2 = – 1. In this section we study the set of complex numbers, which contains solutions to equations such as x2 + 1 = 0. The set of complex numbers C contains the set of real numbers R as well as numbers whose squares are negative.
Introduction In the preceding section we saw that some quadratic equations have no real solutions. For example, x2 + 1 = 0 has no real roots because there is no real number x such that x2 = – 1. In this section we study the set of complex numbers, which contains solutions to equations such as x2 + 1 = 0. The set of complex numbers C contains the set of real numbers R as well as numbers whose squares are negative.
To obtain the complex numbers C, we begin by defining the imaginary unit, denoted by the letter i, as the number that satisfies
![]()
It is common practice to write
![]()
With i we are able to define the principal square root of a negative number, as follows. If c is a positive real number, then the principal square root of – c, denoted ![]() is defined by
is defined by
![]()
EXAMPLE 1 Principal Square Roots
Find the principal square root of (a) ![]() and (b)
and (b) ![]()
Solution From (1),
(a)![]()
(b)![]()
![]() Terminology The complex number system contains the imaginary unit i, all real numbers, products such as bi, b real, and sums such as a + bi, where a and b are real numbers. In particular, a complex number is defined to be any expression of the form
Terminology The complex number system contains the imaginary unit i, all real numbers, products such as bi, b real, and sums such as a + bi, where a and b are real numbers. In particular, a complex number is defined to be any expression of the form
![]()
where a and b are real numbers and i2 = – 1. The form given in (2) is called the standard form of a complex number. The numbers a and b are called the real and imaginary parts of z, respectively. A complex number of the form 0 + bi is said to be a pure imaginary number. Note that by choosing b = 0 in (2), we obtain a real numbe r. Thus the set R of real numbers is a subset of the set C of complex numbers.
EXAMPLE 2 Real and Imaginary Parts
The complex number z = 4 + (–5)i is written as z = 4 – 5i. The real part of z is 4 and its imaginary part is –5.
z = 10i is a pure imaginary number.
z = 6 + 0i = 6 is a real number.
EXAMPLE 3 Writing in the Standard Form a + bi
Express each of the following in the standard form a + bi.
![]()
![]()
Solution Using ![]() we can write
we can write
![]()
![]()
In order to solve certain equations involving complex numbers, it is necessary to specify when two complex numbers are equal.
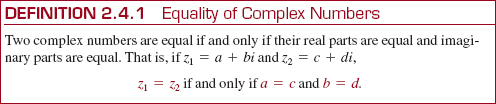
EXAMPLE 4 A Simple Equation
Solve for x and y:
![]()
Solution By Definition 2.4.1 we must have
![]()
Solving each equation yields x = ½ and y = ![]() .
.
Addition and multiplication for complex numbers are defined as follows.

![]() Properties of Complex Numbers In Section 1.1 we stated the basic properties for the real number system. Using the definition of addition and multiplication of complex numbers, it can be shown that these basic properties also apply to the complex number system. In particular, the associative, commutative, and distributive laws hold for complex numbers. We further observe that in Definition 2.4.2(i):
Properties of Complex Numbers In Section 1.1 we stated the basic properties for the real number system. Using the definition of addition and multiplication of complex numbers, it can be shown that these basic properties also apply to the complex number system. In particular, the associative, commutative, and distributive laws hold for complex numbers. We further observe that in Definition 2.4.2(i):
![]() The sum of two complex numbers is obtained by adding their corresponding real and imaginary parts.
The sum of two complex numbers is obtained by adding their corresponding real and imaginary parts.
Similarly, Definition 2.4.2(ii) shows that
The difference of two complex numbers is obtained by subtracting their corresponding real and imaginary parts.
Also, rather than memorizing (iii) of Definition 2.4.2:
The product of two complex numbers can be obtained by using the associative, commutative, and distributive laws and the fact that i2 = –1.
Applying this approach, we find that
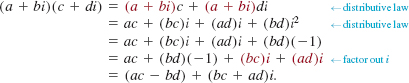
This is the same result as the product given by Definition 2.4.2(iii). These techniques are illustrated in the following example.
EXAMPLE 5 Sum, Difference, and Product
If z1 = 5 – 6i and z2 = 2 + 4i, find (a) z1 + z2, (b) z1 – z2, and (c) z1z2.
Solution(a) The colors in the diagram below show how to add z1 and z2:
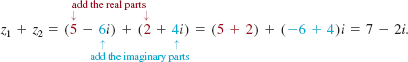
(b)Analogous to part (a) we now subtract the real and imaginary parts:
![]()
(c)Using the distributive law, we write the product (5 – 6i)(2 + 4i) as
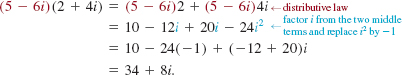
Not all the properties of the real number system hold for complex numbers. In particular, the property of radicals ![]() is not true when both a and b are negative. To see this, consider that
is not true when both a and b are negative. To see this, consider that
![]()
Thus, ![]() However, if only one of a or b is negative, then we do have
However, if only one of a or b is negative, then we do have ![]()
In the set C of complex numbers, the additive identity is the number0 = 0 1 0i, and the multiplicative identity is the number1 = 1 + 0i. The number –z = –a – bi is called the additive inverse of z = a + bi because
![]()
In order to obtain the multiplicative inverse of a nonzero complex number z = a + bi, we introduce the concept of the conjugate of a complex number.

In other words, the conjugate of a complex number z = a + bi is the complex number obtained by changing the sign of its imaginary part. For example, the conjugate of 8 + 13i is 8 – 13i, and the conjugate of –5 – 2i is –5 + 2i.
The following computations show that both the sum and the product of a complex number z and its conjugate ![]() are real numbers:
are real numbers:
![]()
![]()
The latter property makes conjugates very useful in finding the multiplicative inverse 1/z, z ≠ 0, and in dividing two complex numbers.
We summarize the procedure.
![]() To divide a complex number z1 by a complex number z2, multiply the numerator and denominator of z1/z2 by the conjugate of the denominator z2. That is,
To divide a complex number z1 by a complex number z2, multiply the numerator and denominator of z1/z2 by the conjugate of the denominator z2. That is,
![]()
![]() and then use the fact that the product z2
and then use the fact that the product z2![]() 2 is the sum of the squares of the real and imaginary parts of z2.
2 is the sum of the squares of the real and imaginary parts of z2.
EXAMPLE 6 Division
For z1 = 3 – 2i and z2 = 4 + 5i, express the given complex number in the form a + bi.
(a)![]()
(b)![]()
Solution In each case, we multiply both the numerator and the denominator by the conjugate of the denominator and simplify.
(a)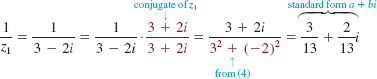
(b)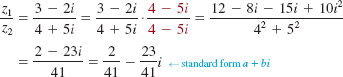
From the definition of addition and subtraction of two complex numbers, it is readily shown that the conjugate of a sum and difference of two complex numbers is the sum and difference of the conjugates. This property, along with three other properties of the conjugate are summarized as a theorem.

Of course, the conjugate of any finite sum (product) of complex numbers is the sum (product) of the conjugates.
![]() Quadratic Equations Complex numbers make it possible to solve quadratic equations ax2 + bx + c = 0 when the discriminant b2 – 4ac is negative. We now see that the solutions from the quadratic formula
Quadratic Equations Complex numbers make it possible to solve quadratic equations ax2 + bx + c = 0 when the discriminant b2 – 4ac is negative. We now see that the solutions from the quadratic formula
![]()
represent complex numbers. Note that in fact the solutions are conjugates of each other. As the next example shows these solutions can be written in the form z = a + bi.
EXAMPLE 7 Complex Solutions
Solve x2 – 8x + 25 =0.
Solution From the quadratic formula, we obtain
![]()
Using ![]() we obtain
we obtain
![]()
Thus, the solution set of the equation is {4 – 3i, 4 + 3i}.
![]() Conjugate Solutions We can now obtain solutions to any quadratic equation. In particular, if the coefficients in ax2 + bx + c = 0 are real numbers and the discriminant is negative, we see from (5) that the roots appear as conjugate pairs. Observe in Example 7 that if x1 = 4 – 3i and x2 = 4 + 3i, then
Conjugate Solutions We can now obtain solutions to any quadratic equation. In particular, if the coefficients in ax2 + bx + c = 0 are real numbers and the discriminant is negative, we see from (5) that the roots appear as conjugate pairs. Observe in Example 7 that if x1 = 4 – 3i and x2 = 4 + 3i, then ![]() . Moreover, it is easily seen that
. Moreover, it is easily seen that ![]()
2.4 Exercises: Answers to selected odd-numbered problems begin on page ANS-3.
In Problems 1–10, find the indicated power of i.
1.i3
2.i4
3.i5
4.i6
5.i7
6.i8
7.i–1
8.i–2
9.i–3
10.i–6
In Problems 11–56, perform the indicated operation. Write the answer in standard form a + bi.
11.![]()
12.![]()
13.![]()
14.![]()
15.(3 + i) – (4 – 3i)
16.(5 + 6i) + (–7 + 2i)
17.2(4 – 5i) + 3(–2 – i)
18.–2(6 + 4i) + 5(4 – 8i)
19.i(– 10 + 9i) – 5i
20.i(4 + 13i) – i(1 – 9i)
21.3i(1 + i) – 4(2 – i)
22.i + i(1 – 2i) + i(4 + 3i)
23.(3 – 2i)(1 – i)
24.(4 + 6i)(–3 + 4i)
25.(7 + 14i)(2 + i)
26.![]()
27.(4 + 5i) – (2 – i)(1 + i)
28.(–3 + 6i) + (2 + 4i)(–3 + 2i)
29.i(1 – 2i)(2 + 5i)
30. ![]()
31. (1 + i)(1 + 2i)(1 + 3i)
32. (2 + i)(2 – i)(4 – 2i)
33. (1 – i)[2(2 – i) – 5(1 + 3i)]
34. (4 + i)[i(1 + 3i) – 2(–5 + 3i)]
35. (4 + i)2
36. (3 – 5i)2
37. (1 – i)2(1 + i)2
38. (2 + i)2(3 + 2i)2
39. ![]()
40. ![]()
41. ![]()
42. ![]()
43. ![]()
44. ![]()
45. ![]()
46. ![]()
47. ![]()
48. ![]()
49. ![]()
50. ![]()
51. ![]()
52. ![]()
53. ![]()
54. ![]()
55. ![]()
56. ![]()
In Problems 57–64, use Definition 2.4.1 to solve for x and y.
57. 2(x + yi) = i(3 – 4i)
58. (x + yi) + 4(1 – i) = 5 – 7i
59. i(x + yi) = (1 – 6i)(2 + 3i)
60. 10 + 6yi = 5x + 24i
61. (1 + i)(x – yi) = i(14 + 7i) – (2 + 13i)
62. i2(1 – i)(1 + i) = 3x + yi + i(y + xi)
63. ![]()
64. 25 – 49i = x2 – y2i
In Problems 65–76, solve the given equation.
65. x2 + 9 = 0
66. x2 + 8 = 0
67. 2x2 = –5
68. 3x2 = –1
69. 2x2 – x + 1 = 0
70. x2 – 2x + 10 = 0
71. x2 + 8x + 52 = 0
72. 3x2 + 2x + 5 = 0
73. 4x2 – x + 2 = 0
74. x2 + x + 2 = 0
75. x4 + 3x2 + 2 = 0
76. 2x4 + 9x2 + 4 = 0
77. The two square roots of the complex number i are the two numbers z1 and z2 that are solutions of the equation z2 = i. Let z = x + iy and find z2. Then use Definition 2.4.1 to find z1 and z2.
78. Proceed as in Problem 77 to find two numbers z1 and z2 that satisfy the equation z2 = –3 + 4i.
For Discussion
In Problems 79–82, prove the given properties involving the conjugates of z1 = a + bi and z2 = c + di.
79. ![]() if and only if z1 is a real number.
if and only if z1 is a real number.
80. ![]()
81. ![]()
82. ![]()
2.5 Linear Inequalities
![]() Introduction In Section 1.2 we defined the order relations “less than,” “less than or equal,” “greater than,” and “greater than or equal,” and we saw how to interpret these relations on the real number line. In this section we are interested in solving various kinds of inequalities containing a variable x. If a real number is substituted for the variable x in an inequality such as
Introduction In Section 1.2 we defined the order relations “less than,” “less than or equal,” “greater than,” and “greater than or equal,” and we saw how to interpret these relations on the real number line. In this section we are interested in solving various kinds of inequalities containing a variable x. If a real number is substituted for the variable x in an inequality such as
![]()
and if the result is a true statement, then that number is said to be a solution of the inequality. For example, 5 is a solution of (1) because if x is replaced by 5, then the resulting inequality 3(5) – 7 > 5 simplifies to the true statement 8 > 5. The word solve means that we are to find the set of all solutions of an inequality such as (1). This set is called the solution set of the inequality. Two inequalities are said to be equivalent if they have exactly the same solution set. The representation of the solution set on the number line is the graph of the inequality.
We solve an inequality by finding an equivalent inequality with obvious solutions. The following list summarizes three operations that yield equivalent inequalities.

PROOF OF (i): To prove part (i), we begin with the assumption that a < b. Then from Definition 1.2.1 it follows that b – a is positive. If we add c – c = 0 to a positive number, the sum is positive. Therefore,
![]()
is a positive number. Thus we have a + c < b + c.
Operations (i)–(iii) of Theorem 2.5.1 also hold with > in place of < and < in place of >. In addition, (i)–(iii) can be stated for the order relations ≤ and ≥. We leave the verification of (ii) and (iii) as exercises. See Problems 55 and 56 in Exercises 2.5.
Property (iii) of Theorem 2.5.1 is frequently forgotten when solving inequalities. In words, property (iii) states that
83. ![]() If an inequality is multiplied by a negative number, then the direction of the resulting inequality is reversed.
If an inequality is multiplied by a negative number, then the direction of the resulting inequality is reversed.
For example, if we multiply the inequality – 2 < 5 by – 3, then the less than symbol is changed to a greater than symbol:
![]()
![]() Solving Linear Inequalities Any inequality that can be written in one of the forms
Solving Linear Inequalities Any inequality that can be written in one of the forms
![]()
![]()
where a and b are real numbers, is said to be a linear inequality in the variable x. The inequality in (1) is an example of a linear inequality since by part (i) of Theorem 2.5.1 we can add –4 to both sides to obtain
![]()
or 3x – 11 > 0, which matches the second form in (2).
In the examples that follow we use operations (i)–(iii) in Theorem 2.5.1 to solve linear inequalities.
EXAMPLE 1 Solving a Linear Inequality
Solve 8x + 4 < 16 + 5x.
Solution We obtain equivalent inequalities using the operations in Theorem 2.5.1:
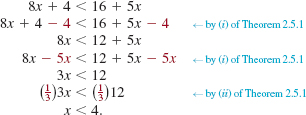
Using set-builder notation, the solution set of the given inequality is
{x | x is real and x < 4}.
EXAMPLE 2 Solving a Linear Inequality
Solve ½ – 3x ≤ ![]() .
.
Solution The following inequalities are equivalent. (You should be able to supply a reason for each step.)

Thus, the solution set of the given inequality is {x | x is real and x ≥ –![]() }.
}.
![]() Interval Notation The solution set in Example 1 is graphed on the number line in FIGURE 2.5.1(a) as a colored arrow over the line pointing to the left. In the figure, the right parenthesis at 4 indicates that number 4 is not included in the solution set. Because the solution set extends indefinitely to the left, or to the negative direction, the inequality x < 4 can also be written as – ∞ < x < 4, where ∞ is the infinity symbol. In other words, the solution set of the inequality x < 4 is
Interval Notation The solution set in Example 1 is graphed on the number line in FIGURE 2.5.1(a) as a colored arrow over the line pointing to the left. In the figure, the right parenthesis at 4 indicates that number 4 is not included in the solution set. Because the solution set extends indefinitely to the left, or to the negative direction, the inequality x < 4 can also be written as – ∞ < x < 4, where ∞ is the infinity symbol. In other words, the solution set of the inequality x < 4 is

Solution sets in Examples 1 and 2 in interval notation
![]()
Using interval notation this set of real numbers is written (–∞, 4) and is an example of an unbounded interval. The graph of the solution set in Example 2,
![]()
is shown in Figure 2.5.1(b), where the left bracket at –![]() indicates that –
indicates that –![]() is included in the solution set. In interval notation, this set is the unbounded interval
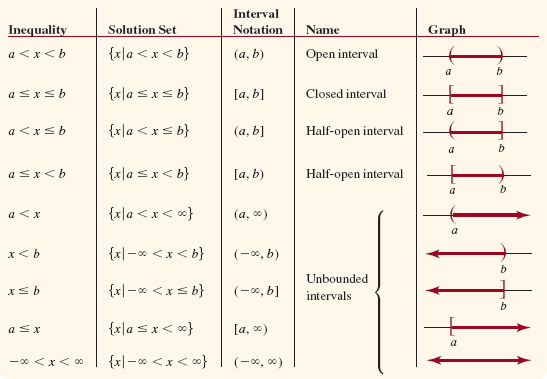
is included in the solution set. In interval notation, this set is the unbounded interval ![]() . Table 2.5.1 that follows summarizes various inequalities and their solution sets, as well as interval notations, names, and graphs. In each of the first four entries of the table, the numbers a and b are called the endpoints of the interval. As a set, the open interval
. Table 2.5.1 that follows summarizes various inequalities and their solution sets, as well as interval notations, names, and graphs. In each of the first four entries of the table, the numbers a and b are called the endpoints of the interval. As a set, the open interval
![]()
does not include either endpoint, whereas the closed interval
![]()
includes both endpoints. Note too, that the graph of the last interval in Table 2.5.1, extending indefinitely both to the left and to the right, is the entire real number line. The interval notation (– ∞, ∞) is generally used to represent the set R of real numbers.
As you peruse Table 2.5.1, keep firmly in mind that the infinity symbols – ∞ (“minus infinity”) and ∞ (“infinity”) do not represent real numbers and should never be manipulated arithmetically like a number. The infinity symbols are merely notational devices; – ∞ and ∞ are used to indicate unboundedness in the negative direction and in the positive direction, respectively. Thus when using interval notation, the symbols – ∞ and ∞ can never appear next to a square bracket; that is, an expression such as (2, ∞] is meaningless. Also, observe that the last entry in Table 2.5.1 states that the unbounded interval (–∞, ∞) is the entire real number line. When referring to the entire set of real numbers, it is common practice to use the symbols R and (–∞, ∞) interchangeably.
Inequalities and Intervals
|
![]() Simultaneous Inequalities An inequality of the form
Simultaneous Inequalities An inequality of the form
![]()
is sometimes referred to as a simultaneous inequality because the number x is between the numbers a and b; in other words, x > a and simultaneously x < b. For example, the set of real numbers that satisfy 2 < x < 5 is the intersection of the intervals (2, ∞)and (– ∞, 5) defined, respectively, by the inequalities 2 < x and x < 5. Recall from Section 1.1 that the intersection of two sets A and B, written A ∩ B, is the set of elements that are in A and in B, in other words, the elements that are common to both sets. As illustrated in FIGURE 2.5.2, the solution set of the inequality 2 < x < 5, is the intersection of sets (2, ∞) and (–∞, 5). The set (2, ∞) ∩ (–∞, 5) = (2, 5) can be visualized by overlapping the red arrows in the figure.

The numbers in (2, 5) are the numbers common to both (2, ∞) and (–∞, 5)
![]() Solving Simultaneous Inequalities As the following examples show, we can usually solve a simultaneous inequality by isolating the variable in the middle. Operations (i)–(iii) of Theorem 2.5.1 are applied to both parts of the inequality at the same time.
Solving Simultaneous Inequalities As the following examples show, we can usually solve a simultaneous inequality by isolating the variable in the middle. Operations (i)–(iii) of Theorem 2.5.1 are applied to both parts of the inequality at the same time.
EXAMPLE 3 Solving a Simultaneous Inequality
Solve –7 ≤ 2x + 1 < 19. Give the solutions in interval notation and sketch the graph.
Solution We obtain equivalent inequalities as follows:
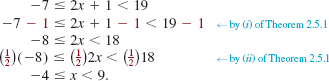
Thus the solutions of the given inequality are all the numbers in the interval [–4, 9).
The graph of the interval is shown in FIGURE 2.5.3.
![]()
Solution set in Example 3
It is customary to write simultaneous inequalities with the smaller number on the left. For example, although 5 > x > 2 is technically correct, it should be rewritten as 2 < x < 5 to reflect the order on the number line. The following example illustrates this point.
EXAMPLE 4 Solving a Simultaneous Inequality
Solve –1 < 1 – 2x < 3. Give the solution set in interval notation and sketch its graph.
Solution You should supply reasons why the following inequalities are equivalent:
![]()
We isolate the variable x in the middle of the last simultaneous inequality by multiplying by –½ Since multiplication by a negative number reverses the direction of an inequality we have,

To express this solution in interval notation, we first rewrite it with the negative number on the left; that is, –1 < x < 1. Thus the solution set can be expressed as the open interval (–1, 1), which is sketched in FIGURE 2.5.4.
![]()
Solution set in Example 4
Example 5 illustrates an application involving inequalities.
EXAMPLE 5 Yearly Number of Sales
Mrs. Johnson is paid $15,000 a year plus a commission of 8% on her sales. What yearly sales would correspond to an annual income between $23,000 and $27,000?
Solution If we let x represent the amount in dollars of Mrs. Johnson's yearly sales, then 15,000 + 0.08x equals her annual income in dollars. Thus we want to find x such that
![]()
We solve this inequality as follows:
![]()
Thus Mrs. Johnson's yearly sales must lie between $100,000 and $150,000 in order for her annual income to be between $23,000 and $27,000.
2.5 Exercises Answers to selected odd-numbered problems begin on page ANS-4.
In Problems 1–8, write the given inequality using interval notation and then graph the interval.
1. x < 0
2. 0 < x < 5
3. x ≥ 5
4. –1 ≤ x
5. 8 < x ≤ 10
6. –5 < x ≤ –3
7. –2 ≤ x ≤ 4
8. x > –7
In Problems 9–14, write the given interval as an inequality.
9. [–7, 9]
10. [1, 15)
11. (–∞, 2)
12. [–5, ∞)
13. (4, 20]
14. (–½, 10)
In Problems 15–18, solve the given inequality and indicate where operations (i)–(iii) of Theorem 2.5.1 are used.
15. 4x + 4 ≥ x
16. –x + 5 < 4x – 10
17. 0 < 2(4 – x) < 6
18. ![]()
In Problems 19–34, solve the given linear inequality. Write the solution set using intervalnotation. Graph the solution set.
19. x + 3 > –2
20. 3x – 9 < 6
21. ![]() x + 4 ≤ 10
x + 4 ≤ 10
22. 5 – ![]() x ≥ –4
x ≥ –4
23. ![]() x > x
x > x
24. –(1 – x) ≥ 2x – 1
25. 2 + x ≥ 3(x – 1)
26. –7x + 3 ≤ 4 – x
27. ![]()
28. –3 ≤ –x < 2
29. –7 < x – 2 < 1
30. 3 < x + 4 ≤ 10
31. 7 < 3 – ½x ≤ 8
32. 100 + x ≤ 41 – 6x ≤ 121 + x
33. ![]()
34. ![]()
In Problems 35–38, write the expression|x – 2| + |x – 5| without the absolute-value symbols if x is a number in the given interval.
35. (–∞, 1)
36. (7, ∞)
37. (3, 4]
38. [2, 5]
In Problems 39–42, write the expression |x + 1| – |x – 3| without the absolute-value symbols if x is a number in the given interval.
39. [–1, 3)
40. (0, 1)
41. (π, ∞)
42. (–∞, –5)
Miscellaneous Applications
43. Playing with Numbers If 7 times a number is decreased by 5, the result is less than 47. What can be determined about the number?
44. Trying for a B James has two test scores of 71 and 82 out of 100. What must he score on a third test in order to have an average of 80 or more?
45. Such a Deal A 50¢ rebate is available on a 4-oz jar of instant coffee, and the 2.5-oz jar sells for $3.00. At what price would the larger jar be more economical?
46. Fever Generally a person is considered to have a fever if he or she has an oral temperature greater than 98.6°F. What temperatures on the Celsius scale indicate a fever? [Hint: Recall from Problem 67 in Exercises 2.1 that TF = ![]() TC + 32, where TC is degrees Celsius and TF is degrees Fahrenheit.]
TC + 32, where TC is degrees Celsius and TF is degrees Fahrenheit.]
47. Taken for a Ride A taxi charges 90¢ for the first quarter mile and 30¢ for each additional quarter mile. How far in quarter miles can a person ride and owe between $3 and $6?
48. At Least It's a Job A successful salesperson normally spends between 5 and 15 hours of a 40-h week working in the office. How much time does the salesperson have left to contact customers outside the office?
For Discussion
In Problems 49–54, answer true or false.
49. If a < b, then a – 16 < b – 16. _____
50. If a < b, then –a < –b. _____
51. If 0 < a, then a < a + a. _____
52. If a < 0, then a + a < a. _____
53. If 1 < a, then ![]() < 1. _____
< 1. _____
54. If a < 0, then ![]() < 0. _____
< 0. _____
55. Prove operation (ii) of Theorem 2.5.1 using the fact that the product of two positive numbers is positive.
56. Prove operation (iii) of Theorem 2.5.1 using the fact that the product of a positive number and a negative number is negative.
57. If 0 < a < b, show that 1/b < 1/a. Is the restriction that a is positive necessary? Explain.
58.(a) If 0 < a < b, show that a2 < b2.
(b) What is the relationship between a2 and b2 if a < b < 0? If b < a < 0?
2.6 Absolute-Value Equations and Inequalities
![]() Introduction We have seen previously that the absolute value of a real number x is a nonnegative quantity defined as
Introduction We have seen previously that the absolute value of a real number x is a nonnegative quantity defined as
![]()
In this section we focus on two things: solving equations and inequalities that involve an absolute value.
![]() Absolute-Value Equations From (1) we see immediately that |6| = 6 since 6 > 0 and | –6| = –(–6) = 6 because –6 < 0. This simple example suggests that the solution of the equation |x| = 6 has two solutions, namely, x = 6 and x = –6. The first theorem succinctly summarizes how to solve an absolute-value equation.
Absolute-Value Equations From (1) we see immediately that |6| = 6 since 6 > 0 and | –6| = –(–6) = 6 because –6 < 0. This simple example suggests that the solution of the equation |x| = 6 has two solutions, namely, x = 6 and x = –6. The first theorem succinctly summarizes how to solve an absolute-value equation.
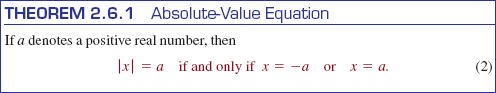
In (2), keep in mind that the symbol x is a placeholder for any quantity.
EXAMPLE 1 Absolute-Value Equations
Solve
(a)|–2x| = 9
(b)|5x – 3| = 8.
Solution
We use (2) with the symbol x replaced by –2x and the identification a = 9:
![]()
(a)We solve each of these equations. From –2x = –9, we obtain ![]() Then from –2x = 9, we get
Then from –2x = 9, we get ![]() The solution set is
The solution set is ![]()
(b)Now from (2) with x replaced by 5x – 3 and a = 8:
![]()
Solving each of these linear equations gives, in turn, x = –1 and x = ![]() . The solution set of the original equation is
. The solution set of the original equation is ![]()
![]() Absolute-Value Inequalities Many important applications of inequalities also involve absolute values. Recall from Section 1.2 that | x | represents the distance along the number line from x to the origin. Thus, the inequality | x | < a, (a > 0), indicates that the distance from x to the origin is less than a. We can see in FIGURE 2.6.1[a] that this is the set of real numbers x such that –a < x < a. On the other hand, | x | > a means that the distance from x to the origin is greater than a. Therefore, as Figure 2.6.1(b) shows, either x < –a or x > a. These geometric observations suggest the following interpretation of two kinds of absolute-value inequalities.
Absolute-Value Inequalities Many important applications of inequalities also involve absolute values. Recall from Section 1.2 that | x | represents the distance along the number line from x to the origin. Thus, the inequality | x | < a, (a > 0), indicates that the distance from x to the origin is less than a. We can see in FIGURE 2.6.1[a] that this is the set of real numbers x such that –a < x < a. On the other hand, | x | > a means that the distance from x to the origin is greater than a. Therefore, as Figure 2.6.1(b) shows, either x < –a or x > a. These geometric observations suggest the following interpretation of two kinds of absolute-value inequalities.

Graphical interpretation of |x| < a and |x| > a

Parts (i) and (ii) of Theorem 2.6.2 also hold with ≤ in place of < and ≥ in place of >.
EXAMPLE 2 Two Absolute-Value Inequalities
Solve the inequalities
|x| < 1
|x| ≥ 5.
Solution(a)From (i) of Theorem 2.6.2 the inequality |x| < 1 is equivalent to the simultaneous inequality – 1 < x < 1. Thus the solution set of |x| < 1 is the interval (–1, 1).
(b)From (ii) of Theorem 2.6.2, the inequality |x| ≥ 5 is equivalent to the pair of inequalities: x ≤ –5 or x ≥ 5. Thus |x| ≥ 5 is satisfied for numbers in either of the intervals (–∞, –5] or [5, ∞).
Because the solution set in part (b) of Example 2 consists of two nonintersecting, or disjoint, intervals it cannot be expressed as a single interval. The best we can do is to write the solution set as the union of the two intervals. Recall from Section 1.1, the union of two sets A and B, written A U B, is the set of elements that are in either A or in B. Thus the solution set in Example 2(b) can be written (–∞, –5] U [5, ∞).
EXAMPLE 3 An Absolute-Value Inequality
Solve |3x – 7| < 1 and graph the solution set.
Solution If we replace x by 3x – 7 and a by the number 1, then property (i) of Theorem 2.6.2 yields the equivalent simultaneous inequality
![]()
To solve we beginning by adding 7 across the inequalities:
![]()
Multiplying the last inequality by ![]() then gives
then gives
![]()
The solution set is the open interval (2, ![]() ) shown in FIGURE 2.6.2.
) shown in FIGURE 2.6.2.
![]()
Solution set in Example 3
EXAMPLE 4 An Absolute-Value Inequality
Solve |3x – 4| ≤ 0.
Solution Since the absolute value of an expression is never negative, the only numbers satisfying the given inequality are those for which
![]()
Thus the solution set consists of the single number ![]() .
.
An inequality such as |x – b| < a can also be interpreted in terms of distance along the number line. Since |x – b| is the distance between x and b, an inequality such as |x – b| < a is satisfied by all real numbers x whose distance between x and b is less than a. This interval is shown in FIGURE 2.6.3. Note when b = 0 we get property (i) above. Similarly, the set of numbers satisfying |x – b| > a are the numbers x whose distance between x and b is greater than a.
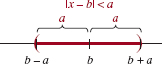
The distance between x and b is less than a
EXAMPLE 5 An Absolute-Value Inequality
Solve |4 – ½x| ≥ 7 and graph the solution set.
Solution By replacing x by 4 – ½x, a = 7, and > replaced by ≥, we see from (ii) of Theorem 2.6.2 that
![]()
is equivalent to the two inequalities
![]()
We solve each of these inequalities separately. First we have
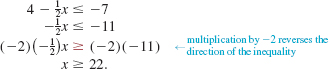
In interval notation this is [22, ∞). Then we solve
![]()
In interval notation this is written (–∞, –6]. Since any real number that satisfies either 4 – ½x ≤ –7 or 4 – ½x ≥ 7 also satisfies |4 – ½x| ≥ 7, the solution set is the union of the two disjoint intervals: (–∞, –6] U [22, ∞). The graph of these solutions is shown in FIGURE 2.6.4.
![]()
Solution set in Example 5 is the union of these two disjoint sets
Notice in Figure 2.6.1(a) that the number 0 is the midpoint of the solution interval for |x| < a and in FIGURE 2.6.3 that the number b is the midpoint of the solution interval for the inequality |x – b| < a. With this in mind, work through the next example.
EXAMPLE 6 Constructing an Absolute-Value Inequality
Find an inequality of the form |x – b| < a for which the open interval (4, 8) is its solution set.
Solution The midpoint of the interval (4, 8) is ![]() The distance between the midpoint m and one of the endpoints of the interval is d(m, 8) = |8 – 6| = 2. Therefore, with b = 6 and a = 2, the required inequality is |x – 6| < 2.
The distance between the midpoint m and one of the endpoints of the interval is d(m, 8) = |8 – 6| = 2. Therefore, with b = 6 and a = 2, the required inequality is |x – 6| < 2.
2.6 Exercises Answers to selected odd-numbered problems begin on page ANS-4.
In Problems 1–10, solve the given equation.
1. |4x – 1| = 2
2. |5v – 4| = 7
3. |¼ – ![]() y| = 1
y| = 1
4. |2 – 16t| = 0
5. ![]()
6. ![]()
7. |x2 – 8| = 1
8. |x2 + 3x| = 4
9. |x2 – 2x| = 1
10. |x2 + 5x – 3| = 3
In Problems 11–22, solve the given inequality. Write the solution set using interval notation. Graph the solution set.
11. |–5x| < 4
12. |3x| > 18
13. |3 + x| > 7
14. |x – 4| ≤ 9
15. |2x – 7| ≤ 1
16. |5 – ![]() x| < ½
x| < ½
17. ![]()
18. |6x + 4| > 4
19. ![]()
20. ![]()
21. |x – 5| < 0.01
22. |x – (–2)| < 0.001
In Problems 23–26, proceed as in Example 6 and find an inequality |x – b| < a or |x – b| > a for which the given interval is its solution set.
23. (–3, 11)
24. (1, 2)
25. (–∞, 1) ![]() (9, ∞)
(9, ∞)
26. (–∞, –3) ![]() (13, ∞)
(13, ∞)
In Problems 27 and 28, find an absolute-value inequality whose solution is the set of real numbers x satisfying the given condition. Express each set using interval notation.
27. Greater than or equal to 2 units from –3
28. Less than ½ unit from 3.5
Miscellaneous Applications
29. Comparing Ages Bill's and Mary's ages, AB and AM, respectively, differ by at most 3 years. Write this fact as an inequality using absolute-value symbols.
30. Survival Your score on the first exam is 72%. The midterm grade is the average of the first exam score with the midterm exam score. If the B range is from 80 to 89%, what scores can you obtain on the midterm exam so that your midsemester grade is B?
31. Weight of Coffee The weight w of the coffee in cans filled by a food processing company satisfies
![]()
where w is measured in ounces. Determine the interval in which w lies.
32. Weight of Cans A grocery scale is designed to be accurate to within 0.25 oz. If two identical cans of soup placed on the scale have a combined weight of 33.15 oz, what are the largest and smallest possible weights of one of the cans?
33. The Right Part A precision part for a small motor is specified to have a diameter of 0.623 cm. In order for the part to fit correctly, its diameter must be within 0.005 cm of the specified diameter. Write an inequality involving an absolute value that has as its solution all possible diameters of parts that will fit. Solve the inequality to determine those diameters.
34. Water Usage The estimated daily requirement for water by a certain city is given by
![]()
where N is the number of gallons of water used each day. Find the largest and the smallest daily water requirements.
For Discussion
In Problems 35 and 36, discuss how you might solve the given inequality and equation. Carry out your ideas.
35. ![]()
36. ![]()
37. The distance between the number x and 5 is |x – 51.
(a) In words, describe the graphical interpretation of the inequalities 0 < |x – 51 and 0 < |x – 5| < 3.
(b) Solve each inequality in part (a) and write each solution set using interval notation.
38. Interpret |x – 3| as the distance between the number x and 3. Sketch on the number line the set of real numbers that satisfy 2 < |x – 3| < 5.
39. Solve the simultaneous inequality 2 < |x – 3| < 5 by first solving | x – 31 < 5 and then 2 < | x – 3|. Take the intersection of the two solution sets and compare with your sketch in Problem 38.
40. Suppose a and b are real numbers and that the point a lies to the left of point b on the real number line. Without actually solving the inequality,
![]()
discuss its solution set.
2.7 Polynomial and Rational Inequalities
![]() Introduction In Sections 2.5 and 2.6 we solved linear inequalities, that is, inequalities containing a single variable x that can be put into the forms ax + b > 0, ax + b ≤ 0, and so on. Because ax + b is a linear polynomial, linear inequalities are just a special case of a larger class of inequalities that involve polynomials. If P(x) polynomial. denotes a polynomial of arbitrary degree, inequalities that can be put into the form
Introduction In Sections 2.5 and 2.6 we solved linear inequalities, that is, inequalities containing a single variable x that can be put into the forms ax + b > 0, ax + b ≤ 0, and so on. Because ax + b is a linear polynomial, linear inequalities are just a special case of a larger class of inequalities that involve polynomials. If P(x) polynomial. denotes a polynomial of arbitrary degree, inequalities that can be put into the form
![]()
are called polynomial inequalities. Inequalities involving the quotient of two polynomials P(x) and Q(x),
![]()
are called rational inequalities. We will assume for a rational inequality that the polynomials P(x) and Q(x) have no common factors. For example,
![]()
are a polynomial inequality and a rational inequality, respectively.
In this section we consider a method for solving polynomial and rational inequalities.
![]() Polynomial Inequalities In the next three examples we illustrate the sign-chart method for solving polynomial inequalities. The sign properties of a product of real numbers given next is fundamental to constructing a sign chart of a polynomial inequality:
Polynomial Inequalities In the next three examples we illustrate the sign-chart method for solving polynomial inequalities. The sign properties of a product of real numbers given next is fundamental to constructing a sign chart of a polynomial inequality:
![]()
That is, if the signs of the numbers are (+)(+) or (–)(–), then their product is positive, and if they have different signs (+)(–) or (–)(+), then their product is negative.
Here are some of the basic steps of the sign-chart method that is illustrated in the first example. We use the fact that a polynomial P(x) can change sign only at a number c for which P(c) = 0. A number c for which P(c) = 0 is called a zero of the polynomial.

EXAMPLE 1 Solving a Polynomial Inequality
Solve x2 ≥ –2x + 15.
Solution We begin by rewriting the inequality with all terms to the left of the inequality symbol and 0 to the right. By the properties of inequalities,
![]()
Factoring, the last expression is the same as (x + 5)(x – 3) ≥ 0.
Then we indicate on the number line where each factor is 0, in this case, x = –5 and x = 3. As shown in FIGURE 2.7.1, this divides the number line into three disjoint, or nonintersecting, intervals (– ∞, –5), (–5, 3), and (3, ∞). Note too, that since the given inequality requires the product to be nonnegative, that is, “greater than or equal to 0,” the numbers –5 and 3 are two solutions. Next, we must determine the signs of the factors x + 5 and x – 3 on each of the three intervals. We are looking for those intervals on which the two factors are either both positive or both negative, for then their product will be positive. Since the linear factors x + 5 and x – 3 cannot change signs within these intervals, it suffices to obtain the sign of each factor at just one test number chosen from inside each interval. For example, on the interval (– ∞, –5), if we use x = –10 as a test number, then
![]()
Three disjoint intervals in Example 1
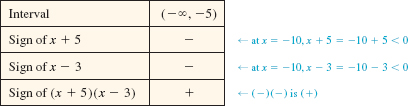
Continuing in this manner for the remaining two intervals we get the sign chart in FIGURE 2.7.2. As can be seen from the third line of this figure, the product (x + 5)(x – 3) is nonnegative on either of the unbounded disjoint intervals (–∞, –5] or [3, ∞). Thus the solution set is (– ∞, –5] ![]() [3, ∞).
[3, ∞).
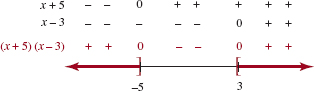
Sign chart for Example 1
EXAMPLE 2 Solving a Polynomial Inequality
Solve x < 10 – 3x2.
Solution We begin by rewriting the inequality with all nonzero terms on the same side: 3x2 + x – 10 < 0. Factoring this quadratic polynomial gives us
![]()
From the sign chart in FIGURE 2.7.3 we see (in red) that the foregoing product is negative for the numbers in the open interval (–2, ![]() ). Because of the strict inequality “less than” symbol, the endpoints of the interval numbers are not included in the solution set.
). Because of the strict inequality “less than” symbol, the endpoints of the interval numbers are not included in the solution set.
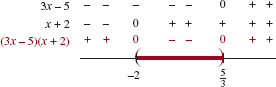
Sign chart for Example 2
EXAMPLE 3 Solving a Polynomial Inequality
Solve (x – 4)2(x + 8)3 > 0.
Solution Since the given inequality already has the form appropriate for the sign-chart method (a factored expression to the left of the inequality symbol and 0 to the right), we begin by finding the numbers where each factor is 0, in this case, x = 4 and x = –8. We place these numbers on the number line and determine three intervals. Then in each interval we consider the signs of the powers of each linear factor. Because of the even power, we see that (x – 4)2 is never negative. But because of the odd power, (x + 8)3 has the same sign as the factor x + 8. Observe that the numbers x = 4 and x = –8 are not solutions of the inequality because of the strict inequality “greater than” symbol. Therefore, as we see (in red) in FIGURE 2.7.4, the product of factors (x – 4)2(x + 8)3 is nonnegative for the numbers in the set (–8, 4) ![]() (4, ∞).
(4, ∞).

Sign chart for Example 3
![]() Rational Inequalities We turn now to rational inequalities of the type shown in (2). Rational inequalities can be solved using the procedure above except we put the zeros of both the numerator P(x) and denominator Q(x) on the number line and use the sign properties of a quotient:
Rational Inequalities We turn now to rational inequalities of the type shown in (2). Rational inequalities can be solved using the procedure above except we put the zeros of both the numerator P(x) and denominator Q(x) on the number line and use the sign properties of a quotient:
![]()
EXAMPLE 4 Solving a Rational Inequality
Solve ![]()
Solution In order to utilize sign properties of a quotient (4), we must have all nonzero terms on the same side of the inequality (just as we did for polynomial inequalities). Thus we add 1 to both sides of the inequality and then combine terms to obtain an equivalent rational inequality:
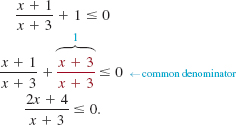
Using the fact that 2x + 4 = 0 when x = –2 and x + 3 = 0 when x = –3, we prepare the sign chart shown in FIGURE 2.7.5. From this chart we see that the number –3 is not a solution since (2x + 4)/(x + 3) is undefined for x = –3, but the number –2 is included in the solution set because (2x + 4)/(x + 3) is zero for x = –2. The solution set is the interval (–3, –2].
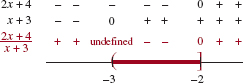
Sign chart for Example 4
EXAMPLE 5 Solving a Rational Inequality
Solve ![]()
Solution We begin by rewriting the inequality with all variables and nonzero constants to the left and 0 to the right of the inequality sign,
![]()
Next we put the terms over a common denominator,
![]()
Now the numbers that make the three linear factors in the last expression equal to 0 are –2,0, and 1. On the number line these three numbers determine four intervals. Because of the “less than or equal to 0” we see that 0 and 1 are members of the solution set. But –2 is excluded from the solution set since substituting this value into the fractional expression results in a zero denominator (making the fraction undefined). As we can see from the sign chart in FIGURE 2.7.6, the solution set is (-∞, –2) ![]() [0, 1].
[0, 1].
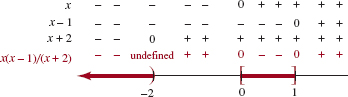
Sign chart for Example 5

2.7 Exercises: Answers to selected odd-numbered problems begin on page ANS-4.
In Problems 1–40, solve the given inequality and express the solution using interval notation.
1. x2 + 2x – 15 ≥ 0
2. 3x2 – x – 2 ≤ 0
3. x2 – 8x + 12 < 0
4. 6x2 + 14x + 4 ≥ 0
5. x2 – 5x ≥ 0
6. x2 – 4x + 4 ≥ 0
7. 3x2 – 27 < 0
8. 4x2 + 7x ≤ 0
9. 4x2 – 4x + 1 < 0
10. 12x2 > 27x + 27
11. x2 – 16 < 0
12. x2 – 5 > 0
13. x2 – 12 ≤ 0
14. 9x > 2x2 – 18
15. x2 + 6x ≤ –9
16. 9x2 + 30x < –25
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25. ![]()
26. ![]()
27. ![]()
28. ![]()
29. ![]()
30. ![]()
31. ![]()
32. ![]()
33. –(x + 1)(x + 2)(x + 3) < 0
34. –2(x – 1)(x + ½)(x – 3) ≤ 0
35. (x2 – 1)(x2 – 4) ≤ 0
36. (x – 1)2(x + 3)(x + 5) > 0
37. (x – ![]() )2(x + 5)3 < 0
)2(x + 5)3 < 0
38. x2(x – 2)(x – 3)5 ≥ 0
39. ![]()
40. ![]()
In Problems 41–44, solve the given inequality and express the solution using interval notation. You may need to use the quadratic formula to factor the quadratic expression.
41. x2 – x – 1 > 0
42. 6x2 < 3x + 5
43. ![]()
44. ![]()
In Problems 45 and 46, solve the given inequalities and express each solution using interval notation.
45. (a) x2 < x
x2 > x
46. (a) ![]()
(b) ![]()
47. If x2 ≤ 1, is it necessarily true that x ≤ 1? Explain.
48. If x2 ≥ 4, is it necessarily true that x ≥ 2? Explain.
49. If 7 times the square of a positive number is decreased by 3, the result is greater than 60. What can be determined about the number?
50. The sides of a square are extended to form a rectangle. As shown in FIGURE 2.7.7, one side is extended 2 cm and the other side is extended 5 cm. If the area of the resulting rectangle is less than 130 cm2, what are the possible lengths of a side of the original square?
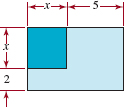
FIGURE 2.7.7 Rectangle in Problem 50
51. A polygon is a closed figure made by joining line segments. For example, a triangle is a three-sided polygon. Shown in FIGURE 2.7.8 is an eight-sided polygon called an octagon. A diagonal of a polygon is defined to be a line segment that joins any two nonadjacent vertices. The number of diagonals d in a polygon with n sides is given by d = ½(n – 1)n – n. For what polygons will the number of diagonals exceed 35?
FIGURE 2.7.8 Octagon in Problem 51
52. The total number of dots, t, in a triangular array with n rows is given by
![]()
See FIGURE 2.7.9. How many rows can the array have if the total number of dots is to be less than 5050?
FIGURE 2.7.9 Triangular arrays of dots in Problem 52
Miscellaneous Applications
53. Flower Garden A rectangular flower bed is to be twice as long as it is wide. If the area enclosed must be greater than 98 m2, what can you conclude about the width of the flower bed?
54. Intensity of Light The intensity I in lumens of a certain light source at a point r centimeters from the source is given by I = 625/r2. At what distances from the light source will the intensity be less than 25 lumens?
55. Parallel Resistors A 5-ohm resistor and a variable resistor are placed in parallel. The resulting resistance RT is given by RT = 5R/(5 + R). Determine the values of the variable resistor R for which the resulting resistance RT will be greater than 2 ohms.
56. What Goes Up… With the aid of calculus it is easy to show that the height s of a projectile launched straight upward from an initial height s0 with an initial velocity v0 is given by s = –½gt2 + v0t + s0, where t is in seconds and g = 32 ft/s2. If a toy rocket is shot straight upward from ground level, then s0 = 0. If its initial velocity is 72 ft/s, during what time interval will the rocket be more than 80 ft above the ground?
For Discussion
57. In Example 5, explain why one should not multiply the last expression in (2) by x + 2.

Chapter 2 Review Exercises: Answers to selected odd-numbered problems begin on page ANS-5.
True/False__________________________________________________
In Problems 1–10, answer true or false.
1. ![]() ___
___
2. ![]() ___
___
3. |–3t + 6| = 3|t – 2| ___
4. If –3x ≥ 6, then x ≥ –2. ___
5. The number 3.5 is in the solution set of ![]() ___
___
6. The solution set of |4x – 6| ≥ – 1 is (–∞, ∞). ___
7. For any real number x, |–x2 – 25| = x2 + 25. ___
8. If ![]() then z must be a real number. ___
then z must be a real number. ___
9. The inequality ![]() has no solution. ___
has no solution. ___
10. If x is a real number, then |x| = |–x|. ___
Fill in the Blanks_____________________________________________
In Problems 1–10, fill in the blanks.
1. An inequality with (–∞, 9] as its solution set is ___________.
2. The solution set of the inequality –3 < x ≤ 8 as an interval is ___________.
3. The imaginary part of the complex number 4 – 6i is ___________.
4. ![]() ___________.
___________.
5. If |15 – 2x| = x, then x = ___________.
6. The solution set for the equation |x| = |x + 1| is ___________.
7. The set of real numbers x whose distance between x and ![]() is greater than 3 is defined by the absolute-value inequality ___________.
is greater than 3 is defined by the absolute-value inequality ___________.
8. If x is in the interval (4, 8), then |x – 4| + |x – 8| = ___________.
9. If a < 0, then |–a| = ___________.
10. If y ≥ 0 and x2 – 2x + 1 = y, then x = ___________.
Review Exercises_____________________________________________
In Problems 1–26, solve the given equation.
1. ![]()
2. 4(1 – x) = x – 3(x + 1)
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. (1 – y)(y – 1) = y2
8. x(2x – 1) = 3
9. 4x2 + 10x – 24 = 0
10. 3x2 + x – 10 = 0
11. 16x2 + 9 = 24x
12. x2 – 17 = 0
13. 2x2 – 6x – 3 = 0
14. 4x2 + 20x + 25 = 0
15. 2x2 + 100 = 0
16. x2 + 2x + 4 = 0
17. x3 – 8 = 0
18. x3 + 8 = 0
19. x4 + 4x2 – 8 = 0
20. 4x4 – 4x2 + 1 = 0
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25. ![]()
26. x + 3 – 28x–1 = 0
In Problems 27–40, solve the given inequality. Write the solution set using interval notation.
27. 2x – 5 ≥ 6x + 7
28. ¼x – 3 < ½x + 1
29. –4 < x – 8 < 4
30. 7 ≤ 3 – 2x < 11
31. |x| > 10
32. |–6x| ≤ 42
33. |3x – 4| < 5
34. |5 – 2x| ≥ 7
35. 3x ≥ 2x2 – 5
36. x2 > 6x – 9
37. x3 > x
38. (x2 – x)(x2 + x) ≤ 0
39. ![]()
40. ![]()
In Problems 41–44, describe the given interval on the real number line using (a) an inequality, (b) interval notation.
41. ![]()
FIGURE 2.R.1 Graph for Problem 41
42. ![]()
FIGURE 2.R.2 Graph for Problem 42
43. ![]()
FIGURE 2.R.3 Graph for Problem 43
44. ![]()
FIGURE 2.R.4 Graph for Problem 44
In Problems 45–50, solve for the indicated variable in terms of the remaining variables. Assume that all variables represent positive real numbers.
45. Surface area of a rectangular parallelepiped
![]()
46. Temperature conversion
![]()
47. Lens equation
![]()
48. Volume of a sphere
![]()
49. Equation of a hyperbola
![]()
50. Projectile motion
![]()
In Problems 51–58, perform the indicated operation and write the answer in the standard form a + bi.
51. (6 – 5i) + (4 + 3i)
52. (8 + 2i) – (5 – i)
53. (3 + 2i)(4 – 5i)
54. (3 + 5i)2
55. ![]()
56. ![]()
57. ![]()
58. ![]()
In Problems 59–62, solve for x and y.
59. (3x – yi)i = 4(1 + yi)
60. (1 + i)2 = (x – yi)i
61. ![]()
62. i2 = – (y + xi)
63. Playing with Numbers If the sum of two numbers is 33 and their quotient is ![]() , find the two numbers.
, find the two numbers.
64. Wind Speed In still air two airplanes fly at a speed of 180 mi/h. One plane leaves Los Angeles and flies with the wind toward Phoenix. The second plane leaves Phoenix at the same time and flies against the wind toward Los Angeles. If the distance between the cities is 400 mi and the planes pass each other 250 mi from Los Angeles, find the speed of the wind.
65. Trying for a B Again On four tests of equal weight a student has an average score of 76. If the final exam is worth twice as much as each of the four tests, find the score on the final exam necessary for the student to have an overall average of 80.
66. How Fast? Two cars travel 40 mi. One car travels 5 mi/h faster than the other car and makes the trip in 16 min less time. Find the rates of the two cars.
67. How Fast? The distance from Minneapolis to Des Moines is approximately 250 mi: 100 mi in Minnesota and 150 mi in Iowa. At one time Iowa had raised its interstate speed limit to 65 mi/h while Minnesota's speed limit was still 55 mi/h. Under these circumstances, suppose a woman wants to drive from Minneapolis to Des Moines in 4 h. If she plans to drive 65 mi/h in Iowa, how fast must she go in Minnesota?
68. Slow Typist Ethan can type 100 addresses in 5 h. He begins and works alone for 2 h. Then Sean starts to help on another computer and they finish the task in another 90 min. How long would it take Sean to type all 100 addresses alone?
69. Width of a Sidewalk A sidewalk is to be constructed around a circular mall. The diameter of the mall is 20 m. If the area of the sidewalk is 44π m2, determine the width of the sidewalk.
70. Playing with Numbers If the digits of a two-digit number are reversed, the ratio of the original number to the new number is equal to ![]() . What is the original number?
. What is the original number?
71. Speed of Current Fran's boat cruises at a rate of 20 mi/h in still water. If she travels the same distance in 3 h against the current that she could travel in 2 h with the current, what is the speed of the current?
72. Dimensions The floor of a house is a rectangle that is 5 m longer than twice its width. An addition is planned that will increase the total area of the house to 135 m2. If the addition increases the width by 4 m, find the original dimensions of the house.
73. Making the Cut A border of uniform width is cut from a rectangular piece of cloth. The resulting piece of cloth is 20 in. by 30 in. See Figure 2.R.5. If the original area was twice the present area, find the width of the border that was cut off.

FIGURE 2.R.5 Cloth in Problem 73
74.Flat Panel TV The “size” of a rectangular television screen is measured along the diagonal. If the length of the screen is 24 in. longer than the width and the size of the screen is given as 64 in., what are the dimensions of the screen?
75.What Goes Up… A toy rocket is shot straight upward from the ground with an initial velocity of 72 ft/s. Its height s in feet above the ground after t seconds is given by s = – 16t2 + 72t. During what interval of time will the rocket be more than 80 ft above the ground?
76.Mixture A nurse has 2 L of a 3% boric acid solution. How much of a 10% solution must be added in order to have a 4% solution?
77.Bond Cost Mr. Diamond bought two bonds for a total of $30,000. One bond pays 6% interest and the other pays 8% interest. The annual interest from the 8% bond exceeds the annual interest from the 6% bond by $1000. Find the cost of each bond.
78.Planning Retirement Teri had worked at an aerospace firm for 21 years when Maria started at the firm. If Teri retires when she has five times as much seniority as Maria, how long will each have worked at the aerospace firm?
79.Music in the Night Mrs. Applebee bought a number of music boxes for her store for a total of $400. If each music box had cost $4 more, she would have obtained five fewer music boxes for the same amount of money. How many did she buy?
80.Children's Dosage Young's rule for converting an adult dosage of a drug to a child's dosage assumes a relationship between age and dosage and is used most frequently for children between the ages of three and twelve:
![]()
At what age is the adult's dosage four times the child's dosage?
81.Avalanche Prevention Engineers concerned with avalanche hazards measure the hardness of a snowpack by hammering a specially designed metal tube into the snow and seeing how far it penetrates. They assign the snowpack a ram number R given by the formula
![]()
where H is the mass of the hammer, T is the mass of the tube, n is the number of blows of the hammer, f is the distance the hammer falls for each blow, and p is the total penetration after n blows. See Figure 2.R.6. Typically, T and H are each 1 kg and f is about 50 cm. If the ram number of a snowpack is 150, how far will the tube penetrate after one blow?
Snowpack ram in Problem 81

Piston in Problem 82
82.Classic Cars The size of an automobile engine is measured by the volume of air that is forced upward or displaced by the motion of the pistons. This volume is given by the formula
![]()
where N is the number of pistons, S is the vertical distance or stroke that each piston moves, and B is the diameter or bore of a piston. See Figure 2.R.7.

(a)Find the size in cubic inches of a V-8 (8-cylinder engine) with a 4-in. bore and a 3-in. stroke.
(b)The 1909 6-cylinder Thomas Flyer had a 5.5-in. bore and stroke. Find its size. (Note: Early engines were large because of their low efficiency.)
(c)The 1911 Oldsmobile Limited displaced 706.9 in3 with a 5-in. bore and a 6-in. stroke. How many cylinders did it have?
(d)Hot-rodders will “soup up” a car by increasing the size of the bore and the length of the stroke. If the stroke is increased by ¼ in. and the bore is increased by ![]() in. in the engine described in part (a), how much displacement is gained?
in. in the engine described in part (a), how much displacement is gained?
83.Air Temperature Vincent's formula for human skin temperature Pv in degrees Celsius is
![]()
where t is the air temperature in degrees Celsius and v is the wind velocity in meters per second.
(a)At which temperature t in still air (v = 0) is skin temperature less than blood temperature (37°C)?
(b)Is there a wind velocity at which both air temperature t and skin temperature Pv equal blood temperature (37° C)? Explain your answer.
(c)According to this formula, at what temperature t does wind velocity cause skin temperature to increase? [Hint: Wind velocity will increase skin temperature when the coefficient of v is positive.]
84.Small Parking Lot A stadium architect has designed a 20,000-car parking lot with four 4-lane exits. Under ideal conditions it is assumed that cars will exit smoothly at 10 mi/h, using all 16 lanes, with a spacing of 10 ft between cars.
(a)If the average car is 15 ft long, how long will it take for the parking lot to empty? [Hint: Convert 10 mi/h to feet per minute.]
(b)Derive a general formula that expresses the time T in minutes that it takes C cars to exit a parking lot, using N exit lanes, with a spacing of s feet between cars, all moving at v miles per hour, if the average car is L feet in length. Include the fact that converts miles per hour to feet per minute.
(c)Solve the formula derived in part (b) for N.
(d)Find the number of exit lanes required for 10,000 cars, each 15 ft long, to exit in no more than 30 min at 10 mi/h with 10 ft between each car.
85.Violent Storms A few years ago, meteorologists used the equation D3 = 216T2 as a mathematical model to describe the size and intensity of four types of violent storms—tornados, thunderstorms, hurricanes, and cyclones—where D is the diameter of the storm in miles and T is the number of hours the storm travels before dissipating. (Source: NCTM Student Math Notes, January 1987.)
(a)Solve for T.
(B)In the United States about 150 tornadoes occur each year. If the diameter of a tornado is 2 mi, use the given mathematical model to determine the number of hours it could be expected to last.
86.Plate Tectonics Geological studies of the Earth's crust indicate that the fresh lithosphere (molten rock) that is forced up at oceanic ridges, sinks as it cools and moves away from the ridge. In plate tectonics the rate at which the lithosphere sinks is predicted by the mathematical model
![]()
Where Z is the depth in meters that the lithosphere has sunk, T is the age of the lithosphere in millions of years, and C is a constant. (The value C = 300 fits the data relatively well.) See Figure 2.R.8.
Oceanic ridge in Problem 86
(a)How far has the lithosphere sunk after 100 million years?
(b)Solve the given equation for T. How old is the lithosphere that has sunk 500 m?