EXERCISES

1. We delete from the set of states Q of an FSM M, all the states not reachable from q₀ and get a new FSM M₁. Is it true that L(M₁) = L(M)?
2. Consider a set A = {1, 2, 3} and a relation R : A → A, R = {(1, 2), (2, 2), (1,1)}. What is the nature of R?
3. In some NDFSM with ε transitions, there is a state with e transition to itself. What is the language recognized by a new machine in which this transition is deleted?
4. State True/False:
   1. The language L(R) for any regular expression R is sometimes finite.
   2. If R does not have any * or +, then L(R) is always finite.
5. Give inductive proofs for:
   1. If REV(x) is reverse of any string x, then REV(REV(X)) = x.
   2. 
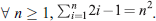
   3. Let a language L be defined as: (i) a ∈ L, (ii) if some x ∈ L then (x) ∈ L. Prove that any string x ∈ L will have at least as many ‘(’ as there are ‘)’.
   4. For n ≥ 0 strings A(n) and B(n) are defined as: A(0) = 0, B(0) = 1, ∀n > 0, A(n) = A(n – 1) B(n – 1), B(n) = B(n – 1) A(n – 1). Prove that A(n) contains neither ‘000’ nor ‘111’ as a substring.
   5. Prove that the above strings A(n) and B(n) differ in every symbol positions.
   6. Consider straight lines drawn in an infinite plane, such that no two lines are parallel and no three lines have a common point of intersection. The lines divide the plane in disjoint regions. Prove that the number r of such regions is given by 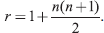Hint: n = 0, r = 1; n = 1, r = 2.
6. Let C and D be regular expressions over some alphabet ∑. Show that the equation R = C + RD is satisfied for an RE R = CD*. Draw a state diagram of a skeleton FSM showing this relationship.
7. Let ∑= {0, 1} be the alphabet. Develop an FSM M₁ recognizing the language L₁ = {x ∈ ∑* |x begins with 00 or 11}. Also develop another FSM M₂ recognizing the language L₂ = {x ∈ ∑* | x ends with 00 or 11}. Could M₁ and M₂ be created out of an FSM accepting the language {00, 11}? If yes, show how it can be done, if No, then prove it.
8. In some programming languages, identifiers may have embedded underscore ‘_’ characters. However the first character may not be an underscore, nor may two underscores appear in succession. Write a regular expression that specifies such identifiers.
9. Write a regular expression that generates the Roman representation of integers from 1 to 99.
10. Write a regular expression to represent a book – with front and back covers, contents, chapters and an index. Each chapter has a section with exercises at end. There has to be at least one chapter in a book.
11. Give a recursive definition of a language L ⊆{a, b}* and ∀x ∈ L, x has number of ‘a’ exactly double the number of ‘b’.
12. Develop a PDA for accepting the language generated by the grammar:

    E –> E ‒ T | T
    T –> T / F | F
    F –> [ E ] | i
    

    and demonstrate the acceptance of string i – i /i.
13. Develop an equivalent grammar without useless NTs for the grammar:

    S –> ABC | BaB
    A –> aA | BaC | aaa
    B –> bBb | a
    C –> CA  | AC
    

14. Develop a grammar in as much details as you can to represent the fprintf(fp, “format”, var-list) function call. Note that the number of format specifiers and number of variables in var-list must match.