9.1 Introduction

In Chapter 7 we saw how to build scalable spin locks that provide mutual exclusion efficiently, even when they are heavily used. We might think that it is now a simple matter to construct scalable concurrent data structures: take a sequential implementation of the class, add a scalable lock field, and ensure that each method call acquires and releases that lock. We call this approach coarse-grained synchronization.

Often, coarse-grained synchronization works well, but there are important cases where it does not. The problem is that a class that uses a single lock to mediate all its method calls is not always scalable, even if the lock itself is scalable. Coarse-grained synchronization works well when levels of concurrency are low, but if too many threads try to access the object at the same time, then the object becomes a sequential bottleneck, forcing threads to wait in line for access.

This chapter introduces several useful techniques that go beyond coarse-grained locking to allow multiple threads to access a single object at the same time.

Each of these techniques can be applied (with appropriate customization) to a variety of common data structures. In this chapter we consider how to use linked lists to implement a set, a collection of items that contains no duplicate elements.

For our purposes, as illustrated in Fig. 9.1, a set provides the following three methods:

Figure 9.1 The Set interface: add() adds an item to the set (no effect if that item is already present), remove() removes it (if present), and contains() returns a Boolean indicating whether the item is present.

For each method, we say that a call is successful if it returns true, and unsuccessful otherwise. It is typical that in applications using sets, there are significantly more contains() calls than add() or remove() calls.

9.2 List-Based Sets

This chapter presents a range of concurrent set algorithms, all based on the same basic idea. A set is implemented as a linked list of nodes. As shown in Fig. 9.2, the Node<T> class has three fields.¹ The item field is the actual item of interest. The key field is the item’s hash code. Nodes are sorted in key order, providing an efficient way to detect when an item is absent. The next field is a reference to the next node in the list. (Some of the algorithms we consider require technical changes to this class, such as adding new fields, or changing the types of existing fields.) For simplicity, we assume that each item’s hash code is unique (relaxing this assumption is left as an exercise). We associate an item with the same node and key throughout any given example, which allows us to abuse notation and use the same symbol to refer to a node, its key, and its item. That is, node a may have key a and item a, and so on.

Figure 9.2 The Node<T> class: this internal class keeps track of the item, the item’s key, and the next node in the list. Some algorithms require technical changes to this class.

The list has two kinds of nodes. In addition to regular nodes that hold items in the set, we use two sentinel nodes, called head and tail, as the first and last list elements. Sentinel nodes are never added, removed, or searched for, and their keys are the minimum and maximum integer values.² Ignoring synchronization for the moment, the top part of Fig. 9.3 schematically describes how an item is added to the set. Each thread A has two local variables used to traverse the list: curr_A is the current node and pred_A is its predecessor. To add an item to the set, thread A sets local variables pred_A and curr_A to head, and moves down the list, comparing curr_A ’s key to the key of the item being added. If they match, the item is already present in the set, so the call returns false. If pred_A precedes curr_A in the list, then pred_A ’s key is lower than that of the inserted item, and curr_A ’s key is higher, so the item is not present in the list. The method creates a new node b to hold the item, sets b ’s next_A field to curr_A, then sets pred_A to b. Removing an item from the set works in a similar way.

Figure 9.3 A seqential Set implementation: adding and removing nodes. In Part (a), a thread adding a node b uses two variables: curr is the current node, and pred is its predecessor. The thread moves down the list comparing the keys for curr and b. If a match is found, the item is already present, so it returns false. If curr reaches a node with a higher key, the item is not in the set so Set b’s next field to curr, and pred’s next field to b. In Part (b), to delete curr, the thread sets pred’s next field to curr’s next field.

9.3 Concurrent Reasoning

Reasoning about concurrent data structures may seem impossibly difficult, but it is a skill that can be learned. Often, the key to understanding a concurrent data structure is to understand its invariants: properties that always hold. We can show that a property is invariant by showing that:

Most interesting invariants hold trivially when the list is created, so it makes sense to focus on how invariants, once established, are preserved.

Specifically, we can check that each invariant is preserved by each invocation of insert(), remove(), and contains() methods. This approach works only if we can assume that these methods are the only ones that modify nodes, a property sometimes called freedom from interference. In the list algorithms considered here, nodes are internal to the list implementation, so freedom from interference is guaranteed because users of the list have no opportunity to modify its internal nodes.

We require freedom from interference even for nodes that have been removed from the list, since some of our algorithms permit a thread to unlink a node while it is being traversed by others. Fortunately, we do not attempt to reuse list nodes that have been removed from the list, relying instead on a garbage collector to recycle that memory. The algorithms described here work in languages without garbage collection, but sometimes require nontrivial modifications that are beyond the scope of this chapter.

When reasoning about concurrent object implementations, it is important to understand the distinction between an object’s abstract value (here, a set of items), and its concrete representation (here, a list of nodes).

Not every list of nodes is a meaningful representation for a set. An algorithm’s representation invariant characterizes which representations make sense as abstract values. If a and b are nodes, we say that a points to b if a ’s next field is a reference to b. We say that b is reachable if there is a sequence of nodes, starting at head, and ending at b, where each node in the sequence points to its successor.

The set algorithms in this chapter require the following invariants (some require more, as explained later). First, sentinels are neither added nor removed. Second, nodes are sorted by key, and keys are unique.

Let us think of the representation invariant as a contract among the object’s methods. Each method call preserves the invariant, and also relies on the other methods to preserve the invariant. In this way, we can reason about each method in isolation, without having to consider all the possible ways they might interact.

Given a list satisfying the representation invariant, which set does it represent? The meaning of such a list is given by an abstraction map carrying lists that satisfy the representation invariant to sets. Here, the abstraction map is simple: an item is in the set if and only if it is reachable from head.

What safety and liveness properties do we need? Our safety property is linearizability. As we saw in Chapter 3, to show that a concurrent data structure is a linearizable implementation of a sequentially specified object, it is enough to identify a linearization point, a single atomic step where the method call “takes effect." This step can be a read, a write, or a more complex atomic operation. Looking at any execution history of a list-based set, it must be the case that if the abstraction map is applied to the representation at the linearization points, the resulting sequence of states and method calls defines a valid sequential set execution. Here, add(a) adds a to the abstract set, remove(a) removes a from the abstract set, and contains(a) returns true or false, depending on whether a was already in the set.

Different list algorithms make different progress guarantees. Some use locks, and care is required to ensure they are deadlock- and starvation-free. Some nonblocking list algorithms do not use locks at all, while others restrict locking to certain methods. Here is a brief summary, from Chapter 3, of the nonblocking properties we use³:

We are now ready to consider a range of list-based set algorithms. We start with algorithms that use coarse-grained synchronization, and successively refine them to reduce granularity of locking. Formal proofs of correctness lie beyond the scope of this book. Instead, we focus on informal reasoning useful in everyday problem-solving.

As mentioned, in each of these algorithms, methods scan through the list using two local variables: curr is the current node and pred is its predecessor. These variables are thread-local,⁴ so we use pred_A and curr_A to denote the instances used by thread A.

9.4 Coarse-Grained Synchronization

We start with a simple algorithm using coarse-grained synchronization. Figs. 9.4 and 9.5 show the add() and remove() methods for this coarse-grained algorithm. (The contains() method works in much the same way, and is left as an exercise.) The list itself has a single lock which every method call must acquire. The principal advantage of this algorithm, which should not be discounted, is that it is obviously correct. All methods act on the list only while holding the lock, so the execution is essentially sequential. To simplify matters, we follow the convention (for now) that the linearization point for any method call that acquires a lock is the instant the lock is acquired.

Figure 9.4 The CoarseList class: the add() method.

Figure 9.5 The CoarseList class: the remove() method. All methods acquire a single lock, which is released on exit by the finally block.

The CoarseList class satisfies the same progress condition as its lock: if the Lock is starvation-free, so is our implementation. If contention is very low, this algorithm is an excellent way to implement a list. If, however, there is contention, then even if the lock itself performs well, threads will still be delayed waiting for one another.

9.5 Fine-Grained Synchronization

We can improve concurrency by locking individual nodes, rather than locking the list as a whole. Instead of placing a lock on the entire list, let us add a Lock to each node, along with lock() and unlock() methods. As a thread traverses the list, it locks each node when it first visits, and sometime later releases it. Such fine-grained locking permits concurrent threads to traverse the list together in a pipelined fashion.

Let us consider two nodes a and b where a points to b. It is not safe to unlock a before locking b because another thread could remove b from the list in the interval between unlocking a and locking b. Instead, thread A must acquire locks in a kind of “hand-over-hand” order: except for the initial head sentinel node, acquire the lock for a node only while holding the lock for its predecessor. This locking protocol is sometimes called lock coupling. (Notice that there is no obvious way to implement lock coupling using Java’s synchronized methods.)

Fig. 9.6 shows the FineList algorithm’s add() method, and Fig. 9.7 its remove() method. Just as in the coarse-grained list, remove() makes curr_A unreachable by setting pred_A ’s next field to curr_A ’s successor. To be safe, remove() must lock both pred_A and curr_A. To see why, let us consider the following scenario, illustrated in Fig. 9.8. Thread A is about to remove node a, the first node in the list, while thread B is about to remove node b, where a points to b. Suppose A locks head, and B locks a. A then sets head.next to b, while B sets a.next to c. The net effect is to remove a, but not b. The problem is that there is no overlap between the locks held by the two remove() calls. Fig. 9.9 illustrates how this “hand-over-hand” locking avoids this problem.

Figure 9.6 The FineList class: the add() method uses hand-over-hand locking to traverse the list. The finally blocks release locks before returning.

Figure 9.7 The FineList class: the remove() method locks both the node to be removed and its predecessor before removing that node.

Figure 9.8 The FineList class: why remove() must acquire two locks. Thread A is about to remove a, the first node in the list, while thread b is about to remove b, where a points to b. Suppose A locks head, and b locks a. Thread A then sets head.next to b, while b sets a’s next field to c. The net effect is to remove a, but not b

Figure 9.9 The FineList class: Hand-over-hand locking ensures that if concurrent remove() calls try to remove adjacent nodes, then they acquire conflicting locks. Thread A is about to remove node a, the first node in the list, while thread b is about to remove node b, where a points to b. Because A must lock both head and a, and b must lock both a and b, they are guaranteed to conflict on a, forcing one call to wait for the other.

To guarantee progress, it is important that all methods acquire locks in the same order, starting at the head and following next references toward the tail. As Fig. 9.10 shows, a deadlock could occur if different method calls were to acquire locks in different orders. In this example, thread A, trying to add a, has locked b and is attempting to lock head, while B, trying to remove b, has locked head and is trying to lock b. Clearly, these method calls will never finish. Avoiding deadlocks is one of the principal challenges of programming with locks.

Figure 9.10 The FineList class: a deadlock can occur if, for example, remove() and add() calls acquire locks in opposite order. Thread A is about to insert a by locking first b and then head, and thread b is about to remove node b by locking first head and then b. Each thread holds the lock the other is waiting to acquire, so neither makes progress.

The FineList algorithm maintains the representation invariant: sentinels are never added or removed, and nodes are sorted by key value without duplicates. The abstraction map is the same as for the course-grained list: an item is in the set if, and only if its node is reachable.

The linearization point for an add(a) call depends on whether the call was successful (i.e., whether a was already present). A successful call (a absent) is linearized when the node with the next higher key is locked (either Line 7 or 13).

The same distinctions apply to remove(a) calls. An unsuccessful call (a present) is linearized when the predecessor node is locked (Lines 36 or 42). An unsuccessful call (a absent) is linearized when the node containing the next higher key is locked (Lines 36 or 42).

Determining linearization points for contains() is left as an exercise.

The FineList algorithm is starvation-free, but arguing this property is harder than in the coarse-grained case. We assume that all individual locks are starvation-free. Because all methods acquire locks in the same down-the-list order, deadlock is impossible. If thread A attempts to lock head, eventually it succeeds. From that point on, because there are no deadlocks, eventually all locks held by threads ahead of A in the list will be released, and A will succeed in locking pred_A and curr_A.

9.6 Optimistic Synchronization

Although fine-grained locking is an improvement over a single, coarse-grained lock, it still imposes a potentially long sequence of lock acquisitions and releases. Moreover, threads accessing disjoint parts of the list may still block one another. For example, a thread removing the second item in the list blocks all concurrent threads searching for later nodes.

One way to reduce synchronization costs is to take a chance: search without acquiring locks, lock the nodes found, and then confirm that the locked nodes are correct. If a synchronization conflict causes the wrong nodes to be locked, then release the locks and start over. Normally, this kind of conflict is rare, which is why we call this technique optimistic synchronization.

In Fig. 9.11, thread A makes an optimistic add(a). It traverses the list without acquiring any locks (Lines 6 through 8). In fact, it ignores the locks completely. It stops the traversal when curr_A ’s key is greater than, or equal to a ’s. It then locks pred_A and curr_A, and calls validate() to check that pred_A is reachable and its next field still refers to curr_A. If validation succeeds, then thread A proceeds as before: if curr_A ’s key is greater than a, thread A adds a new node with item a between pred_A and curr_A, and returns true. Otherwise it returns false. The remove() and contains() methods (Figs. 9.12 and 9.13) operate similarly, traversing the list without locking, then locking the target nodes and validating they are still in the list. To be consistent with the Java memory model, the next fields in the nodes need to be declared volatile.

Figure 9.11 The OptimisticList class: the add() method traverses the list ignoring locks, acquires locks, and validates before adding the new node.

Figure 9.12 The OptimisticList class: the remove() method traverses ignoring locks, acquires locks, and validates before removing the node.

Figure 9.13 The OptimisticList class: the contains() method searches, ignoring locks, then it acquires locks, and validates to determine if the node is in the list.

The code of validate() appears in Fig. 9.14. We are reminded of the following story:

A tourist takes a taxi in a foreign town. The taxi driver speeds through a red light. The tourist, frightened, asks “What are you are doing?” The driver answers: “Do not worry, I am an expert.” He speeds through more red lights, and the tourist, on the verge of hysteria, complains again, more urgently. The driver replies, “Relax, relax, you are in the hands of an expert.” Suddenly, the light turns green, the driver slams on the brakes, and the taxi skids to a halt. The tourist picks himself off the floor of the taxi and asks “For crying out loud, why stop now that the light is finally green?” The driver answers “Too dangerous, could be another expert crossing.”

Figure 9.14 The OptimisticList: validation checks that pred_A points to curr_A and is reachable from head.

Traversing any dynamically changing lock-based data structure while ignoring locks requires careful thought (there are other expert threads out there). We must make sure to use some form of validation and guarantee freedom from interference.

As Fig. 9.15 shows, validation is necessary because the trail of references leading to pred_A or the reference from pred_A to curr_A could have changed between when they were last read by A and when A acquired the locks. In particular, a thread could be traversing parts of the list that have already been removed. For example, the node curr_A and all nodes between curr_A and a (including a) may be removed while A is still traversing curr_A. Thread A discovers that curr_A points to a, and, without validation, “successfully” removes a, even though a is no longer in the list. A validate() call detects that a is no longer in the list, and the caller restarts the method.

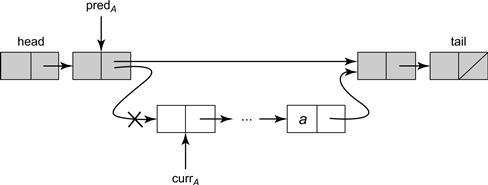
Figure 9.15 The OptimisticList class: why validation is needed. Thread A is attempting to remove a node a. While traversing the list, curr_A and all nodes between curr_A and a (including a) might be removed (denoted by a lighter node color). In such a case, thread A would proceed to the point where curr_A points to a, and, without validation, would successfully remove a, even though it is no longer in the list. Validation is required to determine that a is no longer reachable from head.

Because we are ignoring the locks that protect concurrent modifications, each of the method calls may traverse nodes that have been removed from the list. Nevertheless, absence of interference implies that once a node has been unlinked from the list, the value of its next field does not change, so following a sequence of such links eventually leads back to the list. Absence of interference, in turn, relies on garbage collection to ensure that no node is recycled while it is being traversed.

The OptimisticList algorithm is not starvation-free, even if all node locks are individually starvation-free. A thread might be delayed forever if new nodes are repeatedly added and removed (see Exercise 107). Nevertheless, we would expect this algorithm to do well in practice, since starvation is rare.

9.7 Lazy Synchronization

The OptimisticList implementation works best if the cost of traversing the list twice without locking is significantly less than the cost of traversing the list once with locking. One drawback of this particular algorithm is that contains() acquires locks, which is unattractive since contains() calls are likely to be much more common than calls to other methods.

The next step is to refine this algorithm so that contains() calls are wait-free, and add() and remove() methods, while still blocking, traverse the list only once (in the absence of contention). We add to each node a Boolean marked field indicating whether that node is in the set. Now, traversals do not need to lock the target node, and there is no need to validate that the node is reachable by retraversing the whole list. Instead, the algorithm maintains the invariant that every unmarked node is reachable. If a traversing thread does not find a node, or finds it marked, then that item is not in the set. As a result, contains() needs only one wait-free traversal. To add an element to the list, add() traverses the list, locks the target’s predecessor, and inserts the node. The remove() method is lazy, taking two steps: first, mark the target node, logically removing it, and second, redirect its predecessor’s next field, physically removing it.

In more detail, all methods traverse the list (possibly traversing logically and physically removed nodes) ignoring the locks. The add() and remove() methods lock the pred_A and curr_A nodes as before (Figs. 9.17 and 9.18), but validation does not retraverse the entire list (Fig. 9.16) to determine whether a node is in the set. Instead, because a node must be marked before being physically removed, validation need only check that curr_A has not been marked. However, as Fig. 9.20 shows, for insertion and deletion, since pred_A is the one being modified, one must also check that pred_A itself is not marked, and that it points to curr_A. Logical removals require a small change to the abstraction map: an item is in the set if, and only if it is referred to by an unmarked reachable node. Notice that the path along which the node is reachable may contain marked nodes. The reader should check that any unmarked reachable node remains reachable, even if its predecessor is logically or physically deleted. As in the OptimisticList algorithm, add() and remove() are not starvation-free, because list traversals may be arbitrarily delayed by ongoing modifications.

Figure 9.16 The LazyList class: validation checks that neither the pred nor the curr node has been logically deleted, and that pred points to curr.

Figure 9.17 The LazyList class: add() method.

Figure 9.18 The LazyList class: the remove() method removes nodes in two steps, logical and physical.

The contains() method (Fig. 9.19) traverses the list once ignoring locks and returns true if the node it was searching for is present and unmarked, and falseotherwise. It is thus wait-free.⁵ A marked node’s value is ignored. Each time the traversal moves to a new node, the new node has a larger key than the previous one, even if the node is logically deleted.

Figure 9.19 The LazyList class: the contains() method.

Figure 9.20 The LazyList class: why validation is needed. In Part (a) of the figure, thread A is attempting to remove node a. After it reaches the point where pred_A refers to curr_A, and before it acquires locks on these nodes, the node pred_A is logically and physically removed. After A acquires the locks, validation will detect the problem. In Part (b) of the figure, A is attempting to remove node a. After it reaches the point where pred_A refers to curr_A, and before it acquires locks on these nodes, a new node is added between pred_A and curr_A. After A acquires the locks, even though neither pred_A or curr_A are marked, validation detects that pred_A is not the same as curr_A, and A’s call to remove() will be restarted.

The linearization points for LazyList add() and unsuccessful remove() calls are the same as for the OptimisticList. A successful remove() call is linearized when the mark is set (Line 17), and a successful contains() call is linearized when an unmarked matching node is found.

To understand how to linearize an unsuccessful contains(), let us consider the scenario depicted in Fig. 9.21. In Part (a), node a is marked as removed (its marked field is set) and thread A is attempting to find the node matching a ’s key. While A is traversing the list, curr_A and all nodes between curr_A and a including a are removed, both logically and physically. Thread A would still proceed to the point where curr_A points to a, and would detect that a is marked and no longer in the abstract set. The call could be linearized at this point.

Figure 9.21 The LazyList class: linearizing an unsuccessful contains() call. Dark nodes are physically in the list and white nodes are physically removed. In Part (a), while thread A is traversing the list, a concurrent remove() call disconnects the sublist referred to by curr. Notice that nodes with items a and b are still reachable, so whether an item is actually in the list depends only on whether it is marked. Thread A’s call is linearized at the point when it sees that a is marked and is no longer in the abstract set. Alternatively, let us consider the scenario depicted in Part (b). While thread A is traversing the list leading to marked node a, another thread adds a new node with key a. It would be wrong to linearize thread A’s unsuccessful contains() call to when it found the marked node a, since this point occurs after the insertion of the new node with key a to the list.

Now let us consider the scenario depicted in Part (b). While A is traversing the removed section of the list leading to a, and before it reaches the removed node a, another thread adds a new node with a key a to the reachable part of the list. Linearizing thread A ’s unsuccessful contains() method at the point it finds the marked node a would be wrong, since this point occurs after the insertion of the new node with key a to the list. We therefore linearize an unsuccessful contains() method call within its execution interval at the earlier of the following points: (1) the point where a removed matching node, or a node with a key greater than the one being searched for is found, and (2) the point immediately before a new matching node is added to the list. Notice that the second is guaranteed to be within the execution interval because the insertion of the new node with the same key must have happened after the start of the contains() method, or the contains() method would have found that item. As can be seen, the linearization point of the unsuccessful contains() is determined by the ordering of events in the execution, and is not a predetermined point in the method’s code.

One benefit of lazy synchronization is that we can separate unobtrusive logical steps such as setting a flag, from disruptive physical changes to the structure, such as disconnecting a node. The example presented here is simple because we disconnect one node at a time. In general, however, delayed operations can be batched and performed lazily at a convenient time, reducing the overall disruptiveness of physical modifications to the structure.

The principal disadvantage of the LazyList algorithm is that add() and remove() calls are blocking: if one thread is delayed, then others may also be delayed.

9.8 Non-Blocking Synchronization

We have seen that it is sometimes a good idea to mark nodes as logically removed before physically removing them from the list. We now show how to extend this idea to eliminate locks altogether, allowing all three methods, add(), remove(), and contains(), to be nonblocking. (The first two methods are lock-free and the last wait-free). A nae approach would be to use compareAndSet() to change the next fields. Unfortunately, this idea does not work. In Fig. 9.22, part (a) shows a thread A attempting to remove a node a while thread B is adding a node b. Suppose A applies compareAndSet() to head.next, while B applies compareAndSet() to a.next. The net effect is that a is correctly deleted but b is not added to the list. In part (b) of the figure, A attempts to remove a, the first node in the list, while B is about to remove b, where a points to b. Suppose A applies compareAndSet() to head.next, while B applies compareAndSet() to a.next. The net effect is to remove a, but not b.

Figure 9.22 The LockFreeList class: why mark and reference fields must be modified atomically. In Part (a) of the figure, thread A is about to remove a, the first node in the list, while b is about to add b. Suppose A applies compareAndSet() to head.next, while b applies compareAndSet() to a.next. The net effect is that a is correctly deleted but b is not added to the list. In Part (b) of the figure, thread A is about to remove a, the first node in the list, while b is about to remove b, where a points to b. Suppose A applies compareAndSet() to head.next, while b applies compareAndSet() to a.next. The net effect is to remove a, but not b.

If B wants to remove curr_B from the list, it might call compareAndSet() to set pred_B ’s next field to curr_B ’s successor. It is not hard to see that if these two threads try to remove these adjacent nodes concurrently, the list will end up with b not being removed. A similar situation for a pair of concurrent add() and remove() methods is depicted in the upper part of Fig. 9.22.

Clearly, we need a way to ensure that a node’s fields cannot be updated, after that node has been logically or physically removed from the list. Our approach is to treat the node’s next and marked fields as a single atomic unit: any attempt to update the next field when the marked field is true will fail.

As described in detail in Pragma 9.8.1, an AtomicMarkableReference<T> object encapsulates both a reference to an object of type T and a Boolean mark. These fields can be atomically updated, either together or individually.

We make each node’s next field an AtomicMarkableReference<Node>. Thread A logically removes curr_A by setting the mark bit in the node’s next field, and shares the physical removal with other threads performing add() or remove(): as each thread traverses the list, it cleans up the list by physically removing (using compareAndSet()) any marked nodes it encounters. In other words, threads performing add() and remove() do not traverse marked nodes, they remove them before continuing. The contains() method remains the same as in the LazyList algorithm, traversing all nodes whether they are marked or not, and testing if an item is in the list based on its key and mark.

It is worth pausing to consider a design decision that differentiates the LockFreeList algorithm from the LazyList algorithm. Why do threads that add or remove nodes never traverse marked nodes, and instead physically remove all marked nodes they encounter? Suppose that thread A were to traverse marked nodes without physically removing them, and after logically removing curr_A, were to attempt to physically remove it as well. It could do so by calling compareAndSet() to try to redirect pred_A ’s next field, simultaneously verifying that pred_A is not marked and that it refers to curr_A. The difficulty is that because A is not holding locks on pred_A and curr_A, other threads could insert new nodes or remove pred_A before the compareAndSet() call.

Consider a scenario in which another thread marks pred_A. As illustrated in Fig. 9.22, we cannot safely redirect the next field of a marked node, so A would have to restart the physical removal by retraversing the list. This time, however, A would have to physically remove pred_A before it could remove curr_A. Even worse, if there is a sequence of logically removed nodes leading to pred_A, A must remove them all, one after the other, before it can remove curr_A itself.

This example illustrates why add() and remove() calls do not traverse marked nodes: when they arrive at the node to be modified, they may be forced to retraverse the list to remove previous marked nodes. Instead, we choose to have both add() and remove() physically remove any marked nodes on the path to their target node. The contains() method, by contrast, performs no modification, and therefore need not participate in the cleanup of logically removed nodes, allowing it, as in the LazyList, to traverse both marked and unmarked nodes.

In presenting our LockFreeList algorithm, we factor out functionality common to the add() and remove() methods by creating an inner Window class to help navigation. As shown in Fig. 9.24, a Window object is a structure with pred and curr fields. The find() method takes a head node and a key a, and traverses the list, seeking to set pred to the node with the largest key less than a, and curr to the node with the least key greater than or equal to a. As thread A traverses the list, each time it advances curr_A, it checks whether that node is marked (Line 16). If so, it calls compareAndSet() to attempt to physically remove the node by setting pred_A ’s next field to curr_A’s next field. This call tests both the field’s reference and Boolean mark values, and fails if either value has changed. A concurrent thread could change the mark value by logically removing pred_A, or it could change the reference value by physically removing curr_A. If the call fails, A restarts the traversal from the head of the list; otherwise the traversal continues.

Figure 9.24 The Window class: the find() method returns a structure containing the nodes on either side of the key. It removes marked nodes when it encounters them.

The LockFreeList algorithm uses the same abstraction map as the LazyList algorithm: an item is in the set if, and only if it is in an unmarked reachable node. The compareAndSet() call at Line 17 of the find() method is an example of a benevolent side effect: it changes the concrete list without changing the abstract set, because removing a marked node does not change the value of the abstraction map.

Fig. 9.25 shows the LockFreeList class’s add() method. Suppose thread A calls add(a). A uses find() to locate pred_A and curr_A. If curr_A ’s key is equal to a ’s, the call returns false. Otherwise, add() initializes a new node a to hold a, and sets a to refer to curr_A. It then calls compareAndSet() (Line 11) to set pred_A to a. Because the compareAndSet() tests both the mark and the reference, it succeeds only if pred_A is unmarked and refers to curr_A. If the compareAndSet() is successful, the method returns true, and otherwise it starts over.

Figure 9.25 The LockFreeList class: the add() method calls find() to locate pred_A and curr_A. It adds a new node only if pred_A is unmarked and refers to curr_A.

Fig. 9.26 shows the LockFreeList algorithm’s remove() method. When A calls remove() to remove item a, it uses find() to locate pred_A and curr_A. If curr_A ’s key fails to match a ’s, the call returns false. Otherwise, remove() uses a compareAndSet() to attempt to mark curr_A as logically removed (Line 27). This call succeeds only if no other thread has set the mark first. If it succeeds, the call returns true. A single attempt is made to physically remove the node, but there is no need to try again because the node will be removed by the next thread to traverse that region of the list. If the compareAndSet() call fails, remove() starts over.

Figure 9.26 The LockFreeList class: the remove() method calls find() to locate pred_A and curr_A, and atomically marks the node for removal.

The LockFreeList algorithm’s contains() method is virtually the same as that of the LazyList (Fig. 9.27). There is one small change: to test if curr is marked we must apply curr.next.get(marked) and check that marked[0] is true.

Figure 9.27 The LockFreeList class: the wait-free contains() method is almost the same as in the LazyList class. There is one small difference: it calls curr.next.get(marked) to test whether curr is marked.

9.9 Discussion

We have seen a progression of list-based lock implementations in which the granularity and frequency of locking was gradually reduced, eventually reaching a fully nonblocking list. The final transition from the LazyList to the LockFreeList exposes some of the design decisions that face concurrent programmers. As we will see, approaches such as optimistic and lazy synchronization will appear time and again when designing more complex data structures.

On the one hand, the LockFreeList algorithm guarantees progress in the face of arbitrary delays. However, there is a price for this strong progress guarantee:

On the other hand, the lazy lock-based list does not guarantee progress in the face of arbitrary delays: its add() and remove() methods are blocking. However, unlike the lock-free algorithm, it does not require each node to include an atomically markable reference. It also does not require traversals to clean up logically removed nodes; they progress down the list, ignoring marked nodes.

Which approach is preferable depends on the application. In the end, the balance of factors such as the potential for arbitrary thread delays, the relative frequency of calls to the add() and remove() methods, the overhead of implementing an atomically markable reference, and so on determine the choice of whether to lock, and if so, at what granularity.

9.10 Chapter Notes

Lock coupling was invented by Rudolf Bayer and Mario Schkolnick [19]. The first designs of lock-free linked-list algorithms are credited to John Valois [147]. The Lock-free list implementation shown here is a variation on the lists of Maged Michael [114], who based his work on earlier linked-list algorithms by Tim Harris [53]. This algorithm is referred to by many as the Harris-Michael algorithm. The Harris-Michael algorithm is the one used in the Java Concurrency Package. The OptimisticList algorithm was invented for this chapter, and the lazy algorithm is credited to Steven Heller, Maurice Herlihy, Victor Luchangco, Mark Moir, Nir Shavit, and Bill Scherer [55].