14
Skiplists and Balanced Search
14.1 Introduction
We have seen several concurrent implementations of sets based on linked lists and on hash tables. We now turn our attention to concurrent search structures with logarithmic depth. There are many concurrent logarithmic search structures in the literature. Here, we are interested in search structures intended for in-memory data, as opposed to data residing on outside storage such as disks.
Many popular sequential search structures, such as red-black trees or AVL-trees, require periodic rebalancing to maintain the structure’s logarithmic depth. Rebalancing works well for sequential tree-based search structures, but for concurrent structures, rebalancing may cause bottlenecks and contention. Instead, we focus here on concurrent implementations of a proven data structure that provides expected logarithmic time search without the need to rebalance: the SkipList. In the following sections we present two SkipList implementations. The LazySkipList class is a lock-based implementation, while the LockFreeSkipList class is not. In both algorithms, the typically most frequent method, contains(), which searches for an item, is wait-free. These constructions follow the design patterns outlined earlier in Chapter 9.
14.2 Sequential Skiplists
For simplicity we treat the list as a set, meaning that keys are unique. A SkipList is a collection of sorted linked lists, which mimics, in a subtle way, a balanced search tree. Nodes in a SkipList are ordered by key. Each node is linked into a subset of the lists. Each list has a level, ranging from 0 to a maximum. The bottom-level list contains all the nodes, and each higher-level list is a sublist of the lower-level lists. Fig. 14.1 shows a SkipList with integer keys. The higher-level lists are shortcuts into the lower-level lists, because, roughly speaking, each link at level i skips over about 2i nodes in next lower-level list, (e.g., in the SkipList shown in Fig. 14.1, each reference at level 3 skips over 23 nodes.) Between any two nodes at a given level, the number of nodes in the level immediately below it is effectively constant, so the total height of the SkipList is roughly logarithmic in the number of nodes. One can find a node with a given key by searching first through the lists in higher levels, skipping over large numbers of lower nodes, and progressively descending until a node with the target key is found (or not) at the bottom level.
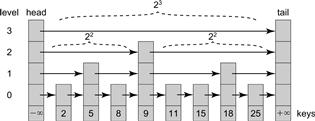
Figure 14.1 The SkipList class: this example has four levels of lists. Each node has a key, and the head and tail sentinels have ±∞ keys. The list at level i is a shortcut where each reference skips over 2i nodes of the next lower level list. For example, at level 3, references skip 23 nodes, at level 2, 22 nodes, and so on.
The SkipList is a probabilistic data structure. (No one knows how to provide this kind of performance without randomization.) Each node is created with a random top level (topLevel), and belongs to all lists up to that level. Top levels are chosen so that the expected number of nodes in each level’s list decreases exponentially. Let 0 < p < 1 be the conditional probability that a node at level i also appears at level i + 1. All nodes appear at level 0. The probability that a node at level 0 also appears at level i > 0 is pi. For example, with p = 1/2, 1/2 of the nodes are expected to appear at level 1, 1/4 at level 2 and so on, providing a balancing property like the classical sequential tree-based search structures, except without the need for complex global restructuring.
We put head and tail sentinel nodes at the beginning and end of the lists with the maximum allowed height. Initially, when the SkipList is empty, the head (left sentinel) is the predecessor of the tail (right sentinel) at every level. The head’s key is less than any key that may be added to the set, and the tail’s key is greater.
Each SkipList node’s next field is an array of references, one for each list to which it belongs and so finding a node means finding its predecessors and successors. Searching the SkipList always begins at the head. The find() method proceeds down the levels one after the other, and traverses each level as in the LazyList using references to a predecessor node pred and a current node curr. Whenever it finds a node with a greater or matching key, it records the pred and curr as the predecessor and successor of a node in arrays called preds[] and succs[], and continues to the next lower level. The traversal ends at the bottom level. Fig. 14.2 (Part a) shows a sequential find() call.

Figure 14.2 The SkipList class: add() and find() methods. In Part (a), find() traverses at each level, starting at the highest level, for as long as curr is less than or equal to the target key 12. Otherwise, it stores pred and curr in the preds[] and succs[] arrays at each level and descends to the next level. For example, the node with key 9 is preds[2] and preds[1], while tail is succs[2] and the node with key 18 is succs[1]. Here, find() returns false since the node with key 12 was not found in the lowest-level list and so an add(12) call in Part (b) can proceed. In Part (b) a new node is created with a random topLevel = 2. The new node’s next references are redirected to the corresponding succs[] nodes, and each predecessor node’s next reference is redirected to the new node.
To add a node to a skiplist, a find() call fills in the preds[] and succs[] arrays. The new node is created and linked between its predecessors and successors. Fig. 14.2, Part (b) shows an add(12) call.
To remove a victim node from the skiplist, the find() method initializes the victim’s preds[] and succs[] arrays. The victim is then removed from the list at all levels by redirecting each predecessor’s next reference to the victim’s successor.
14.3 A Lock-Based Concurrent Skiplist
We now describe the first concurrent skiplist design, the LazySkipList class. This class builds on the LazyList algorithm of Chapter 9: each level of the SkipList structure is a LazyList, and as in the LazyList algorithm, the add() and remove() methods use optimistic fine-grained locking, while the contains() method is wait-free.
14.3.1 A Bird’s-Eye View
Here is a bird’s-eye view of the LazySkipList class. Start with Fig. 14.3. As in the LazyList class, each node has its own lock and a marked field indicating whether it is in the abstract set, or has been logically removed. All along, the algorithm maintains the skiplist property: higher-level lists are always contained in lower-level lists.

Figure 14.3 The LazySkipList class: failed and successful add() and remove() calls. In Part (a) the add(18) call finds the node with key 18 unmarked but not yet fullyLinked. It spins waiting for the node to become fullyLinked in Part (b), at which point it returns false. In Part (a) the remove(8) call finds the node with key 8 unmarked and fully linked, which means that it can acquire the node’s lock in Part (b). It then sets the mark bit, and proceeds to lock the node’s predecessors, in this case the node with key 5. Once the predecessor is locked, it physically removes the node from the list by redirecting the bottom-level reference of the node with key 5, completing the successful remove(). In Part (a) a remove(18) fails, because it found the node not fully linked. The same remove(18) call succeeds in Part (b) because it found that the node is fully linked.
The skiplist property is maintained using locks to prevent structural changes in the vicinity of a node while it is being added or removed, and by delaying any access to a node until it has been inserted into all levels of the list.
To add a node, it must be linked into the list at several levels. Every add() call calls find(), which traverses the skiplist and returns the node’s predecessors and successors at all levels. To prevent changes to the node’s predecessors while the node is being added, add() locks the predecessors, validates that the locked predecessors still refer to their successors, then adds the node in a manner similar to the sequential add() shown in Fig. 14.2. To maintain the skiplist property, a node is not considered to be logically in the set until all references to it at all levels have been properly set. Each node has an additional flag, fullyLinked, set to true once it has been linked in all its levels. We do not allow access to a node until it is fully linked, so for example, the add() method, when trying to determine whether the node it wishes to add is already in the list, must spin waiting for it to become fully linked. Fig. 14.3 shows a call to add(18) that spins waiting until the node with key 18 becomes fully linked.
To remove a node from the list, remove() uses find() to check whether a victim node with the target key is already in the list. If so, it checks whether the victim is ready to be deleted, that is, is fully linked and unmarked. In Part (a) of Fig. 14.3, remove(8) finds the node with key 8 unmarked and fully linked, which means that it can remove it. The remove(18) call fails, because it found that the victim is not fully linked. The same remove(18) call succeeds in Part (b) because it found that the victim is fully linked.
If the victim can be removed, remove() logically removes it by setting its mark bit. It completes the physical deletion of the victim by locking its predecessors at all levels and then the victim node itself, validating that the predecessors are unmarked and still refer to the victim, and then splicing out the victim node one level at a time. To maintain the skiplist property, the victim is spliced out from top to bottom.
For example, in Part (b) of Fig. 14.3, remove(8) locks the predecessor node with key 5. Once this predecessor is locked, remove() physically removes the node from the list by redirecting the bottom-level reference of the node with key 5 to refer to the node with key 9.
In both the add() and remove() methods, if validation fails, find() is called again to find the newly changed set of predecessors, and the attempt to complete the method resumes.
The wait-free contains() method calls find() to locate the node containing the target key. If it finds a node, it determines whether the node is in the set by checking whether it is unmarked and fully linked. This method, like the LazyList class’s contains(), is wait-free because it ignores any locks or concurrent changes in the SkipList structure.
To summarize, the LazySkipList class uses a technique familiar from earlier algorithms: it holds lock on all locations to be modified, validates that nothing important has changed, completes the modifications, and releases the locks (in this context, the fullyLinked flag acts like a lock).
14.3.2 The Algorithm
Fig. 14.4 shows the LazySkipList’s Node class. A key is in the set if, and only if the list contains an unmarked, fully linked node with that key. The key 8 in Part (a) of Fig. 14.3, is an example of such a key.
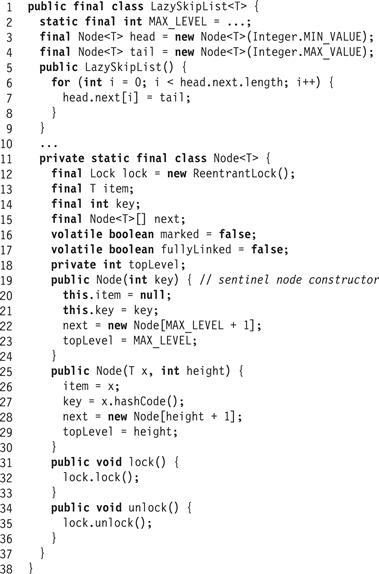
Figure 14.4 The LazySkipList class: constructor, fields, and Node class.
Fig. 14.5 shows the skiplist find() method. (The same method works in both the sequential and concurrent algorithms). The find() method returns −1 if the item is not found. It traverses the SkipList using pred and curr references starting at the head and at the highest level.1 This highest level can be maintained dynamically to reflect the highest level actually in the SkipList, but for brevity, we do not do so here. The find() method goes down the levels one after the other. At each level it sets curr to be the pred node’s successor. If it finds a node with a matching key, it records the level (Line 48). If it does not find a node with a matching key, then find() records the pred and curr as the predecessor and successor at that level in the preds[] and succs[] arrays (Lines 51–52), continuing to the next lower level starting from the current pred node. Part (a) of Fig. 14.2 shows how find() traverses a SkipList. Part (b) shows how find() results would be used to add() a new item to a SkipList.
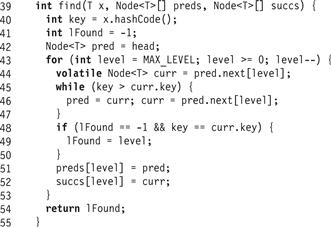
Figure 14.5 The LazySkipList class: the wait-free find() method. This algorithm is the same as in the sequential SkipList implementation. The preds[] and succs[] arrays are filled from the maximum level to level 0 with the predecessor and successor references for the given key.
Because we start with pred at the head sentinel node and always advance the window only if curr is less than the target key, pred is always a predecessor of the target key, and never refers to the node with the key itself. The find() method returns the preds[] and succs[] arrays as well as the level at which the node with a matching key was found.
The add(k) method, shown in Fig. 14.6, uses find() (Fig. 14.5) to determine whether a node with the target key k is already in the list (Line 42). If an unmarked node with the key is found (Lines 62–67) then add(k) returns false, indicating that the key k is already in the set. However, if that node is not yet fully linked (indicated by the fullyLinked field), then the thread waits until it is linked (because the key k is not in the abstract set until the node is fully linked). If the node found is marked, then some other thread is in the process of deleting it, so the add() call simply retries. Otherwise, it checks whether the node is unmarked and fully linked, indicating that the add() call should return false. It is safe to check if the node is unmarked before the node is fully linked, because remove() methods do not mark nodes unless they are fully linked. If a node is unmarked and not yet fully linked, it must become unmarked and fully linked before it can become marked (see Fig. 14.7). This step is the linearization point (Line 66) of an unsuccessful add() method call.

Figure 14.6 The LazySkipList class: the add() method.
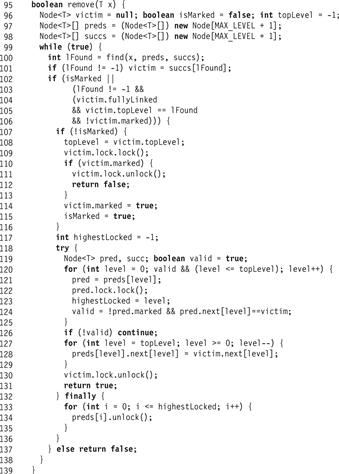
Figure 14.7 The LazySkipList class: the remove() method.
The add() method calls find() to initialize the preds[] and succs[] arrays to hold the ostensible predecessor and successor nodes of the node to be added. These references are unreliable, because they may no longer be accurate by the time the nodes are accessed. If no unmarked fully linked node was found with key k, then the thread proceeds to lock and validate each of the predecessors returned by find() from level 0 up to the topLevel of the new node (Lines 74–80). To avoid deadlocks, both add() and remove() acquire locks in ascending order. The topLevel value is determined at the very beginning of the add() method using the randomLevel() method. 2 The validation (Line 79) at each level checks that the predecessor is still adjacent to the successor and that neither is marked. If validation fails, the thread must have encountered the effects of a conflicting method, so it releases (in the finally block at Line 87) the locks it acquired and retries.
If the thread successfully locks and validates the results of find() up to the topLevel of the new node, then the add() call will succeed because the thread holds all the locks it needs. The thread then allocates a new node with the appropriate key and randomly chosen topLevel, links it in, and sets the new node’s fullyLinked flag. Setting this flag is the linearization point of a successful add() method (Line 87). It then releases all its locks and returns true (Lines 89). The only time a thread modifies an unlocked node’s next field is when it initializes the new node’s next references (Line 83). This initialization is safe because it occurs before the new node is accessible.
The remove() method appears in Fig. 14.7. It calls find() to determine whether a node with the appropriate key is in the list. If so, the thread checks whether the node is ready to be deleted (Line 104): meaning it is fully linked, unmarked, and at its top level. A node found below its top level was either not yet fully linked (see the node with key 18 in Part (a) of Fig. 14.3), or marked and already partially unlinked by a concurrent remove() method call. (The remove() method could continue, but the subsequent validation would fail.)
If the node is ready to be deleted, the thread locks the node (Line 109) and verifies that it is still not marked. If it is still not marked, the thread marks the node, logically deleting that item. This step (Line 114), is the linearization point of a successful remove() call. If the node was marked, then the thread returns false since the node was already deleted. This step is one linearization point of an unsuccessful remove(). Another occurs when find() does not find a node with a matching key, or when the node with the matching key was marked, or not fully linked, or not found at its top level (Line 104).
The rest of the method completes the physical deletion of the victim node. To remove the victim from the list, the remove() method first locks (in ascending order, to avoid deadlock) the victim’s predecessors at all levels up to the victim’s topLevel (Lines 120–124). After locking each predecessor, it validates that the predecessor is still unmarked and still refers to the victim. It then splices out the victim one level at a time (Line 128). To maintain the SkipList property, that any node reachable at a given level is reachable at lower levels, the victim is spliced out from top to bottom. If the validation fails at any level, then the thread releases the locks for the predecessors (but not the victim) and calls find() to acquire the new set of predecessors. Because it has already set the victim’s isMarked field, it does not try to mark the node again. After successfully removing the victim node from the list, the thread releases all its locks and returns true.
Finally, we recall that if no node was found, or the node found was marked, or not fully linked, or not found at its top level, then the method simply returns false. It is easy to see that it is correct to return false if the node is not marked, because for any key, there can at any time be at most one node with this key in the SkipList (i.e., reachable from the head). Moreover, once a node is entered into the list, (which must have occurred before it is found by find()), it cannot be removed until it is marked. It follows that if the node is not marked, and not all its links are in place, it must be in the process of being added into the SkipList, but the adding method has not reached the linearization point (see the node with key 18 in Part (a) of Fig. 14.3).
If the node is marked at the time it is found, it might not be in the list, and some unmarked node with the same key may be in the list. However, in that case, just like for the LazyList remove() method, there must have been some point during the remove() call when the key was not in the abstract set.
The wait-free contains() method (Fig. 14.8) calls find() to locate the node containing the target key. If it finds a node it checks whether it is unmarked and fully linked. This method, like that of the LazyList class of Chapter 9, is wait-free, ignoring any locks or concurrent changes in the SkipList list structure. A successful contains() call’s linearization point occurs when the predecessor’s next reference is traversed, having been observed to be unmarked and fully linked. An unsuccessful contains() call, like the remove() call, occurs if the method finds a node that is marked. Care is needed, because at the time the node is found, it might not be in the list, while an unmarked node with the same key may be in the list. As with remove(), however, there must have been some point during the contains() call when the key was not in the abstract set.
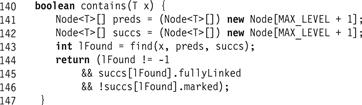
Figure 14.8 The LazySkipList class: the wait-free contains() method.
14.4 A Lock-Free Concurrent Skiplist
The basis of our LockFreeSkipList implementation is the LockFreeList algorithm of Chapter 9: each level of the SkipList structure is a LockFreeList, each next reference in a node is an AtomicMarkableReference<Node>, and list manipulations are performed using compareAndSet().
14.4.1 A Bird’s-Eye View
Here is a bird’s-eye view of the of the LockFreeSkipList class.
Because we cannot use locks to manipulate references at all levels at the same time, the LockFreeSkipList cannot maintain the SkipList property that each list is a sublist of the list at levels below it.
Since we cannot maintain the skiplist property, we take the approach that the abstract set is defined by the bottom-level list: a key is in the set if there is a node with that key whose next reference is unmarked in the bottom-level list. Nodes in higher-level lists in the skiplist serve only as shortcuts to the bottom level. There is no need for a fullyLinked flag as in the LazySkipList.
How do we add or remove a node? We treat each level of the list as a LockFreeList. We use compareAndSet() to insert a node at a given level, and we mark the next references of a node to remove it.
As in the LockFreeList, the find() method cleans up marked nodes. The method traverses the skiplist, proceeding down each list at each level. As in the LockFreeList class’s find() method, it repeatedly snips out marked nodes as they are encountered, so that it never looks at a marked node’s key. Unfortunately, this means that a node may be physically removed while it is in the process of being linked at the higher levels. A find() call that passes through a node’s middle-level references may remove these references, so, as noted earlier, the SkipList property is not maintained.
The add() method calls find() to determine whether a node is already in the list, and to find its set of predecessors and successors. A new node is prepared with a randomly chosen topLevel, and its next references are directed to the potential successors returned by the find() call. The next step is to try to logically add the new node to the abstract set by linking it into the bottom-level list, using the same approach as in the LockFreeList. If the addition succeeds, the item is logically in the set. The add() call then links the node in at higher levels (up to its top level).
Fig. 14.9 shows the LockFreeSkipList class. In Part (a) add(12) calls find(12) while there are three ongoing remove() calls. Part (b) shows the results of redirecting the dashed links. Part (c) shows the subsequent addition of the new node with key 12. Part (d) shows an alternate addition scenario which would occur if the node with key 11 were removed before the addition of the node with key 12.
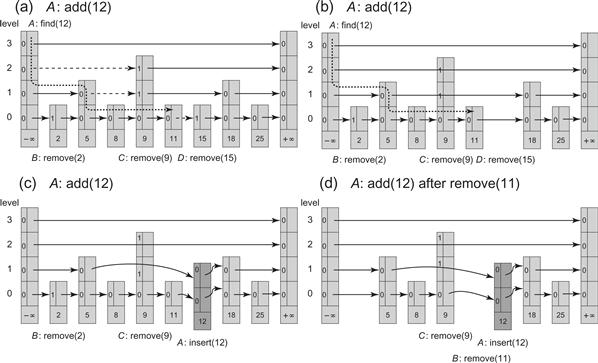
Figure 14.9 The LockFreeSkipList class: an add() call. Each node consists of links that are unmarked (a 0) or marked (a 1). In Part (a), add(12) calls find(12) while there are three ongoing remove() calls. The find() method “cleans” the marked links (denoted by 1s) as it traverses the skiplist. The traversal is not the same as a sequential find(12), because marked nodes are unlinked whenever they are encountered. The path in the figure shows the nodes traversed by the pred reference, which always refers to unmarked nodes with keys less than the target key. Part (b) shows the result of redirecting the dashed links. We denote bypassing a node by placing the link in front of it. Node 15, whose bottom-level next reference was marked, is removed from the skiplist. Part (c) shows the subsequent addition of the new node with key 12. Part (d) shows an alternate addition scenario which would occur if the node with key 11 were removed before the addition of the node with key 12. The bottom-level next reference of the node with key 9 is not yet marked, and so the bottom-level predecessor node, whose next reference is marked, is redirected by the add() method to the new node. Once thread C completes marking this reference, the node with key 9 is removed and the node with key 5 becomes the immediate predecessor of the newly added node.
The remove() method calls find() to determine whether an unmarked node with the target key is in the bottom-level list. If an unmarked node is found, it is marked starting from the topLevel. All next references up to, but not including the bottom-level reference are logically removed from their appropriate level list by marking them. Once all levels but the bottom one have been marked, the method marks the bottom-level’s next reference. This marking, if successful, removes the item from the abstract set. The physical removal of the node is the result of its physical removal from the lists at all levels by the remove() method itself and the find() methods of other threads that access it while traversing the skiplist. In both add() and remove(), if at any point a compareAndSet() fails, the set of predecessors and successors might have changed, and so find() must be called again.
The key to the interaction between the add(), remove(), and find() methods is the order in which list manipulations take place. The add() method sets its next references to the successors before it links the node into the bottom-level list, meaning that a node is ready to be removed from the moment it is logically added to the list. Similarly, the remove() method marks the next references top-down, so that once a node is logically removed, it is not traversed by a find() method call.
As noted, in most applications, calls to contains() usually outnumber calls to other methods. As a result contains() should not call find(). While it may be effective to have individual find() calls physically remove logically deleted nodes, contention results if too many concurrent find() calls try to clean up the same nodes at the same time. This kind of contention is much more likely with frequent contains() calls than with calls to the other methods.
However, contains() cannot use the approach taken by the LockFreeList’s wait-free contains(): look at the keys of all reachable nodes independently of whether they are marked or not. The problem is that add() and remove() may violate the skiplist property. It is possible for a marked node to be reachable in a higher-level list after being physically deleted from the lowest-level list. Ignoring the mark could lead to skipping over nodes reachable in the lowest level.
Notice, however, that the find() method of the LockFreeSkipList is not subject to this problem because it never looks at keys of marked nodes, removing them instead. We will have the contains() method mimic this behavior, but without cleaning up marked nodes. Instead, contains() traverses the skiplist, ignoring the keys of marked nodes, and skipping over them instead of physically removing them. Avoiding the physical removal allows the method to be wait-free.
14.4.2 The Algorithm in Detail
As we present the algorithmic details, the reader should keep in mind that the abstract set is defined only by the bottom-level list. Nodes in the higher-level lists are used only as shortcuts into the bottom-level list. Fig. 14.10 shows the structure of the list’s nodes.

Figure 14.10 The LockFreeSkipList class: fields and constructor.
The add() method, shown in Fig. 14.11, uses find(), shown in Fig. 14.13, to determine whether a node with key k is already in the list (Line 61). As in the LazySkipList, add() calls find() to initialize the preds[] and succs[] arrays to hold the new node’s ostensible predecessors and successors.
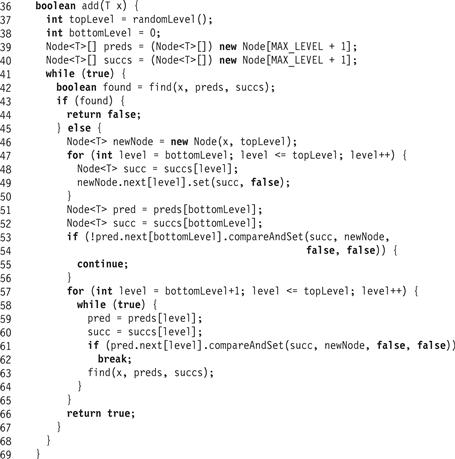
Figure 14.11 The LockFreeSkipList class: the add() method.
If an unmarked node with the target key is found in the bottom-level list, find() returns true and the add() method returns false, indicating that the key is already in the set. The unsuccessful add()’s linearization point is the same as the successful find()’s (Line 42). If no node is found, then the next step is to try to add a new node with the key into the structure.
A new node is created with a randomly chosen topLevel. The node’s next references are unmarked and set to the successors returned by the find() method (Lines 46–49).
The next step is to try to add the new node by linking it into the bottom-level list between the preds[0] and succs[0] nodes returned by find(). As in the LockFreeList, we use compareAndSet() to set the reference while validating that these nodes still refer one to the other and have not been removed from the list (Line 54). If the compareAndSet() fails, something has changed and the call restarts. If the compareAndSet() succeeds, the item is added, and Line 54 is the call’s linearization point.
The add() then links the node in at higher levels (Line 57). For each level, it attempts to splice the node in by setting the predecessor, if it refers to the valid successor, to the new node (Line 61). If successful, it breaks and moves on to the next level. If unsuccessful, then the node referenced by the predecessor must have changed, and find() is called again to find a new valid set of predecessors and successors. We discard the result of calling find() (Line 63) because we care only about recomputing the ostensible predecessors and successors on the remaining unlinked levels. Once all levels are linked, the method returns true (Line 66).
The remove() method, shown in Fig. 14.12, calls find() to determine whether an unmarked node with a matching key is in the bottom-level list. If no node is found in the bottom-level list, or the node with a matching key is marked, the method returns false. The linearization point of the unsuccessful remove() is that of the find() method called in Line 76. If an unmarked node is found, then the method logically removes the associated key from the abstract set, and prepares it for physical removal. This step uses the set of ostensible predecessors (stored by find() in preds[]) and the nodeToRemove (returned from find() in succs[]). First, starting from the topLevel, all links up to and not including the bottom-level link are marked (Lines 82–88) by repeatedly reading next and its mark and applying a compareAndSet(). If the link is found to be marked (either because it was already marked or because the attempt succeeded) the method moves on to the next-level link. Otherwise, the current level’s link is reread since it must have been changed by another concurrent thread, so the marking attempt must be repeated. Once all levels but the bottom one have been marked, the method marks the bottom-level’s next reference. This marking (Line 95), if successful, is the linearization point of a successful remove(). The remove() method tries to mark the next field using compareAndSet(). If successful, it can determine that it was the thread that changed the mark from false to true. Before returning true, the find() method is called again. This call is an optimization: as a side effect, find() physically removes all links to the node it is searching for if that node is already logically removed.

Figure 14.12 The LockFreeSkipList class: the remove() method.
On the other hand, if the compareAndSet() call failed, but the next reference is marked, then another thread must have concurrently removed it, so remove() returns false. The linearization point of this unsuccessful remove() is the linearization point of the remove() method by the thread that successfully marked the next field. Notice that this linearization point must occur during the remove() call because the find() call found the node unmarked before it found it marked.
Finally, if the compareAndSet() fails and the node is unmarked, then the next node must have changed concurrently. Since the nodeToRemove is known, there is no need to call find() again, and remove() simply uses the new value read from next to retry the marking.
As noted, both the add() and remove() methods rely on find(). This method searches the LockFreeSkipList, returning true if and only if a node with the target key is in the set. It fills in the preds[] and succs[] arrays with the target node’s ostensible predecessors and successors at each level. It maintains the following two properties:
![]() It never traverses a marked link. Instead, it removes the node referred to by a marked link from the list at that level.
It never traverses a marked link. Instead, it removes the node referred to by a marked link from the list at that level.
![]() Every preds[] reference is to a node with a key strictly less than the target.
Every preds[] reference is to a node with a key strictly less than the target.
The find() method in Fig. 14.13 proceeds as follows. It starts traversing the SkipList from the topLevel of the head sentinel, which has the maximal allowed node level. It then proceeds in each level down the list, filling in preds and succs nodes that are repeatedly advanced until pred refers to a node with the largest value on that level that is strictly less than the target key (Lines 117–131). As in the LockFreeList, it repeatedly snips out marked nodes from the given level as they are encountered (Lines 119–125) using a compareAndSet(). Notice that the compareAndSet() validates that the next field of the predecessor references the current node. Once an unmarked curr is found (Line 126), it is tested to see if its key is less than the target key. If so, pred is advanced to curr. Otherwise, curr’s key is greater than or equal to the target’s, so the current value of pred is the target node’s immediate predecessor. The find() method breaks out of the current level search loop, saving the current values of pred and curr (Line 132).
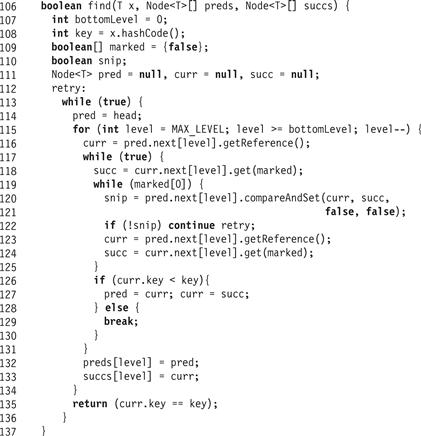
Figure 14.13 The LockFreeSkipList class: a more complex find() than in LazySkipList.
The find() method proceeds this way until it reaches the bottom level. Here is an important point: the traversal at each level maintains the two properties described earlier. In particular, if a node with the target key is in the list, it will be found at the bottom level even if traversed nodes are removed at higher levels. When the traversal stops, pred refers to a predecessor of the target node. The method descends to each next lower level without skipping over the target node. If the node is in the list, it will be found at the bottom level. Moreover, if the node is found, it cannot be marked because if it were marked, it would have been snipped out in Lines 119–125. Therefore, the test in Line 135 need only check if the key of curr is equal to the target key to determine if the target is in the set.
The linearization points of both successful and unsuccessful calls to the find() methods occur when the curr reference at the bottom-level list is set, at either Line 116 or 123, for the last time before the find() call’s success or failure is determined in Line 135. Fig. 14.9 shows how a node is successfully added to the LockFreeSkipList.
The wait-free contains() method appears in Fig. 14.14. It traverses the SkipList in the same way as the find() method, descending level-by-level from the head. Like find(), contains() ignores keys of marked nodes. Unlike find(), it does not try to remove marked nodes. Instead, it simply jumps over them (Line 147–150). For an example execution, see Fig. 14.15.

Figure 14.14 The LockFreeSkipList class: the wait-free contains() method.
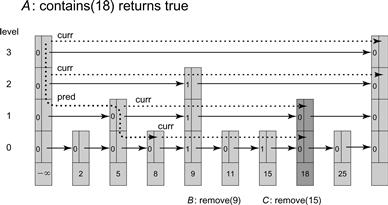
Figure 14.15 Thread A calls contains(18), which traverses the list starting from the top level of the head node. The dotted line marks the traversal by the pred field, and the sparse dotted line marks the path of the curr field. The curr field is advanced to tail on level 3. Since its key is greater than 18, pred descends to level 2. The curr field advances past the marked reference in the node with key 9, again reaching tail which is greater than 18, so pred descends to level 1. Here pred is advanced to the unmarked node with key 5, and curr advances past the marked node with key 9 to reach the unmarked node with key 18, at which point curr is no longer advanced. Though 18 is the target key, the method continues to descend with pred to the bottom level, advancing pred to the node with key 8. From this point, curr traverses past marked Nodes 9 and 15 and Node 11 whose key is smaller than 18. Eventually curr reaches the unmarked node with key 18, returning true.
The method is correct because contains() preserves the same properties as find(), among them, that pred, in any level, never refers to an unmarked node whose key is greater than or equal to the target key. The pred variable arrives at the bottom-level list at a node before, and never after, the target node. If the node is added before the contains() method call starts, then it will be found. Moreover, recall that add() calls find(), which unlinks marked nodes from the bottom-level list before adding the new node. It follows that if contains() does not find the desired node, or finds the desired node at the bottom level but marked, then any concurrently added node that was not found must have been added to the bottom level after the start of the contains() call, so it is correct to return false in Line 159.
Fig. 14.16 shows an execution of the contains() method. In Part (a), a contains(18) call traverses the list starting from the top level of the head node. In Part (b) the contains(18) call traverses the list after the node with key 18 has been logically removed.

Figure 14.16 The LockFreeSkipList class: a contains() call. In Part (a), contains(18) traverses the list starting from the top level of the head node. The dotted line marks the traversal by the pred field. The pred field eventually reaches Node 8 at the bottom level and we show the path of curr from that point on using a sparser dotted line. The curr traverses past Node 9 and reaches the marked Node 15. In Part (b) a new node with key 18 is added to the list by a thread E. Thread E, as part of its find(18) call, physically removes the old nodes with keys 9, 15, and 18. Now thread A continues its traversal with the curr field from the removed node with key 15 (the nodes with keys 15 and 18 are not recycled since they are reachable by thread A). Thread A reaches the node with key 25 which is greater than 18, returning false. Even though at this point there is an unmarked node with key 18 in the LockFreeSkipList, this node was inserted by E concurrently with A’s traversal and is linearized after A’s add(18).
14.5 Concurrent Skiplists
We have seen two highly concurrent SkipList implementations, each providing logarithmic search without the need to rebalance. In the LazySkipList class, the add() and remove() methods use optimistic fine-grained locking, meaning that the method searches for its target node without locking, and acquires locks and validates only when it discovers the target. The contains() method, usually the most common, is wait-free. In the LockFreeSkipList class, the add() and remove() methods are lock-free, building on the LockFreeList class of Chapter 9. In this class too, the contains() method is wait-free.
In Chapter 15 we will see how one can build highly concurrent priority queues based on the concurrent SkipList we presented here.
14.6 Chapter Notes
Bill Pugh invented skiplists, both sequential [128] and concurrent [127]. The LazySkipList is by Yossi Lev, Maurice Herlihy, Victor Luchangco, and Nir Shavit [103]. The LockFreeSkipList presented here is credited to Maurice Herlihy, Yossi Lev, and Nir Shavit [64]. It is partly based on an earlier lock-free SkipList algorithm developed by to Kier Fraser [42], a variant of which was incorporated into the Java Concurrency Package by Doug Lea [100].
Exercise 163. Recall that a skiplist is a probabilistic data structure. Although the expected peformance of a contains() call is O(log n), where n is the number of items in the list, the worst-case peformance could be O(n). Draw a picture of an 8-element skiplist with worst-case performance, and explain how it got that way.
Exercise 164. You are given a skiplist with probability p and MAX_LEVEL M. If the list contains N nodes, what is the expected number of nodes at each level from 0 to M − 1?
Exercise 165. Modify the LazySkipList class so find() starts at the level of the highest node currently in the structure, instead of the highest level possible (MAX_LEVEL).
Exercise 166. Modify the LazySkipList to support multiple items with the same key.
Exercise 167. Suppose we modify the LockFreeSkipList class so that at Line 101 of Fig. 14.12, remove() restarts the main loop instead of returning false. Is the algorithm still correct? Address both safety and liveness issues. That is, what is an unsuccessful remove() call’s new linearization point, and is the class still lock-free?
Exercise 168. Explain how, in the LockFreeSkipList class, a node might end up in the list at levels 0 and 2, but not at level 1. Draw pictures.
Exercise 169. Modify the LockFreeSkipList so that the find() method snips out a sequence of marked nodes with a single compareAndSet(). Explain why your implementation cannot remove a concurrently inserted unmarked node.
Exercise 170. Will the add() method of the LockFreeSkipList work even if the bottom level is linked and then all other levels are linked in some arbitrary order? Is the same true for the marking of the next references in the remove() method: the bottom level next reference is marked last, but references at all other levels are marked in an arbitrary order?
Exercise 171. (Hard) Modify the LazySkipList so that the list at each level is bidirectional, and allows threads to add and remove items in parallel by traversing from either the head or the tail.
Exercise 172.Fig. 14.17 shows a buggy contains() method for the LockFreeSkipList class. Give a scenario where this method returns a wrong answer. Hint: the reason this method is wrong is that it takes into account keys of nodes that have been removed.

Figure 14.17 The LockFreeSkipList class: an incorrect contains().
1 In Fig. 14.5 we make the curr field volatile to prevent compiler optimizations of the loop in Line 45. Recall that making the node array volatile does not make the array entries volatile.
2 The randomLevel() method is designed based on empirical measurements to maintain the SkipList property. For example, in the Java concurrency package, for a maximal SkipList level of 31, randomLevel() returns 0 with probability ![]() , i with probability 2−(i+2) for i ∈ [1, 30], and 31 with probability 2−32.
, i with probability 2−(i+2) for i ∈ [1, 30], and 31 with probability 2−32.
