4
Foundations of Shared Memory
The foundations of sequential computing were established in the 1930s by Alan Turing and Alonzo Church, who independently formulated what has come to be known as the Church-Turing Thesis: anything that can be computed, can be computed by a Turing Machine (or, equivalently, by Church’s Lambda Calculus). Any problem that cannot be solved by a Turing Machine (such as deciding whether a program halts on any input) is universally considered to be unsolvable by any kind of practical computing device. The Turing Thesis is a thesis, not a theorem, because the notion of “what is computable” can never be defined in a precise, mathematically rigorous way. Nevertheless, just about everyone believes it.
This chapter describes the foundations of concurrent shared memory computing. A shared-memory computation consists of multiple threads, each of which is a sequential program in its own right. These threads communicate by calling methods of objects that reside in a shared memory. Threads are asynchronous, meaning that they run at different speeds, and any thread can halt for an unpredictable duration at any time. This notion of asynchrony reflects the realities of modern multiprocessor architectures, where thread delays are unpredictable, ranging from microseconds (cache misses), to milliseconds (page faults), to seconds (scheduling interruptions).
The classical theory of sequential computability proceeds in stages. It starts with finite-state automata, moves on to push-down automata, and culminates in Turing Machines. We, too, consider a progression of models for concurrent computing. In this chapter we start with the simplest form of shared-memory computation: concurrent threads apply simple read–write operations to shared-memory locations, called registers for historical reasons. We start with very simple registers, and we show how to use them to construct a series of more complex registers.
The classical theory of sequential computability is (for the most part) not concerned with efficiency: to show that a problem is computable, it is enough to show that it can be solved by a Turing Machine. There is little incentive to make such a Turing Machine efficient, because a Turing Machine is not a practical means of computation. In the same way, we make little attempt to make our register constructions efficient. We are interested in understanding whether such constructions exist, and how they work. They are not intended to be a practical model for computation. Instead, we prefer easy-to-understand but inefficient constructions over complicated but efficient ones. In particular, some of our constructions use timestamps (counter values) to distinguish older values from newer values.
The problem with timestamps is that they grow without bound, and eventually overflow any fixed-size variable. Bounded solutions (such as the one in Section 2.7 Chapter 2) are (arguably) more intellectually satisfying, and we encourage readers to investigate them further through the references provided in the chapter notes. Here, however, we focus on simpler, unbounded constructions, because they illustrate fundamental principles of concurrent programming with less danger of becoming distracted by technicalities.
4.1 The Space of Registers
At the hardware level, threads communicate by reading and writing shared memory. A good way to understand inter-thread communication is to abstract away from hardware primitives, and to think about communication as happening through shared concurrent objects. Chapter 3 provided a detailed description of shared objects. For now, it suffices to recall the two key properties of their design: safety, defined by consistency conditions, and liveness, defined by progress conditions.
A read–write register (or just a register), is an object that encapsulates a value that can be observed by a read() method and modified by a write() method (in real systems these method calls are often called load and store). Fig. 4.1 illustrates the Register<T> interface implemented by all registers. The type T of the value is typically either Boolean, Integer, or a reference to an object. A register that implements the Register<Boolean> interface is called a Boolean register (we sometimes use 1 and 0 as synonyms for true and false). A register that implements Register<Boolean> for a range of M integer values is called an M-valued register. We do not explicitly discuss any other kind of register, except to note that any algorithm that implements integer registers can be adapted to implement registers that hold references to other objects, simply by treating those references as integers.

Figure 4.1 The Register<T> interface.
If method calls do not overlap, a register implementation should behave as shown in Fig. 4.2. On a multiprocessor, however, we expect method calls to overlap all the time, so we need to specify what the concurrent method calls mean.

Figure 4.2 The SequentialRegister class.
One approach is to rely on mutual exclusion: protect each register with a mutex lock acquired by each read() and write() call. Unfortunately, we cannot use mutual exclusion here. Chapter 2 describes how to accomplish mutual exclusion using registers, so it makes little sense to implement registers using mutual exclusion. Moreover, as we saw in Chapter 3, using mutual exclusion, even if it is deadlock- or starvation-free, would mean that the computation’s progress would depend on the operating system scheduler to guarantee that threads never get stuck in critical sections. Since we wish to examine the basic building blocks of concurrent computation using shared objects, it makes little sense to assume the existence of a separate entity to provide one of their key properties: progress.
Here is a different approach. Recall that an object implementation is wait-free if each method call finishes in a finite number of steps, independently of how its execution is interleaved with steps of other concurrent method calls. The wait-free condition may seem simple and natural, but it has far-reaching consequences. In particular, it rules out any kind of mutual exclusion, and guarantees independent progress, that is, without relying on an operating system scheduler. We therefore require our register implementations to be wait-free.1
An atomic register is a linearizable implementation of the sequential register class shown in Fig. 4.2. Informally, an atomic register behaves exactly as we would expect: each read returns the “last” value written. A model in which threads communicate by reading and writing to atomic registers is intuitively appealing, and for a long time was the standard model of concurrent computation.
It is also important to specify how many readers and writers are expected. Not surprisingly, it is easier to implement a register that supports only a single reader and writer than one that supports multiple readers and writers. For brevity, we use SRSW to mean “single-reader, single-writer,” MRSW to mean “multi-reader, single-writer,” and MRMW to mean “multi-reader, multi-writer.”
In this chapter, we address the following fundamental question:
Can any data structure implemented from the most powerful registers we define also be implemented from the weakest?
We recall from Chapter 1 that any useful form of inter-thread communication must be persistent: the message sent must outlive the active participation of the sender. The weakest form of persistent synchronization is (arguably) the ability to set a single persistent bit in shared memory, and the weakest form of synchronization is (unarguably) none at all: if the act of setting a bit does not overlap the act of reading that bit, then the value read is the same as the value written. Otherwise, a read overlapping a write could return any value.
Different kinds of registers come with different guarantees that make them more or less powerful. For example, we have seen that registers may differ in the range of values they may encapsulate (for example, Boolean vs. M-valued), and in the number of readers and writers they support. Finally, they may differ in the degree of consistency they provide.
A single-writer, multi-reader register implementation is safe if —
![]() A read() call that does not overlap a write() call returns the value written by the most recent write() call.
A read() call that does not overlap a write() call returns the value written by the most recent write() call.
![]() Otherwise, if a read() call overlaps a write() call, then the read() call may return any value within the register’s allowed range of values (for example, 0 to M − 1 for an M-valued register).
Otherwise, if a read() call overlaps a write() call, then the read() call may return any value within the register’s allowed range of values (for example, 0 to M − 1 for an M-valued register).
Be aware that the term “safe” is a historical accident. Because they provide such weak guarantees, “safe” registers are actually quite unsafe.
Consider the history shown in Fig. 4.3. If the register is safe, then the three read calls might behave as follows:
![]() R1 returns 0, the most recently-written value.
R1 returns 0, the most recently-written value.
![]() R2 and R3 are concurrent with W (1), so they could return any value in the range of the register.
R2 and R3 are concurrent with W (1), so they could return any value in the range of the register.
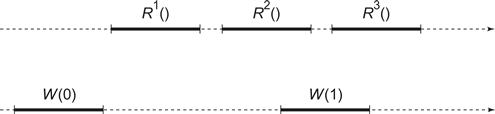
Figure 4.3 A single-reader, single-writer register execution: Ri is the ith read and W(v) is a write of value v. Time flows from left to right. No matter whether the register is safe, regular, or atomic, R1 must return 0, the most recently written value. If the register is safe then because R2 and R3 are concurrent with W(1), they can return any value in the range of the register. If the register is regular, R2 and R3 can each return either 0 or 1. If the register is atomic then if R2 returns 1 then R3 also returns 1, and if R2 returns 0 then R3 could return 0 or 1.
It is convenient to define an intermediate level of consistency between safe and atomic. A regular register is a multi-reader, single-writer register where writes do not happen atomically. Instead, while the write() call is in progress, the value being read may “flicker” between the old and new value before finally replacing the older value. More precisely:
![]() A regular register is safe, so any read() call that does not overlap a write() call returns the most recently written value.
A regular register is safe, so any read() call that does not overlap a write() call returns the most recently written value.
![]() Suppose a read() call overlaps one or more write() calls. Let v0 be the value written by the latest preceding write() call, and let
Suppose a read() call overlaps one or more write() calls. Let v0 be the value written by the latest preceding write() call, and let ![]() be the sequence of values written by overlapping write() calls. The read() call may return any of the vi, for any i in the range 0 … k.
be the sequence of values written by overlapping write() calls. The read() call may return any of the vi, for any i in the range 0 … k.
For the execution in Fig. 4.3, a single-reader regular register might behave as follows:
Regular registers are quiescently consistent (Chapter 3), but not vice versa. We defined both safe and regular registers to permit only a single writer. Note that a regular register is a quiescently consistent single-writer sequential register.
For a single-reader single-writer atomic register, the execution in Fig. 4.3 might produce the following results:
Fig. 4.4 shows a schematic view of the range of possible registers as a three-dimensional space: the register size defines one dimension, the number of readers and writers defines another, and the register’s consistency property defines the third. This view should not be taken literally: there are several combinations, such as multi-writer safe registers, that are not useful to define.

Figure 4.4 The three-dimensional space of possible read–write register-based implementations.
To reason about algorithms for implementing regular and atomic registers, it is convenient to rephrase our definitions directly in terms of object histories. From now on, we consider only histories in which each read() call returns a value written by some write() call (regular and atomic registers do not allow reads to make up return values). We assume values read or written are unique. 2
Recall that an object history is a sequence of invocation and response events, where an invocation event occurs when a thread calls a method, and a matching response event occurs when that call returns. A method call (or just a call) is the interval between matching invocation and response events. Any history induces a partial → order on method calls, defined as follows: if m0 and m1 are method calls, ![]() if m0's response event precedes m1's call event. (See Chapter 3 for complete definitions.)
if m0's response event precedes m1's call event. (See Chapter 3 for complete definitions.)
Any register implementation (whether safe, regular, or atomic) defines a total order on the write() calls called the write order, the order in which writes “take effect” in the register. For safe and regular registers, the write order is trivial, because they allow only one writer at a time. For atomic registers, method calls have a linearization order. We use this order to index the write calls: write call W0 is ordered first, W1 second, and so on. Note that for SRSW or MRSW safe or regular registers, the write order is exactly the same as the precedence order.
We use Ri to denote any read call that returns vi, the unique value written by Wi. Remember that a history contains only one Wi call, but it might contain multiple Ri calls.
One can show that the following conditions provide a precise statement of what it means for a register to be regular. First, no read call returns a value from the future:
![]() (4.1.1)
(4.1.1)
Second, no read call returns a value from the distant past, that is, one that precedes the most recently written non-overlapping value:
![]() (4.1.2)
(4.1.2)
To prove that a register implementation is regular, we must show that its histories satisfy Conditions 4.1.1 and 4.1.2.
An atomic register satisfies one additional condition:
![]() (4.1.3)
(4.1.3)
This condition states that an earlier read cannot return a value later than that returned by a later read. Regular registers are not required to satisfy Condition 4.1.3. To show that a register implementation is atomic, we need first to define a write order, and then to show that its histories satisfy Conditions 4.1.1–4.1.3.
4.2 Register Constructions
We now show how to implement a range of surprisingly powerful registers from simple single-reader single-writer Boolean safe registers. These constructions imply that all read–write register types are equivalent, at least in terms of computability. We consider a series of constructions that implement stronger from weaker registers.
The sequence of constructions appears in Fig. 4.5:

Figure 4.5 The sequence of register constructions.
In the last step, we show how atomic registers (and therefore safe registers) can implement an atomic snapshot: an array of MRSW registers written by different threads, that can be read atomically by any thread. Some of these constructions are more powerful than necessary to complete the sequence of derivations (for example, we do not need to provide the multi-reader property for regular and safe registers to complete the derivation of a SRSW atomic register). We present them anyway because they provide valuable insights.
Our code samples follow these conventions. When we display an algorithm to implement a particular kind of register, say, a safe MRSW Boolean register, we present the algorithm using a form somewhat like this:
class SafeMRSWBooleanRegister implements Register<Boolean>
{
…
}
While this notation makes clear the properties of the register class being implemented, it becomes cumbersome when we want to use this class to implement other classes. Instead, when describing a class implementation, we use the following conventions to indicate whether a particular field is safe, regular, or atomic. A field otherwise named mumble is called s_mumble if it is safe, r_mumble if it is regular, and a_mumble if it is atomic. Other important aspects of the field, such as its type, or whether it supports multiple readers or writers, are noted as comments within the code, and should also be clear from context.
4.2.1 MRSW Safe Registers
Fig. 4.6 shows how to construct a safe MRSW register from safe SRSW registers.

Figure 4.6 The SafeBoolMRSWRegister class: a safe Boolean MRSW register.
Lemma 4.2.1
The construction in Fig. 4.6 is a safe MRSW register.
Proof
If A ’s read() call does not overlap any write() call, then the read() call returns the value of s_table[A], which is the most recently written value. For overlapping method calls, the reader may return any value, because the component registers are safe.
4.2.2 A Regular Boolean MRSW Register
The next construction in Fig. 4.7 builds a regular Boolean MRSW register from a safe Boolean MRSW register. For Boolean registers, the only difference between safe and regular arises when the newly written value x is the same as the old. A regular register can only return x, while a safe register may return either Boolean value. We circumvent this problem simply by ensuring that a value is written only if it is distinct from the previously written value.
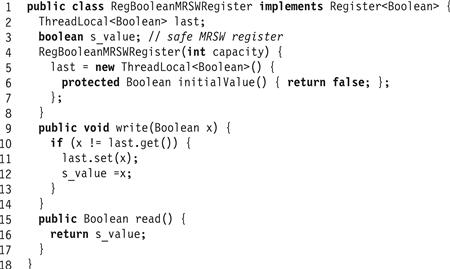
Figure 4.7 The RegBoolMRSWRegister class: a regular Boolean MRSW register constructed from a safe Boolean MRSW register.
Lemma 4.2.2
The construction in Fig. 4.7 is a regular Boolean MRSW register.
Proof
A read() call that does not overlap any write() call returns the most recently written value. If the calls do overlap, there are two cases to consider.
![]() If the value being written is the same as the last value written, then the writer avoids writing to the safe register, ensuring that the reader reads the correct value.
If the value being written is the same as the last value written, then the writer avoids writing to the safe register, ensuring that the reader reads the correct value.
![]() If the value written now is distinct from the last value written, then those values must be true and false because the register is Boolean. A concurrent read returns some value in the range of the register, namely either true or false, either of which is correct.
If the value written now is distinct from the last value written, then those values must be true and false because the register is Boolean. A concurrent read returns some value in the range of the register, namely either true or false, either of which is correct.
4.2.3 A Regular M-Valued MRSW Register
The jump from Boolean to M-valued registers is simple, if astonishingly inefficient: we represent the value in unary notation. In Fig. 4.7 we implement an M-valued register as an array of M Boolean registers. Initially the register is set to value zero, indicated by the “0"-th bit being set to true. A write method of value x writes true in location x and then in descending array-index order sets all lower locations to false. A reading method reads the locations in ascending index order until the first time it reads the value true in some index i. It then returns i. The example in Fig. 4.9 illustrates an 8-valued register.
Lemma 4.2.3
The read() call in the construction in Fig. 4.8 always returns a value corresponding to a bit in 0..M−1 set by some write() call.
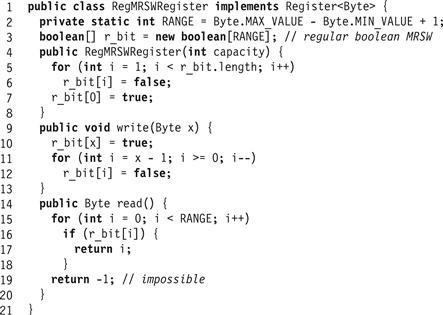
Figure 4.8 The RegMRSWRegister class: a regular M-valued MRSW register.
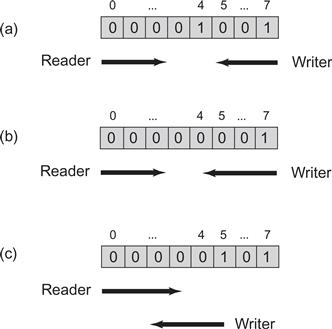
Figure 4.9 The RegMRSWRegister class: an execution of a regular 8-valued MRSW register. The values true and false are represented by 0 and 1. In Part (a), the value prior to the write was 4, thread W’s write of 7 is not read by thread R because R reaches array entry 4 before W overwrites false at that location. In Part (b), entry 4 is overwritten by W before it is read, so the read returns 7. In Part (c), W starts to write 5. Since it wrote array entry 5 before it was read, the reader returns 5 even though entry 7 is also set to true.
Proof
The following property is invariant: if a reading thread is reading r_bit[j], then some bit at index j or higher, written by a write() call, is set to true.
When the register is initialized, there are no readers, and the constructor (we treat the constructor call as a write(0) call) sets r_bit[0] to true. Assume a reader is reading r_bit[j], and that r_bit[k] is true, for ![]() .
.
Lemma 4.2.4
The construction in Fig. 4.8 is a regular M-valued MRSW register.
Proof
For any read, let x be the value written by the most recent non-overlapping write(). At the time the write() completed, a_bit[x] was set to true, and a_bit[i] is false for i < x. By Lemma 4.2.3, if the reader returns a value that is not x, then it observed some a_bit[J], j ≠ x to be true, and that bit must have been set by a concurrent write, proving Conditions 4.1.1 and 4.1.2.
4.2.4 An Atomic SRSW Register
We first show how to construct an atomic SRSW register from a regular SRSW register. (Note that our construction uses unbounded timestamps.)
A regular register satisfies Conditions 4.1.1 and 4.1.2, while an atomic register must also satisfy Condition 4.1.3. Since an SRSW regular register has no concurrent reads, the only way Condition 4.1.3 can be violated is if two reads that overlap the same write read values out-of-order, the first returning vi and the latter returning vj, where j < i.
Fig. 4.10 describes a class of values that each have an added tag that contains a timestamp. As illustrated in Fig. 4.11, our implementation of an AtomicSRSWRegister will use these tags to order write calls so that they can be ordered properly by concurrent read calls. Each read remembers the latest (highest timestamp) timestamp/value pair ever read, so that it is available to future reads. If a later read then reads an earlier value (one having a lower timestamp), it ignores that value and simply uses the remembered latest value. Similarly, the writer remembers the latest timestamp it wrote, and tags each newly written value with a later timestamp (a timestamp greater by 1).

Figure 4.10 The StampedValue<T> class: allows a timestamp and a value to be read or written together.

Figure 4.11 The AtomicSRSWRegister class: an atomic SRSW register constructed from a regular SRSW register.
This algorithm requires the ability to read–write a value and a timestamp as a single unit. In a language such as C, we would treat both the value and the timestamp as uninterpreted bits (“raw seething bits”), and use bit-shifting and logical masking to pack and unpack both values in and out of one or more words. In Java, it is easer to create a StampedValue<T> structure that holds a timestamp/value pair, and to store a reference to that structure in the register.
Lemma 4.2.5
The construction in Fig. 4.11 is an atomic SRSW register.
Proof
The register is regular, so Conditions 4.1.1 and 4.1.2 are met. The algorithm satisfies Condition 4.1.3 because writes are totally ordered by their timestamps, and if a read returns a given value, a later read cannot read an earlier written value, since it would have a lower timestamp.
4.2.5 An Atomic MRSW Register
To understand how to construct an atomic MRSW register from atomic SRSW registers, we first consider a simple algorithm based on direct use of the construction in Section 4.2.1, which took us from SRSW to MRSW safe registers. Let the SRSW registers composing the table array a_table[0..n−1] be atomic instead of safe, with all other calls remaining the same: the writer writes the array locations in increasing index order and then each reader reads and returns its associated array entry. The result is not a multi-reader atomic register. Condition 4.1.3 holds for any single reader because each reader reads from an atomic register, yet it does not hold for distinct readers. Consider, for example, a write that starts by setting the first SRSW register a_table[0], and is delayed before writing the remaining locations a_table[1..n−1]. A subsequent read by thread 0 returns the correct new value, but a subsequent read by thread 1 that completely follows the read by thread 0, reads and returns the earlier value because the writer has yet to update a_table[1..n−1]. We address this problem by having earlier reader threads help out later threads by telling them which value they read.
This implementation appears in Fig. 4.12. The n threads share an n-by-n array a_table[0..n − 1][0..n − 1] of stamped values. As in Section 4.2.4, we use timestamped values to allow early reads to tell later reads which of the values read is the latest. The locations along the diagonal, a_table[i][i] for all i, correspond to the registers in our failed simple construction mentioned earlier. The writer simply writes the diagonal locations one after the other with a new value and a timestamp that increases from one write() call to the next. Each reader A first reads a_table[A][A] as in the earlier algorithm. It then uses the remaining SRSW locations a_table[A][B], A ≠ B for communication between readers A and B. Each reader A, after reading a_table[A][A], checks to see if some other reader has read a later value by traversing its corresponding column (a_table[B][A] for all B), and checking if it contains a later value (one with a higher timestamp). The reader then lets all later readers know the latest value it read by writing this value to all locations in its corresponding row (a_table[A][B] for all B). It thus follows that after a read by A is completed, every later read by a B sees the last value A read (since it reads a_table[A][B]). Fig. 4.13 shows an example execution of the algorithm.

Figure 4.12 The AtomicMRSWRegister class: an atomic MRSW register constructed from atomic SRSW registers.
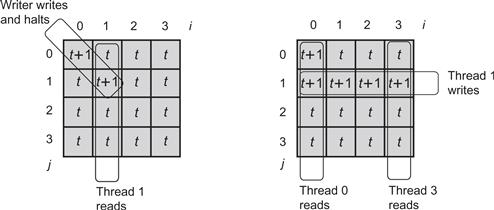
Figure 4.13 An execution of the MRSW atomic register. Each reader thread has an index between 0 and 4, and we refer to each thread by its index. Here, the writer writes a new value with timestamp t + 1 to locations a_table[0][0] and a_table[1][1] and then halts. Then, thread 1 reads its corresponding column a_table[i][1] for all i, and writes its corresponding row a_table[1][i] for all i, returning the new value with timestamp t + 1. Threads 0 and 3 both read completely after thread 1's read. Thread 0 reads a_table[0][0] with value t + 1. Thread 3 cannot read the new value with timestamp t + 1 because the writer has yet to write a_table[3][3]. Nevertheless, it reads a_table[1][3] and returns the correct value with timestamp t + 1 that was read by the earlier thread 1.
Lemma 4.2.6
The construction in Fig. 4.12 is a MRSW atomic register.
Proof
First, no reader returns a value from the future, so Condition 4.1.1 is clearly satisfied. By construction, write() calls write strictly increasing timestamps. The key to understanding this algorithm is the simple observation that the maximum timestamp along any row or column is also strictly increasing. If A writes v with timestamp t, then any read() call by B, where A ’s call completely precedes B ’s, reads (from the diagonal of a_table) a maximum timestamp greater than or equal to t, satisfying Condition 4.1.2. Finally, as noted earlier, if a read call by A completely precedes a read call by B, then A writes a stamped value with timestamp t to B ’s row, so B chooses a value with a timestamp greater than or equal to t, satisfying Condition 4.1.3.
4.2.6 An Atomic MRMW Register
Here is how to construct an atomic MRMW register from an array of atomic MRSW registers, one per thread.
To write to the register, A reads all the array elements, chooses a timestamp higher than any it has observed, and writes a stamped value to array element A. To read the register, a thread reads all the array elements, and returns the one with the highest timestamp. This is exactly the timestamp algorithm used by the Bakery algorithm of Section 2.6. As in the Bakery algorithm, we resolve ties in favor of the thread with the lesser index; in other words, we use a lexicographic order on pairs of timestamp and thread ids.
Lemma 4.2.7
The construction in Fig. 4.14 is an atomic MRMW register.

Figure 4.14 Atomic MRMW register.
Proof
Define the write order among write() calls based on the lexicographic order of their timestamps and thread ids so that the write() call by A with timestamp tA precedes the write() call by B with timestamp tB if ![]() , or if
, or if ![]() and
and ![]() . We leave as an exercise to the reader to show that this lexicographic order is consistent with →. As usual, index write() calls in write order:
. We leave as an exercise to the reader to show that this lexicographic order is consistent with →. As usual, index write() calls in write order: ![]() .
.
Clearly a read() call cannot read a value written in a_table[] after it is completed, and any write() call completely preceded by the read has a timestamp higher than all those written before the read is completed, implying Condition 4.1.1.
Consider Condition 4.1.2, which prohibits skipping over the most recent preceding write(). Suppose a write() call by A preceded a write call by B, which in turn preceded a read() by C. If A = B, then the later write overwrites a_table[A] and the read() does not return the value of the earlier write. If A ≠ B, then since A’s timestamp is smaller than B’s timestamp, any C that sees both returns B’s value (or one with higher timestamp), meeting Condition 4.1.2.
Finally, we consider Condition 4.1.3, which prohibits values from being read out of write order. Consider any read() call by A completely preceding a read() call by B, and any write() call by C which is ordered before the write() by D in the write order. We must show that if A returned D ’s value, then B could not return C ’s value. If ![]() , then if A read timestamp tD from a_table[D], B reads tD or a higher timestamp from a_table[D], and does not return the value associated with tC. If
, then if A read timestamp tD from a_table[D], B reads tD or a higher timestamp from a_table[D], and does not return the value associated with tC. If ![]() , that is, the writes were concurrent, then from the write order,
, that is, the writes were concurrent, then from the write order, ![]() , so if A read timestamp tD from a_table[D], B also reads tD from a_table[D], and returns the value associated with tD(or higher), even if it reads tC in a_table[C].
, so if A read timestamp tD from a_table[D], B also reads tD from a_table[D], and returns the value associated with tD(or higher), even if it reads tC in a_table[C].
Our series of constructions shows that one can construct a wait-free MRMW multi-valued atomic register from SRSW safe Boolean registers. Naturally, no one wants to write a concurrent algorithm using safe registers, but these constructions show that any algorithm using atomic registers can be implemented on an architecture that supports only safe registers. Later on, when we consider more realistic architectures, we return to the theme of implementing algorithms that assume strong synchronization properties on architectures that directly provide only weak properties.
4.3 Atomic Snapshots
We have seen how a register value can be read and written atomically. What if we want to read multiple register values atomically? We call such an operation an atomic snapshot.
An atomic snapshot constructs an instantaneous view of an array of atomic registers. We construct a wait-free snapshot, meaning that a thread can take an instantaneous snapshot of memory without delaying any other thread. Atomic snapshots might be useful for backups or checkpoints.
The snapshot interface (Fig. 4.15) is just an array of atomic MRSW registers, one for each thread. The update() method writes a value v to the calling thread’s register in that array, while the scan() method returns an atomic snapshot of that array.

Figure 4.15 The Snapshot interface.
Our goal is to construct a wait-free implementation that is equivalent (that is, linearizable) to the sequential specification shown in Fig. 4.16. The key property of this sequential implementation is that scan() returns a collection of values, each corresponding to the latest preceding update(), that is, it returns a collection of register values that existed together in the same system state.

Figure 4.16 A sequential snapshot.
4.3.1 An Obstruction-Free Snapshot
We begin with a SimpleSnapshot class for which update() is wait-free, but scan() is obstruction-free. We then extend this algorithm to make scan() wait-free.
Just as for the atomic MRSW register construction, each value includes a StampedValue<T> object with stamp and value fields. Each update() call increments the timestamp.
A collect is the non atomic act of copying the register values one-by-one into an array. If we perform two collects one after the other, and both collects read the same set of timestamps, then we know that there was an interval during which no thread updated its register, so the result of the collect is a snapshot of the system state immediately after the end of the first collect. We call such a pair of collects a clean double collect.
In the construction shown in the SimpleSnapshot<T> <T> class (Fig. 4.17), each thread repeatedly calls collect() (Line 27), and returns as soon as it detects a clean double collect (one in which both sets of timestamps were identical). This construction always returns correct values. The update() calls are wait-free, but scan() is not because any call can be repeatedly interrupted by update(), and may run forever without completing. It is however obstruction-free, since a scan() completes if it runs by itself for long enough.

Figure 4.17 Simple snapshot object.
4.3.2 A Wait-Free Snapshot
To make the scan() method wait-free, each update() call helps a scan() it may interfere with, by taking a snapshot before modifying its register. A scan() that repeatedly fails in taking a double collect can use the snapshot from one of the interfering update() calls as its own. The tricky part is that we must make sure the snapshot taken from the helping update is one that can be linearized within the scan() call’s execution interval.
We say that a thread moves if it completes an update(). If thread A fails to make a clean collect because thread B moved, then can A simply take B ’s most recent snapshot as its own? Unfortunately, no. As illustrated in Fig. 4.18, it is possible for A to see B move when B ’s snapshot was taken before A started its scan() call, so the snapshot did not occur within the interval of A ’s scan.
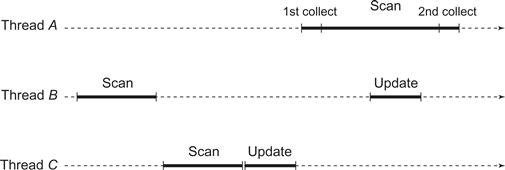
Figure 4.18 Here is why a thread A that fails to complete a clean double collect cannot simply take the latest snapshot of a thread B that performed an update() during A’s second collect. B’s snapshot was taken before A started its scan(), i.e., B’s snapshot did not overlap A’s scan. The danger, illustrated here, is that a thread C could have called update() after B’s scan() and before A’s scan(), making it incorrect for A to use the results of B’s scan().
The wait-free construction is based on the following observation: if a scanning thread A sees a thread B move twice while it is performing repeated collects, then B executed a complete update() call within the interval of A ’s scan(), so it is correct for A to use B ’s snapshot.
Figs. 4.19, 4.20, and 4.21 show the wait-free snapshot algorithm. Each update() call calls scan(), and appends the result of the scan to the value’s label. More precisely, each value written to a register has the structure shown in Fig. 4.19: a stamp field incremented each time the thread updates its value, a value field containing the register’s actual value, and a snap field containing that thread’s most recent scan. The snapshot algorithm is described in Fig. 4.21. A scanning thread creates a Boolean array called moved[] (Line 13), which records which threads have been observed to move in the course of the scan. As before, each thread performs two collects (Lines 14 and 16) and tests whether any thread’s label has changed. If no thread’s label has changed, then the collect is clean, and the scan returns the result of the collect. If any thread’s label has changed (Line 18) the scanning thread tests the moved[] array to detect whether this is the second time this thread has moved (Line 19). If so, it returns that thread’s scan (Line 20), and otherwise it updates moved[] and resumes the outer loop (Line 21).

Figure 4.19 The stamped snapshot class.

Figure 4.20 The single-writer atomic snapshot class and Collect() method.

Figure 4.21 Single-writer atomic snapshot update() and scan() methods.
4.3.3 Correctness Arguments
In this section, we review the correctness arguments for the wait-free snapshot algorithm a little more carefully.
Lemma 4.3.1
If a scanning thread makes a clean double collect, then the values it returns were the values that existed in the registers in some state of the execution.
Proof
Consider the interval between the last read of the first collect, and the first read of the second collect. If any register were updated in that interval, the labels would not match, and the double collect would not be clean.
Lemma 4.3.2
If a scanning thread A observes changes in another thread B ’s label during two different double collects, then the value of B ’s register read during the last collect was written by an update() call that began after the first of the four collects started.
Proof
If during a scan(), two successive reads by A of B ’s register return different label values, then at least one write by B occurs between this pair of reads. Thread B writes to its register as the final step of an update() call, so some update() call by B ended sometime after the first read by A, and the write step of another occurs between the last pair of reads by A. The claim follows because only B writes to its register.
Lemma 4.3.3
The values returned by a scan() were in the registers at some state between the call’s invocation and response.
Proof
If the scan() call made a clean double collect, then the claim follows from Lemma 4.3.1. If the call took the scan value from another thread B ’s register, then by Lemma 4.3.2, the scan value found in B ’s register was obtained by a scan() call by B whose interval lies between A ’s first and second reads of B ’s register. Either B ’s scan() call had a clean double collect, in which case the result follows from Lemma 4.3.1, or there is an embedded scan() call by a thread C occurring within the interval of B ’s scan() call. This argument can be applied inductively, noting that there can be at most n − 1 nested calls before we run out of threads, where n is the maximum number of threads (see Fig. 4.22). Eventually, some nested scan() call must have a clean double collect.
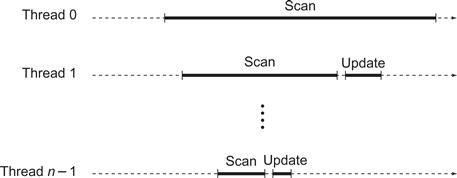
Figure 4.22 There can be at most n−1 nested calls of scan() before we run out of threads, where n is the maximum number of threads. The scan() by thread n−1, contained in the intervals of all other scan() calls, must have a clean double collect.
Lemma 4.3.4
Every scan() or update() returns after at most O(n2) reads or writes.
Proof
For a given scan(), since there are only n−1 other threads, after n + 1 double collects, either one is clean, or some thread is observed to move twice. It follows that scan() calls are wait-free, and so are update() calls.
By Lemma 4.3.3, the values returned by a scan() form a snapshot as they are all in the registers in some state during the call: linearize the call at that point. Similarly, linearize update() calls at the point the register is written.
Theorem 4.3.1
Figs. 4.20 and 4.21 provide a wait-free snapshot implementation.
4.4 Chapter Notes
Alonzo Church introduced Lambda Calculus around 1934-5 [29]. Alan Turing defined the Turing Machine in a classic paper in 1936-7 [146]. Leslie Lamport first defined the notions of safe, regular, and atomic registers and the register hierarchy, and was the first to show that one could implement non trivial shared memory from safe bits [93, 94]. Gary Peterson first suggested the problem of constructing atomic registers [125]. Jaydev Misra gave an axiomatic treatment of atomic registers [116]. The notion of linearizability, which generalizes Leslie Lamport and Jaydev Misra’s notions of atomic registers, is due to Herlihy and Wing [69]. Susmita Haldar and Krishnamurthy Vidyasankar gave a bounded MRSW atomic register construction from regular registers [50]. The problem of constructing a multi-reader atomic register from single-reader atomic registers was mentioned as an open problem by Leslie Lamport [93, 94], and by Paul Vitànyi and Baruch Awerbuch [148]. Paul Vitányi and Baruch Awerbuch were the first to propose an approach for MRMW atomic register design [148]. The first solution is due to Jim Anderson, Mohamed Gouda, and Ambuj Singh [12, 13]. Other atomic register constructions, to name only a few, were proposed by Jim Burns and Gary Peterson [24], Richard Newman-Wolfe [150], Lefteris Kirousis, Paul Spirakis, and Philippas Tsigas [83], Amos Israeli and Amnon Shaham [78], and Ming Li and John Tromp and Paul Vitányi [104]. The simple timestamp-based atomic MRMW construction we present here is due to Danny Dolev and Nir Shavit [34].
Collect operations were first formalized by Mike Saks, Nir Shavit, and Heather Woll [135]. The first atomic snapshot constructions were discovered concurrently and independently by Jim Anderson [10], and by Yehuda Afek, Hagit Attiya, Danny Dolev, Eli Gafni, Michael Merritt and Nir Shavit [2]. The latter algorithm is the one presented here. Later snapshot algorithms are due to Elizabeth Borowsky and Eli Gafni [22] and Yehuda Afek, Gideon Stupp, and Dan Touitou [4].
The timestamps in all the algorithms mentioned in this chapter can be bounded so that the constructions themselves use registers of bounded size. Bounded timestamp systems were introduced by Amos Israeli and Ming Li [77], and bounded concurrent timestamp systems by Danny Dolev and Nir Shavit [34].
Exercise 34. Consider the safe Boolean MRSW construction shown in Fig. 4.6. True or false: if we replace the safe Boolean SRSW register array with an array of safe M-valued SRSW registers, then the construction yields a safe M-valued MRSW register. Justify your answer.
Exercise 35. Consider the safe Boolean MRSW construction shown in Fig. 4.6. True or false: if we replace the safe Boolean SRSW register array with an array of regular Boolean SRSW registers, then the construction yields a regular Boolean MRSW register. Justify your answer.
Exercise 36. Consider the atomic MRSW construction shown in Fig. 4.12. True or false: if we replace the atomic SRSW registers with regular SRSW registers, then the construction still yields an atomic MRSW register. Justify your answer.
Exercise 37. Give an example of a quiescently-consistent register execution that is not regular.
Exercise 38. Consider the safe Boolean MRSW construction shown in Fig. 4.6. True or false: if we replace the safe Boolean SRSW register array with an array of regular M-valued SRSW registers, then the construction yields a regular M-valued MRSW register. Justify your answer.
Exercise 39. Consider the regular Boolean MRSW construction shown in Fig. 4.7. True or false: if we replace the safe Boolean MRSW register with a safe M-valued MRSW register, then the construction yields a regular M-valued MRSW register. Justify your answer.
Exercise 40. Does Peterson’s two-thread mutual exclusion algorithm work if the shared atomic flag registers are replaced by regular registers?
Exercise 41. Consider the following implementation of a Register in a distributed, message-passing system. There are n processors ![]() arranged in a ring, where Pi can send messages only to
arranged in a ring, where Pi can send messages only to ![]() . Messages are delivered in FIFO order along each link.
. Messages are delivered in FIFO order along each link.
Each processor keeps a copy of the shared register.
![]() To read a register, the processor reads the copy in its local memory.
To read a register, the processor reads the copy in its local memory.
![]() A processor Pi starts a write() call of value v to register x, by sending the message "Pi: write v to x " to
A processor Pi starts a write() call of value v to register x, by sending the message "Pi: write v to x " to ![]() .
.
![]() If Pi receives a message “Pj: write v to x,” for
If Pi receives a message “Pj: write v to x,” for ![]() , then it writes v to its local copy of x, and forwards the message to
, then it writes v to its local copy of x, and forwards the message to ![]() .
.
![]() If Pi receives a message “Pi: write v to x,” then it writes v to its local copy of x, and discards the message. The write() call is now complete.
If Pi receives a message “Pi: write v to x,” then it writes v to its local copy of x, and discards the message. The write() call is now complete.
Give a short justification or counterexample.
If write() calls never overlap,
If multiple processors call write(),
Exercise 42. You learn that your competitor, the Acme Atomic Register Company, has developed a way to use Boolean (single-bit) atomic registers to construct an efficient write-once single-reader single-writer atomic register. Through your spies, you acquire the code fragment shown in Fig. 4.23, which is unfortunately missing the code for read(). Your job is to devise a read() method that works for this class, and to justify (informally) why it works. (Remember that the register is write-once, meaning that your read will overlap at most one write.)

Figure 4.23 Partial acme register implementation.
Exercise 43. Prove that the safe Boolean MRSW register construction from safe Boolean SRSW registers illustrated in Fig. 4.6 is a correct implementation of a regular MRSW register if the component registers are regular SRSW registers.
Exercise 44. A monotonic counter is a data structure c = c1… cm(i.e., c is composed of the individual digits cj, ![]() ) such that
) such that ![]() …, where
…, where ![]() … denote the successive values assumed by c.
… denote the successive values assumed by c.
If c is not a single digit, then reading and writing c may involve several separate operations. A read of c which is performed concurrently with one or more writes to c may obtain a value different from any of the versions cj, ![]() . The value obtained may contain traces of several different versions. If a read obtains traces of versions
. The value obtained may contain traces of several different versions. If a read obtains traces of versions ![]() , …,
, …, ![]() , then we say that it obtained a value of
, then we say that it obtained a value of ![]() where k = minimum (i1, …, im) and l = maximum (i1, …, im), so
where k = minimum (i1, …, im) and l = maximum (i1, …, im), so ![]() . If k = l, then
. If k = l, then ![]() and the read obtained is a consistent version of c.
and the read obtained is a consistent version of c.
Hence, the correctness condition for such a counter simply asserts that if a read obtains the value ![]() , then
, then ![]() . The individual digits cj are also assumed to be atomic digits.
. The individual digits cj are also assumed to be atomic digits.
Give an implementation of a monotonic counter, given that the following theorems are true:
Theorem 4.5.1
If ![]() … cm is always written from right to left, then a read from left to right obtains a sequence of values
… cm is always written from right to left, then a read from left to right obtains a sequence of values ![]() with
with ![]() .
.
Note that:
If a read of c obtains traces of version ![]() , then:
, then:
![]() The beginning of the read preceded the end of the write of
The beginning of the read preceded the end of the write of ![]() .
.
![]() The end of the read followed the beginning of the write of cj.
The end of the read followed the beginning of the write of cj.
Furthermore, we say that a read (write) of c is performed from left to right if for each ![]() , the read (write) of cj is completed before the read (write) of
, the read (write) of cj is completed before the read (write) of ![]() has begun. Reading or writing from right to left is defined in the analogous way.
has begun. Reading or writing from right to left is defined in the analogous way.
Finally, always remember that subscripts refer to individual digits of c while superscripts refer to successive values assumed by c.
Exercise 45. Prove Theorem 4.5.1 of Exercise 44. Note that since ![]() , you need only to show that
, you need only to show that ![]() if
if ![]() .
.
(2) Prove Theorem 4.5.3 of Exercise 44, given that the Lemma is true.
Exercise 46. We saw safe and regular registers earlier in this chapter. Define a wraparound register that has the property that there is a value v such that adding 1 to v yields 0, not v + 1.
If we replace the Bakery algorithm’s shared variables with either (a) flickering, (b) safe, (c) or wraparound registers, then does it still satisfy (1) mutual exclusion, (2) first-come-first-served ordering?
You should provide six answers (some may imply others). Justify each claim.
