10
Concurrent Queues and the ABA Problem
10.1 Introduction
In the subsequent chapters, we look at a broad class of objects known as pools. A pool is similar to the Set class studied in Chapter 9, with two main differences: a pool does not necessarily provide a contains() method to test membership, and it allows the same item to appear more than once. The Pool has get() and set() methods as in Fig. 10.1. Pools show up in many places in concurrent systems. For example, in many applications, one or more producer threads produce items to be consumed by one or more consumer threads. These items may be jobs to perform, keystrokes to interpret, purchase orders to execute, or packets to decode. Sometimes, producers are bursty, suddenly and briefly producing items faster than consumers can consume them. To allow consumers to keep up, we can place a buffer between the producers and the consumers. Items produced faster than they can be consumed accumulate in the buffer, from which they are consumed as quickly as possible. Often, pools act as producer–consumer buffers.

Figure 10.1 The Pool<T> interface.
Pools come in several varieties.
![]() A pool can be bounded or unbounded. A bounded pool holds a limited number of items. This limit is called its capacity. By contrast, an unbounded pool can hold any number of items. Bounded pools are useful when we want to keep producer and consumer threads loosely synchronized, ensuring that producers do not get too far ahead of consumers. Bounded pools may also be simpler to implement than unbounded pools. On the other hand, unbounded pools are useful when there is no need to set a fixed limit on how far producers can outstrip consumers.
A pool can be bounded or unbounded. A bounded pool holds a limited number of items. This limit is called its capacity. By contrast, an unbounded pool can hold any number of items. Bounded pools are useful when we want to keep producer and consumer threads loosely synchronized, ensuring that producers do not get too far ahead of consumers. Bounded pools may also be simpler to implement than unbounded pools. On the other hand, unbounded pools are useful when there is no need to set a fixed limit on how far producers can outstrip consumers.
![]() Pool methods may be total, partial, or synchronous.
Pool methods may be total, partial, or synchronous.
— A method is total if calls do not wait for certain conditions to become true. For example, a get() call that tries to remove an item from an empty pool immediately returns a failure code or throws an exception. If the pool is bounded, a total set() that tries to add an item to a full pool immediately returns a failure code or an exception. A total interface makes sense when the producer (or consumer) thread has something better to do than wait for the method call to take effect.
– A method is partial if calls may wait for conditions to hold. For example, a partial get() call that tries to remove an item from an empty pool blocks until an item is available to return. If the pool is bounded, a partial set() call that tries to add an item to a full pool blocks until an empty slot is available to fill. A partial interface makes sense when the producer (or consumer) has nothing better to do than to wait for the pool to become nonfull (or nonempty).
– A method is synchronous if it waits for another method to overlap its call interval. For example, in a synchronous pool, a method call that adds an item to the pool is blocked until that item is removed by another method call. Symmetrically, a method call that removes an item from the pool is blocked until another method call makes an item available to be removed. (Such methods are partial.) Synchronous pools are used for communication in programming languages such as CSP and Ada in which threads rendezvous to exchange information.
![]() Pools provide different fairness guarantees. They can be first-in-first-out (a queue), last-in-first-out (a stack), or other, weaker properties. The importance of fairness when buffering using a pool is clear to anyone who has ever called a bank or a technical support line, only to be placed in a pool of waiting calls. The longer you wait, the more consolation you draw from the recorded message asserting that calls are answered in the order they arrive. Perhaps.
Pools provide different fairness guarantees. They can be first-in-first-out (a queue), last-in-first-out (a stack), or other, weaker properties. The importance of fairness when buffering using a pool is clear to anyone who has ever called a bank or a technical support line, only to be placed in a pool of waiting calls. The longer you wait, the more consolation you draw from the recorded message asserting that calls are answered in the order they arrive. Perhaps.
10.2 Queues
In this chapter we consider a kind of pool that provides first-in-first-out (FIFO) fairness. A sequential Queue<T> is an ordered sequence of items (of type T). It provides an enq(x) method that puts item x at one end of the queue, called the tail, and a deq() method that removes and returns the item at the other end of the queue, called the head. A concurrent queue is linearizable to a sequential queue. Queues are pools, where enq() implements set(), and deq() implements get(). We use queue implementations to illustrate a number of important principles. In later chapters we consider pools that provide other fairness guarantees.
10.3 A Bounded Partial Queue
For simplicity, we assume it is illegal to add a null value to a queue. Of course, there may be circumstances where it makes sense to add and remove null values, but we leave it as an exercise to adapt our algorithms to accommodate null values.
How much concurrency can we expect a bounded queue implementation with multiple concurrent enqueuers and dequeuers to provide? Very informally, the enq() and deq() methods operate on opposite ends of the queue, so as long as the queue is neither full nor empty, an enq() call and a deq() call should, in principle, be able to proceed without interference. For the same reason, concurrent enq() calls probably will interfere, and the same holds for deq() calls. This informal reasoning may sound convincing, and it is in fact mostly correct, but realizing this level of concurrency is not trivial.
Here, we implement a bounded queue as a linked list. (We could also have used an array.) Fig. 10.2 shows the queue’s fields and constructor, Figs. 10.3 and 10.4 show the enq() and deq() methods, and Fig. 10.5 shows a queue node. Like the lists studied in Chapter 9, a queue node has value and next fields.
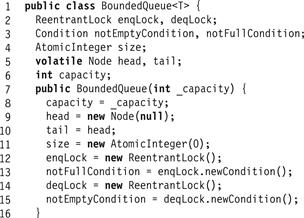
Figure 10.2 The BoundedQueue class: fields and constructor.

Figure 10.3 The BoundedQueue class: the enq() method.

Figure 10.4 The BoundedQueue class: the deq() method.

Figure 10.5 BoundedQueue class: List Node.
As seen in Fig. 10.6, the queue itself has head and tail fields that respectively refer to the first and last nodes in the queue. The queue always contains a sentinel node acting as a place-holder. Like the sentinel nodes in Chapter 9, it marks a position in the queue, though its value is meaningless. Unlike the list algorithms in Chapter 9, in which the same nodes always act as sentinels, the queue repeatedly replaces the sentinel node. We use two distinct locks, enqLock and deqLock, to ensure that at most one enqueuer, and at most one dequeuer at a time can manipulate the queue object’s fields. Using two locks instead of one ensures that an enqueuer does not lock out a dequeuer unnecessarily, and vice versa. Each lock has an associated condition field. The enqLock is associated with the notFullCondition condition, used to notify waiting dequeuers when the queue is no longer full. The deqLock is associated with enqLock, used to notify waiting enqueuers when the queue is no longer empty.

Figure 10.6 The enq() and deq() methods of the BoundedQueue with 4 slots. First a node is enqueued into the queue by acquiring the enqLock. The enq() checks that the size is 3 which is less than the bound. It then redirects the next field of the node referenced by the tail field (step 1), redirects tail to the new node (step 2), increments the size to 4, and releases the lock. Since size is now 4, any further calls to enq() will cause the threads to block until the notFullCondition is signalled by some deq(). Next, a node is dequeued from the queue by some thread. The deq() acquires the deqLock, reads the new value b from the successor of the node referenced by head (this node is the current sentinel), redirects head to this successor node (step 3), decrements the size to 3, and releases the lock. Before completing the deq(), because the size was 4 when it started, the thread acquires the enqLock and signals any enqueuers waiting on notFullCondition that they can proceed.
Since the queue is bounded, we must keep track of the number of empty slots. The size field is an AtomicInteger that tracks the number of objects currently in the queue. This field is decremented by deq() calls and incremented by enq() calls.
The enq() method (Fig. 10.3) works as follows. A thread acquires the enqLock (Line 19), and reads the size field (Line 21). While that field is equal to the capacity, the queue is full, and the enqueuer must wait until a dequeuer makes room. The enqueuer waits on the notFullCondition field (Line 22), releasing the enqueue lock temporarily, and blocking until that condition is signaled. Each time the thread awakens (Line 22), it checks whether there is room, and if not, goes back to sleep.
Once the number of empty slots exceeds zero, however, the enqueuer may proceed. We note that once the enqueuer observes an empty slot, while the enqueue is in progress no other thread can fill the queue, because all the other enqueuers are locked out, and a concurrent dequeuer can only increase the number of empty slots. (Synchronization for the enq() method is symmetric.)
We must carefully check that this implementation does not suffer from the kind of “lost-wakeup” bug described in Chapter 8. Care is needed because an enqueuer encounters a full queue in two steps: first, it sees that size is the queue capacity, and second, it waits on notFullCondition until there is room in the queue. When a dequeuer changes the queue from full to not-full, it acquires enqLock and signals notFullCondition. Even though the size field is not protected by the enqLock, the dequeuer acquires the enqLock before it signals the condition, so the dequeuer cannot signal between the enqueuer’s two steps.
The deq() method proceeds as follows. It reads the size field to check whether the queue is empty. If so, the dequeuer must wait until an item is enqueued. Like the enq() method, the dequeuer waits on enqLock, which temporarily releases deqLock, and blocks until the condition is signaled. Each time the thread awakens, it checks whether the queue is empty, and if so, goes back to sleep.
It is important to understand that the abstract queue’s head and tail items are not always the same as those referenced by head and tail. An item is logically added to the queue as soon as the last node’s next field is redirected to the new item (the linearization point of the enq()), even if the enqueuer has not yet updated tail. For example, a thread can hold the enqLock and be in the process of inserting a new node. Suppose it has not yet redirected the tail field. A concurrent dequeuing thread could acquire the deqLock, read and return the new node’s value, and redirect the head to the new node, all before the enqueuer redirects tail to the newly inserted node.
Once the dequeuer establishes that the queue is nonempty, the queue will remain nonempty for the duration of the deq() call, because all other dequeuers have been locked out. Consider the first nonsentinel node in the queue (i.e., the node referenced by the sentinel node’s next field). The dequeuer reads this node’s value field, and sets the queue’s head to refer to it, making it the new sentinel node. The dequeuer then decrements size and releases deqLock. If the dequeuer found the former size was the queue capacity, then there may be enqueuers waiting on enqLock, so the dequeuer acquires enqLock, and signals all such threads to wake up.
One drawback of this implementation is that concurrent enq() and deq() calls interfere with each other, but not through locks. All method calls apply getAndIncrement() or getAndDecrement() calls to the size field. These methods are more expensive than ordinary reads–writes, and they could cause a sequential bottleneck.
One way to reduce such interactions is to split this field into two counters: enqSideSize is an integer field incremented by enq(), and deqSideSize is an integer field decremented by deq(). A thread calling enq() tests enqSideSize, and as long as it is less than the capacity, it proceeds. When the field reaches capacity, the thread locks deqLock, adds deqSize to EnqSize, and resets deqSideSize to 0. Instead of synchronizing on every method call, this technique synchronizes sporadically when the enqueuer’s size estimate becomes too large.
10.4 An Unbounded Total Queue
We now describe a different kind of queue that can hold an unbounded number of items. The enq() method always enqueues its item, and deq() throws EmptyException if there is no item to dequeue. The representation is the same as the bounded queue, except there is no need to count the number of items in the queue, or to provide conditions on which to wait. As illustrated in Figs. 10.7 and 10.8, this algorithm is simpler than the bounded algorithm.

Figure 10.7 The UnboundedQueue<T> class: the enq() method.

Figure 10.8 The UnboundedQueue<T> class: the deq() method.
This queue cannot deadlock, because each method acquires only one lock, either enqLock or deqLock. A sentinel node alone in the queue will never be deleted, so each enq() call will succeed as soon as it acquires the lock. Of course, a deq() method may fail if the queue is empty (i.e., if head.next is null). As in the earlier queue implementations, an item is actually enqueued when the enq() call sets the last node’s next field to the new node, even before enq() resets tail to refer to the new node. After that instant, the new item is reachable along a chain of the next references. As usual, the queue’s actual head and tail are not necessarily the items referenced by head and tail. Instead, the actual head is the successor of the node referenced by head, and the actual tail is the last item reachable from the head. Both the enq() and deq() methods are total as they do not wait for the queue to become empty or full.
10.5 An Unbounded Lock-Free Queue
We now describe the LockFreeQueue<T> class, an unbounded lock-free queue implementation. This class, depicted in Figs. 10.9 through 10.11, is a natural extension of the unbounded total queue of Section 10.4. Its implementation prevents method calls from starving by having the quicker threads help the slower threads.

Figure 10.9 The LockFreeQueue<T> class: list node.

Figure 10.10 The LockFreeQueue<T> class: the enq() method.

Figure 10.11 The LockFreeQueue<T> class: the deq() method.
As done earlier, we represent the queue as a list of nodes. However, as shown in Fig. 10.9, each node’s next field is an AtomicReference<Node> that refers to the next node in the list. As can be seen in Fig. 10.12, the queue itself consists of two AtomicReference<Node> fields: head refers to the first node in the queue, and tail to the last. Again, the first node in the queue is a sentinel node, whose value is meaningless. The queue constructor sets both head and tail to refer to the sentinel.
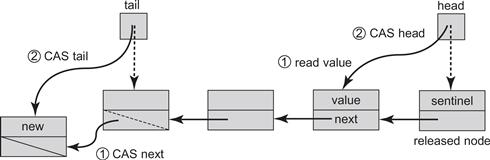
Figure 10.12 The lazy lock-free enq() and deq() methods of the LockFreeQueue. A node is inserted into the queue in two steps. First, a compareAndSet() call changes the next field of the node referenced by the queue's tail from null to the new node. Then a compareAndSet() call advances tail itself to refer to the new node. An item is removed from the queue in two steps. A compareAndSet() call reads the item from the node referred to by the sentinel node, and then redirects head from the current sentinel to the sentinel's next node, making the latter the new sentinel. Both enq() and deq() methods help complete unfinished tail updates.
An interesting aspect of the enq() method is that it is lazy: it takes place in two distinct steps. To make this method lock-free, threads may need to help one another. Fig. 10.12 illustrates these steps.
In the following description the line numbers refer to Figs. 10.9 through 10.11. Normally, the enq() method creates a new node (Line 10), locates the last node in the queue (Lines 12–13), and performs the following two steps:
1. It calls compareAndSet() to append the new node (Line 16), and
2. calls compareAndSet() to change the queue’s tail field from the prior last node to the current last node (Line 17).
Because these two steps are not executed atomically, every other method call must be prepared to encounter a half-finished enq() call, and to finish the job. This is a real-world example of the “helping” technique we first saw in the universal construction of Chapter 6.
We now review all the steps in detail. An enqueuer creates a new node with the new value to be enqueued (Line 10), reads tail, and finds the node that appears to be last (Lines 12–13). To verify that node is indeed last, it checks whether that node has a successor (Line 15). If so, the thread attempts to append the new node by calling compareAndSet() (Line 16). (A compareAndSet() is required because other threads may be trying the same thing.) If the compareAndSet() succeeds, the thread uses a second compareAndSet() to advance tail to the new node (Line 17). Even if this second compareAndSet() call fails, the thread can still return successfully because, as we will see, the call fails only if some other thread “helped” it by advancing tail. If the tail node has a successor (Line 20), then the method tries to “help” other threads by advancing tail to refer directly to the successor (Line 21) before trying again to insert its own node. This enq() is total, meaning that it never waits for a dequeuer. A successful enq() is linearized at the instant where the executing thread (or a concurrent helping thread) calls compareAndSet() to redirect the tail field to the new node at Line 21.
The deq() method is similar to its total counterpart from the UnboundedQueue. If the queue is nonempty, the dequeuer calls compareAndSet() to change head from the sentinel node to its successor, making the successor the new sentinel node. The deq() method makes sure that the queue is not empty in the same way as before: by checking that the next field of the head node is not null.
There is, however, a subtle issue in the lock-free case, depicted in Fig. 10.13: before advancing head one must make sure that tail is not left referring to the sentinel node which is about to be removed from the queue. To avoid this problem we add a test: if head equals tail (Line 32) and the (sentinel) node they refer to has a non-null next field (Line 33), then the tail is deemed to be lagging behind. As in the enq() method, deq() then attempts to help make tail consistent by swinging it to the sentinel node’s successor (Line 36), and only then updates head to remove the sentinel (Line 39). As in the partial queue, the value is read from the successor of the sentinel node (Line 38). If this method returns a value, then its linearization point occurs when it completes a successful compareAndSet() call at Line, and otherwise it is linearized at Line 33.

Figure 10.13 Why dequeuers must help advance tail in Line 36 of Fig. 10.11. Consider the scenario in which a thread enqueuing node b has redirected a’s next field to b, but has yet to redirect tail from a to b. If another thread starts dequeuing, it will read b's value and redirect head from a to b, effectively removing a while tail still refers to it. To avoid this problem, the dequeuing thread must help advance tail from a to b before redirecting head.
It is easy to check that the resulting queue is lock-free. Every method call first checks for an incomplete enq() call, and tries to complete it. In the worst case, all threads are trying to advance the queue’s tail field, and one of them must succeed. A thread fails to enqueue or dequeue a node only if another thread’s method call succeeds in changing the reference, so some method call always completes. As it turns out, being lock-free substantially enhances the performance of queue implementations, and the lock-free algorithms tend to outperform the most efficient blocking ones.
10.6 Memory Reclamation and the ABA Problem
Our queue implementations so far rely on the Java garbage collector to recycle nodes after they have been dequeued. What happens if we choose to do our own memory management? There are several reasons we might want to do this. Languages such as C or C++ do not provide garbage collection. Even if garbage collection is available, it is often more efficient for a class to do its own memory management, particularly if it creates and releases many small objects. Finally, if the garbage collection process is not lock-free, we might want to supply our own lock-free memory reclamation.
A natural way to recycle nodes in a lock-free manner is to have each thread maintain its own private free list of unused queue entries.
ThreadLocal<Node> freeList = new ThreadLocal<Node>() {
protected Node initialValue() { return null; };
};
When an enqueuing thread needs a new node, it tries to remove one from the thread-local free list. If the free list is empty, it simply allocates a node using the new operator. When a dequeuing thread is ready to retire a node, it links it back onto the thread-local list. Because the list is thread-local, there is no need for expensive synchronization. This design works well, as long as each thread performs roughly the same number of enqueues and dequeues. If there is an imbalance, then there may be a need for more complex techniques, such as periodically stealing nodes from other threads.
Surprisingly, perhaps, the lock-free queue will not work if nodes are recycled in the most straightforward way. Consider the scenario depicted in Fig. 10.14. In Part (a) of Fig. 10.14, the dequeuing thread A observes the sentinel node is a, and the next node is b. It then prepares to update head by applying a compareAndSet() with old value a and new value b. Before it takes another step, other threads dequeue b and its successor, placing both a and b in the free pool. Node a is recycled, and eventually reappears as the sentinel node in the queue, as depicted in Part (b) of Fig. 10.14. The thread now wakes up, calls compareAndSet(), and succeeds, since the old value of the head is indeed a. Unfortunately, it has redirected head to a recycled node!
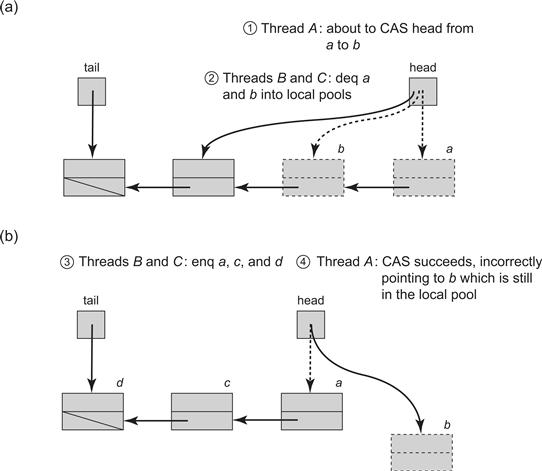
Figure 10.14 An ABA scenario: Assume that we use local pools of recycled nodes in our lock-free queue algorithm. In Part (a), the dequeuer thread A of Fig. 10.11 observes that the sentinel node is a, and next node is b. (Step 1) It then prepares to update head by applying a compareAndSet() with old value a and new value b. (Step 2) Suppose however, that before it takes another step, other threads dequeue b, then its successor, placing both a and b in the free pool. In Part (b) (Step 3) node a is reused, and eventually reappears as the sentinel node in the queue. (Step 4) thread A now wakes up, calls compareAndSet(), and succeeds in setting head to b, since the old value of head is indeed a. Now, head is incorrectly set to a recycled node.
This phenomenon is called the “ABA” problem. It shows up often, especially in dynamic memory algorithms that use conditional synchronization operations such as compareAndSet(). Typically, a reference about to be modified by a compareAndSet() changes from a, to b, and back to a again. As a result, the compareAndSet() call succeeds even though its effect on the data structure has changed, and no longer has the desired effect.
One straightforward way to fix this problem is to tag each atomic reference with a unique stamp. As described in detail in Pragma 10.6.1, an AtomicStampedReference<T> object encapsulates both a reference to an object of Type T and an integer stamp. These fields can be atomically updated either together or individually.
Pragma 10.6.1
The AtomicStampedReference<T> class encapsulates both a reference to an object of Type T and an integer stamp. It generalizes the AtomicMarkableReference<T> class (Pragma 9.8.1), replacing the Boolean mark with an integer stamp.
We usually use this stamp to avoid the ABA problem, incrementing the value of the stamp each time we modify the object, although sometimes, as in the LockFreeExchanger class of Chapter 11, we use the stamp to hold one of a finite set of states.
The stamp and reference fields can be updated atomically, either together or individually. For example, the compareAndSet() method tests expected reference and stamp values, and if both tests succeed, replaces them with updated reference and stamp values. As shorthand, the attemptStamp() method tests an expected reference value and if the test succeeds, replaces it with a new stamp value. The get() method has an unusual interface: it returns the object’s reference value and stores the stamp value in an integer array argument. Fig. 10.15 illustrates the signatures for these methods.
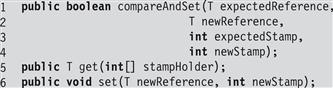
Figure 10.15 The AtomicStampedReference<T> class: the compareAndSet() and get() methods. The compareAndSet() method tests and updates both the stamp and reference fields, the get() method returns the encapsulated reference and stores the stamp at position 0 in the argument array, and set() updates the encapsulated reference and the stamp.
In a language like C or C++, one could provide this functionality efficiently in a 64-bit architecture by “stealing” bits from pointers, although a 32-bit architecture would probably require a level of indirection.
As shown in Fig. 10.16, each time through the loop, deq() reads both the reference and stamp values for the first, next, and last nodes (Lines 6–8). It uses compareAndSet() to compare both the reference and the stamp (Line 17). It increments the stamp each time it uses compareAndSet() to update a reference (Lines 14 and 17).1

Figure 10.16 The LockFreeQueueRecycle<T> class: the deq() method uses stamps to avoid ABA.
The ABA problem can occur in many synchronization scenarios, not just those involving conditional synchronization. For example, it can occur when using only loads and stores. Conditional synchronization operations such as load-linked/store-conditional, available on some architectures (see Appendix B), avoid ABA by testing not whether a value is the same at two points in time, but whether the value has ever changed between those points.
10.6.1 A Na e Synchronous Queue
e Synchronous Queue
We now turn our attention to an even tighter kind of synchronization. One or more producer threads produce items to be removed, in first-in-first-out order, by one or more consumer threads. Here, however, producers and consumers rendezvous with one another: a producer that puts an item in the queue blocks until that item is removed by a consumer, and vice versa. Such rendezvous synchronization is built into languages such as CSP and Ada.
Fig. 10.17 illustrates the SynchronousQueue<T> class, a straightforward monitor-based synchronous queue implementation. It has the following fields: item is the first item waiting to be dequeued, enqueuing is a Boolean value used by enqueuers to synchronize among themselves, lock is the lock used for mutual exclusion, and condition is used to block partial methods. If the enq() method finds enqueuing to be true (Line 10) then another enqueuer has supplied an item and is waiting to rendezvous with a dequeuer, so the enqueuer repeatedly releases the lock, sleeps, and checks whether enqueuing has become false (Line 11). When this condition is satisfied, the enqueuer sets enqueuing to true, which locks out other enqueuers until the current rendezvous is complete, and sets item to refer to the new item (Lines 12–13). It then notifies any waiting threads (Line 14), and waits until item becomes null (Lines 15–16). When the wait is over, the rendezvous has occurred, so the enqueuer sets enqueuing to false, notifies any waiting threads, and returns (Lines 17 and 19).

Figure 10.17 The SynchronousQueue<T> class.
The deq() method simply waits until item is non-null (Lines 26–27), records the item, sets the item field to null, and notifies any waiting threads before returning the item (Lines 28–31).
While the design of the queue is relatively simple, it incurs a high synchronization cost. At every point where one thread might wake up another, both enqueuers and dequeuers wake up all waiting threads, leading to a number of wakeups quadratic in the number of waiting threads. While it is possible to use condition objects to reduce the number of wakeups, it is still necessary to block on every call, which is expensive.
10.7 Dual Data Structures
To reduce the synchronization overheads of the synchronous queue, we consider an alternative synchronous queue implementation that splits enq() and deq() methods into two steps. Here is how a dequeuer tries to remove an item from an empty queue. In the first step, it puts a reservation object in the queue, indicating that the dequeuer is waiting for an enqueuer with which to rendezvous. The dequeuer then spins on a flag in the reservation. Later, when an enqueuer discovers the reservation, it fulfills the reservation by depositing an item and notifying the dequeuer by setting the reservation’s flag. Similarly, an enqueuer can wait for a rendezvous partner by creating its own reservation, and spinning on the reservation’s flag. At any time the queue itself contains either enq() reservations, deq() reservations, or it is empty.
This structure is called a dual data structure, since the methods take effect in two stages, reservation and fulfillment. It has a number of nice properties. First, waiting threads can spin on a locally cached flag, which we have seen is essential for scalability. Second, it ensures fairness in a natural way. Reservations are queued in the order they arrive, ensuring that requests are fulfilled in the same order. Note that this data structure is linearizable, since each partial method call can be ordered when it is fulfilled.
The queue is implemented as a list of nodes, where a node represents either an item waiting to be dequeued, or a reservation waiting to be fulfilled (Fig. 10.18). A node’s type field indicates which. At any time, all queue nodes have the same type: either the queue consists entirely of items waiting to be dequeued, or entirely of reservations waiting to be fulfilled.

Figure 10.18 The SynchronousDualQueue<T> class: queue node.
When an item is enqueued, the node’s item field holds the item, which is reset to null when that item is dequeued. When a reservation is enqueued, the node’s item field is null, and is reset to an item when fulfilled by an enqueuer.
Fig. 10.19 shows the SynchronousDualQueue’s constructor and enq() method. (The deq() method is symmetric.) Just like the earlier queues we have considered, the head field always refers to a sentinel node that serves as a place-holder, and whose actual value is unimportant. The queue is empty when head and tail agree. The constructor creates a sentinel node with an arbitrary value, referred to by both head and tail.
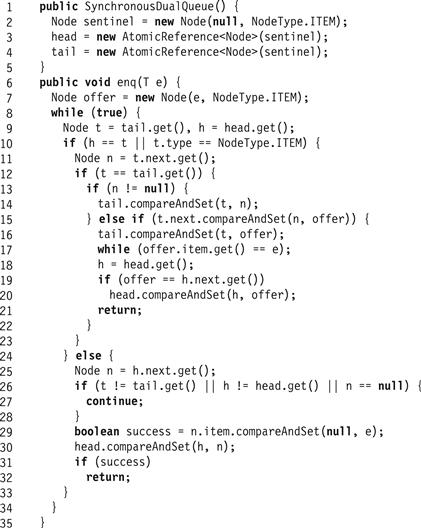
Figure 10.19 The SynchronousDualQueue<T> class: enq() method and constructor.
The enq() method first checks whether the queue is empty or whether it contains enqueued items waiting to be dequeued (Line 10). If so, then just as in the lock-free queue, the method reads the queue’s tail field (Line 11), and checks that the values read are consistent (Line 12). If the tail field does not refer to the last node in the queue, then the method advances the tail field and starts over (Lines 13–14). Otherwise, the enq() method tries to append the new node to the end of the queue by resetting the tail node’s next field to refer to the new node (Line 15). If it succeeds, it tries to advance the tail to the newly appended node (Line 16), and then spins, waiting for a dequeuer to announce that it has dequeued the item by setting the node’s item field to null. Once the item is dequeued, the method tries to clean up by making its node the new sentinel. This last step serves only to enhance performance, because the implementation remains correct, whether or not the method advances the head reference.
If, however, the enq() method discovers that the queue contains dequeuers' reservations waiting to be fulfilled, then it tries to find a reservation to fulfill. Since the queue’s head node is a sentinel with no meaningful value, enq() reads the head’s successor (Line 25), checks that the values it has read are consistent (Lines 26–28), and tries to switch that node’s item field from null to the item being enqueued. Whether or not this step succeeds, the method tries to advance head (Line 30). If the compareAndSet() call succeeds (Line 29), the method returns; otherwise it retries.
10.8 Chapter Notes
The partial queue employs a mixture of techniques adapted from Doug Lea [98] and from an algorithm by Maged Michael and Michael Scott [115]. The lock-free queue is a slightly simplified version of a queue algorithm by Maged Michael and Michael Scott [115]. The synchronous queue implementations are adapted from algorithms by Bill Scherer, Doug Lea, and Michael Scott [136].
Exercise 119.Change the SynchronousDualQueue<T> class to work correctly with null items.
Exercise 120.Consider the simple lock-free queue for a single enqueuer and a single dequeuer, described earlier in Chapter 3. The queue is presented in Fig. 10.20. This queue is blocking, that is, removing an item from an empty queue or inserting an item to a full one causes the threads to block (spin). The surprising thing about this queue is that it requires only loads and stores and not a more powerful read–modify–write synchronization operation. Does it however require the use of a memory barrier? If not, explain, and if so, where in the code is such a barrier needed and why?

Figure 10.20 A Lock-free FIFO queue with blocking semantics for a single enqueuer and single dequeuer. The queue is implemented in an array. Initially the head and tail fields are equal and the queue is empty. If the head and tail differ by capacity, then the queue is full. The enq() method reads the head field, and if the queue is full, it repeatedly checks the head until the queue is no longer full. It then stores the object in the array, and increments the tail field. The deq() method works in a symmetric way.
Exercise 121.Design a bounded lock-based queue implementation using an array instead of a linked list.
1. Allow parallelism by using two separate locks for head and tail.
2. Try to transform your algorithm to be lock-free. Where do you run into difficulty?
Exercise 122.Consider the unbounded lock-based queue’s deq() method in Fig. 10.8. Is it necessary to hold the lock when checking that the queue is not empty? Explain.
Exercise 123.In Dante’s Inferno, he describes a visit to Hell. In a very recently discovered chapter, he encounters five people sitting at a table with a pot of stew in the middle. Although each one holds a spoon that reaches the pot, each spoon’s handle is much longer than each person’s arm, so no one can feed him- or herself. They are famished and desperate.
Dante then suggests “why do not you feed one another?”
The rest of the chapter is lost.
1. Write an algorithm to allow these unfortunates to feed one another. Two or more people may not feed the same person at the same time. Your algorithm must be, well, starvation-free.
2. Discuss the advantages and disadvantages of your algorithm. Is it centralized, decentralized, high or low in contention, deterministic or randomized?
Exercise 124.Consider the linearization points of the enq() and deq() methods of the lock-free queue:
1. Can we choose the point at which the returned value is read from a node as the linearization point of a successful deq()?
2. Can we choose the linearization point of the enq() method to be the point at which the tail field is updated, possibly by other threads (consider if it is within the enq() 's execution interval)? Argue your case.
Exercise 125. Consider the unbounded queue implementation shown in Fig. 10.21. This queue is blocking, meaning that the deq() method does not return until it has found an item to dequeue.
The queue has two fields: items is a very large array, and tail is the index of the next unused element in the array.

Figure 10.21 Queue used in Exercise 125.
1. Are the enq() and deq() methods wait-free? If not, are they lock-free? Explain.
2. Identify the linearization points for enq() and deq(). (Careful! They may be execution-dependent.)
1 We ignore the remote possibility that the stamp could wrap around and cause an error.
