17
Barriers
17.1 Introduction
Imagine you are writing the graphical display for a computer game. Your program prepares a sequence of frames to be displayed by a graphics package (perhaps a hardware coprocessor). This kind of program is sometimes called a soft real-time application: real-time because it must display at least 35 frames per second to be effective, and soft because occasional failure is not catastrophic. On a single-threaded machine, you might write a loop like this:
while (true) {
frame.prepare();
frame.display();
}
If, instead, you have n parallel threads available, then it makes sense to split the frame into n disjoint parts, and to have each thread prepare its own part in parallel with the others.
int me = ThreadID.get();
while (true) {
frame[me].prepare();
frame[me].display();
The problem with this approach is that different threads will require different amounts of time to prepare and display their portions of the frame. Some threads might start displaying the ith frame before others have finished the (i − 1)st.
To avoid such synchronization problems, we can organize computations such as this as a sequence of phases, where no thread should start the ith phase until the others have finished the (i − 1)st. We have already seen this phased computation pattern before. In Chapter 12, the sorting network algorithms required each comparison phase to be separate from the others. Similarly, in the sample sorting algorithm, each phase had to make sure that prior phases had completed before proceeding.
The mechanism for enforcing this kind of synchronization is called a barrier (Fig. 17.1). A barrier is a way of forcing asynchronous threads to act almost as if they were synchronous. When a thread finishing phase i calls the barrier’s await() method, it is blocked until all n threads have also finished that phase. Fig. 17.2 shows how one could use a barrier to make the parallel rendering program work correctly. After preparing frame i, all threads synchronize at a barrier before starting to display that frame. This structure ensures that all threads concurrently displaying a frame display the same frame.
![]()
Figure 17.1 The Barrier interface.

Figure 17.2 Using a barrier to synchronize concurrent displays.
Barrier implementations raise many of the same performance issues as spin locks in Chapter 7, as well as some new issues. Clearly, barriers should be fast, in the sense that we want to minimize the duration between when the last thread reaches the barrier and when the last thread leaves the barrier. It is also important that threads leave the barrier at roughly the same time. A thread’s notification time is the interval between when some thread has detected that all threads have reached the barrier, and when that specific thread leaves the barrier. Having uniform notification times is important for many soft real-time applications. For example, picture quality is enhanced if all portions of the frame are updated at more-or-less the same time.
17.2 Barrier Implementations
Fig. 17.3 shows the SimpleBarrier class, which creates an AtomicInteger counter initialized to n, the barrier size. Each thread applies getAndDecrement() to lower the counter. If the call returns 1 (Line 10), then that thread is the last to reach the barrier, so it resets the counter for the next use (Line 11). Otherwise, the thread spins on the counter, waiting for the value to fall to zero (Line 13). This barrier class may look like it works, but it does not.

Figure 17.3 The SimpleBarrier class.
Unfortunately, the attempt to make the barrier reusable causes it to break (see Fig. 17.2). Suppose there are only two threads. Thread A applies getAndDecrement() to the counter, discovers it is not the last thread to reach the barrier, and spins waiting for the counter value to reach zero. When B arrives, it discovers it is the last thread to arrive, so it resets the counter to n in this case 2. It finishes the next phase and calls await(). Meanwhile, A continues to spin, and the counter never reaches zero. Eventually, A is waiting for phase 0 to finish, while B is waiting for phase 1 to finish, and the two threads starve.
Perhaps the simplest way to fix this problem is just to alternate between two barriers, using one for even-numbered phases, and another for odd-numbered ones. However, such an approach wastes space, and requires too much bookkeeping from applications.
17.3 Sense-Reversing Barrier
A sense-reversing barrier is a more elegant and practical solution to the problem of reusing barriers. As depicted in Fig. 17.4, a phase’s sense is a Boolean value: true for even-numbered phases and false otherwise. Each SenseBarrier object has a Boolean sense field indicating the sense of the currently executing phase. Each thread keeps its current sense as a thread-local object (see Pragma 17.3.1). Initially the barrier’s sense is the complement of the local sense of all the threads. When a thread calls await(), it checks whether it is the last thread to decrement the counter. If so, it reverses the barrier’s sense and continues. Otherwise, it spins waiting for the barrier’s sense field to change to match its own local sense.

Figure 17.4 The SenseBarrier class: a sense-reversing barrier.
Decrementing the shared counter may cause memory contention, since all the threads are trying to access the counter at about the same time. Once the counter has been decremented, each thread spins on the sense field. This implementation is well suited for cache-coherent architectures, since threads spin on locally cached copies of the field, and the field is modified only when threads are ready to leave the barrier. The sense field is an excellent way of maintaining a uniform notification time on symmetric cache-coherent multiprocessors.
Pragma 17.3.1
The constructor code for the sense-reversing barrier, shown in Fig. 17.4, is mostly straightforward. The one exception occurs on lines 5 and 6, where we initialize the thread-local threadSense field. This somewhat complicated syntax defines a thread-local Boolean value whose initial value is the complement of the sense field’s initial value. See Appendix A.2.4 for a more complete explanation of thread-local objects in Java.
17.4 Combining Tree Barrier
One way to reduce memory contention (at the cost of increased latency) is to use the combining paradigm of Chapter 12. Split a large barrier into a tree of smaller barriers, and have threads combine requests going up the tree and distribute notifications going down the tree. As shown in Fig. 17.5, a tree barrier is characterized by a size n, the total number of threads, and a radix r, each node’s number of children. For convenience, we assume there are exactly n = rd+1 threads, where d is the depth of the tree.

Figure 17.5 The TreeBarrier class: each thread indexes into an array of leaf nodes and calls that leaf’s await() method.
Specifically, the combining tree barrier is a tree of nodes, where each node has a counter and a sense, just as in the sense-reversing barrier. A node’s implementation is shown in Fig. 17.6. Thread i starts at leaf node [i/r]. The node’s await() method is similar to the sense-reversing barrier’s await(), the principal difference being that the last thread to arrive, the one that completes the barrier, visits the parent barrier before waking up the other threads. When r threads have arrived at the root, the barrier is complete, and the sense is reversed. As before, thread-local Boolean sense values allow the barrier to be reused without reinitialization.

Figure 17.6 The TreeBarrier class: internal tree node.
The tree-structured barrier reduces memory contention by spreading memory accesses across multiple barriers. It may or may not reduce latency, depending on whether it is faster to decrement a single location or to visit a logarithmic number of barriers.
The root node, once its barrier is complete, lets notifications percolate down the tree. This approach may be good for a NUMA architecture, but it may cause nonuniform notification times. Because threads visit an unpredictable sequence of locations as they move up the tree, this approach may not work well on cacheless NUMA architectures.
Pragma 17.4.1
Tree nodes are declared as an inner class of the tree barrier class, so nodes are not accessible outside the class. As shown in Fig. 17.7, the tree is initialized by a recursive build() method. The method takes a parent node and a depth. If the depth is nonzero, it creates radix children, and recursively creates the children’s children. If the depth is zero, it places each node in a leaf[] array. When a thread enters the barrier, it uses this array to choose a leaf to start from. See Appendix A.2.1 for a more complete discussion of inner classes in Java.

Figure 17.7 The TreeBarrier class: initializing a combining tree barrier. The build() method creates r children for each node, and then recursively creates the children’s children. At the bottom, it places leaves in an array.
17.5 Static Tree Barrier
The barriers seen so far either suffer from contention (the simple and sense-reversing barriers) or have excessive communication (the combining-tree barrier). In the last barrier, threads traverse an unpredictable sequence of nodes, which makes it difficult to lay out the barriers on cacheless NUMA architectures. Surprisingly, there is another simple barrier that allows both static layout and low contention.
The static tree barrier of Fig. 17.8 works as follows. Each thread is assigned to a node in a tree (see Fig. 17.9). The thread at a node waits until all nodes below it in the tree have finished, and then informs its parent. It then spins waiting for the global sense bit to change. Once the root learns that its children are done, it toggles the global sense bit to notify the waiting threads that all threads are done. On a cache-coherent multiprocessor, completing the barrier requires log(n) steps moving up the tree, while notification simply requires changing the global sense, which is propagated by the cache-coherence mechanism. On machines without coherent caches threads propagate notification down the tree as in the combining barrier we saw earlier.

Figure 17.8 The StaticTreeBarrier class: each thread indexes into a statically assigned tree node and calls that node’s await() method.

Figure 17.9 The StaticTreeBarrier class: internal Node class.
17.6 Termination Detecting Barriers
All the barriers considered so far were directed at computations organized in phases, where each thread finishes the work for a phase, reaches the barrier, and then starts a new phase.
There is, however, another interesting class of programs, in which each thread finishes its own part of the computation, only to be put to work again when another thread generates new work. An example of such a program is the simplified work stealing executer pool from Chapter 16 (see Fig. 17.10). Here, once a thread exhausts the tasks in its local queue, it tries to steal work from other threads’ queues. The execute() method itself may push new tasks onto the calling thread’s local queue. Once all threads have exhausted all tasks in their queues, the threads will run forever while repeatedly attempting to steal items. Instead, we would like to devise a termination detection barrier so that these threads can all terminate once they have finished all their tasks.

Figure 17.10 Work stealing executer pool revisited.
Each thread is either active (it has a task to execute) or inactive (it has none). Note that any inactive thread may become active as long as some other thread is active, since an inactive thread may steal a task from an active one. Once all threads have become inactive, then no thread will ever become active again. Detecting that the computation as a whole has terminated is the problem of determining that at some instant in time there are no longer any active threads.
None of the barrier algorithms studied so far can solve this problem. Termination cannot be detected by having each thread announce that it has become inactive, and simply count how many have done so, because threads may repeatedly change from inactive to active and back. For example, consider threads A, B, and C running as shown in Fig. 17.10, and assume that each has a Boolean value indicating whether it is active or inactive. When A becomes inactive, it may then observe that B is also inactive, and then observe that C is inactive. Nevertheless, A cannot conclude that the overall computation has completed; as B might have stolen work from C after A checked B, but before it checked C.
A termination-detection barrier (Fig. 17.11) provides methods setActive(v) and isTerminated(). Each thread calls setActive(true) to notify the barrier when it becomes active, and setActive(false) to notify the barrier when it becomes inactive. The isTerminated() method returns true if and only if all threads had become inactive at some earlier instant. Fig. 17.12 shows a simple implementation of a termination-detection barrier.

Figure 17.11 Termination detection barrier interface.

Figure 17.12 A simple termination detecting barrier.
The barrier encompasses an AtomicInteger initialized to 0. Each thread that becomes active increments the counter (Line 8) and each thread that becomes inactive decrements it (Line 10). The computation is deemed to have terminated when the counter reaches zero (Line 14).
The termination-detection barrier works only if used correctly. Fig. 17.13 shows how to modify the work-stealing thread’s run() method to return when the computation has terminated. Initially, every thread registers as active (Line 3). Once a thread has exhausted its local queue, it registers as inactive (Line 10). Before it tries to steal a new task, however, it must register as active (Line 14). If the theft fails, it registers as inactive again (Line 17).

Figure 17.13 Work-stealing executer pool: the run() method with termination.
Notice that a thread sets its state to active before stealing a task. Otherwise, if a thread were to steal a task while inactive, then the thread whose task was stolen might also declare itself inactive, resulting in a computation where all threads declare themselves inactive while the computation continues.
Here is a subtle point. A thread tests whether the queue is empty (Line 13) before it attempts to steal a task. This way, it avoids declaring itself active if there is no chance the theft will succeed. Without this precaution, it is possible that the threads will not detect termination because each one repeatedly switches to an active state before a steal attempt that is doomed to fail.
Correct use of the termination-detection barrier must satisfy both a safety and a liveness property. The safety property is that if isTerminated() returns true, then the computation really has terminated. Safety requires that no active thread ever declare itself inactive, because it could trigger an incorrect termination detection. For example, the work-stealing thread of Fig. 17.13 would be incorrect if the thread declared itself to be active only after successfully stealing a task. By contrast, it is safe for an inactive thread to declare itself active, which may occur if the thread is unsuccessful in stealing work at Line 15.
The liveness property is that if the computation terminates, then isTerminated() eventually returns true. (It is not necessary that termination be detected instantly.) While safety is not jeopardized if an inactive thread declares itself active, liveness will be violated if a thread that does not succeed in stealing work fails to declare itself inactive again (Line 15), because termination will not be detected when it occurs.
17.7 Chapter Notes
John Mellor–Crummey and Michael Scott [113] provide a survey of several barrier algorithms, though the performance numbers they provide should be viewed from a historical perspective. The combining tree barrier is based on code due to John Mellor–Crummey and Michael Scott [113], which is in turn based on the combining tree algorithm of Pen-Chung Yew, Nian-Feng Tzeng, and Duncan Lawrie [151]. The dissemination barrier is credited to Debra Hensgen, Raphael Finkel, and Udi Manber [59]. The tournament tree barrier used in the exercises is credited to John Mellor–Crummey and Michael Scott [113]. The simple barriers and the static tree barrier are most likely folklore. We learned of the static tree barrier from Beng-Hong Lim. The termination detection barrier and its application to an executer pool are based on a variation suggested by Peter Kessler to an algorithm by Dave Detlefs, Christine Flood, Nir Shavit, and Xiolan Zhang [41].
17.8 Exercises
Exercise 198. Fig. 17.14 shows how to use barriers to make a parallel prefix computation work on an asynchronous architecture.

Figure 17.14 Parallel prefix computation.
A parallel prefix computation, given a sequence a0, …, am−1, of numbers, computes in parallel the partial sums:
![]()
In a synchronous system, where all threads take steps at the same time, there are simple, well-known algorithms for m threads to compute the partial sums in log m steps. The computation proceeds in a sequence of rounds, starting at round zero. In round r, if i ≥ 2r, thread i reads the value at a[i − 2r] into a local variable. Next, it adds that value to a[i]. Rounds continue until 2r ≥ m. It is not hard to see that after log2(m) rounds, the array a contains the partial sums.
1. What could go wrong if we executed the parallel prefix on n > m threads?
2. Modify this program, adding one or more barriers, to make it work properly in a concurrent setting with n threads. What is the minimum number of barriers that are necessary?
Exercise 199. Change the sense-reversing barrier implementation so that waiting threads call wait() instead of spinning.
![]() Give an example of a situation where suspending threads is better than spinning.
Give an example of a situation where suspending threads is better than spinning.
![]() Give an example of a situation where the other choice is better.
Give an example of a situation where the other choice is better.
Exercise 200. Change the tree barrier implementation so that it takes a Runnable object whose run() method is called once after the last thread arrives at the barrier, but before any thread leaves the barrier.
Exercise 201. Modify the combining tree barrier so that nodes can use any barrier implementation, not just the sense-reversing barrier.
Exercise 202. A tournament tree barrier (Class TourBarrier in Fig. 17.15) is an alternative tree-structured barrier. Assume there are n threads, where n is a power of 2. The tree is a binary tree consisting of 2n − 1 nodes. Each leaf is owned by a single, statically determined thread. Each node’s two children are linked as partners. One partner is statically designated as active, and the other as passive. Fig. 17.16 illustrates the tree structure.

Figure 17.15 The TourBarrier class.

Figure 17.16 The TourBarrier class: information flow. Nodes are paired statically in active/passive pairs. Threads start at the leaves. Each thread in an active node waits for its passive partner to show up; then it proceeds up the tree. Each passive thread waits for its active partner for notification of completion. Once an active thread reaches the root, all threads have arrived, and notifications flow down the tree in the reverse order.
Each thread keeps track of the current sense in a thread-local variable. When a thread arrives at a passive node, it sets its active partner’s sense field to the current sense, and spins on its own sense field until its partner changes that field’s value to the current sense. When a thread arrives at an active node, it spins on its sense field until its passive partner sets it to the current sense. When the field changes, that particular barrier is complete, and the active thread follows the parent reference to its parent node. Note that an active thread at one level may become passive at the next level. When the root node barrier is complete, notifications percolate down the tree. Each thread moves back down the tree setting its partner’s sense field to the current sense.
This barrier improves a little on the combining tree barrier of Fig. 17.5. Explain how.
The tournament barrier code uses parent and partner references to navigate the tree. We could save space by eliminating these fields and keeping all the nodes in a single array with the root at index 0, the root’s children at indexes 1 and 2, the grandchildren at indexes 3–6, and so on. Re-implement the tournament barrier to use indexing arithmetic instead of references to navigate the tree.
Exercise 203. The combining tree barrier uses a single thread-local sense field for the entire barrier. Suppose instead we were to associate a thread-local sense with each node as in Fig. 17.8. Either:
![]() Explain why this implementation is equivalent to the other one, except that it consumes more memory, or.
Explain why this implementation is equivalent to the other one, except that it consumes more memory, or.
![]() Give a counterexample showing that this implementation is incorrect.
Give a counterexample showing that this implementation is incorrect.

Figure 17.17 Thread-local tree barrier.
Exercise 204. The tree barrier works “bottom-up,” in the sense that barrier completion moves from the leaves up to the root, while wake-up information moves from the root back down to the leaves. Figs. 17.18 and 17.19 show an alternative design, called a reverse tree barrier, which works just like a tree barrier except for the fact that barrier completion starts at the root and moves down to the leaves. Either:
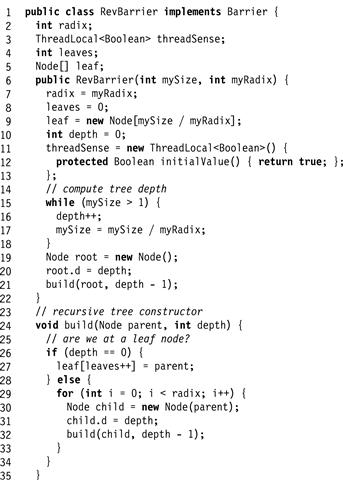
Figure 17.18 Reverse tree barrier Part 1.
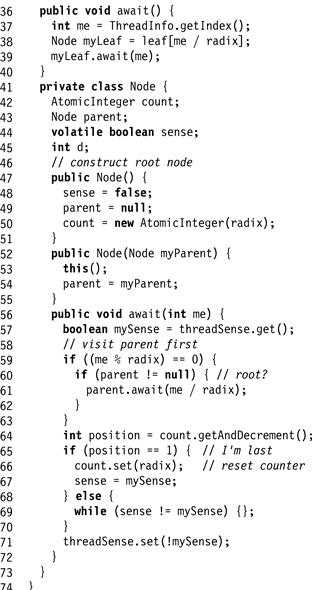
Figure 17.19 Reverse tree barrier Part 2: correct or not?
Exercise 205. Implement an n-thread reusable barrier from an n-wire counting network and a single Boolean variable. Sketch a proof that the barrier works.
Exercise 206. Can you devise a “distributed” termination detection algorithm for the executer pool in which threads do not repeatedly update or test a central location for termination, but rather use only local uncontended variables? Variables may be unbounded, but state changes should take constant time, (so you cannot parallelize the shared counter).
Hint: adapt the atomic snapshot algorithm from Chapter 4.
Exercise 207. A dissemination barrier is a symmetric barrier implementation in which threads spin on statically-assigned locally-cached locations using only loads and stores. As illustrated in Fig. 17.20, the algorithm runs in a series of rounds. At round r, thread i notifies thread i + 2r(mod n), (where n is the number of threads) and waits for notification from thread i − 2r(mod n).

Figure 17.20 Communication in the dissemination barrier. In each round r a thread i communicates with thread i + 2r(mod n).
For how many rounds must this protocol run to implement a barrier? What if n is not a power of 2? Justify your answers.
Exercise 208. Give a reusable implementation of a dissemination barrier in Java.
Hint: you may want to keep track of both the parity and the sense of the current phase.
Exercise 209. Create a table that summarizes the total number of operations in the static tree, combining tree, and dissemination barriers.
Exercise 210. In the termination detection barrier, the state is set to active before stealing the task; otherwise the stealing thread could be declared inactive; then it would steal a task, and before setting its state back to active, the thread it stole from could become inactive. This would lead to an undesirable situation in which all threads are declared inactive yet the computation continues. Can you devise a terminating executer pool in which the state is set to active only after successfully stealing a task?
