4. Operators and Expressions
This chapter describes Python’s built-in operators, expressions, and evaluation rules. Although much of this chapter describes Python’s built-in types, user-defined objects can easily redefine any of the operators to provide their own behavior.
Operations on Numbers
The following operations can be applied to all numeric types:
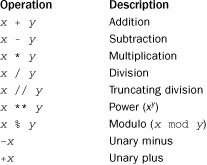
The truncating division operator (//, also known as floor division) truncates the result to an integer and works with both integers and floating-point numbers. In Python 2, the true division operator (/) also truncates the result to an integer if the operands are integers. Therefore, 7/4 is 1, not 1.75. However, this behavior changes in Python 3, where division produces a floating-point result. The modulo operator returns the remainder of the division x // y. For example, 7 % 4 is 3. For floating-point numbers, the modulo operator returns the floating-point remainder of x // y, which is x – (x // y) * y. For complex numbers, the modulo (%) and truncating division operators (//) are invalid.
The following shifting and bitwise logical operators can be applied only to integers:

The bitwise operators assume that integers are represented in a 2’s complement binary representation and that the sign bit is infinitely extended to the left. Some care is required if you are working with raw bit-patterns that are intended to map to native integers on the hardware. This is because Python does not truncate the bits or allow values to overflow—instead, the result will grow arbitrarily large in magnitude.
In addition, you can apply the following built-in functions to all the numerical types:

The abs() function returns the absolute value of a number. The divmod() function returns the quotient and remainder of a division operation and is only valid on non-complex numbers. The pow() function can be used in place of the ** operator but also supports the ternary power-modulo function (often used in cryptographic algorithms). The round() function rounds a floating-point number, x, to the nearest multiple of 10 to the power minus n. If n is omitted, it’s set to 0. If x is equally close to two multiples, Python 2 rounds to the nearest multiple away from zero (for example, 0.5 is rounded to 1.0 and -0.5 is rounded to -1.0). One caution here is that Python 3 rounds equally close values to the nearest even multiple (for example, 0.5 is rounded to 0.0, and 1.5 is rounded to 2.0). This is a subtle portability issue for mathematical programs being ported to Python 3.
The following comparison operators have the standard mathematical interpretation and return a Boolean value of True for true, False for false:

Comparisons can be chained together, such as in w < x < y < z. Such expressions are evaluated as w < x and x < y and y < z. Expressions such as x < y > z are legal but are likely to confuse anyone reading the code (it’s important to note that no comparison is made between x and z in such an expression). Comparisons involving complex numbers are undefined and result in a TypeError.
Operations involving numbers are valid only if the operands are of the same type. For built-in numbers, a coercion operation is performed to convert one of the types to the other, as follows:
1. If either operand is a complex number, the other operand is converted to a complex number.
2. If either operand is a floating-point number, the other is converted to a float.
3. Otherwise, both numbers must be integers and no conversion is performed.
For user-defined objects, the behavior of expressions involving mixed operands depends on the implementation of the object. As a general rule, the interpreter does not try to perform any kind of implicit type conversion.
Operations on Sequences
The following operators can be applied to sequence types, including strings, lists, and tuples:

The + operator concatenates two sequences of the same type. The s * n operator makes n copies of a sequence. However, these are shallow copies that replicate elements by reference only. For example, consider the following code:

Notice how the change to a modified every element of the list c. In this case, a reference to the list a was placed in the list b. When b was replicated, four additional references to a were created. Finally, when a was modified, this change was propagated to all the other “copies” of a. This behavior of sequence multiplication is often unexpected and not the intent of the programmer. One way to work around the problem is to manually construct the replicated sequence by duplicating the contents of a. Here’s an example:
![]()
The copy module in the standard library can also be used to make copies of objects.
All sequences can be unpacked into a sequence of variable names. For example:

When unpacking values into variables, the number of variables must exactly match the number of items in the sequence. In addition, the structure of the variables must match that of the sequence. For example, the last line of the example unpacks values into six variables, organized into two 3-tuples, which is the structure of the sequence on the right. Unpacking sequences into variables works with any kind of sequence, including those created by iterators and generators.
The indexing operator s[n] returns the nth object from a sequence in which s[0] is the first object. Negative indices can be used to fetch characters from the end of a sequence. For example, s[-1] returns the last item. Otherwise, attempts to access elements that are out of range result in an IndexError exception.
The slicing operator s[i:j] extracts a subsequence from s consisting of the elements with index k, where i <= k < j. Both i and j must be integers or long integers. If the starting or ending index is omitted, the beginning or end of the sequence is assumed, respectively. Negative indices are allowed and assumed to be relative to the end of the sequence. If i or j is out of range, they’re assumed to refer to the beginning or end of a sequence, depending on whether their value refers to an element before the first item or after the last item, respectively.
The slicing operator may be given an optional stride, s[i:j:stride], that causes the slice to skip elements. However, the behavior is somewhat more subtle. If a stride is supplied, i is the starting index; j is the ending index; and the produced subsequence is the elements s[i], s[i+stride], s[i+2*stride], and so forth until index j is reached (which is not included). The stride may also be negative. If the starting index i is omitted, it is set to the beginning of the sequence if stride is positive or the end of the sequence if stride is negative. If the ending index j is omitted, it is set to the end of the sequence if stride is positive or the beginning of the sequence if stride is negative. Here are some examples:

The x in s operator tests to see whether the object x is in the sequence s and returns True or False. Similarly, the x not in s operator tests whether x is not in the sequence s. For strings, the in and not in operators accept subtrings. For example, 'hello' in 'hello world' produces True. It is important to note that the in operator does not support wildcards or any kind of pattern matching. For this, you need to use a library module such as the re module for regular expression patterns.
The for x in s operator iterates over all the elements of a sequence and is described further in Chapter 5, “Program Structure and Control Flow.” len(s) returns the number of elements in a sequence. min(s) and max(s) return the minimum and maximum values of a sequence, respectively, although the result may only make sense if the elements can be ordered with respect to the < operator (for example, it would make little sense to find the maximum value of a list of file objects). sum(s) sums all of the items in s but usually works only if the items represent numbers. An optional initial value can be given to sum(). The type of this value usually determines the result. For example, if you used sum(items, decimal.Decimal(0)), the result would be a Decimal object (see more about the decimal module in Chapter 14, “Mathematics”).
Strings and tuples are immutable and cannot be modified after creation. Lists can be modified with the following operators:

The s[i] = x operator changes element i of a list to refer to object x, increasing the reference count of x. Negative indices are relative to the end of the list, and attempts to assign a value to an out-of-range index result in an IndexError exception. The slicing assignment operator s[i:j] = r replaces element k, where i <= k < j, with elements from sequence r. Indices may have the same values as for slicing and are adjusted to the beginning or end of the list if they’re out of range. If necessary, the sequence s is expanded or reduced to accommodate all the elements in r. Here’s an example:
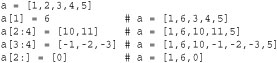
Slicing assignment may be supplied with an optional stride argument. However, the behavior is somewhat more restricted in that the argument on the right side must have exactly the same number of elements as the slice that’s being replaced. Here’s an example:
![]()
The del s[i] operator removes element i from a list and decrements its reference count. del s[i:j] removes all the elements in a slice. A stride may also be supplied, as in del s[i:j:stride].
Sequences are compared using the operators <, >, <=, >=, ==, and !=. When comparing two sequences, the first elements of each sequence are compared. If they differ, this determines the result. If they’re the same, the comparison moves to the second element of each sequence. This process continues until two different elements are found or no more elements exist in either of the sequences. If the end of both sequences is reached, the sequences are considered equal. If a is a subsequence of b, then a < b.
Strings are compared using lexicographical ordering. Each character is assigned a unique numerical index determined by the character set (such as ASCII or Unicode). A character is less than another character if its index is less. One caution concerning character ordering is that the preceding simple comparison operators are not related to the character ordering rules associated with locale or language settings. Thus, you would not use these operations to order strings according to the standard conventions of a foreign language (see the unicodedata and locale modules for more information).
Another caution, this time involving strings. Python has two types of string data: byte strings and Unicode strings. Byte strings differ from their Unicode counterpart in that they are usually assumed to be encoded, whereas Unicode strings represent raw unencoded character values. Because of this, you should never mix byte strings and Unicode together in expressions or comparisons (such as using + to concatenate a byte string and Unicode string or using == to compare mixed strings). In Python 3, mixing string types results in a TypeError exception, but Python 2 attempts to perform an implicit promotion of byte strings to Unicode. This aspect of Python 2 is widely considered to be a design mistake and is often a source of unanticipated exceptions and inexplicable program behavior. So, to keep your head from exploding, don’t mix string types in sequence operations.
String Formatting
The modulo operator (s % d) produces a formatted string, given a format string, s, and a collection of objects in a tuple or mapping object (dictionary) d. The behavior of this operator is similar to the C sprintf() function. The format string contains two types of objects: ordinary characters (which are left unmodified) and conversion specifiers, each of which is replaced with a formatted string representing an element of the associated tuple or mapping. If d is a tuple, the number of conversion specifiers must exactly match the number of objects in d. If d is a mapping, each conversion specifier must be associated with a valid key name in the mapping (using parentheses, as described shortly). Each conversion specifier starts with the % character and ends with one of the conversion characters shown in Table 4.1.
Table 4.1 String Formatting Conversions

Between the % character and the conversion character, the following modifiers may appear, in this order:
1. A key name in parentheses, which selects a specific item out of the mapping object. If no such element exists, a KeyError exception is raised.
2. One or more of the following:
• - sign, indicating left alignment. By default, values are right-aligned.
• + sign, indicating that the numeric sign should be included (even if positive).
• 0, indicating a zero fill.
3. A number specifying the minimum field width. The converted value will be printed in a field at least this wide and padded on the left (or right if the – flag is given) to make up the field width.
4. A period separating the field width from a precision.
5. A number specifying the maximum number of characters to be printed from a string, the number of digits following the decimal point in a floating-point number, or the minimum number of digits for an integer.
In addition, the asterisk (*) character may be used in place of a number in any width field. If present, the width will be read from the next item in the tuple.
The following code illustrates a few examples:
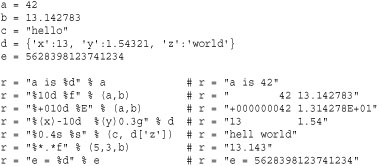
When used with a dictionary, the string formatting operator % is often used to mimic the string interpolation feature often found in scripting languages (e.g., expansion of $var symbols in strings). For example, if you have a dictionary of values, you can expand those values into fields within a formatted string as follows:
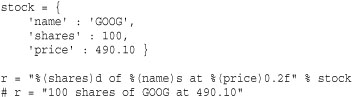
The following code shows how to expand the values of currently defined variables within a string. The vars() function returns a dictionary containing all of the variables defined at the point at which vars() is called.
![]()
Advanced String Formatting
A more advanced form of string formatting is available using the s.format(*args, *kwargs) method on strings. This method collects an arbitrary collection of positional and keyword arguments and substitutes their values into placeholders embedded in s. A placeholder of the form '{n}', where n is a number, gets replaced by positional argument n supplied to format(). A placeholder of the form '{name}' gets replaced by keyword argument name supplied to format. Use '{{' to output a single '{' and '}}' to output a single '}'. For example:

With each placeholder, you can additionally perform both indexing and attribute lookups. For example, in '{name[n]}' where n is an integer, a sequence lookup is performed and in '{name[key]}' where key is a non-numeric string, a dictionary lookup of the form name['key'] is performed. In '{name.attr}', an attribute lookup is performed. Here are some examples:

In these expansions, you are only allowed to use names. Arbitrary expressions, method calls, and other operations are not supported.
You can optionally specify a format specifier that gives more precise control over the output. This is supplied by adding an optional format specifier to each placeholder using a colon (:), as in '{place:format_spec}'. By using this specifier, you can specify column widths, decimal places, and alignment. Here is an example:
![]()
The general format of a specifier is [[fill[align]][sign][0][width][.precision][type] where each part enclosed in [] is optional. The width specifier specifies the minimum field width to use, and the align specifier is one of '<', '>’, or '^' for left, right, and centered alignment within the field. An optional fill character fill is used to pad the space. For example:

The type specifier indicates the type of data. Table 4.2 lists the supported format codes. If not supplied, the default format code is 's' for strings, 'd' for integers, and 'f' for floats.
Table 4.2 Advanced String Formatting Type Specifier Codes

The sign part of a format specifier is one of '+', '-', or ' '. A '+' indicates that a leading sign should be used on all numbers. '-' is the default and only adds a sign character for negative numbers. A ' ' adds a leading space to positive numbers. The precision part of the specifier supplies the number of digits of accuracy to use for decimals. If a leading '0' is added to the field width for numbers, numeric values are padded with leading 0s to fill the space. Here are some examples of formatting different kinds of numbers:

Parts of a format specifier can optionally be supplied by other fields supplied to the format function. They are accessed using the same syntax as normal fields in a format string. For example:
![]()
This nesting of fields can only be one level deep and can only occur in the format specifier portion. In addition, the nested values cannot have any additional format specifiers of their own.
One caution on format specifiers is that objects can define their own custom set of specifiers. Underneath the covers, advanced string formatting invokes the special method _ _format_ _(self, format_spec) on each field value. Thus, the capabilities of the format() operation are open-ended and depend on the objects to which it is applied. For example, dates, times, and other kinds of objects may define their own format codes.
In certain cases, you may want to simply format the str() or repr() representation of an object, bypassing the functionality implemented by its _ _format_ _() method. To do this, you can add the '!s' or '!r' modifier before the format specifier. For example:
![]()
Operations on Dictionaries
Dictionaries provide a mapping between names and objects. You can apply the following operations to dictionaries:

Key values can be any immutable object, such as strings, numbers, and tuples. In addition, dictionary keys can be specified as a comma-separated list of values, like this:
![]()
In this case, the key values represent a tuple, making the preceding assignments identical to the following:
![]()
Operations on Sets
The set and frozenset type support a number of common set operations:

The result of union, intersection, and difference operations will have the same type as the left-most operand. For example, if s is a frozenset, the result will be a frozenset even if t is a set.
Augmented Assignment
Python provides the following set of augmented assignment operators:
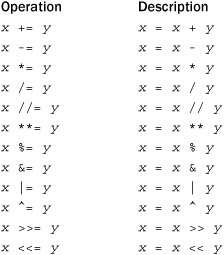
These operators can be used anywhere that ordinary assignment is used. Here’s an example:

Augmented assignment doesn’t violate mutability or perform in-place modification of objects. Therefore, writing x += y creates an entirely new object x with the value x + y. User-defined classes can redefine the augmented assignment operators using the special methods described in Chapter 3, “Types and Objects.”
The Attribute (.) Operator
The dot (.) operator is used to access the attributes of an object. Here’s an example:
![]()
More than one dot operator can appear in a single expression, such as in foo.y.a.b. The dot operator can also be applied to the intermediate results of functions, as in a = foo.bar(3,4,5).spam.
User-defined classes can redefine or customize the behavior of (.). More details are found in Chapter 3 and Chapter 7, “Classes and Object-Oriented Programming.”
The Function Call () Operator
The f(args) operator is used to make a function call on f. Each argument to a function is an expression. Prior to calling the function, all of the argument expressions are fully evaluated from left to right. This is sometimes known as applicative order evaluation.
It is possible to partially evaluate function arguments using the partial() function in the functools module. For example:

The partial() function evaluates some of the arguments to a function and returns an object that you can call to supply the remaining arguments at a later point. In the previous example, the variable f represents a partially evaluated function where the first two arguments have already been calculated. You merely need to supply the last remaining argument value for the function to execute. Partial evaluation of function arguments is closely related to a process known as currying, a mechanism by which a function taking multiple arguments such as f(x,y) is decomposed into a series of functions each taking only one argument (for example, you partially evaluate f by fixing x to get a new function to which you give values of y to produce a result).
Conversion Functions
Sometimes it’s necessary to perform conversions between the built-in types. To convert between types, you simply use the type name as a function. In addition, several built-in functions are supplied to perform special kinds of conversions. All of these functions return a new object representing the converted value.

Note that the str() and repr() functions may return different results. repr() typically creates an expression string that can be evaluated with eval() to re-create the object. On the other hand, str() produces a concise or nicely formatted representation of the object (and is used by the print statement). The format(x, [format_spec]) function produces the same output as that produced by the advanced string formatting operations but applied to a single object x. As input, it accepts an optional format_spec, which is a string containing the formatting code. The ord() function returns the integer ordinal value of a character. For Unicode, this value will be the integer code point. The chr() and unichr() functions convert integers back into characters.
To convert strings back into numbers, use the int(), float(), and complex() functions. The eval() function can also convert a string containing a valid expression to an object. Here’s an example:
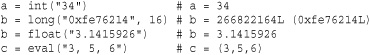
In functions that create containers (list(), tuple(), set(), and so on), the argument may be any object that supports iteration used to generate all the items used to populate the object that’s being created.
Boolean Expressions and Truth Values
The and, or, and not keywords can form Boolean expressions. The behavior of these operators is as follows:

When you use an expression to determine a true or false value, True, any nonzero number, nonempty string, list, tuple, or dictionary is taken to be true. False; zero; None; and empty lists, tuples, and dictionaries evaluate as false. Boolean expressions are evaluated from left to right and consume the right operand only if it’s needed to determine the final value. For example, a and b evaluates b only if a is true. This is sometimes known as “short-circuit” evaluation.
Object Equality and Identity
The equality operator (x == y) tests the values of x and y for equality. In the case of lists and tuples, all the elements are compared and evaluated as true if they’re of equal value. For dictionaries, a true value is returned only if x and y have the same set of keys and all the objects with the same key have equal values. Two sets are equal if they have the same elements, which are compared using equality (==).
The identity operators (x is y and x is not y) test two objects to see whether they refer to the same object in memory. In general, it may be the case that x == y, but x is not y.
Comparison between objects of noncompatible types, such as a file and a floating-point number, may be allowed, but the outcome is arbitrary and may not make any sense. It may also result in an exception depending on the type.
Order of Evaluation
Table 4.3 lists the order of operation (precedence rules) for Python operators. All operators except the power (**) operator are evaluated from left to right and are listed in the table from highest to lowest precedence. That is, operators listed first in the table are evaluated before operators listed later. (Note that operators included together within subsections, such as x * y, x / y, x / y, and x % y, have equal precedence.)
Table 4.3 Order of Evaluation (Highest to Lowest)

The order of evaluation is not determined by the types of x and y in Table 4.3. So, even though user-defined objects can redefine individual operators, it is not possible to customize the underlying evaluation order, precedence, and associativity rules.
Conditional Expressions
A common programming pattern is that of conditionally assigning a value based on the result of an expression. For example:
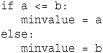
This code can be shortened using a conditional expression. For example:
minvalue = a if a <=b else b
In such expressions, the condition in the middle is evaluated first. The expression to the left of the if is then evaluated if the result is True. Otherwise, the expression after the else is evaluated.
Conditional expressions should probably be used sparingly because they can lead to confusion (especially if they are nested or mixed with other complicated expressions). However, one particularly useful application is in list comprehensions and generator expressions. For example:
![]()
