8.1 optim()

optim() is one of the most used tools in R. It incorporates five methods, three of which are derived from the author's own work (Nash, 1979). The five methods are largely independent but are all called through optim(), using a call such as

 ans<-optim(start, fn=myfn, gr=mygr, method="BFGS",
        X=myx, Y=myY, control=list(trace=1))

where start is the vector of parameters that are used as the initial point of the optimization iteration, myfn is the function to be minimized, mygr is its gradient, and the control list specifies that we want to follow the iterations (trace), while the elements given by X=myX, Y=myY are named variables required by myfn and mygr and are passed to optim() via the “…” arguments. The method is specified via a character string, here using a method called “BFGS” (Broyden–Fletcher–Goldfarb–Shanno).

The methods included in optim() are

• Nelder–Mead. This is the default method and is a variant of that described in Nelder and Mead (1965). This method requires no derivative information to be supplied; indeed it will be ignored. The method builds a polytope (or simplex) of 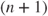points in -space, then reflects the “highest” point through the centroid of the rest of the points, and proceeds to use such geometric information to steadily reduce the function value. The name “Nelder–Mead Simplex method” has in the past caused confusion with the linear programming method of Dantzig (Nash, 2000). I prefer to use “Nelder–Mead polytope method” or simply “Nelder–Mead” or even “NM.”
• BFGS. This is a variable metric method due to Fletcher (1970). This method is a descent method using the gradient, and analytic gradients or very good approximations are recommended. Starting with a simple identity matrix, gradient information built up during the iterations of this method is used to build an approximate inverse Hessian, so that the method “approaches” Newton's method. While experiments show the approximation to be poor, in practice the method performs well. The use of a BFGS formula to “update” the inverse Hessian approximation has led to the naming of this method in R, but readers will more likely find useful information about this method by using the search term “variable metric.”
• L-BFGS-B. This method is the most sophisticated in the optim() set. It uses a limited-memory update of the inverse Hessian so is somewhat similar to the BFGS approach. However, the amount of information kept to build the update can be controlled by the user, the default being to keep information from the last five iterations. See Lu et al. (1994) or the code published by Zhu et al. (1997). The method can, moreover, deal with bounds on the parameters and is the default method if any bound is specified. Generally, L-BFGS-B works well, although its very sophistication does get in the way of success on occasions. At the time of writing, R does not include the updated version of this method (Morales and Nocedal, 2011).
• CG. This is a conjugate gradient descent method. It is based on various codes extant in the 1960s and 1970s. As with BFGS, we start with the gradient as a search direction and then modify this at each iteration. Where the BFGS/variable metric method updated a full matrix, CG simply builds the new search direction from the old one and new and old gradient information. This makes it very attractive for problems in large numbers of parameters. There was much discussion about which of the three main candidates can be used for the computation of the new search direction in papers of the era. These are the Fletcher–Reeves, Polak–Ribière, and Beale–Sorenson updates. (Note that other names are also used, just to confuse us all.) R allows a choice of update via a control-list item type which takes values 1 (default), 2, or 3 respectively. Personally, I have found the second option preferable, but none are definitely better than the others. Overall I have been disappointed in this method. However, a more recent approach (Dai and Yuan, 2001) that cleverly combines and exploits differences in the updates allowed me to prepare Rcgmin with which I have been more than pleased.
• SANN. This is a stochastic method that I believe does NOT belong with optim(). First, it will always evaluate the function a fixed number of times and then report “convergence.” This is exceedingly misleading to most users. Moreover, the idea of “temperature” in the process is inconsistent with the descent ideas of the other methods.

8.2 nlm()

nlm is an interface to a particularized version of UNCMIN, a set of algorithms for unconstrained minimization from Schnabel et al. (1985). The approach is a Newton or quasi-Newton method, but the details are somewhat difficult to understand from the manual. The original code provided for a variety of line search and updating techniques, as well as different gradient approximations.

The calling sequence for nlm() is rather different from that of optim(), and the manual gives the usage as

 nlm(f, p, ..., hessian = FALSE, typsize = rep(1, length(p)),
     fscale = 1, print.level = 0, ndigit = 12, gradtol = 1e-6,
     stepmax = max(1000 * sqrt(sum((p/typsize)^2)), 1000),
     steptol = 1e-6, iterlim = 100, check.analyticals = TRUE)

Note that the function f is given first in the sequence, and the parameters second, a reverse from optim(). Moreover, the gradient and possibly Hessian code are passed as attributes to f, described as

 f: the function to be minimized.  If the function value has an
    attribute called 'gradient' or both 'gradient' and 'hessian'
    attributes, these will be used in the calculation of updated
    parameter values.  Otherwise, numerical derivatives are used.
    'deriv' returns a function with suitable 'gradient'
    attribute.  This should be a function of a vector of the
    length of 'p' followed by any other arguments specified by
    the '...' argument.

As with so many optimization routines, nlm() has a lot of controls that essentially adjust heuristics aimed at tuning the methods. In practice, I have rarely if ever used these, even though I work in the optimization field and should have the expertise to do so. The reality is that each program has different names or ways of implementing relatively similar ideas that concern how “big” or “small” different quantities should be. Users find it tedious to learn the intricacies of each control, and tinkering is time consuming and generally unproductive.

A possible exception is the limit on iterations. I generally want to know if a method gets to a valid solution when allowed to take as many iterations as it likes.

Despite the above criticisms of nlm(), in my experience, it is one of the more reliable and efficient optimization methods for unconstrained functions, even when only the function code is provided. To simplify its use, I generally call it via optimx(), which allows the use of a common, optim-like calling sequence.

8.3 nlminb()

Because nlm() is an unconstrained minimizer, but bounds constraints were needed for a number of maximum likelihood problems, nlminb() was added to the base set of optimizers. The code on which nlminb() is based was written by David Gay at Bell Labs and was part of the PORT Fortran Library (Fox et al. 1978). The S language at Bell Labs used this as its optimizer, and Doug Bates, in an e-mail dated June 2008, states that

> I created the nlminb function because I was unable to get reliable
> convergence on some difficult optimization problems for the nlme and
> lme4 packages using nlm and optim. The nlme package was originally
> written for S from Bell Labs (the forerunner of SPLUS) and the PORT
> package was the optimization code used. Even though it is very old
> style Fortran code I find it quite reliable as an optimizer.

I agree with this general view, although the code in the PORT library is not easy to follow and use. Moreover, as with nlm(), there are many settings and choices that could be helpful, but more R users will want to leave alone. However, nlminb is quite similar in call to optim(), namely,

 nlminb(start, objective, gradient = NULL, hessian = NULL, ...,
   scale = 1, control = list(), lower = -Inf, upper = Inf)

The issue of controls was highlighted in a discovery in 2010 (see https://stat.ethz.ch/pipermail/r-help/2010-July/245194.html) that nlminb() assumed positive objective functions (likely sums of squares) and that a default test for termination was abs.tol, a control parameter to nlminb. Many negative log likelihood functions will not be positive, and it is difficult to know how many incorrect results were used or published. The issue underlines one that is central to open-source software such as R—we need to be able to easily review code if it is to be improved. The PORT library has many fine codes, but in my view, they are not easily understood or changed, especially as implemented for the use by R, where the interface adds another layer of confusion.

8.4 Using the base optimization tools

Let us solve the well-known Rosenbrock (1960) banana-shaped valley problem with the methods of this chapter. We will start from the “standard” point of , and we will not, for the moment, supply the gradient.

fr <- function(x) {
    ## Rosenbrock Banana function
    x1 <- x[1]
    x2 <- x[2]
    100 * (x2 - x1 * x1)^2 + (1 - x1)^2
}
sstart <- c(-1.2, 1)

To keep the output tidy, we will use a little display function.

prtopt <- function(optres, headname) {
    # compact print of optim() result
    cat(headname, ": f(")
    npar <- length(optres$par)
    for (i in 1:(npar - 1)) {
        cat(optres$par[[i]], ", ")
    }
    cat(optres$par[[npar]], ") = ", optres$value, " after ",
        optres$counts[[1]], "f & ", optres$counts[[2]], "g
")
    cat(optres$message, "  convergence code=", optres$convergence,
        "
")
}

First, we try the Nelder–Mead, BFGS, CG, and L-BFGS-B methods of optim()

anm <- optim(sstart, fr)  # Nelder Mead is the default method
prtopt(anm, "anm")
## anm : f(1.0003 , 1.0005 ) =  8.8252e-08  after  195 f &  NA g
##    convergence code= 0
abfgs <- optim(sstart, fr, method = "BFGS")
prtopt(abfgs, "abfgs")
## abfgs : f(0.9998 , 0.99961 ) =  3.8274e-08  after  118 f &  38 g
##    convergence code= 0
acg1 <- optim(sstart, fr, method = "CG", control = list(type = 1))
prtopt(acg1, "acg1")
## acg1 : f(-0.76481 , 0.59271 ) =  3.1065  after  402 f &  101 g
##    convergence code= 1
acg2 <- optim(sstart, fr, method = "CG", control = list(type = 2))
prtopt(acg2, "acg2")
## acg2 : f(0.96767 , 0.93628 ) =  0.0010432  after  384 f &  101 g
##    convergence code= 1
acg3 <- optim(sstart, fr, method = "CG", control = list(type = 3))
prtopt(acg3, "acg3")
## acg3 : f(0.94331 , 0.88953 ) =  0.0032119  after  352 f &  101 g
##    convergence code= 1
albfgsb <- optim(sstart, fr, method = "L-BFGS-B")
prtopt(albfgsb, "albfgsb")
## albfgsb : f(0.9998 , 0.9996 ) =  3.9985e-08  after  49 f &  49 g
## CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH   convergence code= 0

Here we note that Nelder–Mead, BFGS, and L-BFGS-B have essentially found the correct solution at , but the CG examples have hit the maximum allowed gradient computations. Let us check the results using the analytic gradient. Note that we test the gradient code!

frg <- function(x) {
    ## Rosenbrock Banana function gradient
    x1 <- x[1]
    x2 <- x[2]
    g1 <- -400 * (x2 - x1 * x1) * x1 - 2 * (1 - x1)
    g2 <- 200 * (x2 - x1 * x1)
    gg <- c(g1, g2)
}
## test gradient at standard start:
require(numDeriv)
gn <- grad(fr, sstart)
ga <- frg(sstart)
## max(abs(ga-gn))
max(abs(ga - gn))
## [1] 1.47e-08
## analytic gradient results
gabfgs <- optim(sstart, fr, frg, method = "BFGS")
prtopt(gabfgs, "BFGS w. frg")
## BFGS w. frg : f(1 , 1 ) =  9.595e-18  after  110 f &  43 g
##    convergence code= 0
gacg1 <- optim(sstart, fr, frg, method = "CG", control = list(type = 1))
prtopt(gacg1, "CG Fletcher-Reeves w. frg")
## CG Fletcher-Reeves w. frg : f(-0.76484,0.59276) = 3.1066 after 402 f & 101 g
##    convergence code= 1
gacg2 <- optim(sstart, fr, frg, method = "CG", control = list(type = 2))
prtopt(gacg2, "CG Polak-Ribiere w. frg")
## CG Polak-Ribiere w. frg : f(0.99441,0.98882)=3.1238e-05 after 385 f & 101 g
##    convergence code= 1
gacg3 <- optim(sstart, fr, frg, method = "CG", control = list(type = 3))
prtopt(gacg3, "CG Beale-Sorenson w. frg")
## CG Beale-Sorenson w. frg : f(0.89973,0.80901) = 0.010045 after 355 f & 101 g
##    convergence code= 1
galbfgsb <- optim(sstart, fr, method = "L-BFGS-B")
prtopt(galbfgsb, "L-BFGS-B w. frg")
## L-BFGS-B w. frg : f(0.9998 , 0.9996 ) =  3.9985e-08  after  49 f &  49 g
## CONVERGENCE: REL_REDUCTION_OF_F <= FACTR*EPSMCH   convergence code= 0

We observe that the CG methods are still doing poorly compared to other approaches.

References

1. Dai YH and Yuan Y 2001 An efficient hybrid conjugate gradient method for unconstrained optimization. Annals of Operations Research 103(1–4), 33–47.
2. Fletcher R 1970 A new approach to variable metric algorithms. Computer Journal 13(3), 317–322.
3. Fox PA, Hall AD and Schryer NL 1978 The PORT mathematical subroutine library. ACM Transactions on Mathematical Software (TOMS) 4(2), 104–126.
4. Lu P, Nocedal J, Zhu C, Byrd RH and Byrd RH 1994 A limited-memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing 16, 1190–1208.
5. Morales JL and Nocedal J 2011 Remark on Algorithm 778: L-BFGS-B: fortran subroutines for large-scale bound constrained optimization. ACM Transactions on Mathematical Software 38(1), 7:1–7:4.
6. Nash JC 1979 Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation. Hilger, Bristol.
7. Nash JC 2000 The Dantzig simplex method for linear programming. Computing in Science and Engineering 2(1), 29–31.
8. Nelder JA and Mead R 1965 A simplex method for function minimization. Computer Journal 7(4), 308–313.
9. Rosenbrock HH 1960 An automatic method for finding the greatest or least value of a function. Computer Journal 3, 175–184.
10. Schnabel RB, Koonatz JE and Weiss BE 1985 A modular system of algorithms for unconstrained minimization. ACM Transactions on Mathematical Software 11(4), 419–440.
11. Zhu C, Byrd RH, Lu P and Nocedal J 1997 Algorithm 778: L-bfgs-b: fortran subroutines for large-scale bound-constrained optimization. ACM Transactions on Mathematical Software 23(4), 550–560.