3.1 Perspective

In a fairly long career in this area, I have found that there is a common love of “speed.” More correctly, people do not want to feel that they are waiting for their calculations to finish. If they do find that they are waiting, they may begin to judge methods on the basis of timings, sometimes surprisingly few and poorly conducted timings.

While sharing a strong interest in computational efficiency, I take the following views.

• It is important to know that the answer presented is “right,” or at least to provide guidance or information if the result may not be satisfactory. For example, there may be multiple solutions, or the result may be simply the best we can do in a difficult situation. Optimizers can and do stop for reasons other than that there is a satisfactory answer. User functions frequently have errors, despite our best efforts. Uncovering and correcting wrong answers can be very very time consuming for humans, as well as being potentially embarrassing.
• Doing the tests and checks required to provide the diagnostic and explanatory information just mentioned will take computational time. Hence, users will find, for example, that running the optimizers in the package optimx (see Section 9.1) takes longer than running them directly. The penalty generally is not huge, although computing Hessians when the number of parameters is large can take longer than the optimization process. Indeed, optimx does not compute the Hessian and optimality (Karush–Kuhn–Tucker, KKT) tests when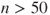 if there are no analytic derivatives available or 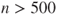when there are. Similarly, the experimental package optplus provides parameter scaling and checking for inadmissible parameters on every function evaluation, but the cost is high enough that I am rethinking how to better provide such features.
• When a problem must be solved very quickly and/or very frequently, so that the time taken by R optimizers is too great, then I believe it is worth considering reimplementing the particular calculation. See Chapter 19. Otherwise, I feel that computer time is “cheap” relative to that of the user.

3.2 Issues of choice

While this book is about optimization in R, more generally users must decide on the system under which they will perform computations. In the past decade, it has become possible to decide to compute in “R” without reference to the hardware or operating system to be used. This is largely true of other major computational choices, such as Matlab or Python or SAS or etc.

Having decided on R, however, there are so many packages—well above 4000 at the time of writing—that it is difficult to discover what each of them does and impossible to decide on whether their features and quality make them suitable to our needs. This is especially difficult for optimization problems. Many packages are targeted at specific domains of research. They may claim great performance or features, but those capabilities may be applicable to a minuscule collection of users.

Clearly, one of the purposes of this book is to provide guidance through this undergrowth, but even though I am active in pursuing the subject of optimization in R, I am painfully conscious that I am going to miss some package or other with a useful capability. Therefore, I have chosen to look at the general tools that can be adapted to many problems rather than tools for specific problems.

It is also notable that there are many packages that include custom-built optimizers, for example, package likelihood (Murphy, 2012). From the perspective of a tool builder like myself, this is unfortunate:

• It requires generally quite a lot of work to abstract the optimizer from the surrounding infrastructure and context in such packages.
• The interests and focus of the package developer are generally on the particularproblems of their domain of work. The optimizer may be well constructed for that domain but risky to use in other areas.
• For similar reasons, the provenance and documentation of the optimizer may be unclear.

Moreover, I am unapologetic about favoring packages that are written entirely in R and which present themselves as simply and generally as possible. This focus is partly due to a level of laziness—I do not enjoy digging through difficult and opaque documentation with idiosyncratic vocabulary. However, I am also convinced that there are far too many situations where using programs written in languages other than R gives rise to errors in interfacing or leaves unsuitable controls in place in the non-R code. Furthermore, it is difficult to pin down the provenance of the codes, even though R does very well in documenting its origins.

For example, in the case of the optimizer L-BFGS-B, a search through the source package yields the routine lbfgs.c that has a comment that it is ‘version 2.3’. Yet the web page of the original authors (http://www.ece.∼northwestern.edu/nocedal/lbfgsb.html) shows only versions 2.1 (1997) and 3.0 (2011). Moreover, both these are in Fortran not C. There are notes in the R source in various places that code has been converted from Fortran to C using a program called f2c (Feldman et al. 1991). It seems likely that a partially updated version of the Fortran code was converted to C in the late 1990s.

I can sympathize with the difficulty of choosing, converting, and interfacing a complicated program such as L-BFGS-B for use in R. Further, I can appreciate why developers would prefer to not have to reimplement the method in R itself. However, I have found that once a code is in R, and especially if the coding is kept plain—I often use the adjective pedestrian—it is much much easier to find and fix bugs, to adjust the code to particular situations, or to improve it as new ideas become current.

3.3 Software issues

There are rather a lot of software issues that arise in connection with attempted computational solution of optimization problems:

• Specifying the objective and constraints to the optimizer
• Communicating exogenous data to problem definition functions
• Masked (i.e., temporarily fixed) optimization parameters
• Dealing with inadmissible results
• Providing derivatives for functions
• Derivative approximations when there are constraints
• Scaling of parameters and function
• Termination tests—normal finish to computations
• Termination tests—abnormal ending
• Output to monitor progress of calculations
• Output of the optimization results
• Controls for the optimizer
• Default control settings
• Appropriate measures of performance
• The optimization interface.

We will explore these issues in the rest of the chapter.

3.4 Specifying the objective and constraints to the optimizer

Unlike statistical computations with a well-established structure, for example, linear regression, the general constrained optimization problem requires the user to supply an objective function as well as any inequality constraints

3.1

or equality constraints

3.2

The wide variety of possible functional forms leads to problems of very diverse levels of difficulty.

The latter, equality, constraints may, of course, be introduced in other ways, ways that may unfortunately destabilize the computations. Overall, this issue is specifying the objective and constraints to the optimizer.

3.5 Communicating exogenous data to problem definition functions

In the real world, the objective function and the constraints and are not only functions of the parameters but also depend on data. In fact, they may depend on vast arrays of data, particularly in statistical problems involving large systems. Typically, such data consists of observations on a number of variables. can be a very large number. Communicating this data to the objective and constraint functions as well as to the functions to compute their derivatives is a sometimes awkward task. Even when it is straightforward, it can be tedious and error prone. This difficulty is magnified when one wishes to apply a number of different minimization algorithms, because each may have its own structure.

In R, data available in the user workspace is generally available to lower level routines. We can see this in the following example, where xx and yy do not need to be passed in the call to nlsLM() of package minpack.lm. On the other hand, function nlxb() of package nlmrt requires us to specify a data frame data as an argument in its call.

xx <- 1:12
yy <- exp(-0.1 * sin(0.3 * xx))
require(minpack.lm, quietly = TRUE)
strt1 <- list(p1 = 0, p2 = 1)
## here we do not specify any exogenous data
anls1 <- nlsLM(yy ∼ exp(p1 * sin(p2 * xx)), start = strt1, trace = FALSE)
anls1
## Nonlinear regression model
##   model: yy ∼ exp(p1 * sin(p2 * xx))
##    data: parent.frame()
##      p1      p2
## -0.0113  0.9643
##  residual sum-of-squares: 0.0496
##
## Number of iterations to convergence: 7
## Achieved convergence tolerance: 1.49e-08
rss <- function(par) {
    p1 <- par[1]
    p2 <- par[2]
    res <- exp(p1 * sin(p2 * xx)) - yy
    sum(res * res)
}
## check the initial sum of squares
print(rss(c(-0.1, 0.3)))
## [1] 0
## and the final sum of squares
print(rss(coef(anls1)))
## [1] 0.04957
# Now try with an optimizer (default method=Nelder-Mead)
anm <- optim(strt1, rss)
anm
## $par
##       p1       p2
## -0.01131  0.96426
##
## $value
## [1] 0.04957
##
## $counts
## function gradient
##       53       NA
##
## $convergence
## [1] 0
##
## $message
## NULL
## But (at time of writing) nlmrt requires explicit data
mydat <- data.frame(xx = xx, yy = yy)
require(nlmrt, quietly = TRUE)
anlxb1 <- nlxb(yy ∼ exp(p1 * sin(p2 * xx)), start = strt1, trace = FALSE, data = mydat)
## Insert following into call to get a more aggressive search
## control=list(roffset=FALSE, smallsstest=FALSE)
print(anlxb1)
## nlmrt class object: x
## residual sumsquares =  0.049565  on  12 observations
##     after  12    Jacobian and  20 function evaluations
## name     coeff        SE       tstat      pval       gradient    JSingval
## p1     -0.0113074   0.02762   -0.4094    0.6909     -2.513e-10    2.552
## p2      0.964283    0.3681     2.62      0.02561     9.805e-09    0.1913

R offers a mechanism in function calls for the provision of data that is to be passed through a function but is not specifically declared for that function. This is the ‘…’ or dot-dot-dot argument(s) to a function. That is, the called function optimizer will be declared as

optimizer<-function(parameters, ufn, ...)
   (code)

while the calling script will be written something like

myanswer<-optimizer(mypar, objective, datax=Xdata, ydata=Y)

R conveniently provides the datax and ydata information to functions within optimizer. Furthermore, within optimizer, we can write

fval<-ufn(parameters, ...)

to evaluate the function with parameters that are initially at values given by mypar and the exogenous data datax and ydata. This assumes that the data have not been altered by optimizer. The parameters clearly will be altered from the initial values mypar to try to find lower function values.

The dot argument mechanism, while fairly straightforward, can still allow of mistakes. Moreover, we need to carry quite a lot of information through the optimizer and possibly subsidiary routines such as those for scaling and numerical derivative approximation. It is, in fact, at the level of these subsidiary routines that the dots mechanism can become cumbersome. However, we can sometimes simplify the process somewhat by making the user data (in our example datax and ydata) essentially global to optimizer.

The four approaches (possibly there are others) to passing data into functions are thus

• using objects that are in the user's workspace;
• passing data via a named argument as in nlxb() above;
• passing objects through the dots mechanism;
• creating a global structure (see Section 3.5.1).

I have generally found that I get into less difficulties if I ensure that I explicitly specify the exogenous data, either with a named object or data frame that is required by the called function, or by named items passed via the dots mechanism.

result <- afunction(x=myx, y=y)

mystart <- function() {
    # JN: Define globals here.
    gtn <- list(x = 0, y = 1, vec = rep(0, 9))
    envjn <- list2env(gtn)
}
y <- 4
myrun <- function() {
    cat("y:", y, "  envjn$y: ")
    print(envjn$y)
    envjn$y <- 9876
    return(0)
}
mystart()
myrun()
## y: 4   envjn$y: [1] 1
## [1] 0
cat("envjn$y:", envjn$y, "
")
## envjn$y: 9876

3.6 Masked (temporarily fixed) optimization parameters

Sometimes we wish to fix some of the parameters. Fixing a parameter implies that there is one fewer element in the parameter vector, but adjusting all the indices is a large task, essentially a rewrite of our objective function and constraint functions. Unfortunately, although the mathematics and even the programming of the use of such fixed or masked parameters is relatively straightforward, it is surprisingly uncommon in optimization codes. Because it can be quite useful, I have included a chapter on masks and their use (Chapter 12) and mention some approaches to specifying fixed parameters there that are different from the following discussion.

The idea of masks has been around quite a long time. The author recalls first recognizing explicit program code in some work of Ron Duggleby of the University of Queensland, and the ideas were incorporated in Nash and Walker-Smith (1987). Masks are a special form of equality constraint. As mentioned, they present an issue of detail and tedium for nonlinear optimization programs rather than a serious mathematical obstacle.

Following Nash and Walker-Smith (1987), in my own R codes, I use an indicator vector bdmsk that puts a 0 in the position of each masked (fixed) parameter. Initially, the other parameters are free, which is indicated by a value of 1 in the corresponding element of bdmsk. This indicator vector is also used for bounds constraints, and on return from one of the optimizers with bounds and masks capability, a bdmsk element of implies a parameter is on an active lower bound, while implies a parameter is on an active upper bound.

The 0's in bdmsk can be applied in a simple way to the gradient, because a fixed parameter will have zero gradient component—it is, after all, fixed. Likewise, the row and column of the Hessian corresponding to a masked parameter will be zero. While it is clear such zeros should not be an essential obstacle to an optimization method, aparticular implementation of a method may inadvertently happen to create a “0/0” situation. To render an optimizer capable of handling masks is actually quite a bit simpler than introducing bounds (box constraints), but the details must nevertheless be handled carefully.

3.7 Dealing with inadmissible results

Sometimes users provide functions to define a problem, namely, the objective function, constraint functions, and sometimes derivative calculations, that gives returned values that cannot be handled by our optimization codes. The returned objects may be infinite, NULL, or NA, causing failure of the optimizer and other computations. Sometimes computations return an object that is a vector, matrix, or array when it should be numeric. For example, the sum of squares of a vector of residuals, resids, in a nonlinear least squares calculation can be efficiently found using

sumsqrs<-crossprod(resids)

Unfortunately, sumsqrs is a 1 1 matrix. We need to use

sumsqrs<-as.numeric(crossprod(resids))

Often such seemingly trivial matters result in a program suddenly stopping. We would ideally wish to have our program simply warn of the issue and proceed sensibly. At the very least, we would like it to terminate in a controlled manner. While it is essentially the inputs to the functions that are inadmissible and cause our troubles, it is the results of attempting a calculation in a particular context that are the source of our difficulty.

I have found that unacceptable returned values from user-written functions are one of the most common sources of failure for users in applying optimization tools to their problems. Indeed, including incorrectly computed derivatives (mostly gradients or Jacobian matrices) and poor scaling of parameters in this category explains almost all the “failures” of optimization codes I see.

Quite often users supply objective or residual functions where there are log() or sqrt() components with arguments that can become negative. The starting parameters may be such that the function is initially computable and the user may not realize that the optimization process may generate a negative argument to a function.

By writing the problem function carefully, we can indicate that inputs are inadmissible (or even undesirable). A simple expedient that often “works” is to return a very large function value. In the experimental package optplus, I used badval=(0.5)∗.Machine$double.xmax, which has a value nearly 1E. Note, however, that simply making the function large at undesirable parameter points may distort the behavior of the optimization method. We do not want to actually use this result as a function value; it is an indicator of a point that should not be part of the domain of our function. Indeed, because it is quite possible that methods that generate points in the parameter space and use them to search in favorable directions will calculate on the returned, and very large, values, I have also used smaller settings, for example, badval=(1e-6)∗.Machine$double.xmax which for all but very extreme functions will serve as an indicator.

In Nash and Walker-Smith (1987), we used a “noncomputability flag” that allowed optimization methods to adjust their search for an optimum. However, we wrote all our own optimizers and could react to the flag appropriately. This is not nearly so easy with optimizers written by others that operate from a different base and perspective. Very few optimization methods in R, including my own, have much capability to exploit this as yet. However, even a minimal capability allows a report of failure to be passed back to a calling program, thereby avoiding an unexpected halt in computations.

R also has the function try() that let us trap errors. This is used in several of my codes to avoid “crashes,” but so far, it mostly does no more than report difficultiesand then stop or exit. That is, we do not fully exploit the capability to backtrack from a dangerous parameter region.

3.8 Providing derivatives for functions

Many optimization tools require derivative information for the objective function. This is sufficiently important that it merits a full chapter in this book (Chapter 10). A general nonlinear objective function will give rise to a gradient . If the objective is a sum of squared residuals, then it is generally preferable to work with the residuals and find their derivatives as the Jacobian matrix and build the gradient as the inner product of the Jacobian and the vector of residuals.

Second derivative information for a general nonlinear objective function is found as the Hessian matrix . For a sum of squares, we find the Hessian elements as a two-term expression. Thus the element of is the inner product of the th and th columns of the Jacobian (i.e., the element of the matrix ) plus the sum of elements of the form

3.3

Requiring the second derivatives of the residuals from users is rare, and rarer than it ought to be in the author's view. However, Hessian matrix information is commonly used in deciding if a solution is acceptable. Moreover, Hessians ought to be more commonly used in nonlinear least squares computations instead of “standard” approximations to the Jacobian of the residuals, which leave out some of the Hessian information.

Computing adequately precise derivatives is important for the proper working of some optimization tools, particularly those that make explicit use of gradient information. This is especially true of methods from the conjugate gradient/truncated Newton and quasi-Newton / variable metric families of methods, of which there are a great many algorithms and implementations, for example, Nielsen 2000, Nash (2011a), Nash (2011b), Nielsen and Mortensen (2012), Byrd et al. 1995, Dai and Yuan 1999.

For such optimization methods, it is generally considered that derivatives calculated from analytic functions are likely to work best. Such functions require either human or computer symbolic mathematics, or else automatic differentiation (there are quite good explanations at http://en.wikipedia.org/wiki/Automatic_differentiation and http://www.autodiff.org/), which programmatically applies the chain rule and other algorithms to the program code of our function. A number of practitioners use automatic differentiation in optimization, for example, the NEOS web-based optimization system (http://www.neos-server.org/) and the AD Model Builder software (http://admb-project.org/). These have justifiably attracted a certain following, but my experience is that they require considerable effort to use. On the other hand, many workers, including some very prominent developers of optimization software, prefer to work with numerically approximated derivatives or with methods that obtain this information implicitly.

When symbolic or automatic derivatives are not available, numerical approximations are generally employed. As a rather poor example, simple forward derivative approximations can be computed by code such as

gr <- function(par, ...) {
    fbase <- myfn(par, ...)  # ensure we have right value, may not be necessary
    df <- rep(NA, length(par))
    teps <- eps * (abs(par) + eps)
    for (i in 1:length(par)) {
        dx <- par
        dx[i] <- dx[i] + teps[i]  # Dangerous step if a constraint is in the way!
        tdf <- (myfn(dx, ...) - fbase)/teps[i]
        if (!is.finite(tdf) || is.nan(tdf))
            tdf <- 0  # Is this a good choice?
        df[i] <- tdf
    }
    df
}

3.9 Derivative approximations when there are constraints

Whatever approach to derivatives is chosen, the situation is seriously magnified when there are bounds or other constraints on the parameters. In principle, we can simply project gradients onto a surface tangential to the constraint. In practice, our methods must discover if they are on or very close to a constraint surface. For my own sanity, I will not attempt to define “very close” in this context.

Worse, if we are using numerical approximations to derivatives, the computations can step out of bounds. Consider the expression for the derivative of the univariate function used above in the forward approximation

3.4

The issue for software development is that can be in bounds when is not, so we need to include checks for constraint violation as well as special code for an alternate computation of the derivative approximation. I have not seen programs that do this. The concept is fairly simple, but the actual code would be very long and detailed.

The step noted as dangerous in the above code chunk presents a challenge to programmers primarily because it imposes quite severe overheads. First, we must check whether the step taken for the th element of the gradient crosses a bound, and if it does, we must then work out how to best approximate the gradient. For example, the code above uses a forward approximation because we add the axial step to the parameter vector. But equally simple are backward approximations based on subtracting the step and then using

tdf <- (fbase - myfn(dx, ...))/teps[i].

3.10 Scaling of parameters and function

Scaling of parameters for user-written functions, and occasionally, the scale of the computed function, are another issue that afflicts optimization computations. When users are aware of scaling, they are generally able to provide appropriate adjustments of parameters and functions. Automatic scaling is not trivial for nonlinear optimization because an essential feature of nonlinearity is that there is different scaling in different regions of the parameter space. Once again, this merits its own treatment in Chapter 17.

3.11 Normal ending of computations

How do we know if our computations are satisfactory? Answering this leads us to the thorny issues of optimality tests and program performance. Almost every piece of code to perform function minimization has its own particular tests for termination—often misidentified as convergence. As we have noted,

Programs terminate, while algorithms (may?) converge.

Optimality tests almost always have some relation to the well-known KKT conditions (Gill et al. 1981), but there are many approximations and shortcuts used, so it is useful to be able to actually compute the final gradient and the final Hessian. We want the gradient to be “small” and the Hessian to be “positive definite,” but the meaning of these concepts in the context of real problems in floating point arithmetic are far from cut and dried. There is more on this subject in Chapter 19.

3.12 Termination tests—abnormal ending

It is very very common that optimization programs do not exit because a satisfactory answer has been found. Instead, they often return control to a calling program because too much effort has been expended, as measured by time, function evaluations, gradient evaluations, or “iterations.” The last measure is unfortunate in that it is unusual to find clear, consistent documentation of what constitutes an “iteration” for a particular method.

Beyond reasons of too much effort, optimization programs may stop for a variety of reasons that are particular to the methods themselves. Let us consider one example.

R's optim() function includes a Nelder–Mead polytope minimizer based on the version in my book (Nash, 1979). This method, as mentioned in Section 2.10.3, takes a preliminary polytope (or simplex) made up of points in -space and modifies it according to various rules. One of these rules is called SHRINK, and it shifts of the points toward the point with the lowest function value.

One would assume that a volume measure of the polytope would bereduced in this operation, but when I was developing the code (in BASIC on a machine with between 4K and 8K of memory for program and data, and very unsatisfactory arithmetic), I noticed that sometimes the polytope volume measure would not decrease because of rounding errors. This was generally when the polytope had collapsed onto a point that was quite often a good approximation to the minimum. Because of the possibility that the SHRINK operation did not achieve its purpose, I calculated size measures before and after the operation, making failure to reduce the polytope volume a reason to exit, as otherwise the program would cycle continuously, trying and failing to shrink the polytope.

3.13 Output to monitor progress of calculations

For large calculations, it is helpful to be able to monitor the progress of the calculations. I like to periodically see the best function value found so far and some measures of function or gradient calculations. The volume of such output is controlled by setting an appropriate option. Unfortunately, there are many names and types for such options. trace is a common choice of name, but it can be either a logical or an integer quantity, depending on the optimizer. There are many other names. If you are using just one method, this is hardly worth thinking about, but if you want to try different methods, the syntax changes are a large nuisance.

The volume and selection of quantities output vary greatly across optimization codes. This lack of consistency is partly due to the internals of the optimizers. However, it makes comparisons between methods much more tedious than it might be if the progress information were consistent across many optimizers. This is one of the major motivations of optimx.

3.14 Output of the optimization results

When optimization programs have finished, even via a successful and normal termination, the returned information may vary considerably across methods. Standardization of output was another goal of the optimx wrapper, and we have put in quite a lot of work to provide useful and consistent output, but there are still some awkward structures. A lot of work has been put in (thanks especially to Gabor Grothendieck) to provide tools to access the returned results from optimx. Similar issues exist for most large R packages that wrap several related tools.

Note that in many cases, we only want the optimal parameters. However, it is almost always worthwhile doing some examination—either automated or manual—of the function value as well as some indicator of the likely acceptability of the solution such as the KKT tests.

In rarer instances, it is important to provide the trajectory of the optimization. This is the set of points, possibly augmented by the function value, which mark iterations or other recognized steps in our methods. This is quite distinct from the needs of different applications for particular information to be returned or saved, which might, as we have suggested, be only the parameters and perhaps the function value and a completion code. By contrast, the trajectory might lead to an unsatisfactory “answer.” What we want to know is how, and eventually why, the method got to this answer.

3.15 Controls for the optimizer

Most packages and functions include a “control” list, often called control. In R this list may be used to provide tolerances for convergence tests, indicators of the level of output to be provided, algorithms for computing derivatives, and similar options. Users can generally comprehend the general purpose of these controls, even if they lack the understanding to use them to best advantage.

Much more difficult for nonspecialists are controls that alter the behavior of the optimizer methods. A relatively comprehensible example of this is the pair of controls used to increase or decrease the so-called Marquardt parameter in the Levenberg–Marquardt approach to nonlinear least squares. safeguards the Gauss–Newton search direction calculation by essentially mixing a steepest-descents component into the Gauss–Newton search direction. However, if it is too large, there is usually a slowing of progress toward a minimum. The tactic to try to work around this possibility is to decrease the Marquardt parameter , for example, multiply it by 0.4, when we improve (that is, decrease) the sum of squares function, and increase it, for example, by a factor of 10, when we fail to get a lower sum of squares. Setting particular values for the decrease and increase controls can be important for performance, On the other hand, we want choices for these numbers, as well as the initial value of , that are widely successful for many objective functions and starting parameters.

3.16 Default control settings

R has a good mechanism for providing default values of function arguments. This allows users to omit mention of these arguments if they are happy to use the default values provided. Thus, if we declare

myfn<-function(parameters, siglevel=0.05){

then we can use the calling syntax

result<-myfn(somepars)

and siglevel will be given the default value of 0.05. If we wish to override this to use a value 0.01, we put

result<-myfn(somepars, siglevel=0.01)

For the control list argument of a function call, we must specify the items to be particularized. Thus, for example, we might write

result<-myfn(somepars, control=list(trace=2))

to set the trace control, which often has a zero default.

3.17 Measuring performance

Performance is often measured by computing time, but other measures of effort are possible, such as the number of evaluations of functions, gradients, and Hessians, or “iterations” of a method. The amount of memory or number of double-precision numbers that must be stored may also be important. Unfortunately, all these are subject to the vagaries of implementation choices.

3.18 The optimization interface

Finally, there is a huge issue related to the overall way in which human users provide input to and receive output from the optimization tools. Traditionally, R is operated by typing in program lines that execute a function and return the output as a result object. Sometimes the functions we run also write data to a file or the screen. Because some early terminals were teleprinters, the command print is used even for writing to a screen.

As we store programs as files, we can also run them outside the R command terminal. There are tools such as Rscript and the construct R CMD to allow this.

Today many users are uncomfortable with having to type commands and prefer to use a pointing device such as a mouse to drag icons around a screen, choose from menu items, and generally do most of their work without touching a keyboard. R has a number of tools that allow such graphical user interfaces (GUIs) to be constructed. There are many variations on the GUI theme, each with its advantages and disadvantages for particular uses. I mentored Yixuan Qiu in a 2011 Google Summer of Code project called optimgui which demonstrated capabilities in this area. In particular, the interface allowed the objective function to be coded (we typed code into a template), data to be provided by selection, and the function executed for a set of parameters. Testing and checking were actions we wanted to make default behavior. The user could easily select an optimizer and attempt to run it to solve the problem.

As with most optimization tools, this was relatively easy to get running to a demonstration level. The unseen bulk of the iceberg is, however, the many small but critical checks for things that are not or should not be allowed, things that will make the results unsatisfactory. Thus optimgui is “working” but unfinished at the time of writing and is not part of the CRAN repository.

References

1. Byrd RH, Lu P, Nocedal J and Zhu CY 1995 A limited memory algorithm for bound constrained optimization. SIAM Journal on Scientific Computing 16(5), 1190–1208.
2. Dai YH and Yuan Y 1999 A nonlinear conjugate gradient method with a strong global convergence property. SIAM Journal on Optimization 10, 177–182.
3. Feldman SI, Gay DM, Maimone MW and Schryer NL 1991 Availability of f2c - a fortran to c converter. SIGPLAN Fortran Forum 10(2), 14–15.
4. Gill PE, Murray W and Wright MH 1981 Practical Optimization. Academic Press, London.
5. Murphy L 2012 likelihood: Methods for maximum likelihood estimation. R package version 1.5.
6. Nash JC 1979 Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation. Adam Hilger, Bristol. Second Edition, 1990, Bristol: Institute of Physics Publications.
7. Nash JC 2011a Rcgmin: Conjugate Gradient Minimization of Nonlinear Functions with Box Constraints. Nash Information Services Inc. R package version 2011-2.10.
8. Nash JC 2011b Rvmmin: Variable Metric Nonlinear Function Minimization with Bounds Constraints. Nash Information Services Inc. R package version 2011-2.25.
9. Nash JC and Walker-Smith M 1987 Nonlinear Parameter Estimation: An Integrated System in BASIC. Marcel Dekker, New York. See http://www.nashinfo.com/nlpe.htm for an expanded downloadable version.
10. Nielsen HB 2000 UCMINF - an algorithm for unconstrained, nonlinear optimization. Technical report, Department of Mathematical Modelling, Technical University of Denmark. Report IMM-REP-2000-18.
11. Nielsen HB and Mortensen SB 2012 ucminf: General-purpose unconstrained non-linear optimization. R package version 1.1-3.