1.2
Conditional and Biconditional Connectives

1.2.1 The Conditional Sentence

The conditional sentence (or implication), is a compound sentence of the form

“if P then Q”

From a purely logical point of view, conditional sentences do not necessarily imply a cause and effect between P and Q, although generally there is a definite cause and effect. For example the conditional sentence

If 1 + 1 = 3, then pigs fly.

is a true conditional sentence, although the reader would have to think long and hard to find a cause and effect relation between 1 + 1 = 3 and flying pigs. A more common implication in mathematics would be

If a positive integer n is composite, then n has a prime divisor less than or equal to images.

which provides an important cause and effect between P and Q. No doubt the reader has seen conditional sentences in Euclidean geometry, where the subject is explained through cause and effect implications of this type. The sentence, “If a polygon has three sides, then it is a triangle,” is a conditional sentence relating two important concepts in geometry.

The conditional statement P ⇒ Q can be visualized by the Euler (or Venn) diagram as drawn in Figure 1.4.

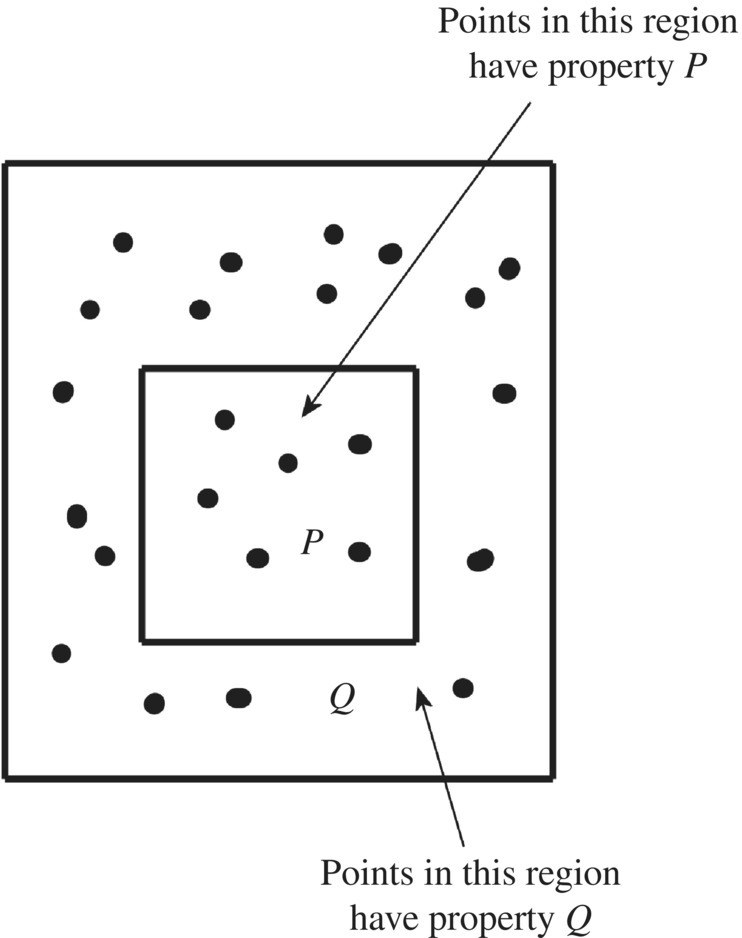
Euler diagram for P ⇒ Q displaying a box labeled Q enclosing smaller box labeled P with solid circle markers and arrows marking Points in this region have property P and Points in this region have property Q.

Figure 1.4 Euler diagram for P ⇒ Q.

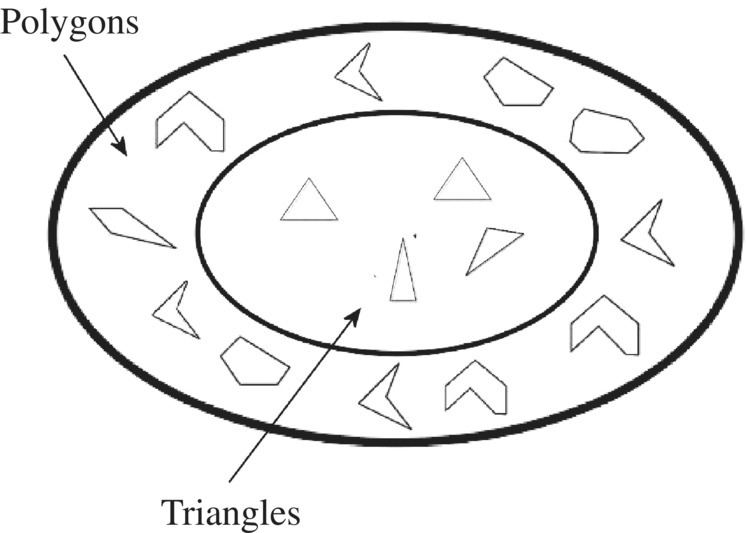
Diagram displaying subsets of triangles inside an ellipse enclosed by bigger ellipse with various patterns of polygons.

Figure 1.5 Subsets of triangles.

For example all polygons are triangles that we illustrate by the diagram in Figure 1.5.

1.2.2 Understanding the Conditional Sentence

The conditional sentence “if P, then Q” is best understood as a promise, where if the promise is kept, the conditional sentence is true, otherwise the sentence is false. As an illustration suppose your professor makes you the promise:

If pigs fly, then you will receive an A for the course.

The proposition is true since your professor has only promised an A if pigs fly, but since they do not, all bets are off. However, if you see a flying pig outside your classroom and your professor gives you a C, then you have reason to complain to your professor since the promise was broken, hence the proposition false.

The conditional sentence P ⇒ Q is often called an inference, and we say P implies Q. Another way of stating P ⇒ Q is to say P is a sufficient condition for Q, which means the truth of P is sufficient for the truth of Q. We also say that Q is a necessary condition for P, meaning the truth of Q necessarily follows from the truth of P.

1.2.3 Converse, Inverse, and the Contrapositive

The implication P ⇒ Q gives rise to three related implications shown in Table 1.22, one equivalent to the implication, the others not.

Table 1.22 Converse, inverse, contrapositive.

Implication Converse Inverse Contrapositive
P ⇒ Q Q ⇒ P ∼P ⇒  ∼ Q ∼Q ⇒  ∼ P

It is easy to show by truth tables that

equation

1.2.4 Law of the Syllogism

A fundamental principle of logic, called the law of the syllogism, states:

“if P implies Q, and Q implies R, then P implies R”

which is equivalent to the compound conditional sentence

equation

This sentence is a tautology since Table 1.23 shows all T's in column (5).

Table 1.23 Truth table verification of the syllogism.

images images images images (5)
P Q R images images images images images
T T T T T T T T
T T F T F F F T
T F T F T T F T
T F F F T F F T
F T T T T T T T
F T F T F T F T
F F T T T T T T
F F F T T T T T

1.2.5 A Useful Equivalence for the Implication

The implication P ⇒ Q is true if either P is false or Q is true. Hence, we have the useful logical equivalence

equation

which we verify by means of the truth table in Table 1.24.

Table 1.24 Equivalence of P ⇒ Q ≡  ∼ P ∨ Q.

P Q P ⇒ Q ∼P ∼P ∨ Q
T T T F T
T F F F F
F T T T T
F F T T T

Also the negation of the implication P ⇒ Q is another useful equivalence that we obtain by one of De Morgan's laws:

equation

In other words, an implication is (only) false when the premise is true and the conclusion false.

1.2.6 The Biconditional

Compound sentences of the form

“P if and only if Q”

are fundamental in mathematics, which leads to the following definition.

Problems

  1. True or False

    Identify the assumption and conclusion in the following conditional sentences and tell if the implication is true or false.

    1. If pigs fly, then I am richer than Bill Gates.
    2. If a person got the plague in the seventeenth century, they die.
    3. If you miss class over 75% of the time, you are in trouble.
    4. If x is a prime number, then x2 is prime too.
    5. If x and y are prime numbers, then so is x + y.
    6. If the determinant of a matrix is nonzero, the matrix has an inverse.
    7. If f is a 1–1 function, then f has an inverse.
  2. Contrapositive

    Write the contrapositive of the conditional sentences in Problem 1.

  3. True or False

    Let P be the sentence “4 > 6,” Q the sentence “1 + 1 = 2,” and R the sentence “1 + 1 = 3.” What is the truth value of the following sentences?

    1. P ∧  ∼ Q
    2. ∼(P ∧ Q)
    3. ∼(P ∨ Q)
    4. ∼P ∧  ∼ Q
    5. P ∧ Q
    6. P ⇒ Q
    7. Q ⇔ R
    8. P ⇒ (Q ⇒ R)
    9. (P ⇒ Q) ⇒ R
    10. (R ∨ Q ∨ R) ⇔ (P ∧ Q ∧ R)
  4. True or False

    Let P be the sentence “Jerry is richer than Mary,” Q is the sentence “Jerry is taller than Mary,” and R is the sentence “Mary is taller than Jerry.” For the following sentences, what can you conclude about Jerry and Mary if the given sentence is true?

    1. P ∨ Q
    2. P ∧ Q
    3. ∼P ∨ Q
    4. Q ∧ R
    5. ∼Q ∧  ∼ R
    6. P ∧ (P ⇒ Q)
    7. P ⇔ (Q ∨ R)
    8. Q ∧ (P ⇒ R)
    9. P ∨ Q ∨ R
    10. P ∨ (Q ∧ R)
  5. Truth Tables

    Construct truth tables to verify the following logical equivalences.

    1. (P ⇔ Q) ≡ (∼P ⇔  ∼ Q)
    2. [∼(P ⇔ Q)] ≡ [(P ∧  ∼ Q) ∨ (∼P ∧ Q)]
    3. (P ⇒ Q) ≡ (∼P ∨ Q)
  6. Conditional Sentences

    Translate the given English language sentences to the form P ⇒ Q.

    1. Unless you study, you will not get a good grade.
    2. “Do you like it? It is yours.”
    3. Get out or I will call the cops.
    4. Anyone who does not study deserves to flunk.
    5. Criticize her and she will slap you.
    6. With his toupee on, the professor looks younger.
  7. In Plain English

    Without making a truth table, say why the following implications are true.

    1. [(P ∨ Q) ∧  ∼ P] ⇒ Q
    2. [P ∧ (Q ∧  ∼ Q)] ⇒  ∼ P
    3. (P ∨ Q) ⇒ (∼P ⇒ Q)
  8. Distributive Laws for AND and OR

    For P, Q, and R verify the distributive laws

    1. P ∧ (Q ∨ R) ≡ (P ∧ Q) ∨ (P ∧ R)
    2. P ∨ (Q ∧ R) ≡ (P ∨ Q) ∧ (P ∨ R)
  9. Inverse, Converse, and Contrapositive

    One of the following sentences is logically equivalent to the implication P ⇒ Q. Which one is it?

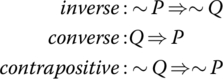
    equation

    For the two sentences not equivalent to P ⇒ Q, find examples illustrating this fact.

  10. True or False

    Is the following statement a tautology, a contradiction, or neither?

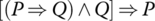
    equation
  11. Logical Equivalent Implications

    Show that the following five implications are all logically equivalent.

    1. P ⇒ Q (direct form of an implication)
    2. ∼Q ⇒  ∼ P (contrapositive form)
    3. (P ∧  ∼ Q) ⇒  ∼ P (proof by contradiction)
    4. (P ∧  ∼ Q) ⇒ Q (proof by contradiction)
    5. (P ∧  ∼ Q) ⇒ R ∧  ∼ R (reduction ad absurdum)
  12. Hmmmmmmmmmmm

    Is the statement

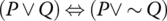
    equation

    true for all truth values of P and Q, or is it false for all values, or is it sometimes true and sometimes false?

  13. Interesting Biconditional

    Is the statement

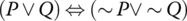
    equation

    true for all truth values of P and Q, or is it false for all values, or is it sometimes true and sometimes false?

  14. Finding Negations

    Find the negation of the following sentences.

    1. (P ∨ Q) ∧ R
    2. (P ∨ Q) ∧ (R ∨ S)
    3. (∼P ∨ Q) ∧ R
  15. If possible, find an example of a true conditional for which
    1. its contrapositive is true.
    2. its contrapositive is false.
    3. its converse is true.
    4. its converse is false.
  16. The inverse of the implication P ⇒ Q is ∼P ⇒  ∼ Q.
    1. Prove or disprove that an implication and its inverse are equivalent.
    2. What are the truth values of P and Q for which an implication and its inverse are both true?
    3. What are the truth values of P and Q for which the implication and its inverse are both false?
  17. For the sentence

    “If N is an integer, then 2N is an even integer.”

    write the converse, contrapositive, and inverse sentences.

  18. Let P, Q, and R be sentences. Show that
    1. P ⇒ (Q ⇔ R) requires the given paranthesis
    2. (P ∧ Q) ∨ R requires the given paranthesis
    3. (∼P ∨ Q) ⇒ R can not be written as ∼ P ∨ (Q ⇒ R)
  19. Challenge

    Rewrite the sentence

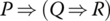
    equation

    in an equivalent form in which the symbol “⇒” does not occur.

  20. Nonobvious Statement

    The statement

    equation

    can be read “If P is true, then P follows from any Q.” Is this a tautology, contradiction, or does its truth value depend on the truth or falsity of P and Q?

  21. Another Nonobvious Statement

    The statement

    equation

    can be read “For any two sentences P and Q, it is always true that P implies Q or Q implies P.”

    Is this a tautology, contradiction, or does its true value depend on the truth or falsity of P and Q?

  22. Three‐Valued Logic

    Two‐valued (T and F) truth tables were basic in logic until 1921 when the Polish logician Jan Lukasiewicz (1878–1956) and American logician Emil Post (1897–1954) introduced n‐valued logical systems, where n is any integer greater than one. For example, sentences in a three‐valued logic might have values True, False, and Unknown. Three‐value logic is useful in computer science in database work. The truth tables for the AND, OR, and NOT connectives are given in Table 1.28.

    Table 1.28 Three‐valued logic.

    P Q P OR Q P AND Q NOT P
    True True True True False
    True Unknown True Unknown False
    True False True False False
    Unknown True True Unknown Unknown
    Unknown Unknown Unknown Unknown Unknown
    Unknown False Unknown False Unknown
    False True True False True
    False Unknown Unknown False True
    False False False False True

    From these connectives, derive the conditional P ⇒ Q and biconditional P ⇔ Q by drawing a truth table.

  23. Modus Ponens 3 and Modus Tollens?4 are systematic ways of making logical arguments of the form:
    equation

    Write Modus Ponens and Modus Tollens as compound sentences, and show they are both tautologies.

  24. Interesting

    Are the following two statements equivalent?

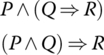
    equation
  25. Sixteen Logical Functions of Two Variables

    Figure 1.6 below shows the totality of 16 relations between 2 logical variables. One expression can be proven from another if it lies on an upward path from the first. For example

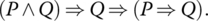
    equation
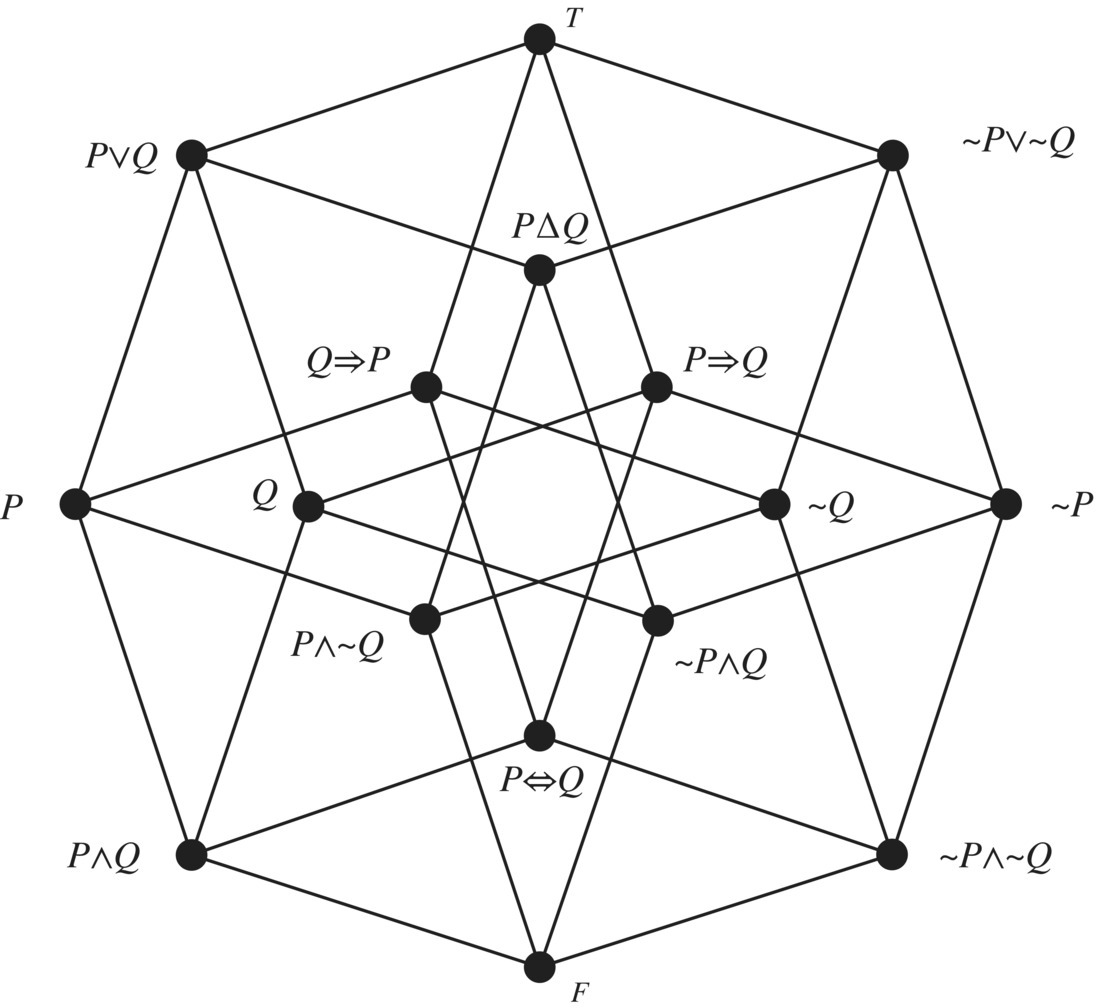
    Diagram of sixteen logical functions displaying a 3-dimensional polygon with vertices labeled P∨Q, P, PΔQ, P⇒Q, ~Q, ~P, P⇔Q, ~P∧~Q, ~P∧Q, T, Q⇒P, Q, P∧~Q, F, P∨Q, and ~P∨~Q.

    Figure 1.6 Sixteen logical functions.

    Verify a few of these implications using truth tables. The compound sentence PΔQ refers to the exclusive OR, which means either P or Q true but not both.

  26. Internet Research

    There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward conditional connectives, biconditional, truth tables, and necessary and sufficient conditions.

Notes

  1. 1 In pure logical systems, P and Q are generally referred to as antecedent and consequent, respectively. In mathematics, they are more likely to be called the assumption and conclusion.
  2. 2 You get an A for the course if you can prove this statement. Just slide your solution under your professor's door. The truth value of this conjecture, called the Goldbach Conjecture, is unknown.
  3. 3 Latin: mode that affirms.
  4. 4 Latin: mode that denies.
..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
3.139.238.76