3.1
Relations
3.1.1 Introduction and the Cartesian Product
The idea of things being related enters our consciousness a dozen times a day. We talk about people being related in many way, such as gender, race, height, age, and so on. In mathematics, the word relation is used to show the relations between pairs of objects, as when we say
| “is less than” | “is a subset of” |
| “is perpendicular to” | “divides” |
| “is greater than” | “is congruent to” |
| “is parallel to” | “is equivalent to” |
| “is homeomorphic to” | “is isomorphic to?” |
However, before defining a relation, it is necessary that we introduce the Cartesian product of two sets.
You are already familiar with one Cartesian product, namely the Cartesian plane, which is ℝ × ℝ, often denoted by ℝ2.
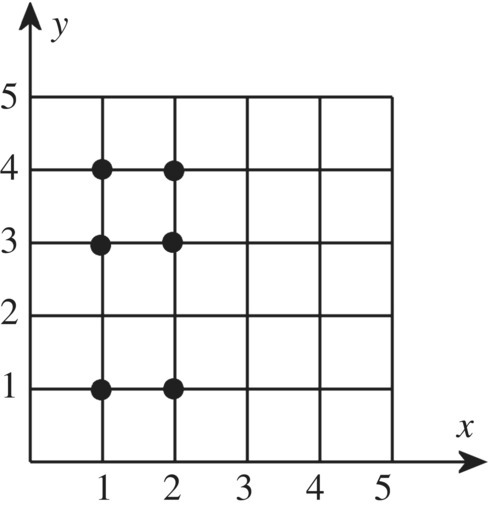
Figure 3.1 Graph of the {1, 2} × {1, 3, 4}.
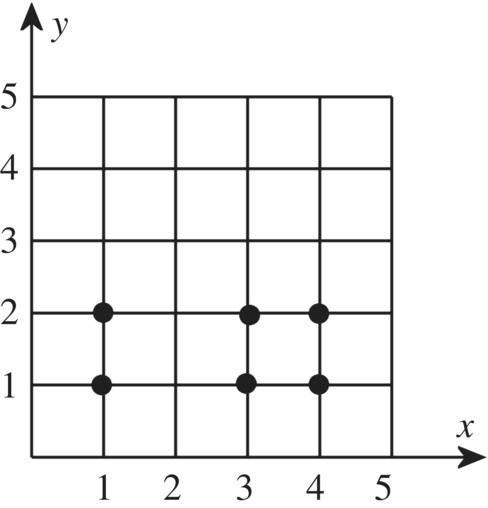
Figure 3.2 Graph of {1, 3, 4} × {1, 2}.

Figure 3.3 Visualization of A × (B ∪ C) = (A × B) ∪ (A × C).
![Four Cartesian planes with specified markers and line for [0,1]×[0,1], ℤ×ℝ, ℤ×ℤ, and {1,2}×ℤ.](http://images-20200215.ebookreading.net/2/5/5/9781119563518/9781119563518__advanced-mathematics__9781119563518__images__c03f001_4.gif)
Figure 3.4 Typical Cartesian products.
3.1.2 Relations
A (binary) relation is a rule that assigns truth values (true or false) to two things, which normally are numbers, sets, functions, and so on. When the value assigned by the relation is true, we say the things are related. For example, the pair of numbers (2, 3) would be assigned “true” for the relation “is less than” since 2 < 3. The reader is well familiar with many relations, such as the equal relation “=,” which would assign a truth value to the pair (3, 3) but not to the pair (3, 4). What this chapter does is it provides a general theory behind many of the relations you already known, and some you do not know.
The following examples will familiarize you with some common relations.
Table 3.1 Relation “likes class” on {Students} × {Classes}.
| Math | x | x | |||
| Literature | x | x | x | ||
| Chemistry | x | x | |||
| Psychology | x | x | x | ||
| Mary | John | Ann | Sally | Jim |
3.1.3 Visualization of Relations with Directed Graphs
Another way to visualize a relation is with a directed graph, which consists of a collection of dots representing members of A, and arrows connecting the dots if members are related. For example, the relation
on A = {1, 2, 3, 4, 5} can be visualized by the directed graph drawn in Figure 3.6.
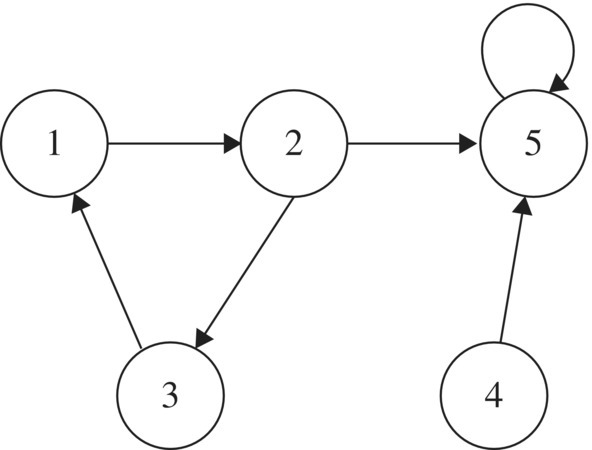
Figure 3.6 Directed graph of a relation on {1, 2, 3, 4, 5}.
3.1.4 Domain and Range of a Relation
A relation R is a generalization of a function f in the sense that every function is also a relation, but not vice versa. When the relation is a function, the relation maps a single element x ∈ A into a single value f(x) ∈ B, whereas for a general relation, a single value of x ∈ A can be related to none or many values of y ∈ B. But like functions, relations also have domains and ranges.
In Plain English: The domain of a relation R from A to B is the set of first members of the ordered pairs in R and the range of R is the set of second members of the ordered pairs. By definition, we have
For example, if A = {1, 2, 3, 4} and B = {2, 3, 4} with relation R from A to B, given by
we have
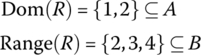
3.1.5 Inverses and Compositions
Two common ways of constructing new relations from old ones are inverse relations and compositions of relations.

Figure 3.8 Graphs of R and R−1.
3.1.6 Composition of Relations
The composition of two (or more) relations is similar to the composition of functions that the reader might be familiar. Recall that the composition of functions f and g, written f ∘ g, is defined by
for all x in the domain of g, where g(x) in the domain of f. The generalization of this definition to relations goes as follows.
In plain language, the composition is the collection of all “paths” from A to C as illustrated in Example 7.
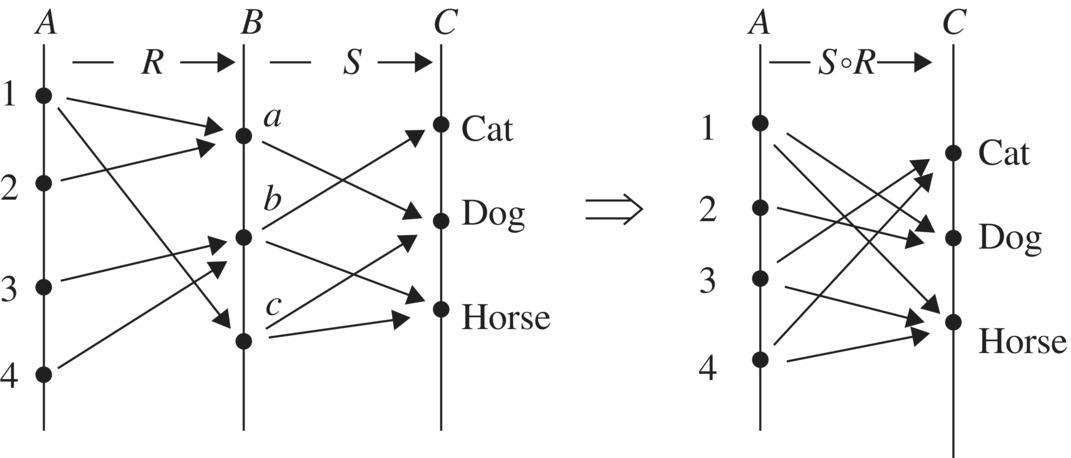
Figure 3.9 Composition S ∘ R.
Problems
- True or False
Tell whether the following statements are true or false.
- ℚ × ℚ ⊆ ℝ × ℝ
- aRb ⇒ (a, b) ∈ R
- aRb ⇒ bRa
- aRa
- For any two sets A, B, A × B = B × A
- For some sets A, B, A × B = B × A
- Relations
For the set A = {1, 2, 3, 4}, write out the ordered pairs in the relation R on A if
- xRy ⇔ x < y
- xRy ⇔ x = y
- xRy ⇔ x divides y
- xRy ⇔ x is a multiple of y
- Four Basic Cartesian Products
Given A = {1, 2, 3}, B = {a, b}. Find the following Cartesian products.
- A × B
- B × A
- A × A
- B × B
- Cartesian Products
For each of the following pair of sets A and B, find the Cartesian products A × B and B × A.
- A = {0, 2}, B = {−1, 0}
- A = {a, b}, B = {b, c}
- A = ℝ, B = ℕ
- A = ℤ, B = ℕ
- A = ℝ, B = {−1, 0, 1}
- Graphing a Relation
Draw a sketch of the following relations.
- R = {(x, y) ∈ ℝ × ℝ : x2 + y2 = 1}
- R = {(x, y) ∈ ℝ × ℝ : y = sin x}
- R = {(x, y) ∈ ℝ × ℝ : x = y2}
- R = {(x, y) ∈ ℝ × ℝ : |x| ≤ 1, |y| ≥ 1}
- R = {(x, y) ∈ ℕ × ℕ : x ≡ 0(mod3), y ≡ 1(mod3)}
- R = {(x, y) ∈ ℕ × ℕ : x divides y}
- Algebra of Relations
Given are the closed intervals

on the real line ℝ. Sketch the following relations in the plane.
- R = (A ∪ B) × C ⊆ ℝ × ℝ
- R = (A ∩ B) × C ⊆ ℝ × ℝ
- R = (A × B) ∪ (A × C) ⊆ ℝ × ℝ
- R = A × (A ∪ C) ⊆ ℝ × ℝ
- Naming a Relation
Give common names that describe the following relations on
 . Then find the inverse relation. What is a name for the relation and inverse relation?
. Then find the inverse relation. What is a name for the relation and inverse relation?- R = {(1, 1), (2, 2), (3, 3)}
- R = {(1, 2), (1, 3), (2, 3)}
- R = {(1, 1), (1, 2), (1, 3), (2, 2), (2, 3), (3, 3)}
- Important Types of Relations
Two important types of relations are injections (1–1) and surjections (onto), whose definitions we have seen in Section 2.4 in conjunction with the cardinality of sets. The definition of an injection and surjection defined especially for relations are as follows:
- Surjective Relation: A relation R ⊆ X × Y is surjective if
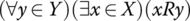
- Injective Relation: A relation R ⊆ X × Y is injective if

For X = Y = {1, 2, 3}, give an example of an injective and surjective relation from X to Y.
- Surjective Relation: A relation R ⊆ X × Y is surjective if
- Meaning of Relations
For each of the following, describe the members of the relation R.
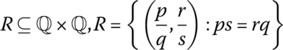
- R ⊆ ℚ × ℚ, R = Ø
- R ⊆ ℝ × ℝ, R = ℝ × ℝ
- Inverse Relation of Compositions
Given A = {1, 2, 3} verify the following identity for the inverse of a composition:
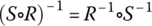
for relations

- Composition of Relations
Find the composition of the relations S ∘ R given the sets

and the relations

- Cartesian Product Identities
Prove the identity

- Number of Relations
If a set A has m elements and B has n elements, show that the number of relations from A to B is 2mn.
- Graphing Relations and Their Inverses
Graph the following relations and their inverses.
- R ⊆ ℝ × ℝ, xRy ⇔ y = 1/x
- R ⊆ ℝ × ℝ, xRy ⇔ y = ex
- R ⊆ ℝ × ℝ, R = {(x, y) : |x| + |y| = 1}
- Counting Relations I
What is the total number of relations that can be defined on the set A = {1, 2}?
- Counting Relations II
What is the total number of relations that can be defined on the set A = {1, 2, 3}?
- Converse of a Binary Relation
If R is a binary relation on a set A, then the converse relation
 on A is defined by the relation
on A is defined by the relation  . State in English or write out in ordered pairs the converse of the following relations R.
. State in English or write out in ordered pairs the converse of the following relations R.- The relation “is the mother of.”
- The relation “is a uncle of.”
- The relation “<” on the real numbers.
- The relation “=” on the real numbers.
- Blood Typing
There are four blood, types A, B, AB, and O.
- Type A can receive blood from type A and O.
- Type B can receive blood from type B and O.
- Type AB can receive blood from all types.
- Type O can receive blood from only type O.
Given the set S = {A, B, AB, O}, define a binary relation R on S as follows:

- Write out the ordered pairs of R.
- Draw a directed graph of the relation R.
- Define the converse
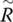 of R by
of R by 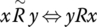 . What is the interpretation of the converse?
. What is the interpretation of the converse?
- Internet Research
There is a wealth of information related to topics introduced in this section just waiting for curious minds. Try aiming your favorite search engine toward important relations in mathematics, visualizing mathematical relations, and composition of relations.
