3

Risk

3.1 Risk and Uncertainty

Economists attach a precise meaning to the words risk and uncertainty. Pandora makes a decision under risk if unambiguous probabilities can be assigned to the states of the world in her belief space B. Otherwise, she decides under uncertainty. The importance of distinguishing decision problems in which unambiguous probabilities are available from those in which they aren’t was first brought to the attention of the world by Frank Knight (1921). For this reason, people often speak of Knightian uncertainty to emphasize that they are using the word in its technical sense.

The archetypal case of risk is playing roulette in a casino. The archetypal case of uncertainty is betting at the race track. Who knows what the probability is that Punter’s Folly will win? Does it even make sense to attribute a probability to such a one-off occurrence?

Problems about when it makes sense to attach probabilities to events are the subject of an ongoing controversy in philosophy, but these problems will be put on the shelf until chapter 6. Our concern in the current chapter will be with issues that are nicely illustrated by the following paradox.

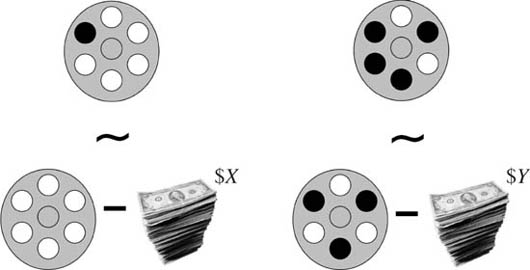
Zeckhauser’s paradox. Some bullets are loaded into a revolver with six chambers, as illustrated in figure 3.1. The cylinder is then spun and the gun pointed at your head. Would you be prepared to pay more to get one bullet removed when only one bullet was loaded, or when four bullets were loaded? People usually say they would pay more in the first case, because they would then be buying their lives for certain.

I made this mistake myself when the paradox was first put to me, but I changed my mind when I learned that my decision was inconsistent with my preferring being alive to being dead and having more money rather than less. However, we shall have to wait for the reasons why until after the Von Neumann and Morgenstern theory of making decisions under risk has been examined.

Figure 3.1. Zeckhauser’s paradox. The diagram on the left shows that Pandora is indifferent between leaving one bullet in the revolver and paying $X to get the bullet removed. The diagram on the right shows that Pandora is indifferent between leaving four bullets in the revolver and paying $Y to get one bullet removed. Is Pandora’s choice behavior consistent if X > Y?

3.2 Von Neumann and Morgenstern

John Von Neumann was an all-round genius. Inventing game theory was just a sideline for him. Critics of game theory choose to caricature him as the archetypal cold warrior—the original for Dr. Strangelove in the well-known movie. He was indeed a hawk in the cold war, but far from being a mad cyborg, he was a genial soul, whose parties were famous in Princeton for their relaxed atmosphere.

Von Neumann had proved the famous minimax theorem of game theory in 1928, but left the wider implications of the result unexplored until Oskar Morgenstern persuaded him that they should write a book they called The Theory of Games and Economic Behavior (Von Neumann and Morgenstern 1944), which put game theory on the map.

They were well into this enterprise when Morgenstern turned up at Von Neumann’s house one day in the 1940s complaining that they didn’t have a proper basis for the cardinal utilities they had been taking for granted in the book. Fortunately, Von Neumann didn’t know or care that the reigning orthodoxy at the time was that cardinal utility scales are intrinsically nonsensical (section 1.7). So he invented a theory on the spot that measures how much Pandora wants something by the size of the risk she is willing to take to get it.

How does Von Neumann’s theory work? Von Neumann’s approach to utility is still sometimes regarded as an abstruse mathematical theory beyond the comprehension of ordinary folk. I think that this mistaken attitude is a hangover from the time when cardinal utility was controversial. After all, the old-time gurus who denounced cardinal utility as nonsensical were hardly likely to admit that they were wrong for a very simple reason.

Suppose that Pandora is wondering how much effort it is worth expending to get a date with Quentin tonight. How many utils should she assign to this outcome in her set C of consequences?

We first need to decide what utility scale to use. For this purpose, Pandora needs to pick two outcomes that are respectively better and worse than any other outcome she is likely to encounter. For example, the worst outcome might be that she has to spend the evening home alone. Her best outcome might be that she somehow gets a date with Johnny Depp. These two extremes will correspond to the boiling and freezing points of water used to calibrate a thermometer, except that the utility scale to be constructed will assign 0 utils to the worst outcome, and 1 util to the best outcome (rather than 32° and 212° as on the Fahrenheit scale).

Next consider a bunch of (free) lottery tickets for which the only prizes are either the best outcome or the worst outcome. When we offer Pandora lottery tickets with higher and higher probabilities of getting the best outcome as an alternative to a date with Quentin, she will eventually switch from saying no to saying yes. If the probability of the best outcome on the lottery ticket that makes her switch is 0.2, then Von Neumann’s theory says that a date with Quentin is worth 0.2 utils to her.

Pandora needs to know that a date with Quentin is worth 0.2 utils in order to determine the expected value of her Von Neumann and Morgenstern utility function. But why should a rational agent maximize the long-run average of such a utility function and not something else? This question was first asked by Nicholas Bernoulli way back in the eighteenth century when he formulated the St Petersburg paradox.

3.3 The St Petersburg Paradox

In the heyday of the Czars, a casino in St Petersburg was supposedly willing to run any lottery whatever, provided that the management could set the price of a ticket to participate.¹

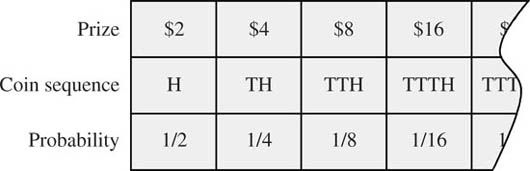
In the lottery of figure 3.2, a fair coin is tossed until it shows heads for the first time. If the first head appears on the kth trial, a player wins $2^k. How much should Pandora be willing to pay to participate in this lottery?

A player wins 2^k dollars in the St Petersburg lottery with probability 1/2^k. For example, the probability of the sequence TTH, which wins 8 dollars, is 1/2³ = 1/8. So a player expects to win

Figure 3.2. The St Petersburg paradox. How much should Pandora be willing to pay to win 2^k dollars with probability 1/2^k?

2/2 + 2²/2² + 2³/2³ + · · · = 1 + 1 + 1 + · · ·

dollars on average. The expected dollar value of the lottery is therefore infinite.

If it made sense for Pandora to choose whatever maximizes her dollar expectation, she would liquidate her entire assets and borrow whatever she could in order to buy a ticket for the lottery. But the probability is that Pandora will end up with no more than $8, and so she is unlikely to find the odds attractive.

The moral isn’t that the policy of always choosing the lottery with the largest expectation in dollars is irrational. It isn’t for us to tell Pandora what her aims should be. The St Petersburg story only casts doubt on the idea that no other policy can be rational. The same goes for any theory which claims that there is only one rational way to respond to risk. An adequate theory needs to recognize that the extent to which Pandora is willing to bear risk is as much a part of her preference profile as her attitude to getting a date with Quentin or Johnny.

Decreasing marginal utility. The St Petersburg paradox shows that maximizing your dollar expectation may not always be a good idea. It suggests that an agent in a risky situation might sometimes want to maximize the expectation of some utility function with decreasing marginal utility. This just means that each extra dollar is assigned a smaller number of utils than the dollar that went before. Paul Samuelson famously explained that this is why rich men take a cab when it rains but poor men get wet—the cab fare is worth more to you if you are poor than if you are rich. As Jeremy Bentham (1863) put it: “The quantity of happiness produced by a particle of wealth will be less and less at every particle.”

If Pandora’s utility for x dollars is u(x), then her expected utility in the St Petersburg lottery becomes

u(2) × + u(4) × + u(8) ×; + · · ·.

The St Petersburg paradox assumes that u(x) = x, but Daniel Bernoulli suggested taking the utility function to be the logarithm of Pandora’s dollar winnings. If we adopt his suggestion using logarithms to base 2,² then the expected utility of the St Petersburg lottery is reduced all the way from infinity to 2. It follows that Pandora would only be willing to pay $4 to participate in the St Petersburg lottery.

Daniel Bernoulli’s conclusion accords with our intuitions about how ordinary people would behave in the mind experiment envisaged in the St Petersburg paradox. Nobody I know would be prepared to pay more than $10 to participate. But, although Daniel Bernoulli predates Bentham by many years, his proposal is Benthamite in character. We are left wondering what is special about the logarithm of income. Why not take Pandora’s utility function to be the square root or some other function of income? For example, if , then Pandora would be willing to pay $5.86 to participate in the St Petersburg lottery.

Why are we maximizing the long-run average of a utility function anyway? Why shouldn’t Pandora be ultracautious and maximize her minimum possible income, as assumed by John Rawls (1972) in his famous Theory of Justice? Since her minimum possible prize in the St Petersburg lottery is $2, she would then be unwilling to pay more than this amount to participate.

The theory of revealed preference allows us to see our way around such questions. In particular, the Von Neumann and Morgenstern theory of decision under risk explains why Pandora will necessarily act as though maximizing the expected value of something if she honors their consistency requirements.

3.4 Expected Utility Theory

This section offers a simple version of Von Neumann and Morgenstern’s theory.

Lotteries. In a decision problem D : A × B → C the feasible set A of actions is a subset of the set of all acts α : B → C (section 1.2). In the Von Neumann and Morgenstern theory, each state of the world in Pandora’s belief set B comes equipped with a precise probability. When making decisions, Pandora is assumed to pay no attention to any other features of a state.

In the Von Neumann and Morgenstern theory, Pandora’s beliefs over the states in the set B and her preferences over the consequences in the set C are separated right from the outset. The probabilities of the states in B are assumed to be exogenously determined, and so not open to any bias that Pandora’s preferences might induce. Nor does the theory allow any bias to arise from the nature of Pandora’s feasible set A, since a Von Neumann and Morgenstern utility function is derived from the preferences she reveals over the whole set of acts.

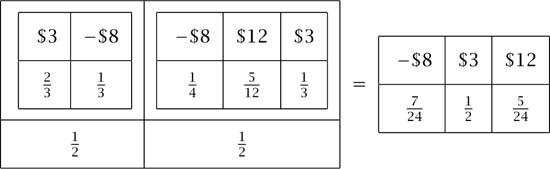
Figure 3.3. Reducing a compound lottery. For example, the total probability of losing $8 in the compound lottery is .

Given that only the probabilities of states are to be counted as relevant, the first step in the derivation is to identify with the set lott(C) of lotteries with prizes in C. For example, if C consists of possible money payments, then the lottery in which Pandora loses $8 with probability , wins $12 with probability , and wins $3 with probability is represented by

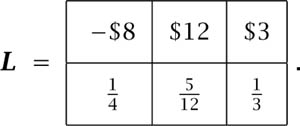
The expected dollar value of this lottery is

One of the prizes in a raffle at an Irish county fair is sometimes a ticket for the Irish National Sweepstake. If you buy a raffle ticket, you are then participating in a compound lottery in which the prizes may themselves be lotteries. All the lotteries involved in a compound lottery are always assumed to be independent of each other (unless something is said to the contrary), and so it is easy to reduce a compound lottery to a simple lottery, as in figure 3.3.

3.4.1 Rationality Postulates

The following list of postulates are simplifications of those proposed by Von Neumann and Morgenstern (1944).³ They require that the preferences over lotteries that Pandora reveals in risky situations be consistent.

Postulate 1. Pandora prefers whichever of two win-or-lose lotteries offers the larger probability of winning.

Recall from section 3.2 that Pandora must identify outcomes that are respectively better and worse than any outcome she needs to consider in her decision problem. These outcomes will be called and . A win-or-lose lottery is simply a lottery in which the only outcomes are and .

Postulate 2. Pandora is always indifferent between each prize and some lottery involving only and .

The second postulate says that, for each prize in Pandora’s set of consequences, there is a probability q for which

The postulate is sometimes called the Archimedean axiom for reasons that aren’t worth remembering. It is needed to justify the method used to construct a Von Neumann and Morgenstern utility function u : C → in section 3.2. We simply make u() equal to the probability q of (3.1).

However, it isn’t enough to have constructed a utility function that represents Pandora’s revealed preferences over the prizes in her consequence space C. For u to be a Von Neumann and Morgenstern utility function, Pandora must choose among the lotteries in lott(C) as though she were maximizing the expected utility u(L) of the lottery L. Not only do we require that u represents Pandora’s preferences over C, we therefore also require that u represents Pandora’s preferences over lott(C).

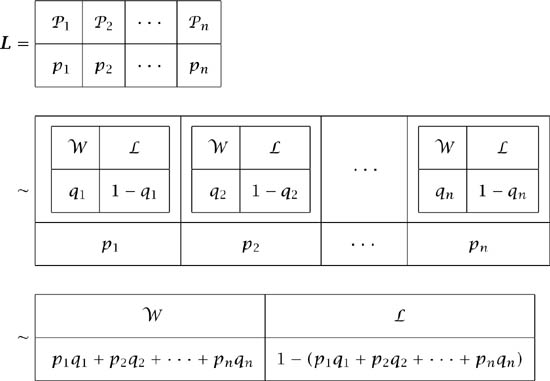
Figure 3.4 illustrates the two steps in the argument that justifies this conclusion. Each step requires a further postulate.

Postulate 3. Pandora doesn’t care if a prize in a lottery is replaced by an independent prize if she is indifferent between the new prize and the prize it replaces.

Versions of postulate 3 are often called the independence axiom. This terminology serves as a reminder that it is implicitly assumed that if one of the prizes is itself a lottery, then this lottery must be independent of all other lotteries involved.

Figure 3.4. Von Neumann and Morgenstern’s argument. The first indifference is justified by postulate 3. The second indifference is justified by postulate 4.

The prizes available in the arbitrary lottery L of figure 3.4 are ₁, ₂, . . . , _n. By postulate 2, Pandora is indifferent between each such prize _k and some win-or-lose lottery in which she wins with probability q_k. Postulate 3 is then used to justify replacing each prize _k by the corresponding win-or-lose lottery. We then need a final assumption to reduce the resulting compound lottery to a simple lottery.

Postulate 4. Pandora only cares about the total probability with which she gets each prize in a compound lottery.

The total probability of in figure 3.4 is r = p₁q₁ + p₂q₂ + · · · + p_nq_n. So postulate 4 says that we can replace the compound lottery by the win-or-lose lottery on the final line, thereby justifying the second of the two steps the figure illustrates.

By postulate 1, Pandora prefers whichever of two lotteries like L in figure 3.4 has the larger value of r = p₁q₁ + p₂q₂ + · · · + p_nq_n. She therefore acts as though seeking to maximize

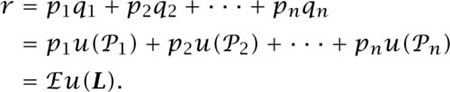
It follows that u is a utility function that represents Pandora’s preferences over lotteries. But this is what it means to say that u is a Von Neumann and Morgenstern utility function for her preferences over prizes.

Standing Quentin up. The following example emphasizes the importance of the independence proviso in the vital postulate 3.

Suppose that Pandora is indifferent between a date with Quentin and the lottery Q in which a fair coin is tossed that results in her getting a date with Johnny Depp if it falls heads and a date with nobody at all if it falls tails. Now imagine that Pandora is offered a lottery L in which she gets a date with Johnny if a fair coin falls tails and a date with Quentin if it falls heads. Will she be ready to swap the unfortunate Quentin in this lottery for Q?

She most certainly would if we were talking about the same coin toss in each lottery, because she would then be guaranteed a date with Johnny whatever happens! Even if the coins were different but positively correlated she would still strictly prefer standing Quentin up.

3.5 Paradoxes from A to Z

This section examines Allais’ paradox and Zeckhauser’s paradox as examples of how the Von Neumann and Morgenstern theory works in practice.

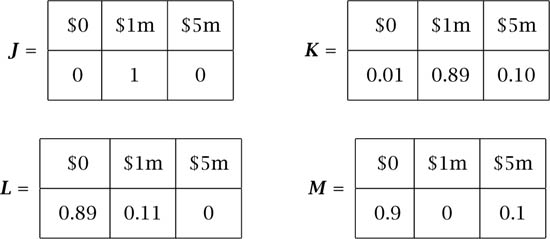
Allais’ paradox. Allais asked Savage to compare the lotteries J and K of figure 3.5, and then to compare the lotteries L and M (section 1.10). When Savage reported that he would choose J rather than K, and M rather than L, Allais triumphantly pointed out that the preferences he thereby revealed are inconsistent with the Von Neumann and Morgenstern theory.

To see that the preferences K J and L M violate the Von Neumann and Morgenstern postulates, it is only necessary to show that they can’t be described by a Von Neumann and Morgenstern utility function.

The best and worst prizes available are $0 and $5m. We therefore look for a Von Neumann and Morgenstern utility function with u(0) = 0 and u(5) = 1. What can then be said about Savage’s value for x = u(1)? Observe that

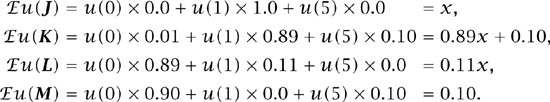
Since J K, we have that x > 0.89x + 0.10, and so . Since L M, we also have that 0.11x < 0.10, and so . But it can’t be simultaneously true that and . So the preferences that Savage expressed can’t be described with a Von Neumann and Morgenstern utility function.

Figure 3.5. Allais’ paradox. The prizes are given in millions of dollars to dramatize the situation.

Experiments are said to show that most laboratory subjects express the same preferences as Savage. Allais’ paradox then provides ammunition for people who deny that the Von Neumann and Morgenstern theory is a good model of how real people behave in risky situations. My own view is that such critics are right to challenge the kind of positive application of the theory that is standard in economics, but wrong to think that Allais’ paradox adds much to their case.

Most people presumably express the preference J K because J guarantees $1m for sure, whereas K carries the risk of getting nothing at all. On the other hand, when M is compared with L, the risk of ending up with nothing at all can’t be avoided. On the contrary, the risk of this final outcome is high in both cases. But if the probability 0.89 in L is rounded up to 0.90 and 0.11 is rounded down to 0.10, then someone who understands what is going on will prefer M to the new L. If the new L is thought to be essentially the same as the old L, one then has a reason for expressing the preference M L. In other words, the version of the Allais’ paradox presented here can be explained in terms of rounding errors.

Zeckhauser’s paradox. Suppose, as in figure 3.1, that $X is the most that Pandora is willing to pay to get one bullet removed from a gun containing one bullet, and that $Y is the most that she is willing to pay to get one bullet removed from a gun containing four bullets (section 3.1). Let mean death, and mean being alive after paying nothing. Let C mean being alive after paying $X, and mean being alive after paying $Y.

The aim is to assign Von Neumann and Morgenstern utilities to the consequences C and . If we find that u() < u(C), then it follows that C, and so it must be the case that X < Y because Pandora is assumed to prefer more money to less.

We shall follow our practice so far of making u() = 0 and u() = 1 (section 3.2). Sometimes people complain that death is so terrible an outcome that it should be assigned a utility of −∞. But even if this were allowed in the Von Neumann and Morgenstern theory, it would be completely unrealistic. If u() = −∞, then Pandora wouldn’t be willing to do anything whatever that involved the slightest risk of dying. She wouldn’t even go for a walk in the park in case a meteor fell on her head. In fact, estimates derived from driving behavior suggest that ordinary people value their lives at something less than ten million dollars.

Returning to Zeckhauser’s paradox, we are given that Pandora is indifferent between C and the lottery in which she gets with probability and with probability . Thus,

Similarly, Pandora is indifferent between the lottery in which she gets and each with probability , and the lottery in which she gets with probability and with probability . Thus,

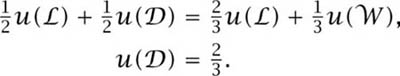
So C, and thus Pandora will necessarily be ready to pay less to get one bullet removed when only one bullet was loaded than when four bullets were loaded.

After seeing the calculation, the result begins to seem more plausible. Would I be willing to pay more to get a bullet removed from a six-shooter containing one bullet than to get a bullet removed from a six-shooter containing six bullets? Definitely not! But getting a bullet removed when there are six bullets isn’t so different from getting a bullet removed when there are five bullets, which isn’t so different from getting a bullet removed when there are four bullets. How different is the difference between each of these cases? Appealing to our gut feelings doesn’t get us very far when such questions are asked. We need to calculate.⁴

3.6 Utility Scales

We have seen that there is always an infinite number of possible utility functions that represent any consistent preference relation. If U is an ordinal utility function, then any strictly increasing transformation of U is also an ordinal utility function that represents the same preference relation (section 1.7). However, a Von Neumann and Morgenstern utility function u is cardinal. Given any two Von Neumann and Morgenstern utility functions u₁ and u₂ that represent the same preferences over lott(C), we can write

where A > 0 and B are constants.

3.6.1 Analogy with Temperature

Von Neumann and Morgenstern emphasize the analogy between their kind of utility scale and temperature scales. In both cases, we are free to assign the zero and the unit on the scale in any way we find convenient. We therefore assign 0° to the freezing point of water on the Celsius scale and 100° to the boiling point. The reason that it was once convenient to assign 32° to the freezing point of water on the Fahrenheit scale and 212° to the boiling point of water are nowadays forgotten. However, it doesn’t matter very much that the Fahrenheit scale seems arbitrary, because we can pass back and forward between the two scales using the affine transformation

In a similar way, we don’t need to use a utility scale that assigns a utility of 0 to and 1 to . We can assign them any utilities we find convenient, provided that the utility we assign to exceeds the utility we assign to . However, once we have determined the zero and the unit on a Von Neumann and Morgenstern utility scale, we have exhausted all our room for maneuver.

Justifying the analogy. What justifies equation (3.2)? It is obvious that maximizing the expected utility of u₁ is equivalent to maximizing the expected utility of u₂ = Au₁ + B. It is not so obvious that if u₁ and u₂ are alternative Von Neumann and Morgenstern utility functions for a preference relation defined on lott(C), then they must be linked as in (3.2).

To see why, begin by choosing constants A_i > 0 and B_i to make the Von Neumann and Morgenstern utility functions ν_i = A_iu_i + B_i satisfy ν_i () = 0 and ν_i () = 1. Recall that postulate 2 implies that, for any prize in C, there is a probability q for which

This observation allows us to deduce that ν₁ () = ν₂ () because both sides are equal to (1 − q)ν_i () + qν_i () = q. Then rewrite ν_i in terms of u_i, and solve for u₂ in terms of u₁.

The domain of a Von Neumann and Morgenstern utility function. The domain of a Von Neumann and Morgenstern utility function u : C → is Pandora’s set C of consequences. The domain of its expected value Eu : lott(C) → is the set lott(C) of lotteries with prizes in C.

Confusion can arise because some authors say that Eu is the Von Neumann and Morgenstern utility function rather than u. The difference is large because Eu has only ordinal status on lott(C), whereas u has cardinal status on C. It is hard to believe in retrospect, but this misunderstanding once created a major controversy in the utilitarianism literature (Elster and Roemer 1992).

Von Neumann and Morgenstern utility functions are sometimes said to be linear for similar reasons. There need be nothing linear about u : C → , but there is a sense that we need not worry about in which Eu : lott(C) → always defines a linear mapping from a set of probability vectors to the real numbers.

3.6.2 Isolating Decision Problems

The lectures that gave rise to this book were given in honor of William (Terence) Gorman. This section uses his idea that the satisfaction people find in commodities can sometimes be regarded as deriving from separable characteristics (Gorman and Myles 1988). I hope he would also have liked my pursuing the analogy of utility with temperature even to the extent of contemplating the possibility of an absolute zero on a Von Neumann and Morgenstern utility scale.

Separating preferences. Pandora may like oranges for two reasons: they are healthy and they taste nice. Her preferences can then be separated into a health dimension and a taste dimension. Pandora needs to be able to separate her preferences in this kind of way, because she would otherwise never be able to squeeze a decision problem into a small-world format. Even deciding between a vanilla and a strawberry ice cream would become problematic if she always had to take account of the totality of her environment when doing so. The ability to isolate only the preference dimensions that matter in a particular problem is therefore of great importance. But how can this be done?

Figure 3.6. Evaluating lotteries separately. The lottery (L, M) is obtained by combining the separate lotteries L and M.

The first step in addressing the separation question is to write C = C₁ × C₂, so that each consequence c = (c₁, c₂) in C can be evaluated in terms of two characteristics c₁ and c₂. If Pandora evaluates these two dimensions separately, then her preferences on one dimension should be unaffected by how well she is doing on the other dimension. When this requirement is expressed in terms of lotteries, the result is surprisingly strong (Keeney and Raiffa 1975).

Figure 3.6 shows two lotteries L and M with prizes in C₁ and C₂ respectively. The lottery (L, M) (with prizes in C = C₁ × C₂) is one particular way of combining L and M. We shall say that a preference relation defined on lott(C) evaluates lott(C₁) and lott(C₂) separately if it is always true that

(1) (L, M) (L, M′) implies (L′, M) (L′, M′);

(2) (L, M) (L′, M) implies (L, M′) (L′, M′).

Separating utilities. If satisfies the Von Neumann and Morgenstern postulates, then we can represent it with a Von Neumann and Morgenstern utility function u : C → satisfying u () = 0 and u () = 1, where = (₁, ₂) and = (₁, ₂) are the best and worst outcomes in C. We shall also need to consider A = u(₁, ₂) and B = u(₁, ₂).

If evaluates lott(C₁) and lott(C₂) separately, section 10.1 shows that

where the functions u₁ : C₁ → and u₂ : C₂ → can be regarded as Von Neumann and Morgenstern utility functions on C₁ and C₂, with u₁(₁) = u₂(₂) = 0 and u₁ (₁) = u₂(₂) = 1.

Three cases need to be distinguished: A + B < 1, A + B = 1, and A + B > 1. Rationality can’t decide between these cases. Pandora reveals which case applies to her when she chooses between the lottery L, in which she has an equal chance of getting (₁, ₂) or (₁, ₂), and the lottery M, in which she has an equal chance of getting (₁, ₂) or (₁, ₂). Case 1 applies if she always chooses L. Case 3 applies if she always chooses M. Case 2 applies if she is indifferent.

Absolute zero? Where the matter is considered at all, the rational choice literature commonly makes assumptions that instantiate case 2 (Fishburn and Rubinstein 1982). More often, as in section 2.5.1, it is simply taken for granted that Pandora behaves as though seeking to maximize the (discounted) sum of utilities derived from separate consequence spaces. I have used case 1 in defending the Nash bargaining solution, but this is quite unusual (Binmore 1984).

Without denying that all three cases may arise in different applications, I think that case 1 is the best candidate for a default assumption. To see why, suppose that C₁ is the set of consequences that appears in Pandora’s decision problem, and C₂ takes account of everything else. To deny case 1 is then to deny that the worst outcome ₂ in C₂ is so bad that its realization makes Pandora regard the distinctions between the consequences of C₁ as irrelevant. In Zeckhauser’s paradox, Pandora’s death eliminated her interest in money (section 3.1), but the bad event need not be so drastic. For example, if Pandora learns that Quentin is unfaithful, she may temporarily cease to care what lipstick she wears.

The point here is that if A = u(₁, ₂) = 0, then A + B = B 1. If it is also true that B = u(₁, ₂) = 1, then u(c₁, c₂) = u₂(c₂), so that Pandora doesn’t ever care what consequence is realized in C₁.⁵ If this extreme possibility is eliminated, then B < 1 and so we are left with case 1.

When case 1 applies, we have a reason for identifying an absolute zero on Pandora’s Von Neumann and Morgenstern utility scale. Since no temperature can fall below −273.15°C, scientists make this the zero temperature on the Kelvin scale, and say that 0°K is absolute zero. Similarly, no utility can fall below whatever Pandora gets when ₂ occurs, and so it is natural to use a Von Neumann and Morgenstern utility scale whose zero corresponds to this outcome.

3.7 Attitudes to Risk

Pandora must choose between:

1. an equal chance of getting either $4 or $36;

2. an equal chance of getting $9 or $25.

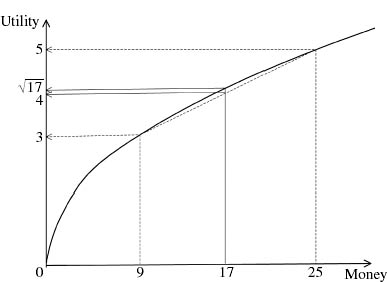
Pandora’s Von Neumann and Morgenstern utility for $x is , and so her expected utility for both lotteries is 4 utils, but she tells us that she plans to choose the second lottery because it has a smaller variance, and she is averse to taking risks.⁶

Pandora’s story is irrational, because a rational person is necessarily indifferent between two lotteries if their expected utilities are the same. We aren’t thereby denying that Pandora might be risk averse. Her risk aversion is built into the shape of her utility function (figure 3.9). In general, the Von Neumann and Morgenstern utility functions of risk-averse people are concave, and the Von Neumann and Morgenstern utility functions of risk-loving people are convex (figure 3.7).

Note that the degree of risk aversion a person reveals is a matter of personal preference in the Von Neumann and Morgenstern theory. Just as Pandora may or may not prefer Mozart to Wagner, so she may or may not prefer to spend $500 on insuring her house. Some philosophers insist to the contrary that rationality implies prudence, and it is prudent for Pandora to be risk averse. But such considerations go beyond the consistency requirements of the Von Neumann and Morgenstern theory.

Concavity. Concave functions have many pleasant properties. In particular, the slope of a concave function always decreases. The slope u′ (x) is Pandora’s marginal utility at x.⁷ So a risk-averse person has decreasing marginal utility (section 3.3).

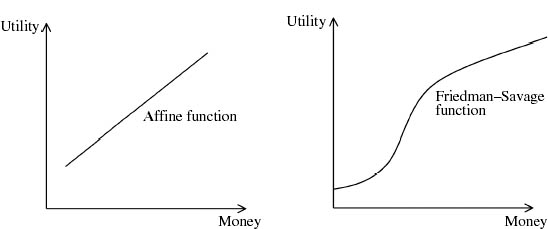
A function can be simultaneously concave and convex. Its graph is then a straight line. Mathematicians say that such a function is affine. If Pandora has an affine utility function, she is said to be risk neutral.

Figure 3.8 shows an affine utility function alongside a utility function that is neither concave nor convex. Friedman and Savage (1948) suggest that we can explain the behavior of people who insure their houses against fire but take their vacations in Las Vegas by attributing such a utility function to them. They are risk loving for small amounts and so bet in casinos. They are risk averse for large amounts and so also take out insurance.

Figure 3.7. Concave and convex functions. Chords drawn to a concave function lie on or below the graph. Chords drawn to a convex function lie on or above the graph.

Figure 3.8. More utility functions. An affine function has a straight-line graph. The Friedman–Savage function starts out being convex and then switches to being concave.

Risk aversion. Why are people with concave utility functions risk averse? The formal definition says that Pandora is risk averse if she always prefers the dollar average of any set of money prizes for certain to participating in a lottery in which she has an equal chance of ending up with each prize. In mathematics:

where L is a lottery with money prizes and u is Pandora’s Von Neumann and Morgenstern utility function. Figure 3.9 explains why this criterion holds if and only if u is concave.

Figure 3.9. Risk aversion. Pandora’s Von Neumann and Morgenstern utility for $x is . The expected utility of the lottery L in which Pandora has an equal chance of getting $9 or $25 is . Pandora therefore prefers getting 17 = (9 + 25)/2 dollars for sure to L because . Her utility function u therefore satisfies the requirement for risk aversion. The same argument goes through for any concave utility function u.

It is often useful in applications to know to what degree a person is risk averse. Economists use various coefficients of risk aversion for this purpose, which are explained very clearly by Hirshleifer and Riley (1992).

Maximin criterion. John Rawls (1972) argues that the maximin criterion corresponds to the case of extreme risk aversion, but this view is incompatible with the Von Neumann and Morgenstern theory.⁸

The maximin criterion says that Pandora should ignore everything about a lottery except the smallest prize that it offers with positive probability. She should then choose the lottery in her feasible set whose smallest prize is largest. For example, J should be chosen over K in figure 3.5 because J guarantees $1m, whereas there is a positive probability of getting nothing at all from K.

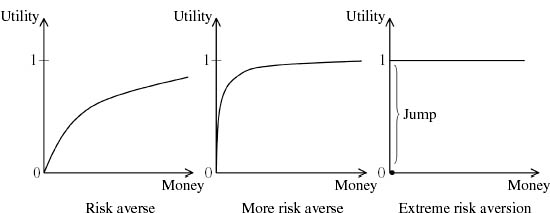
Figure 3.10 shows a sequence of Von Neumann and Morgenstern utility functions for Pandora as she becomes more and more risk averse. In the limiting case, she cares only about not ending up with nothing at all. She will therefore be indifferent between $2 for certain and an even chance of $1 or $100. But the maximin criterion says that she should choose the former.

Figure 3.10. Extreme risk aversion. The graphs show Pandora’s risk aversion increasing from left to right. In the extreme case, she is indifferent between all positive sums of money. She only cares about avoiding ending up with nothing at all.

The important point here isn’t so much that the maximin criterion doesn’t correspond to extreme risk aversion, but that it is incompatible with maximizing any kind of Von Neumann and Morgenstern utility function at all. It seems popular with some authors only because Von Neumann’s theory of two-person zero-sum games recommends its use. But who would want to play a game against nature as though it were a zero-sum game in which nature’s aim is to cause you as much damage as possible?

Risk neutrality. Pandora is risk neutral if she is always indifferent between having the dollar average of any set of money prizes for certain and participating in a lottery in which she has an equal chance of ending up with each prize. We then have equality in (3.4).

If Pandora is risk neutral, her Von Neumann and Morgenstern utility function can always be rescaled so that her utils can be identified with dollars. She therefore acts as though seeking to maximize her dollar profit. For example, insurance companies arguably behave as though they are risk neutral when insuring your house against fire. The reason is that they are also insuring very large numbers of other houses, and so the law of large numbers operates in their favor. If Pandora is risk averse, inequality (3.4) therefore explains why she can make a deal with an insurance company that profits both parties.

Suppose that Pandora’s house is worth $H and her other assets total $W. If the probability that the house burns down is r, then Pandora faces a lottery L in which she gets W + H dollars with probability 1 − r and W with probability r. Inequality (3.4) tells us that she prefers having W + H − rH dollars for certain to this lottery. So if the insurance company offers to insure her house for a premium not too much larger than P = rH dollars, Pandora will accept. However, P = rH dollars is the break-even premium for a risk-neutral insurance company.

3.7.1 Taste for Gambling?

Pandora is risk loving if she always prefers participating in a lottery in which she has an equal chance of ending up with any one of a set of money prizes to having the average of the prizes for certain. The inequality in (3.4) is then reversed.

It is often taken for granted that gambling can be explained as rational behavior on the part of a risk-loving agent. Friedman and Savage (1948), for example, offer this explanation when trying to reconcile the behavior of people who both gamble and buy insurance.

The mistake is easily made, because to speak of “attitudes to risk” is a positive invitation to regard the shape of Pandora’s Von Neumann and Morgenstern utility function u as embodying the thrill that she derives from the act of gambling. But if we fall into this error, we have no answer to the critics who ask why Von Neumann and Morgenstern utility functions should be thought to have any relevance to how Pandora chooses in riskless situations.

However, Von Neumann and Morgenstern’s fourth postulate takes for granted that Pandora is entirely neutral about the actual act of gambling. She doesn’t bet because she enjoys betting—she bets only when she judges that the odds are in her favor. If she liked or disliked the act of gambling itself, we would have no reason to assume that she is indifferent between a compound lottery and a simple lottery in which the prizes are available with the same probabilities. After all, it wouldn’t be much fun to walk into a casino and bet all your money on one turn of the wheel at roulette. Gamblers choose instead to lose their money in dribs and drabs in return for the thrill of winning now and again.

To be rational in the sense of Von Neumann and Morgenstern, Pandora needs to be as unemotional about gambling as a Presbyterian minister of the old school when he insures his church against fire. Quentin may bet at the racetrack because he enjoys the excitement of the race. Rupert may refuse even to buy insurance because he believes any kind of gambling whatever is evil. Neither satisfy the Von Neumann and Morgenstern postulates, because they each like or dislike gambling for its own sake.

It doesn’t follow that gambling for fun is necessarily irrational; only that the lotteries which give Pandora a thrill need to be excluded from those to which the Von Neumann and Morgenstern theory is applied. However, my guess is that most betting behavior is in fact irrational. Indeed, part of the reason that people enjoy gambling may be that they like the feeling of behaving irrationally now and again. I recall, for example, suggesting to a regular loser at a weekly poker game that he keep a record of his winnings and losses. His response was that he used to do so but had given up because it proved to be unlucky.

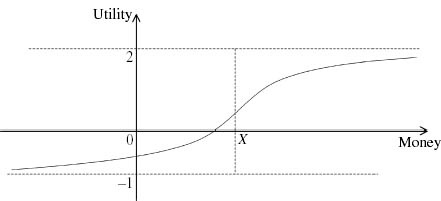
Figure 3.11. Bounded utility. This utility function is bounded above by 2 and below by −1. It is convex to the left of the point of inflexion X, and concave to the right.

3.8 Unbounded Utility?

The utility function drawn in figure 3.11 is bounded above by 2 and below by −1. The particular function drawn has a unique point of inflexion at X, and hence is concave to the right of X and convex to the left. It shares this property with the Friedman–Savage utility function of figure 3.8, but we have just seen that we aren’t entitled to use this fact to explain why people gamble. On the other hand, to the small extent that the choice behavior of laboratory subjects can be explained in terms of maximizing expected utility functions, the functions that fit the data do seem to have such a unique point of inflexion (Kahneman and Tversky 1979).

My version of the Von Neumann and Morgenstern theory necessarily generates bounded utility functions because each lottery considered must lie between a best outcome and a worst outcome . So what of the various examples involving money that we have been using? All of these involve unbounded utility functions.

Working with unbounded utility functions is unproblematic, provided we only do things that are sanctioned by Von Neumann and Morgenstern’s postulates. What this means in practice is that we don’t need to worry that a Von Neumann and Morgenstern utility function is unbounded if we only plan to consider lotteries whose expected utility is bounded. We can even allow lotteries with an infinite number of prizes if this constraint is observed.

What if we were to try to create a more glamorous theory in which we allow lotteries whose expected utility is infinite? Not only would we then be working outside the Von Neumann and Morgenstern theory, but we would have to face a whole morass of paradoxes.

Paradox of the infinite. Daniel Bernoulli’s idea that people will maximize the expected value of a concave utility function doesn’t make the St Petersburg paradox go away. Given any utility function u for money that is unbounded above, we can find a lottery with an infinite number of prizes whose expected utility is infinite.

To see why, simply replace the nth prize of $2ⁿ in the St Petersburg lottery of figure 3.2 by a dollar prize _n that is so large that (n = 1, 2, . . .). The expected utility of the resulting lottery is then

Swapping envelopes. The devil offers Pandora a choice between two identical sealed envelopes, one of which is known to contain twice as much money as the other. Pandora chooses one of the envelopes and finds that it contains $2n. So the other envelope contains either $n or $4n. Pandora computes its expected dollar value to be

If she is risk neutral, Pandora will therefore always want to swap whatever envelope she chose for the other envelope.

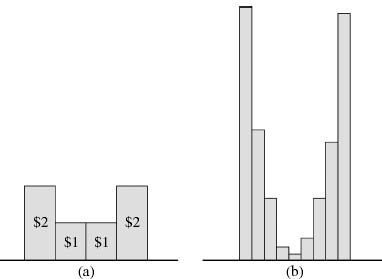
The swapping envelopes paradox isn’t so sharp as it may at first appear. There is nothing paradoxical about the fact that Pandora might prefer to swap whichever of two envelopes she opens first for the other. For example, Pandora might be offered two envelopes containing any adjacent pair of the prizes shown in figure 3.12(a). If she is offered the pair in the middle, then both envelopes will contain $1, and she will want to swap whichever she opens for the other because it might possibly contain $2 rather than $1.

The paradox therefore lies in the fact that Pandora will wish to swap whichever envelope she chooses from any pair of envelopes she might be offered. Figure 3.12(b) illustrates that the devil can make Pandora want to swap whichever of two envelopes she is offered, except in the case when the pair of envelopes lies at one of the two extremes of the range of possibilities. It doesn’t matter whether Pandora is risk neutral or not. Nor does it matter with what positive probability each pair of envelopes is offered. We only require that each prize has a neighbor to which Pandora assigns a large enough utility.

We can’t make this argument work for every prize in the finite case, because the two extremal prizes will always be exceptions. But if we allow an infinite number of prizes, we can eliminate the extremal cases altogether. If Pandora’s Von Neumann and Morgenstern utility function is unbounded above, the devil can put sums of money in each of the infinite number of envelopes so as to guarantee that each prize has a neighbor with a sufficiently larger utility that Pandora always wants to swap whatever envelope she opens.

Figure 3.12. Swapping envelopes. Each of a pair of adjacent prizes is concealed in an envelope. Pandora chooses one of the two envelopes. Each prize not lying at an extreme has a neighbor whose utility is sufficiently large that Pandora wants to swap envelopes if she finds a nonextremal prize in the envelope she chose. If Pandora’s utility function is unbounded, the extremes can be eliminated by allowing an infinite number of prizes.

A subplot is sometimes allowed to confuse the issue. In the original story, Pandora always assigns probability to the other envelope containing either $n or $4n. She is correct to do so only if the probability of each pair of envelopes that she might be offered is the same. But this can’t be true in the infinite case, because an infinity of equal positive numbers must sum to infinity, and probabilities of nonoverlapping events can never sum to more than one. However, to focus on this error in the standard formulation of the paradox is to miss its essential point.

Pascal’s wager. Infinite utilities are thought worthy of attention partly because of Pascal’s wager. In this attempt to apply decision theory to theology, Pandora can choose to follow the straight and narrow path of rectitude, or she can indulge her passions. If there is an afterlife, the ultimate reward for living a good life will be infinitely more important than anything that might happen on this earth. Pascal’s argument is therefore that Pandora ought to be good, even if she believes that the probability of an afterlife is very small.

It isn’t interesting to challenge the prejudices built into Pascal’s assumptions. Given his premises, the question is whether his argument is sound. The appearance of infinite magnitudes makes it clear that he can’t appeal to the version of the Von Neumann and Morgenstern theory presented here in arguing that it is rational for Pandora to maximize her expected utility. If we don’t allow infinite magnitudes, then all we learn is that it is rational for Pandora to be good if the probability of an afterlife isn’t too small.

But is living a good life enough? God is commonly thought to demand belief in His existence as well as observance of His laws. It is said that adopting the good habits of believers is likely to result in your coming to believe as well. But to start living a good life for this reason is to fall foul of Aesop’s principle.

3.9 Positive Applications?

Von Neumann and Morgenstern theory has been the subject of much debate in recent years. Are economists entitled to take for granted that the theory will predict the behavior of real people in risky situations? That is to say, is it safe to reinterpret the normative theory of Von Neumann and Morgenstern as a positive theory?

The chief exponents of the idea that it isn’t safe are the psychologists Kahneman and Tversky (1979). Their laboratory experiments and those of their followers seem to me a knockdown refutation of the claim that the Von Neumann and Morgenstern theory is usually a good predictor of how ordinary people behave. For example, the indifference curves of someone who honors the Von Neumann and Morgenstern theory should all be parallel straight lines, as in figure 3.13. But experimental data shows most people reveal indifference curves that are neither straight nor parallel.

Various behavioral theories have been proposed as alternatives to the Von Neumann and Morgenstern theory (Machina 2004). The best known of these is Kahneman and Tversky’s (1979) prospect theory. However, none of these rival theories are very successful in predicting the outcome of experiments whose results haven’t been used already in calibrating the theory.

In fact, at the time of writing, the combatants in the debate seem largely to have retired from the scene after two papers appeared back-to-back in the journal Econometrica offering data which suggests that all extant positive theories are bad predictors—but that the least bad theory is the Von Neumann and Morgenstern theory of expected utility! (See Camerer and Harless (1994) and Hey and Orme (1994); and also Schmidt and Neugebauer (2007).)

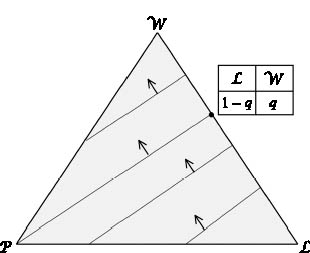
Figure 3.13. Rational indifference curves. Each point in the triangle represents a lottery with prizes , , and . The lottery it represents lies at the center of gravity of weights located at each prize that are equal to the probability with which the prize is available. For example, the lottery Q in which Pandora gets with probability 1 − q and with probability q lies on the line segment joining and . If , then Q is one third of the way down the line segment from . Pandora is indifferent between and the particular lottery Q shown in the figure. If we choose a Von Neumann and Morgenstern utility scale with u() = 0 and u() = 1, it follows that u() = q.

My own views on when one might reasonably expect a normative theory of behavior to predict successfully in positive applications are given in section 1.10. Enthusiasts who somehow manage to convince themselves that the Von Neumann and Morgenstern theory always applies in every positive context only succeed in providing ammunition for skeptics looking for an excuse to junk the theory altogether. It is an unwelcome truth that the best we can say of positive applications of the theory is that it doesn’t perform as badly overall as any of its behavioral rivals, but Aesop’s principle tells us that it should be irrelevant whether a truth is welcome or not.

¹ The story is good, but the paradox probably got its name for the more prosaic reason that Daniel Bernoulli published it in the Proceedings of the St Petersburg Academy of 1738. The brothers Daniel and Nicholas are only two of a whole family of mathematical Bernoullis.

² Recall that k = log₂ 2^k, and so Pandora’s expected utility is

³ Von Neumann and Morgenstern’s own exposition is best read as presented in the third edition (1953) of their book on pages 15–31.

⁴ Kahneman and Tversky (1979) think the example misleading on the grounds that matters are confused by the question of whether money has value for you after you are dead. However, the result would remain the same even if one were to distinguish different types of death depending on how much money you left for your heirs. The only necessary assumption would be that the Von Neumann and Morgenstern utilities of these different types of death not be too far apart.

⁵ When ₂ is hell and ₂ is heaven, who cares about the joys and sorrows of our earthly lives?

⁶ The variance of a lottery measures how far the money prizes deviate from their mean value.

⁷ When working with a continuous variable x, we assume that the units δx in which x is measured are so small that the extra utility Pandora gains from one extra unit of x is approximately u′ (x)δx.

⁸ Rawls’s intuition in favor of the maximin criterion is perhaps better captured by John Milnor’s (1954) theory of decisions under complete ignorance (section 9.1.1).