2
Game Theory
2.1 Introduction
Game theory is perhaps the most important arena for the application of rational decision theory. It is also a breeding ground for innumerable fallacies and paradoxes. However, this book isn’t the place to learn the subject, because I plan to say only enough to allow me to use a few examples here and there. My book Playing for Real is a fairly comprehensive introduction that isn’t mathematically demanding (Binmore 2007b).
2.2 What Is a Game?
A game arises when several players have to make decisions in a situation in which the outcome for each player is partly determined by the choices made by the other players. The states of the world that appear in Pandora’s decision problem must therefore include the end products of the reasoning processes of her opponents in the game. Sometimes people speak of strategic uncertainty in such a situation.
A one-person decision problem in which Pandora has no opponents is sometimes called a one-player game, or a game against nature. The traditional aim of a game-theoretic analysis is to deduce how players will choose when playing a game against each other from how they each individually play games against nature. The latter information is assumed to be sufficiently complete that it can be summarized in terms of utilities that are called payoffs when they appear in the context of a game.
Critics commonly assume that a payoff in a game must be measured in dollars, and so game theorists get included in the class of mean-minded, money-grubbing misfits who supposedly think that everybody is as selfish as they are themselves. However, game theory is no less a daughter of the theory of revealed preference than any other branch of decision theory. It is therefore entirely neutral about what motivates the players, provided only that their choice behavior is consistent.
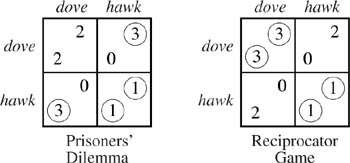
Figure 2.1. Paradox of rationality?
Nash equilibrium. Alice and Bob are using a Nash equilibrium in a two-player game if both choose a strategy that is a best reply to the strategy choice of the other (Nash 1951). There are two reasons why game theorists care about Nash equilibria.
The first reason is that a game theory book can’t authoritatively point to a pair of strategies (a, b) as the rational solution of a game unless it is a Nash equilibrium. Suppose, for example, that b weren’t a best reply to a. Bob would then reason that if Alice follows the book’s advice and plays a, then he would do better not to play b. But a book can’t be authoritative on what is rational if rational people don’t play as it predicts (Binmore 2007b, p. 17).
Since this book is about making rational decisions, it is the rationalist defense of Nash equilibria that will always be relevant when game theory examples are mentioned. However, a second reason for caring about Nash equilibria is that they can be used to characterize the end product of an interactive evolutionary process (section 1.6). The idea is very simple. If the payoffs in a game correspond to how fit the players are, then adjustment processes that favor the more fit at the expense of the less fit will stop working when we get to a Nash equilibrium, because all the survivors will then be as fit as it is possible to be in the circumstances.
2.3 Paradox of Rationality?
The Prisoners’ Dilemma is considered here as an example of how the payoffs in a game are determined by an appeal to the theory of revealed preference.
In the payoff table of figure 2.1, we assume that Alice must choose one of the rows labeled dove or hawk. Bob must simultaneously choose one of the columns labeled dove or hawk. The payoff that Alice receives is written in the southwest of each cell of the payoff table. Bob’s payoff is written in the northeast of each cell.
The Prisoners’ Dilemma is famous because it was once widely thought that it embodies the essence of the problem of human cooperation. It therefore seemed paradoxical that a rational analysis implies that both players will play hawk and so obtain a payoff of 1, when they could both play dove for a payoff of 2. Numerous fallacies purporting to show that it is rational to cooperate in the Prisoners’ Dilemma were therefore invented (Binmore 1994, chapter 3).
Game theorists think it plain wrong to claim that the Prisoners’ Dilemma is an appropriate setting within which to study the problem of human cooperation. On the contrary, it represents a situation in which the dice are as loaded against the emergence of cooperation as they could possibly be. If the game of life played by the human species resembled the Prisoners’ Dilemma, we wouldn’t have evolved as social animals!
Nor is there any paradox of rationality. Rational players don’t cooperate in the Prisoners’ Dilemma, because the conditions necessary for rational cooperation are absent. The following argument explains why game theorists are so emphatic in rejecting the idea that it might be rational to cooperate in the Prisoners’ Dilemma.
Revealed preference in the Prisoners’ Dilemma. So as not to beg any questions, we begin by asking where the payoff table that represents the players’ preferences in the Prisoners’ Dilemma comes from. The official answer is that we discover the players’ preferences by observing the choices they make (or would make) when solving one-person decision problems.
What would Alice choose in the one-person decision problem she would face if she knew in advance that Bob is sure to play dove in the Prisoners’ Dilemma? The circle in the southwest corner of the bottom-left cell of the payoff table indicates that we are given the information that she would then choose hawk. Similarly, the circle in the southwest corner of the bottom-right cell indicates that we are given the information that she would choose hawk if she knew in advance that Bob is sure to play hawk.
Writing a larger payoff for Alice in the bottom-left cell of the payoff table than in the top-left cell is just another way of registering that she would choose hawk if she knew that Bob were going to choose dove. Writing a larger payoff in the bottom-right cell is just another way of registering that she would choose hawk if she knew that Bob were going to choose hawk. If we want to retain a sense of paradox, we can also add the information that Alice would choose (dove, dove) over (hawk, hawk) if offered the opportunity. We must then ensure that Alice’s payoff in the top-left cell exceeds her payoff in the bottom-right cell.
The circled payoffs are said to indicate Alice’s best replies to Bob’s strategies. This language invites the Causal Utility Fallacy, but we must remember that Alice doesn’t choose hawk because she then gets a larger payoff. Alice assigns a larger payoff to (hawk, dove) than to (dove, dove) because she would choose the former if given the choice.
Game theory is needed because Alice has to choose her strategy in the Prisoners’ Dilemma without knowing in advance what strategy Bob is going to choose. To predict what she will then do, we need to assume that she is sufficiently rational that the choices she makes in the game are consistent with the choices she would make when solving the simple one-person decision problems we have considered.
The trivial consistency requirement we require is a simplified variant of the sure-thing principle that we shall meet in a later chapter (section 7.2). I call it the umbrella principle to honor Reinhard Selten, who is a famous game theorist with an even more famous golfing umbrella. He always carries it on rainy days, and he always carries it on sunny days. But will he carry it tomorrow? We don’t know whether tomorrow will be rainy or sunny, but the umbrella principle says that we don’t need to know, because we can count on his carrying the umbrella anyway.
In the Prisoners’ Dilemma, our data says that Alice will choose hawk if she learns that Bob is to play dove, and that she will also choose hawk if she learns that he is to play hawk. She thereby reveals that her choice doesn’t depend on what she knows about Bob’s choice. If her behavior is consistent with the umbrella principle, she will therefore play hawk whatever she guesses Bob’s choice will be.
In game theory, hawk is said to be a strongly dominant strategy for Alice. After circling best replies in a payoff table, it is easy to spot a strongly dominant strategy because only her payoffs in the corresponding row will be circled.
Collective rationality? The Prisoners’ Dilemma teaches the important lesson that rationality need not be good for a society. For example, everybody in a society of rational individuals can be made worse off if certain pieces of information become common knowledge. However, the response that we should therefore junk the orthodox theory in favor of some notion of collective rationality makes no sense. One might as well propose abandoning arithmetic because two loaves and seven fishes won’t feed a multitude.
Transparent dispositions? A common objection to the preceding analysis of the Prisoners’ Dilemma denies its premises. People say that Alice wouldn’t choose hawk if she knew that Bob were going to choose dove.
For example, Alice might choose dove if she knew that Bob were going to choose dove because she has a reciprocating disposition. If it is transparent to both players that they both have a reciprocating disposition, then we are faced with a game like the Reciprocator Game of figure 2.1. No strategy is now dominant. Instead, both the strategy pairs (dove, dove) and (hawk, hawk) are Nash equilibria, because they correspond to cells in which both payoffs are circled, which implies that both players are simultaneously making best replies to each other.
But the fact that (dove, dove) is a Nash equilibrium in the Reciprocator Game doesn’t imply that we have found a reason why it is rational to cooperate in the Prisoners’ Dilemma. We have only found a reason why it might be rational to cooperate in the Reciprocator Game.
Whether Alice would or wouldn’t choose hawk if she knew that Bob were going to choose dove is an empirical issue that is irrelevant to what is rational in the Prisoners’ Dilemma. If Alice wouldn’t choose hawk, she wouldn’t be playing the Prisoners’ Dilemma, but it would still be rational for her to play hawk if she were to play the Prisoners’ Dilemma.
2.3.1 Anything Goes?
Critics sometimes reject rational decision theory on the grounds that it is just a bunch of tautologies, which can be ignored because they fail to exclude any outcome whatever of the game being played. In making this criticism, they miss the point that rational decision theory is about means rather than ends. This isn’t to say that the players’ ends are unimportant; only that it isn’t part of rational decision theory to determine them.
Determining a player’s ends takes place outside the theory. For example, in the usual story that accompanies the Prisoners’ Dilemma, Alice and Bob are Chicago gangsters who are offered incentives by the District Attorney to fink on each other. Depending on who does or doesn’t fink, Alice and Bob will spend more or less time in jail. But rational choice theory can’t tell them how much they ought to value their honor as thieves in terms of years in jail, because this is an empirical question.
Empirical questions are settled by looking at the data. Since Chicago gangsters were apparently unscrupulous in seeking to avoid being jailed, we are led to model the problem faced by Alice and Bob in Chicago as the Prisoners’ Dilemma. Rational decision theory then says that the solution of their problem is for both to fink on the other by playing hawk. If Alice and Bob had been Mother Theresa and St Francis of Assisi, we would have been led to another game with a different solution.
2.4 Newcomb’s Problem
Rational decision theory is sometimes criticized because it is supposedly unable to deal with Newcomb’s problem. Rival decision theories have even been invented to accommodate the difficulties it is thought to create. It is relevant here because David Lewis (1979) argued that the Prisoners’ Dilemma reduces to two back-to-back Newcomb problems.
Newcomb’s problem involves two boxes that may have money inside. Pandora is free to take either the first box or both boxes. If she cares only for money, what choice should she make? This seems an easy problem. If dove represents taking only the first box and hawk represents taking both boxes, then Pandora should choose hawk, because this choice always results in her getting at least as much money as dove. That is to say, hawk dominates dove.
However, there is a catch. It is certain that there is one dollar bill in the second box. The first box may contain nothing or it may contain two dollar bills. The decision about whether to put money in the first box is made by Quentin, who knows Pandora so well that he can always make a perfect prediction of what she will do, whether or not she behaves rationally. Like Pandora, he has two choices, dove and hawk. His dove-like choice is to put two dollar bills in the first box. His hawkish choice is to put nothing in the first box. His motivation is to catch Pandora out. He therefore plays dove if and only if he predicts that Pandora will choose dove. He plays hawk if and only if he predicts that Pandora will choose hawk.
Pandora’s choice of hawk now doesn’t look so good. If she chooses hawk, Quentin predicts her choice and puts nothing in the first box, so that Pandora gets only the single dollar in the second box. If Pandora chooses dove, Quentin predicts her choice and puts two dollars in the first box. Pandora then gets two dollars, but is left regretting the dollar in the second box that she failed to pick.
Robert Nozick (1969) argues that Newcomb’s problem shows that maximizing your payoff can be consistent with using a strictly dominated strategy, but this obviously can’t be right. I think that we are led to this contradiction because the premises of the Newcomb problem are contradictory. Binmore (1994, p. 242) shows that it is simply impossible to write down a game in which
1. Pandora has a genuine choice;
2. Quentin predicts before Pandora chooses;
3. Quentin’s prediction is always accurate whatever Pandora may choose.
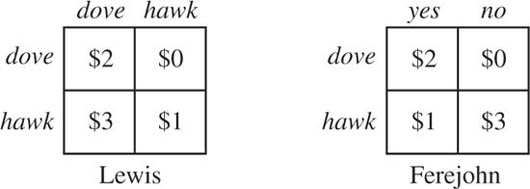
Figure 2.2. Newcomb’s problem? Lewis reduces Pandora’s problem to that of the row player in the Prisoners’ Dilemma. In so doing, he fails to capture the assumption in Newcomb’s problem that Quentin will predict her choice whether it is rational or not. Ferejohn makes the states of the world correspond to whether Quentin predicts Pandora’s choice correctly or not. In so doing, he violates Aesop’s principle.
For example, David Lewis’s claim that the Prisoners’ Dilemma is two back-to-back Newcomb problems fails to take into account that Quentin must predict Pandora’s choice even if she were to choose irrationally. However, going over this old ground would take us too far afield, and so I shall simply draw attention to two attempts to solve Newcomb’s problem that fail to honor Aesop’s principle.
Richard Jeffrey’s (1965) decision theory allows Pandora to count her own choice of action as evidence of the prediction that Quentin will make. In so doing, she fails to separate what is going on in her set A of actions from her beliefs in the set B of states of the world.
According to Steve Brams (1975), John Ferejohn suggests modeling the problem as in figure 2.2. In this model, the states of the world represent Quentin’s success in predicting Pandora’s choice. They are therefore labeled yes and no. If the probability that Quentin guesses correctly is sufficiently large, Pandora will then choose dove. However, Ferejohn’s model violates Aesop’s principle because the definitions of the states in B depend on what action is chosen in A.
2.5 Extensive Form of a Game
The payoff tables of figure 2.1 are strategic forms, in which the players are envisaged as choosing their strategies simultaneously. When the order of moves is important, a game is represented as an extensive form.
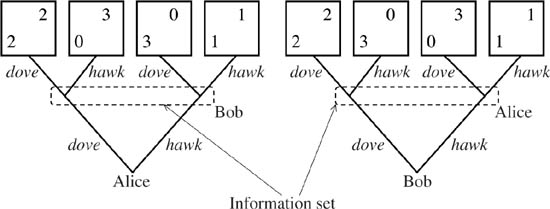
Figure 2.3 shows two versions of an extensive form for the Prisoners’ Dilemma. In both cases, the game is represented as a tree whose root corresponds to the opening move. Alice moves first in one case and Bob does so in the other. It doesn’t matter who is treated as moving first, because the information set enclosing the second player’s two possible moves indicates that he or she doesn’t know whether the first player chose dove or hawk at the first move.
Figure 2.3. An extensive form. The figure shows two extensive forms for the Prisoners’ Dilemma. In the left-hand case, Alice moves first. In the right-hand case, Bob moves first. It doesn’t matter who moves first, because the information set enclosing the second player’s two possible moves indicates that he or she doesn’t know whether the first player chose dove or hawk at the first move.
2.5.1 Backward Induction
To analyze a game by backward induction, one assumes that Nash equilibria will be played, not only in the game as a whole, but in all of its subgames. Starting with the smallest subgames, one then replaces each subgame by a pair of payoffs that would be obtained by playing a Nash equilibrium in that subgame if it were reached.
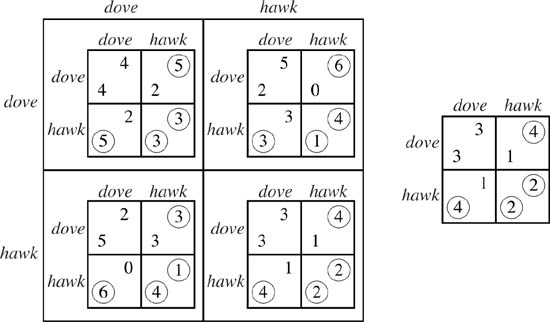
The method is illustrated in figure 2.4 for the Prisoner’s Dilemma of figure 2.1 played twice in succession. The repeated game has four subgames, consisting of four copies of the one-shot Prisoners’ Dilemma that might be reached at the second stage of the repeated game depending on how Alice and Bob play at the first stage. The four copies differ because their payoffs take account of how much Alice and Bob gained at the first stage. For example, if the strategy pair (dove, hawk) is played at the first stage, then a payoff of 3 is added to each of Bob’s payoffs at the second stage.
Since hawk dominates dove in each subgame, we replace each subgame by the payoff pair that is obtained when Alice and Bob both play hawk in the subgame. The result is the game on the right of figure 2.4, in which hawk again dominates dove. A backward induction analysis of the twice-repeated Prisoners’ Dilemma therefore predicts that each player will always play hawk.
2.5.2 Possible Worlds
The chief reason for introducing games in extensive form is to draw attention to the importance of the idea of possible worlds. This idea was introduced by Leibniz and taken up in modern times by David Lewis (1976), who entertained the delightful conceit that all possible worlds actually exist in some metaphysical sense.
Figure 2.4. Playing the Prisoners’ Dilemma twice. Alice and Bob’s final payoffs are the sum of the payoffs in the two games. There are four possible subgames that can result from the players’ strategy choices at the first stage of the repeated game. If the dominant strategy were played in each of these subgames, the result would be the game on the right, in which it is again a dominant strategy to play hawk. Backward induction in the finitely repeated Prisoners’ Dilemma therefore always calls for the play of hawk.
Possible worlds matter a great deal in game theory because they help Pandora make sense of subjunctive conditionals of the form,
What would happen if I were to do that?
Such conditionals frequently express counterfactuals. In particular, if a rational analysis persuades Pandora to take action a rather than action b, then she won’t take action b. But the reason that she takes action a is that she believes that if she were to take action b, she wouldn’t get a better payoff.
In the twice-repeated Prisoners’ Dilemma, there are four possible worlds that Alice and Bob need to consider. Each possible world corresponds to playing a copy of the Prisoners’ Dilemma at the second stage after experiencing one of the four possible ways the Prisoners’ Dilemma might be played at the first stage. The players need to predict what would happen if each of these possible worlds were to be reached.
In the case of the repeated Prisoners’ Dilemma, the prediction is easy because hawk strongly dominates dove and it is therefore optimal to play hawk whatever a player might believe about the other player’s plans. However, it is instructive for Alice if she observes Bob play dove at the first stage, because this tells her that Bob doesn’t always play rationally. So there is some chance that he will play irrationally in the future. In a game less simple than the twice-repeated Prisoners’ Dilemma, this information might well lead her to seek to exploit Bob’s perceived irrationality by deviating from Nash equilibrium play in some subgame—thereby subverting the logic of backward induction.
Bob Aumann (1995) argues that common knowledge of the players’ rationality nevertheless implies that the backward induction path will be followed in finite games of perfect information. To pursue this controversy would take us way off course, but the issue will be mentioned again briefly in section 8.5 when discussing how knowledge should be interpreted in games.