8

Epistemology

8.1 Knowledge

Philosophers traditionally treat knowledge as justified true belief, and then argue about what their definition means. This chapter contributes little to this debate, because it defends an entirely different way of thinking about knowledge. However, before describing the approach to knowledge that I think most useful in decision theory, it is necessary to review Bayesian epistemology—the study of how knowledge is treated in Bayesian decision theory.

8.2 Bayesian Epistemology

When Pandora uses Bayes’ rule to update her prior probability prob(E) of an event E to a posterior probability prob(E|F) on learning that the event F has occurred, everybody understands that we are taking for granted that she has received a signal that results in her knowing that F has occurred. For example, after Pandora sees a black raven in Hempel’s paradox, she deduces that the event F of figure 5.1 has occurred. However, when deciding what Pandora may reasonably be assumed to know after receiving a signal, Bayesians assume more than they often realize about how rational agents supposedly organize their knowledge.

This section therefore reviews what Bayesian decision theory implicitly assumes about what Pandora can or can’t know if she is to be regarded as consistent. The simple mathematics behind the discussion are omitted since they can be found in chapter 12 of my book Playing for Real (Binmore 2007b).

Knowledge operators. We specify what Pandora knows with a knowledge operator . The event E is the set of states of the world in which Pandora knows that the event E has occurred. So E is the event that Pandora knows E. Not knowing that something didn’t happen is equivalent to thinking it possible that it did happen. So the possibility operator is defined by E = ~ ~E (where ~F is the complement of F).

Figure 8.1. The knowledge operator. The five properties that characterize the knowledge operator are jointly equivalent to the five properties that characterize the possibility operator. Properties (K0) and (K3) are strictly redundant, because they can be deduced from the other knowledge properties. One can also replace ⊆ in (K3) and (K4) by =. If B is infinite, then (K1) needs to be modified to allow to commute with infinite intersections.

The properties of knowledge and possibility operators usually taken for granted in Bayesian decision theory are listed in figure 8.1 for a finite state space B.¹

Consistency and completeness. Property (K0) looks innocent, but it embodies a completeness assumption that Pandora may not always be willing to make. It says that she always knows the universe of discourse she is working in. But do we want to say that our current language will always be adequate to describe all future scientific discoveries? Are we comfortable in claiming that we have already conceived of all possibilities that we may think of in the future?

Property (K2) is a consistency assumption. It says that Pandora is infallible—she never knows something that isn’t true. But do we ever know what is really true? Even if we somehow hit upon the truth, how could we be sure we were right?

Both the completeness assumption and the consistency assumption are therefore open to philosophical doubt. But we shall find that matters are worse when we seek to apply them simultaneously in the kind of large world to which Bayesian decision theory doesn’t apply (section 8.4). The tension between completeness and consistency mentioned in section 7.3.1 then becomes so strong that one or the other has to be abandoned.

Knowing that you know. Thomas Hobbes must have been desperate to rescue a losing argument in 1654 when he asked René Descartes whether we really know that we know that we know that we know something. If Descartes had been a Bayesian, he would have replied that it is only necessary to iterate (K3) many times to ensure that someone who knows something knows that they know to any depth of knowing that we choose.

Not knowing that you don’t know. Donald Rumsfeld will probably be forgotten as one of the authors of the Iraq War by the time this book is published, but he deserves to go down in history for systematically considering all the ways of juxtaposing the operators and ~ at a news conference. When he got to ~ ~, he revealed that he was no Bayesian by failing to deduce from (K4) that ~ ~E = E.

The claim that we necessarily know any facts that we don’t know that we don’t know is hard to swallow. But the logic that supports ~ ~E = E in a small world is inescapable. Pandora doesn’t know that she doesn’t know that she has been dealt the Queen of Hearts. But she would know she hadn’t been dealt the Queen of Hearts if she had been dealt some other card. She therefore knows that she wasn’t dealt some other card. So she knows she was dealt the Queen of Hearts.

All things considered. The preceding discussion makes it clear that Bayesian epistemology only makes good sense when Pandora has carefully thought through all the logical implications of all the data at her disposal. Philosophers sometimes express this assumption of omniscience by saying Pandora’s decisions are only taken after “all things have been considered.”

However, Donald Rumsfeld was right to doubt that all things can be considered in a large world. In a large world, some bridges can only be crossed when you come to them. Only in a small world, in which you can always look before you leap, is it possible to consider everything that might be relevant to the decisions you take.

8.3 Information Sets

How does Pandora come to know things? In Bayesian epistemology, Pandora can only know something if it is implied by a truism, which is an event that can’t occur without Pandora knowing it has occurred.

The idea is more powerful in the case of common knowledge, which is the knowledge that groups of people hold in common. The common knowledge operator satisfies all the properties listed in figure 8.1, and so nothing can be common knowledge unless it is implied by a public event—which is an event that can’t occur without it becoming common knowledge that it has occurred. Public events are therefore rare. They happen only when we all observe each other observing the same occurrence.

Possibility sets. The smallest truism P(s) containing a state s of the world is called a possibility set. The event P(s) consists of all the states t that Pandora thinks are possible when the actual state of the world is s. So if s occurs, the events that Pandora knows have occurred consist of P(s) and all its supersets.

The assumptions of Bayesian epistemology can be neatly expressed in terms of possibility sets. It is in this form that they are commonly learned by Bayesians—who are sometimes a little surprised to discover that they are equivalent to (K0)-(K4). The equivalence is established by defining and P in terms of each other using the formula

The formulation of Bayesian epistemology in terms of possibility sets requires only two assumptions:

(Q1) Pandora never thinks the true state is impossible;

(Q2) Pandora’s possibility sets partition the state space B.

The requirement (Q1) is the infallibility or consistency requirement that we met as (K2) in section 8.2. It says that s always lies in P(s). To partition B is to break it down into a collection of subsets so that each state in B belongs to one and only one subset in the collection (section 5.2.1). Given (Q1), the requirement (Q2) therefore reduces to demanding that P(s) and P(t) either have no states in common or else are different names for the same set.

One can think of Pandora’s possibility sets as partitioning her universe of discourse into units of knowledge. When the true state is determined, Pandora necessarily learns that one and only one of these units of knowledge has occurred. Everything else she knows can then be deduced from this fact.

8.3.1 Applications to Game Theory

A case can be made for crediting John Von Neumann with the discovery of Bayesian epistemology. The information sets he introduced into game theory are versions of possibility sets modified to allow updating over time to be carried out conveniently. When first reading Von Neumann and Morgenstern’s (1944) Theory of Games and Economic Behavior, I recall being astonished that so many problems with time and information could be handled with such a simple and flexible formalism.

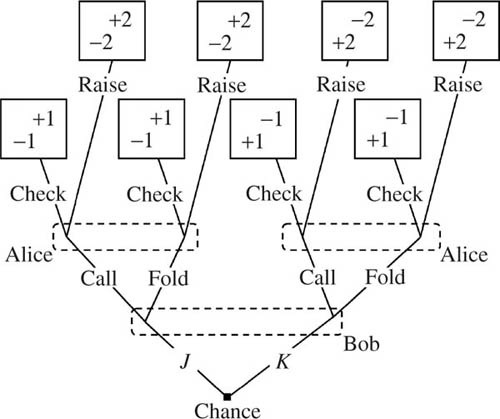
Figure 8.2. Mini-Poker. Alice is dealt a Jack or a King with equal probability. She sees her card but Bob doesn’t. Everybody knows that Bob has been dealt a Queen. The left-hand game tree shows the betting rules. Bob only gets to act if Alice raises. He then knows that Alice has raised, but not whether she holds a Jack or a King. This information is represented by the information set labeled Q. Bob knows he is at one of the two nodes in Q, but not whether he is at the left node or the right node. It is always optimal for Alice to raise when dealt a King, and so this choice has been thickened in the left-hand game tree to indicate that Bob believes that she will raise with probability one when holding a King. If Bob knew that she never checks when holding the King, this fact would be indicated as in the right-hand game tree by omitting this possibility from the model.

Mini-Poker. Translating Von Neumann’s formalism into the official language of epistemic logic is nearly always a very bad idea when trying to solve a game, since epistemic logic isn’t designed for practical problem-solving. However, this section goes some way down this road for the game of Mini-Poker, whose rules are illustrated in figure 8.2.²

All poker games begin with the players contributing a fixed sum of money to the pot. In Mini-Poker, Alice and Bob each contribute one dollar. Bob is then dealt a Queen face up. Alice is then dealt either a Jack or a King face down. Alice may then check or raise one dollar. If she checks, the game is over. Both players show their cards, and whoever has the higher card takes the pot. If Alice raises, Bob may call or fold. If he folds, Alice takes the pot regardless of who has the better card. If Bob calls, he must join Alice in putting an extra dollar in the pot. Both players then show their cards, and whoever has the higher card takes the pot.

The most significant feature of the rules of the game illustrated in figure 8.2 is the information set labeled Q. If this information set is reached, then Bob knows he is at one of the two decision nodes in Q, but not whether he is at the left node or the right node. The fact that he knows Q has been reached corresponds to his knowing that Alice has raised the pot. The fact that he doesn’t know which node in Q has been reached corresponds to his not knowing whether Alice has been dealt a Jack or a King.

How should Alice and Bob play if the Jack or the King is dealt with equal probability and both players are risk neutral?³ Alice should always raise when holding the King. When holding the Jack she should raise with probability . (Some bluffing is necessary, because Bob would always fold if Alice never raised when holding a Jack.) Bob should keep Alice honest by calling with probability .

It would be too painful to deduce this result using the formal language of possibility sets, but it isn’t so hard to check that Bob is indifferent between calling and folding if Alice plays according to the game-theoretic solution. (If he weren’t indifferent, the solution would be wrong, since it can never be optimal for Bob to sometimes play one strategy and sometimes another if he believes one of them is strictly better than the other.)

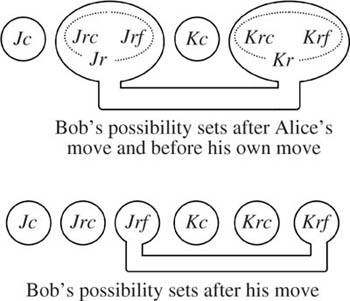
Bob’s possibility sets. In principle, the states of the world in a game are all possible paths through the tree. In Mini-Poker, there are six such plays of the game, which can be labeled Jc, Jrc, Jrf, Kc, Krc, and Krf. For example, Krf is the play in which Alice is dealt a King and raises, whereupon Bob folds.

As the game proceeds, Alice and Bob update their knowledge partitions as they learn things about what has happened in the game so far. For example, figure 8.3 shows Bob’s possibility sets after Alice’s move, both before and after he makes his own move. (If he folds, Alice won’t show him what she was dealt, because only novices reveal whether or not they were bluffing in such situations.)

Bayesian updating. Bob believes that Alice is dealt a Jack or a King with probability . He also believes that Alice will play according to the recommendations of game theory and so raise with probability . His prior probabilities for the events Jc, Jr, Kc, Kr in figure 8.3 are therefore

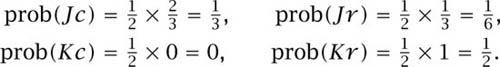
Figure 8.3. Possibility sets for Bob in Mini-Poker. When Bob observes Alice raise the pot, he knows that the outcome of the game will be one of the four plays Jrc, Jrf, Krc, Krf. He will himself determine whether he calls or folds, and so he is only interested in the conditional probability of the events that Alice was dealt a Jack or a King given that he has observed her raise the pot. These are the events Jr = {Jrc, Jrf} and Kr = {Krc, Krf}.

After Bob learns that Alice has raised, his possibility set becomes F = {Jr, Kr}. His probabilities for the events Jr and Kr have to be updated to take account of this information. Applying Kolmogorov’s definition of a conditional probability (5.4), we find that Bob’s posterior probabilities are

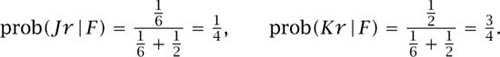
Bob’s expected payoff if he calls a raise by Alice is therefore × 2 + × (−2) = −1, which is the same payoff he gets from folding. He is therefore indifferent between the two actions.

Perfect recall. Von Neumann overlooked the need that sometimes arises to insist that rational players never forget any information. However, the deficiency was made up by Harold Kuhn (1953).

Kuhn’s requirement of perfect recall is particularly easy to express in terms of possibility sets. One simply requires that any new information that Pandora receives results in a refinement of her knowledge partition—which means that each of her new possibility sets is always a subset of one of her previous possibility sets. Mini-Poker provides an example. In figure 8.3, Bob’s later knowledge partition is a refinement of his earlier knowledge partition.

There is a continuing debate on how to cope with decision problems with imperfect recall that centers around the Absent-Minded Driver’s problem. Terence must make two right turns to get to his destination.⁴ He gets to a turning but can’t remember whether he has already taken a right turn or not. What should he do?

Most attempts to answer the question take Bayesian decision theory for granted. But if Terence satisfies the omniscience requirement how could he have imperfect recall? Worse still, his possibility sets overlap, in flagrant contradiction of (Q2).

Knowledge versus belief. I think there is a strong case for distinguishing between knowledge and belief with probability one (section 8.5.2).

Mini-Poker again provides an example. In the left-hand game tree of figure 8.2, the branch of the tree that represents Alice’s choice of raising after being dealt a King has been thickened to indicate that the players believe that, in equilibrium, she will take this action with probability one. In the right-hand game tree, her alternative choice of checking has been deleted to indicate that the players know from the outset that she will raise when holding a King.

The difference lies in the reason that the players act as though they are sure that Alice will raise when holding the King. In the knowledge case, she raises when holding a King in all possible worlds that are consistent with the model represented by the right-hand game tree. These possible worlds are all the available strategy profiles. Since the model rules out the possibility that Alice will check when holding a King, it is impossible that a rational analysis will predict that she will. In the belief case represented by the left-hand game tree, the set of all strategy profiles includes possibilities in which Alice checks when holding a King, but a rational analysis predicts that she won’t actually do so.

In brief, when we know that Alice won’t check, we don’t consider the possibility that she might. When we don’t know that she won’t check, we consider the possibility that she might, but end up believing that she won’t.

Alternative models. We don’t need possibility sets to see that Alice is indifferent between checking and raising in Mini-Poker when holding a Jack. Bob plans to call a raise with probability , and so Alice’s expected payoff from raising is , which is the same as she gets from checking.

How would we obtain the same result using the apparatus of possibility sets? If we want to copy the method we employed for Bob, we can appeal to the new game tree for Mini-Poker shown in figure 8.4. In this formulation of the game, Bob decides whether to call or fold if Alice raises before she does anything at all. It doesn’t matter when Bob makes this decision, as long as Alice doesn’t discover what he has decided to do until after she makes her own decision.

Figure 8.4. A different model for Mini-Poker. Bob decides in advance of Alice’s move whether to call or fold if she raises. It doesn’t matter when Bob makes this decision, as long as Alice doesn’t discover what he has decided until after she makes her own decision.

When we ask how Alice’s possibility sets evolve as the game proceeds, we now find that she has to consider a different state space than Bob, since our new model for Mini-Poker has eight possible plays instead of six. However, I won’t pursue the analysis further because the point I want to make is already on the table.

If we were better disciplined, we would continually remind ourselves that everything we say is always relative to some model. When we forget to do so, we risk treating the underlying model as though it were set in concrete.

The game of Mini-Poker is only one of many examples that show that many alternative models are usually available. Much of the art of successful problem-solving lies in choosing a model from all these alternatives that is easy to analyze. It is for this reason that chapter 1 goes on at length about the advantages of formulating a model that satisfies Aesop’s principle so that we can validly apply orthodox decision theory.

Metaphysicians prefer to think of their formalisms as attempts to represent the one-and-only true model, but I think such inflexible thinking is a major handicap in the kinds of problems that arise in ordinary life (section 8.5).

8.4 Knowledge in a Large World

Bayesian epistemology makes perfectly good sense in a small enough world, but we don’t need to expand our horizons very far before we find ourselves in a large world. As soon as we seek to predict the behavior of other human beings, we should begin to be suspicious of discussions that take Bayesian decision theory for granted. After all, if Bob is as complex as Alice, it is impossible for her to create a model of the world that incorporates a model of Bob that is adequate for all purposes. Worse still, the kind of game-theoretic arguments that begin:

If I think that he thinks that I think . . .

require that she contemplates models of the world that incorporate models of herself.

This section seeks to discredit the use of Bayesian epistemology in worlds in which such self-reference can’t be avoided. I don’t argue that it is only in such worlds that Bayesian epistemology is inappropriate. In most situations to which Bayesian decision theory is thoughtlessly applied—such as financial economics—the underlying world is so immensely large that nobody could possibly disagree with Savage that it is “utterly ridiculous” to imagine applying his massaging process to generate consistent beliefs (section 7.5.1). However, in worlds where self-reference is intrinsic, a knockdown argument against Bayesian epistemology is available.

I have to apologize to audiences at various seminars for claiming credit for this argument, but I only learned recently from Johan van Bentham that Kaplan and Montague (1960) proved a similar result more than forty years ago.

A possibility machine. How do rational people come to know things? What is the process of justification that philosophers have traditionally thought turns belief into knowledge? A fully satisfactory answer to this question would describe the process as an algorithm, in the manner first envisaged by Leibniz.

A modern Leibniz engine would not be a mechanical device of springs and cogs, but the program for a computer. We need not worry about what kind of computer or in what language the program is written. According to the Church–Turing hypothesis, all possible computations can be carried through on a highly simplified computer called a Turing machine.

Consider a hypothetical Leibniz engine L that may depend on whatever the true state of the world happens to be. The engine L decides what events Pandora will regard as possible under all possible circumstances. For each event E, it therefore determines the event E.

In this setup, we show that (P0) and (P2) are incompatible (figure 8.1). It follows that the same is true of (K0) and (K2). As Gödel showed for provability in arithmetic, we therefore can’t hang on to both completeness and consistency in a large enough world when knowledge is algorithmic.

The Turing halting problem. We first need to be precise about how L decides possibility questions. It is assumed that L sometimes answers NO when asked suitably coded questions that begin:

Is it possible that . . . ?

Issues of timing are obviously relevant here. How long should Pandora wait for an answer? Such timing problems are idealized away by assuming that she can wait for ever. If L never says NO, she regards it as possible that the answer is YES.

As in the Turing halting problem, we suppose that [N] is the code for some question about the Turing machine N. We then take {M} to be code for:

Is it possible that M answers NO to [M]?

Let T be the Turing machine that outputs {x} on receiving the input [x]. Now employ the Turing machine I = LT that first runs an input through T, and then runs the output of T through the Leibniz engine L. Then the Turing machine I responds to [M] as L responds to {M}.

An event E is now defined to be the set of states in which I responds to [I] with NO. We then have the following equivalences:

It follows from (P2) that , which implies E = B. Thus, , and so . But (P0) says that .

What is the moral? If the states in B are sufficiently widely construed and knowledge is algorithmic, then another way of reporting the preceding result is that we can’t retain the infallibility assumption (K2) without abandoning (K0).

But we can’t just throw away (K0) without also throwing away either (K1) or (K4).⁵ It is unthinkable to abandon (K1), and so (K4) must go along with (K0). But (K4) is the property that bears the brunt of the requirement that all things have been considered in Pandora’s world.

8.4.1 Algorithmic Properties?

The preceding impossibility result not only forces us to abandon either , it also tells us that implies that . One can translate this property into the assertion that Pandora never knows in what world she is operating. But what does this mean in practice?

One way of interpreting the result is to rethink what is involved in saying that an event E has occurred. The standard view is that E is said to occur if the true state s of the world has whatever property defines E. But how do we determine whether s has the necessary property?

If we are committed to an algorithmic approach, we need an algorithmic procedure for the defining property P of each event E. This procedure can then be used to interrogate s with a view to getting a YES or NO answer to the question:

Does s have property P?

We can then say that E has occurred when we get the answer YES and that ~E has occurred when we get the answer NO.

But in a sufficiently large world, there will necessarily be properties for which the relevant algorithm sometimes won’t stop and give an answer, but will rattle on forever. Our methodology will then fail to classify s as belonging to either E or ~E. We won’t then be able to implement Ken Arrow’s (1971, p. 45) ideal recipe for a state of the world—which requires that it be described so completely that, if true and known, the consequences of every action would be known (section 1.2).

In decision theory, we are particularly interested in questions like:

Is prob(s) p?

Our algorithmic procedure might say YES for values of and NO for values of but leave the question open for intermediate values of p. So we have another reason for assessing events in large worlds in terms of upper and lower probabilities.

8.4.2 Updating

We have just explored the implications of holding on to the infallibility or consistency requirement (K2). However, my attempt in section 9.2 to extend Bayesian decision theory to a minimal set of large worlds doesn’t take this line. I hold on instead to the completeness requirement (K0).

To see why, consider what happens when Pandora replaces her belief space B by a new belief space F after receiving some information. In Bayesian decision theory, we take for granted that so that F is a truism in her new situation (section 8.3). If we didn’t, it would take some fancy footwork to make sense of what is going on when we update prob(E) to prob(E|F). In section 9.2, I therefore assume that Pandora never has to condition on events F that aren’t truisms. To retain Bayes’ rule, I go even further by insisting that any such F is measurable, and so can be assigned a unique probability.

For example, rational players in game theory are assumed to know that their opponents are also rational (section 8.5.3). As long as everybody behaves rationally and so play follows an equilibrium path, no inconsistency in what the players regard as known can occur. But rational players stay on the equilibrium path because of what would happen if they were to deviate. In the counterfactual world that would be created by such a deviation, the players would have to live with the fact that their knowledge that nobody will play irrationally has proved fallible. The more general case I consider in section 9.2 has the same character. It is only in counterfactual worlds that anything unorthodox is allowed—but it is what would happen if such counterfactual worlds were reached which ensures that they aren’t reached.

8.5 Revealed Knowledge?

What are the implications of abandoning consistency (K2) in favor of completeness (K0)? If we were talking about knowledge of some absolute conception of truth, then I imagine everybody would agree that (K2) must be sacrosanct. But I plan to argue that absolute truth—whatever that may be—is irrelevant to rational decision theory. We can’t dispense with some Tarskian notion of truth relative to a model, but as long as we don’t get above ourselves by imagining we have some handle on the problem of scientific induction, then that seems to be all we need.

8.5.1 Jesting Pilate

Pontius Pilate has been vilified down the ages for asking:

What is truth?

His crime was to jest about a matter too serious for philosophical jokes. But is the answer to his question so obvious? Xenophanes didn’t think so:

But as for certain truth, no man knows it,
And even if by chance he were to utter
The final truth, he would himself not know it;
For all is but a woven web of guesses.

Sir Arthur Eddington put the same point more strongly: “Not only is the universe stranger than we imagine, it is stranger than we can imagine.” J. B. S. Haldane said the same thing in almost the same words. I too doubt whether human beings have the capacity to formulate a language adequate to describe whatever the ultimate reality may be by labeling some of its sentences as true and others as false. Some philosophers are scornful of such skepticism (Maxwell 1998). More commonly, they deny Quine’s (1976) view that truth must be relative to a language. But how can any arguments they offer fail to beg the relevant questions?

In the absence of an ultimate model of possible realities, we make do in practice with a bunch of gimcrack models that everybody agrees are inadequate. We say that sentences within these models are true or false, even though we usually know that the entities between which relationships are asserted are mere fictions. As in quantum physics, we often tolerate models that are mutually contradictory because they seem to offer different insights in different contexts.

The game we play with the notion of truth when manipulating such models isn’t at all satisfactory, but it seems to me the only genuine game in town. I therefore seek guidance in how to model knowledge and truth from the way these notions are actually used when making scientific decisions in real life, rather than appealing to metaphysical fancies of doubtful practicality.

8.5.2 Knowledge as Commitment to a Model

Bayesian decision theory attributes preferences and beliefs to Pandora on the basis of her choice behavior. We misleadingly say that her preferences and her beliefs are revealed by her choice behavior, as though we had reason to suppose her choices were really caused by preferences and beliefs. Perhaps Pandora actually does have preferences and beliefs, but all the theory of revealed preference entitles us to say is that Pandora makes decisions as though she were maximizing an expected utility function relative to a subjective probability measure.

Without denying that other interpretations may be more useful in other contexts, I advocate taking a similar revealed-preference approach to knowledge in the context of decision theory. The result represents a radical departure from the orthodox view of knowledge as justified true belief. With the new interpretation, knowledge need neither be justified nor true in the sense usually attributed to these terms. It won’t even be classified as a particular kind of belief.

Revealed knowledge. Instead of asking whether Pandora actually does know truths about the nature of the universe, I suggest that we ask instead what choice behavior on her part would lead us to regard her acting as though she knew some fact within her basic model.

To behave as though you know something is to act as though it were true. But we don’t update truths like beliefs. If Pandora once knew that a proposition is true, we wouldn’t allow her to say that she now knows that the same proposition is false without admitting that she was mistaken when she previously said the proposition was true. I therefore suggest saying that Pandora reveals that she knows something if she acts as though it were true in all possible worlds generated by her model.

In game theory, for example, the rules of a game are always taken to be common knowledge among the players (unless something is said to the contrary). The understanding is that, whatever the future behavior of the players, the rules will never be questioned. If Alice moves a bishop like a knight, we don’t attempt to explain her maneuver by touting the possibility that we have misunderstood the rules of chess; we say that she cheated or made a mistake. In Bayesian decision theory, Pandora is similarly regarded as knowing the structure D: A × B → C of her decision problem because she never varies this structure when considering the various possible worlds that may arise as a result of her choice of an action in A.

I think this attitude to knowledge is actually the de facto norm in scientific enquiry. Do electrons “really” exist? Physicists seem utterly uninterested in such metaphysical questions. Even when you are asked to “explain your ontology,” nobody expects a disquisition on the ultimate nature of reality. You are simply being invited to clarify the working hypotheses built into your model.

Necessity. Philosophers say something is necessary if it is true in all possible worlds. The necessity operator and the corresponding possibility operator are then sometimes deemed to satisfy the requirements of figure 8.1. When knowledge is interpreted as commitment to a model, such arguments can be transferred immediately to the knowledge operator. However, there is a kick in the tail, because the arguments we have offered against assuming both (K0) and (K2) in a large world also militate against the same properties being attributed to the necessity operator.

Updating parameters. Bayesianism casts Bayes’ rule in a leading role. But my separation of knowledge from belief allows Bayesian updating to be viewed simply as a humdrum updating of Pandora’s beliefs about the parameters of a model whose structure she treats as known.

From this perspective, Bayesian updating has little or nothing to do with the problem of scientific induction. The kind of scientific revolution that Karl Popper (1959) studied arises when the data no longer allows Pandora to maintain her commitment to a particular model. She therefore throws away her old model and adopts a new model—freely admitting as she does so that she is being inconsistent.

It seems to me that the manner in which human beings manage this trick remains as much a mystery now as when David Hume first exposed the problem. There are Bayesians who imagine that prior probabilities could be assigned to all possible models of the universe, but this extreme form of Bayesianism has lost all contact with the reasons that Savage gave for restricting the application of his theory to small worlds. An even more extreme form of Bayesianism holds that scientists actually do use some form of Bayesian updating when revising a theory—but that they are unconscious of doing so. This latter notion has been put to me with great urgency on several occasions, but you might as well seek to persuade me that fairies live at the bottom of my garden.

Belief with probability one. How is belief with probability one to be distinguished from knowledge? On this subject, I share the views of Bayesians who insist that one should never allow subjective probabilities to go all the way to zero or one. Otherwise any attempt by Pandora to massage her system of beliefs into consistency would fail when she found herself trying to condition on a zero-probability event. This isn’t to say that models in which events with extreme probabilities appear may not often be useful, but they should be regarded as limiting cases of models in which extreme probabilities don’t appear (section 5.5.1).

8.5.3 Common Knowledge of Rationality

I want to conclude this chapter by returning to the issue of whether common knowledge of rationality implies backward induction (section 2.5.1). I have disputed this claim with Robert Aumann (Binmore 1996, 1997), but my arguments were based on the orthodox idea that we should treat common knowledge as the limiting case of common belief. In such a conceptual framework, Bob would find it necessary to update his belief about the probability that Alice will behave irrationally in the future if he finds that she has behaved irrationally in the past.

However, if knowledge is understood as being impervious to revision within a particular model (as I recommend in this section), then it becomes trivially true that common knowledge of rationality implies backward induction. No history of play can disturb the initial assumption that there is common knowledge of rationality, because knowledge isn’t subject to revision. In predicting the behavior of the players in any subgame, we can therefore count on this hypothesis being available. It may be that some of these subgames couldn’t be reached without Alice repeatedly choosing actions that game theorists would classify as irrational, but if Bob knows that Alice is rational, her history of irrational behavior is irrelevant. He will continue to act as though it were true that she is rational in all possible worlds that may arise.

¹ They are equivalent to the properties attributed to the operators □ and ◊ by the modal logic S-5. It is usual in epistemic logic to write the requirements for S-5 differently. They are standardly written in terms of propositions (rather than events) and include the assumption that (Hintikka 1962).

² Mini-Poker is a simplification of a version of poker analyzed in Binmore (2007b, chapter 15) in which Alice and Bob are each dealt one card from a shuffled deck containing only the King, Queen, and Jack of Hearts. This game is itself a simplification of Von Neumann’s (1944) second model of poker in which Alice and Bob are each dealt a real number between 0 and 1.

³ We solve such problems by computing Nash equilibria. Since Mini-Poker is a two-person zero-sum game, this is the same as finding the players’ maximin strategies.

⁴ Terence Gorman was the most absent-minded professor the world has ever seen.

⁵ It follows from (K1) that implies . In particular, , and so . Thus . Therefore, by (K4). It is similarly easy to deduce (K3): .