This chapter introduces the concepts of a tuple, a table, and a database predicate (using the meaning of predicate that was established in Chapter 1). You can use tuple, table, and database predicates to describe the data integrity constraints of a database design. The goal of this chapter is to establish these three different classes of predicates—which jointly we’ll refer to as data integrity predicates—and to give ample examples of predicates within each class.

A data integrity predicate deals with data. We classify data integrity predicates into three classes by looking at the scope of data that they deal with. In increasing scope, a predicate can deal with a tuple, a table, or a database state.

The section “Tuple Predicates” establishes the concept of a tuple predicate. This type of data integrity predicate has a single parameter of type tuple. You can use it to accept or reject a tuple (loosely speaking, a set of attribute values).

The next section, “Table Predicates,” will introduce you to table predicates. A table predicate deals with a table, and consequently has a single parameter of type table. We’ll use them to accept or reject a table (a set of tuples).

We familiarize you with the concept of database predicates in the section “Database Predicates.” Database predicates deal with database states. We’ll use them to accept or reject a database state (loosely speaking, a set of tables).

The section “Common Patterns of Table and Database Predicates” will explore five data integrity predicate patterns that often play a role in a database design: unique identification, subset requirement, specialization, generalization, and tuple-in-join predicates.

In a database design you always (rare cases excluded) encounter data integrity constraints that are based on unique identification and subset requirement predicates. You’ll probably identify these two predicate patterns with the relational concepts of unique and foreign key constraints, respectively. The specialization and generalization predicate patterns will probably remind you of the ERD concepts of a subtype and a supertype. The tuple-in-join predicate pattern involves a join between two or more tables, and is at the basis of a type of constraint that is also often encountered in database designs.

As usual, you’ll find a “Chapter Summary” at the end, followed by an “Exercises” section.

Tuple Predicates

Let’s explain right away what a tuple predicate is and then quickly demonstrate this concept with a few examples. A tuple predicate is a predicate with one parameter. This parameter is of type tuple. Listing 6-1 displays a few examples of tuple predicates.

Predicate P0 states that the sex attribute value of a tuple should be 'male' or 'female'. Predicate P1 states that if the price (attribute) value of a tuple is greater than or equal to 20, then the instock (attribute) value should be 10 or less. P2 states that the status value is either F or it is I, but then at the same time the total value should be greater than 0. Predicate P3 states that salary should be less then 5000 or sex is female. Finally, predicate P4 states that the begindate value should be less than enddate.

We’ll use a tuple predicate (in Chapter 7) to accept or reject a given tuple. If the predicate—when instantiated with a given tuple as the argument—turns into a FALSE proposition, then we will reject the tuple; otherwise, we will accept it. In the latter case, we say that the given tuple satisfies the predicate. In the former case, the tuple violates the predicate.

Again, let’s demonstrate this with a few example tuples (see Listing 6-2).

Instantiating predicate P0 with tuple t5—rendering expression P0(t5)—results in the proposition 'male'∈{'male', 'female'}, which is a TRUE proposition, and we say that t5 satisfies P0. Instantiating predicate P1 with tuple t1—expression P1(t1)—results in the proposition 30 ≥ 20 ⇒ 4 ≤ 10. This is also a TRUE proposition; therefore t1 satisfies P1. Check for yourself that the following propositions are TRUE propositions: P0(t6), P2(t3), P3(t6), P4(t0). The following are FALSE propositions: P1(t2), P3(t5).

Note that we cannot instantiate a tuple predicate with just any tuple. For instance, instantiating predicate P2 with tuple t4 cannot be done because t4 lacks a status attribute. This brings us to the concept of a tuple predicate over a set.

We call predicate P1 a tuple predicate over {price,instock}; the components of this predicate assume that there is a price and an instock attribute available within the tuple that is provided as the argument. In the same way that predicate P0 is a tuple predicate over {sex}, P2 is a tuple predicate over {status,total}, P3 is a tuple predicate over {salary,sex}, and P4 is a tuple predicate over {begindate,enddate}. In general, if a given predicate, say P(t), is a predicate over some set A, then we can only meaningfully instantiate predicate P with tuples whose domain is a superset of A. For instance, the domain of t5—{salary,sex,name}—is a (proper) superset of {salary,sex}. Therefore, we can instantiate predicate P3—a predicate over {salary,sex}—with t5.

As you can see by the examples given, a tuple predicate is allowed to be compound; that is, one that involves logical connectives. The components of this predicate typically compare the attribute values of the tuple supplied as the argument with certain given values.

We need to make two more observations with regards to tuple predicates. The first one deals with the number of attributes involved in the predicate. Note that predicate P0 only references the sex attribute; it is a tuple predicate over a singleton.

We consider a tuple predicate—say P(t)—over a singleton—say A—a degenerate case of a tuple predicate. In Chapter 7, and also later on in Chapter 11, we’ll deal with such a degenerate case of a tuple predicate as a condition on the attribute value set of attribute ↵A (see the section “The Choose Operator” in Chapter 2 to refresh your mind on the choose operator ↵).

Second, tuple predicates shouldn’t be decomposable into multiple conjuncts. In Chapters 7 and 11, we’ll require that a tuple predicate when written in conjunctive normal form (CNF) will consist of only one conjunct. If the CNF version of the predicate has more than one conjunct, then we are in fact dealing with multiple (as many conjuncts as there are) potential tuple predicates.

Predicate P2 from Listing 6-1 violates this second observation; it has more than one conjunct in CNF. Here is predicate P2 rewritten into CNF (you can quickly achieve this by using the distribution rewrite rules):

Predicate P2 has two conjuncts in CNF; therefore, we’re dealing with two tuple predicates. We’ll name them P2a and P2b, respectively:

As you can see, predicate P2a is a tuple predicate over singleton {status}. Therefore, according to our first observation, P2a is a degenerate case of a tuple predicate. We have broken down what seemed like a tuple predicate, P2, into a combination of a (simpler) tuple predicate P2b and a condition on the attribute value set of the status attribute (P2a).

Table Predicates

In the previous section you were introduced to a certain type of predicate: the tuple predicate. In this section we’ll introduce you to the concept of a table predicate. Table predicates deal with multiple tuples within a single table. They are predicates that have a single parameter of type table. Listing 6-3 displays a few examples of table predicates.

Predicate P5 states that there are no two distinct tuples (parts) in table T such that they have the same partno value. Assuming predicate P6 also deals with parts tables, it states—loosely speaking—that the total stock value represented by the parts table T does not exceed 2500. Predicate P7 states that whenever a certain part is out of stock, then there should be a different part (one with a different part number) that has the same name and is still in stock.

In the same way as with tuple predicates, we say that P5 is a table predicate over {partno}, P6 is a table predicate over {instock,price}, and P7 is a table predicate over {instock,partno, name}.

Now take a look at table PAR1 in Figure 6-1.

Figure 6-1. Table PAR1

PAR1 is a table over {partno,name,instock,price}. This is a superset of all sets that P5, P6, and P7 are table predicates over; we can therefore meaningfully supply PAR1 as an argument to these predicates.

As you’ve probably already noticed, PAR1 satisfies predicate P5; there are no two different parts in PAR1 that have the same partno value. The total stock value represented by PAR1 is 675, which is less than 2500, so PAR1 also satisfies P6. However, it violates predicate P7; part 3 is out of stock but there isn’t a different part with the same name (axe) that’s in stock.

In the remainder of this book, we’ll consider a table predicate a degenerate case of a table predicate if it can be rewritten into a predicate with the following pattern:

Here Q(t) represents a tuple predicate. If a table predicate is of the preceding form, then we consider it a tuple predicate in disguise. In the next chapter, we’ll specify these degenerate cases of table predicates differently than the other table predicates; in fact, for these cases we’ll specify tuple predicate Q(t) in a different layer than the other table predicates, and table predicate P(T) is discarded as a table predicate.

A degenerate case of a table predicate disguising a tuple predicate would be this:

This is the table predicate variation of tuple predicate P1(t) from Listing 6-1 that we won’t allow as a table predicate.

Without loss of generality we will also—just like tuple predicates—confine our attention to table predicates consisting of a single conjunct. If you can rewrite a given table predicate P(T) into an expression of the form Q(T) ∧ R(T), then you are in fact dealing with two table predicates. Here is an example to illustrate this:

This predicate states that if for a given part we have more than 100 items in stock, then there should not exist another part that has the same name, nor should the price of the given part be equal to 200 or more. This table predicate is of the following form:

Using the following rewrite rule

together with the distributive property of a universal quantification (see Listing 3-12), you can rewrite this into a conjunction of two predicates:

This shows that you’re dealing with two predicates. The first conjunct is indeed a table predicate, and the second one is actually a tuple predicate in disguise!

We conclude this section on table predicates with another example introducing three more table predicates. Listing 6-4 first introduces characterization chr_EMP that models an employee.

For an employee, the employee number (empno), its name (ename), the employee’s job (job), the salary (sal), and the number (deptno) of the department that employs the employee are the relevant attributes that are captured by this characterization. Using this characterization, you can generate an employee table by choosing a subset from Π(chr_EMP). Such a table can be provided as the argument to a table predicate. Listing 6-5 introduces three table predicates that can accept a table over dom(chr_EMP) through parameter T.

Table predicate P8 states that managers earn more than trainers, and trainers earn more than clerks. Predicate P9 states that every department should have at least three employees. Predicate P10 states that departmental salary budgets cannot exceed 40000.

Figure 6-2 displays an example subset of Π(chr_EMP) named EMP1.

Figure 6-2. Example table EMP1

Verify for yourself that EMP1 is indeed a subset of Π(chr_EMP) and that it satisfies predicates P8, P9, and P10.

Database Predicates

We continue now by further increasing the scope of data that a predicate deals with. After tuple predicates (scope of data is a tuple) and table predicates (scope of data is a table), the next level up is predicates that deal with multiple tables. We’ll call this kind of predicate a database predicate. A database predicate has one parameter of type database state.

To show a few examples of predicates that deal with a database state, we first introduce a department characterization alongside the earlier introduced employee characterization. Listing 6-6 defines characterization chr_DEPT that models a department.

For a department, the department number (deptno), its name (dname), the department’s location (loc), and the salary budget (salbudget) are the relevant attributes this characterization captures.

Figure 6-3 displays an example department table that we name DEP1.

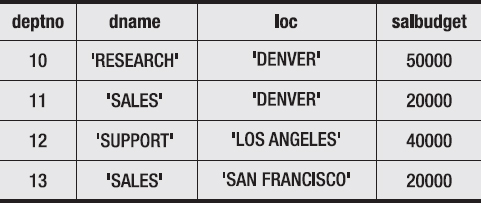
Figure 6-3. Example table DEP1

Check that table DEP1 is a subset of Π(chr_DEPT) and that it satisfies the table predicates shown in Listing 6-7.

Table predicate P11 states that there cannot be two different departments that share the same department number. P12 states that two different departments either have different names or different locations (or both).

By the way, do you see that these two predicates are of the same form? You can transform predicate P11 into a universal quantification using rewrite rules, as follows:

Here we have used a rewrite rule that transforms an existential quantifier into a universal quantifier, a De Morgan Law, and a rewrite rule that transforms disjunction into implication. Predicates P11 and P12 are both of the form of one of the common patterns of data integrity predicates that we’ll treat in the next section.

You can now construct a database state, say S1, as follows:

In this expression, EMP1 and DEP1 represent the tables that were introduced in Figures 6-2 and 6-3. You can also represent database state S1 in this way (see Figure 6-4).

Figure 6-4. Database state S1

S1 represents a database state over the skeleton { (employee;{empno,ename,job,sal, deptno}), (department;{deptno,dname,loc,salbudget}) }. As a reminder from the previous chapter, you can write expressions such as S1(employee) and S1(department), which respectively evaluate to EMP1 (the employee table from Figure 6-2) and DEP1(the department table from Figure 6-3).

Now let’s take a look at database predicates P13 and P14 in Listing 6-8. Remember parameter S represents a database state.

Predicate P13 states that every employee is employed within a department that is known in the department table.

This type of database predicate (the set of values of a specified attribute of one table forms a subset of the set of values of a specified attribute of another table) is commonly found in database designs and will be treated in more detail in the next section. Supplying database state S1 as the argument to predicate P13 results in the following proposition:

This is a TRUE proposition. The set of numbers at the left-hand side is a subset of the set of numbers at the right-hand side. Again we say that database state S1 satisfies (does not violate) database predicate P13. A somewhat more succinct way to specify predicate P13 is as follows:

We now use table projection. Supplying state S1 as the value for the parameter results in this proposition:

This is again a TRUE proposition. The set of two functions at the left-hand side is a subset of the set of four functions at the right-hand side.

Predicate P14 states that the sum of the salaries of all employees in the employee table that work in a particular department should not exceed the salary budget for that department as found in the department table. Database state S1 also satisfies P14.

As with tuple and table predicates, some cases of database predicates are considered degenerate cases. If a database predicate, say P, can be rewritten into a predicate with the following pattern, we consider the database predicate a degenerate case:

If a database predicate is of the preceding form, then it involves only one table structure. In the right-hand side expression, T represents one of the table structure names in a database state S. S(T) then represents the corresponding table, and Q represents a table predicate. Database predicates that involve just one table structure (in the preceding case, T) are considered degenerate. These degenerate cases are in fact disguising a table predicate. In the next chapter we’ll require for these cases that Q is introduced as a table predicate and that database predicate P is discarded.

Without loss of generality, we again confine our attention to database predicates that cannot be decomposed into multiple conjuncts. If you can rewrite a given database predicate P(S) into an expression of the form Pa(S) ∧ Pb(S), then you are in fact dealing with two database predicates.

A Few Remarks on Data Integrity Predicates

We conclude the introduction of the preceding three classes of data integrity predicates with a few observations.

As you’ve seen through the various examples, we can elegantly use tuple, table, and database predicates to formally define the conditions (business rules) that are part of the real world and that need to be reflected somehow in the specification of a database design. The predicate class (tuple, table, or database) to which a business rule maps is fully dependent on the given database skeleton of the database design. For instance, predicate P8 (see Listing 6-5) is a table predicate because all the information to formally specify the business rule that managers earn more than trainers, and trainers earn more than clerks, is available within the employee table structure. Now, if for some reason a separate table structure, say trainer, was introduced to hold all trainer information (rendering employee to hold only manager and clerk information), then this realworld constraint would map to a database predicate involving both table structures employee and trainer.

You might have a question regarding the way we’ve introduced data integrity predicates in this chapter. In the various examples you’ve seen, we’ve employed these predicates to show whether a given tuple, table, or database state satisfies them. However, when formally specifying a database design, we aren’t interested in a single database state (or table or tuple). We are interested in a database state space: a set that holds all values that we allow for our database. We intend to mathematically model such a database state space that represents the value set for a database variable (this will be done in Chapter 7). When we do so, we’ll use the three classes of data integrity predicates introduced in this chapter, in a sophisticated manner such that they represent data integrity constraints that play a role at the database state space level.

Common Patterns of Table and Database Predicates

This section will establish five common patterns of table and database predicates: unique identification predicates, subset requirement predicates, specialization predicates, generalization predicates, and tuple-in-join predicates. These five patterns of data integrity predicates are common in database designs and are therefore important enough to justify a separate section dealing with them.

Unique Identification Predicate

We’ve mentioned before that every tuple that is an element of a given table is unique within that table. The attribute values make a tuple unique inside a table, not its attributes. Often it doesn’t take all attribute values to identify a tuple uniquely in a table; a proper subset of the attribute values suffices. The way this property can be stated for a certain table is through a special kind of table predicate called a unique identification predicate. A unique identification predicate is a table predicate as defined in Definition 6-1.

A unique identification predicate states that if any two tuples in a table have the same attribute values on a given subset of the attributes, then they must be the same tuple. Using rewrite rules introduced in Part 1 of this book, you can also express a unique identification predicate in the forms listed in Listing 6-9.

The first form listed might be a more intuitive formal version of the unique identification predicate; two different tuples in a table must differ on the given subset of attributes. Predicate P12 in Listing 6-7 was written in this form; it states that {dname,loc} is uniquely identifying in table T. Predicate P11 in the same listing is also a unique identification predicate. It is written in the third form displayed in Listing 6-9 and states that {deptno} is uniquely identifying in table T. The first predicate in Listing 6-3 also uses this form.

Given that a set A is uniquely identifying in table T (with heading H), then every subset of H that is a proper superset of A is of course also uniquely identifying in table T. In a unique identification predicate, you want to specify an irreducible subset A of heading H that is uniquely identifying in table T.

If you choose a reducible subset of H, then the resulting unique identification predicate is too weak. The weakest unique identification predicate would be that the heading of T (the largest possible superset) is uniquely identifying in table T. In fact, this wouldn’t add any constraint at all on the set of tuples that is admissible for table T; as mentioned at the beginning of this section, we already know that tuples are unique within a table.

You can also conclude this by taking a more formal approach. Take a look what happens if you substitute the heading of T for set A in the unique identification predicate pattern:

Note that if t is an element of T, then you can refer to the heading of T via expression dom(t): the domain of tuple t. Using the rewrite rule t↓dom(t) = t (the restriction of a tuple to all its attributes is the same as the tuple itself), we can rewrite the preceding predicate into this:

The predicate is now a tautology; it is always TRUE, irrespective of the value of T. Therefore it doesn’t constrain T in any way at all.

Subset Requirement Predicate

The different table structures that you capture in a database design are not all independent of each other. Many pairs of these table structures have a relationship that is referred to as a subset requirement. Definition 6-2 defines the concept of a subset requirement predicate. The structure of the predicate in this definition shows why it is referred to as a subset requirement.

Let’s demonstrate this with tables EMP1 and DEP1 (see Figures 6-2 and 6-3). If we substitute EMP1 for T1, DEP1 for T2, and {deptno} for A, we end up with the following expression:

This evaluates to the following expression:

This is a TRUE proposition; every department number in EMP1 also appears in DEP1.

If the cardinality of A equals 1 (that is, if A represents a singleton), then we will often use function application instead of function limitation to specify a subset requirement predicate. Using the preceding example, we would write this:

This subset requirement is analogous to predicate P13 in Listing 6-8.

A subset requirement predicate is often accompanied by a unique identification predicate. Using the names from Definition 6-2, you’ll often encounter that “A is uniquely identifying in T2;” in the preceding example {deptno} is indeed uniquely identifying in DEP1. This is not mandatory; the example database design that will be given in Chapter 7 actually has a subset requirement where the accompanying unique identification predicate is absent.

When using function limitation to specify a subset requirement, you must sometimes apply function composition to rename one or more attributes in one of the tables involved. Let’s illustrate this through an example. Take a look at table DEP2, displayed in Figure 6-5, which very much resembles table DEP1.

Figure 6-5. Example table DEP2

Table DEP2 differs from table DEP1 in that the attribute used to hold the department number is now named dno instead of deptno. You can express a subset requirement from EMP1 (see Figure 6-2) to DEP2 using function application, as follows:

However, if you want to specify this subset requirement using function limitation, you must first either rename the deptno attribute in table EMP1 into dno, or rename the dno attribute in table DEP2 into deptno. Here is the specification for this subset requirement, where the attribute renaming is applied to EMP1 tuples:

In this expression, the function {(dno;deptno)} represents an attribute renaming function. It renames the deptno attribute in tuples from table EMP1 to dno.

By using the more elaborate function limitation as opposed to the function application that was used in Listing 6-8, you are able to express subset requirements that involve multiple attributes of both involved tables at the same time. The database design that will be introduced in Chapter 7 has an example subset requirement that involves multiple attributes.

A subset requirement predicate usually involves two different table structures, and therefore represents a database predicate. However, this need not always be the case; sometimes they involve just one table structure. In these cases, they represent a table predicate. For instance, assume that table EMP1 is extended with a mgr (manager) attribute that holds the employee number of the manager of the employee. You would require that every manager number that appears in EMP1 also appears as an employee number in EMP1. Formally, you can express this as a subset requirement:

You might even require that every manager number that appears in EMP1 also appears as an employee number in a certain restriction of EMP1. Perhaps the referenced tuples must each have a JOB value indicating that the employee in question is indeed a manager. Formally, you can express this as follows:

We consider the preceding expression also a subset requirement.

Subset requirements can be visualized by a picture. You can draw a picture for a subset requirement “A in T1 references A in T2” by drawing two rectangles (or some other shape)—one for T1 and one for T2—and connecting the two rectangles with a directed arrow going from T1 to T2. The arrow represents that every tuple in table T1 references at least one tuple in table T2. Figure 6-6 shows the subset requirement from EMP1 to DEP2.

Figure 6-6. Visualization of subset requirement from EMP1 to DEP2

Note that this picture of a subset requirement doesn’t tell you what the involved attributes are at both sides of the arrow, nor if any attribute renaming is involved. It is just a picture and should always be accompanied by the formal predicate that tells you exactly what the intended meaning of the arrow is.

Sometimes you know that the subset requirement is actually a proper subset requirement. Suppose you want to specify the requirement that the set of department numbers found in an employee table is a proper subset of the set of department numbers found in a department table. You can specify this database predicate as follows:

In this book, we’ll call this special case a subset requirement too. Another way of dealing with this is to still use the subset operator (instead of the proper subset) and to specify a second database predicate that expresses the existence of at least one department number in thedepartment table that does not appear in the employee table. The following database predicate P15b does just that:

Tables EMP1 (employee) and DEP2 (department) conform to both database predicate P15a and P15b. At other times you know that the subset requirement is actually an equality requirement. Suppose you want to specify the requirement that every department must have employees. You can specify this as follows:

In this book we’ll call this special case a subset requirement too. Again, another way of dealing with this is to use the subset operation (instead of the equality) and to add a second integrity constraint that expresses the existence of at least one employee for every department. Database predicate P16b expresses just that:

By the way, do you see that predicate P15b is just the negation of predicate P16b? This is because these two special cases—proper subset and equality—are mutually exclusive.

Specialization Predicate

Take a look at table TRN1 displayed in Figure 6-7.

Figure 6-7. Table TRN1

The propositions regarding tables EMP1 and TRN1 listed in Listing 6-10 are TRUE propositions.

It follows from proposition P7 that the uniquely identifying attributes of tables TRN1 and EMP1 are the same. Proposition P8 states that the employee numbers of trainers in table EMP1 equal the employee numbers found in table TRN1 (loosely speaking). Note the equality. For every trainer that can be found in table EMP1, you can find a related tuple in table TRN1. And vice versa, for every tuple in TRN1 you can find a trainer in EMP1.

Table TRN1 can be considered to hold additional information regarding trainers (and only trainers): the date on which they got certified (again loosely speaking).

This type of circumstance is often found in database designs; for a certain subset of tuples in a given table—specifiable through some predicate (in the preceding case e(job)='TRAINER')—additional information is found in another given table where both tables share the same uniquely identifying attributes. In this case, table TRN1 is referred to as a specialization of table EMP1. Definition 6-3 formally specifies this concept.

You’ll usually find that set A is uniquely identifying in both tables T1 and T2. In the example from Listing 6-10, you saw that {empno} is uniquely identifying in both EMP1 and TRN1.

A given table can have more than one specialization. Assume that you want to hold additional information for managers too; for instance, the agreed yearly bonus for a manager. For the sake of this example, assume that trainers and clerks do not have a yearly bonus, only managers do. Take a look at table MAN1(see Figure 6-8) that holds the yearly bonus for managers; it is also a specialization of EMP1.

Figure 6-8. Table MAN1

The following proposition holds between tables EMP1 and MAN1. It is of the form introduced in Definition 6-3.

In the next section we’ll discuss a concept that is related to specializations.

Generalization

If a given table T has multiple specializations, say tables S1 through Sn (n>1), such that for every tuple in T there exists exactly one related tuple in exactly one of the specializations, then we say that “table T is a generalization of tables S1 through Sn.”

Let’s build on the example of the previous section. Suppose you also want to hold additional information for clerks; for instance, the type of contract they have (full time or part time) and the manager that they report to. Table CLK1, shown in Figure 6-9, is a specialization of table EMP1 that holds this extra information for clerks.

Figure 6-9. Table CLK1

Specializations TRN1, MAN1, and CLK1 now have seven tuples in total. For every tuple in table EMP1—there are seven—there exists exactly one tuple in exactly one of the tables TRN1, MAN1, or CLK1. This makes table EMP1 a generalization of tables TRN1, MAN1, and CLK1.

In a generalization table, you’ll often find a specific attribute that determines in which specialization table the additional information can be found. In the example used, this attribute is the job attribute. For the tuples in table EMP1 that have job='TRAINER', additional information is found in specialization TRN1. For tuples with job='MANAGER', additional information can be found in table MAN1, and for tuples with job='CLERK', additional information can be found in table CLK1. Such an attribute in a generalization table is referred to as the inspection attribute.

Note that an inspection attribute is a redundant attribute; that is, its value can be derived from other tuples. For a given tuple of EMP1, a corresponding tuple exists in either TRN1, MAN1, or CLK1. You can directly deduce the job value of the EMP1 tuple from where this corresponding tuple appears; its value should be 'TRAINER', 'MANAGER', or 'CLERK', respectively.

In general, you shouldn’t introduce data redundancy in a database design; it forces you to maintain the redundancy whenever you update data that determines the redundant data. Or, viewed from a database design perspective, it forces you to introduce a constraint that imposes the data redundancy. However, an inspection attribute is very helpful when specifying a generalization property in a database design (there is an exercise on this at the end of this chapter).

Tuple-in-Join Predicate

Often two tables are related through a subset requirement. When two tables are thus related, the need to join them arises often, for obvious reasons. You can join tuples from tables EMP1 and DEP1 that correspond on the attributes that are involved in the subset requirement between these two tables, in this case the deptno attribute. The resulting table from this combination will have as its heading the union of the heading of EMP1 and the heading of DEP1.

Figure 6-10 displays the result of such a combination of tables EMP1 and DEP1.

Figure 6-10. Table EMPDEP1, the join of tables EMP1 and DEP1

Every tuple in table EMPDEP1 is called a tuple in the join of EMP1 and DEP1. Tuple-in-join predicates are tuple predicates dealing with these tuples in a join; the joined tuple is the parameter for the tuple predicate. Here is an example of a tuple predicate regarding EMPDEP1:

This proposition states that all tuples in EMPDEP1—the join of EMP1 and DEP1—have a sal attribute value that doesn’t exceed 20 percent of the salbudget attribute value. In this proposition the expression t(sal)≤t(salbudget)/5 represents the tuple predicate. If you express this proposition not in terms of table EMPDEP1, but in terms of the two tables that are joined—EMP1 and DEP1—you’ll end up with a proposition looking like this:

It states that no employee can earn more than a fifth of the departmental salary budget (of the department where he or she is employed). Another way of formally specifying this is as follows:

In this proposition, the expression t(sal)≤t(salbudget)/5 represents a tuple predicate that constrains the tuples in the join. This predicate pattern is commonly found in database designs and is referred to as a tuple-in-join predicate. Definition 6-4 formally specifies it.

In the preceding definition, you will typically find that tables T1 and T2 are related via a subset requirement that involves the join attributes.

Listing 6-11 demonstrates two more instantiations of a tuple-in-join predicate involving tables EMP1 and DEP1.

P9 states that managers cannot be employed in Los Angeles. P10 states that employees working in San Francisco must either be trainers or clerks. Given the sample values EMP1 and DEP1 in Figure 6-10 both propositions are TRUE; there are no managers working in Los Angeles and all employees working in San Francisco—there are none—are either trainers or clerks.

In this section, we’ve defined the tuple-in-join predicate to involve only two tables. However, it is often meaningful to combine three or even more tables with the join operator. Of course, tuples in these joins can also be constrained by a tuple predicate. Here is the pattern of a tuple-in-join predicate involving three tables (T1, T2, and T3):

In this pattern, A represents the set of join attributes for tables T1 and T2, and B represents the set of join attributes for tables T2 and T3. Predicate P represents a predicate whose argument is the tuple in the join. In the next chapter, you’ll see examples of tuple-in-join predicates involving more than two tables.

Chapter Summary

This section provides a summary of this chapter, formatted as a bulleted list. You can use it to check your understanding of the various concepts introduced in this chapter before continuing with the exercises in the next section.

• A tuple predicate is a predicate with one parameter of type tuple. It can be used to accept (or reject) tuples based on the combination of attribute values that they hold.
• A table predicate is a predicate with one parameter of type table. It can be used to accept (or reject) tables based on the combination of tuples that they hold.
• A database (multi-table) predicate is a predicate with one parameter of type database state. It can be used to accept (or reject) database states based on the combination of tables that they hold.
• Five patterns of table and database predicates are commonly found in database designs: unique identification, subset requirement, specialization, generalization, and tuple-in-join predicates.
• A unique identification predicate is a table predicate of the following form (T represents a table): ( ∀t1,t2∈T: t1↓A=t2↓A ⇒ t1=t2 ).

  In this expression, A represents the set of attributes that uniquely identify tuples in table T.

• A subset requirement predicate is a predicate of the following form (T1 and T2 represent tables): { t1↓A| t1∈T1 } ⊆ { t2↓A| t2∈T2 }.

  In this expression, A often represents the set of attributes that uniquely identify tuples in table T2.

• A specialization predicate is a database predicate of the following form (T1 and T2 represent tables): { t1↓A| t1∈T1 ∧ P(t1) } = { t2↓A| t2∈T2 }.

  In this expression, A represents the set of attributes that uniquely identify tuples in both tables T1 and T2. Predicate P is a predicate specifying a subset of table T1. We say that “T2 is a specialization of T1.” T2 is considered to hold additional information for the subset of tuples in T1 specified by predicate P.

• If a given table, say T, has more than one specialization such that for every tuple in T there exists exactly one tuple in exactly one of the specialization tables that holds additional information for that tuple, then table T is referred to as the generalization of the specializations.
• A tuple-in-join predicate is a predicate of the following form (T1 and T2 represent tables): ( ∀t1∈T1: ( ∀t2∈T2: t1↓A=t2↓A ⇒ P(t1∪t2) ) ).

In this expression, A represents the set of attributes that is typically involved in a subset requirement between tables T1 and T2. Predicate P is a tuple predicate.

Exercises

1. Evaluate the truth value of the following propositions (PAR1 was introduced in Figure 6-1):
   • ( ∀p∈PAR1: mod(p(partno),2)=0 ⇒ p(price)≤15 )
   • ¬( ∃p∈PAR1: p(price)≠5 ∨ p(instock)=0 )
   • #{ p | p∈PAR1 ∧ ( p(instock)>10 ⇒ p(price)≤10 ) } = 6
2. Let A be a subset of the heading of PAR1. Give all possible values for A such that “A is uniquely identifying in PAR1” (only give the smallest possible subsets).
3. Specify a subset requirement predicate from CLK1 and EMP1 stating that the manager of a clerk must be an employee whose job is 'MANAGER'.
4. Formally specify the fact that table EMP1 is a generalization of tables TRN1, MAN1, and CLK1.
5. In EMP1 the job attribute is a (redundant) inspection attribute. Formally specify the fact that EMP1 is a generalization of TRN1, MAN1, and CLK1 given that EMP1 does not have this attribute.
6. Using rewrite rules for implication and quantifiers that have been introduced in Part 1, give at least three alternative formal expressions for proposition P12.
7. Using the semantics introduced by tables EMP1 and CLK1, give a formal specification for the database predicate “A manager of a clerk must work in the same department as the clerk.”

   Is this proposition TRUE for tables EMP1 and CLK1?

8. Using the semantics introduced by tables DEP1, EMP1, and CLK1, give a formal specification for the database predicate “A manager of a clerk must work in a department that is located in Denver.”

   Is this proposition TRUE for these tables?