Chapter 4

Decision Trees: Theory and Algorithms

Victor E. Lee

John Carroll University
University Heights, OH
[email protected]

Lin Liu

Kent State University
Kent, OH
[email protected]

Ruoming Jin

Kent State University
Kent, OH
[email protected]

4.1 Introduction

One of the most intuitive tools for data classification is the decision tree. It hierarchically partitions the input space until it reaches a subspace associated with a class label. Decision trees are appreciated for being easy to interpret and easy to use. They are enthusiastically used in a range of business, scientific, and health care applications [12, 15, 71] because they provide an intuitive means of solving complex decision-making tasks. For example, in business, decision trees are used for everything from codifying how employees should deal with customer needs to making high-value investments. In medicine, decision trees are used for diagnosing illnesses and making treatment decisions for individuals or for communities.

A decision tree is a rooted, directed tree akin to a flowchart. Each internal node corresponds to a partitioning decision, and each leaf node is mapped to a class label prediction. To classify a data item, we imagine the data item to be traversing the tree, beginning at the root. Each internal node is programmed with a splitting rule, which partitions the domain of one (or more) of the data’s attributes. Based on the splitting rule, the data item is sent forward to one of the node’s children. This testing and forwarding is repeated until the data item reaches a leaf node.

Decision trees are nonparametric in the statistical sense: they are not modeled on a probability distribution for which parameters must be learned. Moreover, decision tree induction is almost always nonparametric in the algorithmic sense: there are no weight parameters which affect the results.

Each directed edge of the tree can be translated to a Boolean expression (e.g., x1 > 5); therefore, a decision tree can easily be converted to a set of production rules. Each path from root to leaf generates one rule as follows: form the conjunction (logical AND) of all the decisions from parent to child.

Decision trees can be used with both numerical (ordered) and categorical (unordered) attributes. There are also techniques to deal with missing or uncertain values. Typically, the decision rules are univariate. That is, each partitioning rule considers a single attribute. Multivariate decision rules have also been studied [8, 9]. They sometimes yield better results, but the added complexity is often not justified. Many decision trees are binary, with each partitioning rule dividing its subspace into two parts. Even binary trees can be used to choose among several class labels. Multiway splits are also common, but if the partitioning is into more than a handful of subdivisions, then both the interpretability and the stability of the tree suffers. Regression trees are a generalization of decision trees, where the output is a real value over a continuous range, instead of a categorical value. For the remainder of the chapter, we will assume binary, univariate trees, unless otherwise stated.

Table 4.1 shows a set of training data to answer the classification question, “What sort of contact lenses are suitable for the patient?” This data was derived from a public dataset available from the UCI Machine Learning Repository [3]. In the original data, the age attribute was categorical with three age groups. We have modified it to be a numerical attribute with age in years. The next three attributes are binary-valued. The last attribute is the class label. It is shown with three values (lenses types): {hard, soft, no}. Some decision tree methods support only binary decisions. In this case, we can combine hard and soft to be simply yes.

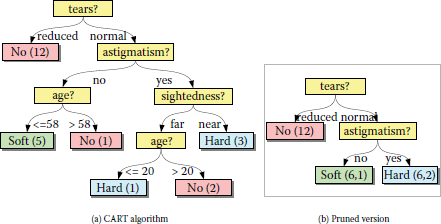
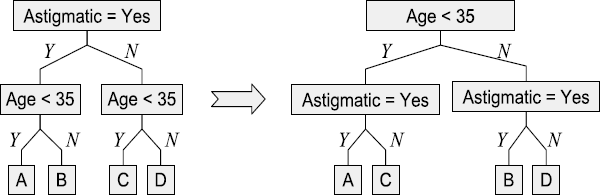
Next, we show four different decision trees, all induced from the same data. Figure 4.1(a) shows the tree generated by using the Gini index [8] to select split rules when the classifier is targeting all three class values. This tree classifies the training data exactly, with no errors. In the leaf nodes, the number in parentheses indicates how many records from the training dataset were classified into this bin. Some leaf nodes indicate a single data item. In real applications, it may be unwise to permit the tree to branch based on a single training item because we expect the data to have some noise or uncertainty. Figure 4.1(b) is the result of pruning the previous tree, in order to achieve a smaller tree while maintaining nearly the same classification accuracy. Some leaf nodes now have a pair of number: (record count, classification errors).

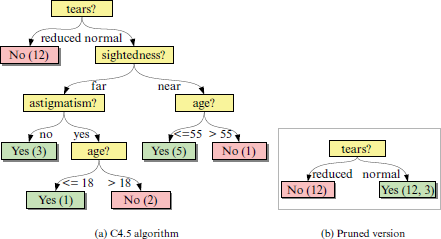
Figure 4.2(a) shows a 2-class classifier (yes, no) and uses the C4.5 algorithm for selecting the splits [66]. A very aggressively pruned tree is shown in Figure 4.2(b). It misclassifies 3 out of 24 training records.

Optimality and Complexity

Constructing a decision tree that correctly classifies a consistent1 data set is not difficult. Our problem, then, is to construct an optimal tree, but what does optimal mean? Ideally, we would like a method with fast tree construction, fast predictions (shallow tree depth), accurate predictions, and robustness with respect to noise, missing values, or concept drift. Should it treat all errors the same, or it is more important to avoid certain types of false positives or false negatives? For example, if this were a medical diagnostic test, it may be better for a screening test to incorrectly predict that a few individuals have an illness than to incorrectly decide that some other individuals are healthy.

Regardless of the chosen measure of goodness, finding a globally optimal result is not feasible for large data sets. The number of possible trees grows exponentially with the number of attributes and with the number of distinct values for each attribute. For example, if one path in the tree from root to leaf tests d attributes, there are d! different ways to order the tests. Hyafil and Rivest [35] proved that constructing a binary decision tree that correctly classifies a set of N data items such that the expected number of steps to classify an item is minimal is NP-complete. Even for more esoteric schemes, namely randomized decision trees and quantum decision trees, the complexity is still NP-complete [10].

In most real applications, however, we know we cannot make a perfect predictor anyway (due to unknown differences between training data and test data, noise and missing values, and concept drift over time). Instead, we favor a tree that is efficient to construct and/or update and that matches the training set “well enough.”

Notation We will use the following notation (further summarized for data and partition in Table 4.2) to describe the data, its attributes, the class labels, and the tree structure. A data item x is a vector of d attribute values with an optional class label y. We denote the set of attributes as A = {A1,A2 , … ,Ad}. Thus, we can characterize x as {x1,x2 , … ,xd}, where x1 ∈ A1,x2 £ A2 , … ,xd £ Ad. Let Y = {y1,y2 , … ,ym} be the set of class labels. Each training item x is mapped to a class value y where y ∈ Y. Together they constitute a data tuple 〈x, y〉. The complete set of training data is X.

A partitioning rule S subdivides data set X into a set of subsets collectively known as XS; that is, XS = {X1,X2, … ,Xk} where ⋃i Xi = X. A decision tree is a rooted tree in which each set of children of each parent node corresponds to a partitioning (XS) of the parent’s data set, with the full data set associated with the root. The number of items in Xi that belong to class yj is |Xij|. The probability that a randomly selected member of Xi is of class yi is pij = pij=|Xij||Xi|$p_{ij}=\frac{\left|X_{ij}\right|}{\left|X_i\right|}$.

The remainder of the chapter is organized as follows. Section 4.2 describes the operation of classical top-down decision tree induction. We break the task down into several subtasks, examining and comparing specific splitting and pruning algorithms that have been proposed. Section 4.3 features case studies of two influential decision tree algorithms, C4.5 [66] and CART [8]. Here we delve into the details of start-to-finish decision tree induction and prediction. In Section 4.4, we describe how data summarization and parallelism can be used to achieve scalability with very large datasets. Then, in Section 4.5, we introduce techniques and algorithms that enable incremental tree induction, especially in the case of streaming data. We conclude with a review of the advantages and disadvantages of decision trees compared to other classification methods.

4.2 Top-Down Decision Tree Induction

The process of learning the structure of a decision tree, to construct the classifier, is called decision tree induction [63]. We first describe the classical approach, top-down selection of partitioning rules on a static dataset. We introduce a high-level generic algorithm to convey the basic idea, and then look deeper at various steps and subfunctions within the algorithm.

The decision tree concept and algorithm can be tracked back to two independent sources: AID (Morgan and Sonquist, 1963) [56] and CLS in Experiments in Induction (Hunt, Marin, and Stone, 1966) [34]. The algorithm can be written almost entirely as a single recursive function, as shown in Algorithm 4.1. Given a set of data items, which are each described by their attribute values, the function builds and returns a subtree. The key subfunctions are shown in small capital letters. First, the function checks if it should stop further refinement of this branch of the decision tree (line 3, subfunction STOP). If so, it returns a leaf node, labeled with the class that occurs most frequently in the current data subset X’. Otherwise, it procedes to try all feasible splitting options and selects the best one (line 6, FINDBESTSPLITTINGRULE). A splitting rule partitions the dataset into subsets. What constitutes the “best” rule is perhaps the most distinctive aspect of one tree induction algorithm versus another. The algorithm creates a tree node for the chosen rule (line 8).

If a splitting rule draws all the classification information out of its attribute, then the attribute is exhausted and is ineligible to be used for splitting in any subtree (lines 9-11). For example, if a discrete attribute with k different values is used to create k subsets, then the attribute is “exhausted.”

As a final but vital step, for each of the data subsets generated by the splitting rule, we recursively call BUILDSUBTREE (lines 13-15). Each call generates a subtree that is then attached as a child to the principal node. We now have a tree, which is returned as the output of the function.

 1: tree ← BUILDSUBTREE(X,A,0);

 2: function BUILDSUBTREE(X’,A’,depth)

 3:  if STOP(X’,depth) then

 4:   return CreateNode(nullRule, majorityClass(X’));

 5:  else

 6:   rule ← FINDBESTSPLITTINGRULE(X’ ,A’);

 7:   attr ← attributeUsed(rule);

 8:   node ← CreateNode(rule,nullClass);

 9:   if rule “exhausts” attr then

10:   remove attr from A’;

11:  end if

12:  DataSubsets ← ApplyRule(X’,rule);

13:  for Xi ∈ DataSubsets do

14:   child ← BUILDSUBTREE(Xi,A’,depth+1);

15:   node.addChild(child);

16:  end for

17:  return node;

18: end if

19: end function

4.2.1 Node Splitting

Selecting a splitting rule has two aspects: (1) What possible splits shall be considered, and (2) which of these is the best one? Each attribute contributes a set of candidate splits. This set is determined by the attribute’s data type, the actual values present in the training data, and possible restrictions set by the algorithm.

• Binary attributes: only one split is possible.
• Categorical (unordered) attributes: If an attribute A is unordered, then the domain of A is a mathematical set. Any nonempty proper subset S of A defines a binary split {S,AS}. After ruling out redundant and empty partitions, we have 2k—1 -1 possible binary splits. However, some algorithms make k-way splits instead.
• Numerical (ordered) attributes:If there are k different values, then we can make either (k -1) different binary splits or one single k-way split.

These rules are summarized in Table 4.3. For the data set in Table 4.1, the age attribute has 20 distinct values, so there are 19 possible splits. The other three attributes are binary, so they each offer one split. There are a total of 22 ways to split the root node.

We now look at how each splitting rule is evaluated for its goodness. An ideal rule would form subsets that exhibit class purity: each subset would contain members belonging to only one class y. To optimize the decision tree, we seek the splitting rule S which minimizes the impurity function F(XS). Alternately, we can seek to maximize the amount that the impurity decreases due to the split:

ΔF (S) = F(X) — F(XS). The authors of CART [8] provide an axiomatic definition of an impurity function F :

Definition 4.1 An impurity function F for a m-state discrete variable Y is a function defined on the set of all m-tuple discrete probability vectors (p1,p2, … ,pm) such that

1. F is maximum only at $\left(\frac{1}{m},\frac{1}{m},\dots ,\frac{1}{m}\right)$,
2. F is minimum only at the “purity points” (1,0, … ,0),(0,1 ,… ,0), … ,(0,0, … ,1),
3. F is symmetric with respect to p1,p2, … ,pm.

We now consider several basic impurity functions that meet this definition.

1. Error Rate

   A simple measure is the percentage of misclassified items. If yj is the class value that appears most frequently in partition Xi, then the error rate for Xi is E(Xi) = $\frac{\left|\left\{y\ne y_j:\left(x,y\right)\in X_i\right\}\right|}{\left|X_i\right|}=1-p_{ij}$ The error rate for the entire split XS is the weighted sum of the error rates for each subset. This equals the total number of misclassifications, normalized by the size of X.

   $$\begin{array}{ccc}\Delta F_{error}\left(S\right)=E\left(X\right)-{\displaystyle \sum _{i\in S}\frac{\left|X_i\right|}{\left|X\right|}E\left(X_i\right).}& & \left(4.1\right)\end{array}$$

   This measure does not have good discriminating power. Suppose we have a two-class system, in which y is the majority class not only in X, but in every available partitioning of X. Error rate will consider all such partitions equal in preference.

2. Entropy and Information Gain (ID3)

   Quinlan’s first decision tree algorithm, ID3 [62], uses information gain, or equivalently, entropy loss, as the goodness function for dataset partitions. In his seminal work on information theory, Shannnon [70] defined information entropy as the degree of uncertainty of a (discrete) random variable Y, formulated as

   $$\begin{array}{ccc}H\left(Y\right)=-{\displaystyle \sum _{y\in Y}{p}_y\log p_y}& & \left(4.2\right)\end{array}$$

   where py is the probability that a random selection would have state y. We add a subscript (e.g., X) when it is necessary to indicate the dataset being measured. Information entropy can be interpreted at the expected amount of information, measured in bits, needed to describe the state of a system. Pure systems require the least information. If all objects in the system are in the same state k, then pk = 1, log pk = 0, so entropy Η = 0. There is no randomness in the system; no additional classification information is needed. At the other extreme is maximal uncertainty, when there are an equal number of objects in each of the |Y| states, so $p_y=\frac{1}{\left|Y\right|},$ for all y. Then, H(Y) = $-\left|Y\right|\left(\frac{1}{\left|Y\right|}\log \frac{1}{\left|Y\right|}\right)=\log \left|Y\right|.$ To describe the system we have to fully specify all the possible states using log|Y| bits. If the system is pre-partitioned into subsets according to another variable (or splitting rule) S, then the information entropy of the overall system is the weighted sum of the entropies for each partition, HXi(Y). This is equivalent to the conditional entropy HX(Y|S).

   $$\begin{array}{c}\Delta F_{infoGain}\left(S\right)=-{\displaystyle \sum _{y\in Y}{p}_y\log p_y}\\ =H_X\left(Y\right)\\ =H_X\left(Y\right)\end{array}\begin{array}{rrr}\hfill +{\displaystyle \sum _{i\in Y}\frac{\left|X_i\right|}{\left|X\right|}{\displaystyle \sum _{y\in Y}{p}_{iy}\log p_{iy}}}& \hfill & \hfill \left(4.3\right)\\ \hfill -{\displaystyle \sum _{i\in S}{p}_i{H}_{X_i}\left(Y\right)}& \hfill & \hfill \\ \hfill -H_X\left(Y|S\right).& \hfill & \hfill \end{array}$$

   We know limp→0p log p goes to 0, so if a particular class value y is not represented in a dataset, then it does not contribute to the system’s entropy.

   A shortcoming of the information gain criterion is that it is biased towards splits with larger k. Given a candidate split, if subdividing any subset provides additional class differentiation, then the information gain score will always be better. That is, there is no cost to making a split. In practice, making splits into many small subsets increases the sensitivity to individual training data items, leading to overfit. If the split’s cardinality k is greater than the number of class values m, then we might be “overclassifying” the data.

   For example, suppose we want to decide whether conditions are suitable for holding a seminar, and one of the attributes is day of the week. The “correct” answer is Monday through Friday are candidates for a seminar, while Saturday and Sunday are not. This is naturally a binary split, but ID3 would select a 7-way split.

3. Gini Criterion (CART)

   Another influential and popular decision tree program, CART [8], uses the Gini index for a splitting criterion. This can be interpreted as the expected error if each individual item were randomly classified according to the probability distribution of class membership within each subset. Like ID3, the Gini index is biased towards splits with larger k.

   $$\begin{array}{ccc}Gini\left(X_i\right)={\displaystyle \sum _{y\in Y}{p}_{iy}\left(1-p_{iy}\right)=1-{\displaystyle \sum _{y\in Y}{p}_{iy}^2}}& & \left(4.4\right)\end{array}$$

   $$\begin{array}{ccc}\Delta F_{Gini}\left(S\right)=Gini\left(X\right)-{\displaystyle \sum _{i\in S}\frac{\left|X_i\right|}{\left|X\right|}Gini\left(X_i\right).}& & \left(4.5\right)\end{array}$$

4. Normalized Measures — Gain Ratio (C4.5)

   To remedy ID3’s bias towards higher k splits, Quinlan normalized the information gain to create a new measure called gain ratio [63]. Gain ratio is featured in Quinlan’s well-known decision tree tool, C4.5 [66].

   $$\begin{array}{cccc}splitbinfo\left(S\right)=-{\displaystyle \sum _{i\in S}\frac{\left|X_i\right|}{\left|X\right|}\log \frac{\left|X_i\right|}{\left|X\right|}}& =H\left(S\right)& & \left(4.6\right)\end{array}$$

   $$\begin{array}{cccc}\Delta F_{gainRatio\left(S\right)}=\frac{\Delta F_{infoGain}\left(S\right)}{splitinfo\left(S\right)}& =\frac{H\left(Y\right)-H\left(Y|S\right)}{H\left(S\right)}.& & \left(4.7\right)\end{array}$$

   SplitInfo considers only the number of subdivisions and their relative sizes, not their purity. It is higher when there are more subdivisions and when they are more balanced in size. In fact, splitInfo is the entropy of the split where S is the random variable of interest, not Y. Thus, the gain ratio seeks to factor out the information gained from the type of partitioning as opposed to what classes were contained in the partitions.

   The gain ratio still has a drawback. A very imbalanced partitioning will yield a low value for Η(S) and thus a high value for ΔFgainRatio, even if the information gain is not very good. To overcome this, C4.5 only considers splits whose information gain scores are better than the average value [66].

5. Normalized Measures — Information Distance

   López de Mantaras has proposed using normalized information distance as a splitting criterion [51]. The distance between a target attribute Y and a splitting rule S is the sum of the two conditional entropies, which is then normalized by dividing by their joint entropy:

   $$\begin{array}{cccc}\hfill d_N\left(Y,S\right)& =\frac{H\left(Y|S\right)+H\left(S|Y\right)}{H\left(Y|S\right)}\hfill & \hfill & \left(4.8\right)\hfill \\ & =\frac{{\displaystyle \sum _{i\in S}{p}_i{\displaystyle \sum _{y\in Y}{p}_{iy}\log p_{iy}+{\displaystyle \sum _{y\in Y}{p}_i{\displaystyle \sum _{i\in S}{p}_{yi}\log p_{yi}}}}}}{{\displaystyle \sum _{i\in S}{\displaystyle \sum _{y\in Y}{p}_{iy}\log p_{iy}}}}.& & \end{array}$$

   This function is a distance metric; that is, it meets the nonnegative, symmetry, and triangle inequality properties, and dN(Y,S) = 0 when Y = S. Moreover its range is normalized to [0, 1]. Due to its construction, it solves both the high-k bias and the imbalanced partition problems of information gain (ID3) and gain ratio (C4.5).

6. DKM Criterion for Binary Classes

   In cases where the class attribute is binary, the DKM splitting criterion, named after Dietterich, Kearns, and Mansour [17, 43] offers some advantages. The authors have proven that for a given level of prediction accuracy, the expected size of a DKM-based tree is smaller than for those constructed using C4.5 or Gini.

   $$\begin{array}{lll}DKM\left(X_i\right)=2\sqrt{p_i\left(1-p_i\right)}\hfill & \hfill & \left(4.9\right)\hfill \\ \Delta F_{DKM}\left(S\right)=DKM\left(X\right)-{\displaystyle \sum _{i\in S}\frac{\left|X_i\right|}{\left|X\right|}DKM\left(X_i\right)}.\hfill & \hfill & \hfill \end{array}$$

7. Binary Splitting Criteria

   Binary decision trees as often used, for a variety of reasons. Many attributes are naturally binary, binary trees are easy to interpret, and binary architecture avails itself of additional mathematical properties. Below are a few splitting criteria especially for binary splits. The two partitions are designated 0 and 1.

   1. (a) Twoing Criterion

      This criterion is presented in CART [8] as an alternative to the Gini index. Its value coincides with the Gini index value for two-way splits.

      $$\begin{array}{ccc}\Delta F_{twoing}\left(S\right)=\frac{p_0\cdot p_1}{4}{({\displaystyle \sum _{y\in Y}\left|p_y{}_0-p_y{}_1\right|})}^2.& & \left(4.10\right)\end{array}$$

   2. (b) Orthogonality Measure

      Fayyad and Irani measure the cosine angle between the class probability vectors from the two partitions [22]. (Recall the use of probability vectors in Definition 4.1 for an impurity function.) If the split puts all instances of a given class in one partition but not the other, then the two vectors are orthogonal, and the cosine is 0. The measure is formulated as (1 –cos)θ so that we seek a maximum value.

      $$\begin{array}{ccc}ORT\left(S\right)=1-cos\left(P_0,P_1\right)=1-\frac{{\displaystyle \sum _{y\in Y}{p}_y{}_0{p}_y{}_1}}{||P_0||\cdot ||P_1||.}& & \left(4.11\right)\end{array}$$

   3. (c) Other Vector Distance Measures

      Once we see that a vector representation and cosine distance can be used, many other distance or divergence criteria come to mind, such as Jensen-Shannon divergence [75], Kolmogorov-Smirmov distance [24], and Hellinger distance [13].

8. Minimum Description Length

   Quinlan and Rivest [65] use the Minimum Description Length (MDL) approach to simultaneous work towards the best splits and the most compact tree. A description of a solution consists of an encoded classification model (tree) plus discrepancies between the model and the actual data (misclassifications). To find the minimum description, we must find the best balance between a small tree with relatively high errors and a more expansive tree with little or no misclassifications. Improved algorithms are offered in [83] and [82].

9. Comparing Splitting Criteria

   When a new splitting criterion is introduced, it is compared to others for tree size and accuracy, and sometimes for robustness, training time, or performance with specific types of data. The baselines for comparison are often C4.5(Gain ratio), CART(Gini), and sometimes DKM. For example, Shannon entropy is compared to Rényi and Tsallis entropies in [50]. While one might not be too concerned about tree size, perhaps because one does not have a large number of attributes, a smaller (but equally accurate) tree implies that each decision is accomplishing more classification work. In that sense, a smaller tree is a better tree.

   In 1999, Lim and Loh compared decision tree, nine statistical, and two neural network algorithms [49]. A key result was that there was no statistically significant difference in classification accuracy among the top 21 algorithms. However, there were large differences in training time. The most accurate algorithm, POLYCAST, required hours while similarly accurate algorithms took seconds. It is also good to remember that if high quality training data are not available, then algorithms do not have the opportunity to perform at their best. The best strategy may be to pick a fast, robust, and competitively accurate algorithm. In Lim and Loh’s tests, C4.5 and an implementation of CART were among the best in terms of balanced speed and accuracy.

Weighted error penalties

All of the above criteria have assumed that all errors have equal significance. However, for many appliations this is not the case. For a binary classifier (class is either Yes or No), there are four possible prediction results, two correct results and two errors:

1. Actual class = Yes; Predicted class = Yes: True Positive
2. Actual class = Yes; Predicted class = No: False Negative
3. Actual class = No; Predicted class = Yes: False Positive
4. Actual class = No; Predicted class = No: True Negative

If there are k different class values, then there are k(k—1) different types of errors. We can assign each type of error a weight and then modify the split goodness criterion to include these weights. For example, a binary classifier could have wFP and wFN for False Positive and False Negative, respectively. More generally, we can say the weight is wp,t, where p is the predicted class and t is the true class. wtt =0 because this represents a correct classification, hence no error.

Let us look at a few examples of weights being incorporated into an impurity function. Let Ti be the class predicted for partition Xi, which would be the most populous class value in Xi.

Weighted Error Rate : Instead of simply counting all the misclassifications, we count how many of each type of classification occurs, multiplied by its weight.

$$\begin{array}{ccc}{F}_{error,wt}=\frac{{\displaystyle {\sum }_{i\in S}{\displaystyle {\sum }_{y\in Y}{w}_{T_i,y}\left|X_{iy}\right|}}}{||X||}{\displaystyle \sum _{i\in S}{\displaystyle \sum _{y\in Y}{w}_{T_i}{}_{,y}{p}_{iy}.}}& & \left(4.12\right)\end{array}$$

Weighted Entropy : The modified entropy can be incorporated into the information gain, gain ratio, or information distance criterion.

$$\begin{array}{ccc}H{\left(Y\right)}_{wt}=-{\displaystyle \sum _{y\in Y}{w}_{T_i}{}_{,y}{p}_y\log p_y.}& & \left(4.13\right)\end{array}$$

4.2.2 Tree Pruning

Using the splitting rules presented above, the recursive decision tree induction procedure will keep splitting nodes as long as the goodness function indicates some improvement. However, this greedy strategy can lead to overfitting, a phenomenon where a more precise model decreases the error rate for the training dataset but increases the error rate for the testing dataset. Additionally, a large tree might offer only a slight accuracy improvement over a smaller tree. Overfit and tree size can be reduced by pruning, replacing subtrees with leaf nodes or simpler subtrees that have the same or nearly the same classification accuracy as the unpruned tree. As Breiman et al. have observed, pruning algorithms affect the final tree much more than the splitting rule.

Pruning is basically tree growth in reverse. However, the splitting criteria must be different than what was used during the growth phase; otherwise, the criteria would indicate that no pruning is needed. Mingers (1989) [55] lists five different pruning algorithms. Most of them require using a different data sample for pruning than for the initial tree growth, and most of them introduce a new impurity function. We describe each of them below.

1. Cost Complexity Pruning, also called Error Complexity Pruning (CART) [8]

   This multi-step pruning process aims to replace subtrees with a single node. First, we define a cost-benefit ratio for a subtree: the number of misclassification errors it removes divided by the number of leaf nodes it adds. If LX is the set of leaf node data subsets of X, then

   $$\begin{array}{ccc}error\_complexity=\frac{E\left(X\right)-{\displaystyle {\sum }_{L_i\in L_X}E\left(L_i\right)}}{\left|L_X\right|-1}.& & \left(4.14\right)\end{array}$$

   Compute error_complexity for each internal node, and convert the one with the smallest value (least increase in error per leaf) to a leaf node. Recompute values and repeat pruning until only the root remains, but save each intermediate tree. Now, compute new (estimated) error rates for every pruned tree, using a new test dataset, different than the original training set. Let T0 be the pruned tree with the lowest error rate. For the final selection, pick the smallest tree T’ whose error rate is within one standard error of T0’s error rate, where standard error is defined as $SE=\sqrt{\frac{E\left(T_0\right)\left(1-E\left(T_0\right)\right)}{N}}.$

   For example, in Figure 4.2(a), the [age > 55?] decision node receives 6 training items: 5 items have age ≤ 55, and 1 item has age > 55. The subtree has no misclassification errors and 2 leaves. If we replace the subtree with a single node, it will have an error rate of 1/6. Thus, error_complexity (age55) = $\frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.-0}{2-1}=\mathrm{0.167.}$ This is better than the [age > 18?] node, which has an error complexity of 0.333.

2. Critical Value Pruning [54]

   This pruning strategy follows the same progressive pruning approach as cost-complexity pruning, but rather than defining a new goodness measure just for pruning, it reuses the same criterion that was used for tree growth. It records the splitting criteria values for each node during the growth phase. After tree growth is finished, it goes back in search of interior nodes whose splitting criteria values fall below some threshold. If all the splitting criteria values in a node’s subtree are also below the threshold, then the subtree is replaced with a single leaf node. However, due to the difficulty of selecting the right threshold value, the practical approach is to prune the weakest subtree, remember this pruned tree, prune the next weakest subtree, remember the new tree, and so on, until only the root remains. Finally, among these several pruned trees, the one with the lowest error rate is selected.

3. Minimum Error Pruning [58]

   The error rate defined in Equation 4.1 is the actual error rate for the sample (training) data. Assuming that all classes are in fact equally likely, Niblett and Bratko [58] prove that the expected error rate is

   $$\begin{array}{ccc}{E}^{\prime }\left(X_i\right)=\frac{\left|X_i\right|\cdot E\left(X_i\right)+m-1}{\left|X_i\right|+m},& & \left(4.15\right)\end{array}$$

   where m is the number of different classes. Using this as an impurity criterion, this pruning method works just like the tree growth step, except it merges instead of splits. Starting from the parent of a leaf node, it compares its expected error rate with the size-weighted sum of the error rates of its children. If the parent has a lower expected error rate, the subtree is converted to a leaf. The process is repeated for all parents of leaves until the tree has been optimized. Mingers [54] notes a few flaws with this approach: 1) the assumption of equally likely classes is unreasonable, and 2) the number of classes strongly affects the degree of pruning.

   Looking at the [age > 55?] node in Figure 4.2(a) again, the current subtree has a score $E^{\prime }\left(subtree\right)=\left(5/6\right)\frac{5\left(0\right)+2-1}{5+2}+\left(1/6\right)\frac{1\left(0\right)+2-1}{1+2}=\left(5/6\right)\left(1/7\right)+\left(1/6\right)\left(1/3\right)=\mathrm{0.175.}$ If we change the node to a leaf, we get $E\text{'}\left(leaf\right)=\frac{6\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.\right)+2-1}{6+2}=\raisebox{1ex}{$2$}\!\left/ \!\raisebox{-1ex}{$8$}\right.=0.250$ The pruned version has a higher expected error, so the subtree is not pruned.

4. Reduced Error Pruning (ID3) [64]

   This method uses the same goodness criteria for both tree growth and pruning, but uses different data samples for the two phases. Before the initial tree induction, the training dataset is divided into a growth dataset and a pruning dataset. Initial tree induction is performed using the growth dataset. Then, just as in minimum error pruning, we work bottom-to-top, but this time the pruning dataset is used. We retest each parent of children to see if the split is still advantageous, when a different data sample is used. One weakness of this method is that it requires a larger quantity of training data. Furthermore, using the same criteria for growing and pruning will tend to under-prune.

5. Pessimistic Error Pruning (ID3, C4.5) [63, 66]

   This method eliminates the need for a second dataset by estimating the training set bias and compensating for it. A modified error function is created (as in minimum error pruning), which is used for bottom-up retesting of splits. In Quinlan’s original version, the adjusted error is estimated to be $\frac{1}{2}$ per leaf in a subtree. Given tree node v, let T(v) be the subtree rooted at v, and L(v) be the leaf nodes under v. Then,

   $$\begin{array}{ccc}\text{not}\text{purned:}{E}_{pess}\left(T\left(v\right)\right)={\displaystyle \sum _{l\in L\left(v\right)}E\left(l\right)+\frac{\left|L\left(v\right)\right|}{2}}& & \left(4.16\right)\end{array}$$

   $$\begin{array}{ll}\text{if}\text{purned:}{E}_{pess}\left(v\right)=E\left(v\right)+\frac{1}{2}.\hfill & \left(4.17\right)\hfill \end{array}$$

   Because this adjustment alone might still be too optimistic, the actual rule is that a subtree will be pruned if the decrease in error is larger than the Standard Error.

   In C4.5, Quinlan modified pessimistic error pruning to be more pessimistic. The new estimated error is the upper bound of the binomial distribution confidence interval, UCF(E,|Xi|). C4.5 uses 25% confidence by default. Note that the binomial distribution should not be approximated by the normal distribution, because the approximation is not good for small error rates.

   For our [age > 55?] example in Figure 4.2(a), C4.5 would assign the subtree an error score of $\raisebox{1ex}{$5$}\!\left/ \!\raisebox{-1ex}{$6$}\right.U_{CF}\left(0,5\right)+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$6$}\right.\right)U_{CF}\left(0,1\right)=\left(0.833\right)0.242+\left(0.166\right).750=0.327$ If we prune, then the new root has a score of UCF (1,6) = 0.390. The original split has a better error score, so we retain the split.

6. Additional Pruning Methods

   Mansour [52] has computed a different upper bound for pessimistic error pruning, based on the Chernoff bound. The formula is simpler than Quinlan’s but requires setting two parameters. Kearns and Mansour [44] describe an algorithm with good theoretical guarantees for near- optimal tree size. Mehta et al. present an MDL-based method that offers a better combination of tree size and speed than C4.5 or CART on their test data.

Esposito et al. [20] have compared the five earlier pruning techniques. They find that cost-complexity pruning and reduced error pruning tend to overprune, i.e., create smaller but less accurate decision trees. Other methods (error-based pruning, pessimistic error pruning, and minimum error pruning) tend to underprune. However, no method clearly outperforms others on all measures. The wisest strategy for the user seems to be to try several methods, in order to have a choice.

4.3 Case Studies with C4.5 and CART

To illustrate how a complete decision tree classifier works, we look at the two most prominent algorithms: CART and C4.5. Interestingly, both are listed among the top 10 algorithms in all of data mining, as chosen at the 2006 International Conference on Data Mining [85].

CART was developed by Breiman, Friedman, Olshen, and Stone, as a research work. The decision tree induction problem and their solution is described in detail in their 1984 book, Classification and Regression Trees [8]. C4.5 gradually evolved out of ID3 during the late 1980s and early 1990s. Both were developed by J. Ross Quinlan. Early on C4.5 was put to industrial use, so there has been a steady stream of enhancements and added features. We focus on the version described in Quinlan’s 1993 book, C4.5: Programs for Machine Learning [66].

4.3.1 Splitting Criteria

CART: CART was designed to construct binary trees only. It introduced both the Gini and twoing criteria. Numerical attributes are first sorted, and then the k−1 midpoints between adjacent numerical values are used as candidate split points. Categorical attributes with large domains must try all 2k−1 −1 possible binary splits. To avoid excessive computation, the authors recommend not having a large number of different categories.

C4.5: In default mode, C4.5 makes binary splits for numerical attributes and k-way splits for categorical attributes. ID3 used the Information Gain criterion. C4.5 normally uses the Gain Ratio, with the caveat that the chosen splitting rule must also have an Information Gain that is stronger than the average Information Gain. Numerical attributes are first sorted. However, instead of selecting the midpoints, C4.5 considers each of the values themselves as the split points. If the sorted values are (x1,x2, …,xn), then the candidate rules are {x > x1,x > x2, … ,x > xn—1}. Optionally, instead of splitting categorical attributes into k branches, one branch for each different attribute value, they can be split into b branches, where b is a user-designated number. To implement this, C4.5 first performs the k-way split and then greedily merges the most similar children until there are b children remaining.

4.3.2 Stopping Conditions

In top-down tree induction, each split produces new nodes that recursively become the starting points for new splits. Splitting continues as long as it is possible to continue and to achieve a net improvement, as measured by the particular algorithm. Any algorithm will naturally stop trying to split a node when either the node achieves class purity or the node contain only a single item. The node is then designated a leaf node, and the algorithm chooses a class label for it.

However, stopping only under these absolute conditions tends to form very large trees that are overfit to the training data. Therefore, additional stopping conditions that apply pre-pruning may be used. Below are several possible conditions. Each is independent of the other and employs some threshold parameter.

• Data set size reaches a minimum.
• Splitting the data set would make children that are below the minimize size.
• Splitting criteria improvement is too small.
• Tree depth reaches a maximum.
• Number of nodes reaches a maximum.

CART: Earlier, the authors experimented with a minimum improvement rule: $\left|\Delta F_{Gini}\right|>\text{β}.$ How-ever, this was abandoned because there was no right value for β. While the immediate benefit of splitting a node may be small, the cumulative benefit from multiple levels of splitting might be substantial. In fact, even if splitting the current node offers only a small reduction of impurity, its chidren could offer a much larger reduction. Consequently, CART’s only stopping condition is a minimum node size. Instead, it strives to perform high-quality pruning.

C4.5: In ID3, a Chi-squared test was used as a stopping condition. Seeing that this sometimes caused overpruning, Quinlan removed this stopping condition in C4.5. Like CART, the tree is allowed to grow unfettered, with only one size constraint: any split must have at least two children containing at least nmin training items each, where nmin defaults to 2.

4.3.3 Pruning Strategy

CART uses cost complexity pruning. This is one of the most theoretically sound pruning methods. To remove data and algorithmic bias from the tree growth phase, it uses a different goodness criterion and a different dataset for pruning. Acknowledging that there is still statistical uncertainty about the computations, a standard error statistic is computed, and the smallest tree that is with the error range is chosen.

C4.5 uses pessimistic error pruning with the binomial confidence interval. Quinlan himself acknowledges that C4.5 may be applying statistical concepts loosely [66]. As a heuristic method, however, it works about as well as any other method. Its major advantage is that it does not require a separate dataset for pruning. Moreover, it allows a subtree to be replaced not only by a single node but also by the most commonly selected child.

4.3.4 Handling Unknown Values: Induction and Prediction

One real-world complication is that some data items have missing attribute values. Using the notation x = {x1,x2, … ,xd}, some of the xi values may be missing (null). Missing values generate three concerns:

1. Choosing the Best Split: If a candidate splitting criterion uses attribute Ai but some items have no values for Ai, how should we account for this? How do we select the best criteria, when they have different proportions of missing values?
2. Partitioning the Training Set: Once a splitting criteria is selected, to which child node will the imcomplete data items be assigned?
3. Making Predictions: If making class predictions for items with missing attribute values, how will they proceed down the tree?

Recent studies have compared different techniques for handling missing values in decision trees [18, 67]. CART and C4.5 take very different approaches for addressing these concerns.

CART: CART assumes that missing values are sparse. It calculates and compares splitting criteria using only data that contain values for the relevant attributes. However, if the top scoring splitting criteria is on an attribute with some missing values, then CART selects the best surrogate split that has no missing attribute values. For any splitting rule S, a surrogate rule generates similar partitioning results, and the surrogate S’ is the one that is most strongly correlated. For each actual rule selected, CART computes and saves a small ordered list of top surrogate rules. Recall that CART performs binary splits. For dataset Xi, p11 is the fraction of items that is classified by both S and S’ as state 1; p00 is the fraction that is classifed by both as state 0. The probability that a random item is classified the same by both S and S’ is p(S,S’) = p11(S,S’) + p00(S,S’). This measure is further refined in light of the discriminating power of S. The final predictive measure of association between S and S’ is

$$\begin{array}{ccc}\text{λ}\left(S^{\prime }|S\right)=\frac{min\left(p_0\left(S\right),p_1\left(S\right)\right)-\left(1-p\left(S,S^{\prime }\right)\right)}{min\left(p_0\left(S\right),p_1\left(S\right)\right)}.& & \left(4.18\right)\end{array}$$

The scaling factor min(p0(S),p1(S)) estimates the probability that S correctly classifies an item. Due to the use of surrogates, we need not worry about how to partition items with missing attribute values.

When trying to predict the class of a new item, if a missing attribute is encountered, CART looks for the best surrogate rule for which the data item does have an attribute value. This rule is used instead. So, underneath the primary splitting rules in a CART tree are a set of backup rules. This method seems to depend much on there being highly correlated attributes. In practice, decision trees can have some robustness; even if an item is misdirected at one level, there is some probability that it will be correctly classified in a later level.

C4.5: To compute the splitting criteria, C4.5 computes the information gain using only the items with known attribute values, then weights this result by the fraction of total items that have known values for A. Let XA be the data subset of X that has known values for attribute A.

$$\begin{array}{ccc}\Delta F_{infoGain}\left(S\right)=\frac{\left|X_A\right|}{\left|X\right|}\left(H_{X_A}\left(Y\right)-H_{X_A}\left(Y|S\right)\right).& & \left(4.19\right)\end{array}$$

Additionally, splitlnfo(S), the denominator in C4.5’s Gain Ratio, is adjusted so that the set of items with unknown values is considered a separate partition. If S previously made a k-way split, splitlnfo(S) is computed as though it were a (k +1)-way split.

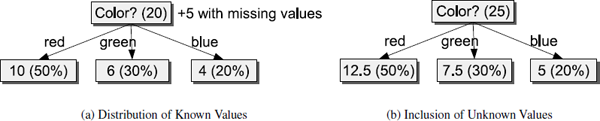
To partitioning the training set, C4.5 spreads the items with unknown values according to the same distribution ratios as the items with known attribute values. In the example in Figure 4.3, we have 25 items. Twenty of them have known colors and are partitioned as in Figure 4.3(a). The 5 remaining items are distributed in the same proportions as shown in Figure 4.3(b). This generates fractional training items. In subsequent tree levels, we may make fractions of fractions. We now have a probabilistic tree.

If such a node is encountered while classifying unlabeled items, then all children are selected, not just one, and the probabilities are noted. The prediction process will end at several leaf nodes, which collectively describe a probability distribution. The class with the highest probability can be used for the prediction.

4.3.5 Other Issues: Windowing and Multivariate Criteria

To conclude our case studies, we take a look at a few notable features that distinguish C4.5 and CART.

Windowing in C4.5: Windowing is the name that Quinlan uses for a sampling technique that was originally intended to speed up C4.5’s tree induction process. In short, a small sample, the window, of the training set is used to construct an initial decision tree. The initial tree is tested using the remaining training data. A portion of the misclassified items are added to the window, a new tree is inducted, and the non-window training data are again used for testing. This process is repeated until the decision tree’s error rate falls below a target threshold or the error rate converges to a constant level.

In early versions, the initial window was selected uniformly randomly. By the time of this 1993 book, Quinlan had discovered that selecting the window so that the different class values were represented about equally yielded better results. Also by that time, computer memory size and processor speeds had improved enough so that the multiple rounds with windowed data were not always faster than a single round with all the data. However, it was discovered that the multiple rounds improve classification accuracy. This is logical, since the windowing algorithm is a form of boosting.

Multivariate Rules in CART: Breiman et al. investigated the use of multivariate splitting criteria, decision rules that are a function of more than one variable. They considered three different forms: linear combinations, Boolean combinations, and ad hoc combinations. CART considers combining only numerical attributes. For this discussion, assume A = (A1, … ,Ad) are all numerical. In the univariable case, for Ai, we search the |Ai|−1 possible split points for the one that yields the maximal value of C. Using a geometric analogy, if d = 3, we have a 3-dimensional data space. A univariable rule, such as xi < C, defines a half-space that is orthogonal to one of the axes. However, if we lift the restriction that the plane is orthogonal to an axis, then we have the more general half-space ${\displaystyle {\sum }_i{c}_i{x}_i<C}.$ Note that a coefficient ci can be positive or negative. Thus, to find the best multivariable split, we want to find the values of C and c = (c1, … ,cd), normalized to ${\displaystyle {\sum }_i{c}_i^2=1},$ such that ΔF is optimized. This is clearly an expensive search. There are many search heuristics that could accelerate the search, but they cannot guarantee to find the globally best rule. If a rule using all d different attributes is found, it is likely that some of the attributes will not contribute much. The weakest coefficients can be pruned out.

CART also offers to search for Boolean combinations of rules. It is limited to rules containing only conjunction or disjuction. If Si is a rule on attribute Ai, then candidate rules have the form $S=S_1\wedge S_2\wedge \mathrm{...}\wedge S_d$ or $S=S_1\vee S_2\vee \mathrm{...}\vee S_d$. A series of conjunctions is equivalent to walking down a branch of the tree. A series of disjunctions is equavalent to merging children. Unlike linear combinations of rules that offer possible splits that are unavailable with univariate splits, Boolean combinations do not offer a new capability. They simply compress what would otherwise be a large, bushy decision tree.

The ad hoc combination is a manual pre-processing to generate new attributes. Rather than a specific computational technique, this is an acknowledgment that the given attributes might not have good linear correlation with the class variable, but that humans sometimes can study a smal dataset and have helpful intuitions. We might see that a new intermediate function, say the log or square of any existing parameter, might fit better.

None of these features have been aggressively adapted in modern decision trees. In the end, a standard univariate decision tree induction algorithm can always create a tree to classify a training set. The tree might not be as compact or as accurate on new data as we would like, but more often than not, the results are competitive with those of other classification techniques.

4.4 Scalable Decision Tree Construction

The basic decision tree algorithms, such as C4.5 and CART, work well when the dataset can fit into main memory. However, as datasets tend to grow faster than computer memory, decision trees often need to be constructed over disk-resident datasets. There are two major challenges in scaling a decision tree construction algorithm to support large datasets. The first is the very large number of candidate splitting conditions associated with numerical attributes. The second is the recursive nature of the algorithm. For the computer hardware to work efficiently, the data for each node should be stored in sequential blocks. However, each node split conceptually regroups the data. To maintain disk and memory efficiency, we must either relocate the data after every split or maintain special data structures.

One of the first decision tree construction methods for disk-resident datasets was SLIQ [53]. To find splitting points for a numerical attribute, SLIQ requires separation of the input dataset into attribute lists and sorting of attribute lists associated with a numerical attribute. An attribute list in SLIQ has a record-id and attribute value for each training record. To be able to determine the records associated with a non-root node, a data-structure called a class list is also maintained. For each training record, the class list stores the class label and a pointer to the current node in the tree. The need for maintaining the class list limits the scalability of this algorithm. Because the class list is accessed randomly and frequently, it must be maintained in main memory. Moreover, in parallelizing the algorithm, it needs to be either replicated, or a high communication overhead is incurred.

A somewhat related approach is SPRINT [69]. SPRINT also requires separation of the dataset into class labels and sorting of attribute lists associated with numerical attributes. The attribute lists in SPRINT store the class label for the record, as well as the record-id and attribute value. SPRINT does not require a class list data structure. However, the attribute lists must be partitioned and written back when a node is partitioned. Thus, there may be a significant overhead for rewriting a disk-resident data set. Efforts have been made to reduce the memory and I/O requirements of SPRINT [41, 72]. However, they do not guarantee the same precision from the resulting decision tree, and do not eliminate the need for writing-back the datasets.

In 1998, Gehrke proposed RainForest [31], a general framework for scaling decision tree construction. It can be used with any splitting criteria. We provide a brief overview below.

4.4.1 RainForest-Based Approach

RainForest scales decision tree construction to larger datasets, while also effectively exploiting the available main memory. This is done by isolating an AVC (Attribute-Value, Classlabel) set for a given attribute and node being processed. An AVC set for an attribute simply records the number of occurrences of each class label for each distinct value the attribute can take. The size of the AVC set for a given node and attribute is proportional to the product of the number of distinct values of the attribute and the number of distinct class labels. The AVC set can be constructed by taking one pass through the training records associated with the node.

Each node has an AVC group, which is the collection of AVC sets for all attributes. The key observation is that though an AVC group does not contain sufficient information to reconstruct the training dataset, it contains all the necessary information for selecting the node’s splitting criterion. One can expect the AVC group for a node to easily fit in main memory, though the RainForest framework includes algorithms that do not require this. The algorithm initiates by reading the training dataset once and constructing the AVC group of the root node. Then, the criteria for splitting the root node is selected.

The original RainForest proposal includes a number of algorithms within the RainForest framework to split decision tree nodes at lower levels. In the RF-read algorithm, the dataset is never partitioned. The algorithm progresses level by level. In the first step, the AVC group for the root node is built and a splitting criteria is selected. At any of the lower levels, all nodes at that level are processed in a single pass if the AVC group for all the nodes fit in main memory. If not, multiple passes over the input dataset are made to split nodes at the same level of the tree. Because the training dataset is not partitioned, this can mean reading each record multiple times for one level of the tree.

Another algorithm, RF-write, partitions and rewrites the dataset after each pass. The algorithm RF-hybrid combines the previous two algorithms. Overall, RF-read and RF-hybrid algorithms are able to exploit the available main memory to speed up computations, but without requiring the dataset to be main memory resident.

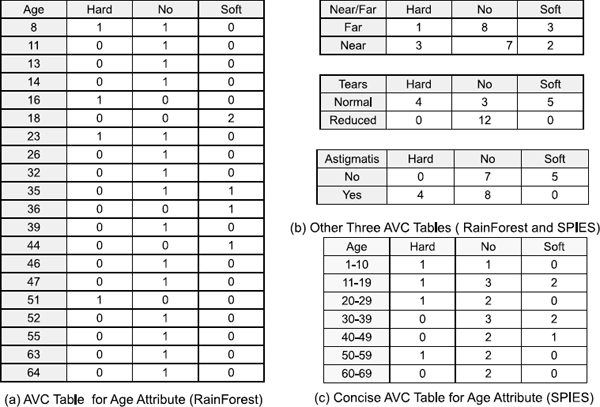
Figure 4.4(a) and 4.4(b) show the AVC tables for our Contact Lens dataset from Table 4.1. The Age table is largest because it is a numeric attribute with several values. The other three tables are small because their attributes have only two possible values.

4.4.2 SPIES Approach

In [39], a new approach, referred to as SPIES (Statistical Pruning of Intervals for Enhanced Scalability), is developed to make decision tree construction more memory and communication efficient. The algorithm is presented in the procedure SPIES-Classifier (Figure 4.2). The SPIES method is based on AVC groups, like the RainForest approach. The key difference is in how the numerical attributes are handled. In SPIES, the AVC group for a node is comprised of three subgroups:

Small AVC group: This is primarily comprised of AVC sets for all categorical attributes. Since the number of distinct elements for a categorical attribute is usually not very large, the size of these AVC sets is small. In addition, SPIES also adds the AVC sets for numerical attributes that only have a small number of distinct elements. These are built and treated in the same fashion as in the RainForest approach.

Concise AVC group: The range of numerical attributes that have a large number of distinct elements in the dataset is divided into intervals. The number of intervals and how the intervals are constructed are important parameters to the algorithm. The original SPIES implementation uses equal-width intervals. The concise AVC group records the class histogram (i.e., the frequency of occurrence of each class) for each interval.

Partial AVC group: Based upon the concise AVC group, the algorithm computes a subset of the values in the range of the numerical attributes that are likely to contain the split point. The partial AVC group stores the class histogram for the points in the range of a numerical attribute that has been determined to be a candidate for being the split condition.

SPIES uses two passes to efficiently construct the above AVC groups. The first pass is a quick Sampling Step. Here, a sample from the dataset is used to estimate small AVC groups and concise numerical attributes. Based on these, it obtains an estimate of the best (highest) gain, denoted as g’. Then, using g’, the intervals that do not appear likely to include the split point will be pruned. The second pass is the Completion Step. Here, the entire dataset is used to construct complete versions of the three AVC subgroups. The partial AVC groups will record the class histogram for all of the points in the unpruned intervals.

 l: function SPIES-CLASSlFlER(Level L, Dataset X)

 2:  for Node v ∈ Level L do

 {*Sampling Step*}

 3:   Sample S ← Sampling (X);

 4:   Build_Small_AVCGroup(S);

 5:   Build_Concise_AVCGroup(S);

 6:   g’ ← Find_Best_Gain(AVCGroup);

 7:   Partial-AVCGroup ← Pruning(g’, Concise_AVCGroup);

 {*Completion Step*}

 8:   Build_Small_AVCGroup(X);

 9:   Build_Concise_AVCGroup(X);

10:   Build_Partial_AVCGroup(X);

1l:   g ← Find_Best_Gain(AVCGroup);

12:   if False_Pruning(g, Concise_AVCGroup)

 {*Additional Step*}

13:   Partial-AVCGroup ← Pruning(g, Concise_AVCGroup);

14:   Build_Partial_AVCGroup(X);

15:   g ← Find_Best_Gain(AVCGroup);

16:   if not satisfy_stop_condition(v)

17:   Split_Node(v);

18: end for

19: end function

After that, the best gain g from these AVC groups can be obtained. Because the pruning is based upon only an estimate of small and concise AVC groups, false pruning may occur. However, false pruning can be detected using the updated values of small and concise AVC groups during the completion step. If false pruning has occurred, SPIES can make another pass on the data to construct partial AVC groups for points in falsely pruned intervals. The experimental evaluation shows SPIES significantly reduces the memory requirements, typically by 85% to 95%, and that false pruning rarely happens.

In Figure 4.4(c), we show the concise AVC set for the Age attribute, assuming 10-year ranges. The table size depends on the selected range size. Compare its size to the RainForest AVC in Figure 4.4(a). For discrete attributes and numerical attributes with small distinct values, RainForest and SPIES generate the same small AVC tables, as in Figure 4.4(b).

Other scalable decision tree construction algorithms have been developed over the years; the representatives include BOAT [30] and CLOUDS [2]. BOAT uses a statistical technique called bootstrapping to reduce decision tree construction to as few as two passes over the entire dataset. In addition, BOAT can handle insertions and deletions of the data. CLOUDS is another algorithm that uses intervals to speed up processing of numerical attributes [2]. However, CLOUDS’ method does not guarantee the same level of accuracy as one would achieve by considering all possible numerical splitting points (though in their experiments, the difference is usually small). Further, CLOUDS always requires two scans over the dataset for partitioning the nodes at one level of the tree. More recently, SURPASS [47] makes use of linear discriminants during the recursive partitioning process. The summary statistics (like AVC tables) are obtained incrementally. Rather than using summary statistics, [74] samples the training data, with confidence levels determined by PAC learning theory.

4.4.3 Parallel Decision Tree Construction

Several studies have sought to further speed up the decision tree construction using parallel machines. One of the first such studies is by Zaki et al. [88], who develop a shared memory paral-lelization of the SPRINT algorithm on disk-resident datasets. In parallelizing SPRINT, each attribute list is assigned to a separate processor. Also, Narlikar has used a fine-grained threaded library for parallelizing a decision tree algorithm [57], but the work is limited to memory-resident datasets. A shared memory parallelization has been proposed for the RF-read algorithm [38].

The SPIES approach has been parallelized [39] using a middleware system, FREERIDE (Framework for Rapid Implementation of Datamining Engines) [36, 37], which supports both distributed and shared memory parallelization on disk-resident datasets. FREERIDE was developed in early 2000 and can be considered an early prototype of the popular MapReduce/Hadoop system [16]. It is based on the observation that a number of popular data mining algorithms share a relatively similar structure. Their common processing structure is essentially that of generalized reductions. During each phase of the algorithm, the computation involves reading the data instances in an arbitrary order, processing each data instance (similar to Map in MapReduce), and updating elements of a Reduction object using associative and commutative operators (similar to Reduce in MapReduce).

In a distributed memory setting, such algorithms can be parallelized by dividing the data items among the processors and replicating the reduction object. Each node can process the data items it owns to perform a local reduction. After local reduction on all processors, a global reduction is performed. In a shared memory setting, parallelization can be done by assigning different data items to different threads. The main challenge in maintaining the correctness is avoiding race conditions when different threads may be trying to update the same element of the reduction object. FREERIDE has provided a number of techniques for avoiding such race conditions, particularly focusing on the memory hierarchy impact of the use of locking. However, if the size of the reduction object is relatively small, race conditions can be avoided by simply replicating the reduction object.

The key observation in parallelizing the SPIES-based algorithm is that construction of each type of AVC group, i.e., small, concise, and partial, essentially involves a reduction operation. Each data item is read, and the class histograms for appropriate AVC sets are updated. The order in which the data items are read and processed does not impact the final value of AVC groups. Moreover, if separate copies of the AVC groups are initialized and updated by processing different portions of the data set, a final copy can be created by simply adding the corresponding values from the class histograms. Therefore, this algorithm can be easily parallelized using the FREERIDE middleware system.

More recently, a general strategy was proposed in [11] to transform centralized algorithms into algorithms for learning from distributed data. Decision tree induction is demonstrated as an example, and the resulting decision tree learned from distributed data sets is identical to that obtained in the centralized setting. In [4] a distributed hierarchical decision tree algorithm is proposed for a group of computers, each having its own local data set. Similarly, this distributed algorithm induces the same decision tree that would come from a sequential algorithm with full data on each computer. Two univariate decision tree algorithms, C4.5 and univariate linear discriminant tree, are parallelized in [87] in three ways: feature-based, node-based, and data-based. Fisher’s linear discriminant function is the basis for a method to generate a multivariate decision tree from distributed data [59]. In [61] MapReduce is employed for massively parallel learning of tree ensembles. Ye et al. [86] take on the challenging task of combining bootstrapping, which implies sequential improvement, with distributed processing.

4.5 Incremental Decision Tree Induction

Non-incremental decision tree learning methods assume that the training items can be accommodated simultaneously in the main memory or disk. This assumption grieviously limits the power of decision trees when dealing with the following situations: 1) training data sets are too large to fit into the main memory or disk, 2) the entire training data sets are not available at the time the tree is learned, and 3) the underlying distribution of training data sets is changed. Therefore, incremental decision tree learning methods have received much attention from the very beginning [68]. In this section, we examine the techniques for learning decision tree incrementally, especially in a streaming data setting.

Streaming data, represented by an endless sequence of data items, often arrive at high rates. Unlike traditional data available for batch (or off-line) prcessing, the labeled and unlabeled items are mixed together in the stream as shown in Figure 4.5.

In Figure 4.5, the shaded blocks are labeled records. We can see that labeled items can arrive unexpectedly. Therefore, this situation proposes new requirements for learning algorithms from streaming data, such as iterative, single pass, any-time learning [23].

To learn decision trees from streaming data, there are two main strategies: a greedy approach [14, 68, 78–80] and a statistical approach [19, 33]. In this section, we introduce both approaches, which are illustrated by two famous families of decision trees, respectively: ID3 and VFDT.

4.5.1 ID3 Family

Incremental induction has been discussed almost from the start. Schlimmer [68] considers incremental concept induction in general, and develops an incremental algorithm named ID4 with a modification of Quinlan’s top-down ID3 as a case study. The basic idea of ID4 is listed in Algorithm 4.3.

In Algorithm 4.3, Av stands for all the attributes contained in tree node v, and $A_v^{*}$ for the attribute with the lowest E-score. Meanwhile count nijy(v) records the number of records observed by node v having value xij for attribute Ai and being in class y. In [68], the authors only consider positive and negative classes. That means |Y| = 2. vr stands for the immediate child of v containing item r.

Here, the E-score is the result of computing Quinlan’s expected information function E of an attribute at any node. Specificially, at node v,

• np: # positive records;
• nn:# negative records;
• $n_{ij}^P$: # positive records with value xij for attribute Ai;
• $n_{ij}^n$: # negative records with value xij for attribute Ai;

 1: for each Ai ∈ Av, where Av ⊆ A do

 2: Increment count nijy(v) of class y for Ai;

 3: end for

 4: if all items observed by v are from class y then

 5: return;

 6: else

 7: if v is a leaf node then

 8:  Change v to be an internal node;

 9:  Update $A_v^{*}$ with lowest E-score;

10: else if $A_v^{*}$ does not have the lowest E-score then

11:  Remove all children Child (v) of v;

12:  Update $A_v^{*}$;

13: end if

14: if Child(v) = $\cancel{0}$ then

15:  Generate the set Child(v) for all values of attribute $A_v^{*}$;

16: end if

17: ID4(vr,r);

18: end if

Then

$$\begin{array}{ccc}E\left(A_i\right)={\displaystyle \sum _{j=1}^{\left|A_i\right|}\frac{n_{ij}^p+n_{ij}^n}{n^p+n^n}I\left(n_{ij}^p,n_{ij}^n\right)},& & \left(4.20\right)\end{array}$$

With

$$I\left(x,y\right)=\{\begin{array}{ll}0\hfill & \text{if}x=0\text{or}y=0\hfill \\ -\frac{x}{x+y}\log \frac{x}{x+y}-\frac{y}{x+y}\log \frac{y}{x+y}\hfill & \text{otherwise}.\hfill \end{array}$$

In Algorithm 4.3, we can see that whenever an erroneous splitting attribute is found at v (Line 10), ID4 simply removes all the subtrees rooted at v’s immediate children (Line 11), and computes the correct splitting attribute $A_v^{*}$ (Line 12).

Clearly ID4 is not efficient because it removes the entire subtree when a new $A_v^{*}$ is found, and this situation could render certain concepts unlearnable by ID4, which could be induced by ID3. Utgoff introduced two improved algorithms: ID5 [77] and ID5R [78]. In particular, ID5R guarantees it will produce the same decision tree that ID3 would have if presented with the same training items.

In Algorithm 4.4, when a splitting test is needed at node v, an arbitrary attribute Ao ∈ Av is chosen; further, according to counts nijy(v) the optimal splitting attribute $A_v^{*}$ is calculated based on E-score. If $A_v^{*}$ ≠ Ao, the splitting attribute $A_v^{*}$ is pulled up from all its subtrees (Line 10) to v, and all its subtrees are recursively updated similarly (Line 11 and 13).

The fundamental difference between ID4 (Algorithm 4.3) and ID5R (Algorithm 4.4) is that when ID5R finds a wrong subtree, it restructures the subtree (Line 11 and 13) instead of discarding it and replacing it with a leaf node for the current splitting attribute. The restructuring process in Algorithm 4.4 is called the pull-up procedure. The general pull-up procedure is as follows, and illustrated in Figure 4.6. In Figure 4.6, left branches satisfy the splitting tests, and right ones do not.

1. if attribute $A_v^{*}$ is already at the root, then stop;
2. otherwise,

 1: If v = null, make v a leaf node; return;

 2: If v is a leaf, and all items observed by v are from class y; return;

 3: if v is a leaf node then

 4: Split v by choosing an arbitrary attribute;

 5: end if

 6: for Ai ∈ Av, where Av ⊆ A do

 7: Increment count nijy(v) of class y for $A_v^{*}$;

 8: end for

 9: if $A_v^{*}$ does not have the lowest E-score then

10: Update $A_v^{*}$, and restructure v;

11: Recursively reestablish vc ∈ Child(v) except the branch vr for r;

12: end if

13: Recursively update subtree vr along the branches with the value occuring in x;

1. Recursively pull the attribute $A_v^{*}$ to the root of each immediate subtree of v. Convert any leaves to internal nodes as necessary, choosing $A_v^{*}$ as splitting attribute.
2. Transpose the subtree rooted at v, resulting in a new subtree with $A_v^{*}$ at the root, and the old root attribute Ao at the root of each immediate subtree of v.

There are several other works that fall into the ID3 family. A variation for multivariate splits appears in [81], and an improvement of this work appears in [79], which is able to handle numerical attributes. Having achieved an arguably efficient technique for incrementally restructuring a tree, Utgoff applies this technique to develop Direct Metric Tree Induction (DMTI). DMTI leverages fast tree restructuring to fashion an algorithm that can explore more options than traditional greedy top-down induction [80]. Kalles [42] speeds up ID5R by estimating the minimum number of training items for a new attribute to be selected as the splitting attribute.

4.5.2 VFDT Family

In the Big Data era, applications that generate vast streams of data are ever-present. Large retail chain stores like Walmart produce millions of transaction records every day or even every hour, giant telecommunication companies connect millions of calls and text messages in the world, and large banks receive millions of ATM requests throughout the world. These applications need machine learning algorithms that can learn from extremely large (probably infinite) data sets, but spend only a small time with each record. The VFDT learning system was proposed by Domingos [19] to handle this very situation.

VFDT (Very Fast Decision Tree learner) is based on the Hoeffding tree, a decision tree learning method. The intuition of the Hoeffding tree is that to find the best splitting attribute it is sufficient to consider only a small portion of the training items available at a node. To acheive this goal, the Hoeffding bound is utilized. Basically, given a real-valued random variable r having range R, if we have observed n values for this random variable, and the sample mean is r, then the Hoeffding bound states that, with probability 1−δ, the true mean of r is at least r - ɛ, where

$$\begin{array}{ccc}\text{ε}=\sqrt{\frac{R^{2}ln\left(1/\text{δ}\right)}{2n}}.& & \left(4.21\right)\end{array}$$

Based on the above analysis, if at one node we find that F(Ai) — F(Aj) ≥ ɛ, where F is the splitting criterion, and Ai and Aj are the two attributes with the best and second best F respectively, then Ai is the correct choice with probability 1−δ. Using this novel observation, the Hoeffding tree algorithm is developed (Algorithm 4.5).

 1: Let T be a tree with a single leaf v1;

 2: Let A1 = A;

 3: Set count nijy(v1) = 0 for each y ∈ Y, each value xij of each attribute Ai ∈ A

 4: for each training record 〈x,y㌉ in S do

 5: Leaf v = classify(〈x,y〉,T);

 6: For each xijy ∈ x: Increment count nijy(v);

 7: if nijy(v) does not satisfy any stop conditions then

 8:  $A_v^{*}$ = F(nijy(v), δ);

 9:  Replace v by an internal node that splits on $A_v^{*}$;

10:  for each child vm of v do

11:    Let Am = Av − {$A_v^{*}$};

12:    Initialize nijy(vm);

13:  end for

14: end if

15: end for

16: return T;

In Algorithm 4.5, the nijy counts are sufficient to calculate F. Initially decision tree T only contains a leaf node v1 (Line 1), and v1 is labeled by predicting the most frequent class. For each item 〈x,y〉, it is first classified into a leaf node v through T (Line 5). If the items in v are from more than one class, then v is split according to the Hoeffding bound (Line 8). The key property of the Hoeffding tree is that under realistic assumptions (see [19] for details), it is possible to guarantee that the generated tree is asymptotically close to the one produced by a batch learner.

When dealing with streaming data, one practical problem that needs considerable attention is concept drift, which does not satisfy the assumption of VFDT: that the sequential data is a random sample drawn from a stationary distribution. For example, the behavior of customers of online shopping may change from weekdays to weekends, from season to season. CVFDT [33] has been developed to deal with concept drift.

CVFDT utilizes two strategies: a sliding window W of training items, and alternate subtrees ALT(v) for each internal node v. The decision tree records the statistics for the |W| most recent unique training items. More specifically, instead of learning a new model from scratch when a new training item 〈x,y〉 comes, CVFDT increments the sufficient statistics nijy at corresponding nodes for the new item and decrements the counts for the oldest records 〈xo,yo) in the window. Periodically, CVFDT reevaluates the classification quality and replaces a subtree with one of the alternate subtrees if needed.

 1: let T be a tree with a single leaf v1;

 2: let ALT(v1) be an initially empty set of alternate trees for v1;

 3: let A1 = A;

 4: Set count nijy(v1) = 0 for each y ∈ Y and each value xij for Ai ∈ A;

 5: Set record window W = 0;

 6: for each training record 〈x,y〉 in S do

 7: L = classify({〈x,y〉, T), where L contains all nodes that {〈x,y〉 passes through using T and all trees in ALT;

 8: W = W ⋃{{〈x,y〉};

 9: if |W| > w then

10:  let {〈xo,yo〉 be the oldest element of W;

11:  ForgetExample(T,ALT, {〈xo,yo〉);

12:  let W = W {〈xo,yo〉};

13: end if

14: CVFDTGrow(T,L, 〈x,y〉,δ);

15: if there have been f examples since the last checking of alternate trees

16:  CheckSplitValidity(T,δ);

17: end for

18: return T;

An outline of CVFDT is shown in Algorithm 4.6. When a new record 〈x,y〉 is received, we classify it according to the current tree. We record in a structure L every node in the tree T and in the alternate subtrees ALT that are encountered by 〈x,y〉 (Line 7). Lines 8 to 14 keep the sliding window up to date. If the tree’s number of data items has now exceeded the maximum window size (Line 9), we remove the oldest data item from the statistics (Line 11) and from W (Line 12). ForgetExample traverses the decision tree and decrements the corresponding counts nijy for 〈xo,yo) in any node of or ALT. We then add 〈x,y〉 to the tree, increasing nijy statistics according to L (Line 14). Finally, once every f items, we invoke Procedure CheckSplitValidity, which scans T and ALT looking for better splitting attributes for each internal node. It revises T and ALT as necessary.

Of course, more recent works can be found following this family. Both VFDT and CVFDT only consider discrete attributes; the VFDTc [26] system extends VFDT in two major directions: 1) VFDTc is equipped with the ability to deal with numerical attributes; and 2) a naïve Bayesian classifier is utilized in each leaf. Jin [40] presents a numerical interval pruning (NIP) approach to efficiently handle numerical attributes, and speeds up the algorithm by reducing the sample size. Further, Bifet [6] proposes a more efficient decision tree learning method than [26] by replacing naïve Bayes with perceptron classifiers, while maintaining competitive accuracy. Hashemi [32] develops a flexible decision tree (FlexDT) based on fuzzy logic to deal with noise and missing values in streaming data. Liang [48] builds a decision tree for uncertain streaming data.

Notice that there are some general works on handling concept drifting for streaming data. Gama [27, 28] detects drifts by tracing the classification errors for the training items based on PAC framework.

4.5.3 Ensemble Method for Streaming Data

An ensemble classifier is a collection of several base classifiers combined together for greater prediction accuracy. There are two well-known ensemble learning approaches: Bagging and Boosting.

Online bagging and boosting algorithms are introduced in [60]. They rely on the following observation: The probability for each base model to contain each of the original training items k times follows the binomial distribution. As the number of training items goes to infinity, k follows the Possion(1) distribution, and this assumption is suitable for streaming data.

In [73], Street et al. propose an ensemble method to read training items sequentially as blocks. When a new training block D comes, a new classifier Ci is learned, and Ci will be evaluated by the next training block. If the ensemble committee E is not full, Ci is inserted into E; otherwise, Ci could replace some member classifier Ci in E if the quality of Ci is better than that of C. However, both [73] and [60] fail to explicitly take into consideration the concept drift problem.

Based on Turner’s work [76], Wang et al. [84] prove that ensemble classifier E produces a smaller error than a single classifier G ∈ E, if all the classifiers in E have weights based on their expected classification accuracy on the test data. Accordingly they propose a new ensemble classification method that handles concept drift as follows: When a new chunk D of training items arrives, not only is a new classifier C trained, but also the weights of the previously trained classifiers are recomputed.

They propose the following training method for classifiers on streaming chunks of data, shown in Algorithm 4.7.

1: Train a new classifier C’ based on S;

2: Compute the weight w’ for C’;

3: for each Ci ∈ C do

4: Recompute the weight wi for Ci based on S;

5: end for

6: C ← top K weighted classifiers from C⋃{C’};

In Algorithm 4.7, we can see that when a new chunk S arrives, not only a new classifier C’ is trained, but also the weights of the previous trained classifiers are recomputed in this way to handle the concept drifting.

Kolter et al. [45] propose another ensemble classifier to detect concept drift in streaming data. Similar to [84], their method dynamically adjusts the weight of each base classifier according to its accuracy. In contrast, their method has a weight parameter threshold to remove bad classifiers and trains a new classifier for the new item if the existing ensemble classifier fails to identity the correct class.

Fan [21] notices that the previous works did not answer the following questions: When would the old data help detect concept drift and which old data would help? To answer these questions, the author develops a method to sift the old data and proposes a simple cross-validation decision tree ensemble method.

Gama [29] extends the Hoeffding-based Ultra Fast Forest of Trees (UFFT) [25] system to handle concept drifting in streaming data. In a similar vein, Abulsalam [1] extends the random forests ensemble method to run in amortized O(1) time, handles concept drift, and judges whether a sufficient quantity of labeled data has been received to make reasonable predictions. This algorithm also handles multiple class values. Bifet [7] provides a new experimental framework for detecting concept drift and two new variants of bagging methods: ADWIN Bagging and Adaptive-Size Hoeffding Tree (ASHT). In [5], Bifet et al. combine Hoeffding trees using stacking to classify streaming data, in which each Hoeffding tree is built using a subset of item attributes, and ADWIN is utilized both for the perceptron meta-classifier for resetting learning rate and for the ensemble members to detect concept drifting.

4.6 Summary

Compared to other classification methods [46], the following stand out as advantages of decision trees:

• Easy to interpret. A small decision tree can be visualized, used, and understood by a layperson.
• Handling both numerical and categorical attributes. Classification methods that rely on weights or distances (neural networks, k-nearest neighbor, and support vector machines) do not directly handle categorical data.
• Fast. Training time is competitive with other classification methods.
• Tolerant of missing values and irrelevant attributes.
• Can learn incrementally.

The shortcomings tend to be less obvious and require a little more explanation. The following are some weaknesses of decision trees:

• Not well-suited for multivariate partitions. Support vector machines and neural networks are particularly good at making discriminations based on a weighted sum of all the attributes. However, this very feature makes them harder to interpret.
• Not sensitive to relative spacing of numerical values. Earlier, we cited decision trees’ ability to work with either categorical or numerical data as an advantage. However, most split criteria do not use the numerical values directly to measure a split’s goodness. Instead, they use the values to sort the items, which produces an ordered sequence. The ordering then determines the candidate splits; a set of n ordered items has n−1 splits.
• Greedy approach may focus too strongly on the training data, leading to overfit.
• Sensitivity of induction time to data diversity. To determine the next split, decision tree induction needs to compare every possible split. As the number of different attribute values increases, so does the number of possible splits.

Despite some shortcomings, the decision tree continues to be an attractive choice among classification methods. Improvements continue to be made: more accurate and robust split criteria, ensemble methods for even greater accuracy, incremental methods that handle streaming data and concept drift, and scalability features to handle larger and distributed datasets. A simple concept that began well before the invention of the computer, the decision tree remains a valuable tool in the machine learning toolkit.

Bibliography

[1] Hanady Abdulsalam, David B. Skillicorn, and Patrick Martin. Classification using streaming random forests. IEEE Transactions on Knowledge and Data Engineering, 23(1):22–36, 2011.

[2] Khaled Alsabti, Sanjay Ranka, and Vineet Singh. Clouds: A decision tree classifier for large datasets. In Proceedings of the Fourth International Conference on Knowledge Discovery and Data Mining, KDD’98, pages 2–8. AAAI, 1998.

[3] K. Bache and M. Lichman. UCI machine learning repository. http://archive.ics.uci.edu/ml, 2013.

[4] Amir Bar-Or, Assaf Schuster, Ran Wolff, and Daniel Keren. Decision tree induction in high dimensional, hierarchically distributed databases. In Proceedings of the Fifth SIAM International Conference on Data Mining, SDM’05, pages 466–470. SIAM, 2005.

[5] Albert Bifet, Eibe Frank, Geoffrey Holmes, and Bernhard Pfahringer. Accurate ensembles for data streams: Combining restricted hoeffding trees using stacking. Journal of Machine Learning Research: Workshop and Conference Proceedings, 13:225–240, 2010.

[6] Albert Bifet, Geoff Holmes, Bernhard Pfahringer, and Eibe Frank. Fast perceptron decision tree learning from evolving data streams. Advances in Knowledge Discovery and Data Mining, pages 299–310, 2010.

[7] Albert Bifet, Geoff Holmes, Bernhard Pfahringer, Richard Kirkby, and Ricard Gavalda. New ensemble methods for evolving data streams. In Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’09, pages 139–148. ACM, 2009.

[8] Leo Breiman, Jerome Friedman, Charles J. Stone, and Richard A. Olshen. Classification and Regression Trees. Chapman & Hall/CRC, 1984.

[9] Carla E. Brodley and Paul E. Utgoff. Multivariate decision trees. Machine Learning, 19(1):45–77, 1995.

[10] Harry Buhrman and Ronald De Wolf. Complexity measures and decision tree complexity: A survey. Theoretical Computer Science, 288(1):21–43,2002.

[11] Doina Caragea, Adrian Silvescu, and Vasant Honavar. A framework for learning from distributed data using sufficient statistics and its application to learning decision trees. International Journal of Hybrid Intelligent Systems, 1(1):80–89, 2004.

[12] Xiang Chen, Minghui Wang, and Heping Zhang. The use of classification trees for bioinformatics. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, 1(1):55–63, 2011.

[13] David A. Cieslak and Nitesh V. Chawla. Learning decision trees for unbalanced data. In Proceedings of the 2008 European Conference on Machine Learning and Knowledge Discovery in Databases - Part I, ECML PKDD’08, pages 241–256. Springer, 2008.

[14] S. L. Crawford. Extensions to the cart algorithm. International Journal of Man-Machine Studies, 31(2): 197–217, September 1989.

[15] Barry De Ville. Decision Trees for Business Intelligence and Data Mining: Using SAS Enterprise Miner. SAS Institute Inc., 2006.

[16] Jeffrey Dean and Sanjay Ghemawat. Mapreduce: Simplified data processing on large clusters. Communications of the ACM, 51(1):107–113, 2008. Originally presented at OSDI ’04: 6th Symposium on Operating Systems Design and Implementation.

[17] Tom Dietterich, Michael Kearns, and Yishay Mansour. Applying the weak learning framework to understand and improve C4.5. In Proceedings of the Thirteenth International Conference on Machine Learning, ICML’96, pages 96–104. Morgan Kaufmann, 1996.

[18] Yufeng Ding and Jeffrey S. Simonoff. An investigation of missing data methods for classification trees applied to binary response data. The Journal of Machine Learning Research, 11:131–170, 2010.

[19] Pedro Domingos and Geoff Hulten. Mining high-speed data streams. In Proceedings of the Sixth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’00, pages 71–80. ACM, 2000.

[20] Floriana Esposito, Donato Malerba, Giovanni Semeraro, and J. Kay. A comparative analysis of methods for pruning decision trees. IEEE Transactions on Pattern Analysis and Machine Intelligence, 19(5):476–491, 1997.

[21] Wei Fan. Systematic data selection to mine concept-drifting data streams. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 128–137. ACM, 2004.

[22] Usama M. Fayyad and Keki B. Irani. The attribute selection problem in decision tree generation. In Proceedings of the Tenth National Conference on Artificial Intelligence, AAAI’92, pages 104–110. AAAI Press, 1992.

[23] Usama M. Fayyad, Gregory Piatetsky-Shapiro, Padhraic Smyth, and Ramasamy Uthurusamy. Advances in Knowledge Discovery and Data Mining. The MIT Press, February 1996.

[24] Jerome H. Friedman. A recursive partitioning decision rule for nonparametric classification. IEEE Transactions on Computers, 100(4):404–408, 1977.

[25] João Gama, Pedro Medas, and Ricardo Rocha. Forest trees for on-line data. In Proceedings of the 2004 ACM Symposium on Applied Computing, SAC’04, pages 632–636. ACM, 2004.

[26] João Gama, Ricardo Rocha, and Pedro Medas. Accurate decision trees for mining high-speed data streams. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’03, pages 523–528. ACM, 2003.

[27] João Gama and Gladys Castillo. Learning with local drift detection. In Advanced Data Mining and Applications, volume 4093, pages 42–55. Springer-Verlag, 2006.

[28] João Gama, Pedro Medas, Gladys Castillo, and Pedro Rodrigues. Learning with drift detection. Advances in Artificial Intelligence-SBIA 2004, pages 66–112, 2004.

[29] João Gama, Pedro Medas, and Pedro Rodrigues. Learning decision trees from dynamic data streams. In Proceedings of the 2005 ACM Symposium on Applied Computing, SAC’05, pages 573–577. ACM, 2005.

[30] Johannes Gehrke, Venkatesh Ganti, Raghu Ramakrishnan, and Wei-Yin Loh. Boat- optimistic decision tree construction. ACM SIGM0D Record, 28(2): 169–180, 1999.

[31] Johannes Gehrke, Raghu Ramakrishnan, and Venkatesh Ganti. Rainforest — A framework for fast decision tree construction of large datasets. In Proceedings of the International Conference on Very Large Data Bases, VLDB’98, pages 127–162, 1998.

[32] Sattar Hashemi and Ying Yang. Flexible decision tree for data stream classification in the presence of concept change, noise and missing values. Data Mining and Knowledge Discovery, 19(1):95–131, 2009.

[33] Geoff Hulten, Laurie Spencer, and Pedro Domingos. Mining time-changing data streams. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’01, pages 97–106. ACM, 2001.

[34] Earl Busby Hunt, Janet Marin, and Philip J. Stone. Experiments in Induction. Academic Press, New York, London, 1966.

[35] Laurent Hyafil and Ronald L. Rivest. Constructing optimal binary decision trees is np-complete. Information Processing Letters, 5(1):15–17, 1976.

[36] Ruoming Jin and Gagan Agrawal. A middleware for developing parallel data mining implementations. In Proceedings of the 2001 SIAM International Conference on Data Mining, SDM’01, April 2001.

[37] Ruoming Jin and Gagan Agrawal. Shared memory parallelization of data mining agorithms: Techniques, programming interface, and performance. In Proceedings of the Second SIAM International Conference on Data Mining, SDM’02, pages 71–89, April 2002.

[38] Ruoming Jin and Gagan Agrawal. Shared memory parallelization of decision tree construction using a general middleware. In Proceedings of the 8th International Euro-Par Parallel Processing Conference, Euro-Par’02, pages 346–354, Aug 2002.

[39] Ruoming Jin and Gagan Agrawal. Communication and memory efficient parallel decision tree construction. In Proceedings of the Third SIAM International Conference on Data Mining, SDM’03, pages 119–129, May 2003.

[40] Ruoming Jin and Gagan Agrawal. Efficient decision tree construction on streaming data. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’03, pages 571–576. ACM, 2003.

[41] Mahesh V. Joshi, George Karypis, and Vipin Kumar. Scalparc: A new scalable and efficient parallel classification algorithm for mining large datasets. In First Merged Symp. IPPS/SPDP 1998: 12th International Parallel Processing Symposium and 9th Symposium on Parallel and Distributed Processing, pages 573–579. IEEE, 1998.

[42] Dimitrios Kalles and Tim Morris. Efficient incremental induction of decision trees. Machine Learning, 24(3):231–242, 1996.

[43] Michael Kearns and Yishay Mansour. On the boosting ability of top-down decision tree learning algorithms. In Proceedings of the 28th Annual ACM Symposium on Theory of Computing, STOC’96, pages 459–468. ACM, 1996.

[44] Michael Kearns and Yishay Mansour. A fast, bottom-up decision tree pruning algorithm with near-optimal generalization. In Proceedings of the 15th International Conference on Machine Learning, pages 269–277, 1998.

[45] Jeremy Z. Kolter and Marcus A. Maloof. Dynamic weighted majority: A new ensemble method for tracking concept drift. In Proceedings of the Third IEEE International Conference on Data Mining, 2003., ICDM’03, pages 123–130. IEEE, 2003.

[46] S. B. Kotsiantis. Supervised machine learning: A review of classification techniques. In Proceedings of the 2007 Conference on Emerging Artifical Intelligence Applications in Computer Engineering, pages 3–24. IOS Press, 2007.

[47] Xiao-Bai Li. A scalable decision tree system and its application in pattern recognition and intrusion detection. Decision Support Systems, 41(1):112–130, 2005.

[48] Chunquan Liang, Yang Zhang, and Qun Song. Decision tree for dynamic and uncertain data streams. In 2nd Asian Conference on Machine Learning, volume 3, pages 209–224, 2010.

[49] Tjen-Sien Lim, Wei-Yin Loh, and Yu-Shan Shih. A comparison of prediction accuracy, complexity, and training time of thirty-three old and new classification algorithms. Machine Learning, 40(3):203–228, 2000.

[50] Christiane Ferreira Lemos Lima, Francisco Marcos de Assis, and Cleonilson Protásio de Souza. Decision tree based on shannon, rényi and tsallis entropies for intrusion tolerant systems. In Proceedings of the Fifth International Conference on Internet Monitoring and Protection, ICIMP’10, pages 117–122. IEEE, 2010.

[51] R. López de Mántaras. A distance-based attribute selection measure for decision tree induction. Machine Learning, 6(1):81–92, 1991.

[52] Yishay Mansour. Pessimistic decision tree pruning based on tree size. In Proceedings of the 14th International Conference on Machine Learning, pages 195–201, 1997.

[53] Manish Mehta, Rakesh Agrawal, and Jorma Rissanen. Sliq: A fast scalable classifier for data mining. In Proceedings of the Fifth International Conference on Extending Database Technology, pages 18–32, Avignon, France, 1996.

[54] John Mingers. Expert systems—Rule induction with statistical data. Journal of the Operational Research Society, 38(1): 39–47, 1987.

[55] John Mingers. An empirical comparison of pruning methods for decision tree induction. Machine Learning, 4(2):227–243, 1989.

[56] James N. Morgan and John A. Sonquist. Problems in the analysis of survey data, and a proposal. Journal of the American Statistical Association, 58(302):415–434, 1963.

[57] G. J. Narlikar. A parallel, multithreaded decision tree builder. Technical Report CMU-CS-98-184, School of Computer Science, Carnegie Mellon University, 1998.

[58] Tim Niblett. Constructing decision trees in noisy domains. In I. Bratko and N. Lavrac, editors, Progress in Machine Learning. Sigma, 1987.

[59] Jie Ouyang, Nilesh Patel, and Ishwar Sethi. Induction of multiclass multifeature split decision trees from distributed data. Pattern Recognition, 42(9): 1786–1794, 2009.

[60] Nikunj C. Oza and Stuart Russell. Online bagging and boosting. In Eighth International Workshop on Artificial Intelligence and Statistics, pages 105–112. Morgan Kaufmann, 2001.

[61] Biswanath Panda, Joshua S. Herbach, Sugato Basu, and Roberto J. Bayardo. Planet: Massively parallel learning of tree ensembles with mapreduce. Proceedings of the VLDB Endowment, 2(2):1426–1437, 2009.

[62] J. Ross Quinlan. Learning efficient classification procedures and their application to chess end-games. In Machine Learrning: An Artificial Intelligence Approach. Tioga Publishing Company, 1983.

[63] J. Ross Quinlan. Induction of decision trees. Machine Learning, 1(1):81–106, March 1986.

[64] J. Ross Quinlan. Simplifying decision trees. International Journal of Man-Machine Studies, 27(3):221–234, 1987.

[65] J. Ross Quinlan and Ronald L. Rivest. Inferring decision trees using the minimum description length principle. Information and Computing, 80:227–248, 1989.

[66] John Ross Quinlan. C4.5: Programs for Machine Learning. Morgan Kaufmann, 1993.

[67] Maytal Saar-Tsechansky and Foster Provost. Handling missing values when applying classification models. Journal of Machine Learning Research, 8:1623–1657, 2007.

[68] Jeffrey C. Schlimmer and Douglas Fisher. A case study of incremental concept induction. In Proceedings of the Fifth National Conference on Artificial Intelligence, pages 495–501. Morgan Kaufmann, 1986.

[69] John Shafer, Rakeeh Agrawal, and Manish Mehta. SPRINT: A scalable parallel classifier for data mining. In Proceedings of the 22nd International Conference on Very Large Databases (VLDB), pages 544–555, September 1996.

[70] Claude E. Shannon. A mathematical theory of communication. Bell System Technical Journal, 27(3):379–423, July/October 1948.

[71] Harold C. Sox and Michael C. Higgins. Medical Decision Making. Royal Society of Medicine, 1988.

[72] Anurag Srivastava, Eui-Hong Han, Vipin Kumar, and Vineet Singh. Parallel formulations of decision-tree classification algorithms. In Proceedings of the 1998 International Conference on Parallel Processing, ICPP’98, pages 237–261, 1998.

[73] W. Nick Street and YongSeog Kim. A streaming ensemble algorithm (sea) for large-scale classification. In Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD’01, pages 377–382. ACM, 2001.

[74] Hyontai Sug. A comprehensively sized decision tree generation method for interactive data mining of very large databases. In Advanced Data Mining and Applications, pages 141–148. Springer, 2005.

[75] Umar Syed and Golan Yona. Using a mixture of probabilistic decision trees for direct prediction of protein function. In Proceedings of the Seventh Annual International Conference on Research in Computational Molecular Biology, RECOMB’03, pages 289–300. ACM, 2003.

[76] Kagan Tumer and Joydeep Ghosh. Error correlation and error reduction in ensemble classifiers. Connection Science, 8(3–4):385–404, 1996.

[77] Paul E. Utgoff. Id5: An incremental id3. In Proceedings of the Fifth International Conference on Machine Learning, ICML’88, pages 107–120, 1988.

[78] Paul E. Utgoff. Incremental induction of decision trees. Machine Learning, 4(2):161–186, 1989.

[79] Paul E. Utgoff. An improved algorithm for incremental induction of decision trees. In Proceedings of the Eleventh International Conference on Machine Learning, ICML’94, pages 318–325, 1994.

[80] Paul E Utgoff, Neil C Berkman, and Jeffery A Clouse. Decision tree induction based on efficient tree restructuring. Machine Learning, 29(1):5–44, 1997.

[81] Paul E. Utgoff and Carla E. Brodley. An incremental method for finding multivariate splits for decision trees. In Proceedings of the Seventh International Conference on Machine Learning, ICML’90, pages 58–65, 1990.

[82] Paul A. J. Volf and Frans M.J. Willems. Context maximizing: Finding mdl decision trees. In Symposium on Information Theory in the Benelux, volume 15, pages 192–200, 1994.

[83] Chris S. Wallace and J. D. Patrick. Coding decision trees. Machine Learning, 11(1):7–22, 1993.

[84] Haixun Wang, Wei Fan, Philip S. Yu, and Jiawei Han. Mining concept-drifting data streams using ensemble classifiers. In Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pages 226–235. ACM, 2003.

[85] Xindong Wu, Vipin Kumar, J. Ross Quinlan, Joydeep Ghosh, Qiang Yang, Hiroshi Motoda, Geoffrey J. McLachlan, Angus Ng, Bing Liu, Philip S. Yu, Zhi-Hua Zhou, Michael Steinbach, David J. Hand, and Dan Steinberg. Top 10 algorithms in data mining. Knowledge and Information Systems, 14(1): 1–37, 2008.

[86] Jerry Ye, Jyh-Herng Chow, Jiang Chen, and Zhaohui Zheng. Stochastic gradient boosted distributed decision trees. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, CIKM’09, pages 2061–2064. ACM, 2009.

[87] Olcay Taner Yildiz and Onur Dikmen. Parallel univariate decision trees. Pattern Recognition Letters, 28(7):825–832, 2007.

[88] M. J. Zaki, Ching-Tien Ho, and Rakesh Agrawal. Parallel classification for data mining on shared-memory multiprocessors. In Proceedings of the Fifteenth International Conference on Data Engineering, ICDE’99, pages 198–205, May 1999.

1A training set is inconsistent if two items have different class values but are identical in all other attribute values.