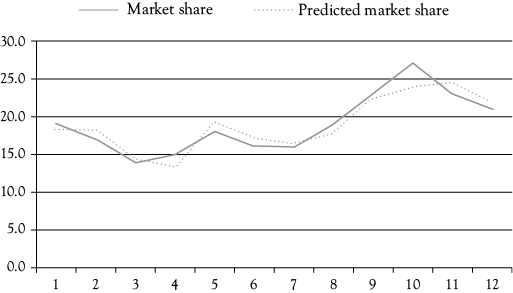
Figure 7.1. Miller’s Foods’ market share: actual and regression estimates. The dotted line representing the estimated market share for Miller’s Foods’ is derived from the following regression model: MS = 80.011 – 8.458(P) + 0.020(AD) – 2.541(CAD).
A Market Share Multiple Regression Model
Chapter 7 Preview
When you have completed reading this chapter you will be able to:
• Identify what constitutes a market share multiple regression model.
• Arrange your data for use in a market share multiple regression model.
• Determine whether a particular variable ought to be in the model.
• Evaluate the market share model.
• Make a point estimate from the model.
• Calculate a confidence interval for your estimate.
In the previous chapters, you have seen examples of simple linear regressions (those with a single independent variable) and multiple linear regressions (those with more than one independent variable). Now, you will apply these concepts of regression analysis to estimate a model for the market share of a company. Table 7.1 contains the data used in this example: 3 years of quarterly data related to the market share for Miller’s Foods’. The objective is to develop a regression model that explains how Miller’s Foods’ price (P) and advertising (AD), as well as an index of competitors’ advertising (CAD), have influenced the firm’s market share (MS).
Table 7.1. Three Years of Miller’s Foods’ Market Share Multiple Regression Data
|
Period (quarter) |
Market share in M$ (MS) |
Price in $ (P) |
Advertising in $ (AD) |
Competitors’ advertising index (CAD) |
|
1 |
19 |
5.20 |
500 |
11 |
|
2 |
17 |
5.32 |
550 |
11 |
|
3 |
14 |
5.48 |
550 |
12 |
|
4 |
15 |
5.60 |
550 |
12 |
|
5 |
18 |
5.80 |
550 |
9 |
|
6 |
16 |
6.03 |
660 |
10 |
|
7 |
16 |
6.01 |
615 |
10 |
|
8 |
19 |
5.92 |
650 |
10 |
|
9 |
23 |
5.90 |
745 |
9 |
|
10 |
27 |
5.85 |
920 |
10 |
|
11 |
23 |
5.80 |
1,053 |
11 |
|
12 |
21 |
5.85 |
950 |
11 |
Source: Proprietary data.
Estimating a Simple Linear Regression Market Share Model
It would be reasonable to assume that the market share for MF would be related to their price variable. If you estimate a simple linear regression to represent this assumption, using only price as an independent variable, you receive the following result (MS as a function of P):
![]()
This is a rather disappointing result in at least two dimensions. First, this estimated coefficient for price (+3.673) has a positive sign! How would you interpret this? The positive sign and the value of 3.673 infer that if price were to increase by one, market share would increase by 3.673 (measured in percentage terms). That is a very unusual result to say the least. If this is correct, you could increase the market share (a good thing) by simply raising prices. But is this logical? Secondly, the t-stat on the coefficient of the independent variable (price) is far below the “rule-of-thumb” value of 2; this would infer that the estimated coefficient (+3.673) is not significantly different from zero. In other words, the coefficient is not statistically significant; it is not a reliable coefficient and you should be suspect of using it in any manner even if it was logical.
So, this model should not be used. Is the regression result incorrect? No, the regression result is accurate, but you may have made an incorrect assumption by constricting the regression model to relate market share to only a single independent variable. It appears that in the real world of MF, market share depends upon more than just price (the model is under specified). That is the reason you use multiple linear regression; you recognize that not only price is important in determining market share, but also their advertising effort, and some measure of their competitors’ advertising effort.
Estimating a Multiple Linear Regression Market Share Model
Putting this disappointing simple linear regression result away, you can estimate a multiple linear regression using three independent variables: price (P),advertising (AD), and an index of their competitors’ advertising (CAD).
The Excel regression results for this example are summarized in Table 7.2. From the results given in Table 7.2, you could write the appropriate regression equation as:
Table 7.2. Excel Regression Results for Miller’s Foods’ Market Share Model
|
Regression statistics |
|||||
|
Multiple R |
0.929 |
DW = 2.17 |
|||
|
R-square |
0.863 |
||||
|
Adjusted R-square |
0.812 |
||||
|
Standard error |
1.676 |
||||
|
Observations |
12 |
||||
|
ANOVA |
|||||
|
|
df |
SS |
MS |
F |
Sig F |
|
Regression |
3 |
141.537 |
47.179 |
16.802 |
0.001 |
|
Residual |
8 |
22.463 |
2.808 |
||
|
Total |
11 |
164 |
|||
|
Coefficients |
Std error |
t Stat |
p-Value |
P/2 |
|
|
Intercept |
80.011 |
19.479 |
4.107 |
0.003 |
0.002 |
|
P |
–8.458 |
2.705 |
–3.127 |
0.014 |
0.007 |
|
AD |
0.020 |
0.003 |
6.404 |
0.000 |
0.000 |
|
CAD |
–2.541 |
0.647 |
–3.924 |
0.004 |
0.002 |
![]()
Evaluating the Estimated Market Share Model
In order to complete the examination of this model, you should use the five-step process described previously (see chapter 6) to evaluate multiple regression models.
Evaluation Step 1: Evaluate Whether the Model Makes Sense
Does the model make sense? The signs on the coefficients for all three independent variables do make economic sense as described below. The interpretation of the slope terms for price, advertising, and the competitors’ advertising index are as follows:
1. Price. The coefficient –8.458 has a negative sign, which indicates that as price goes up, market share goes down. Note that this is different from the sign you received in the simple linear regression. For every $1 increase in price, now market share could be expected to fall by 8.458 market share percentage points; or for every 10 cent increase in price, market share would be expected to fall by .8458 market share percentage points. Price cuts would be expected to increase market share by like amounts.
2. Advertising. The coefficient 0.02 has a positive sign, which indicates that increasing advertising is expected to increase market share. Each $100 increase in advertising would increase market share by 2.0 market share percentage points. Decreases in advertising would lower market share in a like manner.
3. Index of Competitors’ Advertising. The negative sign for the index indicates that this firm’s market share would fall when competitors advertise more. Every 1 unit rise in the index is expected to lower market share by 2.541 market share percentage points. Decreases in the index would be expected to increase market share in a like manner.
Therefore, this model passes our test for sound business/economic logic.
Evaluation Step 2: Check for Statistical Significance
Are the slope terms significantly different from zero? That is, does each of the independent variables have a statistically significant influence on the dependent variable? The hypotheses you would want to evaluate for each of the slope terms are as follows:

These all imply a one-tailed test. From the t-table presented earlier (Appendix 4B), you find that the critical value of t at 8 degrees of freedom (df = 12 – (3 + 1) = 8) and a 95% confidence level (5% confidence level) for a one-tailed test is 1.860. Thus,
1. For price, you reject H0, since the absolute value of tc(|–3.13|) is greater than the critical t-table value (1.860). This implies that the coefficient for price is statistically less than zero.
2. For advertising, you reject H0, since the absolute value of tc(|6.40|) is greater than the critical t-table value (1.860). This implies that the coefficient for advertising is statistically greater than zero.
3. For competitors’ advertising, the absolute value of tc(|–3.92|) is greater than the critical t-table value (1.860). This implies that the coefficient for competitors’ advertising is statistically less than zero.
Note that, in Table 7.2, all the p-values divided by 2 (relevant for one-tailed tests) are far below the desired level of significance (0.05) also implying statistical significance.
Based on rejecting all three of these null hypotheses you conclude, at a 95% confidence level, that all three independent variables have a significant effect on the market share of Miller’s Foods’. In other words, you can rely on the three coefficients and use them in describing how Miller’s market share is affected by each of the variables. Note that when you ran the simple linear regression with only price as an independent variable, you were not able to rely on the estimated slope of the price variable. What has changed? The market share and price variables are identical in the simple regression and the multiple regression. But, what has changed is the addition of the two independent variables in the multiple regression; the multiple linear regression recognizes that market share is not only dependent upon price, but it is also dependent upon advertising and competitors’ advertising at the same time.
Evaluation Step 3: Determine Explanatory Power of Model
How much of the variation (i.e., “up and down movement”) in Miller’s Foods’ market share does this regression model explain? Because this is a multiple linear regression model you want to use the adjusted R2 to answer this question. From Table 7.2, you see that the adjusted R2 is 0.812. Thus, over 81% of the variation in Miller’s Foods’ market share (MS) is explained by this model. You can infer that most of the change you see in market share over the 3 years for which you have data is due to changes in price, advertising, and Miller’s competitors’ advertising.
You can also use the F-test to evaluate the overall statistical significance of this model. The calculated F-statistic from Table 7.2 is compared with the critical F-table value (Appendix 6A) at k degrees of freedom for the numerator and n – (k + 1) degrees of freedom for the denominator. In this example for the numerator df = 3 and the denominator df = 8. From the F-table (Appendix 6A) you see that the critical F-table value is 4.07. Since the computed F-statistic from Table 7.2(16.8) is greater than the critical F-table value (4.07) you would reject the null hypothesis that all of the slope terms are simultaneously equal to zero (or alternatively that the adjusted R2 equals zero). Thus, this full regression test infers that the estimated relationships are reasonably accurate.
Evaluation Step 4: Check for Serial Correlation
You need to check for serial correlation because the Miller’s Foods’ Market Share regression uses time-series data. To do this, you need to evaluate the Durbin–Watson statistic explained previously. Your calculated value is DW = 2.17 (refer to Appendix 4D on how to calculate the DW statistic). Recall that the DW values may range from 0 to 4. If the DW is exactly 2, there is little chance of serial correlation. However, if the calculated DW is close to 0, or close to 4, the chance of serial correlation is high. A shortcut (or an approximation) often used by practitioners is to examine whether the DW statistic is between 1.5 and 2.5. If the calculated value is between these limits, you might assume that serial correlation is not a serious problem. In this case, the calculated value for DW of 2.17 is between dl (0.368) and du (2.287) of the DW table (Appendix 4C). This satisfies Test 5 of Table 4.2, so the result is actually indeterminate.
Evaluation Step 5: Check for Multicollinearity
You should evaluate the model for possible multicollinearity since you have multiple independent variables in the regression. The signs for the coefficients all make sense and the t-ratios are all high so there is no suggestion on these grounds to suspect multicollinearity (the model does not appear to be over specified). The correlation coefficients for all pairs of independent variables can be found in the correlation matrix in Table 7.3.
Table 7.3. Correlation Matrix for Independent Variables in Miller’s Foods’ Market Share Regression
|
P |
AD |
CAD |
|
|
P |
1 |
||
|
AD |
0.468 |
1 |
|
|
CAD |
–0.590 |
–0.092 |
1 |
Obviously, each variable is perfectly correlated with itself (i.e., correlations of 1). Since none of the other correlation coefficients is particularly large (all below 0.7 in absolute value), it is unlikely that there is a multicollinearity problem in this regression.
Making an Estimate from the Market Share Model
Suppose you want to know what market share would be expected if MF set their price at $5.70 and spent $700 on advertising, and if the competitors’ advertising index was 10%. You could make this point estimate by substituting these values into the regression model as follows:
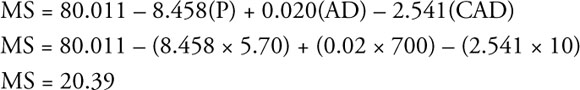
How would you estimate an approximate 95% confidence interval for market share? From the Excel regression results in Table 7.2, you see that the standard error of the estimate (SEE) is 1.676. Thus, the approximate 95% confidence interval is
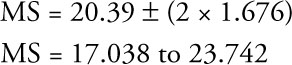
This means that you would be 95% confident that the market share of Miller’s Foods’ would fall in the interval from 17.038% through 23.742% if the firm set a $5.70 price and spent $700 on advertising, and if the competitors’ advertising index was 10%.
The graph in Figure 7.1 further illustrates how well this regression model explains variations in MF’s market share. You see that the estimated market share follows the actual market share quite well, except during the second quarter of the final year. You will learn more about this quarter in the next chapter.
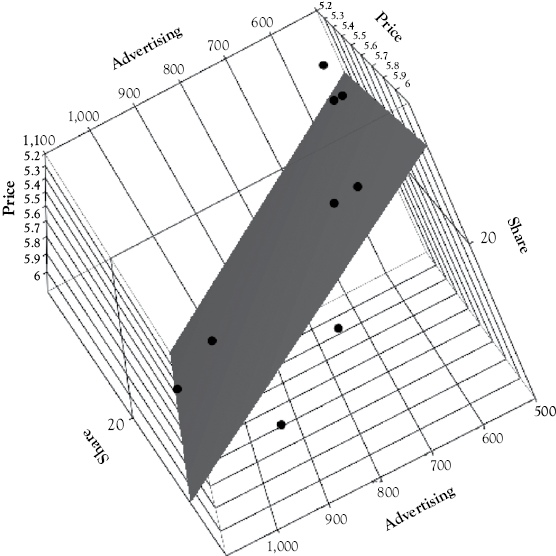
A Three-Dimensional Visual Representation
To help you get a visual feel for what a multiple regression data set might look like, see the three-dimensional plot of market share, price, and advertising in Figure 7.2. You could not include the third independent variable in such a plot since the human mind cannot visualize beyond three dimensions. The regression plane for market share (MS) as a function of price (P) and advertising (AD) is shown in Figure 7.2. The equation for that plane is:
![]()
The actual data points in Figure 7.2 are shown by the dark circles and the regression plane is the shaded rectangle.
What You Have Learned in Chapter 7
• You know what constitutes a market share multiple regression model.
• You know how to arrange your data for use in a market share multiple regression model.
• You know how to determine whether a particular variable ought to be in the model.
• You know how to evaluate the market share model.
• You know how to make a point estimate from the model.
• You know how to estimate a confidence interval for your estimate.
