The naive parallel prefix algorithm is the original version of this algorithm; this algorithm is "naive" because it makes an assumption that given n input elements, , with the further assumption that n is dyadic (that is,  for some positive integer, k), and we can run the algorithm in parallel over n processors (or n threads). Obviously, this will impose strong limits on the cardinality n of sets that we may process. However, given these conditions are satisfied, we have a nice result in that its computational time complexity is only O(log n). We can see this from the pseudocode of the algorithm. Here, we'll indicate the input values with  and the output values as :

input: x0, ..., xn-1
initialize:
for k=0 to n-1:
    yk := xk
begin:
parfor i=0 to n-1 :
    for j=0 to log2(n):
        if i >= 2j :
            yi := yi  yi - 2j
            else:
            continue
        end if
    end for
end parfor
end
output: y0, ..., yn-1

Now, we can clearly see that this will take O(log n) asymptotic time, as the outer loop is parallelized over the parfor and the inner loop takes log₂(n). It should be easy to see after a few minutes of thought that the y_i values will yield our desired output.

Now let's begin our implementation; here, our binary operator will simply be addition. Since this example is illustrative, this kernel will be strictly over 1,024 threads.

Let's just set up the header and dive right into writing our kernel:

import pycuda.autoinit
import pycuda.driver as drv
import numpy as np
from pycuda import gpuarray
from pycuda.compiler import SourceModule
from time import time

naive_ker = SourceModule("""
__global__ void naive_prefix(double *vec, double *out)
{
     __shared__ double sum_buf[1024]; 
     int tid = threadIdx.x; 
     sum_buf[tid] = vec[tid];

So, let's look at what we have: we represent our input elements as a GPU array of doubles, that is double *vec, and represent the output values with double *out. We declare a shared memory sum_buf array that we'll use for the calculation of our output. Now, let's look at the implementation of the algorithm itself:

 int iter = 1;
 for (int i=0; i < 10; i++)
 {
     __syncthreads();
     if (tid >= iter )
     {
         sum_buf[tid] = sum_buf[tid] + sum_buf[tid - iter]; 
     } 
     iter *= 2;
 }
 __syncthreads();

Of course, there is no parfor, which is implicit over the tid variable, which indicates the thread number. We are also able to omit the use of log₂ and 2ⁱ by starting with a variable that is initialized to 1, and then iteratively multiplying by 2 every iteration of i. (Note that if we want to be even more technical, we can do this with the bitwise shift operators .) We bound the iterations of i by 10, since 2¹⁰ = 1024. Now we'll close off our new kernel as follows:

 __syncthreads();
 out[tid] = sum_buf[tid];
 __syncthreads();
 
}
""")
naive_gpu = naive_ker.get_function("naive_prefix")
 

Let's now look at the test code following the kernel:

if __name__ == '__main__':
 testvec = np.random.randn(1024).astype(np.float64)
 testvec_gpu = gpuarray.to_gpu(testvec)
 
 outvec_gpu = gpuarray.empty_like(testvec_gpu)
 naive_gpu( testvec_gpu , outvec_gpu, block=(1024,1,1), grid=(1,1,1))
 
 total_sum = sum( testvec)
 total_sum_gpu = outvec_gpu[-1].get()
 
 print "Does our kernel work correctly? : {}".format(np.allclose(total_sum_gpu , total_sum) )

We're only going to concern ourselves with the final sum in the output, which we retrieve with outvec_gpu[-1].get(), recalling that the "-1" index gives the last member of an array in Python. This will be the sum of every element in vec; the partial sums are in the prior values of outvec_gpu. (This example can be seen in the naive_prefix.py file in the GitHub repository.)

By its nature, the parallel prefix algorithm has to run over n threads, corresponding to a size-n array, where n is dyadic (again, this means that n is some power of 2). However, we can extend this algorithm to an arbitrary non-dyadic size assuming that our operator has a identity element (or equivalently, neutral element)—that is to say, that there is some value e so that for any x value, we have—.  In the case that our operator is + , the identity element is 0; in the case that it is , it is 1; all we do then is just pad the elements  with a series of e values so that we have the a dyadic cardinality of the new set 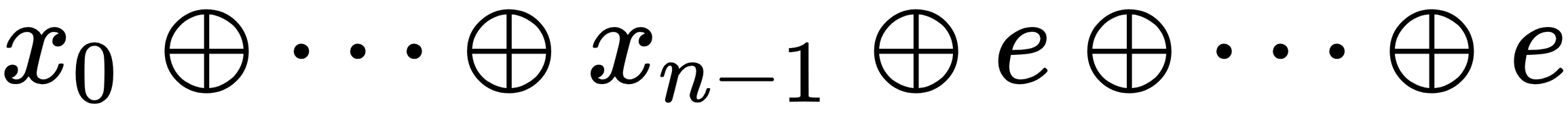.