Now let's look at how we can do some basic fast Fourier transforms (FFT) with cuFFT.  First, let's briefly review what exactly a Fourier transform is. If you have taken an advanced Calculus or Analysis class, you might have seen the Fourier transform defined as an integral formula, like so:

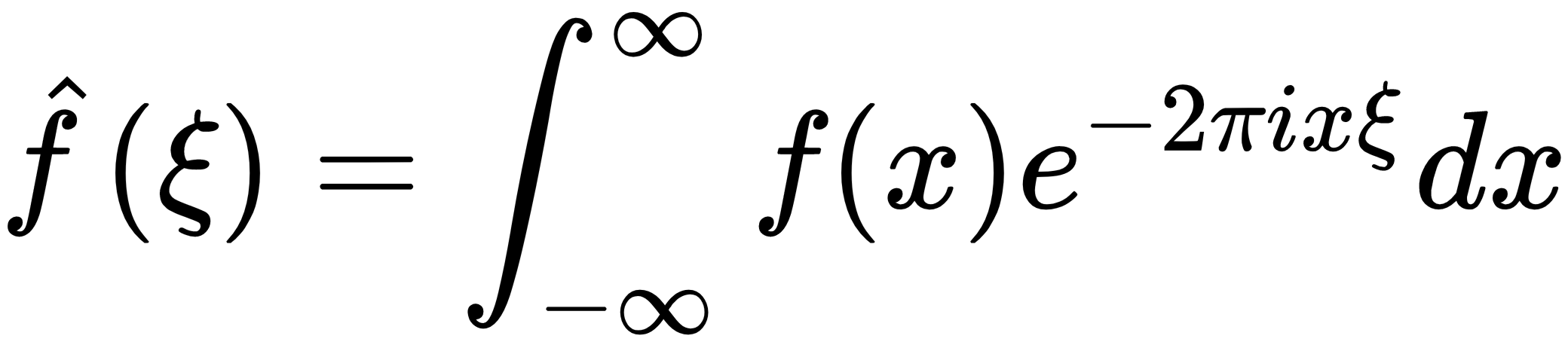
What this does is take f as a time domain function over x. This gives us a corresponding frequency domain function over "ξ".  This turns out to be an incredibly useful tool that touches virtually all branches of science and engineering.

Let's remember that the integral can be thought of as a sum; likewise, there is a corresponding discrete, finite version of the Fourier Transform called the discrete Fourier transform (DFT). This operates on vectors of a finite length and allows them to be analyzed or modified in the frequency domain. The DFT of an n-dimensional vector x is defined as follows:

In other words, we can multiply a vector, x, by the complex N x N matrix  
(here, k corresponds to row number, while n corresponds to column number) to find its DFT. We should also note the inverse formula that lets us retrieve x from its DFT (replace y with the DFT of x here, and the output will be the original x):

Normally, computing a matrix-vector operation is of computational complexity O(N²) for a vector of length N. However, due to symmetries in the DFT matrix, this can always be reduced to O(N log N) by using an FFT. Let's look at how we can use an FFT with CuBLAS, and then we will move on to a more interesting example.