Student's t-distribution was introduced by William Sealy Gosset under the pseudonym student (hence the name) while working at Guinness Brewery. The family of t-tests highly relies on the student's t-distribution in order to infer; in fact, t-test is the general name given to any HT for which the test statistic is assumed to follow a t-distribution. Although normal distributions are very popular and common, a rigorous approach would rather trust a t-distribution instead of the normal one whenever the population's standard deviation is unknown and a sample's estimation is trusted instead.

In case you may be wondering how these distributions look, here is a visual explanation:

x <- seq(-4,4,.1)
par(lwd = 2)
plot(x, dnorm(x), type = 'l', ylab = 'density',
 main = 'prob. density distributions')
lines(x, dt(x, 5), col = '#e66101', lty = 2)
lines(x, dt(x, 10), col = '#5e3c99', lty = 3)
legend('topright', 
 legend = c('normal','t-student (df = 5)', 't-student (df = 10)'), 
 col = c('#000000','#e66101','#5e3c99'), lty = 1:3)

The last code block will generate a visual comparison across normal and t-student distributions' formats:

Both normal and t-student distributions are very similar; both are sort of bell-shaped. The thing is that t-student's distributions will depend on the degrees of freedom; greater degrees of freedom lead to t-student curves more similar to standardized normal curves. As you can see from the previous figure, normal curves are more concentrated around the center, while t-student curves have fatter tails.

Back in the early days of hypothesis testing, people would have to make several calculations by hand and then look at a table to see where the t statistic fit. The computations are now done by computer and there is no need to consult a table anymore, yet the core ideas and concepts remain the same. Given a sample (X) that is i.i.d. and follows a normal distribution with limited mean, µ, and unknown variance, so the following applies:

The value t will follow a Student's t-distribution with n-1 degrees of freedom, where the following applies:

• n: Number of observations
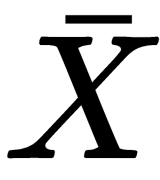• : Arithmetic mean (estimation)
• μ: Expected mean (parameter/true mean), stated by the null hypothesis
• S: A non-biased standard deviation estimator calculated from the sample as follows:

That is how the test statistic is calculated; imagine computing all of these by hand. When Marley says don't worry about a thing, it's only because R will handle all of the computation for you. Once you are aware of what's going on, you can call t.test() to run the test for you. Let's run a simple mean test so we can walk through the output:

# set.seed(10)
# small_sample <- rnorm(n = 10, mean = 10, sd = 5)
# big_sample <- rnorm(n = 10^5, mean = 10, sd = 5)
t.test(big_sample, mu = 10, alternative = 'two.sided')

If you are missing the big_sample object, simply uncomment and run the first three lines of code. So, here we are. The t.test() function will run the test for us. The way it's designed, it will check the null hypothesis, that states that the true (populational) mean is equal to 10 against the alternative hypothesis that states that the true mean is not equal 10; it's something like this:

This is a simple t-test for the mean. A functions' first argument points towards the data. The mean assumed by the null hypothesis is declared into µ argument. A two-sided test asked by the alternative = 'two.sided' argument. Alternative inputs would be 'less' or 'greater'; both would ask for one-sided tests. Let's check the output we will get from the previous code:

#  One Sample t-test
#
# data: big_sample
# t = -1.8583, df = 99999, p-value = 0.06313
# alternative hypothesis: true mean is not equal to 10
# 95 percent confidence interval:
#   9.939406 10.001614
# sample estimates:
# mean of x 
#   9.97051 

R begins by telling us that it's a one sample t-test because, of course, two sample t-tests are also available. It goes on and tells us that the data tested comes from the big_sample data. Calculated statistic (t), degrees of freedom (df) and p-value are shown next. The p-value is the lowest level of confidence that allows us to reject the null hypothesis; for this case, it is 6,313%, so we failed to reject the null hypothesis at 5% level of confidence—which is good, given that the data came from a normal distribution with a mean equal to 10. 

Next comes the alternative hypothesis. Sometimes, it is useful to state your null hypothesis in terms of greater or less instead of not equal. Tweak the alternative argument to do so. In the following section, we can see the 95% confidence interval; be careful while interpreting this one. Given the alternative hypothesis, if repeated samples were taken and this same interval were calculated for all of them, 95% of the intervals would contain the populational mean. You can set a custom interval of your own by naming the conf.level argument. Last but not least, we have the mean of x. The output also told us that the sample estimated mean of x was 9.97051.