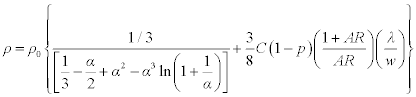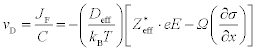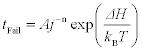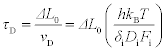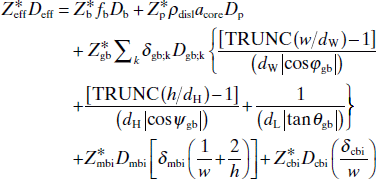Electromigration failure in nanoscale copper interconnects
Abstract:
An introductory discussion is presented to provide specific context to understand reliability trending as nanoscale dimensions (tens of nm) for advanced complementary metal oxide semiconductor (CMOS) technology become ubiquitous, i.e., not just at the transistor gate. There are three main sections: (1) process solutions being developed for Cu interconnects; (2) improving electromigration (EM) margin of Cu-based interconnects; and (3) microstructure effects on EM reliability. Finally, some discussion beyond the use of the canonical Cu interconnect are discussed.
8.1 Process solutions being developed for copper interconnects
8.1.1 Introduction to copper-based interconnect technology
There is perhaps some irony in the fact that ‘interconnects’, consisting of the metallization and surrounding dielectrics that route all electrical signals within advanced microchips, are most appreciated when they do essentially nothing (at least to the naked eye). An interconnects primary function is to connect an electrical output to another electrical input, all at chip level, and vice versa, and as long as such interconnects transmit electrical signals without loss of fidelity and with minimal latency or supply electrical bias without detrimental power loss, then microelectronics devices should only be functionally limited by the behavior of the transistors that make up the bulk of the active circuitry within a given microchip. More realistically, however, functionally passive metallization does not behave so passively at the atomic scale, and its consequences can be significant. Metal atoms within interconnects jostle about under the action of external forces and, if long enough times are sampled, the nanoscopic movements of these atoms can be microscopic enough to lead to macroscopic device failure. The movement of metal ions under the influence of some driving force has several manifestations that lead to interconnect failure. Such failure mechanisms include stress-migration (metal void-generated electrical contact failures under thermomechanical stress), metallic corrosion shorting (interaction of metals with corrosive ambient and residual electrical bias present during processing), and metallic bridging under electrical stress owing to metal ionic drift into the adjacent interconnect dielectric (leading to dielectric breakdown between adjacent metals during electrical stress).
Electromigration (EM), that is metal void-generated contact failures under applied electrical current, is probably the most well-known interconnect failure mechanism and has been both an important topic in reliability physics and a key reliability metric for robust process technology development since the mid-1960s (Blech and Sello, 1966; d’Heurle and Ho, 1978; Ho and Kwok, 1989; Kwok, 1993; Hu et al., 1995; Clement, 2001). During EM, the application of current through a metal creates the so-called ‘electron wind’ and causes metal ions to hop in aggregate from lattice site to lattice site along the direction of electron flow from the cathode end (the electron source side) to anode end. The continued flow of these metal ions from a given site can eventually trigger void nucleation and subsequent void growth. The void growth can then lead to interconnect failure by open circuit. This classical representation of EM is necessary to understand EM for advanced interconnect applications; however, a more nuanced picture of EM will be needed to understand the potential reliability trends for advanced Cu interconnects beyond 32 nm node.
During the earlier era of microelectronics, spanning from the mid-1960s to 1997, Al-based metallization was the primary metallization used to form the interconnections between transistor elements within a microelectronic device such as a microprocessor. Starting around 1997, Cu-based metallization was introduced to enable the necessary performance scaling (Edelstein et al., 1997). Because Cu metallization became the new manufacturing process for advanced interconnects, much refinement in the basic Cu integration process has been done to improve on interconnect defectivity and uniformity so that technology scaling can continue at least up to the year 2015 (ITRS, 2009) before new solutions must be developed to keep pace with scaling requirements. Furthermore, tweaks to the basic Cu process and integration approach have been developed to improve either interconnect performance and/or reliability. These improvements have a direct bearing on EM performance and, in this chapter, we attempt to assess how EM performance might be expected to trend for the remainder of this decade.
8.1.2 The canonical copper interconnect and technology scaling
The canonical or standard picture of a Cu interconnect used in advanced CMOS-based technology appears little changed from its first use around 1997 (Edelstein et al., 1997; Li et al., 2004) and is depicted in Fig. 8.1. Interconnects are fabricated using a so-called ‘damascene’ approach, where a blanket film dielectric on a Si wafer is patterned and etched to form open spaces (trench and via openings). Via openings, for connection to the metal level immediately below, are made either before or after a trench pattern is created. Cu metallization is deposited within the trench and via features using electrochemical deposition (ECD). Before such Cu deposition, however, a metal diffusion barrier, typically Ta-based, and Cu seed layer must be deposited, using physical vapor deposition, to enable conformal growth of Cu metallization during an ECD plating process. Good quality metal diffusion barrier is needed to keep any Cu from ‘out-diffusing’ into the low-k dielectric (Michael et al., 2003a, 2003b; Augur et al., 2003; Lu et al., 2005; Pyun et al., 2005) and potentially allowing the dielectric to be shorted out under electrical bias, since Cu is known to be a ready diffuser into such dielectrics under electrical bias (Tsu et al., 2000), if pin hole defects exist within the metal barrier. After out-diffusion, the Cu then subsequently oxidizes within the inter-metal dielectric (Michael et al., 2003a, 2003b). The Cu plating creates a blanket film overburden above the trench feature that needs to be removed by chemical mechanical polishing (CMP) to eventually form the metal interconnect. CMP flattens or ‘planarizes’ the trench top surface for subsequent capping by a dielectric diffusion barrier. The Cu microstructure is usually improved and stabilized somewhat (increased grain size and stabilized Cu grain texture) by use of a thermal anneal treatment (Hu et al., 2007b) with overburden present or maybe after overburden removal by CMP, depending on the integration approach used.
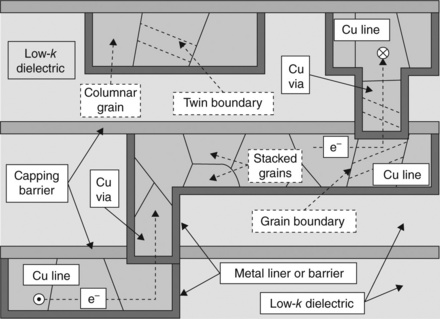
8.1 Cross-sections of a dual-damascene interconnect structure in advanced Cu-based interconnects since 130 nm node, including lower trench, connecting via, intermediate interconnect, next level via and trench. Each trench feature is surrounded by diffusion barriers, on the bottom and sidewalls by a Ta-based metallization and on the top by a capping dielectric. In between the layers of interconnect metal is usually a low-k dielectric; this and the capping dielectric are in continual need of replacement to lower-k dielectric as technology scaling continues, but doing so is a great challenge for process and integration engineering. The Cu metallization within the trench consists of multiple grains along the interconnect length. Some segments can contain more than one grain along the width or height directions. Cu grains are also prone to ‘twinning’. Finally, the electron flow during EM is also depicted. The circle with dot within it and circle with ‘X’ within it represent out-of-page and into-page directions, respectively.
Overburden anneal is usually preferred, however, because it minimizes the potential for void generation within the interconnect or hillock formation on the trench surface during anneal. The overburden presence also allows microstructure evolution during anneal from the overburden to penetrate into the trench feature and improve the resulting trench microstructure (Harper et al., 1999; Lingk and Gross, 1998; van den Boom et al., 2007), at least for interconnects greater than 250 nm in width. Following CMP, a dielectric film, typically a form of SiCxNy in presently available 90, 65, and maybe 45 nm technology nodes, covers or ‘caps’ the remaining free Cu surface so that Cu is fully confined within its trench by diffusion barriers. The dielectric cap layer can also function as an etch stop during via etch when a metal layer above must be connected to a metal layer below.
A procedure whereby such via are formed in conjunction with trench formation above is known as a ‘dual-damascene’ integration scheme where metal barrier/Cu-seed/Cu-plating steps are subsequently carried out into both via and trench concurrently. Typically, the first Back-end-of-Line (BeoL) metal layer, generally called ‘M1’, is made using a ‘single damascene’ integration scheme for connection to a lower tungsten (W) contact plug and eventual connection to transistors or Si substrate. At M2, a dual damascene process is used to connect to the M1 interconnect. This dual-damascene process is then repeated level-by-level until the complete metallization stack is generated. Generally, the interconnect feature size (width and often length) at lower or intermediate metal level is at or near the minimum allowable critical dimensions at a given technology node. The interconnect dimensions at the upper metal level tend to be larger, especially at the highest metal levels, where power and signal routing are used and finally where bond pad connections for access to device package wiring or solder bumping are needed. Thus, the interconnect layout tends to be ‘hierarchical’ in the sense that lower level interconnect dimensions tend to be smaller than those found toward the top levels; however, such dimensional transitions and the extent of such hierarchy are entirely dependent upon product type, cost, performance, and potential reliability issues that are not specifically related to EM.
8.1.3 Issues and evolution of the canonical copper interconnect
The ‘canonical Cu interconnect’ model above has not, however, stayed constant with time because its evolution is needed to keep pace with pressing technology needs. Manufacturing feasibility at a given point in time is an important consideration because the ITRS roadmap has required several adjustments to the rate of implementation of low-k dielectrics because of difficulties encountered incorporating them into a high yielding manufacturing process (Shaviv, 2008; Gambino, 2008; Lu, 2009). Although the overall integration scheme is pretty much the same, a number of improvements have occurred since Cu was first introduced. The intra- and inter-metal effective dielectric constant has decreased owing to new materials substitutions such as SiCxOyHz (carbon-doped oxide; k ~ 2.9) for fluorinated silica glass (FSG; k ~ 3.5), which replaced tetraethyl orthosilicate (TEOS; k ~ 4.0) and capping dielectric SiCxNy (k ≤ 6) for SiNx (k > 6). Etch and CMP processes have evolved for better overall uniformity across a Si wafer and for addressing differences in metal density and feature size. The dielectric cap process has been gradually improved through utilization of surface pre-treatments and time-window management before capping dielectric deposition for better adhesion/mechanical strength, EM performance, and corrosion prevention. The barrier metal has been gradually thinned in each generation to reduce the overall interconnect resistivity. Additional changes for more advanced technologies are also pending. Somewhere before the 15 nm node, ultra low-k porous interconnect dielectrics (k ≤ 2.5), EM mitigation process enhancements (such as metal capping, alloying, and/or interface treatment), and possibly atomic layer deposition (ALD) barriers will be implemented, provided that they are proven to be suitable for large-scale manufacturing (van Roosmalen, 2006). Beyond 15 nm, the inherent difficulty in mitigating the progressively worsened resistivity of Cu metallization while simultaneously placing increased demands on the process margin and performance poses a formidable challenge. Table 8.1 shows how the maximum current density, resistivity, and metal barrier thickness might be expected to scale down to the 7 nm node. Whereas other trends found in the ITRS roadmap are also very important, these three items are of particular interest to EM reliability, although, for brevity, the matter of barrier thickness scaling is only touched upon in this chapter (Traving et al., 2004).
Table 8.1
ITRS values used to predict EM drift velocities at each technology node
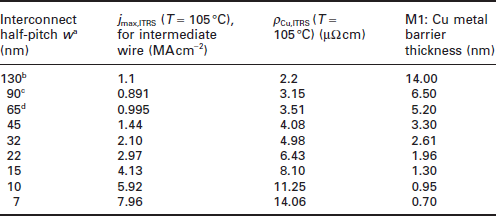
aFrom ITRS (2001, 2005, 2007, and, primarily, 2009);
bFrom ITRS (2001);
cFrom ITRS (2005);
dFrom ITRS (2007).
A significant increase in resistivity from both grain boundary and interface electron scattering has been well-characterized by multiple authors (Besling et al., 2004; Gignac et al., 2007; Im et al., 2005; Kim et al., 2003; Rossnagel and Kuan, 2004; Shimada et al., 2006; Steinhögl et al., 2002, 2004, 2005; Sun et al., 2009; Tay et al., 2005; Wada et al., 2009; Yarimbiyik et al., 2006; Zhang et al., 2004a, 2004b) to the point that their respective interconnect delay contributions are well-predicted in the ITRS roadmap for the rest of this decade. In Fig. 8.2, Cu interconnect resistivity as a function of the technology node is shown along with data from some representative authors. The resistivity contributions are modeled using the formalism developed by Steinhögl et al. (2002, 2004, 2005), and the primary drivers for interconnect resistivity increase are shown to come from grain boundary (Mayadas and Shatzkes, 1970) and surface (interface) scattering (Fuchs, 1938; Sondheimer, 1952). The form provided by Steinhögl et al. (2002, 2004, 2005) is as follows:
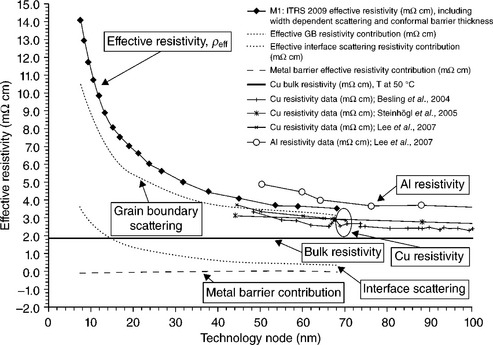
8.2 Expected interconnect resistivity as a function of technology node (based on metal half-pitch dimension), showing expected trending contributions from different components of resistivity increase. For the model used [Steinhögl et al. (2002, 2004, 2005)], grain boundary scattering is dominant. The redundant path provided by the metal barrier does not add to the effective resistivity. The representative Cu resistivity data (Besling et al., 2004; Steinhögl et al., 2005; Lee et al., 2007) shown agrees well with the model trending down to presently accessible metal line widths. Al resistivity data (Lee et al., 2007), shown for reference, lie above the trend graphs found for Cu. The presence of a high resistivity liner that is not easily scaled does not provide a strong argument for Al replacing Cu should increase in the Cu resistivity become intolerable.
where 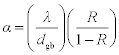 , w is the width, AR the aspect ratio (height over width), ρ0 the bulk material resistivity, λ the mean free path, dgb the average distance between grain boundaries, p the specularity parameter at the metal surface, and R the grain boundary reflectivity coefficient. The parameter C is a constant and equals 1.2 for rectangular cross-sections. Equation [8.1] is an approximation to the exact solution of the transport problem in a conductor with surface scattering. The approximation accuracy compared with the exact integral relationship is estimated by Steinhögl et al. (2005) to be better than 3.5% for linewidths between 50 and 1000 nm. The first term in equation [8.1] corresponds with the grain boundary scattering contribution and the second with interface scattering. The values of the other parameters are taken directly from Im (2005) with the exception of the bulk resistivity, where ρ0 = 1.85 μΩ cm at ~ 50 °C (348 K) is assumed: λ = 37.3 nm (300 K), p = 0.41, and R = 0.22. Similar plots are found in the studies previously noted, and data from those align well with those shown in Fig. 8.2. The parameters w and AR are necessary geometrical parameters that are determined by the ITRS roadmap, and the trending curve for effective resistivity in Fig. 8.2 is directly tied to ITRS predictions from 2007 and 2009. Using these parameters, the grain boundary contribution seems larger than that from interface scattering, but surface scattering is argued as being as least as important by others (Gignac, 2007; Graham et al., 2008) in Cu interconnect microstructures where the mean grain size exceeds the electron mean free path. It is likely that there will be improvements in process and integration to improve on the grain structure, size and interface smoothness, but such improvements will not be easily achieved. In fact, the evidence appears to indicate that microstructure development (Brandstetter et al., 2010) and interface quality because of line edge roughness (LER) (Noguchi, 2005) are less easily controlled or perhaps more complicated to address when the line width is decreased. An LER contribution that does not improve with scaling would significantly worsen the resistivity trend (Lopez et al., 2009). Thus, interconnect microstructure that becomes progressively more difficult to control as trench width narrows, adds further complexity to the expected Cu resistivity increase as interconnect critical dimensions scale downwards (ITRS, 2009) in width and thickness.
, w is the width, AR the aspect ratio (height over width), ρ0 the bulk material resistivity, λ the mean free path, dgb the average distance between grain boundaries, p the specularity parameter at the metal surface, and R the grain boundary reflectivity coefficient. The parameter C is a constant and equals 1.2 for rectangular cross-sections. Equation [8.1] is an approximation to the exact solution of the transport problem in a conductor with surface scattering. The approximation accuracy compared with the exact integral relationship is estimated by Steinhögl et al. (2005) to be better than 3.5% for linewidths between 50 and 1000 nm. The first term in equation [8.1] corresponds with the grain boundary scattering contribution and the second with interface scattering. The values of the other parameters are taken directly from Im (2005) with the exception of the bulk resistivity, where ρ0 = 1.85 μΩ cm at ~ 50 °C (348 K) is assumed: λ = 37.3 nm (300 K), p = 0.41, and R = 0.22. Similar plots are found in the studies previously noted, and data from those align well with those shown in Fig. 8.2. The parameters w and AR are necessary geometrical parameters that are determined by the ITRS roadmap, and the trending curve for effective resistivity in Fig. 8.2 is directly tied to ITRS predictions from 2007 and 2009. Using these parameters, the grain boundary contribution seems larger than that from interface scattering, but surface scattering is argued as being as least as important by others (Gignac, 2007; Graham et al., 2008) in Cu interconnect microstructures where the mean grain size exceeds the electron mean free path. It is likely that there will be improvements in process and integration to improve on the grain structure, size and interface smoothness, but such improvements will not be easily achieved. In fact, the evidence appears to indicate that microstructure development (Brandstetter et al., 2010) and interface quality because of line edge roughness (LER) (Noguchi, 2005) are less easily controlled or perhaps more complicated to address when the line width is decreased. An LER contribution that does not improve with scaling would significantly worsen the resistivity trend (Lopez et al., 2009). Thus, interconnect microstructure that becomes progressively more difficult to control as trench width narrows, adds further complexity to the expected Cu resistivity increase as interconnect critical dimensions scale downwards (ITRS, 2009) in width and thickness.
The result in Fig. 8.2 demonstrates the dramatic resistivity increase expected beyond the 32 nm node, although the accuracy of the prediction needs verification because the result is based on an integral approximation. The published data obtained so far for technologically relevant Cu interconnect does not yet extend down below 40 nm so that the worst of the projected resistivity increase has yet to be verified. Interestingly, resistivity trending for Al interconnect (from Lee et al., 2007) is also shown for reference, and it is clear that Al metallization remains an inferior option down to 50 nm and probably beyond. The reason is that present Al interconnect technology requires the use of TiN antireflective coating (ARC) and a high resistivity Ti/TiN redundant metal liner to mitigate Al susceptibility to stress-induced voids (Okabayashi, 1993; Walls, 1997) or EM (Gambino, 2008; Murphy et al., 2008), and it will be difficult to thin the liners with technology scaling (Rosenberg et al., 2000).
The contributions for grain boundary, interface scattering and the barrier metal are also shown in Fig. 8.2. The barrier contribution shows as a negative because it provides an additional current pathway, which reduces effective resistivity by a very minor amount. This barrier contribution analysis can be seen by treating the interconnect as stemming from two parallel pathways owing to the Cu metal and the metal barrier. The total resistance can be shown to have a form where the barrier metal contribution can be expanded out as (1 + x)− 1 ≅ 1 − x + x2, where x is a term consisting of metal barrier resistivity and cross-sectional area contributions. Note that the above analysis completely ignores vias, which necessarily have barrier metal at the bottom, so that it will have a serial, in addition to the already present parallel, contribution to the via resistance or effective via resistivity. This serial contribution is a seriously detrimental contributor to via resistance and can only be scaled downwards by thinning the barrier. This scaling impact of via resistance is presently not a well-addressed or well-documented problem. How via bottom barrier thickness is addressed will potentially have impact on the use of the Short Length Effect (Blech, 1976, 1997, 1998; Filippi et al., 1995; Wang and Filippi, 2001; Christiansen et al., 2008; Oates and Lin, 2008, 2009) for current density enhancement in short-length interconnects because the via bottom barrier serves both as the flux blocking barrier from one lower level interconnect to an upper level interconnect and as the thin membrane to support back-stress development in sufficiently short-length interconnects (Aubel et al., 2007).
According to Meindl et al. (2002), interconnect signal latency can be generically expressed as a product of three factors:
where τ is latency of a single isolated interconnect, ρε is the resistivity– permittivity factor, h is the metal height, t is the dielectric thickness, and l is the interconnect length. As technology scales, assuming the rather ideal situation that no additional chip functions are added with scaling, all the physical dimensions in the BeoL stack shrink proportionately so that the only simple way to decrease latency is to improve the properties of the materials used in interconnects; namely, by reducing either the metal resistivity ρ, or the effective dielectric permittivity ε. From the metallization perspective, Cu is as good a conductor as can be expected, for a presently available technology. Although improved metallization alternatives to Cu are being investigated (e.g., metal silicides, nano-Ag, carbon nanotubes, nano-graphene, phonon engineering, on-chip optical interconnects, and positive quantum confinement effects; ITRS, 2009), there is little clarity on which technology or technologies will be an appropriate future interconnect medium from a performance, reliability, and manufacturability standpoint; however, the increasing resistivity of Cu metallization as interconnect dimensions scale downwards means that such improvements are critical. Otherwise, the dimensional scaling benefit will be easily lost.
Unfortunately, no new and realistic materials solution presently exists to fully eliminate this upwards resistivity trend of Cu metallization. At this stage, the main effort is to improve on the effective dielectric constant by substituting materials with progressively lower dielectric constant k, where ε = kε0 and ε0 is the permittivity of free space. It is clear, however, that any materials improvement through the use of an ultra low-k dielectric (k ≤ 2.5) is limited by the presence of higher k etch stop layers (4.0 < k < 6) in the present BeoL stack. Significant process optimization effort is required to integrate new materials into a given integration scheme and, although the transition to much lower k materials is a priority for future scaling, such effort may come at the possible cost of decreasing the process margin. For BeoL technology at 22 nm and beyond, use of air-gap technology between the interconnect metal and the use of an ultra-thin metal barrier will be necessary to achieve the required performance improvements (Chen et al., 2008). For metal 1 and intermediate layers, the increased BeoL interconnect delay for a fixed length is likely to be very significant by the end of this decade, and, although capacitance is considered to be more important at these levels than resistance, this resistivity trending may not be easily countered by simple chip shrinkage (See Meindl’s equation [8.2]) as is presently done. Interconnect delay issues are also a major concern for global (across chip) interconnect wiring because their length does not scale as easily as lower level metal interconnects, but because their lateral dimensions remain large relative to the electron mean free path, they still benefit from the incorporation of ultra low-k solutions. Moreover, increased functionality for a given device with technology scaling (so-called system-on-chip or SOC integration) inevitably keeps the overall total wiring length from decreasing as fast from technology node to technology node. Generally, interconnect delay issues can be expected to progressively worsen with each generation and are not easily addressed by new materials substitution in the BeoL, although it might be expected that better process control over the Cu microstructure and interface quality will be forthcoming and that it will provide additional relief from resistivity scaling. By that time, three-dimensional (3D) integration (die stacking and chip-to-chip connection through the Si die) will probably be a stronger technology driving force. In a sense, these latest pre-15 nm Cu-based interconnect technology advances could spell the ‘last hey-day’ for advanced Cu-based interconnect technology development.
8.2 Electromigration (EM) scaling by generation
One of the major reliability benefits that occurred as a consequence of the transition from Al(Cu)-based to Cu-based interconnects was greatly improved EM performance. Such improvement is desired because the trend towards smaller dimensions means that the applied current density increases progressively with each succeeding generation. Beyond a certain point, the increased current density requirements render the use of Al interconnects impractical, except at maybe the highest metal level, where the routing between bond pads is permitted. EM improvement in Cu over Al is naively predictable in that Cu has a significantly higher melting temperature (Tm) than Al (1090 versus 660 °C). Thus, for a given temperature, stress on the metal that can lead to metal atom movement would seem less of a problem for Cu than for Al. As an example of the relative difference in EM performance between Al and Cu, work by Hu et al. (1999b) demonstrates a roughly 100 times improvement in EM performance by Cu interconnect over Al at EM stress conditions.
The actual details about Cu versus Al EM are a bit more complicated owing to differences in how Al interconnects are processed compared with Cu. Al interconnects are created by subtractive etch of the metal film after patterning so that the metal microstructure tends to form grain boundaries that are orthogonal to the substrate plane. Al metal film is doped with a small amount of Cu (ranging from 0.5 to 3 at. wt. %) for improved EM performance by ‘grain boundary stuffing’ (Hu et al., 1992; Spolenak et al., 1999) and is usually sandwiched between thin layers of Ti below and Ti/TiN above the Al film (Hu et al., 1995). These layers form a so-called redundant shunting layer so that any significant voiding that develops in Al metallization by either EM or SM can be mitigated to a certain degree. The more conventional Al-based interconnects are also terminated by via plugs made of tungsten (W) material to connect overlapping interconnects between adjacent layers. From an EM perspective then, the final flux divergence occurs where the Al interconnect and W plug connect. The Al grains tend to grow vertically from the Si substrate and show preferential (111) orientation, and because the deposition temperature is normally relatively high (≥ 350 °C), the as-deposited grain size is rather large (≥ 1 μm). Thus, the as-deposited grains are more or less columnar in nature owing to the relatively high deposition temperature (compared with Tm,Al). Furthermore, Al benefits from having a naturally forming native and self-limiting surface oxide that creates a very clean and strong interface between metal and oxide layer. This layer tends to limit but not block, any tendency for atomic movement through its surface interface under EM stress. Such a stable interface layer means that the ‘fastest pathway’ for EM damage is likely to be found through the grain boundaries in several micrometers wide Al interconnects, where polygranularity is more likely (Cho and Thompson, 1989; Walton, 1992). The doping effect from Cu is also important. Research indicates that the Cu dopant depletion from the interconnect cathode end is necessary to initiate EM voiding from grain boundary pathways (Hu et al., 1991, 1992 and 1995). Only after Cu dopant depletion through Al interfaces has extended beyond the EM critical length (Blech, 1976), is grain boundary EM possible. This effect yields a latency effect in observed relative resistance increase during EM stressing. During EM stress, voids can grow across an interconnect line owing to grain boundary diffusion at some point so that resistance increase may be significant enough to be considered an interconnect failure (Sanchez and Morris, 1991), but eventually such voids tend to migrate towards the cathode end where the Al interconnect and W plug meet (Kawasaki and Hu, 1993).
As the Al(Cu) interconnect feature dimension is shrunk toward 250 nm (Hu et al., 1995), grains are found to be generally longer (in the direction of the interconnect length) than wide (the width being defined by the metal patterning) for basically the same Al film microstructure so that the Al interconnect grain structure outwardly resembles ‘bamboo’ shoots lying down on the silicon wafer. Bamboo grain boundaries tend to lie orthogonal to the interconnect length direction. In bamboo-grained, narrow interconnects (~ 250 nm width) grain boundary pathway EM is constrained by the grain boundary orientation, which is orthogonal to the electron flow (interconnect length) direction, and may be the primary geometrical reason for EM performance enhancement (Oates, 1997). In this instance, both interfacial and grain boundary EM mutually contribute to interconnect EM damage, but interface EM is considered dominant (Hu et al., 1995). Finally, Al interconnects are not an extinct species in advanced technology because they are used as a top metal routing layer, especially for ‘mixed signal’ devices that combine both analog and digital functions (Hein, 2008). Given the discussion above, it is clear that lessons learned about Al interconnect reliability cannot be forgotten and are actually very relevant to the approaches taken to improve EM in Cu nanoscale interconnects.
For Cu, however, use of a damascene integration scheme means that the metal microstructure is formed within the boundaries of the trench features rather than having the interconnect features defined upon an already existing metal film as is the case for Al interconnects. The Cu is deposited using electroplating at relatively low temperature (compared with Tm,Cu). The Cu microstructure is thus unstable and can be greatly affected by a subsequent thermal anneal or even by just simply leaving the Cu film with overburden intact at room temperature for extended periods (Lingk and Gross, 1998; Harper et al., 1999; Detavernier et al., 2003). The Cu microstructure evolution is three-dimensional with interface boundaries at the trench bottom and sidewalls affecting microstructure evolution. Thus, final grain structure is less bamboo in character, even for the narrowest line widths. The resulting Cu microstructure and texture are thus more variable, although the primary grain orientation may still be more (111) than not. The smaller Cu grain size for very narrow interconnects also has a significant bearing on EM reliability as will be shown later. It is also notable that the Ta-based diffusion barrier along the Cu trench bottom and sidewalls are quite thin and getting necessarily thinner with each technology generation, although possessing a much higher intrinsic electrical resistivity compared with Cu. Thus, this metal barrier liner does not function particularly well as a redundant shunting layer in comparison with the role played by the Ti/TiN in the older Al(Cu) interconnect technology, although its presence does provide the additional benefit of avoiding EM failure by sudden open-circuit (Li et al., 2003 and 2005; Yang, 2005).
Another interesting characteristic of Cu metallization as opposed to Al is that Cu does not possess a stable native oxide like Al does. So, unless the Cu surface is well-passivated, this Cu interface is prone to diffusion-controlled damage such as can happen during EM and stress migration (Hartfield et al., 2004). It is then reasonable to suggest that EM in Cu interconnects is generally driven mostly by interface diffusion along a particularly weak interface (Hartfield et al., 2004; Hu et al., 1999a; Lin et al., 2004; Lloyd and Clement, 1995; Michael et al., 2003a; Usui et al., 2004; Vairagar et al., 2004a). Other pathways such as grain boundary diffusion, may also be significant contributors for a given microstructure (Gan et al., 2004 and 2005; Huang et al., 2005; Sukharev et al., 2009; Zschech et al., 2009), especially when linewidth impact on microstructure development becomes important. Presumably, the quality of the interface between the Cu surface and the capping dielectric is controlled mainly by the exposure environment before capping deposition (Birringer et al., 2009). This intuitively reasonable assessment about the EM interface pathway was confirmed by results showing a very strong correlation between interfacial adhesion strength, between a given passivation material and a Cu surface, and EM activation energy (Lane et al., 2003; Lloyd et al., 2005). In this instance, the weakest interface is observed to lie at the trench top, and a primary focus of improving EM reliability has been in developing interface engineering methods to reduce the EM drift velocity at the trench top. In 8.3, process integration approaches that strive to improve the EM performance of known weak interface pathways are described.
Any basic discussion of EM usually starts with the EM drift equation and is expressed as follows:
where vD is the atomic drift velocity, JF is the atomic flux, C is the local atomic concentration, Deff is the effective diffusivity, kB is Boltzman’s constant, T is the temperature, Zeff∗e is the effective charge, E (= ρj, where ρ is the electrical resistivity and j is the electrical current density) is the electric field strength, Ω is the atomic volume, and ∂σ/∂x is the stress gradient along the interconnect length (which leads to the Blech or short-length effect). The above equation is derived from the Nernst–Einstein relation. Note that the E = ρj factor captures nicely the impact of scaling on EM. As interconnects scale dimensionally, both j and ρ necessarily increase. The current density j increases because the interconnect cross-sectional area shrinks by about two-fold each generation and because the sustaining transistor drive currents probably increase. The Cu resistivity ρ increases because increasing contributions by grain boundary and interface scattering are found as interconnects narrow (Besling et al., 2004; Rossnagel and Kuan, 2004; Zhang et al., 2004a, 2004b; Steinhögl et al., 2002, 2004, 2005; Tay et al., 2005; Shimada et al., 2006; Yarimbiyik et al., 2006). Other potentially important chemical potential gradient terms such as the Soret effect (temperature gradient) and entropy gradient (Lloyd, 1999; Croes et al., 2010) should be taken into account but for brevity they are not covered in this chapter. Hu et al. (1999a) have previously demonstrated how EM lifetime and interconnect scaling track with one another. The interconnect lifetime is estimated typically using the venerable Black’s Equation (Black, 1967; 1969), which is given as
where tF is the average time to fail, A is a constant, j is the current density, n is the current exponent, ΔH is the activation enthalpy, kB is Boltzman’s constant, and T is the absolute temperature. The value of n should range between 1 and 2, where n = 1 represents void-growth-limited failure and n = 2 represents void-nucleation-limited failure. Equation [8.4] above is used to characterize the generic behavior of the interconnect population, and statistical analysis is necessary to fully characterize the entire population of interconnects within a microelectronics device. Cu interconnect EM tends to preferentially exhibit void-growth limited behavior with n ranging experimentally between 1 and 1.4 (Hau-Riege et al., 2003; Hau-Riege, 2004; Lloyd, 2007). Current exponent values > 1 indicate that a fraction of the interconnect population is void-growth limited although the remaining fraction is void nucleation limited. Note that when 1 < n < 2, Equation 8.4 tends to lose its physical meaning somewhat, although it is rather convenient to use it regardless. Bear in mind, however, where n does not equal 1 or 2 exactly, Black’s equation should be used with some care (Lloyd, 2007).
Using the drift velocity equation [8.3], the characteristic lifetime, τD, is written as
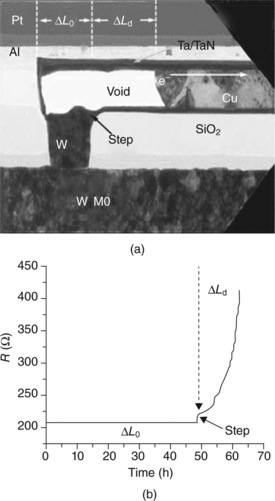
where ΔL0 is the critical void size for interconnect failure and is demonstrated by Fig. 8.3a. The other parameters are the thickness h, temperature T, interface pathway thickness δi, pathway diffusivity Di, and the interface EM driving force Fi. In Fig. 8.3b, the corresponding points in the resistance trace for when a critical void size ΔL0 is reached and where additional material drift to an extent ΔLd occurs are shown. This parameter ΔL0 scales with the via size for a given technology node (e.g. 130 to 90 to 65 to 45 to 32 to 22 nm). The via size decreases roughly by about 70% per side, per technology transition, although the maximum current density jmax is projected to scale upwards by roughly 30% per generation (ITRS, 2009; Iwai, 2009). The characteristic lifetime would then be expected to decrease 0.7/1.3 ~ 0.5 per technology generation (Hu et al., 1999a) or a nearly 10-fold decrease in EM performance within three generations! This critical void size-constrained trending of EM lifetime is demonstrated by the plot in Fig. 8.4 for single damascene W plug terminated lines from Hu et al. (2004). Yokogawa and Tsuchiya (2004) showed a line width dependence of EM lifetime following a power law behavior (t50 = AwN) with exponent N ~ 1.8 using standard Kawasaki–Hu test structures; however, the picture of a decreasing EM margin remains unchanged. Hence, the substantial EM margin originally afforded by a transition to Cu-based interconnects will have been seriously eroded for pending technology generations unless new integration or process strategies are implemented to restore the EM performance margin.
8.3 (a) Void formation at the cathode end must reach a certain size to generate interconnect failure. This critical volume is conveniently defined by a length parameter ΔL0, which is roughly the size of the contact via. This critical size scales downwards with the technology node and is essentially one of the root factors in the decrease in EM lifetime with technology node. Additional material depletion, represented by ΔLd, generates gradual resistance increase by the so-called material ‘drift.’ (b) The change in resistance overtime shows resistance features that correspond to ΔL0 and ΔLd. [from Hu et al., 2004 (© 2004 IEEE); permission IEEE; images have been digitally enhanced from the original for publication purposes]
8.4 Relative impact of critical void volume on EM lifetime. (From Hu et al., 2004 (© 2004 IEEE); permission IEEE)
Equation [8.3] strictly applies before complicated void nucleation and growth events occur, but it can be used to illustrate that EM in Cu interconnects is happening across several separate pathways (Hau-Riege, 2004; Hu et al., 1995 and 1999a; Li et al., 2004; Ogawa et al., 2002; Yokogawa, 2008). A depiction of these pathways is shown in Fig. 8.5. At the expense of some complexity, a somewhat different representation of the pathway dependences from those shown in the other studies is used for further discussion:
8.5 (a) Exploded view of major EM pathways; for simplicity, bulk and pipe EM pathways are not shown. (b) Cross-sectional view of EM pathways showing the multiple possibilities for mass transport within a given microvolume. Within such a microvolume, various pathways connect to enable mass transport over larger distances. Grain boundaries are inherently unable to transport mass of over distances if they do not form a continuous mass transport pathway along the entire interconnect length. Interfaces, however, run along the entire interconnect length to enable long-distance mass transport of EM-driven atoms. Thus, interfaces do not need to be the fastest mass EM pathway locally, only globally, and it is the fastest of the interface pathways that acts as the ‘rate-limiting path’ for long-distance EM mass transport. Such multiple pathway connections intuitively indicate that localized flux divergences where pathways with different mass transport capabilities may meet are a natural consequence of the multi-pathway model.
where Deff is the effective EM diffusivity and DA are the respective diffusivities for each pathway (A ≡ b, gb, mbi, cbi, and p for bulk, grain boundary, metal barrier interface, capping barrier interface, and pipe diffusion pathways, respectively). Zeff∗ is the effective charge parameter, and the parameters Zeff∗ are the effective charges for the different EM pathways (B ≡ b, gb, mbi, cbi, and p for bulk, grain boundary, metal barrier interface, capping barrier interface, and pipe diffusion pathways, respectively). The other parameters are fb (fraction of atoms in the bulk), w (line width), h (line height), dC [average grain size in the C ≡ w (width), l (length) and h (height) directions, respectively], ρdisl (dislocation density), acore (dislocation core cross-sectional area), and δD (pathway width, D ≡ gb, mbi, and cbi for grain boundary, metal barrier interface, and capping barrier interface pathways, respectively). For clarity, δgb;k is the grain boundary width of the kth grain boundary within a given pathway volume and not the identity matrix element, δij. The EM path is assumed to cover a given volume, such as Vpath = lhw, so that the grain boundary and dislocation sums account for all grain boundary and pipe diffusion pathways, respectively, within that volume. This pathway model is illustrated in Fig. 8.6. It is convenient to partition the sum for grain boundary EM as a sum within an average grain length dL. In Fig. 8.6a, such a boundary volume is shown that contains a single width spanning grain boundary with angle θgb. There are three grain boundary terms to cover grain boundaries that lie parallel, or nearly parallel, to the interconnect length, width or height. The factor tanθgb defines the average grain boundary angle for a grain boundary spanning along the interconnect height and width relative to the surface normal from the trench bottom (0 < θgb < 180°). The angle φgb defines the average grain boundary angle for one lying along the interconnect height and length, where φgb = 0 means that such a grain boundary is parallel to the interconnect sidewall. The angle ψgb defines the grain boundary angle for one lying along the interconnect width and length. Likewise, ψgb = 0 means that such a grain boundary is parallel to the interconnect trench bottom. For simplicity, one assumes that both φgb and ψgb are ~ 0°. The truncation function, ‘TRUNC()’ calculates the average number of grain boundaries that lie within the grain length dL for a given grain orientation (Excel, 2007). For example, if 2 ≤ w/dW < 3 for grain boundaries along the height (i.e., interconnect trench thickness) direction, then effectively one grain boundary is found along this direction. The tanθgb parameter takes care of the fact that interconnects with grain boundaries spanning the interconnect cross-section and lying parallel to the surface normal (θgb = 90°) cannot contribute to EM since the current flows along the length direction. Thus, an interconnect with grain boundaries that all have their surface normal vectors pointing parallel with the length direction is a bamboo interconnect; however, the previous statement is an idealization in the sense that a grain boundary path at the point where the grains terminate at the interfaces is likely to have some rounding so that θgb = 90° cannot strictly apply to the grain boundary at that juncture. In that case, a grain boundary triple point exists where a local flux divergence can occur and is a possible site for void nucleation and growth. The factors within each interface transport term that involve a ratio of geometrical parameters such as the pathway width δC to a physical dimension such as line width w or line height h provide a rough estimate of the fraction of atoms involved within a given pathway. A similar statement is made for the product of the dislocation density ρdisl and core area acore. For calculations, the effect of grain boundaries on core diffusivity is neglected for simplicity (Budiman et al., 2009).
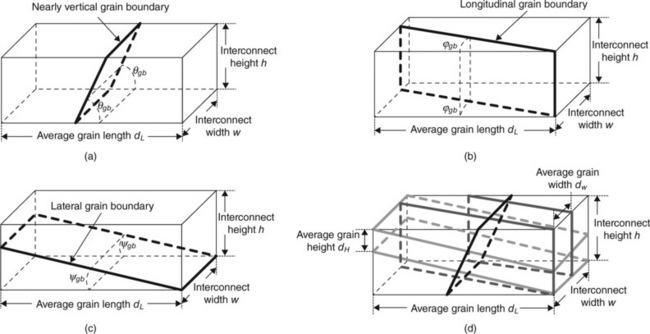
8.6 Grain boundary angles and averaged grain sizes with interconnect microvolume illustrating the geometrical parameters for the grain boundary pathway calculation: (a) nearly vertical grain boundary; (b) longitudinal grain boundary; (c) lateral grain boundary; and (d) all grain boundaries.
To get a sense of the relative fractional atomic contributions, it is worthwhile to calculate some EM numbers. To do so, we make some simplifications by breaking up a long interconnect into simple sub-units limited by the average longitudinal grain size dL. We assume that the volume of interest occurs within a grain boundary length, i.e. l = dL = 200 nm, so that the sums are greatly simplified. We also assume that the lateral and vertical grain sizes dw and dH respectively, equal the line width w and line height h (‘bamboo-ish grains’) and that the other interconnect dimensions are w = 100 nm and h = 200 nm. The dislocation density ρdisl is assumed ~ 1 × 10–3 dislocations nm–2 (Budiman, 2007) and acore = 0.82 nm2 (Frost and Ashby, 1982a, 1982b). With these values, one finds that 98.34% of the Cu atoms lie within the bulk. Interestingly, only ~ 0.09% is available for the grain boundary. For the interfaces, the metal barrier interface occupies 1%, whereas the capping dielectric interface uses 0.49% of the atoms. The pipe dislocation fraction is ~ 0.08%. In Fig. 8.7a and 8.7b, we show how the relative contributions to the EM pathway changes with interconnect dimension, where we compare the relative fractional EM contributions per pathway. Here, we assume that the aspect ratio, AR = h/w = 2 throughout and that the longitudinal grain boundary dimension scales as 2w. We also assume for simplicity the presence of rectangular grains. The average grain boundary angle is arbitrarily assumed to be θgb = 70° from the trench bottom plane for grains that span the interconnect cross-section. For grains with boundaries lying roughly parallel to sidewall or trench bottom, we assume that the boundaries are perfectly parallel with the current flow direction. In Fig. 8.7a, only dimensional scaling is assumed. With technology scaling down to 7 nm, we can clearly see the increasing fractional contribution from the interfaces; however, the grain boundary contribution is not significant because the grains are roughly columnar. In Fig. 8.7b, we assume an average of two grains in the vertical direction and average lateral grain size equaling the width. In this instance, the grain boundary fraction continues to increase with technology scaling so that by the 7 nm node, more than nearly 30% of the available atomic volume follows a non-bulk pathway. Much wider leads (> 2 μm) have different weighting because a single average grain is unlikely to span the width so that for polycrystalline interconnects, the grain boundary contribution has additional significance (Hu et al., 1999a).
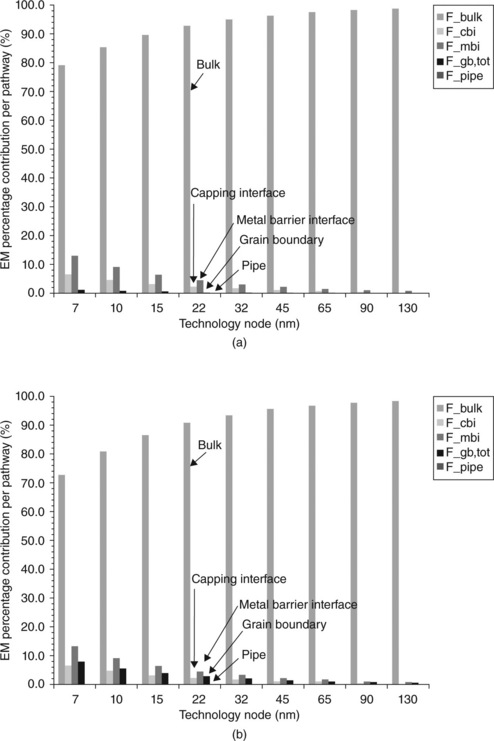
8.7 Estimated atomic fraction for given EM pathway as a function of technology node: (a) assuming that Cu grains are basically columnar across all technology generations; (b) assuming that Cu grains are somewhat polygranular along the depth of the trench across all technology generations. For both cases, an aspect ratio AR = h/w is assumed to have a fixed value, AR = 2, where h and w are, respectively, the interconnect height and width. The terms F_x, where x = bulk, cbi, mbi, gb, and pipe, refer, respectively, to bulk/lattice, capping barrier, metal barrier, grain boundary, and pipe diffusion EM pathways. With continued technology scaling, there is an increasing fraction of Cu atoms within an interconnect lying at interfaces. Polygranular interconnects also show increasing pathway contribution from grain boundaries as technology scales below 15 nm.
The individual diffusivities have the form DPath = D0,Pathexp(− ΔHPath/kBT), where ΔHPath is the activation enthalpy for a given mass transport pathway. Convenient reference values for the Cu pathway-dependent activation energies can be found in Lloyd’s paper (1999): (i) ΔHb = 2.3 eV for bulk diffusion, (ii) ΔHgb = 1.2 eV for grain boundary diffusion, (iii) ΔHi = 0.7–1.0 eV for interface diffusion. For surface diffusion, we use the value provided by Jo and Vook (1995), ΔHs ≅ 0.5 eV since EM was done under ultra-high vacuum conditions. Actually determining, for example, the individual Z* parameters is not simple because of the complication of developing and testing a number of test structure types where the impact of the certain EM pathway contributors are limited, relative to other pathways. Table 8.2 shows some representative values for ΔH, D0, and Z*. The range of value obtained is quite large and shows the inherent difficulty in using these values for quantitative reliability assessment or projection. Both the ZPath∗ and DPath values at a given temperature dominate the relative EM contribution. So, simple atomistic bookkeeping does not tell the whole story. To provide a picture of the EM trending as a function of EM pathway, some calculations can be made using values from Tables 8.1 and 8.2. For this calculation, one goes back to equation [8.3], ignoring the back-stress term, and calculates the drift rates for the different pathways. Several assumptions also need to be made. First, representative values from the literature are chosen from Table 8.2. Second, a grain size characteristic is chosen to distinguish between microstructure that is essentially bamboo or columnar and one that has transverse grains whose boundaries lie parallel to the EM current. Third, where values are not found in the literature, a ‘guess’ value is used that is based on the reported value for somewhat related work (a dangerous assumption but used here to illustrate some points). These simplistic calculations are then assuming that all pathways are continuous from the interconnect cathode to the anode.
Table 8.2
Pathway dependent Cu electromigration diffusion and kinetic parameters
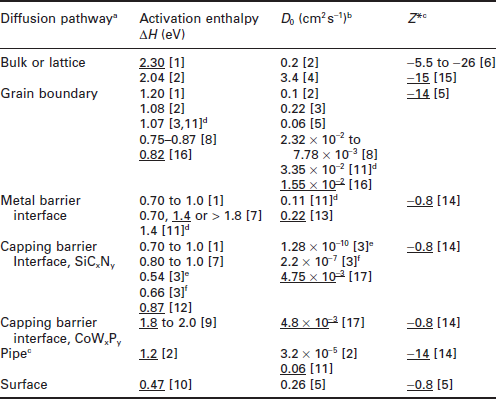
a[1]Lloyd, 1999; [2] Frost and Ashby, 1982a, 1982b; [3] Gan et al., 2005; [4] Chao et al., 2007; [5] Hu et al., 1999; [6] Butrymowicz et al., 1973; [7] Hu et al., 2003, 2010; [8] Surholt and Herzig, 1997; [9] Hu et al., 2004a; [10] Jo and Vook, 1995; [11] Singh et al., 2004; [12] value assumed by author, using [1], and seems good fit overall from literature; [13] value assumed by author, using [3] grain boundary diffusion value; [14] value assumed by author, using [5]; [15] assumed by author, using [6]; [16] value assumed by author, using [8]; [17] value assumed by author, based on comparing published EM data from 130 to 500 nm, where the dielectric capping interface diffusion is still dominant. This value is not necessarily true to CoWP capping; however, I have used it simply for comparison purposes. Underlined values were chosen for calculations to compare relative EM drift velocities. Where possible, parameters such as D0 and ΔH were matched to the same paper, although it is generally not possible to do so for all parameters at the same time, especially Z*.
bFor D0 estimate, results are usually quoted as δbndryD0, where δbndry is the boundary width. To convert to D0, a value of δbndrv = 0.5 nm is assumed. For pipe diffusion, the core cross-section is estimated by assuming that the core radius, R0 ~ 2b ~ 0.5 nm, where b is the Bergers vector value for Cu.
cCertain values, such as Z* for interfaces, have been assumed for calculations described in the text and these generally should not be used as reference values if better values are available. Calculations using such assumed values should be considered with care.
dFor reference [11], GB D0 is calculated using grain boundary width of 0.5 nm and activation energy of 1.07 eV, consistent with reference [3]. For the metal barrier interface, interface width is assumed to be 0.5 nm and activation energy used is 1.4 eV from reference [7].
eFrom reference [3], D0 = 1.28 × 10–10 cm2 s–1 goes with activation energy 0.54 eV.
fFrom reference [3], D0 = 2.2 × 10–7 cm2 s–1 goes with activation energy 0.66 eV.
By assuming the above, one immediately finds a slight conundrum with regards to the grain boundary drift rate. The drift rate can turn out much higher than would be expected during typical EM testing at high temperature because the D0 values reported (measured by other means) are essentially much higher than that obtained for interface diffusion from 25 to 400 °C (see Fig. 8.8). In Fig. 8.8, the grain boundary pathway only becomes slower than the capping interface pathway when the columnar grain boundary is very close to 90° and actually still outpaces the interface pathway at a higher temperature. From Table 8.2, the grain boundary D0 value can be greater than 1 × 106 times the value estimated for capping dielectric interface diffusion. One major flaw with the present analysis is that D0 parameters are not directly coupled with appropriate Z* values, which are typically measured together during EM stress and are not easily decoupled without additional characterization; however, it is still instructive to examine where the analysis breaks down. Although the capping barrier and metal barrier interface D0 values are also guessed values, they lead to EM lifetimes (when coupled with appropriate Z* values in Table 8.2) that appear reasonable at test and use conditions previously reported (when comparing results from different studies). It is natural to ask why reported values for diffusion parameters do not translate directly to EM drift analysis when there should be nothing inherently different about a diffusion process that involves different driving forces such as thermal stress or a chemical potential or EM.
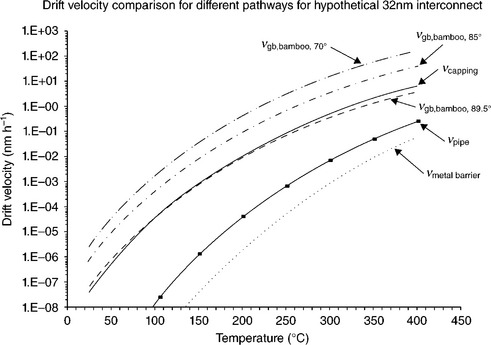
8.8 Calculated drift velocities for hypothetical 32 nm interconnect using ITRS 2009 values for jmax = 2.0 MA cm−2 and ρCu corrected for pathway but using estimated value at 105 °C. D0, ΔH, and Z* assumed underlined values from Table 8.2. Drift rate for grain boundary diffusion can outpace that for interface diffusion depending on columnar grain boundary angle. It should be noted here that the drift picture probably changes once the void is generated and the transport pathway involves free surfaces and alters the local grain boundary structure.
For the simple pathway model to strictly apply, a continuous pathway for grains must exist that is essentially along the interconnect length; i.e., the grains need to be polygranular within the interconnect for the entire length; however, this situation is not likely for interconnects used in advanced technology. There are bound to be certain sections where polygranularity exists, but these regions will be interrupted by regions consisting of bamboo-type grains or very low-diffusivity twin grain boundaries. Thus, the mass transport is inevitably gated by the movement of material from grain boundaries to the interface pathways that extend along the entire interconnect length. Hence, the EM picture for damascene interconnects is not unlike that found for the earlier Al(Cu) technology. When grains become bamboo-like, EM lifetime becomes rate-limited by the interfaces. This argument then requires that certain grain boundaries that form a 90° angle with the trench bottom must completely span the interconnect width and block or at least delay the mass transport; otherwise, a percolative path through the interconnect for grain boundary mass transport exists. Alternatively, the more mundane explanation is that the Z*D0 values need to be recalibrated and better reconciled with diffusivity values estimated by other methods so that the parameters used for grain boundary transport yield drift rates that are slower than interface diffusion.
However, the risk associated with longitudinal grain boundary pathways should not be ignored, because the occurrence of polygranularity at certain vulnerable locations (under or within vias) leads to less desirable early EM failures. For example, small grains placed under vias can be likely candidates for early EM failure where the void appears more slit-like but along a horizontal plane, and such slit void EM failures may be more prevalent in narrow interconnects where the effect of the Cu overburden has very little impact on the evolving trench microstructure during anneal. In such a case, the overburden-controlled microstructure may only partially penetrate into the damascene trench and leave only a shallow footprint of a Cu grain at the top of the trench after CMP removal of the overburden. Such a shallow grain could then lead to horizontal slit voids under EM stress if a via happened to be placed over it during subsequent processing because the critical void volume for interconnect failure is smaller than the expected via area X trench height (see equation [8.5]). In fact, Oates and Lee (2006) have argued that such horizontal slit-voids fundamentally limit EM reliability.
Although equation 12.4 is conceptually important, it is also a simplification in the sense that the pathways are not really independent but rather contribute in parallel and in series simultaneously along the interconnect length. As an example, grain boundary paths inevitably intersect interface paths and vice versa; these are known as ‘triple points’ at which localized void nucleation is possible and thus alters the local EM pathway environment. For simulations, only the most important contributions to the EM flux are included into the more general mass balance equation that includes contributions from diffusion, EM, thermal migration, and stress migration (Kteyan et al., 2007; Sukharev and Zschech, 2004; Sukharev et al., 2009; Zaporozhets et al., 2005). From the process engineering perspective, equation [8.4] points to potential avenues where improvement efforts should be focused to increase Cu EM reliability.
8.3 Suppression by metal capping: blocking rate-limiting EM pathways
The multiple pathways for EM mass transport and the architecture of the Cu dual damascene process provide various means by which Cu interconnects can fail through void generation and growth. From an EM perspective the ultimate flux boundary lies at the bottom of a dual damascene via, which separates lower interconnect from upper. Thus, fatal interconnect voids can be formed above or below the via bottom barrier liner, and these locations are the likely final void location after long-term EM stress. Whether the void forms above or below the via bottom depends, of course, on the electron flow direction so that the terms ‘up-’ and ‘down-direction’ (Ogawa et al., 2002) or ‘via-’ and ‘line-depletion’ (Li et al., 2004)) EM have been used to distinguish the two major EM damage modes. Furthermore, different critical void failure locations during up-direction EM stress have led to bi-modal lifetime behavior. Critically large enough voids can form either within the via or the trench so that two lifetime distributions may be evident (Ogawa et al., 2001) and depend upon whether small defects are present within the via that lead to premature EM failure within the via or not (Kim and Wong, 2003). When comparing EM lifetimes for down- versus up-direction, lifetimes are typically shorter for the down-direction because the necessary critical void size is apparently smaller for voids under a via than for voids forming within a via or trench during up-direction EM stressing (Gan et al., 2001; Lee and Oates, 2006). If the voiding is severe enough within the trench, failure can also occur when the void size has increased enough to span the interconnect trench (Meyer and Zschech, 2007; Sukarev and Zschech, 2004; Sukarev et al., 2009; Zschech et al., 2009).
From a scaling perspective, certain trends continue to lower the EM advantage found generally in Cu interconnects. Firstly, the pathway model shows that, as the interconnect cross-section is generically decreased, the interface EM contribution increases because the relative fraction of atoms within a given pathway increases as the interconnect dimensions decrease when compared with the bulk fraction nb. For example, for the capping dielectric pathway, the atomic fraction scales as δcdi/h. A smaller required critical volume for interconnect failure along with an increased contribution to voiding at the trench top interface is thus not an ideal situation. Secondly, although the metal barrier thickness is projected to thin proportionately with interconnect dimension, the ability to thin the barrier depends strongly on its effectiveness in preventing Cu from entering into the adjacent low-k dielectric; otherwise, a catastrophic interconnect failure owing to Cu metal shorting between adjacent interconnects results. Because the relative amount of current flowing through the barrier metal compared with the Cu is proportional to the ratio of the resistivity of Cu to the barrier metal (say 4 μΩ cm versus 200 μΩ cm), only about 2% of the current would be expected to pass through the barrier metal. Thus, unless the barrier thickness is reduced to keep pace with technology needs appropriately, the current density burden becomes progressively worse than might be expected from simple dimensional scaling. Another concern about a progressively thinning barrier with scaling might be the resulting Cu microstructure because Cu seed quality is affected by barrier quality. Thirdly, the inevitably increased current density that results from interconnect dimensional scaling (and increasing transistor drive current requirements) and ultra low-k dielectrics possessing very poor thermal conduction properties lead to significant increases in the Joule heating burden. Thus, the need to develop improved EM reliability performance is critical for additional technological progress.
Because of the critical role played by the interfaces in EM, interface engineering at the trench top has been a primary area of research focus to improve the EM margin. Such interface engineering effort has led to novel solutions to improve EM reliability. Studies have compared several different types of trench capping metallization, such as CoWxPy, CoSnxPy, CoWxByPz, Pd, Ta/TaNx (physical vapor deposition or PVD), W and Ru (Almog et al., 2007; Hu et al., 2002, 2003, 2004, 2008; Saito et al., 2004; Yang et al., 2009). The general method for such a metal cladding uses selective electroless deposition (Petrov et al., 2002). Selective electroless deposition (SED) is a process where autocatalytic or chemical reduction of aqueous metal ions in conjunction with anodic oxidation of a reducing agent takes place on a metal surface without application of an electrical current. SED is attractive from a processing perspective for several reasons. It has generally low process temperature, high surface deposition selectivity, and good self-alignment properties. The metal cladding selectively coats itself on top of the Cu trench after Cu metallization has undergone CMP and does not generally deposit itself onto exposed dielectric lying between any Cu trenches. In Fig. 8.9, an interconnect with a CoWxPy capping layer on top of a Cu trench is shown.
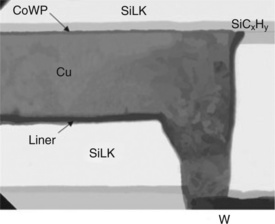
8.9 TEM cross-sectional image of a Cu interconnect coated with CoWP is shown. Note that the metal cap is also covered by a second dielectric cap. (Reprinted with permission from Hu C-K et al., (2002) copyright 2002, American Institute of Physics.) The image has been digitally enhanced from the original for publication purposes and is probably unsuitable for interpretation of the detailed microstructure.
The CoWxPy was initially suggested as a corrosion and diffusion barrier as well as a potential redundant metal liner (Shacham-Diamand et al., 1999; Kohn et al., 2001; Petrov et al., 2002) because of its relatively low resistivity of 80 μΩ cm. CoWxPy diffusion barrier properties have been demonstrated at ~ 100 nm thickness and as low as 30 nm with a higher temperature anneal. W and P atomic placement into the Co grain boundaries is apparently necessary for good barrier performance (Kohn et al., 2001). Subsequently, Hu et al. (2002) showed that very substantial gains in EM performance can be obtained by capping the Cu trench top with CoWxPy metallization. The characteristic EM lifetime is at least as much as 100 times larger than that found for a canonical interconnect at stressing conditions (Aubel et al., 2008; Hu and Rosenberg, 2004; Hu et al., 2004), and given that the CoWP cladding lies over the known fastest global EM path in damascene interconnects, it is clear that significant alteration of the top interface of the Cu metallization has been achieved to reduce Cu transport and void growth. TEM work by Meyer and Zschech (2007) (see also Zhang et al., 2010a) shows that an interface layer is clearly seen for conventional dielectric cap over Cu, whereas the resulting interface for CoWP capping over Cu is very smooth and nearly epitaxial (Fig. 8.10). Lane et al. (2003) have also demonstrated that high interface adhesion strength is achieved so that the CoWxPy/Cu interface no longer limits EM reliability performance (Lane et al., 2003; Lloyd et al., 2005).

8.10 (a) TEM cross section of SiNx capped dielectric over Cu metal is shown. An interface layer about 2 nm thick is visible. (b) In contrast, the TEM cross-section of CoWP capped Cu metallization shows a very smooth transition from Cu to CoWP. The higher resolution inset indicates that regions of near-epitaxial quality CoWP film are generated over Cu. (Reprinted with permission from Meyer and Zschech (2007), copyright 2007, American Institute of Physics.)
Interestingly, the observed activation energy is observed to be a rather bulk-like 2.0 eV (Hu et al., 2004). To understand this, one can perform some simple calculations. If one assumes a 100 nm line width and interface width of 0.5 nm, then the estimated interfacial atomic fraction is given by δcdi/h ~ 1/100. If the fraction of atoms at the capping interface is about 1/100th of the number of atoms in the bulk, then a Cu/CoWP interface with activation energy ≥ 1.8 eV (depending on Z*, D0 values assumed) would be sufficient to mimic the kinetic behavior of Cu self-diffusion (Hu and Rosenberg, 2004; Hu et al., 2004). To estimate, one assumes that the drift velocities of the bulk versus capping interface are the same. Then, one can directly calculate what the activation energy for capping dielectric must be for a given value of bulk activation energy. For the values that assumed in Table 8.2, a capping activation energy as low as 1.3 eV would be sufficient, but again, this value is dependent upon what values are used for the EM parameters. CoWP capping has the added benefit of not significantly increasing the Cu metal resistivity. Although a few percent increase in resistance can be observed owing to Co diffusion into Cu metal during EM stress at 400 °C (Hu and Rosenberg, 2004; Hu et al., 2004), the magnitude of resistance increase by Co penetration in real-world applications (125 °C or less) would be less significant. In situ SEM imaging by Meyer and Zschech (2007) shows that the strong EM resistance of the CoWP capping layer to Cu allows void formation downward across a grain boundary (and across the line width) can be complete enough to cause interconnect failure even if the vertical slit void forms some distance away from the cathode end (Fig. 8.11). The generation of such ‘slit-like’ voids shows that grain boundary diffusion plays a larger role for strongly capped interconnects. Consequently, microstructural details such as the grain boundary angle to the line direction and type of grain boundary are important characteristics to monitor.

8.11 Post-EM SEM/electron back scatter diffraction (EBSD) analysis of Cu interconnect with CoWP capping shows that slits voids are found at locations where vertical grain boundaries spanned the entire interconnect width. (Reprinted with permission from Meyer and Zschech (2007), copyright 2007, American Institute of Physics.)
There may be some concern, however, with the integrity of this process against intermetal dielectric breakdown because CoWxPy tends to lose its deposition selectivity with decreased spacing between adjacent Cu metal lines (Moon et al., 2009). This loss of selectivity means that protrusions from a metal line, small islands of CoWP metal, or poorly capped areas over the Cu metal surface can form after CoWP deposition, which erodes interconnect reliability against low-k dielectric breakdown. Despite this concern, process solutions against such risk and with no demonstrable yield impact have been found down to at least the 32 nm node (Gambino et al., 2006; Nopper et al., 2009; Huang et al., 2009; Moon et al., 2009). Furthermore, Co capping using a chemical vapor deposition (CVD) process has been demonstrated (Nakazawa et al., 2008) which may have fewer problems with selectivity loss. Ru capping using selective CVD has also been demonstrated (Yang et al., 2009). Other novel approaches such as usage of an aqueous molecular masking layer to modify the low-k dielectric surface to become more hydrophilic are being investigated (Besser et al., 2008). Also, use of CoWxByPz in the integrated BeoL process must be considered with some care because of an inherent soft error failure risk associated with elemental boron (B) (Baumann et al., 1995). Another road block is the additional cost of implementing electroless plating technology to already existing processes used for canonical Cu interconnect integration (Shaviv, 2008) and would possibly require careful economic calculation in situations where cost control is at a premium.
The more conventional approach by doping the Cu metal (e.g., with Al) is also shown to improve EM (Vanypre et al., 2007; Yokogawa and Tsuchiya, 2007; Yokogawa et al., 2008), although the expected increase in resistivity associated with such doping is a drawback, especially when the intrinsic Cu interconnect resistivity increases with decreasing line width (Tada, 2004). In this scenario, the Cu seed deposited by physical vapor deposition (PVD) and doped with Al is used, and during subsequent processing, the dopant spreads through the grain boundaries and can also spread into the capping interface. Hu et al. (2010) argues that Al doping actually arrests interface diffusion and is less effective against grain boundary EM (Michael and Kim, 2001). A variant using a CuMn seed alloy is shown to have similar benefits, and in addition, it is more compatible with lower resistivity metal liners such as Ru and Co (Nogami et al., 2010a). A Ti/TaN barrier layer doping scheme where TiOx reactant formed after Ti gettering of low-k oxygen or moisture within low-k enters into the grain boundaries to lessen grain boundary migration has shown promising results (Hamada et al., 2010). Interconnect line or via resistivity impact is not mentioned however. A strong EM performance benefit by using a Ti liner as a dopant source has also been demonstrated but with a resultant resistivity increase penalty (Kakuhara et al., 2010). Use of Co as a part of the metal liner has shown good EM results because Co has presumably diffused into the grain boundaries (Nogami et al., 2010b). One other variant is the combination of SiGe surface preparation along with CuAl seed process to improve the reliability margin (Shaviv et al., 2008).
An alternative method to improve EM is the generation of an interface layer that allows stronger adhesion of conventional dielectric capping to trench top. Silicidation of the trench top interface (Lin et al., 2004, 2005; Chattopadhyay et al., 2006; Usami et al., 2006) is a promising approach because the EM performance enhancement is about two- to threefold, and the approach is attractive because it requires little modification from the processes used already (positive cost-benefit); however, there is a performance penalty owing to the resistivity increase from Si penetration into the Cu metal. Therefore, to take advantage of this approach, precise control of the interface is needed to benefit from improved EM performance without sacrificing the resistivity increase to an unacceptable extent. An alternative approach using SiNx film precursor gas without significant resistivity fall-off has been demonstrated; however, the EM performance benefit remains somewhat modest at a threefold improvement over a canonical reference process (Le-Friec et al., 2009) under EM stress conditions. A SiGexNy process also shows promise with a relatively modest 5% resistance increase and about a fourfold lifetime improvement under EM stress conditions over a canonical reference process (Liu et al., 2008). Work by Hohage et al. (2009) has shown that careful silicidation pretreatment of the exposed Cu surface before capping by a dielectric barrier can result in strong EM performance (3.5 times compared with a canonical reference under stress conditions) with less that a 2% increase in resistivity owing to the creation of an epitaxial CuSix layer sandwiched between the Cu and capping dielectric. Interestingly, the approach is also shown to negate the trending found between adhesion strength and interfacial EM activation energy because the adhesion between the CuSix and the capping dielectric can be rather low compared with a canonical Cu interconnect with a SiCxNy capping process. Because the EM mass transport interface is effectively blocked by the epitaxial CuSix layer, interfacial quality between CuSix and SiCxNy is then not relevant for EM performance. The silicidation process has also been combined with a MgO self-forming barrier process (Koike and Wada, 2005) to increase the EM margin substantially (Kudo et al., 2008); however, the MgO barrier does not leave a conductive liner at the via bottom so that use of the Blech effect in design is obviously not possible (Nogami et al., 2010a). Finally, utilization of silicide capping with a Ti barrier metal appears to provide an increased EM margin (~ 100 times compared with a canonical reference in under stress conditions), and for narrow interconnects less than 100 nm, Ti and Si penetration into the line appears to prevent the occurrence of a severe resistance increase penalty due to alloying to Cu metal. The drawback, however, appears for wider interconnects (> 130 nm) which do suffer a significant resistance increase compared with the use of Ta-based barrier metal. A later combination of the above with a controlled amount of surface copper oxide to prevent Si penetration into grain boundaries, provided further improvement (Hayashi et al., 2009, 2010).
Given this need to improve the EM performance margin through some form of interface engineering, it is instructive to see how EM has been tackled in research and to see how the drift model shown in equation [8.6] can fit the reliability trending. The results are shown in Fig. 8.12. The median time-to-failure for different EM pathways at 105 °C are found using EM parameter values taken from Table 8.1 (ITRS, 2009) and from the EM parameters in Table 8.2. Overlaid on top of these trend curves, a compilation of median EM lifetimes reported are shown. There is a reasonable amount of EM data available, but most of the data is virtually useless for such comparisons because of the sparseness of the details provided. Figuring out lifetime values for extrapolation to a single usage condition is thus quite messy because authors are generally reluctant to divulge specific details of their EM results, typically plotting data using arbitrary lifetime units and not explicitly stating their test conditions (no failure criterion, no current density value, no current exponent, no temperature, etc.) and test structure details (no width, no length, no thickness, etc.). In some cases, the details were not so vague, so some extrapolation was possible, provided certain generic conditions for EM parameters were used to perform the lifetime extrapolations. For example, the activation energy of 0.9 eV and a current exponent of one were used when no equivalent value was provided for each. When such details were provided, however, those values were used. Errors in the extrapolations and a large spread in the results are inevitable, but the extent of the errors lies somewhere near unity. The extracted values (miraculously) appear to match the lifetime projection for a capping dielectric interface without wildly excessive variation. The expected lifetime trending with technology scaling appears consistent with the lifetime extrapolations of the literature data. The result also generally agrees with the trending found by Croes et al. (2007), where it is predicted that canonical interconnect EM will be suitable down to the 32 nm node. The trends shown in Fig. 8.12 seem slightly more pessimistic because the median life is plotted instead of the 100 ppm projection used by Croes et al. Croes et al. also assumed a higher current exponent of 1.2, which would decrease further his projected lifetime compared with that of Fig. 8.12. Furthermore, the interface engineering approaches to EM improvement do seem to provide a substantial EM margin that is well above the noise of the EM lifetime projections for the canonical pathway model. The presence of stacked grains in the EM pathway is truly a fast EM pathway, and it will be critical to ensure that such pathways are not extensive (continuous and long) and not present around vias, even when the interface engineering methods have been implemented (Lin et al., 2010). Vias are the most vulnerable location for EM failures because they are necessarily placed at the interconnect ends. Results by Arnaud et al. (2010) with regards to interconnect early failures seem to mirror this concern. Finally, as a caveat, Lin et al. (2010) using a statistical-based approach to combine the effects of bamboo and polygranular segments provided estimates of the Z*D0δ products for interface and grain boundary EM along with their respective activation energies. The Z*D0δ product values differ substantially from the corresponding product values used in the above calculations. In this instance, the difference appears not to have made a large impact because the calculations in Fig. 8.12 assumed that the grain boundary diffusion was rate-limited by interface diffusion; i.e., that the grains were fully columnar. Of course, discrepancies would probably be more obvious when more detailed or direct EM data are examined. However, the comparison does point to the dangers or difficulties in trying to construct a detailed analysis of EM trends from disparate literature resources.
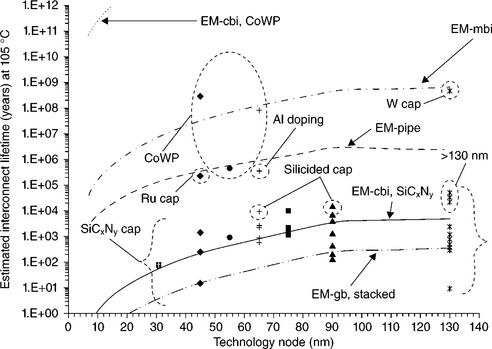
8.12 Expected lifetime trending using ITRS-2009 parameters and reported data on diffusion and kinetic parameters for Cu EM is shown along with data on EM lifetimes projected to a single condition at 105 °C. The data show reasonable agreement with expected values and also illustrate the increased EM lifetime advantage for recently developed methods to improve on capping interface quality. Metal capping EM extrapolations may be somewhat optimistic because microstructure impact is not quantified. Data points were obtained from Cheng et al. (2006), Croes et al. (2010), Hamada et al. (2010), Hartfield et al. (2004), Hohage et al. (2009), Hu et al. (2003, 2007a), Kakuhara et al. (2010), Leaming-Sphabmixay et al. (2007), Lee et al. (2005), Lin M et al. (2004, 2005, 2009, 2010), Lloyd et al. (2005), Ogawa et al. (2002), Pyun et al. (2005), Rosenberg et al. (2000), Saito et al. (2004), Tada et al. (2004), Wang et al. (2005), Yang et al. (2009), Yokogawa and Tsuchiya (2004, 2007), Zhang et al. (2010b), Zschech et al. (2009).
The ability to improve the interface properties at the trench top has increased industry confidence in meeting reliability needs for future scaling; however, there is a complication to this picture. It is clear that, as the critical feature size continues to shrink, it is becoming increasingly difficult to effectively control the microstructure within the Cu trenches. The grain structure shows greater degrees of polygranular character within the trench for interconnects beyond the 65 nm node (Hinode et al., 2001; Hu et al., 2007b) so an increasing contribution from the grain boundary pathway is expected and this may be the limiting factor for EM performance (and resistivity improvement) in future. Unless practical methods (i.e., manufacturable) to increase the grain size for the narrowest leads are invented, approaches to improve EM performance through metal doping may be needed to provide additional EM margin but at the expense of additional resistivity increase (Yokogawa et al., 2008).
8.4 Copper microstructure impact
8.4.1 Microstructure development in damascene copper interconnects
The microstructure that develops in Cu damascene interconnects is greatly affected by a number of process-related factors, including etch profile and uniformity (Choi et al., 2010), barrier/seed deposition, ECD conditions such as the impact of impurity concentration (Neuner et al., 2010), anneal conditions (Barmak et al., 2003; Brandstetter et al., 2010; Carreau et al., 2007), defect generation (Detavernier et al., 2003), overburden thickness (Dubreuil et al., 2008; Field et al., 2003), and metallization stress or strain (Harper et al., 1999). The main factors affecting grain size within a damascene trench, however, are the interconnect dimensions (Besser et al., 2001; Brandstetter et al., 2010; Cho et al., 2005; Lingk et al., 1999; Vanasupa et al., 1999b; Wu et al., 2004). The as-plated grain size is small, somewhere on the order of 50 to 100 nm, and depends on the plating conditions used. Generally, the most characteristic film texture for as-deposited and annealed Cu films is (111)-oriented with contributions from other secondary grain orientations such as (200) and (311) (Cho et al., 2005; Lee et al., 2003; Neuner et al., 2003; Rosenberg et al., 2000; Vanasupa et al., 1999a). The microtexture found in Cu interconnects has a much less preferred orientation (Ji et al., 2004) than that in Al metallization found in microelectronics (Rosenberg et al., 2000). In Cu lines, (111) oriented grains from the trench bottom and sidewalls are found (Besser et al., 2001; Cho et al., 2005; Ganesh et al., 2010). A (111) oriented fiber texture is considered advantageous for grain boundary EM for Al(Cu) metallization (Knorr and Rodbell, 1996; Knorr et al., 1991) and has been confirmed for Cu metallization (Abe et al., 2004; Ryu et al., 1999); however, developing the preferred (111) orientation trenches within ultranarrow trenches is difficult to achieve because side-wall grain growth is prevalent (Leaming-Sphabmixay et al., 2007). For wider interconnects (>~0.5 μm), the grains tend to be polygranular so that smaller grains bunched together can span a given line width. The presence of the overburden has a stronger effect on the microstructure development within wider trenches so that grains can extend from the trench bottom to the overburden surface. The grain boundaries in such instances tend to be more or less vertical, but if several grains are needed to span the interconnect width, a clear longitudinal grain boundary EM pathway would exist for extended lengths over large sections along the interconnect.
When the interconnect line width is reduced, the overburden is found to have limited relation to microtexture development within the trench (Besser et al., 2001; Brandstetter et al., 2010) below 250 nm and virtually no effect at 80 nm or less, although its effect may be more pronounced when the overburden is purposely reduced (Dubreuil et al., 2008). For a narrow interconnect, sidewall growth is thought to increasingly lead to greater complexity in the microstructure (Besser et al., 2001); however, it has recently been argued that a superconformal filling process (Andricacos et al., 1998; Josell et al., 2001) may limit such sidewall orientation contribution for interconnects with widths at least down to 140 nm, especially after thermal anneal treatment. Furthermore, it is argued that stress profiles along the length and depth of the trench during anneal have a greater impact on the final texture than sidewall growth (Cho et al., 2005). As for grain size, it scales roughly with the interconnect width so that, for the narrowest interconnects (80 nm and below), the grains can be longer than wide (Graham et al., 2008); however, it is also found that the interconnect grains show regions of bamboo and polygranular character with smaller grains found deeper in the trench than higher in the trench (Hu et al., 2007b). Interestingly, electrochemical deposition (ECD) actually yields a larger grain size than other deposition methods such as physical vapor deposition (PVD) or chemical vapor deposition (CVD) (Ryu et al., 1999). Twinning is evident in Cu grains regardless of the line width, although the grain size increases and twinning density decreases after thermal anneal treatments (Cho et al., 2005; Hübner et al., 2010). Grain boundaries defined by twins generally have low energy so that they are very unlikely to be effective pathways for EM mass transport (Chen et al., 2008b).
Brandstetter et al. (2010) has shown that high temperature annealing (400 °C for 6 h) has a pronounced effect (16-fold increase with overburden) on grain size only for the larger width interconnects, and a lower temperature anneal (150 °C for 6 h) has somewhat less effect (10-fold). Below 250 nm, the annealing impact on grain size is less significant even for 400 °C annealing (70 nm increased to 100 nm at 80 nm line width). The resulting changes to the microstructure appear to reduce the overall strain present within the Cu grains (Lingk and Gross, 1998; Harper et al., 1999; Moriyama et al., 2003; Lee et al., 2003; Ito et al., 2007); however, the overburden-driven strain energy minimization process of grain growth is stunted by the presence of the interconnect side walls (Wu et al., 2004). When considering such general trends, however, one should be aware that the microstructure found in actual production environments depends upon the explicit process flow used and is not necessarily optimized for grain size or microtexture uniformity.
8.4.2 Microstructure impact on copper EM
When EM is rate-limited by interface mass transport, as is the case for canonical damascene Cu, little evidence of microstructure impact on EM will be apparent (Arnaud et al., 1999; Hu et al., 1999a; Hau-Riege and Thompson, 2001). Hau-Riege and Thompson ran an interesting experiment where direct alteration of the microstructure using a scanned laser annealing method yielded little difference in EM performance in 500 nm wide interconnects. It should be noted that these results pertain to intermediate width interconnects, where the overburden grain growth can extend deeper into the trench. In such intermediate width interconnects, the grain microstructure is found to exhibit bamboo or near-bamboo character (Hu et al., 2007a; Brandstetter et al., 2010). Thus, changing the microstructure for such an interconnect could possibly mean a change from a smaller density of shorter length bamboo grains to a larger density of longer ones. Ryu et al. (1999) did find differences in EM performance in Cu CVD-deposited long test lines with larger dimensions (1.5 μm width and 0.5 μm thickness). It was found that the (111)-preferred orientation had a four-fold better EM performance than the (200) oriented test lines so that some microstructure effects are likely present. In this instance, the test lines would be expected to show polygranular character, especially since the deposition method is CVD and not ECD, so that a microstructure dependence seems reasonable. These CVD metal lines, however, were not passivated, and the effects observed may have been manifested by differences in surface diffusion along differently oriented grain surfaces (which is maybe a more subtle microstructure effect). In summary, the natural conclusions are the following: (a) for wider polygranular interconnects (more than 1 μm), one would expect to have significant contributions from both interfacial and grain boundary EM; (b) for intermediate width interconnects (say, 200 to 3000 nm width), Cu grain boundaries in ECD-deposited interconnects do not matter so much after annealing. Such microstructure is not as important because (i) they are not able to form fast percolative pathways throughout the interconnect length [perhaps because they are blocked by individual bamboo grains or maybe width spanning twinned grains (Hübner et al., 2010)] or (ii) the interface pathway is much faster than any grain boundary pathway even when a percolative path exists. Regardless, any means of increasing the interface pathway resistance to EM increases the influence of the grain boundaries on EM performance as Hau-Riege and Thompson astutely noted in 2001 before the described methods of capping interface improvement were introduced. Similar conclusions have been formed by Ogurtani and Oren (2001) using a more theoretical analysis.
For much narrower interconnects, the grain size may have a clearer role because they probably define the vertical component of the critical void volume, equation [8.5] for EM failure (Arnaud et al., 2010; Li et al., 2004; Oates and Lee, 2006). Thus, the presence of small grains within and under vias may set the conditions for EM early failures. Furthermore, polygranularity in narrow interconnects probably enhances the role of grain boundary diffusion during EM (Hu et al., 2007a, 2010). Then, when interface engineering to arrest interface EM is implemented, the role of grain boundary formation in void nucleation and growth is enhanced (as is evident from Fig. 8.11). Recent observations confirm that EM in CoWP-capped interfaces does not provide as large an EM margin as expected if extended grain boundary paths exist (Hu et al., 2010; Zhang et al., 2010a, 2010b). Hence, microstructure control, and not just interface engineering, is absolutely vital to retain an EM margin in well-capped interconnects below the 32 nm node (Lin et al., 2010).
If grain boundary EM does become a more critical factor, then presumably much of the learning from grain boundary EM in Al should find relevance. Suo et al. (1994) have shown that circular voids will preferentially follow an instability located on a hemispherical void during EM stress so that the instability is extended in opposition to the healing forces owing to surface energy (void surface tension). In contrast to maybe an interface dominant situation but under the same types of EM and surface tension effects, the voids would be expected to extend along the current flow direction (Choy and Kavanagh, 2004). In this context, a grain boundary that connects to an interface is a natural generator of local instability, should a hemispherical void pass through it (Zaporozhets et al., 2005), and such void growth and void translation physics appears to be similar to what is observed by in situ SEM studies (Meyer and Zschech, 2007). Stress modeling of the microstructure effect on void nucleation indicates that small grains at an interface may be susceptible to fracture and are candidates for void nucleation events (Kteyan et al., 2007). Hau-Riege et al. (2004) showed that the critical stress for void nucleation decreases as the Young’s modulus of the surrounding dielectric decreases and has implications for scaling with the need to incorporate ultra-low-k dielectrics or air gap technology and reduced metal barrier thickness. Because grain boundary triple points remain at the capping interface, voids probably nucleate there (Vairagar et al., 2004b), especially at non- Σ3n boundaries that intersect an interface wall (Arnaud et al., 2006; Cayron, 2007). Grain boundary triple points within the metal may also become important sites for void nucleation too. When a grain boundary EM pathway begins to dominate (at least locally around the grain boundary), voids can grow along the grain boundary and generate width spanning slit voids (Sukharev et al., 2009). Ogurtani and Oren (2004) developed a detailed model of void dynamics occurring in bamboo-type interconnects and identified a time-to-failure equation based on the average number of bamboo grains that need to be passed before a given fatal void reaches the cathode end.
Not all grain boundaries provide sufficiently fast EM pathways and, at present, detailed analysis has not been done to identify those grain boundaries that are most susceptible to forming trans-width slit voids. From Al-based EM (Hu et al., 1995), it is expected that (111) tilt grain boundaries with low misorientation angles (< 11° to 15°) are poor pathways for EM voiding. High-angle misorientation boundaries probably provide faster diffusivity paths with the exception of certain special boundaries known as ‘coincident site lattices’ (CSL). Because Cu is also an FCC metal, similar arguments would be expected to apply; however, for Cu damascene interconnects, the Cu lines do not show as strong (111) fiber texture so that a higher density of grain boundary pathways should be active. Thus, more detailed analysis will be needed.
More pragmatically, if horizontal or vertical slit voids only form well beyond the expected life for microelectronics devices under regular use conditions, then the detailed microstructure EM physics is only a minor concern to those more interested in simply meeting the performance demands of the ITRS roadmap. The question remains whether such a reliability margin can be met by the billions of interconnects undergoing some degree of EM amount in a customer environment. To address those concerns, more detailed statistical analysis to identify the extent of EM early failures is necessary. Such discussion, however, is beyond the scope of this chapter, but suitable references are provided because it is an important topic (Gall et al., 1997; Hauschildt et al., 2007, 2008; Lee and Ho, 2004; Li et al., 2006; Oates and Lee, 2006; Ogawa et al., 2001; Tsuchiya and Yokogawa, 2006). Layout effects on EM are also an important consideration and are also listed for reference (Girault et al., 2008; Hau-Riege and Klein, 2008; Hau-Riege and Thompson, 2000; Kakuhara et al., 2009; Park et al., 2010; Roy et al., 2009).
8.5 Conclusions
Although the basic integration scheme has remained the same since the first implementation of Cu metallization into advanced CMOS technology, significant evolutionary improvements have been found to increase the EM reliability margin so that Cu interconnects probably remain the interconnect of choice well-beyond the 22 nm node. Such adjustments to the canonical integration scheme for Cu interconnects are necessary to keep pace with the performance demands from dimensional scaling. Dimensional shrinkage, resistivity increase, and increased current density requirements are key technology drivers that are steadily eroding the EM reliability margin by roughly 50% per technology generation. Key to these evolutionary changes are the different methods of interface engineering to be used to stop the mass transport pathway at the top interface of the Cu damascene trench, although increased contribution from grain boundary pathways should arise and may reduce the expected reliability margin. Such improvements must be achieved without seriously contributing to the expected increase in Cu metallization resistivity with dimensional scaling from increased grain boundary and interface scattering effects. The EM contributions from grain boundary diffusion pathway in ultra-narrow interconnects cannot be dismissed because narrow void failures have been observed and will place greater demands on the ability of redundant metal liners to maintain current carrying capabilities should such catastrophic slit voids develop. Thus, unless an optimal balance between interface and microstructure control is obtained but not at the expense of increased intrinsic Cu resistivity, the EM reliability margin under dimensional scaling pressure will steadily erode to an unacceptable level of intrinsic reliability performance. Even with these changes and with the expected difficulties in finding alternative metallization schemes that provide the same magnitude of manufacturability yet improved interconnect performance, Cu metallization is the foreseeable choice for interconnect technology at least to the end of this decade.
8.6 Acknowledgements
I would first like to thank Professor C. U. Kim at University of Texas at Arlington for the opportunity to write this manuscript, and I would like to thank J. K. Wang, R. Lutze, N. Kim, K. Bult, and H. Samueli for their support at Broadcom. I would like to extend my gratitude to Professor P. S. Ho and Ms J. A. Smith (at The University of Texas at Austin) for technical support and to C. K. Hu (IBM Research) and M. A. Meyer (GLOBALFOUNDRIES) for providing the graphic images for publication in this chapter. Finally, I would like to thank my family for their great patience and understanding while I struggled to put this manuscript together.
8.7 References
Abe, K., Harada, Y., Yoshimaru, M., Onoda, H. Texture and electromigration performance in damascene interconnects formed by reflow sputtered Cu film. Journal of Vacuum Science and Technolology B. 2004; 22(2):721–728.
Almog, R.O., Sverdlov, Y., Shacham-Diamand, Y. A surface adsorption limited model of CoWBP capping barriers for sub 45 nm Cu interconnects. In: McKerrow A.J., Shacham-Diamand Y., Shingubara S., Shimogaki Y., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2007:11–16.
Andricacos, P.C., Uzoh, C., Dukovic, J.O., Horkans, J., Deligianni, H. Damascene copper electroplating for chip interconnections. IBM Journal of Research and Development. 1998; 42(5):567–574.
Arnaud, L., Cacho, F., Doyen, L., Terrier, F., Galpin, D., Monget, C. Analysis of electromigration induced early failures in Cu interconnects for 45 nm node. Microelectronic Engineering. 2010; 87(3):355–360.
Arnaud, L., Guillaumond, J.F., Claret, M., Cayron, C., Guedj, C., Dupeux, M., Arnal, V., Reimbold, G., Passemard, G., Torres, J. Analysis of electromigration voiding phenomena in Cu interconnects. In: 44th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers; 2006:675–676.
Arnaud, L., Tartavel, G., Berger, T., Mariolle, D., Gobil, Y., Toue, I. Microstructure and electromigration in copper damascene lines. In: 37th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 1999:263–269.
Aubel, O., Thierbach, S., Koschinsky, F., Feustel, F., Hau-Riege, C.S., Zistland, C. Investigation of via bottom barrier integrity impact on electromigration. In: 45th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2007:648–649.
Aubel, O., Thierbach, S., Seidel, R., Freudenberg, B., Meyer, M.A., Feustel, F., Poppe, J., Nopper, M., Preusse, A., Zistl, C., Weide-Zaage, K., Comprehensive reliability analysis of CoWP metal cap unit processes for high volume production in sub-μm dimensions. 46th annual IEEE international reliability physics symposium proceedings, Piscataway, NJ, 2008:675–676.
Augur, R.A., Kim, C.U., Blaschke, V., Michael, N.L., Gillespie, P., Rasco, M., Lin, J.C., Kim, S.Y., Pfeifer, K. New reliability failure mechanism in porous low-k dual damascene interconnects. In: Ray G.W., Smy T., Ohta T., Tsujimura M., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2003:277–281.
Barmak, K., Gungor, A., Cabral, C., Jr., Harper, J.M.E. Annealing behavior of Cu and dilute Cu-alloy films: precipitation, grain growth, and resistivity. Journal of Applied Physics. 2003; 94(3):1605–1616.
Baumann, R., Hossain, T., Murata, S., Kitagawa, H. Boron compounds as a dominant source of alpha particles in semiconductor devices. In: 33th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 1995:297–302.
Besling, W.F.A., Broekaart, M., Arnal, V., Torres, J. Line resistance behaviour in narrow lines patterned by a TiN hard mask spacer for 45 nm node interconnects. Microelectronic Engineering. 2004; 76(1–4):167–174.
Besser, P.R., Preusse, A., Lang, C.-I., Fiordalice, B., Nopper, M., Seidel, R., Aubel, O., Berhe, D., Tong, J., Kumar, N., Chiang, T. A novel materials solution to enable CoWP metal capping by reducing line-to-line leakage. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2008:61–68.
Besser, P.R., Zschech, E., Blum, W., Winter, D., Ortega, R., Rose, S., Herrick, M., Gall, M., Thrasher, S., Tiner, M., Baker, B., Braeckelmann, G., Zhao, L., Simpson, C., Capasso, C., Kawasaki, H., Weitzman, E. Microstructural characterization of inlaid copper interconnect lines. Journal of Electronic Materials. 2001; 30(4):320–330.
Birringer, R., Shaviv, R., Mountsier, T., Reid, J., Zhou, J., Geiss, R.H., Read, D., Dauskardt, R. Adhesion, copper voiding, and debonding kinetics of copper/dielectric diffusion barrier films. In: Edelstein D.C., Schulz S.E., eds. Advanced Metallization Conference. Warrendale, PA: Materials Research Society; 2009:207–212.
Black, J.R., Mass transport of aluminum by momentum exchange with conducting electrons. Proceedings of the 1967 annual symposium on reliability physics. 1967:148–159.
Black, J.R. Electromigration – a brief survey and some recent results. IEEE Transactions on Electron Devices. 1969; ED-16(4):338–347.
Blech, I.A. Electromigration in thin aluminum films on titanium nitride. Journal of Applied Physics. 1976; 47(4):1203–1208.
Blech, I.A., Critical length in electromigration – experiments and theoryOkabayashi, H., Shingubara, S., Ho, P.S., eds. Stress-induced phenomena in metallization; 418. American Institute of Physics conference proceedings, 1997:3–13.
Blech, I.A. Diffusional back flows during electromigration. Acta Materialia. 1998; 46(11):3717–3723.
Blech, I.A., Sello, H., A study of failure mechanisms in silicon planar epitaxial transistorsShilliday, T.S., Vaccaro, J., eds. Physics of failure in electronics; 5. USAF, Rome Air Development Center, 1966:496–505.
Brandstetter, S., Carreau, V., Maîtrejean, S., Verdier, M., Legros, M. Grain morphology of Cu damascene lines. Microelectronic Engineering. 2010; 87(3):383–386.
Budiman, A.S., Besser, P.R., Hau-Riege, C.S., Marathe, A., Joo, Y.-C., Tamura, N., Patel, J.R., Nix, W.D. Electromigration-Induced plasticity: texture correlation and implications for reliability assessment. Journal of Electronic Materials. 2009; 38(3):379–391.
Budiman, A.S., Hau-Riege, C.S., Besser, P.R., Marathe, A., Joo, Y.-C., Tamura, N., Patel, J.R., Nix, W.D., Electromigration-induced plasticity and texture in Cu interconnectsOgawa, S., Ho, P.S., Zschech, E., eds. Stress-induced phenomena in metallization; 945. American Institute of Physics, Melville, NY, 2007:56–65.
Butrymowicz, D.B., Manning, J.R., Read, M.E. Diffusion in copper and copper alloys. Part I. Volume and surface self-diffusion in copper. Journal of Physical and Chemical Reference Data. 1973; 2(3):643–655.
Carreau, V., Maîtrejean, S., Verdier, M., Bréchet, Y., Roule, A., Toffoli, A., Delaye, V., Passemard, G. Evolution of Cu microstructure and resistivity during thermal treatment of damascene line: influence of line width and temperature. Microelectronic Engineering. 2007; 84(11):2723–2728.
Cayron, C. Multiple twinning in cubic crystals: geometric/algebraic study and its application for the identification of the Σ3n grain boundaries. Acta Crystallographica, Section A (Foundations of Crystallography). 2007; A63(1):11–29.
Chao, B., Chae, S.H., Zhang, X.F., Lu, K.H., Im, J., Ho, P.S. Investigation of diffusion and electromigration parameters for Cu-Sn intermetallic compounds in Pb-free solders using simulated annealing. Acta Materialia. 2007; 55(8):2805–2814.
Chattopadhyay, K., van Schravendijk, B., Mountsier, T.W., Alers, G.B., Hornbeck, M., Wu, H.J., Shaviv, R., Harm, G., Vitkavage, D., Apen, E., Yu, Y., Havemann, R. In-situ formation of a copper silicide cap for TDDB and electromigration improvement. Proceedings of the 44th annual, IEEE international reliability physics symposium. 2006; 2006:128–130.
Chen, J.H.-C., Jiang, L., Deutsch, A., Angyal, M.S., Spooner, T.A. Interconnect performance and scaling strategy for the 22 nm node and beyond. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2008:83–90.
Chen, K.-C., Wu, W.W., Liao, C.N., Chen, L.J., Tu, K.N. Observation of atomic diffusion at twin-modified grain boundaries in copper. Science. 2008; 321(5892):1066–1069.
Cheng, Y.L., Wang, Y.L., Chen, H.C., Lin, J.H. Effect of inter-level dielectrics on electromigration in damascene copper interconnect. Thin Solid Films. 2006; 494(1–2):315–319.
Cho, J., Thompson, C.V. Grain size dependence of electromigration- induced failures in narrow interconnects. Applied Physics Letters. 1989; 54(25):2577–2579.
Cho, J.-Y., Lee, H.-Y., 2 Kim, H., Szpunar, J.A. Textural and microstructural transformation of Cu damascene interconnects after annealing. Journal of Electronic Materials. 2005; 30(4):506–514.
Choi, D.-Y., Han, S.-J., Kim, N.-H., Kim, S.-Y. Stabilization of sheet resistance for metal lines by formation of etch stop layer (ESL) trench structure. Microelectronic Engineering. 2010; 87(3):343–347.
Choy, J.-H., Kavanagh, K.L. Effects of capillary forces on copper/dielectric interfacial void evolution. Applied Physics Letters. 2004; 84(25):5201–5203.
Christiansen, C., Li, B., Gill, J., Blech effect and lifetime projection for Cu/low-K interconnects. Proceedings of the IEEE 2008 International Interconnect Technology Conference. 2008:114–116.
Clement, J.J. Electromigration modeling for integrated circuit interconnect reliability analysis. IEEE Transactions on Device and Materials Reliability. 2001; 1(1):33–42.
Croes, K., Moon, K.J., Carbonell, L., Struyl, H., Heylen, N., T![]() kei, Z., Beyer, G.P. Electromigration study of ultra narrow copper lines in low-k dielectric. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2007:711–721.
kei, Z., Beyer, G.P. Electromigration study of ultra narrow copper lines in low-k dielectric. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2007:711–721.
Croes, K., Wilson, C.J., Lofrano, M., Vereecke, B., Beyer, G.P., T![]() kei, Z. Electromigration and stress-induced-voiding in dual damascene Cu/low-k interconnects: a complex balance between vacancy and stress gradients. In: 48th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2010:591–598.
kei, Z. Electromigration and stress-induced-voiding in dual damascene Cu/low-k interconnects: a complex balance between vacancy and stress gradients. In: 48th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2010:591–598.
d’Heurle, F.M., Ho, P.S. Electromigration in thin films. In: Poate J., Tu K.N., Mayer J.B., eds. Thin films: interdiffusion and reactions. John Wiley; 1978:243–303. [Ch. 8].
Detavernier, C., Rossnagel, S., Noyan, C., Guha, S., Cabral, C., Jr., Lavoie, C. Thermodynamics and kinetics of room-temperature microstructural evolution in copper films. Journal of Applied Physics. 2003; 94(5):2874–2881.
Dubreuil, O., Cordeau, M., Mourier, Th., Chausse, P., Mellier, M., Bellet, D., Torres, J. Characterization of copper grain growth limitations inside narrow wires depending of overburden thickness. Microelectronic Engineering. 2008; 85(10):1988–1991.
Edelstein, D., Heidenreich, J., Goldblatt, R., Cote, W., Uzoh, C., Lustig, N., Roper, P., Mc- Devitt, T., Motsiff, W., Simon, A., Dukovic, J., Wachnik, R., Rathore, H., Schulz, R., Su, L., Luce, S., Slattery, J. Full copper wiring in a sub-0.25 μm CMOS ULSI technology. In: Technical Digest, IEEE International Electron Devices Meeting. Piscataway, NJ: The Institute of Electrical and Electronics Engineers, Inc; 1997:773–776.
ExcelOffice Suite Software. Redmond, WA: Microsoft Corporation, 2007.
Field, D.P., Nowell, M.M., Kononenko, O.V., Observation of grain growth in Cu films by in-situ EBSD analysisMcKerrow A.J., Leu J., Kraft O., Kikkawa T., eds. Materials, technology and reliability for advanced interconnects and low-k dielectrics – 2003, symposium E, materials research society symposium proceedings. 2003:766. [E4.5.1–E4.5.6].
Filippi, R.G., Biery, G.A., Wachnik, R.A. The electromigration short-length effect in Ti–AlCu–Ti metallization with tungsten studs. Journal of Applied Physics. 1995; 78(6):3756–3768.
Frost, H.J., Ashby, M.F. Deformation-mechanism maps the plasticity and creep of metals and ceramics (1st edition). Oxford: Pergamon Press; 1982.
Frost, H.J., Ashby, M.F. Deformation-mechanism maps, the plasticity and creep of metals and ceramics (1st edition), Chapter 4. Pergamon Press and Dartmouth University, Oxford, 1982. Available from, (accessed 12 December, 2010). http://engineering.dartmouth.edu/defmech/
Fuchs, L., Conduction electrons in thin metallic films. Proceedings of the Philosophical Society; 34. Cambridge University, 1938:100.
Gall, M., Capasso, C., Jawarani, D., Hernandez, R., Kawasaki, H., Ho, P.S., Statistical Evaluation of Device-Level Electromigration ReliabilityOkabayashi, H., Shingubara, S., Ho, P.S., eds. Stress-induced phenomena in metallization; 418. American Institute of Physics, Woodbury, NY, 1997:483–494.
Gambino, J. 22 nm CMOS technology: BEOL technology for the 22 nm node. International electron devices meeting (IEDM) short course. 2008; 1–71.
Gambino, J., Wynne, J., Gill, J., Mongeon, S., Meatyard, D., Lee, B., Bamnolker, H., Hall, L., Li, N., Hernandez, M., Little, P., Hamed, M., Ivanov, I., Gan, C.L. Self-aligned metal capping layers for copper interconnects using electroless plating. Microelectronic Engineering. 2006; 83(11–12):2059–2067.
Gan, C.L., Thompson, C.V., Pey, K.L., Choi, W.K., Tay, H.L., Yu, B., Radhakrishnan, M.K. Effect of current direction on the lifetime of different levels of Cu dual-damascene metallization. Applied Physics Letters. 2001; 79(27):4592–4594.
Gan, D., Ho, P.S., Huang, R., Leu, J., Maiz, J., Scherban, T., Effects of passivation layer on stress relaxation and mass transport in electroplated Cu filmsHo, P.S., Baker, S.P., Nakamura, T., Volkert, C.A., eds. Stress-induced phenomena in metallization; 741. American Institute of Physics, Melville, NY, 2004:256–267.
Gan, D., Ho, P.S., Huang, R., Leu, J., Maiz, J., Scherban, T. Isothermal stress relaxation in electroplated Cu films. I. Mass transport measurements. Journal of Applied Physics. 2005; 97(10):103531-1–103531-8.
Ganesh, K.J., Rajasekhara, S., Ferreira, P.J., Correlating texture with local stresses in Cu interconnects using D-STEM and precession electron diffractionHo P.S., Ogawa S., Zschech E., eds. presentation for Stress-induced phenomena in metallization. American Institute of Physics: Melville, NY, 2010 Available from. http://stress.malab.com/talks.html [(Accessed 26 September, 2010)].
Gignac, L.M., Hu, C.K., Herbst, B., Baker-O’Neal, B.C. The effect of microstructure on resistivity and reliability in copper interconnects. In: McKerrow A.J., Shacham-Diamand S., Shingubara S., Shimogaki Y., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2007:641–651.
Girault, V., Terrier, F., Ney, D. Reservoir effect in SiCN capped copper/SiO2 interconnects. Microelectronics Reliability. 2008; 48(2):219–224.
Graham, R.L., Alers, G.B., Shamma, N., Mountsier, T., Kooi, G., Rairkar, A., Karim, I., Hakim, L., Ponnuswamy, T., Chou, W.B., Dhuey, S., Cabrini, S., Peddeti, S., Geiss, R.H. Grain growth in sub-50 nm Cu lines. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2008:393–399.
Hamada, M., Ohmori, K., Mori, K., Kobori, E., Suzumura, N., Etou, R., Maekawa, K., Fujisawa, M., Miyatake, H., Ikeda, A., Highly reliable 45-nm-half-pitch Cu interconnects incorporating a Ti/TaN multilayer barrier. Proceedings of the IEEE 2010 international interconnect technology conference. IEEE Service Center, Piscataway, NJ, 2010. [Paper 13.4].
Harper, J.M.E., Cabral, C., Jr., Andricacos, P.C., Gignac, L., Noyan, I.C., Rodbell, K.P., Hu, C.K. Mechanisms for microstructure evolution in electroplated copper thin films near room temperature. Journal of Applied Physics. 1999; 86(5):2516–2525.
Hartfield, C.D., Ogawa, E.T., Park, Y.-J., Chiu, T.-C. Interface reliability assessments for copper/low-k products. IEEE transactions on device and materials reliability. 2004; 4(2):129–141.
Hau-Riege, C.S. An introduction to Cu electromigration. Microelectronics Reliability. 2004; 44(2):195–205.
Hau-Riege, C.S., Hau-Riege, S.P., Marathe, A.P., The effect of interlevel dielectric on the critical tensile stress to void nucleation for the reliability of Cu interconnects. Journal of Applied Physics. 2004:5792–5796.
Hau-Riege, C.S., Marathe, A.P., Pham, V. The effect of low-k ILD on the electromigration reliability of Cu interconnects with different line lengths. In: 41st annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2003:173–177.
Hau-Riege, C.S., Klein, R. The effect of a width transition on the electromigration reliability of Cu Interconnects. In: 46th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2008:377–380.
Hau-Riege, C.S., Thompson, C.V. The effects of microstructural transitions at width transitions on interconnect reliability. Journal of Applied Physics. 2000; 87(12):8467–8472.
Hau-Riege, C.S., Thompson, C.V. Electromigration in Cu interconnects with very different grain structures. Applied Physics Letters. 2001; 78(22):3451–3453.
Hauschildt, M., Gall, M., Hernandez, R., Large-scale statistics for Cu electromigrationHo, P.S., Ogawa, S., Zschech, E., eds. Stress-induced phenomena in metallization; 1143. American Institute of Physics, Melville, NY, 2008:31–46.
Hauschildt, M., Gall, M., Justison, P., Hernandez, R., Herrick, M., Large-scale statistical study of electromigration early failure for Cu/low-k interconnectsOgawa, S., Ho, P.S., Zschech, E., eds. Stress-induced phenomena in metallization; 945. American Institute of Physics, Melville, NY, 2007:66–81.
Hayashi, Y., Matsunaga, N., Wada, M., Nakao, S., Watanabe, K., Kato, S., Sakata, A., Kajita, A., Shibata, H. Impact of oxygen on Cu surface for highly reliable low-k/Cu interconnects with CuSiN and Ti-based barrier metal. In: Proceedings of the IEEE 2010 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2010. [Paper 13.3].
Hayashi, Y., Matsunaga, N., Wada, M., Nakao, S., Watanabe, K., Sakata, A., Shibata, H. Low resistive and highly reliable copper interconnects in combination of silicide-cap with Ti-barrier for 32 nm-node and beyond. In: Proceedings of the IEEE 2009 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2009:252–254.
Hein, V., Design of via and stacked via test structures to evaluate electromigration in thick metal AlCu metallizationHo, P.S., Ogawa, S., Zschech, E., eds. Stress-induced phenomena in metallization; 1143. American Institute of Physics, Melville, NY, 2008:63–68.
Hinode, K., Hanaoka, Y., Takeda, K., Kondo, S. Resistivity increase in ultrafine-line copper conductor for ULSIs. Japanese Journal of Applied Physics, Part 2. 2001; 40(10B):L1097–L1099.
Ho, P.S., Kwok, T. Electromigration in metals. Reports on progress in physics. 1989; 52:301–348.
Hohage, J., Lehr, M.U., Kahlert, V. A copper-dielectric cap interface with high resistance to electromigration for high performance semiconductor devices. Microelectronic Engineering. 2009; 86(3):408–413.
Hu, C.-K., Angyal, M., Baker, B., Bonilla, G., Cabral, C., Canaperi, D.F., Clevenger, L., Edelstein, D., Gignac, L., Huang, E., Kelly, J., Kim, B.Y., Kyei-Fordjour, V., Manikonda, S.L., Maniscalco, J., Mittal, S., Nogami, T., Parks, C., Rosenberg, R., Simon, A., Su, T.Y., Vo, A., Witt, C., Effect of impurity on Cu electromigrationHo P.S., Ogawa S., Zschech E., eds. presentation for Stress-induced phenomena in metallization. American Institute of Physics: Melville, NY, 2010 Available from. http://stress.malab.com/talks.html [(accessed 26 September, 2010)].
Hu, C.-K., Canaperi, D., Chen, S.T., Gignac, L.M., Herbst, B., Kaldor, S., Krishnan, M., Liniger, E., Rath, D.L., Restaino, D., Rosenberg, R., Rubino, J., Seo, S.-C., Simon, A., Smith, S., Tseng, W.-T. Effects of overlayers on electromigration reliability improvement for Cu/low k interconnects. In: 42nd annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2004:222–228.
Hu, C.-K., Gignac, L., Baker, B., Liniger, E., Yu, R., Flaitz, P. Impact of Cu microstructure on electromigration reliability. In: Proceedings of the IEEE 2007 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2007:93–95.
Hu, C.-K., Gignac, L., Liniger, E., Herbst, B., Rath, D.L., Chen, S.T., Kaldor, S., Simon, A., Tseng, W.T. Comparison of Cu electromigration lifetime in Cu interconnects coated with various caps. Applied Physics Letters. 2003; 83(5):869–871.
Hu, C.-K., Gignac, L., Rosenberg, R., Liniger, E., Rubino, J., Sambucetti, C., Domenicucci, A., Chen, X., Stamper, A.K. Reduced electromigration of Cu wires by surface coating. Applied Physics Letters. 2002; 81(10):1782–1784.
Hu, C.-K., Gignac, L.M., Baker-O’Neal, B., Liniger, E., Yu, R., Flaitz, P., Stamper, A.K., Electromigration in advanced interconnectsOgawa, S., Ho, P.S., Zschech, E., eds. Stress-induced phenomena in metallization; 945. American Institute of Physics, Melville, NY, 2007:27–41.
Hu, C.-K., Gignac, L.M., Liniger, E., Huang, E., Greco, S., McLaughlin, P., Yang, C.-C., Demarest, J.J., Electromigration challenges for nanoscale Cu wiringHo, P.S., Ogawa, S., Zschech, E., eds. Stress-induced phenomena in metallization; 1143. American Institute of Physics, Melville, NY, 2008:3–11.
Hu, C.-K., Ho, P.S., Small, M.B. Electromigration in two-level interconnect structures with Al alloy lines and W studs. Journal of Applied Physics. 1992; 72(1):291–293.
Hu, C.-K., Ho, P.S., Small, M.B., Kelleher, K. Electromigration in Al/W and Al(Cu)/W interconnect structures. Materials research society symposium proceedings. 1991; 225:99–105.
Hu, C.-K., Rodbell, K.P., Sullivan, T.D., Lee, K.Y., Bouldin, D.P. Electromigration and stress-induced voiding in fine Al and Al-alloy thin-film lines. IBM Journal of Research and Development. 1995; 39(4):465–497.
Hu, C.-K., Rosenberg, R., Lee, K.Y. Electromigration path in thin-film lines. Applied Physics Letters. 1999; 74(20):2945–2947.
Hu, C.-K., Rosenberg, R., Rathore, H.S., Nguyen, D.B., Agarwala, B. Scaling effect on electromigration in on-chip Cu wiring. In: Proceeding of the IEEE 1999 International Interconnect Technology Conference. Piscataway, NJ: IEEE Service Center; 1999:267–269.
Hu, C.-K., Rosenberg, R., Capping layer effects on electromigration in narrow Cu linesHo P.S., Baker S.P., Nakamura T., Volkert C.A., eds. Stress-induced phenomena in metallization. Hu C-K and Rosenberg R; 741. American Institute of Physics, Melville, NY, 2004:97–111.
Huang, E., Oh, M., Law, S.B., Petitdidier, S., Ko, T.-M., Sawada, H., Tang, T.J., Hu, C.-K., Cohen, S., Liniger, E., Bonilla, G., Rath, D., Shaw, T., Gignac, L., Edelstein, D., Permana, D., Child, C., Buengener, R., Fitzsimmons, J., Findeis, P., Taft, C., Angyal, M., Ogunsola, O., King, J., Flaitz, P., Baumann, F., Molis, S., Dziobkowski, C., Coffin, J., Davis, R., Zaitz, M., Kapur, A., Kermel, L., Truong, C., Grunow, S., Chen, X., Sankarapandian, M., Li, B., Chen, F., Lee, T., Christiansen, C., Kolics, A., Gilbert, N., Rigoutat, O., Li, N. CoWP metal caps for reliable 32 nm 1 × Cu interconnects in porous ULK (k = 2.4). In: Edelstein D.C., Schulz S.E., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2009:179–184.
Huang, R., Gan, D., Ho, P.S. Isothermal stress relaxation in electroplated Cu films. II. Kinetic modeling. Journal of Applied Physics. 2005; 97(10):103532-1–103532-9.
Hübner, R., Engelmann, H.-J., Zschech, E. Small grain and twin characterization in sub-100 nm Cu interconnects using the conical dark-field technique in the transmission electron microscope. In: Proceedings of the IEEE 2010 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2010. [Paper 7.1].
Im, S., Srivastava, N., Banerjee, K., Goodson, K.E. Scaling analysis of multilevel interconnect temperatures for high-performance ICs. IEEE Transactions on Electron Devices. 2005; 52(12):2710–2719.
Ito, K., Tsukimoto, S., Moriyama, M., Murakami, M., Resistivity reduction of Cu InterconnectsOgawa, S., Ho, P.S., Zschech, E., eds. Stress-induced phenomena in metallization; 945. American Institute of Physics, Melville, NY, 2007:1–10.
ITRS International technology roadmap for semiconductors. 2001 Edition, 2001. Interconnect. Available from. http://www.itrs.net [(accessed 22 October, 2010)].
ITRS International technology roadmap for semiconductors. 2005 Edition, 2005. Interconnect. Available from. http://www.itrs.net [(accessed 22 October, 2010)].
ITRS International technology roadmap for semiconductors. 2007 Edition, 2007. Interconnect. Available from. http://www.itrs.net [(accessed 22 October, 2010)].
ITRS International technology roadmap for semiconductors. 2009 Edition, 2009. Interconnect. Available from. http://www.itrs.net [(accessed 22 October, 2010)].
Iwai, H. Roadmap for 22 nm and beyond. Microelectronic Engineering. 2009; 86(7–9):1520–1528.
Ji, Y., Zhong, T., Li, Z., Wang, X., Luo, D., Xia, Y., Liu, Z. Grain structure and crystallographic orientation in Cu damascene lines. Microelectronic Engineering. 2004; 71(1):182–189.
Jo, B.H., Vook, R.W. ‘In-situ ultra-high vacuum studies of electromigration in copper films. Thin Solid Films. 1995; 262(1–2):129–134.
Josell, D., Wheeler, D., Huber, W.H., Moffat, T.P. Superconformal electrode-position in submicron features. Physical Review Letters. 2001; 87(1):016102-1–016102-4.
Kakuhara, Y., Yokogawa, S., Ueno, K. Comparison of lifetime improvements in electromigration between Ti barrier metal and chemical vapor deposition Co capping. Japanese Journal of Applied Physics. 2010; 49(4):04DB08-1. [04DB08-5].
Kakuhara, Y., Yokogawa, S., Hiroi, M., Takewaki, T., Ueno, K. Suppression of electromigration early failure of Cu/porous low-k interconnects using dummy metal. Japanese Journal of Applied Physics, Part 1. 2009; 9:096504-1–096504-5.
Kawasaki, H., Hu, C.K. An electromigration failure model of tungsten plug contacts/vias for realistic lifetime prediction. Symposium on VLSI Technology Digest. 1993; 192–193.
Kim, C.U., Park, J., Michael, N., Gillespie, P., Augur, R. Study of electron- scattering mechanism in nanoscale Cu interconnects. Journal of Electronic Materials. 2003; 32(10):982–987.
Kim, D.-Y., Wong, S.S. Mechanism for early failure in Cu dual damascene structure. In: Proceeding of the IEEE 2003 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2003:265–267.
Knorr, D., Tracy, D.P., Rodbell, K.P. Correlation of texture with electromigration behavior in Al metallization. Applied Physics Letters. 1991; 59(25):3241–3243.
Knorr, D., Rodbell, K.P. The role of texture in the electromigration behavior of pure aluminum lines. Journal of Applied Physics. 1996; 79(5):2409–2417.
Kohn, A., Eizenberg, M., Shacham-Diamand, Y., Israel, B., Sverdlov, Y. Evaluation of electroless deposited Co(W, P) thin films as diffusion barriers for copper metallization. Microelectronic Engineering. 2001; 55(1–4):297–303.
Koike, J., Wada, M. Self-forming diffusion barrier layer in Cu–Mn alloy metallization. Applied Physics Letters. 87(4), 2005. [041911-01–041911-03].
Kteyan, A., Sukharev, V., Meyer, M.A., Zschech, E., Nix, W.D., Microstructure effect on EM-induced degradations in dual-inlaid copper interconnectOgawa, S., Ho, P.S., Zschech, E., eds. Stress-induced phenomena in metallization; 945. American Institute of Physics, Melville, NY, 2007:42–55.
Kudo, H., Haneda, M., Tabira, T., Sunayama, M., Ohtsuka, N., Shimizu, N., Ochimizu, H., Tsukune, A., Suzuki, T., Kitada, H., Amari, S., Matsuyama, H., Owada, T., Watatani, H., Futatsugi, T., Nakamura, T., Sugii, T. Further enhancement of electromigration resistance by combination of self-aligned barrier and copper wiring encapsulation techniques for 32-nm nodes and beyond. In: Proceedings of the IEEE 2008 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2008:117–119.
Kwok, T. Electromigration and reliability in submicron metallization and multilevel interconnection. Materials Chemistry and Physics. 1993; 33(3–4):176–188.
Lane, M.W., Liniger, E.G., Lloyd, J.R. Relationship between interfacial adhesion and electromigration in Cu metallization. Journal of Applied Physics. 2003; 93(3):1417–1421.
Le-Friec, Y., Ye, W., Zubkov, V., Conti, G., Shek, M.Y., Xia, L.-Q., Witty, D.R., Chhun, S., Arnaud, L., Petitprez, E., Clement, L., Monget, C., Galpin, D., Hong, S., Fort, J. Electromigration improvement for 40 nm and below through diffusion barrier interface engineering using a new precursor. In: Edelstein D.C., Schulz S.E., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2009:201–206.
Leaming-Sphabmixay, K., Van Olmen, J., Moon, K.J., Vanstreels, K., D’Haen, J., Tokei, Z., List, S., Beyer, G. Electrical performance, reliability and microstructure of sub-45 nm copper damascene lines fabricated with TEOS backfill. Microelectronic Engineering. 2007; 84(11):2681–2685.
Lee, H., Wong, S.S., Lopatin, S.D. Correlation of stress and texture evolution during self- and thermal annealing of electroplated Cu films. Journal of Applied Physics. 2003; 93(7):3796–3804.
Lee, H.B., Hong, J.W., Seong, G.J., Lee, J.M., Park, H., Baek, J.M., Choi, K.I., Park, B.L., Bae, J.Y., Choi, G.H., Kim, S.T., Chung, U.I., Moon, J.T., Oh, J.H., Son, J.H., Jung, J.H., Hah, S., Lee, S.Y. A highly reliable Cu interconnect technology for memory device. In: Proceedings of the IEEE 2007 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2007:64–66.
Lee, K.-D., Ho, P.S. Statistical study for electromigration reliability in dual-damascene Cu interconnects. IEEE Transactions on Device and Materials Reliability. 2004; 4(2):237–245.
Lee, K.-D., Park, Y.-J., Hunter, B. The impact of partially scaled metal barrier shunting on failure criteria for copper electromigration resistance increase in 65 nm technology. In: 43rd annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2005:31–35.
Lee, S.-C., Oates, A.S. Identification and analysis of dominant electromigration failure modes in copper/low-k dual damascene interconnects. In: 44th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2006:107–114.
Li, B., Sullivan, T.D., Lee, T.C. Line depletion electromigration characteristics of Cu interconnects. In: 41st annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2003:140–145.
Li, B., Sullivan, T.D., Lee, T.C., Badami, D. Reliability challenges for copper interconnects. Microelectronics Reliability. 2004; 44(3):365–380.
Li, B., Christiansen, C., Gill, J., Filippi, R., Sullivan, T., Yashchin, E. Minimum void size and 3-parameter lognormal distribution for EM failures in Cu interconnects. In: 44th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2006:115–122.
Li, B., Gill, J., Christiansen, C.J., Sullivan, T.D., McLaughlin, P.S. Impact of via-line contact on Cu interconnect electromigration performance. In: 43rd annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2005:24–30.
Lin, M., Jou, N., Liang, J.W., Juan, A., Su, K.C. Upstream electromigration study on multiple via structures in copper interconnect. In: Proceedings of the IEEE 2009 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2009:86–88.
Lin, M.H., Lee, S.C., Oates, A.S. Electromigration mechanisms in Cu nano-wires. In: 48th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2010:705–711.
Lin, M.H., Lin, Y.L., Chen, J.M., Tsai, C.C., Yeh, M.-S., Liu, C.C., Hsu, S., Wang, C.H., Sheng, Y.C., Chang, K.P., Su, K.C., Chang, Y.J., Wang, T. The improvement of copper interconnect electromigration resistance by cap/dielectic interface treatment and geometrical design. In: 42nd annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2004:229–233.
Lin, M.-H., Lin, Y.L., Chen, J.M., Yeh, M.-S., Chang, K.P., Su, K.C., Wang, T. Electromigration lifetime improvement of copper interconnect by cap/dielectric interface treatment and geometrical design. IEEE Transactions on Electron Devices. 2005; 52(12):2602–2608.
Lingk, C., Gross, M.E. Recrystallization kinetics of electroplated Cu in damascene trenches at room temperature. Journal of Applied Physics. 1998; 84(10):5547–5553.
Lingk, C., Gross, M.E., Brown, W.L. X-ray diffraction pole figure evidence for (111) sidewall texture of electroplated Cu in submicron damascene trenches. Applied Physics Letters. 1999; 74(5):682–684.
Liu, C.S., Chen, H.C., Bao, T.I., VanOlmen, J., Croes, K., VanBesien, E., Pantouvaki, M., Zhao, C., Sleeckx, E., Beyer, G., Yu, C.H. Self aligned CuGeN process for 32/22 nm nodes and beyond. In: Proceeding of the IEEE 2008 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2008:199–201.
Lloyd, J.R. Electromigration in integrated circuit conductors. Journal of Physics D: Applied Physics. 1999; 32(17):R109–R118.
Lloyd, J.R. Black’s law revisited–nucleation and growth in electromigration failure. Microelectronics Reliability. 2007; 47(9–11):1468–1472.
Lloyd, J.R., Lane, M.W., Liniger, E.G., Hu, C.K., Shaw, T.M., Rosenberg, R. Electromigration and Adhesion. IEEE Transactions on Device and Materials Reliability. 2005; 5(1):113–118.
Lloyd, J.R., Clement, J.J. Electromigration in copper conductors. Thin Solid Films. 1995; 262(1–2):135–141.
Lopez, G., Davis, J., Meindl, J. A new physical model and experimental measurements of copper interconnect resistivity considering size effects and line-edge roughness (LER). In: Proceedings of the IEEE 2009 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2009:231–233.
Lu, J.J.-Q. Low power/low energy circuits: from device to system aspects short course – BEOL, 3D, SiP, and 3D integration technologies. International Electron Devices Meeting (IEDM) ShortCourse. 2009; 1–72.
Lu, X., Pyun, J.W., Li, B., Henis, N., Neuman, K., Pfeifer, K., Ho, P.S. Barrier layer effects on electromigration reliability of Cu/low k interconnects. In: Proceedings of the IEEE 2005 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2005:033–035.
Mayadas, A.F., Shatzkes, M. Electrical resistivity model for polycrystalline films: The case of arbitrary reflection at external surfaces. Physical Review B, Condensed Matter. 1970; 1(4):1382–1389.
Meindl, J.D., Davis, J.A., Zarkesh-Ha, P., Patel, C.S., Martin, K.P., Kohl, P.A. Interconnect opportunities for gigascale integration. IBM Journal of Research and Development. 2002; 46(2/3):245–263.
Meyer, M.A., Zschech, E. ‘New microstructure-related EM degradation and failure mechanisms in Cu interconnects with CoWP coating’, in Ogawa S. Ho PS, and Zschech E, Stress-induced phenomena in metallization, Melville, NY, American Institute of Physics. 2007; 945:107–114.
Michael, N.L., Kim, C.U., Gillespie, P., Augur, R. Electromigration failure in ultra-fine copper interconnects. Journal of Electronic Materials. 2003; 32(10):988–993.
Michael, N.L., Kim, C.U., Gillespie, P., Augur, R. Mechanism of reliability failure in Cu interconnects with ultralow-k materials. Applied Physics Letters. 2003; 83(10):1959–1961.
Michael, N.L., Kim, C.U. Electromigration in Cu thin films with Sn and Al cross strips. Journal of Applied Physics. 2001; 90(9):4370–4376.
Moon, K.-J., Yun, J.-H., Choi, Z.-S., Jung, H.-K., Lee, J.-M., Choi, G.-H., Choi, S., Moon, J.-T. Electroless CoWP integration scheme to enhance Cu interconnect reliability at ultra narrow line. In: Edelstein D.C., Schulz S.E., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2009:193–198.
Moriyama, M., Matsunaga, K., Murakami, M. The effect of strain on abnormal grain growth in Cu thin films. Journal of Electronic Materials. 2003; 32(4):261–267.
Murphy, W.J., Thomas, D.C., Lee, T.C., Chapple-Sokol, J., Gambino, J.P., Sullivan, T.D., Delibac, D.A., Vanslette, D.S., He, Z.-X., Mongeon, S.A., Luce, S.E. Extending Al interconnect technology beyond the classical performance limits. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2008:231–236.
Nakazawa, E., Arita, K., Tsuchiya, Y., Kakuhara, Y., Yokogawa, S., Kurokawa, T., Sasaki, N., Ganguli, S., Ha, H.-C., Lee, W.T., Yu, S.-H., Sekine, M. Development of selective Co CVD capping process for reliability improvement of advance Cu interconnect. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2008:19–23.
Neuner, J., Zienert, I., Peeva, A., Preuße, A., Kücher, P., Bartha, J.W. Microstructure in copper interconnects – influence of plating additive concentration. Microelectronic Engineering. 2010; 87(3):254–257.
Nogami, T., Bolom, T., Simon, A., Kim, B.-Y., Hu, C.-K., Tsumura, K., Madan, A., Baumann, F., Wang, Y., Flaitz, P., Parks, C., DeHaven, P., Davis, R., Zaitz, M., St. Lawrence, B., Murphy, R., Tai, L., Molis, S., Rhee, S.-H., Usui, T., Cabral, C., Jr., Maniscalco, J., Clevenger, L., Li, B., Christiansen, C., Chen, F., Lee, T., Schmatz, J., Shobha, H., Ito, F., Ryan, T., Nguyen, S., Canaperi, D., Arnold, J., Choi, S., Cohen, S., Liniger, E., Chen, H.-C., Chen, S.-T., Vo, T., Kelly, J., Straten, O., Penny, C., Bonilla, G., Kozlowski, P., Spooner, T., Edelstein, D., High reliability 32 nm Cu/ULK BEOL based on PVD CuMn seed, and its extendibilityTechnical digest, IEEE international electron devices meeting. Piscataway, NJ: The Institute of Electrical and Electronics Engineers, Inc, 2010. [33.5.1–33.5.4].
Nogami, T., Maniscalco, J., Madan, A., Flaitz, P., DeHaven, P., Parks, C., Tai, L., St. Lawrence, B., Davis, R., Murphy, R., Shaw, T., Cohen, S., Hu, C.K., Cabral, C., Jr., Chiang, S., Kelly, J., Zaitz, M., Schmatz, M., Choi, S., Tsumura, K., Penny, C., Chen, H.-C., Canaperi, D., Vo, T., Ito, F., Straten, O., Simon, A., Rhee, S.-H., Kim, B.-Y., Bolom, T., Ryan, V., Ma, P., Ren, J., Aubuchon, J., Fine, J., Kozlowski, P., Spooner, T., Edelstein, D., CVD Co and its application to Cu damascene interconnectionsProceedings of the IEEE 2010 international interconnect technology conference. Piscataway, NJ: IEEE Service Center, 2010. [Paper 3.1].
Noguchi, J. Dominant factors in TDDB degradation of Cu interconnects. IEEE Transactions on Electron Devices. 2005; 52(8):1743–1750.
Nopper, M., Bömmels, J., Aubel, O., Hartz, H., Preusse, A. Key aspects of CoWP and ULK implementation into high-volume manufacturing for future technologies. In: Edelstein D.C., Schulz S.E., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2009:157–165.
Oates, A.S. ‘Electromigration mass transport phenomena in Al thin-film conductors with bamboo microstructure’, in Okabayashi H. Shingubara S, and Ho PS, Stress-induced phenomena in metallization, Woodbury, NY, American Institute of Physics. 1997; 418:39–51.
Oates, A.S., Lee, S.C. Electromigration failure distributions of dual damascene Cu/low-k interconnects. Microelectronics Reliability. 2006; 46(9–11):1581–1586.
Oates, A.S., Lin, M.H. Analysis and modeling of critical current density effects on electromigration failure distributions of Cu dual-damascene vias. In: 46th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2008:385–391.
Oates, A.S., Lin, M.H. Void nucleation and growth contributions to the critical current density for failure of Cu vias. In: 47th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2009:452–456.
Ogawa, E.T., Lee, K.D., Blaschke, V.A., Ho, P.S. Electromigration reliability issues in dual-damascene Cu interconnections. IEEE Transactions on Reliability. 2002; 51(4):403–419.
Ogawa, E.T., Lee, K.D., Matsuhashi, H., Ko, K.S., Justison, P.R., Ramamurthi, A.N., Bierwag, A.J., Ho, P.S. Statistics of electromigration early failures in Cu/oxide dual-damascene interconnects. In: 39th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2001:341–349.
Ogurtani, T.O., Oren, E.E. Computer simulation of void growth dynamics under the action of electromigration and capillary forces in narrow thin interconnects. Journal of Applied Physics. 2001; 90(3):1564–1572.
Ogurtani, T.O., Oren, E.E. Electromigration-induced void grain-boundary interactions: the mean time to failure for copper interconnects with bamboo and near-bamboo structures. Journal of Applied Physics. 2004; 96(12):7246–7253.
Okabayashi, H. Stress-induced void formation in metallization for integrated circuits. Materials Science and Engineering. 1993; R11:191–241.
Park, Y.-J., Jain, P., Krishnan, S., New electromigration validation: via node vector method48th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc, 2010. [6A.01-01–6A.01-07].
Petrov, N., Sverdlov, Y., Shacham-Diamand, Y. Electrochemical study of the electroless deposition of Co(P) and Co(W, P) alloys. Journal of the Electrochemical Society. 2002; 149(4):C187–C194.
Pyun, J.W., Lu, X., Yoon, S., Henis, N., Neuman, K., Pfeifer, K., Ho, P.S. Scaling effect on electromigration reliability for Cu/low-k interconnects. In: 43rd annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2005:191–194.
Rosenberg, R., Edelstein, D.C., Hu, C.-K., Rodbell, K.P. ‘Copper metallization for high performance silicon technology’, in Kaufmann EN. Annual Review of Materials Science. 2000; 30:229–262.
Rossnagel, S.M., Kuan, T.S. Alteration of Cu conductivity in the size effect regime. Journal of Vacuum Science and Technology B. 2004; 22(1):240–247.
Roy, A., Hou, Y., Tan, C.M. Electromigration in width transition copper interconnect. Microelectronics Reliability. 2009; 49(9–11):1086–1089.
Ryu, C., Kwon, K.-W., Loke, A.L.S., Lee, H., Nogami, T., Dubin, V.M., Kavari, R.A., Ray, G.W., Wong, S.S. Microstructure and reliability of copper interconnects. IEEE Transactions on Electron Devices. 1999; 46(6):1113–1120.
Saito, T., Ashihara, H., Ishikawa, K., Miyauchi, M., Yamada, Y., Nakano, H. A reliability study of barrier-metal-clad copper interconnects with self-aligned metallic caps. IEEE Transactions on Electron Devices. 2004; 51(12):2129–2135.
Sanchez, J.E., Morris, J.W., Jr. Microstructural analysis of electromigration-induced voids and hillocks. Materials Research Society Symposium Proceedings. 1991; 225:53–58.
Shacham-Diamand, Y., Sverdlov, Y., Petrov, N., Zhou, L., Croitoru, N., Inberg, A., Gileadi, E., Kohn, A., Eizenberg, M., Material properties of electroless 100–200 nm thick coWP filmsMadore C., Osaka T., Romankiw L.T., Yamazaki Y., eds. Proceedings of Electrochemical Society: Electrochemical Technology Applications in Electronics III. 1999:102–110. [PV 99–34].
Shaviv, R. Reliability at the heart of scaling: challenges and emerging solutions for 32 and 22 nm technology. In: Tutorial Notes, IEEE International Reliability Physics Symposium. Rome, NY: SAR Associates; 2008:42.
Shaviv, R., Wu, H.-J., Sriram, M., Wu, W., Pradhan, A., O’Loughlin, J., Chattopadhyay, K., Mountsier, T., Dixit, G. Improvements in electromigration to meet the requirements of advanced technology. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2008:681–688.
Shimada, M., Moriyama, M., Ito, K., Tsukimoto, S., Murakami, M. Electrical resistivity of polycrystalline Cu interconnects with nano-scale linewidth. Journal of Vacuum Science and Technolology B. 2006; 24(1):190–194.
Singh, N., Bower, A.F., Gan, D., Yoon, S., Ho, P.S., Leu, J., Shankar, S. ‘Numerical simulations of stress relaxation by interface diffusion in patterned copper lines’, in Ho PS. Baker SP, Nakamura T, and Uolkert CA, Stress-induced phenomena in metallization, Melville, NY, American Institute of Physics. 2004; 741:62–69.
Sondheimer, E.H. The mean free path of electrons in metals. Advances in Physics. 1952; 1(1):1–42.
Spolenak, R., Kraft, O., Arzt, E. ‘Alloying effects in electromigration: what controls the electromigration drift’, in Kraft O. Arzt E, Volkert CA, Ho PS, and Okabayashi H, Stress-induced phenomena in metallization, Melville, NY, American Institute of Physics. 1999; 491:126–137.
Steinhögl, W., Schindler, G., Steinlesberger, G., Engelhardt, M. Size- dependent resistivity of metallic wires in the mesoscopic range. Physical Review B, Condensed Matter and Materials Physics. 66(7), 2002. [075414-01–075414-04].
Steinhögl, W., Schindler, G., Steinlesberger, G., Traving, M., Engelhardt, M. Impact of line edge roughness on the resistivity of nanometer-scale interconnects. Microelectronic Engineering. 2004; 76(1–4):126–130.
Steinhögl, W., Schindler, G., Steinlesberger, G., Traving, M., Engelhardt, M. Comprehensive study of the resistivity of copper wires with lateral dimensions of 100 nm and smaller. Journal of Applied Physics. 97(2), 2005. [023706-1–023706-10].
Sukharev, V., Kteyan, A., Zschech, E., Nix, W.D. Microstructure effect on em-induced degradations in dual inlaid copper interconnects. IEEE Transactions on Device and Materials Reliability. 2009; 9(1):87–97.
Sukharev, V., Zschech, E. A model for electromigration-induced degradation mechanisms in dual-inlaid copper interconnects: effect of interface bonding strength. Journal of Applied Physics. 2004; 96(11):6337–6343.
Sun, T., Yao, B., Warren, A.P., Barmak, K., Toney, M., Peale, R., Coffey, K.R. Quantitative analysis of the impact of surface and grain boundary scattering on the resistivity of nanometric Cu films. In: Edelstein D., Schulz S.E., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2009:11–18.
Suo, Z., Wang, W., Yang, M. Electromigration instability: transgranular slits in interconnects. Applied Physics Letters. 1994; 64(15):1944–1946.
Surholt, T., Herzig, C. Grain boundary self-diffusion in Cu polycrystals of different purity. Acta Materialia. 1997; 45(9):3817–3823.
Tada, M., Ohtake, H., Kawahara, J., Hayashi, Y. Effects of material interfaces in Cu/low-damascene interconnects on their performance and reliability. IEEE Transactions on Electron Devices. 2004; 51(11):1867–1876.
Tay, M., Li, K., Wu, Y. Electrical transport properties of ultrathin metallic films. Journal of Vacuum Science and Technology B. 2005; 23(4):1412–1416.
Traving, M., Schindler, G., Steinlesberger, G., Steinhögl, W., Engelhardt, M. Reconsidering the barrier tasks. In: Erb D., Ramm P., Masu K., Osaki A., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2004:671–677.
Tsu, R., McPherson, J.W., McKee, W.R. Leakage and breakdown reliability issues associated with low-k dielectrics in a dual-damascene Cu process. In: 38th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2000:348–353.
Tsuchiya, H., Yokogawa, S. Electromigration lifetimes and void growth at low cumulative failure probability. Microelectronics Reliability. 2006; 46(9–11):1415–1420.
Usami, T., Ide, T., Kakuhara, Y., Ajima, Y., Ueno, K., Maruyama, T., Yu, Y., Apen, E., Chattopadhyay, K., van Schravendijk, B., Oda, N., Sekine, M. Highly reliable interface of self-aligned CuSiN process with low-k SiC barrier dielectric (k = 3.5) for 65 nm node and beyond. In: Proceedings of the IEEE 2006 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2006:125–127.
Usui, Oki T., Miyajima, H., Tabuchi, K., Watanabe, K., Hasegawa, T., Shibata, H. Identification of electromigration dominant diffusion path for Cu damascene interconnects and effect of plasma treatment and barrier dielectrics on electromigration performance. In: 42nd annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2004:246–250.
van den Boom, R.J.J., Lifshin, E., Dunn, K.A. Evolution of grain size and crystallographic orientation in narrow lines. In: McKerrow A.J., Shacham-Diamand Y., Shingubara S., Shimogaki Y., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2007:607–611.
van Roosmalen, A.J., Zhang, G.Q. Reliability challenges in the nanoelectronics era. Microelectronics Reliability. 2006; 46(9–11):1403–1414.
Vairagar, A.V., Mhaisalkar, S.G., Krishnamoorthy, A. Electromigration behavior of dual-damascene Cu interconnects – structure, width, and length dependences. Microelectronics Reliability. 2004; 44(5):747–754.
Vairagar, A.V., Mhaisalkar, S.G., Krishnamoorthy, A., Tu, K.N., Gusak, A.M., Meyer, M.A., Zschech, E. In situ observation of electromigration-induced void migration in dual-damascene Cu interconnect structures. Applied Physics Letters. 2004; 85(13):2502–2504.
Vanasupa, L., Joo, Y.C., Besser, P.R., Pramanick, S. Texture analysis of damascene-fabricated Cu lines by X-ray diffraction and electron backscatter diffraction and its impact on electromigration performance. Journal of Applied Physics. 1999; 85(5):2583–2590.
Vanasupa, L., Pinck, D., Joo, Y.C., Nogami, T., Pramanick, S., Lopatin, S., Yang, K. The impact of linewidth and line density on the texture of electroplated Cu in damascene-fabricated lines. Electrochemical and Solid-State Letters. 1999; 2(6):275–277.
Vanypre, T., Mourier, T., Jourdan, N., Cordeau, M., Torres, J. CuAl alloy: a robust solution for 45/32 nm integration. In: McKerrow A.J., Shacham-Diamand Y., Shingubara S., Shimogaki Y., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2007:385–389.
Wada, M., Kurusu, T., Akimoto, Y., Matsunaga, N., Tanimoto, H., Aoki, N., Toyoshima, Y., Shibata, H. A study on resistivity increase of copper interconnects with the dimension comparable to electron mean free path utilizing Monte Carlo simulations. In: Edelstein D., Schulz S.E., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2009:1–10.
Walton, J.T., Frost, H.J., Thompson, C.V. Development of near-bamboo and bamboo microstructures in thin-film strips. Applied Physics Letters. 1992; 61(1):40–42.
Walls, J.A. The influence of TiN ARC thickness on stress-induced void formation in tungsten-plug vias. IEEE Transactions on Electron Devices. 1997; 44(12):2213–2219.
Wang, P.C., Filippi, R.G. Electromigration threshold in copper interconnects. Applied Physics Letters. 2001; 78(23):3598–3600.
Wang, T.C., Hsieh, T.E., Wang, M.-T., Su, D.-S., Chang, C.-H., Wang, Y.L., Lee, J.Y.-M. Stress migration and electromigration improvement for copper dual damascene interconnection. Journal of the Electrochemical Society. 2005; 152(1):G45–G49.
Wu, W., Ernur, D., Brongersma, S.H., Van Hove, M., Maex, K. Grain growth in copper interconnect lines. Microelectronic Engineering. 2004; 76(1–4):190–194.
Yang, C.-C., Edelstein, D., Chanda, K., Wang, P., Hu, C.-K., Liniger, E., Cohen, S., Lloyd, J.R., Li, B., McFeely, F., Wisneiff, R., Ishizaka, T., Cerio, F., Suzuki, K., Rullan, J., Selsley, A., Joman, M. Integration and reliability of CVD Ru cap for Cu/low-k development. In: Proceedings of the IEEE 2009 international interconnect technology conference. Piscataway, NJ: IEEE Service Center; 2009:255–257.
Yang, C.-C., Edelstein, D., Clevenger, L., Cowley, A., Gill, J., Chanda, K., Simon, A., Dalton, T., Agarwala, B., Cooney, E., III., Nguyen, D., Spooner, T., Stamper, A., Extendibility of PVD barrier/seed for BEOL Cu metallizationProceedings of the IEEE 2005 international interconnect technology conference. Piscataway, NJ: IEEE Service Center, 2005. [Paper 7–7].
Yarimbiyik, A.E., Schafft, H.A., Allen, R.A., Zaghloul, M.E., Blackburn, D.L. Modeling and simulation of resistivity of nanometer scale copper. Microelectronics Reliability. 2006; 46(7):1050–1057.
Yokogawa, S. Scaling impacts and challenges on reliability in Cu/low-k interconnects. In: Naik M., Shaviv R., Yoda T., Ueno K., eds. Advanced metallization conference. Warrendale, PA: Materials Research Society; 2008:695–701.
Yokogawa, S., Tsuchiya, H., Kakuhara, Y., Kikuta, K. Analysis of Al doping effects on resistivity and electromigration of copper interconnects. IEEE Transactions on Device and Materials Reliability. 2008; 8(1):216–221.
Yokogawa, S., Tsuchiya, H. ‘Scaling impacts on electromigration in narrow single-damascene Cu interconnects’, in Ho PS. Baker SP, Nakamura T, and Volkert CA, Stress-induced phenomena in metallization, Melville, NY, American Institute of Physics. 2004; 741:124–134.
Yokogawa, S., Tsuchiya, H. Effects of Al doping on the electromigration performance of damascene Cu interconnects. Journal of Applied Physics. 101(1), 2007. [013513-01–013513-06].
Zaporozhets, T.V., Gusak, A.M., Tu, K.N., Mhaisalkar, S.G. Three-dimensional simulation of void migration at the interface between thin metallic film and dielectric under electromigration. Journal of Applied Physics. 98(10), 2005. [103508-1–103508-10].
Zhang, L., Kraatz, M., Aubel, O., Hennesthal, C., Im, J., Zschech, E., Ho, P.S. ‘Cap layer and grain size effects on electromigration reliability in Cu/low-k interconnects’, Proceedings of the IEEE 2010 International Interconnect Technology Conference. Piscataway, NJ, IEEE Service Center, paper. 2010; 13:2.
Zhang, L., Zhou, J.P., Im, J., Ho, P.S., Aubel, O., Hennesthal, C., Zschech, E. Effects of cap layer and grain structure on electromigration reliability of Cu/low-k interconnects for 45 nm technology node. In: 48th annual IEEE international reliability physics symposium proceedings. Piscataway, NJ: Institute of Electrical and Electronic Engineers, Inc; 2010:581–585.
Zhang, W., Brongersma, S.H., Clarysse, T., Terzieva, V., Rosseel, E., Vandervorst, W., Maex, K. Surface and grain boundary scattering studied in beveled polycrystalline thin copper films. Journal of Vacuum Science and Technology B. 2004; 22(4):1830–1833.
Zhang, W., Brongersma, S.H., Richard, O., Brijs, B., Palmans, R., Froyen, L., Maex, K. Influence of the electron mean free path on the resistivity of thin metal films. Microelectronic Engineering. 2004; 76(1–4):146–152.
Zschech, E., Ho, P.S., Schmeisser, D., Meyer, M.A., Vairagar, A.V., Schneider, G., Hauschildt, M., Kraatz, M., Sukharev, V. Geometry and microstructure effect on EM-induced copper interconnect degradation. IEEE Transactions on Device and Materials Reliability. 2009; 9(1):20–30.