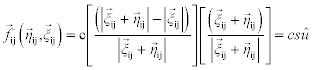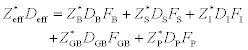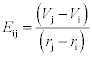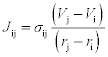Modeling electromigration using the peridynamics approach
Abstract:
This chapter presents a summary of the information and reasoning needed to justify learning about peridynamics for the purpose of analyzing electromigration and provides guidance for the development of a complete peridynamics analysis. The additions needed to convert the original peridynamics model as developed for mechanics problems to a multiphysics model capable of treating electromigration are reviewed. Experimental data on void drift by electromigration are introduced to provide a specific target for a demonstration of the peridynamical approach. Model results for the basic phenomena of this experiment are presented. The peridynamics approach appears capable of simultaneously accommodating both constitutive laws and explicit treatment of multibody interactions, for handling different aspects of the behavior of the material system to be modeled.
2.1 Introduction
2.1.1 Electromigration (EM)
Electromigration (EM) is a key reliability challenge for the economically very important electronics industry. EM in copper damascene interconnect structures is an extremely complex phenomenon because of the multitude of possible diffusion paths, including surfaces, grain boundaries, other internal interfaces, and ‘bulk’ material, and the multitude of driving forces for diffusion, which include gradients in atom or vacancy concentration, temperature, stress, and electrical current density, as well as the basic driving force of current density itself (Tan and Roy, 2007). Modeling EM with quantitative detail is an important aid in tracing physical EM phenomena back to their root causes, so that the damaging effects of EM, illustrated in Fig. 2.1, can be minimized in practical devices.

2.1 Scanning electron micrographs of the open circuit induced by EM in an n-MOS LSI (metal-oxide semiconductor for large-scale integration) bias metallization: (a) normal topographic image; (b) voltage contrast image. From Scorzoni et al. (1991). The contrast shown in (b) between the left and right portions of the wide conductor in the center of the image (white arrow) shows that the line is electrically discontinuous, and also shows that the location of the discontinuity coincides with the visible damage to the line.
2.1.2 Motivation for applying peridynamics (PD) to EM
Because practical failure mechanisms arising from EM include the nucleation, growth, motion, and agglomeration of voids, material discontinuities must be treated in a robust and efficient manner in any complete model of EM. The recently developed peridynamics (PD) approach to solid modeling has the key strength that its intrinsic nonlocal approach is tolerant of material discontinuities. Moreover, some of the key successes of the PD approach have been the realistic predictions of crack initiation and propagation in dynamic fracture experiments (Askari et al., 2008).
2.1.3 Applicability of PD to EM
The application of PD to heat transport in solid bodies was suggested by Silling and Lehoucq (2008). We previously suggested the use of PD for simulating EM (Gerstle et al., 2008, referred to here as PD-EM1) and gave details of the treatment within PD of the four important physical processes involved in EM, which are electrical conduction, thermal conduction, deformation and stress, and diffusion. The importance of these different mechanisms in EM led us to describe the PD approach to EM as a multiphysics model.
2.1.4 Scope
The first part of this chapter summarizes the detailed discussion given in PD-EM1. The latter part reports the computational implementation of a multiphysics PD model for EM along the lines previously proposed. This implementation was created as an extension of a publicly available PD code that was developed as part of a more general molecular dynamics (MD) code (lammps.sandia.gov). Finally, we present computational results for drift of a void impelled by EM, and point out certain correspondences between the model results and recent experimental observations. We suggest that this result is evidence of at least the possibility that modeling EM by use of a PD approach will prove useful.
2.2 Previous approaches to modeling electromigration (EM)
Each of the standard modeling approaches to EM has its obstacles. The PD-EM approach also has its own obstacles, which are explored in the context of the computational model discussed in the latter part of this chapter. Here we summarize the key obstacles for each of the standard approaches: MD; classical continuum analysis; and finite element analysis.
2.2.1 Molecular dynamics (MD) and EM
MD has been applied to EM by, for example, Bachlechner et al. (2005) and Chen et al. (2007). But such simulations, even on today’s massive parallel computers, are limited to model sizes of perhaps ten million atoms for perhaps 100 ps. Thus, it remains true that the time/size scale accessible to MD is insufficient to model even a single crystallite, much less entire interconnect lines in integrated circuits.
2.2.2 Classical continuum modeling and EM
Classical continuum mechanical models have also been employed for EM (Maroudas and Gungor, 2002; Kim and Lu, 2006). Classical continuum mechanics is, however, not efficacious for analysis of fields that are, or may become, manifestly discontinuous, as shown for example in Fig. 2.1. Silling (2000) and subsequent publications have discussed the mismatch between the classical, field-based treatment of solid mechanics and several present-day problems that involve interfaces. Analogous arguments clearly apply to field-based treatments of the other physical phenomena involved in EM, namely, electricity, heat, and diffusion.
On a more philosophical level, because continuum mechanics allows singular solutions (for example, in stress and strain at the tip of a crack), continuum mechanics is not a complete physical theory of solids, because such singularities are clearly non-physical. To remedy the situation, entirely new fields (fracture mechanics; nonlocal damage mechanics) have been developed over the course of the last century to augment continuum mechanics. PD has the favorable attribute that if the PD kernel is well-behaved, the theory does not allow singularities. Thus, PD is a complete theory that does not require auxiliary theories, such as fracture mechanics. This significantly simplifies computational implementation and ease of interpretation.
2.2.3 Finite element modeling and EM
Finite element analysis has been applied to EM in many studies, such as that by Tan et al. (2007). Indeed, the geometrical adaptability of the finite element approach is a key advantage. But finite element analysis requires a mesh; typically the meshes are matched to the solid surfaces, making applicability to moving voids difficult. The finite element treatment of fracture, taken as a representative example of problems with changing interfaces, is typically carried out by remeshing as the crack grows. Mesh dependences of both the initiation site of the crack and the path it takes are difficult to avoid. At a more fundamental level, the finite element approach is based upon the classical field equations, meaning explicit boundary conditions are needed at all boundaries.
2.2.4 Reasons for attempting a PD model of EM
The various approaches to modeling EM are described in more detail elsewhere in this book. Additional information can be found in PD-EM1. However, most of the previous efforts have focused on specific aspects of the problem, and therefore have an intrinsically limited regime of applicability, so they lack predictive capability for different cases. Our goal here as well as in PD-EM1 remains to significantly broaden the regime of applicability and to simplify multiphysical modeling of integrated circuits, by developing a modeling paradigm that can accurately and usefully predict the physical behavior of interconnects using today’s computational capabilities. We choose, as reported in PD-EM1, to model EM using ideas from the PD model (Silling, 1998; 2000; 2002; Silling et al., 2007). In contrast to classical continuum models, this model has several advantages, the foremost being that the response functions need not be continuous or differentiable. In addition, PD is a potential technique for multiscale modeling since it can relate the processes at the atomistic level to observable macroscopic quantities (Shen and Atluri, 2004; Tewary and Read, 2004; Read and Tewary, 2007) More details on the attractive features of the PD approach to EM modeling can be found in PD-EM1.
2.3 Peridynamics (PD)
2.3.1 PD: mathematical basics
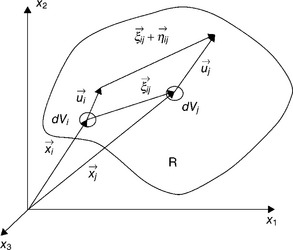
The PD approach to solid mechanics has been described in abundant detail in several publications including PD-EM1. The PD model starts with the assumption that Newton’s second law holds true on every infinitesimally small differential volume within the domain of analysis. A force density function, called the pairwise force function (or PD kernel) f (with units of force per unit volume per unit volume) between each pair of infinitesimally small differentiable volumes is postulated to act if the particles are closer together than some finite distance, called the material horizon, δ. The pairwise force function may be assumed to be a function of the relative position and the relative displacement between the two particles, as indicated in Fig. 2.2. A spatial integration process is employed to determine the total force acting upon each differential volume, and a time integration process is employed to track the positions of the particles owing to the applied body forces and applied displacements. One of the advantages of the PD approach is that no finite element meshes are required. It is a mesh-less method. As described by Silling (1998 and subsequent publications), the PD model may be implemented on the computer as an array of interacting discrete particles or elements in a three-dimensional (3D) geometrical space. Computational implementations of PD models utilize elements of a size appropriate to the problem at hand.
The description of the inter-element forces is phenomenological, like the elastic constants of solid mechanics, rather than an attempt to capture the complexity of atomic bonding. Unlike an MD model, a PD model has constitutive equations. However, unlike a finite element model, a PD model does not require continuous response fields. Silling and Lehoucq (2008) have given an extremely detailed treatment of how the interelement forces in PD describe the same physical behavior as the classical stress tensor field. Silling (2000) noted that the PD approach allows a reference position of the elements to be retained and used, in contrast to the MD approach.
Using the terminology given in Fig. 2.2, we assume that Newton’s second law holds true on an infinitesimally small particle dVi of mass dm, undeformed position ![]() , and displacement,
, and displacement, ![]() , located within domain R:
, located within domain R:
where ![]() is the force vector acting on the free body, and
is the force vector acting on the free body, and ![]() is particle i’s acceleration.
is particle i’s acceleration.
Dividing both sides of equation [2.1] by the differential volume of particle i, dVi, and partitioning the force into components internal and external to the system of particles under consideration gives
where ρ is the mass density at position ![]() ,
, ![]() is the force vector per unit volume acting upon dVi owing to interaction with all other particles (for example, particle j) in domain R, and
is the force vector per unit volume acting upon dVi owing to interaction with all other particles (for example, particle j) in domain R, and ![]() is the externally applied body force vector per unit volume at position
is the externally applied body force vector per unit volume at position ![]() .
.
The internal material force density per unit volume ![]() acting upon particle i is an integral over all other particles j within the domain R:
acting upon particle i is an integral over all other particles j within the domain R:
where ![]() is the PD force between dVi and dVj. The pairwise force function,
is the PD force between dVi and dVj. The pairwise force function, ![]() which has units of force per unit volume squared, can be viewed as a material constitutive property. In the simplest case, let us assume elastic behavior:
which has units of force per unit volume squared, can be viewed as a material constitutive property. In the simplest case, let us assume elastic behavior:
where the pairwise force function is a function of relative displacement ![]() and relative position
and relative position ![]() between particles i and j. More complex constitutive relations, incorporating internal material state variables (such as damage), may also be contemplated.
between particles i and j. More complex constitutive relations, incorporating internal material state variables (such as damage), may also be contemplated.
Silling (1998) proposed a simple nonlocal PD constitutive model:
where c, δ, and u* are positive ‘microelastic’ constants, s is the stretch of the bond, and û is a unit vector directed from particle i to particle j. Thus, the ‘spring’ connecting any two particles is linear for small relative displacements, but it breaks when the relative displacement between the two particles exceeds u*. Only particles within a distance from each other δ (the material horizon) in the deformed configuration interact. A simple microelastic PD model (with tensile limit) for brittle materials is shown in Fig. 2.3.
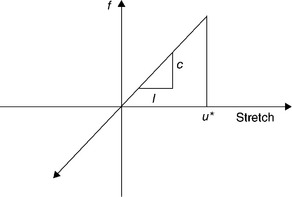
2.3 Microelastic PD model for quasibrittle material. This model governs the forces between two particles situated within the material horizon δ of each other.
The PD model does not specify how the base-space (the particles) nor how the solution fields (such as displacements and temperatures) are to be represented. In most implementations to date, the particles are represented as finite-mass/volume discrete particles. Gerstle et al. (2007) represented the PD base-space using finite elements that may or may not be connected at the nodes. Fourier series or other wavelet-type functions to represent both the base-space and the solution fields can also be contemplated.
In a multiphysics setting, the constitutive model is expanded to account for thermal, electrical and diffusive effects. Each PD bond is generalized to become a conduction path for electrical current, heat transport, and mass transport. In PD-EM1 we gave the generalized constitutive laws listed in Table 2.1.
Table 2.1
Multiphysics fields and equations for PD

Definition of symbols: ![]() displacement; T temperature; Φ electrical potential; C atomic concentration (number of atoms per total number of initial lattice sites, equal to one minus the vacancy concentration);
displacement; T temperature; Φ electrical potential; C atomic concentration (number of atoms per total number of initial lattice sites, equal to one minus the vacancy concentration); ![]() peridynamic force per unit volume squared; fq peridynamic heat flow per unit volume squared; fj peridynamic current flow per unit volume squared; fJ peridynamic concentration flow per unit volume squared; HF, Hq, Hj, HJ peridynamic neighborhoods of various fluxes for point i;
peridynamic force per unit volume squared; fq peridynamic heat flow per unit volume squared; fj peridynamic current flow per unit volume squared; fJ peridynamic concentration flow per unit volume squared; HF, Hq, Hj, HJ peridynamic neighborhoods of various fluxes for point i; ![]() relative position in reference configuration of particle j relative to particle i,
relative position in reference configuration of particle j relative to particle i, ![]() ;
; ![]() difference in displacement between points i and j,
difference in displacement between points i and j, ![]() ; τ difference in temperature between points i and j, Tj – Ti; ϕ difference in electric potential between points i and j, Φj–Φi; χ difference in atomic concentration between points i and j, Cj – Ci;
; τ difference in temperature between points i and j, Tj – Ti; ϕ difference in electric potential between points i and j, Φj–Φi; χ difference in atomic concentration between points i and j, Cj – Ci; ![]() applied body force per unit volume; ρ mass density;
applied body force per unit volume; ρ mass density; ![]() acceleration of particle i;
acceleration of particle i; ![]() applied heat flux (analogous to body force); cT heat capacity per unit mass; cE electrical capacitance (electrical charge per unit electrical potential per unit volume, analogous to body force); cD atomic concentration capacity (atoms per unit concentration change per reference volume).
applied heat flux (analogous to body force); cT heat capacity per unit mass; cE electrical capacitance (electrical charge per unit electrical potential per unit volume, analogous to body force); cD atomic concentration capacity (atoms per unit concentration change per reference volume).
2.3.2 PD as applied: comparison and contrast with MD
A grossly oversimplified functional description would be that PD is a coarse-grained generalization of classical MD. MD analysis is described by Rapaport (1995). In an MD simulation, mathematical constructs representing atoms interact through interatomic potential functions that are designed to mimic actual interatomic forces in solids. Uniform strains can be applied by deforming the mathematical box containing the MD atoms; this allows the evaluation of the elastic constants predicted by the MD model. Special configurations such as surfaces and grain boundaries can be modeled. Forces from electrical charges on the atoms in MD, if present, are considered separately from the short-range interatomic forces. Such forces greatly complicate the MD computation, because of their long range. A computational PD model would implement these same capabilities.
Although MD models are structureless, meaning that the atoms of MD have no reference position, but rather can move freely in response to the sum of the forces from their neighbor atoms, PD models can accommodate numerical storage of states of several types, for example, the accumulated damage in each PD bond between particles. PD also makes use of constitutive laws, as indicated in Table 2.1, whereas in MD these laws are emergent from the behavior of the individual atoms. It is this use of constitutive laws that allows PD models to use time steps that are much longer than the femtosecond steps needed in MD.
2.4 PD and EM
2.4.1 EM master equation
EM is described by the drift equation, equation [2.6]. This is an Einstein–Nernst diffusion equation. However, certain terms in this equation represent complex material behavior rather than specific material properties.
where vd is the drift velocity of the migrating atoms; Deff is the effective diffusion coefficient; for the case where only a single diffusion mechanism is effective, Deff = D0exp(− Ea/kT); D0 is an experimentally determined constant (units: m2 s−1). See for example Butrymowicz et al. (1973); Ea is the activation energy for diffusion. For bulk diffusion near room temperature, this includes the energy to create a vacancy at an atomic position in the crystal lattice plus the energy required to excite the vacancy to the saddle point between two atomic positions; k is the Boltzmann constant; T is the absolute temperature; Zeff∗ is the effective charge of the atoms. It represents the strength of the interaction of the ‘electron wind’ with the atoms, as a multiplier of the electrostatic interaction between a charged atom and the applied electric field that is producing the current; e is the fundamental charge; ρ is the resistivity; j is the current density (A m−2); ∂τ/∂x is the partial derivative of stress with respect to position; and Ω is the atomic volume.
Equation [2.6] lists only two driving forces for EM, namely, the electric current and the stress gradient. Others are possible, foremost among them being temperature gradients and gradients in the concentration of atoms or vacancies (Tan and Roy, 2007). Equation [2.6] includes only one diffusion path, but, in reality, EM results from multiple pathways including surface, interface, grain boundary, pipe, and lattice diffusion (Ogawa et al. 2002; Tan and Roy, 2007).
Ogawa et al. (2002) indicate that the various pathways for EM damage formation can be examined using the first term on the right-hand side of equation [2.6]. The various pathways can be expressed as:
Equation [2.7] illustrates the analysis of the product of the effective charge number and the effective diffusivity into its component parts. The subscripts identify pathways of diffusion by
Fj(j = B, S, I, G, P) is the fraction of atoms diffusing through a given pathway, which depends on the material and the specimen geometry, and probably on other quantities such as the temperature as well. Ogawa et al. (2002) explain that each pathway is anticipated to have a different Z* component because the wind-force varies according to the local electronic environment surrounding a given atom (Sorbello, 1996).
2.4.2 Assumptions for modeling EM by PD
The importance of interfaces in the modeling of EM has already been emphasized. A second important and challenging aspect of EM is that the diffusion pathways can be modified during EM. For example, a void can grow, changing the area available for surface diffusion. An important consideration in the modeling of EM is the capacity of a modeling approach to handle these changes. Our interest in PD as a modeling approach for EM stems from our opinion that PD offers a more workable treatment of these key features of the EM problem. We believe that PD is ‘scalable’, so that the different diffusion paths and driving forces can be treated with a controllable degree of effort according to the goal of the modeling.
Equation [2.6] shows how the electric current, the temperature, and the stress enter into the EM problem. A key issue for the application of PD to EM is whether PD’s nonlocal approach to solid-state phenomena is applicable to electric charges and fields, heat transport, and diffusion. In PD-EM1 we gave a detailed statement of a set of equations for fields, fluxes, constitutive relations, and conservation rules developed by analogy between solid mechanics and these various physical phenomena. Here, as in PD-EM1, we simply assume that because the field equations for electricity, heat, and diffusion are similar to those for deformation, and because the PD approach is mathematically consistent with the field equations for deformation (Silling and Lehoucq, 2008), then the PD approach is also consistent with the field equations for electricity, heat transport, and diffusion. The treatment of these different physical phenomena within PD probably involves mathematical restrictions; here we simply assume that these are not prohibitive.
2.4.3 Mathematical specifics for EM by PD
The problem of long-range electrical interactions is not addressed in the PD model used here. The PD elements are uncharged, so they feel no electrostatic forces. To treat the electrical currents that drive EM, the model includes charge transport among elements, according to the usual relation
where J is the electric current density, E is the electric field vector, and σ is the electrical conductivity. The electric field is notionally given by the standard relation from electricity theory:
for calculating charge transport from element i to element j. We take Vi, the potential on element i, as simply proportional to the charge on element i. This approximation, in particular, clearly requires further study. The result is
where the conductivity σij can be chosen based on the properties of the PD elements i and j.
As in PD-EM1, the conduction of heat and the diffusion of atom concentration are handled similarly, with temperature and atom concentration analogous to voltage and heat and number of atoms analogous to charge in the relations above. In PD-EM1 we showed that a one-dimensional PD model of a conductor reproduced the classical linear distribution of electrical potential and the parabolic distribution of temperature for a wire heated by Joule heating with no loss of heat at the lateral boundaries. Here, again, we show that a 3-dimensional PD approach reproduces the same simple classical solutions to the model problem.
2.5 Illustrative example
2.5.1 Problem to be modeled
Of the many reports in the literature on observations of EM in electronic interconnects, the vast majority focus on either voiding or voids. Voiding refers to the complete disappearance of a certain segment of the length of a conductor, whereas voids are cavities or holes in a conductor. Here we focus on the motion of a single void in a conductor enclosed in dielectric. We note in passing that other aspects of void behavior, such as the evolution of void shape, have been both observed and modeled. We also note that the nucleation of voids is a critical issue in the reliability of microelectronic interconnects, although here we take a void as given. The objective of this section is to identify a particular observed instance of an EM phenomenon, and construct a preliminary PD model of this experimental situation. Here we are only attempting to show the plausibility of modeling this situation by PD. It becomes evident from this example that constitutive laws have a key role in PD modeling.
The motion of a void in a current-carrying conductor was examined by Ho (1970); the approach was continuum mechanics. Few observations of the situation modeled by Ho have been carried out. We have obtained experimental data on a similar system. The main difference is that whereas Ho predicted the speeds of spherical and cylindrical voids, we observed the motion of surface voids. We created voids in copper conductors by the application of high amplitude alternating current (ac) (Read et al., 2009). The specimens were damascene copper lines with width 3 μm, thickness 0.5 μm, and length 200 μm, completely enclosed in SiO2 dielectric. A typical scanning electron microscopy (SEM) micrograph, taken after stressing a line with ac and later removing the dielectric on top of the copper, is shown in Fig. 2.4. The voids appear as round dark regions in the conductor. The void depth is not measurable from the plan-view SEM images. Because we have detected the presence of copper in the center of these voided regions by use of energy dispersive X-ray spectroscopy (EDS), we believe they penetrate only part-way through the thickness. The particular experiment of interest here was performed on a different line, with the dielectric cap still present. After the line was stressed with ac, several voids were visible optically on the top surface, as shown in Fig. 2.5a.

2.4 SEM micrograph showing typical appearance of a wide copper damascene line constrained in SiO2 after ac stress. The peak current density was 14.4 A cm-2. The lifetime was 1498 s. The peak temperature rise, from Joule heating, was 396 °C.

2.5 Enhanced optical images of a line of the same type as shown in the previous figure: (a) voids (dark spots) in fully contained copper damascene line; (b) same line after dc stress, showing that some of the voids have moved by electromigration. Eight additional intermediate images acquired during the experiment, not shown, allowed unambiguous identification of the moving voids.
Because this image has been enhanced to increase the contrast between the voids (dark spots) and the copper (lighter strip), the dark spots reveal only the presence and locations of the voids, but do not portray their shapes accurately.
When we applied a direct voltage and current (dc), the voids moved steadily under the effect of the current, and their changing positions were captured by optical imaging. Over the course of the experiment about 100 images were obtained. Figure 2.5a shows the first and Fig. 2.5b shows the tenth. Each void was sufficiently far from the others that its behavior was independent of the other voids. The fastest-moving voids moved at a similar rate of approximately 0.08 μm s−1 for the particular experimental conditions, approximate current density 15 MA cm−2 and temperature 380 °C. Other voids moved more slowly, and still others at varying rates.
2.5.2 Implementation of PD model
A hypothetical copper conductor with a total length of 310 nm and a width and height of 90 nm was modeled as a rectangular parallelepiped of 2511 PD elements, of which 324 were in boundary regions and 2187 were fully active elements. Each PD element represents a cube 10 nm on each side. A constant voltage was applied between the end boundary regions of the conductor. The sides of the conductor were treated as adiabatic, while the ends were maintained at a fixed temperature. As noted in previous chapters, the surface diffusion rate of copper is known to be much greater than the bulk diffusion rate. For this reason the surfaces of copper conductors in practical interconnects are coated with barrier layers that prevent surface diffusion. Therefore, the lateral surfaces of the model conductor were assigned diffusion rates equal to the bulk rate. A surface void was modeled by assigning an initial atomic concentration of 0.99 to a 3 × 3 block of nine adjacent elements on the surface of the conductor.
The PD elements of the model were visualized as blocks containing variable electric charge, temperature, and atomic concentration. In this initial demonstration, the PD elements were not allowed to move. The physical justification for this was that actual interconnect conductors are fixed in a rigid framework of dielectric supported by a silicon slab, and so are highly constrained mechanically. The transport of atomic concentration between blocks was treated under the framework listed in Table 2.1. The master equation for EM given in equation [2.6], was applied to calculate the amount of atomic concentration transported at each time step between each pair of interacting elements. The formula used was that the fraction of atomic concentration dC transported through each PD bond during a single time step dt was:
where v is the drift velocity from equation [2.6] and l is the size of an element, in this case, 10 nm. The units in equation [2.12] are consistent because the atomic concentration C is dimensionless. In the present calculation, the stress gradient term on the right hand side of equation [2.6] was not considered. Stresses in a more detailed model could be calculated from the inter-element forces given by equation [2.5]. These forces could also be used to displace the elements, but this was not done here as discussed above. The current density in the PD model was calculated within the framework listed in Table 2.1 by allowing electrical charge to flow between neighboring elements according to equations [2.8]–[2.11]. This charge was used to establish the voltage on each PD element, beginning with the usual formula that relates the geometry of a conductor to its resistivity:
where R is the electrical resistance, ρ is the electrical resistivity, L is the length of the conductor, and A is the cross-sectional area. In the present model, the length L was taken as the element size, 10 nm; if the area A had been taken as the block area, here 100 nm2, an incorrect value of the electrical resistance of the modeled copper conductor as a whole would have resulted. The reason for this is that charge is transported through the PD model conductor through each PD bond between neighboring elements; this produces an effective area different from the simple geometrical value of 100 nm2. An ‘effective area factor’ was used to account for this effect. This factor is different for different values of the interaction horizon among the PD elements. In the present model with its simple cubic lattice of elements, each element is assumed to interact with its 26 nearest neighbors.
Below a calculated temperature distribution is presented, based on electrical fields and currents calculated using equations [2.8]–[2.11] and the relationship:
where p is power density and j is current density. However, another simplification in the present calculation of void motion was that the temperature was assumed to be a constant independent of position. This was done to simulate the present experimental case, where the temperature over the region of the conductor that was traversed by the voids is constant. In practice an alternative form of equation [2.6] was formulated by replacing jρ with E since by definition (for scalar conductivity, as is appropriate for copper):
The physical sense of this substitution is that the interaction between the electron wind and the lattice ions is proportional to the electric field because, although the amount of current flowing increases with increasing conductivity, the interaction between the flowing electrons and the fixed ions increases in strength with increasing resistivity. The effects of conductivity and resistivity cancel, leaving the electric field term.
The constitutive parameters used in the present calculation are listed in Table 2.2. Customary units for each parameter are used.
Table 2.2
Constitutive parameters and temperature used in calculations. Customary units for each parameter are used

The numerical calculations for the new multiphysics PD model of EM were implemented through the use of a computer code for the PD model of mechanics that has been made available by Sandia National Laboratories (lammps.sandia.gov). The organization of the source code facilitates modifications for new situations such as EM. Code was added to input the additional constants needed in the constitutive laws used here, such as electrical resistivity, thermal conductivity, heat capacity, and diffusion constants. Arrays for storage of the values of the additional physical quantities needed in this multiphysics version of PD, specifically, voltage, temperature, and atom concentration, were added to the code. Routines for the flow of electrical current, heat, and atom concentration were inserted. The new results, voltage, temperature, and atom concentration at each PD element, were listed by use of existing routines in the code. Graphical representations of the results were created using a companion set of software.
We introduced various timescales appropriate to the various physical quantities involved, which were electrical charge and potential, heat and temperature, and stress and deformation. It is apparent from the physics of this problem that the first event to be modeled is the establishment of electrical current through the conductor, and that this must occur rapidly compared with other events in the problem. We found that thousands of time steps were needed to stabilize the charge and potential distributions. These were iterated on the fastest model time scale. The temperature distribution was then stabilized based on an independent time scale. For this first attempt, we neglected the temperature dependence of the electrical conductivity. To treat variable thermal and electrical conductivities, the electrical and thermal quantities would have to be converged by iterating them repeatedly in turn. The transport of electrical charge, heat, and force between PD elements within the same ‘horizon’ were treated according to the prescriptions given in Table 2.1 as explained in PD-EM1. Figure 2.6 shows that the resulting voltage and temperature distributions converged to their ideal values, which were, respectively, linear and parabolic, for this simple situation. This convergence demonstration was calculated in the absence of a model void, to allow direct comparison to available ideal values. The data shown required 9816 iterations of the voltage calculation and 814 for the temperature calculation.
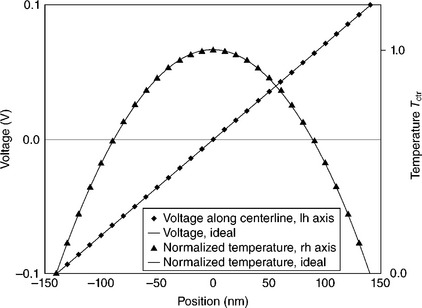
2.6 Voltage and temperature variation along the centerline of the modeled conductor as calculated iteratively by the PD approach, compared with their ideal values.
With current, temperature, and stress all stabilized, the diffusion steps were allowed to begin. Under these extremely oversimplified assumptions, the void gradually dissolved and dispersed through the conductor.
More realistic physical modeling assumptions were deduced by considering the physics of an actual surface void. A void has an internal surface; diffusion on this surface is responsible for the drift of the void under EM, as modeled by Ho (1970). Rapid diffusion on the void surface was introduced into the present model by assigning diffusion constants according to the local atom concentration. The surface diffusion rate, which is thousands of times faster than the bulk rate that corresponds to regions of normal atomic concentration, was assigned to regions of low concentration, considered as representing a void. For this case the void migrated steadily along the conductor, but it dissolved at the same time. This was inconsistent with the experimental observations. Most of the experimentally observed voids, especially those toward the cathode end of the line, appeared to be stable. They did not decrease in size or dissolve. Therefore to model this behavior, two correction terms were included. One was a ‘surface energy’ term that increased the diffusion rate when it would promote the increase of void concentration in one element by absorbing void fraction from a neighboring element with a much smaller concentration. The idea is that for two equal volumes of voids, one volume composed of many small voids and the other composed of a single larger void, the multiple smaller voids have a total surface energy larger than the single larger void. The thermodynamics should therefore favor the growth of the larger void, because this lowers the surface energy. The other correction tested was a ‘stress energy’ term that penalized the diffusion of atoms into regions where the atom concentration was 1 or larger.
Under these ad hoc constitutive laws, the initial void grew in size as it migrated along the line, but it retained its visibility and reached the other end of the line. Initial, intermediate, and final state images are shown in Fig. 2.7 a–c. The small spheres in the graphic represent PD elements. Darker areas indicate reduced atomic concentrations, which is the numerical representation of a void in this model. Figure 2.7 represents a calculation where a 1% reduction in atomic concentration corresponds to the model void. For this case, the criterion for application of the surface diffusion rate was an atomic concentration below 0.996. Because each PD element in the model represents 1000 nm3, a literal interpretation of this calculation would be that the initial void had a volume of 10 nm3 for each of the dark-colored elements in the figure, for a total of 90 nm3. Its velocity was about 453 nm s−1. A similar calculation was carried out for an initial assumption of a 10% reduction in the atomic concentration within the void region. In this case, the criterion for the use of the surface diffusion rate had to be adjusted to an atomic concentration of 0.96, and a slight adjustment in the surface energy improved the stability of the void. This larger model void traveled more slowly by almost a factor of 10. This is generally consistent with Ho’s (1970) result, which had the void speed inversely proportional to the radius (larger voids drift more slowly).
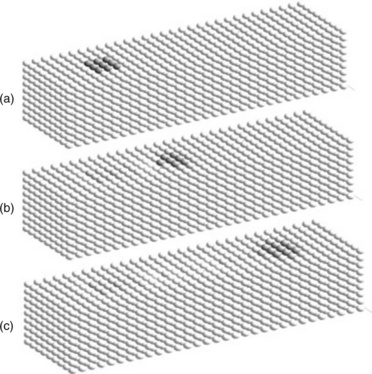
2.7 PD model calculation results showing (a) initial, (b) intermediate, and (c) final stages of PD calculation of void motion. The darker areas indicate reduced atomic concentrations, which is the numerical representation of a void in this model
The run time on a single-processor desktop computer was 203 s. Most of this time was required to converge the charge and temperature distributions. The run included 750 diffusion time steps.
2.6 Computational requirements: present and future
The computational effort involved in PD modeling a problem involving a number N of PD elements is roughly similar to that in involved in a MD model of N atoms. Although the PD force law described in equation [2.5] is simpler than many interatomic force laws, the addition of additional types of physics in a multiphysics PD model consumes additional computational effort. Gerstle et al. (2010) reported the computational effort involved in the use of PD to model the failure of a concrete joint. It was found that, by use of today’s massively parallel computer systems, it is possible to model 3D reinforced concrete components of significant size (such as parts of beams and columns, and connections) using the PD model. However, modeling entire buildings or bridges using PD is not currently feasible.
Simulation of EM problems is somewhat more computationally intensive because of the more complex types of physics involved. However, it appears that simulation of million-particle EM problems are well within the reach of present high-performance computing systems.
2.6.1 Green’s function method for improving the computational efficiency of the PD model of EM
As is apparent in the preceding sections, the PD model involves solution of a many-body problem of N interacting discrete elements. As such, it is closely analogous to an N-atom problem in solid-state physics. Powerful computationally efficient techniques have been established for solution of such problems. These techniques can be, in principle, incorporated into the PD model. One such technique is the lattice Green’s function method for static as well as time dependent problems. The lattice static Green’s function method (Tewary, 1973) has been successfully used for modeling defects in crystal lattices. A hybrid technique based upon the use of both MD and Green’s functions has also been developed (Tewary and Read, 2004; Read and Tewary, 2007) and applied for multiscale modeling of nanomaterials. For time dependent problems, the causal Green’s function method has been shown to extend the time scales by several orders of magnitude (Tewary, 2009). In this section, we briefly review these techniques and indicate their possible application to PD problems.
In the example given in 2.5, we made several simplifying assumptions in order to illustrate the application of the PD model to EM without clouding it with mathematical details. A fully-fledged three-dimensional calculation, which has not yet been carried out for EM using the PD model, consists of solving equation [2.2] for relative displacements that are time dependent. This equation can be solved by using the methods similar to MD. However, for realistic modeling, N needs to be of the order 104 or even larger. For large values of N, the solution of equation [2.2] becomes computationally very expensive. A major problem in MD is its extremely limited time scale. Most MD calculations are limited to 10–100 ps. For modeling many physical processes such as EM, it is necessary to model time up to a few microseconds or even more. For realistic values of N, this is a formidable task even for modern computers. We propose that it should be possible to address this problem by using the causal Green’s function technique (Tewary, 2009). Here we outline the approach.
2.6.2 Mathematics for application of causal Green’s function to PD
The PD force as defined by equation [2.4] must be an analytic function of the displacements. We can, therefore, expand it in a Taylor series in the displacements uj about the equilibrium sites of the elements, as follows:
where f0ij is the constant term and Φij(uj) is the linear Taylor coefficient evaluated at the equilibrium values of ξij. The remaining term ΔfijΦij(uj) represents the nonlinear contributions and contains quadratic and higher powers of uj.
In equation [2.16], ϕij can be identified as a 3 N × 3 N matrix, and f0ij, uj and Δfij as 3 N × 1 column matrices corresponding to N PD elements. The factor 3 arises because each element has three degrees of freedom in the 3D Euclidian space. The integration over the volume element dVj and the functional dependence of fij on position co-ordinates in equation [2.16] and subsequent equations are not explicitly shown for reasons of brevity.
Note that fij in equation [2.16] depends only upon the displacement of a single element uj, whereas it depends upon the relative displacement ηij = uj – ui in equation [2.2]. This apparent inconsistency can be removed by defining the self PD force fii using the following relation:
where the sum includes j = i. This gives the following value for the self-peridynamical force:
The self force is not normally defined in the PD model.
Using equation [2.16], we can write equation [2.2] in the form
where M is an operator defined by
Equation [2.19] is analogous to the Born von Karman equation for N atoms in lattice dynamics (see, for example, Maradudin et al., 1971), except for the nonlinear term Δf(u) on the right in equation [2.21] for b*. The Fourier transform of M is exactly the lattice dynamical matrix of the Born von Karman model and Φij corresponds to the force constant matrix connecting atoms i and j. Equation [2.17] corresponds to the condition of invariance of the crystal energy against rigid body translation [Maradudin et al., 1971] that yields the self force constant of each atom as in equation [2.18].
Equation [2.19] should therefore be amenable to the powerful computational techniques developed for the nonlinear Born von Karman model for static as well as time-dependent problems. The operator on the left of equation [2.19] is linear, so we can define the corresponding Green’s function operator as follows:
This gives the following formal solution of equation [2.19] in the operator form:
In the static case, the time derivative of u is zero and G becomes the static Green’s function (Tewary, 1973). Equation [2.23] can then be used to calculate u for modeling cases when one (or a finite number) of the PD elements is ‘defective’. A defective element is defined as the element that is different from the other elements and has a different fij. It can represent a void or a hillock or some other defect in the solid. In such cases, we have to calculate the defect Green’s function (Tewary, 1973). The effective force term b*(u) can be identified as the Kanzaki force (Tewary, 1973; Tewary, 2004). Calculation of the Kanzaki force in the nonlinear case by using MD has been given by Read and Tewary (2007) for a quantum dot in silicon.
In the time dependent case, the inverse of M can be obtained by taking the Laplace transform of equation [2.22]. This gives:
where I is the 3 N × 3 N unit matrix, G^(s) is the Laplace transform of the Green’s function, and s is the Laplace variable. Equation [2.24] shows that G^(s) has poles in the complex s plane at the eigenvalues of Φ. If Φ is positive definite, all the poles are on the real axis. The causal Green’s function can be obtained analytically by taking the inverse Laplace transform of G^(s) by choosing a suitable contour in the s-plane (Tewary, 2009).
In the linear case when b*(u) = b, the causal Green’s function yields an exact analytical solution of equation [2.23] for u that is valid at all times. In many cases of physical interest u may be small enough for the linear approximation to be valid. In EM and other similar problems involving large displacements of the elements, Δf is, in general, nonzero. In such cases equation [2.23] is solved numerically by using a step-by-step iterative technique in space (Tewary, 2009). At each step, f is expanded locally keeping only the linear terms in u as given by equation [2.16]. The integration over time is obtained exactly by taking the inverse Laplace transform of G^(s) (Tewary, 2009). Each step size is chosen to be small enough so that Δf(u) is negligible during that step. Because the force is recalculated at each step, the final solution includes the nonlinear effects as in conventional MD. However, neglecting Δf(u) at each step introduces a constraint on the time step, but it is much less severe than that in the conventional MD because (Tewary, 2009):
1. In the conventional MD, the force during each time step is approximated by f0 and both the linear term Φ and the nonlinear term Δf in equation [2.16] are neglected. In the GF method the linear term is also retained in addition to f0. This gives a much better approximation of the variation of the force during the time step.
2. The time integration in the conventional MD is carried out numerically using the linear approximation. In more refined versions of the MD, quadratic terms in time are also included. In the GF method, the time integration is carried out analytically to give the exact result for each time step.
In general, the Green’s function method requires inversion of a matrix. In symmetric cases, the matrix inversion is easily performed by using the discrete Fourier transform in space (Tewary, 1973; Tewary, 2004). In more general cases, the inversion can be done by iteration and is facilitated by the fact that Φ is a sparse matrix. The choice of method of calculating G would depend upon the specific physical problem.
More details on the static and causal Green’s function methods and their application to the PD model for EM will be presented in a forthcoming paper. The other associated multiphysics PD problems such as distribution of electrical charge, current, and temperature, as for example in the solution of equation [2.8], can also be solved by using the Green’s function approach. The Green’s functions for these problems are well known (see, for example, the classic text by Morse and Feshbach, 1953). These techniques may be useful for modeling EM in complex and variable geometries.
2.7 Conclusions
The ‘lessons learned’ in this initial attempt to construct a multiphysics PD modeling approach to EM include:
1. The PD treatment of interaction among solid elements, which may be individual atoms or larger blocks, appears capable of handling the transport of electrical charge, heat and matter with physically sensible results for the elementary situations attempted.
2. It was necessary to use separate time scales for the transport of electrical charge, heat, and matter. The distributions of electrical potential and temperature were converged, using iterations as necessary, as a preliminary part of each full time step. The number of calculation steps required to reach convergence of the distribution of electrical potential was substantial. Only after this convergence was mass transport (diffusion) calculated at each time step.
3. The main contrast between the PD approach and the classical continuum approach is that PD naturally accommodates dynamic internal (and external) interfaces.
4. The main contrast between the PD approach and the MD approach is that PD accommodates constitutive laws for its transport properties. This allows treatment of slow processes, in particular, mass transport by diffusion.
5. The adaptation of constitutive laws for diffusion to the particular PD model at hand is an ad hoc process, which depends on the coarseness of the model both in time and in spatial extent. In this illustrative model of EM, a criterion for where to apply the surface diffusion rate and a surface energy function were applied.
6. Continuing advances in the cost-effectiveness of computational power and in the power of mathematical formulations such as Green’s functions provide assurance that available computational resources are sufficient for useful application of PD to various physical phenomena including EM.
2.8 References
Askari, E., Bobaru, F., Lehoucq, R., Parks, M., Silling, S., Weckner, O. Peridynamics for multiscale materials modeling. Journal of Physics: Conference Series. 2008; 125:012078.
Bachlechner, M.E., Zhang, J., Wang, Y., Schiffbauer, J., Knudsen, S.R., Korakakis, D. Molecular dynamics simulations of the mechanical strength of Si/Si3N4 interfaces. Physical Review B. 2005; 72:094115.
Butrymowicz, D.B., Manning, J.R., Read, M.E. Diffusion in copper and copper-alloys. 1. Volume and surface self-diffusion in copper. Journal of Physical and Chemical Reference Data. 1973; 2:643–655.
Chen, W.H., Cheng, H.C., Hsu, Y.C. Mechanical properties of carbon nanotubes using molecular dynamics simulations with the inlayer van der Waals interactions. CMES-Computer Modeling in Engineering & Sciences. 2007; 20:123–145.
Gerstle, W., Sau, N., Silling, S. Peridynamic modeling of concrete structures. Nuclear Engineering and Design. 2007; 237:1250–1258.
Gerstle, W., Sakhavand, N., Chapman, S. ‘Peridynamic and continuum models of reinforced concrete lap splice compared’, in FraMCo5-7, recent advances in fracture mechanics of concrete. Korea Concrete Institute: Eds. B. H. Oh et al. Seoul; 2010.
Gerstle, W., Silling, S., Read, D., Tewary, V., Lehoucq, R. Peridynamic simulation of electromigration. CMC-Computers Materials & Continua. 2008; 8:75–92.
Ho, P.S. Motion of inclusion induced by a direct current and a temperature gradient. Journal of Applied Physics. 1970; 41:64–68.
Kim, D., Lu, W. Creep flow, diffusion, and electromigration in small scale interconects. Journal of the Mechanics and Physics of Solids. 2006; 54:2554–2568.
Maradudin, A.A., Montroll, E.W., Weiss, G.H., Ipatova, I.P. ‘Theory of lattice dynamics in the harmonic approximation’, Solid State Physics, Supplement 3, II edition, Eds. Ehrenreich H, Seitz F and Turnbull D. New York: Academic; 1971.
Maroudas, D., Gungor, M.R. Continuum and atomistic modeling of electromechanically-induced failure if ductile metallic thin films. Computational Materials Science. 2002; 23:242–249.
Morse, P.M., Feshbach, H. Methods of mathematical physics. New York: McGraw-Hill; 1953. [Parts 1 and 2.].
Ogawa, E.T., Lee, K.-D., Blaschke, V.A., Ho, P.S. Electromigration reliability issues in dual-damascene Cu interconnections. IEEE Transactions on Reliability. 2002; 51:403–419.
Rapaport, D.C. The art of molecular dynamics simulation. Cambridge, UK: Cambridge University Press; 1995.
Read, D.T., Tewary, V.K. Multiscale model of near-spherical germanium quantum dots in silicon. Nanotechnology. 2007; 18:105402.
Read, D.T., Geiss, R.H., Barbosa, N. Constraint effect in deformation of copper interconnect lines subjected to cyclic Joule heating. Journal of Strain Analysis for Engineering Design. 2009; 44:543–553.
Sandia National Laboratories. Large-scale atomic/molecular massively parallel simulator (computer code). http://lammps.sandia.gov.
Scorzoni, A., Neri, B., Caprile, C., Fantini, F. Electromigration in thin-film interconnection lines: models, methods and results. Materials Science Reports. 1991; 7:143–220.
Shen, S., Atluri, S.N. Computational nano-mechanics and multi-scale simulation. Tech Science Press CMC. 2004; 1:59–90.
Silling, S. Reformulation of elasticity theory for discontinuous and longrange forces. Albuquerque, NM: Sandia National Laboratories; 1998. [SAND98-2176].
Silling, S. Reformulation of elasticity theory for discontinuities and longrange forces. Journal of the Mechanics and Physics of Solids. 2000; 48:175–209.
Silling, S. ‘Dynamic fracture modeling with a meshfree peridynamic code’, SAND2002–2959C. Albuquerque, NM: Sandia National Laboratories; 2002.
Silling, S.A., Lehoucq, R.B. Convergence of peridynamics to classical elasticity theary. Journal of Elasticity. 2008; 93:13–37.
Silling, S.A., Epton, M., Weckner, O., Xu, J., Askari, E. Peridynamic states and constitutive modeling. Journal of Elasticity. 2007; 88:151–184.
Sorbello, R.S. ‘Microscopic driving forces for electromigration’, in Advanced Metallization for Future ULSI. Materials Research Society Symposium Proceedings. 1996; 427:73–81.
Tan, C.M., Hou, Y.J., Li, W. Revisit to the finite element modeling of electromigration for narrow interconnects. Journal of Applied Physics. 2007; 102:033705.
Tan, C.M., Roy, A. Electromigration in ULSI interconnects. Materials Science & Engineering R-Reports. 2007; 58:3–75.
Tewary, V.K. Green’s function method for lattice statics. Advances in Physics. 1973; 22:757.
Tewary, V.K. Multiscale Green’s-function method for modeling point defects and extended defects in anisotropic solids: application to a vacancy and free surface in copper. Physical Review B. 2004; 69:094109.
Tewary, V.K. Extending the time scale in molecular dynamics simulations: propagation of ripples in graphene. Physical Review (Rapid Communications) B. 2009; 80:161409.
Tewary, V.K., Read, D.T. ‘Integrated Green’s function molecular dynamics method for multiscale modeling of nanostructures: application to Au nanoisland in Cu’, CMES–Computer. Modeling in Engineering & Science. 2004; 6:359–371.