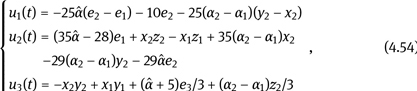Definition 4.1 ([95]): Consider two nonlinear systems as follows:

where state variables x, y ∈ Rn, and F, F′ : [R+ × Rn] → Rn is the nonlinear map. U : [R+ × Rn × Rn] → Rn is the synchronization control variable of chaotic system. R+ is the nonnegative real number set. If we have D(t0) ⊆ Rn,∀x0, y0 ∈ D(t0), and lim‖ x(t; t0, x0) – y(t; t0, y0)‖ = 0 when t → ∞, then systems (4.2) and (4.1) are synchronous. We call system (4.1) as the drive system, and system (4.2) as the response system, and D(t0) is the synchronization region. If D(t0) belongs to the whole space Rn, then the synchronization is defined as global (complete) synchronization. If D(t0) is a subset of Rn, then the synchronization is defined as local (partial) synchronization. If F = F′, then it is called self-synchronization.

If we set error vector e = x–y, then the synchronization error system of systems (4.1) and (4.2) is

Similarly, based on the stability of error system (4.3) at the origin of the system, the stability conditions of the system are derived.

In the study of chaos synchronization, the stability of the synchronization system is determined mainly by the Lyapunov stability principle or by the condition Lyapunov exponent (CLE) criterion proposed by Pecora and Carroll. The former is the main criterion, and the latter is a necessary condition for synchronization. But the linear stability theorem shows that the necessary condition is also a sufficient condition for most of the dynamic systems, and it is used as a criterion during the synchronization research [96].

The above synchronization definition is suitable for synchronization of not only chaotic systems, but also nonchaotic systems. It is suitable for both of the synchronization of autonomous systems and nonautonomous systems, and it can be extended to the synchronization of hyperchaotic systems and spatiotemporal chaotic systems.

4.2Performance Index of Chaotic Synchronization System

The study of the performance of the synchronization system is directly related to the practical application of the chaotic system, and it is of great significance to study the mechanism of the synchronization performance. Control parameters have a great influence on the performance of the synchronization system, and how to choose the control parameters to make the optimal synchronization performance is an important part of the study of chaos synchronization. The synchronization performance of the system can be improved by choosing the initial value and controlling parameters of the system, such as shortening the setup time of synchronization, improving the stability and convergence speed, and increasing the anti-disturbance ability for the synchronization system. Here, we put forward the performance index of chaotic synchronization system first, including synchronization stability, synchronization robustness, synchronization steady-state error, synchronization accuracy, synchronization setup time, synchronization region, synchronization dynamic characteristics, and so on [97].

Definition 4.2: Synchronization stability refers to that the chaos synchronization system with different initial states satisfies the Lyapunov asymptotic stability conditions, namely the solution of system equation is convergent. It is the primary characteristic of the chaotic synchronization system, and it is the necessary condition for the synchronization system to work. It is the key to realize the application of the secure communication. Stability is divided into large-scale (global) asymptotic stability and small-scale (local) asymptotic stability.

Definition 4.3: Synchronization robustness refers to the drive–response system that maintains stability in the case of the system parameters mismatch. From the practical view, if the system’s robustness is better, then the system is easier to implement. But from the view of communication security, if the system’s robustness is better, then the security is worse. This is a contradiction, which must be considered in the practical application.

Definition 4.4: Synchronization steady-state error is the accurate degree of synchronization of the two chaotic systems to achieve synchronization. In general, it is denoted by Δφ.

Definition 4.5: Synchronization accuracy refers to the consistent degree of the chaotic signal generated by the controlled system and the target system in the amplitude and phase, and it is denoted by δ. The relationship between the steady-state error and the synchronization accuracy is δ = 10[lg Δφ], where [Δφ] is the smallest integer that is not more than Δφ.

Definition 4.6: Synchronization setup time is an important index for the application of chaotic secure communication, and it is the transition time experienced by the response signal for the given synchronization accuracy, and it is denoted by Ts. To describe the synchronization of chaotic systems, the synchronization accuracy can be calculated by

or

where n is the number of system variables. When p ≤ δ, synchronization is achieved.

Definition 4.7: Synchronization region is the initial value range for the synchronization of the chaotic system. He and Vaidya proved the solution of the system is asymptotically stable when the initial value of chaotic system is in a certain region (synchronization region) [98]. That is, the response system will eventually be synchronized with the drive system. Obviously, a successful or practical synchronization method should have sufficiently large synchronous region.

Table 4.1: Comparison of the maximum CLE with the synchronization setup time.

Definition 4.8: Synchronization dynamic characteristics are also known as the transient characteristics of the synchronization establishment. It shows as monotonic or nonmonotonic decay. Nonmonotonic decay shows that there is a trend of nonsynchronization in the synchronization process, which should be avoided.

Research shows that the control parameters are closely related to the performance index of the synchronization. Reasonable choice of control parameters can make the CLE of the response system from positive to negative, so that the response system can be controlled. That all CLEs of the response system are negative is a sufficient condition for the realization of chaos synchronization control, and it is a necessary condition in most cases. The smaller the CLE is, the faster the error convergence is, and the shorter the synchronization setup time is. The maximum CLE in Table 4.1 is calculated by employing the algorithm presented in Chapter 2. When the maximum CLE of the response system is negative, and it is significantly less than zero, then it can guarantee a large enough synchronization region. So changing the control parameters means changing the system’s CLE, and it can improve the performance of the synchronous system.

4.3Principle and Performance of Feedback Control Synchronization

4.3.1Multivariable drive feedback synchronization for chaotic system

Consider two continuous chaotic systems with the same structure and different initial values as follows:

where drive variables X ∈ Rn and Y ∈ Rn, and matrices A ∈ Rn×m and B ∈ Rn×m; F: Rn ×R → Rm is the nonlinear function. AX is the linear part, and Bf(X) is the nonlinear part. Control variable U ∈ Rm, and (A, B) is controllable. If the state variable error E = X–Y, then the synchronization problem between response system (4.7) and drive system (4.6) is used to find a suitable control law U(X, Y) to satisfy

Obviously, the synchronization control problem of two continuous chaotic systems is transformed into the control problem of the error system.

According to Lyapunov stability theorem, we design a positive definite quadratic function V(E) = ETPE as a Lyapunov function. If V̇(E) = –ETQE, and Q is positive definite (that is, V̇(E) is negative definite), then the system is asymptotically stable. The synchronous error system equation for eqs (4.6) and (4.7) is

So the problem of synchronization of two systems is transformed into the problem of the control law and the choice of the control parameters. In addition, how to select a set of control parameters from a certain range of parameters must be based on the principle of synchronization performance optimization. It is very important whether it is from the study of the synchronization control itself, or the practical application of the synchronization system.

4.3.1.1Control Law of the Feedback Controller

The multivariable drive feedback synchronization principle for continuous chaotic system is shown in Figure 4.1. The response system is driven by all the variables of the drive system, and the error feedback controller is composed of a linear feedback part and a nonlinear feedback part.

Figure 4.1: Synchronization principle block diagram for continuous chaotic system.

Theorem 4.1: For the n-dimensional continuous chaotic system and its replication system, the synchronous control method based on multivariable drive error feedback control is employed. The drive system is Ẋ= AX + Bf(X), and the response system is Ẏ= AY + Bf(Y) + U, where X, Y ∈ Rn and K ∈ Rn×m. The control variable U = K(X–Y) + B(f(X)–f(Y)). If the elements in the parameter control matrix K satisfy: when i = j, then kij > aij; or when i ≠ j, then kij = aij, and then the asymptotically stable synchronization is achieved between the response system and the drive system.

Proof. Let E = X–Y, then the error system equation Ė= AE + B(f(X) – f(Y)) – U(X, Y). If the control law of the controller is U = KE + B(f(X) – f(Y)), then Ė= (A – K)E.

Define V(E) as the Lyapunov function

where P is a positive definite matrix. Its differential is

Obviously, as long as the feedback controller parameter kij meet: when i = j, kij > aij; when i ≠ j, kij = aij, then Q = (A – K)TP + P(A – K) is positive definite. That is, (E) is negative definite. If and only if E = 0, the equality is right. That is, the drive–response system is asymptotically stable. ∎

Inference 4.1 When i = j, then kij > aij; When i ≠ j, and aij = aji, then kij = kji = 0, the asymptotic stability synchronization is realized and the structure of the controller is simplified, which can be proved by Lyapunov stability theorem (omitted).

Because the response system is driven by all drive system variables, and the synchronization of two systems is achieved by linear and nonlinear feedback controls, it is called multivariable driving feedback synchronization control method. The method does not need to decompose the system, which is not only suitable for simple chaotic systems, such as the Lorenz chaotic system, but also be applied to hyperchaotic system, such as the Rössler hyperchaotic system. In this method, the selection of feedback parameters is presented, and the performance of the synchronization system can be effectively improved by choosing proper feedback control parameters.

4.3.1.2Synchronization Simulation and Discussion

Example 1: Multivariable drive feedback synchronization control for Rössler hyperchaotic system.

As shown in Section 3.3.1, the Rössler hyperchaotic system equation is

When system parameters a = 0.25, b = 3.0, c = 0.05, and d = 0.5, it is hyperchaotic.

According to Theorem 4.1 and Inference 4.1, the drive system is

and the response system is

The synchronization control law is

When feedback coefficient k11 > 0, k22 > a, k33 > 0, and k44 > c, then the synchronization is achieved for the drive system and the response system. Set the initial conditions of the drive system and the response system as (–20, –30, 20, 45) and (–40, 25, 40, 15), respectively. The control parameter kii = 1, and the simulation time is 20 s. The synchronization phase portrait between x1 and y1 is shown in Figure 4.2.

The error curves are obtained with the same initial values and the different control parameters as shown in Figure 4.3, where |E| = [(x1 – y1)2 + (x2 – y2)2 + (x3 – y3)2 + (x4 – y4)2]1/2. The corresponding feedback control parameters of curves a, b, and c are (0.6, 0.6, 0.6, 0.6), (1, 1, 1, 1), and (2, 2, 2, 2). Obviously, in a certain range, the greater the control parameters, i.e., the greater the control energy, the shorter the synchronization setup time, and the better the dynamic performance in a certain convergence error range. The simulation results show that the error feedback control can realize the synchronization of two hyperchaotic systems. To realize the synchronization control, the feedback control parameters must be selected correctly. The synchronization performance of the hyperchaotic synchronization system can be improved by choosing appropriate parameters.

Figure 4.2: Synchronization phase portrait for Rössler hyperchaotic system.

Figure 4.3: Error curves with different control parameters.

then the response system is

and the control law is

where Xn, Yn ∈ Rm. f is the nonlinear function and U is the feedback control law. The feedback parameters K= diag[k1, k2, . . . , km], P = diag[p1, p2, . . . , pm], where ki ≥ 0 and pi ≥ 0 (i = 1,2,. . . ,m). The synchronization of the response system and the drive system is actually the problem of the stability of the synchronous manifold S = {(Xn, Yn) : Yn = Xn}.

Here the problem is analyzed by using local linearization. Set

where δn is a small synchronization error. From eqs (4.16) to (4.19), we obtain the linear evolution equation of the synchronization error as

Obviously, if Dn is the constant matrix, and all the characteristic roots are within the unit circle, then δn → 0 withn →∞, that is, Yn → Xn. So the synchronization manifold is stable, and the two systems will be synchronized. But if Dn in eq. (4.20) is a time-varying matrix, then the above method does not work.

Pecora–Carroll Chaos Synchronization Theorem For all the time t, the zero solution of the nonlinear unstable system ẋ = A(t)x + O(x, t) with O(x, t) will be asymptotically stable, as long as the system meets the following conditions.

That is to say, the Pecora–Carroll chaos synchronization theorem can be concluded as follows. Only when all the Lyapunov exponents of the response system are negative, we can achieve the chaos synchronization between the response system and drive system. This theorem is a sufficient condition for synchronization, but the linear stability theorem proves that the sufficient condition is also a necessary condition for many dynamical systems, so it is used as a criterion in the study of chaos synchronization.

Define the maximum conditional Lyapunov exponent of response system (4.17) as

Obviously, λ is an average statistic. It reflects the global characteristics of the system and determines the final behavior of the system. When λ > 0, the error δn will increase by exponential law. When λ < 0, the error δn will decrease by exponential law and leads to δn = 0 finally. That is,

It means that the synchronization is achieved between the response system and drive system. So, we can determine whether the synchronization is realized and obtain the range of the feedback parameters by calculating the maximum CLE of the response system.

The control law U(Xn, Yn) consists of a linear feedback and nonlinear feedback, so it is called the linear and nonlinear feedback synchronization method. This method has many advantages, such as simple structure, optional parameters, and fast synchronous speed.

4.3.2.1Control Law of the Synchronization Controller

The synchronization principle of discrete chaotic system is shown in Figure 4.4.

According to the stability criterion, the parameter selection theorem for the synchronization of two discrete chaotic systems is given.

Theorem 4.2: For an m-dimensional discrete-time chaotic system Xn + 1 = AXn + Bf(Xn), its response system is Yn+1 = AYn + Bf(Yn) + U(Xn, Yn). By employing the linear and nonlinear feedback control synchronization method, the control law is U(Xn, Yn) = K(Xn – Yn) + P(f(Xn) – f(Yn)), where Xn, Yn ∈ Rm, K=diag[k1, k2, . . . , km]. When P = B, the necessary and sufficient condition for the synchronization between the response system and the drive system is that all poles of the characteristic polynomial T(z) = |Iz – (A – K)| are located in the unit circle.

Proof. For the drive and response systems, the error system equation is

Figure 4.4: Synchronization principle block diagram of discrete chaotic system.

Obviously, the coefficient of the characteristic polynomial of the error system is a function of the linear feedback coefficient K, which is independent of the initial value. If T(z) = |Iz –(A–K)| is a Hurwitz polynomial, then all the eigenvalues of the matrix A–K are located in the unit circle. δn → 0 with n → ∞, that is, Yn → Xn. Synchronization between the drive system and the response system is achieved. ∎

Theorem 4.3: For a one-dimensional discrete chaotic system xn+1 = axn + bf(xn), its response system is yn+1 = ayn+bf(yn)+u(xn, yn). By employing the linear and nonlinear feedback synchronization control method, the control law is u(xn, yn) = k(xn – yn) + p(f(xn) – f(yn)), where xn, yn ∈ R. When k ≥ 0, and p ≥ b, then the sufficient condition for the asymptotic stability synchronization between the response system and the drive system is |a–k| < 1.

Proof. For a one-dimensional discrete chaotic system, the error system equation is

So we have

where represents the ith iteration from x0. According to the definition in eq. (4.21), the maximum CLE is

If p = b, we have

According to eq. (4.28), as long as k meets |a – k| < 1, then we have λ < 0. ∎

Theorem 4.4: For an m-dimensional discrete chaotic system Xn+1 = AXn + Bf(Xn), its response system is Yn+1 = AYn + Bf(Yn) + U(Xn, Yn). By employing the linear and nonlinear feedback control synchronization method, the control law of the controller is U(Xn, Yn) = K(Xn – Yn)+P(f(Xn)–f(Yn)), where Xn, Yn ∈ Rm. When K = dA, and P = dB, d > 0, then the sufficient condition for the asymptotic stability between the response system and the drive system is 1–e–λ′ < d < 1+e–λ′, where λ′ is the maximum Lyapunov exponent of the drive system. Obviously, λ′ > 0. (Proof omitted.)

For one-dimensional discrete chaotic system, we have the following theorem.

Theorem 4.5: For a one-dimensional discrete chaotic system xn+1 = axn + bf(xn), its response system is yn+1 = ayn + bf(yn) + u(xn, yn). By employing the linear and nonlinear feedback control synchronization method, the control law of the controller is u(xn, yn) = k(xn – yn) + p(f(xn) – f(yn)), where xn, yn ∈ R. When k = ma, p =mb, m > 0. The sufficient conditions for the asymptotic stability of the response system and the drive system are a – ae–λ′ < k < a + ae–λ′ , b – be–λ′ < p < b + be–λ′, that is, 1 – e–λ′ < m < 1 + e–λ′, where λ′ is the maximum Lyapunov exponent of the drive system, and λ′ > 0.

According to the above theorems, the linear and nonlinear feedback control can be used to realize the synchronization of two discrete chaotic systems by choosing appropriate feedback coefficient. Although Theorems 4.4 and 4.5 are sufficient conditions to guarantee the synchronization of two chaotic systems, it is also a necessary condition for most of the dynamical systems. It is worth noting that the synchronization speed is very fast. When d = 1 or m = 1, the synchronization can be achieved as D-B synchronization.

4.3.2.2Simulation and Discussion

Example 2: Linear and nonlinear feedback synchronization for logistic map.

Logistic map is

where x ∈ (0, 1) and μ ∈ (0, 4]. When μ = 4, the system is chaotic. The experimental conditions are as follows. The initial value is 0.2. The step size of parameter p and k is 0.05. The iteration number is 40,000.

The drive system is

The response system is

The control law is

Figure 4.5: CLE versus feedback coefficient k.

Figure 4.6: CLE versus feedback coefficient p.

Figure 4.7: CLE versus feedback coefficient k.

Figure 4.8: CLE versus feedback coefficient.

Figure 4.9: Synchronization error curves with different feedback coefficients: (a) k = p = 3.2 and (b) k = p = 4.

Example 3: Linear and nonlinear feedback synchronization for Hénon map.

Hénon map is

When a = 1.4 and b = 0.3, the system is chaotic. Next, we apply Theorem 4.2 to Hénon map.

The drive system is

The response system is

The control law is

Then the error system is

Obviously, the characteristic equation of matrix D is

According to Jury stability criteria, the necessary and sufficient condition of all the characteristic roots of T(z) to locate in the unit circle is

According to eq. (4.39), when k1 = 0 and |k2| < 0.7, or when k2 = 0 and |k1| < 0.7, or when k1 = k2 = k and |k| < 0.4522, the error system is asymptotically stable. That is to say, the response system can be synchronized with the drive system. When we set the initial values as [0.1 1.0]T and [0 0.1]T, respectively, then the control parameters are k1 = 0, k2 = 0.2, and P = B. The error convergence curve of the two systems is shown in Figure 4.10(a). It shows that there exist nonsynchronization trends in the synchronization process. When the steady-state error is Δφ = 10–4, the synchronization setup time is about 22 s. The synchronization performance of the synchronization system can be improved by choosing the appropriate parameters. For example, when k1 = k2 = 0 and P = B, the error convergence curve is shown in Figure 4.10(b). It can be seen that the synchronous speed is accelerated, and the synchronization time is shortened. The simulation synchronization time is about 17 s under the same steady-state error, and it realizes the monotonous synchronization.

By applying Theorem 4.4 to Hénon map and setting the simulation conditions, the initial value is [0.1, 0.5]T, the step size of parameter is 0.05, and the iteration number is 40,000.

Figure 4.10: Synchronization error curves with different feedback parameters: (a) k1 = 0, k2 = 0.2 and (b) k1 = k2 = 0.

Figure 4.11: Maximum CLE curves with linear or nonlinear feedback: (a) p = 0 and (b) k = 0.

Both the stability criterion of discrete system and the Pecora–Carroll asymptotic synchronization theorem can synchronize two discrete chaotic systems, but they are different. The selection of the control parameters obtained by the stability criterion of the discrete system is a necessary and sufficient condition for the synchronization of the systems. While the selection of the control parameters according to the Pecora–Carroll chaos synchronization theorem is a sufficient condition for the synchronization of the systems. That is, it is possible to choose the control parameters to synchronize the drive system and the response system, but the maximum CLE is not negative. For example, for Hénon map, when K = diag[k, k] and P = B, the maximum CLE is greater than zero as shown in Figure 4.14. But according to Theorem 4.2, when |k| < 0.4522, the response system and drive system can be synchronized.

Figure 4.12: Maximum CLE curves with linear or nonlinear feedback: (a) p = 1, k ≠ 0 and (b) k = dA, p = dB.

Figure 4.13: Synchronization error curve with k = A, p = B.

Figure 4.14: CLE versus k.

where the state variable x ∈ Rn, the system parameter α ∈ Rm, and nonlinear function f : Rn×m → Rn.

The given system that generates the desired orbit is

where y ∈ Rn, α ∈ Rm. The variable y starts from the initial and evolves with the known parameter α∗, and one obit O(y) is obtained, which is called as a desired orbit or reference orbit. System (4.42) that produces the orbit is called a target system or a reference system. The adaptive control synchronization method is to introduce a control mechanism for the parameter α in system (4.41), so that the orbit O(x) of system (4.41) from any initial value follows the orbit O(y) of the target system. System (4.41) is called a controlled system or response system. If lim ‖y – x‖ = 0, then the controlled system and the target system are synchronized.

The parameter αj in system (4.41) can be obtained by introducing a certain amount of perturbation to modify the evolution of its orbit, which can make the O(x) and O(y) realize the synchronization. For parameter αj, the control law is

where is the parameter value to generate the desired obit. h(⋅, ⋅) and g(⋅) are control laws, respectively, and ε, δ are positive control constants. When the control law is selected, by changing ε and δ, the combined system from systems (4.43) and (4.41) is

If all the CLEs are less than zero, the synchronization between the two autonomous chaotic systems is realized.

4.4.2Choose Control Law and Control Parameters

Formula (4.43) only gives a general parameter control law, and it does not make a specific description for the choice of h and g. On the other hand, that all the Lyapunov exponents of the combined system are less than zero is only the sufficient conditions for the synchronization of chaotic systems. Therefore, it is necessary to make a further discussion about the control law and control parameter for the chaos synchronization.

In the following simulation, the control law is chosen as

Therefore, the adaptive control law of the controllable parameter is

So the change of controlled parameters depends on two factors. One is the difference (xi–yi) between the state variable x in eq. (4.41) and the corresponding variable y of the desired ∗orbit. The second is the difference between the values of the controlled parameters and the corresponding parameter values of the desired orbit.

Here, we take the unified chaotic system (3.35) as an example to illustrate the synchronization principle. To realize the synchronization control of two unified chaotic systems, the adaptive control law for parameter α is given according to eqs (4.45) and (4.46), that is,

Figure 4.15: Principle block diagram of the adaptive synchronization.

According to the Pecora–Carroll synchronization stability criterion, the sufficient condition for the synchronization of two unified chaotic systems with different parameters is determined by the fact that the maximum CLE of the combined system is less than zero. The principle block diagram is shown in Figure 4.15.

4.4.3Determine the Boundary and Range of the Control Constant

According to the analysis above, once adaptive control law (4.48) of the parameter is determined, the size of ε and δ becomes the key to achieve synchronization. The ranges can be determined by two methods, such as numerical calculation and theoretical analysis.

The numerical calculation method is used mainly to determine the range of ε and δ by calculating the Lyapunov exponent of the composite system which is composed of the unified chaotic system and formula (4.48). The boundary of the constants ε and δ is determined by the fact that the maximum CLE of the composite system is equal to zero.

The theoretical analysis method is described as follows. Assuming the reference system is at equilibrium, set y = y∗ as the equilibrium point of the reference system. α∗ is the parameter corresponding to y∗. So α∗ and y∗ satisfy f(y∗, α∗). Obviously, the most basic requirement for the synchronization control is that the composite system is stable in the neighborhood of y∗. That is, all the eigenvalues of the Jacobian matrix of the composite system have negative real part, or the characteristic polynomial of Jacobian matrix is Hurwitz polynomial. So we can obtain the range of control constant ε and δ. Here the Jacobian matrix of the composite system is

where a = 25α+10, b = 25(x2 –x1), c = –35x1 + 29x2, d = –(8+α)/3, and e = –x3/3. Obviously, the Jacobian matrix contains not only variables but also the symbol function, so the characteristic polynomial is very complex, and it is difficult to determine the range of ε and δ. So here the numerical calculation method of the maximum CLE presented in the second chapter is used to determine the range of ε and δ.

4.4.4Simulation Results and Discussion

When α ∈ [0, 1], the reference system is chaotic. The initial values of the controlled system (response system) are (10, 10, 10) and α(0) = 0.5. The initial values of the reference system (drive system) are (–5, –5, –5) and α∗ = 0.3. Let |e| = [(x1–y1)2 +(x2–y2)2 + (x3–y3)2]1/2, and we have the following conclusions.

Table 4.2: Values of ε and δ with different desired parameters for synchronization.

Figure 4.16: Error curves with ε = 40 and varying δ: (a) δ = 140 and (b) δ = 200.

Figure 4.17: Error curves with δ = 220 and varying ε: (a) ε = 35 and (b) ε = 50.

The response system equation is

To realize the synchronization, the control functions u1(t), u2(t), and u3(t) are added to the right-hand side of each equation, and the response system becomes

The error system is obtained by subtracting eq. (4.52) from eq. (4.50)

where synchronization error e1 = x2 – x1, e2 = y2 – y1, and e3 = z2 – z1. Obviously, the problem of synchronization between two chaotic systems with different parameter is transformed into the stability problem of error system (4.53) at the origin e1 = 0, e2 = 0, and e3 = 0. If the appropriate control variables u = [u1(t), u2(t), u3(t)]T is chosen to make error system (4.53) stable, then response system (4.51) can be synchronized with drive system (4.50).

Theorem 4.6: For drive system (4.50) and response system (4.51), if we choose the control function

where the parameter is an estimate of the parameter α1, and the adaptive law of the estimate parameter is If the control parameter satisfy λ ≥ 0, then the equilibrium point e = 0 and α1 = α̂ exist in the error system, and the asymptotic synchronization is realized between the response system and drive system. That is, for any initial values.

Proof. Substitute control function (4.54) into error system (4.53), then we have

So error dynamics system (4.55) has no relationship with the response system parameter α2. As long as the error system is stable, it can realize the synchronization of two chaotic systems with different parameters. According to the Lyapunov stable theory, the Lyapunov function is constructed as

where e = [e1, e2, e3]T, = α1 – α̂. If the adaptive law of the estimate parameter is

then the derivative of eq. (4.56) is

Substituting eq. (4.55) and eq. (4.57) into eq. (4.58), we have

According to the Lyapunov stable theory, when λ ≥ 0, Ė≤ 0, and equilibrium point e = 0, α1 = α̂. The error system is asymptotically stable, so the two systems are synchronized. ∎

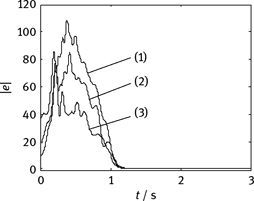
We use Matlab/Simulink for numerical simulation. Set α1 = 0.8, α2 = 0.3, and initial values x1(0) = 10, y1(0) = 10, z1(0) = 10, x2(0) = –5, y2(0) = –5, z2(0) = –5 and α̂(0) = 0.5, and do numerical simulation for control parameter λ = –0.1, λ = 1, λ = 2, and λ = 5. The synchronization error curves between the two chaotic systems with different control parameters are shown in Figure 4.18.

Figure 4.18: Synchronization error curve with different control parameters: (a) + = –0.1; (b) + = 1; (c) + = 2; and (d) + = 5.

where v = [v1, v2, v3]T is the control vector and α is the unknown parameter. Set the error variables as e1 = x2–x1, e2 = y2–y1, and e3 = z2–z1, then the error system of systems (4.60) and (4.61) is

To make the error system stable and realize the synchronization between the two systems, the following theorem is proposed for the control function and the estimated parameters.

Theorem 4.7: For drive system (4.60) and response system (4.61), if the control function is defined as

the parameter is the estimate of the parameter α. If the adaptive law of the estimate parameter is then there exist the equilibrium points e = 0 and α = α̂ in the error system, and the asymptotic synchronization is realized between the response system and drive system. That is, for any initial values.

Proof. Substituting control function (4.63) into error system (4.62), we have

As long as the error system is stable, the synchronization of two chaotic systems with uncertain parameters is realized. According to the Lyapunov stable theory, the Lyapunov function V is constructed as

where α = α – α̂, and α̂ is the estimate of uncertain α. If we choose the adaptive law of the estimate parameter then the derivative of eq. (4.65) is

Because V is positive, and α ≥ 0, V̇ is negative. According to the Lyapunov stable theory, there are equilibrium points e = 0 and α = α̂, that is,

The response system and the drive system are synchronized. ∎

We use Matlab/Simulink for numerical simulation. When α ∈ [0, 1], both drive system (4.60) and response system (4.61) are chaotic. Let the initial values x1(0) = 10, y1(0) = 10, z1(0) = 10, x2(0) = –5, y2(0) = –5, z2(0) = –5, and α ∈ [0, 1], α̂(0) = 0.5. The synchronization error curve of two chaotic systems with unknown parameters is shown in Figure 4.19. The phase diagram of variables x1 and x2 is displayed in Figure 4.20.

The following conclusions are obtained by theoretical analysis and simulations. (1) The performance of the synchronization is stable as shown in Figure 4.19. When steady-state error is Δφ = 10–4, the setup time of synchronization system is short (t < 2 s), and the monotonous synchronization of two systems is achieved. (2) The selection of the initial value of the adaptive parameters has no effect on the results. For example, the synchronization error curve with α̂(0) = 2 is the same with that with α̂(0) = 0.5. (3) By the Lyapunov stability theory, the synchronization condition is only a sufficient condition.

Figure 4.19: Error curve of chaotic synchronization system.

Figure 4.20: Phase portrait of x1 and x2.

When the parameter α ∈ [0, 1], the system is chaotic.

The deformation system of the unified chaotic system is [100]

Correspondingly, when α = 0.8, systems (4.68) and (4.69) are Lü system and deformation Lü system, respectively. The phase portraits with the initial value [–1, 1, 0] are shown in Figure 4.21. Obviously, the phase track curves of Lü system and deformation Lü system are similar, but the evolution of the deformation system in the phase space is more divergent and the system is more complex.

Figure 4.21: Strange attractors with α = 0.8: (a) Lü system and (b) deformation Lü system.

Set ei = xi–yi, then the error system equation is

Set the control variables to

where p(t) is a pulse signal with period T and the ratio D of pulse length and pulse period, and it is defined by

It can be seen that eq. (4.72) is a composite controller composed of nonlinear continuous feedback and linear intermittent feedback. So, eq. (4.71) becomes

If it is asymptotically stable at the origin, the synchronization between systems (4.68) and (4.70) is achieved.

Theorem 4.8: For systems (4.68) and (4.69), if it is controlled by eq. (4.72), and the feedback parameter satisfies k > 27–6α, and D ≥ 0.4, then the asymptotically stable synchronization will be realized between systems (4.70) and (4.68).

Proof. Decompose the error system eq. (4.74), and when iT < t < iT + TD, we have

where A1 is the Jacobian matrix of the error system when the system has a control pulse

When iT + TD < t < (i + 1)T, we have

where A2 is the Jacobian matrix of the error system when the system has no control pulse

and is the nonlinear term of the error system. For all t, when ‖e‖ →0, , so the evolution of errors depends on A1 and A2. During iT < t < iT + TD, the error is controlled by A1. For α ∈ [0, 1], according to the stability criterion of continuous system, if k satisfies k > 27–6α, then the eigenvalues of the matrix A1 have negative real part. The zero point of the error system is asymptotically stable at this time. During iT + TD < t < (i + 1)T, the controlled systems lose some additional feedback, and the error is controlled by A2. Because A2 does not satisfy the stability condition, the trajectory of the two systems will diverge, and the synchronization of the two systems will be lost. As long as the error is still small enough, and the exert control pulse is applied again, it can ensure that the error will not deviate too far, so that the synchronization of the two systems will be achieved gradually. After the continuous system is discretized, the error equation is written as

where e(i) is the error vector of the ith pulse period. DT = m1h, (1 – D)T = m2h, where h is the integral step size, and m1, m2 are the integral iteration numbers for a pulse and no pulse, respectively. Obviously, in the process of synchronization, the system will generate oscillation due to (A2)m2, and the stable synchronization process will depend on |(A1)m1 (A2)m2 |. If |(A1)m1 (A2)m2| = |J| < 1, then the system will become stable [101]. The exact range of D can be obtained by numerical experiments. Simulations show that when D ≥ 0.4, the exact synchronization can be achieved within 10 s. ∎

4.6.2Synchronization Simulation and Performance Analysis

The synchronization control and performance improvement for the unified chaotic system and its deformation system are studied based on Matlab simulation. Here, we observe the changes of the time performance of the synchronization from the aspects of the initial value, the feedback coefficient k, the proportion factor D, the step size h, and the system parameter α.

4.6.2.1Effect of Initial Value on Synchronization Performance

Set α=0.8, k =40, T =0.1 s, D=0.6, h = 0.001, and the initial values are (1) X(0) = [20, 0, 0], Y(0) = [–2, 1, 0]; (2) X(0) = [10, 0, 0], Y(0) = [–2, 1, 0]; and (3) X(0) = [5, 0, 0], Y(0) = [–2, 1, 0]. The synchronization error curve is shown in Figure 4.22. So, the synchronization between the two systems is achieved within 1.5 s. The oscillation phenomenon occurs in the process of establishing the synchronization, which is related to the characteristic value of A2. Because at the beginning of iT + TD < t < (i + 1)T, the error has not reached the steady state. In addition, the oscillation for initial value (3) is minimum, while the oscillation for initial value (1) is maximum. It can be seen that the initial value of the two systems is more; the larger the oscillation, the more the time required to establish accurate synchronization. But in general, it can achieve satisfactory results even when the initial value is large.

Figure 4.22: Synchronization error curves for different initial values.

Figure 4.23: Synchronization error curves with different k.

Figure 4.24: Relation curve of synchronization setup time tb with parameter α.

where x ∈ Rn, u ∈ Rk, and w ∈ Rm are the state variables, nonlinear feedback input, and random noise of the system, respectively. y is the output in the sender. A, B, C, and E are known constant matrices.

In the receiver, when the nonlinear feedback input u is measurable, then the state observer of the system can be expressed as [102]

where z ∈ Rn and ∈ Rn. F, G, H, and J are unknown constant matrices.

Suppose In is a unit matrix with n order, the error of the state observer is defined as e = x̂ – x = z – (In + JCT)x. Let M = In + JCT, then the dynamic equation of the error system is

When error system (4.82) satisfies

then the error system becomes ė = Fe. Obviously, if all eigenvalues of the matrix F are less than zero, then converges to x exponentially.

Substitute M = In + JCT into the third term of HCT – MA + FM = 0, then we have

Let

and substitute eq. (4.84) into eq. (4.85), then we obtain

At this point, the state observer equation is changed to

So, the design problem of the state observer with random disturbance is turned into the problem of how to find the appropriate J, which satisfies (In + JCT)E = 0, and how to choose the appropriate N, which satisfies the eigenvalues of F are less than zero. As F = MA–NCT, the condition that the eigenvalues of F are less than zero must be satisfied by choosing appropriate N. That is to say, in this case, we can always find a suitable N, so that when t →∞, x̂ converges to x exponentially.

From eq. (4.83), we obtain JCTE = –E, and according to matrix knowledge, we have

where (CTE)+ is the generalized inverse matrix of (CTE). V is the matrix with appropriate dimensions. For the convenience of application, we often let V = 0. Then we have J = –E(CTE)+. At the same time, we can obtain M = Ip + JCT.

4.7.2Design of State Observer for Unified Chaotic System

By applying the state observer method to the unified chaotic system, the sender matrix is described as

The receiver equation is

where

Here, n1, n2, and n3 are the three values of the one-dimensional vector N, which can ensure that the eigenvalues of matrix F are less than zero, and these lead the synchronization error for ė = Fe to zero finally. For simple calculation, we set n1 = 25α+10, n2 > 0, n3 = 0. When t →∞, x̂ converges to x exponentially.

4.7.3Simulation and Discussion

Based on Matlab simulation platform, the synchronization of the unified chaotic system is investigated in this section. We set the initial values x1(0) = 15, x2(0) = 15, x3(0) = 15, x̂1(0) = 10–10, x̂2(0) = –10, x̂3(0) = 10–10; n1 = 25α + 10, n3 = 0, and let the synchronization error

Next, we study the synchronization performance of the synchronization system.

4.7.3.1Synchronization Performance with Different Parameter α

When n2 = 3 and w(t) = 100 sin(3t), we obtain the synchronization error curves for α = 0.5, α = 0.8, α = 0.9, respectively, as shown in Figure 4.25. It can be seen, although the difference between the two initial values is very far, that the system can achieve synchronization within t = 2 s for different system parameters. It shows that the system has strong robustness to parameter variation.

4.7.3.2Effect of Noise Interference on the Performance of System Synchronization

When n2 = 3 and α = 0.8, we obtain the synchronization error curves for w(t) = 5 sin(3t), w(t) = 100 sin(3t), and white noise, respectively, as shown in Figure 4.26. It can be seen that the type and size of the noise have little effect on the synchronization error signal. The system can achieve the precise synchronization within t = 2 s. It shows the method has strong antinoise performance.

4.7.3.3Effect of Initial Values on the Performance of System Synchronization

When n2 = 3, α = 0.8, and w(t) = 100 sin(3t), we obtain the synchronization error curves for following initial values as shown in Figure 4.27.

Figure 4.25: Synchronization error curves for different α.

Figure 4.26: Synchronization error curve for different noise interferences.

Figure 4.27: Synchronization error curves for different initial conditions.

Figure 4.28: Synchronization error curves for different n2.

where x ∈ Rn, F: Rn →Rn; s is the scalar output of the system. Set k(x) is a scalar differentiable function, and V(x) is vector field, where V: Rn →Rn. Lee derivative of the vector field V(x) along the scalar differentiable function k(x) is defined as Lvk, then Lvk = <V(x) ● grad k(x)>, where < ● > is the Euclidean inner product. The ith Lee derivative of the vector field V(x) along the scalar differentiable function k(x) is defined as

Lemma 4.1 [103]: If is diffeomorphism, then all the state variables of system (4.92) are observable by using scalar output s and it is the ith (i ≤ n – 1) Lee derivative, and x = ϕ–1[s(t), s(1)(t), . . . , s(n–1)(t)]T.

If a state variable xi is selected as the output of system (4.92), then the remaining state variables of system (4.92) can be expressed as where j ≠ i. So system (4.92) is written as

where A is a constant matrix, and is a matrix with n×1 order, which includes all the nonlinear terms of system (4.92).

Lemma 4.2 [104]: Set the output of system (4.92) as

where B = diag[b1, b2, . . . , bn]. If we select an appropriate diagonal matrix B so that the eigenvalues of the matrix A–B have a negative real part, then system ẏ = F(y) + s(x) – s(y) is the chaos observer of chaotic system (4.92), where

4.8.2Chaos Observer of the Unified Chaotic System

The state observer synchronization scheme is applied to the unified chaotic system, and we have

Here, the drive system is driven by

where

The state observer system in the receiver can be expressed as

where is similar with s(x).

By eq. (4.95), when the appropriate B is taken, the characteristic value of the A–B is negative, and then the accurate synchronization between the chaotic system in the sender and the state observer in the receiver can be achieved.

4.8.3Synchronization Simulation and Performance Analysis

The synchronization simulation of the unified chaotic system is carried out on Matlab, and we set the system’s initial conditions x1(0) = 1, x2(0) = 1, x3(0) = 1, x̂1(0) = 15, x̂2(0) = 15, x̂3(0) = 15,

where b22 > 19α – 1, and let ei = (x̂i – xi).

Next, we will study the synchronization performance of the synchronization system.

4.8.3.1Effect of Different Parameter α on the Performance of System Synchronization

For simulation, we set α = 0.5, α = 0.8, and α = 0.9 (it means the system is the generalized Lorenz system, the generalized Lü system, and the generalized Chen system respectively). The synchronization error curves are obtained as shown in Figure 4.29. Obviously, for different parameter α, the unified chaotic system and the state observer will achieve accurate synchronization, but the synchronization performance is not exactly the same. This is mainly due to the use of a single parameter transmission, and the function between x2 and x̂2 is complex. So this calculation will have a greater impact on the synchronization performance between x2 and x̂2 with different α values. Overall, the synchronization performance is good for different α values.

4.8.3.2Effect of Initial Values on the Performance of System Synchronization

Setting b22 = 29 and α = 0.8, the changes of the synchronous error signals with the following three different initial conditions are analyzed, respectively. The synchronization error curves of the system are shown in Figure 4.30:

Initial condition (1): X(0) = [ 15, 15, 15 ] X̂(0) = [ 10–10, –10, 10–10 ].

Initial condition (2): X(0) = [ 50, 50, 50 ] X̂(0) = [ 10–10, –10, 10–10 ].

Initial condition (3): X(0) = [ 15, 15, 15 ] X̂(0) = [ 10, 5, 10 ].

From Figure 4.30, when the initial values between the unified chaotic system and the state observer are further away from each other, the oscillation is more obvious, and the time required for synchronization is longer, which is consistent with the conclusion obtained by the previous state observer method. However, even if the initial value of the two is far, the system can still achieve accurate synchronization.

Figure 4.29: Synchronization error curves for different α: (a) α = 0.5; (b) α = 0.8; and (c) α = 0.9.

Figure 4.30: Synchronization error curves for different initial conditions: (a) initial value (1); (b) initial value (2); and (c) initial value (3).

Figure 4.31: Synchronization error curves for different b22: (a) b22 = 24; (b) b22 = 30; and (c) b22 = 50.

where the state variable X = (x1, x2, . . . , xn)T ∈ Rn, and the continuous vector function F: Rn → Rn. The function F (X) is decomposed into

where ÃX is the linear part of F (X), and (X) is the nonlinear part of F (X). Then, ÃX is decomposed into

where A is a full rank constant matrix, and the real part of the eigenvalue is negative. Let

then eq. (4.96) can be rewritten as

Now, we take system (4.100) as the drive system and employ the projective synchronization control method. Then the response system is

where Y ∈ Rn is the n-dimensional state vector of the response system, and α is the proportional coefficient. If the synchronization error between drive system (4.100) and response system (4.101) is E = X – αY, then the synchronous error equation is

The real part of all eigenvalues of matrix A is negative, so synchronous error system (4.102) is asymptotically stable at the origin according to the stability criterion of linear system. That is, So the synchronization is achieved between response system (4.101) and drive system (4.100).

Applying the projective synchronization method to the simplified Lorenz chaotic system, the drive system becomes

and the response system becomes

where α is the proportional coefficient (α ≠ 0), and b is the synchronization control parameter. For the synchronization system comprising systems (4.103) and (4.104), the following synchronization theorem is proposed.

Theorem 4.9: For the projection synchronization system composed by drive system (4.103) and response system (4.104), if the synchronization control parameter b < min[10, 4c–24], then the synchronization error system is asymptotically stable at the origin point. That is, response system (4.104) will be synchronized with drive system (4.103) according to the proportional α.

Proof. According to the principle of projective synchronization, for the projection synchronization system comprising drive system (4.103) and response system (4.104), the full rank matrix A and H(X) are, respectively,

If λ is the eigenvalue of the matrix A, then we have

Obviously, one of the eigenvalues λ1 = –8/3 and the other two characteristic roots satisfy the equation

According to the Routh–Hurwitz criterion, if the synchronization control parameter satisfies b < min[10, 4c–24], then the real part of the root of eq. (4.106) is negative. The parameter of the system c ∈ [–1.59, 7.75], so we get b < –17.64. That is, when the control parameter of the synchronization system is b < –17.64, the real part of all eigenvalues of the matrix A of the synchronization error system is negative, and the synchronization error is It means response system (4.104) will be synchronized with drive system (4.103) according to the ratio α. ∎

On Simulink dynamic simulation platform, we set c = 5. According to Theorem 4.9, when b < –4, the synchronization will be achieved. Here we set b = –5 and α = –2, and system initial values x1(0) = 4.4356, x2(0) = 6.1771, x3(0) = 7.2330; y1(0) = 2.0883, y2(0) = 0.4535, y3(0) = –5.8578. The error convergence curve, the evolution of the attractor, and variable of the chaotic synchronization system are shown in Figure 4.32, where the synchronization error is defined by Figure 4.32(a) shows that the two chaotic systems with different initial values can achieve the projective synchronization at about 7.0 s, and the dynamic characteristics of the synchronization is good. Figure 4.32(b) shows that the attractor of the response system and drive system is inverse, and the size ratio is 2:1. According to Figure 4.32(c), we can see that the response system variable y3 is synchronized with the drive system variable x3 according to the projection ratio.

Figure 4.32: Projective synchronization between systems (4.103) and (4.104): (a) synchronization error curve; (b) attractors; and (c) waves of variables x3 and y3.

Figure 4.33: Synchronization error curves for different control parameter b: (a) b = –5; (b) b = –6; and (c) b = –15.

where X = (x1, x2, . . . , xn)T ∈ Rn is the state variable. AX is the linear part, and F (X) is the nonlinear part. Copy eq. (4.107), and add the controller U: R2n → Rn into the system, then the response system is

where Y = (y1, y2, . . . , yn)T ∈ Rn is the state vector. Set as the function matrix, and the error function of the synchronization system is E = X – Φ(t)Y. By designing the controller U (X, Y), we can get and then the generalized function projective synchronization is achieved between systems (4.107) and system (4.108).

Applying the generalized function projective synchronization method to the simplified Lorenz system, the drive system and response system are, respectively,

where c is the system parameter, and U = [u1, u2, u3]T is the nonlinear controller. We have the following synchronization theorem for the synchronization system comprising systems (4.109) and (4.110).

Theorem 4.10: For systems (4.109) and (4.110), the control law is U(X, Y) = Φ–1(t)[–(t)Y + F (X) – Φ(t)G(Y) + (A – B)X + DE], where Φ(t) is the projective function, and D = diag[d1, d2, d3] is the control parameter matrix. When the controller parameter satisfies d1 + d2 > c–10, d1d2–d1c + 10d2 > 240–30c, and d3 > –8/3, systems (4.109) and (4.110) can realize the function projective synchronization, that is, for any initial value.

Proof. For the projection synchronization system comprising drive system (4.109) and response system (4.110), the error function of the synchronization system is

where Φ(t) is the diagonal function matrix. Then the error system equation is

we

Substituting eqs (4.109) and

If the controller is U (X, Y) = Φ–1(t)[–Φ̇ (t)Y + F (X) – Φ(t)G(Y) + (A–B)X + DE], then we obtain

Construct Lyapunov function V(t) as

Then its differential is

Substituting eq. (4.114) into the above formula, we have

Set the control matrix D = diag[d1, d2, d3], when d1+d2 > c–10, d1d2–d1c+10d2 > 240– 30c, and d3 > –8/3, D–B is positive, and then ≤ 0 if and only if E = 0 for equality. By the Lyapunov stability theorem, the error system of the drive–response system is asymptotically stable at the origin. That is, The function projection synchronization is implemented. ∎

On Simulink dynamic simulation platform, we set c = 5. According to Theorem 4.10, when the control parameters are d1 =40, d2 =20, d3 = – 2, the synchronization will be achieved. Set the projective function Φ(t) = – 3 + 2 sin t, and the initial values x1(0) = 4.4356, x2(0) = 6.1771, x3(0) = 7.2330; y1(0) = – 1.8028, y2(0) = – 2.3247, y3(0) = – 2.2974. The synchronization error convergence curve, the evolution of the attractor, and variable of the chaotic synchronization system are shown in Figure 4.34. Figure 4.34(a) shows that the two chaotic systems with different initial values can achieve the projective synchronization within 4.8 s, and the dynamic characteristics of the synchronization are good. Figure 4.34(b) shows that the attractor of the response system and drive system is inverse, and the size ratio satisfies the projective function. According to Figure 4.34(c), we can see that the response system variable y3 is synchronized with the drive system variable x3 according to the projection function.

Figure 4.34: Projective synchronization between systems (4.109) and (4.110): (a) Synchronization error curve; (b) attractors; and (c) waves of variables x3 and y3.

where θ and δ are unknown parameter vectors in the drive system and the response system, respectively. f (X) and g(Y) are vector functions of state variables X and Y. F (X) and G(Y) are function matrices. U (X, Y) is the control law.

Supposing the projective function is Φ(t), and the error function of the synchronization system is E = X –Φ(t)Y, then the synchronization error system equation is

Due to eqs (4.118) and (4.119), we have

where M(X, Y) = f(X)–Φ(t)g(Y)+(A–B)X. Obviously, the adaptive function projective synchronization problem of drive system (4.118) and response system (4.119) is transformed into the stability problem of eq. (4.121). By designing the controller U(X, Y) and the adaptive law, to make the adaptive function projective synchronization between systems (4.118) and (4.119) can be realized and the unknown parameters can be identified.

Theorem 4.11: For the chaotic synchronization system with unknown parameter, which is composed of drive system (4.118) and response system (4.119), if the control function of the system is U(X, Y) = Φ–1(t)[M(X, Y) + F(X)θ̂ – Φ̇ (t)Y – Φ(t)G(Y)δ̂̇ + DE], where M(X, Y) = f(X) – Φ(t)g(Y) + (A – B)X, and D = diag[d1, d2, d3]. If the appropriate control parameters and the adaptive law of the system parameters are selected as = FT(X)E + Bθ, ˙δ̂ = –Φ(t)GT(Y)E + Bδ, where θ̂ = θ – θ̂, δ̄ = δ – δ̂̇. The adaptive function projective synchronization is realized between systems (4.118) and (4.119), and the unknown parameters are identified correctly. That is, for any initial values, we have = θ, and = δ.

Proof. Choose U(X, Y) =Φ–1(t)[M(X, Y) + F(X)θ̂ – Φ̇ (t)Y –Φ(t)G(Y)δ̂ + DE] as the controller, then the error system eq. (4.120) becomes

Constructing Lyapunov function

where θ̄ = θ – θ̂ , δ̄ = δ – δ̂, then its differential is

Set the adaptive law as = FT(X)E + θ̄ and = – Φ(t)GT(Y)E + δ̄, and substitute eq. (4.121) into eq. (4.124), then we have

Obviously, if we choose control parameters d1, d2, and d3, to make (D–B) positive definite, then we have V̇ ≤ 0. If and only if E = 0, θ̄= 0, δ̄ = 0 for equality. By the Lyapunov stability theorem, the error system of the drive–response system is asymptotically stable at the origin. That is, and the adaptive function projection synchronization is implemented. At the same time, when t→∞, we have θ̂→θ and δ̂→δ. That is, the unknown parameters are identified correctly. ∎

Remark 1: If A = B, f (⋅) = g(⋅), and F(⋅) =G(⋅), then the two chaotic systems are homogeneous systems, and vice versa they are heterogeneous systems. Therefore, the adaptive function projective synchronization theorem can be applied to both homogeneous and heterogeneous systems with unknown parameters.

Remark 2: If the parameters of the drive system or response system are known, using the above control method, the parameter adaptation law is removed, and the corresponding generalized function projective synchronization can be realized.

4.9.3.1Adaptive Function Projective Synchronization and Simulation for Driving System with Unknown Parameters

Applying the adaptive function projective method to the simplified Lorenz system, the drive system and response system are, respectively,

where c is the system parameter. C = [θ1, θ2, θ3]T is the unknown parameter of the drive system. U = [u1, u2, u3]T is the nonlinear controller. If we set the projective function as Φ(t) = –3 + 2sin(t), according to Theorem 4.11, the control law and the parameter adaptive law of the synchronization system consisting of systems (4.126) and (4.127) are

There is a following inference for the synchronization system consisting of systems (4.126) and (4.127).

Inference 4.2 For the adaptive function projective synchronization system comprising drive system (4.126) and response system (4.127), when the controller parameters satisfy d1 + d2 > c–10, d1d2–d1c + 10d2 > 240–30c, and d3 > –8/3, the adaptive function projective synchronization is achieved between systems (4.126) and (4.127). That is, for any initial values. (Proof omitted.)

On Simulink platform, we set c = 5. According to Inference 4.2, when the control parameters are d1 =40, d2 =20, and d3 = – 2, the synchronization will be achieved. Set the projective function Φ(t) = – 3 + 2 sin(t), and the initial values X(0) = [4.4356, 6.1771, 7.2330]T, Y(0) = [0.5431, 0.0995, 2.8096]T, θ̂1(0) = – 1, θ̂2(0) = – 1. The synchronization error convergence curve, the evolution of the attractor, and variable waves of the chaotic synchronization system are shown in Figure 4.36. Figure 4.36(a) shows that the two chaotic systems with different initial values can achieve the projective synchronization in 4 s, and the dynamic characteristics of the synchronization are good. Figure 4.36(b) shows that the attractor of the response system and drive system is inverse phase, and the size ratio satisfies the projective function. Figure 4.36(c) shows that in a relatively short period of time (about 2 s), the estimated parameters θ̂1 and θ̂2 converge to the target value and realize the identification of unknown parameters.

Figure 4.36: Projective synchronization between systems (4.126) and (4.127): (a) Synchronization error curve; (b) attractors; and (c) waves of the estimated parameters θ̂1 and θ̂2.

Figure 4.37: Synchronization error curves for different control parameter d1.

where θ = [θ1, θ2, θ3]T and δ = [δ1, δ2, δ3]T are unknown parameters of the chaotic systems. U = [u1, u2, u3]T is the nonlinear controller. If the projective function is Φ(t) = –3 + 2 sin(t), then according to Theorem 4.11, the control law and parameter adaptive law of the synchronization are, respectively,

On Simulink platform, we set the unknown parameter c = 5. It means the true value of the estimated parameter is θ = δ = [0,4, 5]T. If the initial conditions of the synchronization system are X(0) = [4.4356, 6.1771, 7.2330]T, Y(0) = [–0.5431, 0.0995, –2.8096]T, (0) = [–1, –1, 0]T, δ̂(0) = [–2, –2, 0]T, respectively, and d1 = d2 = d3 = 5, we obtain the synchronization error curves, attractors, and error curves of the estimated parameters as shown in Figure 4.38. Figure 4.38(a) shows that the two chaotic systems with different initial values and unknown parameters can achieve the function projective synchronization in about 2.5 s, and it has oscillation attenuation characteristic. Figure 4.38(b) shows that the attractor of the response system and drive system is inverse, and the size ratio satisfies the projective function. From Figure 4.38(c) and (d), it can be seen that in a short time, the error of the estimated parameters θ̂1, θ̂2 and δ̂̇1, δ̂̇2 converges to zero, which indicates that the unknown parameters are identified. The results also show that the larger the control parameter di is, the better the synchronization performance is, which is important for secure communication application.

Figure 4.38: Projective synchronization between systems (4.130) and (4.131); (a) synchronization error curve; (b) attractors; (c) error curves for estimated parameters ^θ1 and θ̂2; and (d) error curves for estimated parameters δ̂1 and δ̂2.

where θ = [θ1, θ2, θ3]T and δ = [δ1, δ2, δ3]T are the unknown parameters of the two systems, and U = [u1, u2, u3]T is the nonlinear controller. If we set the projective function as Φ(t) = –3 + 2 sin(t), according to Theorem 4.11, the control law and parameter adaptive law of the synchronization system are

For simulation, we set the unknown parameter of the simplified Lorenz system c = 5, which means that the true value of the estimated parameter is θ = [0,4,5]T. At the same time, we choose the true value of the unknown parameter of the Chen system δ = [25, 28, 1/3]T. If the initial conditions of the system and unknown parameter are X(0) = [4.4356, 6.1771, 7.2330]T, Y(0) = [–0.62, –0.4261, –4.0838]T, θ̂(0) = [–1, –1, 0]T, δ(0) 2, 2, 2]T, and d1 d2 d3 5, then we obtain the synchronization error curves, attractors, and error curves of the estimated parameters as shown in Figure 4.39. Figure 4.39(a) shows that the two chaotic systems with different initial values and unknown parameters can achieve the function projective synchronization in about 2 s, and it has oscillation attenuation characteristic. Figure 4.39(b) shows that the attractor of the response system and drive system is inverse phase, and the size ratio satisfies the projective function. From Figure 4.39(c) and (d), we know that in a short time, the error of the estimated parameters θ̂1, θ̂2 and δ̂̇1, δ̂̇2, δ̂̇3 converges to zero, which indicates the unknown parameters are identified. The results also show that the larger the control parameter di is, the better the synchronization performance is. That is, the setup time of the synchronization is shorter.

Figure 4.39: Projective synchronization between systems (4.135) and (4.136): (a) synchronization error curve; (b) attractors; (c) error curves for estimated parameters θ̂and θ̂2; and (d) error curves for 1 estimated parameters δ̂1, δ̂2, and δ̂3.