D.1 Problems for Chapter 4: Parsers
D.1.1 Top-down Parsing
Problem 1.1.1 Is this a LL(1) grammar?
0. S‘–> S# 3. A –> abS
1. S –> aAa 4. A –> c
2. S –> empty
First of all, we note that it is a CFG (single NT's on the LHS of all rules), it has ∊-rule, there is no left recursion. So it is a candidate for being an LL(1) grammar. In FIRST(A), the RHS are disjoint, so we need test only productions from S.As one of the S productions is an ∊-rule, we find the FOLLOW(S)= {#,a}. Now, FIRST(aAaFOLLOW(S)) ∩ FIRST(∊FOLLOW(S)) = {a}∩{#, a}≠ Ø. Therefore, this is not an LL(1) grammar.
For example, consider a string “aaba…#”. The productions for this strings can be: S# →aAa#→aabSa … #.
Now at this stage, we do not know whether to use rule 1 or rule 2 for the next substitution for S, looking at the look-ahead symbol ‘a’.
Problem 1.1.2 Verify that the following grammar is LL(1).
0. S –> A# 3. B –> aB 5. C –> cC
1. A –> Bb 4. B –> empty 6. C –> empty
2. A –> Cd
We note that it is a CFG; there is no left recursion, but has ∊-rules. So it is an LL(1) candidate grammar.
Verifying for:
A: there are no ∊-rules, so we apply simple test:
FIRST(Bb)∩FIRST(Cd) = {a, b}∩{c, d} = Ø, OK.
B: FOLLOW(B) = {b}, FIRST(aBb)∩FIRST(b)= Ø, OK.
C: FOLLOW(C) = {d}, FIRST(cCd)∩ FIRST(d)= Ø, OK.
Therefore, the grammar is LL(1).
Problem 1.1.3 Obtain the parsing function for the following LL(1) grammar with ∊-rules.
0. S’ –> S# 3. A –> c
1. S –> aSA 4. A –> empty
2. S –> empty
FOLLOW(S) = {c, #},FOLLOW(A) = {#}
FIRST(aSA) = {a}, FIRST(c) = {c}
Verifying for:
A: FIRST(c)∩FOLLOW (A) = {c}∩{#} = Ø, OK.
S: FIRST(aSA)∩FOLLOW(S) = {a}∩{c, #} = Ø, OK.
The parsing function is given in Table D.1.
Problem 1.1.4 Verify that the following grammar is LL(1) and prepare the table of parsing function.
1. S –> aABC 4. B –> a 7. C –> empty
2. A –> a 5. B –> empty 8. D –> c
3. A –> bbD 6. C –> b 9. D –> empty
Verifying for:
A: FIRST(a)∩FIRST(bbD) = Ø, OK.
B: FIRST(a)∩FOLLOW(B) = {a}∩FIRST(C) = {a}∩{b} = Ø, OK.
C: FIRST(b)∩FOLLOW(C) = {b}∩{#} = Ø, OK.
D: FIRST(c)∩FOLLOW(D) = {c}∩{#, b, a} = Ø, OK.
Therefore, it is an LL(1) grammar.
The parsing function is given in Table D.2.
Problem 1.1.5 Is the following grammar LL(1)? If so, build the parsing function.
1. S –> aSA 3. A –> bS
2. S –> empty 4. A –> c
It is a CFG, no left recursion, but an ∊-rule, so possibly an LL(1) grammar.
FOLLOW(S) = {b,c}.
Testing for:
S: FIRST(aSA)∩FOLLOW(S)= Ø, OK.
A: FIRST(bS)∩FIRST(c) = Ø, OK.
Therefore, it is an LL(1) grammar.
The parsing function is given in Table D.3.
Problem 1.1.6 Verify that the following grammar is LL(1).
1. V –> S# 4. A –> empty
2. S –> AB 5. B –> b
3. A –> a 6. B –> empty
It is a CFG, no left recursion, with ∊-rules, so possibly an LL(1) grammar.
FOLLOW{A) = {b,#}, FOLLOW(B)= {#}. Verifying for:
A: FIRST(a)∩FOLLOW (A)= Ø, OK.
B: FIRST(b)∩FOLLOW(B)= Ø, OK.
Therefore, the grammar is LL(1).
Problem 1.1.7 Consider the following grammar RE over {a, b}, with union ‘+’ and star ‘*’ operations.
1. E –> TE’ 7.F –> PF’ 13. P –> empty
2. E’ –> +E 8.F’ –> *F’
3. E’ –> empty 9.F’ –> empty
4. T –> FT’ 10.P –> (E)
5. T’ –> T 11.P –> a
6. T’ –> empty 12.P –> b
Compute the FIRST and FOLLOW sets. Then show that the grammar is LL(1).
Construct a parsing table, or, convert for a RDP and construct RDP.
FIRST(TE’)= {(, a, b, +, *, empty}, FIRST(FT) = {(, a, b, *, empty}
FOLLOW(E)= {)}, FOLLOW(E’)= {)}, FOLLOW(T)= {), +},
FOLLOW(F’) = {(, a, b, empty},
Testing for LL(1):
For E’: FIRST(+E)∩FOLLOW(E’) = Ø, OK.
For T’: FIRST(T)∩FOLLOW(T’)= {(, a, b, *, empty}∩{), +} = Ø, OK.
For F’: FIRST(*F’)∩FOLLOW{F’)= Ø, OK.
Therefore, the grammar is an LL(1).
Parsing table:
Conversion of the grammar for RDP: we have to convert it to extended BNF.
1. E -> T {+T} 4. P -> (E) | a | b | empty
2. T –> F {F}
3. F –> P {*P}
A skeleton RDP for the grammar:
pE(){pT(); while(next() == ’+’){pplus(); pT();}}
pT(){pF(); while(strchr(next(),"(ab+"){pF();}}
pF(){pP(); while(next() == ‘*’{past();pP();}}
pP(){if(next() == ‘(’){plp(); pE(); prp();}
else if(next() == ‘a’) pa();
else if(next() == ‘b’) pb();
else error(“unexpected token");
}
pplus(){if(symbol() != ‘+’) error("+ expected");}
past(){if(symbol() != ‘*’) error("* expected");}
plp(){if(symbol() != ‘(’) error("(expected");}
prp(){if(symbol() != ‘)’) error(") expected");}
pa(){if(symbol() != ‘a’) error("a or b expected");}
pb(){if(symbol() != ‘b’) error("a or b expected");}
D.1.2 Bottom-up Parsing
Problem 1.2.8 Consider the following grammar defining a list structure:
1. S –> a 4. T –> T,S
2. S –> n 5. T –> S
3. S –> (T)
Here ‘n’ stands for an empty list. An empty list is still a list, different from an empty production.
Give leftmost and rightmost derivations for (a,(a,a)) and indicate the handle at each stage in the rightmost derivation. Then develop an LR(0) machine for this grammar. Identify inadequate states, if any, and check if SLR(1) resolution is possible.
Leftmost derivation:
S → (T) → (T, S) → (S, S) → (a, S) → (a, (T)) → (a, (T, S)) → (a, (S, S)) → (a, (a, S)) → (a, (a, a))
Rightmost derivation – handles are underlined:
![]()
The LR(0) machine is:
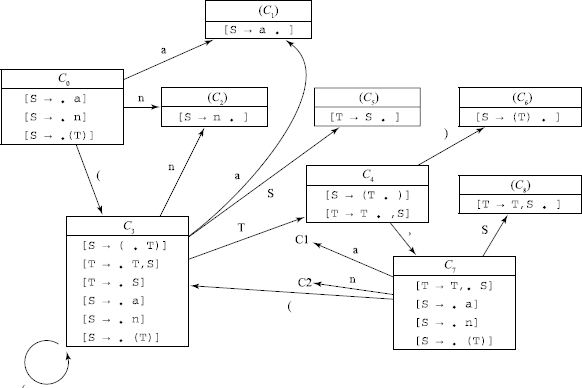
Seemingly, there are no inadequate states.
Problem 1.2.9 For the grammar given below, find the viable prefixes for the sentential forms E + a * a# and E + P˄(a + a)#.
1. s –> E# 4. T –> p 7. p –> p* F
2. E –> T 5. T –> P ˄ T 8. F –> a
3. E –> E + T 6. P –> F 9. F –> ( E )
For the sentential form E + a * a#: the derivation is: ![]() then the viable prefixes are: E, E+, E + a.
then the viable prefixes are: E, E+, E + a.
For sentential form E + P ˄(a + a)#: The derivation is:![]() then the viable prefixes are: E, E+, E + P, E + P˄, E + P˄(, E + P˄(a.
then the viable prefixes are: E, E+, E + P, E + P˄, E + P˄(, E + P˄(a.
Problem 1.2.10 Consider the grammar:
1. S –> E# 4. X –> yX 6. Y –> yY
2. E –> wX 5. X –> z 7. Y –> z
3. E –> xY
Compute the LR(0) machine. Does it have any inadequate states? Show how will an example string wyyz# be parsed.
The LR(0) machine is:
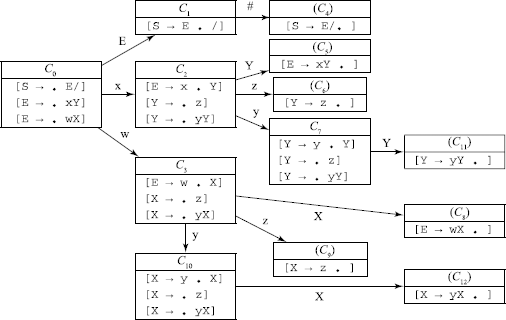
The machine does not have any inadequate states. The parsing and acceptance of the example string wyyz# is shown in Table D.5.
Table D.5 Parsing of an example string wyyz#
| Stack | Input | Handle, rule |
|---|---|---|
| 0 | wyyz# | |
| 0w3 | yyz# | |
| 0 w3 y7 | yz# | |
| 0 w3 y7 y7 | z# | |
| 0 w3 y7 y7 z8 | # | X → z, 5 |
| 0 w3 y7 y7 X9 | # | X → yX, 4 |
| 0 w3 y7 X9 | # | X → yX, 4 |
| 0 w3 X4 | # | E →wX |
| 0 E1 | # | |
| 0 E1 # | S →E# | |
| 0 S | Accept |
Problem 1.2.11 Develop an LR(0) machine for the following grammar. Does it have any inadequate states?
1. S –> E# 4. X –> aX 7. Y –> c
2. E –> X 5. X –> b
3. E –> Y 6. Y –> aY
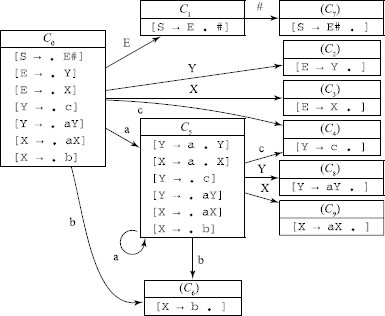
From the LR(0) machine, it is seen that there are no inadequate states.
Problem 1.2.12 For the grammar given in Problem 9, compute the LR(0) machine, show that it is an SLR(1) grammar, prepare an SLR(1) parsing table, and trace of parse of a + a ˄ (a + a)#.
The LR(0) machine is:
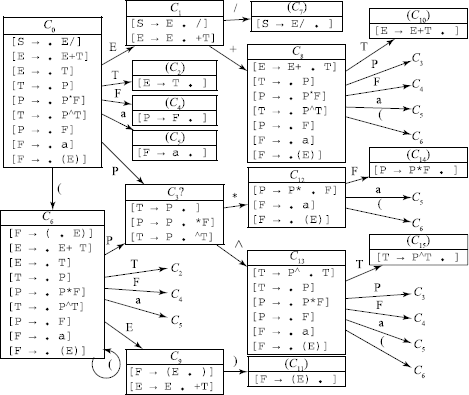
There is only one inadequate state 3, where we have Shift/Reduce conflict – shift on ‘*’ and ‘˄‘, reduce to T.
To show that this is an SLR(1) grammar, we have to construct the FOLLOW(T) set.
which is disjoint with respect to {*, ˄}, so we have an SLR(1) grammar.
To compute the f() and g() functions, we need the following FOLLOW sets:
FOLLOW(E) = {+, ), /}, while reducing by rules 2, 3;
FOLLOW (T) = {+, ), /}, while reducing by rules 4, 5;
FOLLOW(P) = {*, ˄+, ), /}, while reducing by rules 6, 7;
FOLLOW(F) = {*, ˄+, ), /}, while reducing by rules 8, 9.
The SLR(1) parse functions are given in Table D.6.
Table D.7 shows the trace of parse of an input string a + a ˄ (a + a)/
Table D.7 Trace of parse of a + a ˄ (a + a)/ – Problem 12
| Stack | Input | Action and rule |
|---|---|---|
| 0 | a+a ˄ (a+a)/ | Shift |
| 0 a5 | +a ˄ (a+a)/ | Reduce by 8 |
| 0 F4 | +a ˄ (a+a)/ | Reduce by 6 |
| 0 P3 | +a ˄ (a+a)/ | Reduce by 4 |
| 0 T2 | +a ˄ (a+a)/ | Reduce by 2 |
| 0 E1 | a ˄ (a+a)/ | Shift |
| 0 E1 + 8 | ˄ (a+a)/ | Shift |
| 0 E1 + 8 a5 | ˄ (a+a)/ | Reduce by 8 |
| 0 E1 + 8 F4 | ˄ (a+a)/ | Reduce by 6 |
| 0 E1 + 8 P3 | (a+a)/ | Shift |
| 0 E1 + 8 P3 ˄ 13 | a+a)/ | Shift |
| 0 E1 + 8 P3 ˄ 13(6 | a)/ | Shift |
| 0 E1 + 8 P3 ˄ 13(6 a5 | +a)/ | Reduce by 8 |
| 0 E1 + 8 P3 ˄ 13(6F4 | +a)/ | Reduce by 8 |
| 0 E1 + 8 P3 ˄ 13(6P3 | +a)/ | Reduce by 8 |
| 0 E1 + 8 P3 ˄ 13(6T2 | +a)/ | Reduce by 2 |
| 0 E1 + 8 P3 ˄ 13(6E9 | +a)/ | Shift |
| 0 E1 + 8 P3 ˄ 13(6E9 + 8 | a)/ | Shift |
| 0 E1 + 8 P3 ˄ 13(6E9 + 8a5 | )/ | Reduce by 8 |
| 0 E1 + 8 P3 ˄ 13(6E9 + 8F4 | )/ | Reduce by 6 |
| 0 E1 + 8 P3 ˄ 13(6E9 + 8P3 | )/ | Reduce by 4 |
| 0 E1 + 8 P3 ˄ 13(6E9 + 8T10 | )/ | Reduce by 3 |
| 0 E1 + 8 P3 ˄ 13(6E9 | )/ | Shift |
| 0 E1 + 8 P3 ˄ 13(6E9)11 | / | Reduce by 9 |
| 0 E1 + 8 P3 ˄ 13E4 | / | Reduce by 6 |
| 0 E1 + 8 P3 ˄ 13T15 | / | Reduce by 5 |
| 0 E1 + 8 T10 | / | Reduce by 3 |
| 0 E1 | / | Shift |
| 0 E1/7 | Reduce | |
| 0 S | Accept |
Problem 1.2.13 Consider the following grammar.
1. S –> aAd#
2. S –> bAc
3. S –> aec
4. A –> e
Obtain it's LR(0) machine and LALR(1) LA sets for the inadequate states if any.
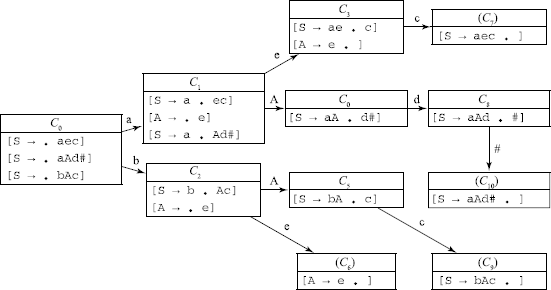
The only inadequate state is 3, which has Shift/Reduce conflict. We find that FOLLOW(A)∩{c} = {d, c}∩{c} ≠ Ø.
Therefore, SLR(1) technique cannot be used. We should then find the look-ahead set (LA) for A when the FSM is in state 3, LA(3, A) = {d}.
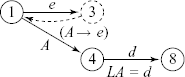
This gives us LA(3, A)∩{c} = {d}∩{c} = Ø; thus, LALR(1) resolution is possible.
Problem 1.2.14 Consider the following grammar.
1. S –> A# 4. B –> cC
2. A –> bB 5. B –> cCe
3. A –> a 6. C –> dA
Is it an LALR(1) grammar? If so, obtain the LA sets for the inadequate states if any.
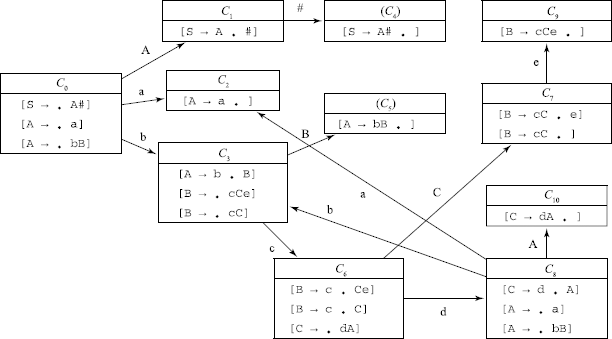
The only inadequate state is 7, with Shift/Reduce conflict on B.So we find
so it is not an SLR(1) grammar.
Then in order to check if LASL(1) can be applied, we find LA(7,B).Suppose we have reduction at state 7, then two symbols ‘C nd ‘c’ are unstacked and state 3 is uncovered.On taking a transition on ‘B’ from here, we arrive at state 5, where another reduction takes place on ‘b’‘B’ and state 0 is uncovered. Taking transition ‘A’ from there we arrive at state 2, where the look-ahead symbol is #. Therefore LA(7,B)= {#} and as this is disjoint with {e}, we can apply LALR(1) resolution for the inadequate state 7.





