▶ 7.3 Computer-Based Encryption
Modern, computer-based encryption algorithms are far more complicated than the older mechanical or hand-operated ciphers. Their sophisticated design and operation foils traditional known-plaintext and known-ciphertext attacks. In general, the only practical attack is to try to guess the key through trial and error. This is the same as trial-and-error attacks on passwords, except that we try harder to avoid biases in key selection. A realistic, general-purpose trial-and-error attack must examine a crypto key’s entire search space.
The Data Encryption Standard
In 1975, the U.S. government unveiled the algorithm that became the Data Encryption Standard, commonly called DES. The algorithm was quickly adopted by the banking industry and was the foundation of our modern electronic banking networks, from electronic funds transfers to ATMs. The DES algorithm allowed a very large number of keys:
72,057,594,037,927,900: over 72 quadrillion keys (7 × 1016)
DES, like other modern encryption algorithms, uses a binary integer as its key. We talk about the size of such keys in terms of bits: the DES keys were 56 bits long. Thus, the key could be any number between zero and 256 or 72 quadrillion.
As soon as DES was announced, however, researchers argued that the key size was too small. At the time, DES seemed uncrackable, but Moore’s law suggested that trial-and-error attacks might become practical within decades. Less than 20 years later, researcher David Winer proposed the design of a $1 million machine that would crack one key every 3.5 hours. The machine was never built.
In 1997, however, a collection of volunteers on the internet worked together to crack a DES message by trial and error. The effort, nicknamed DESCHALL, used a distributed collection of tens of thousands of computers. It found the key in 5 months. The next year, a larger group cracked another DES message in 39 days. Finally, in 1998, the EFF unveiled their DES Cracker. At $250,000, the machine could crack a DES key in an average of less than 5 days, guessing over 92 billion keys per second.
Today, off-the-shelf computing clusters from Pico Computing and SciEngines can crack DES keys even faster. The CloudCracker website claims to crack individual DES keys in about 23 hours using a Pico Computing cluster.
The Advanced Encryption Standard
In 2002, the U.S. government introduced the Advanced Encryption Standard (AES) as the replacement for DES. AES keys come in three different sizes (TABLE 7.1). The smallest AES key is over twice as large as a DES key. The table also shows how long it would take to crack different-sized AES keys if a modified DES Cracker could search for the keys at the same rate. A modern cracker would be significantly faster due to technology improvements. Even so, the cracking time for the smallest AES key vastly exceeds trillions of years (1012 years).
TABLE 7.1 AES Key Sizes and Average Cracking Times |
||
|---|---|---|
Number of Bits in the Key |
Number of Keys |
Average Time Required by a DES Cracker-Style Device |
128 |
3 × 1038 |
6 × 1019 years |
192 |
6 × 1057 |
1 × 1039 years |
256 |
1 × 1077 |
2 × 1058 years |
The average cracking time is the time it takes to search half of the total search space. This is because there are no biases in a well-chosen encryption key. Unlike passwords, we shouldn’t assume that there will be biases when selecting crypto keys.
Digital cryptography succeeds when we give the attacker too many possible keys to test in a practical amount of time. We do this by using a key size that is large enough to present the attacker with too many alternatives. This is why DES is obsolete.
This also is why “exportable” software produced in the 1990s is obsolete. U.S. export laws classify encryption as a weapon of war and restrict its export. Until the end of the century, U.S. export laws effectively limited encryption keys to 40 bits in length. University researchers could crack such keys in a week using 1990s-era campus computing resources.
Predicting Cracking Speeds
According to legend, the NSA dedicates a great deal of computing power to the problem of cracking other countries’ cipher keys. The precise numbers are highly classified, so we can’t accurately estimate how large a key they can crack. We do, however, have hard information about how quickly various efforts could cover a search space while cracking 56-bit DES keys:
■ DESCHALL on one desktop PC: 1 million keys/second, 1997
■ DES Cracker: 92 billion keys/second, 1998
■ Pico Computing/CloudCracker: 870 billion keys/second, 2012
If we apply Moore’s law, we can estimate future cracking speeds that use similar levels of effort. Moore’s law predicts that computing power doubles every 18 months; in other words, the number of keys per second should double every 18 months. If we consult Table 7.1, the time required should reduce by half every 18 months.
For example, if a desktop key cracker could try 1 million keys/second in 1997, how many can it crack per second in 2015? Here is the calculation:

Moore’s law estimates that computing power increased by a factor of over 131,000 in 17 years. Although this yields a significant improvement, it only makes a tiny dent in the strength of AES keys. Let’s assume we can crack AES keys as quickly as DES keys (we can’t) and that performance improves another factor of eight, giving us a million-fold improvement in performance. Now, apply that to the time required to crack the smallest AES key in Table 7.1. The performance improvement reduces the attack time to 1013 years, which remains impractical.
7.3.1 Exclusive Or: A Crypto Building Block
Computers process all data in a binary format; everything is rendered into numbers that are themselves formatted into rows of zeros and ones. If a cipher operates in terms of fundamental symbols, then a binary cipher encrypts data by substituting zeros and ones.
Binary encryption began with the work of Gilbert Vernam, an engineer at Western Electric in the 1920s. Vernam’s goal was to provide encryption for digital teletype traffic. Although teletypes were used as early computer terminals (as in Figure 6.4), the earliest commercial models appeared around 1910.
Teletypes were electromechanical devices that converted a typist’s keystrokes into a series of zeros and ones in a standard, well-known code. At the receiving end, the teletype would type the appropriate character, typewriter style, upon receiving a particular series of zeros and ones.
If two teletypes used the same code, one could type out any message it received from the other. The standard codes made it easy to construct a large teletype network, because compatible teletypes could transmit messages to each other. On the other hand, it also meant that anyone with the right teletype could print out any message traveling on the teletype network.
Vernam needed a way to encrypt teletype data being sent by customers who needed to keep their traffic secret. Vernam developed the simple bit-by-bit substitution cipher shown in FIGURE 7.8. He encrypted the message by adding each bit in the message to one bit taken from the key stream and discarding any overflow.
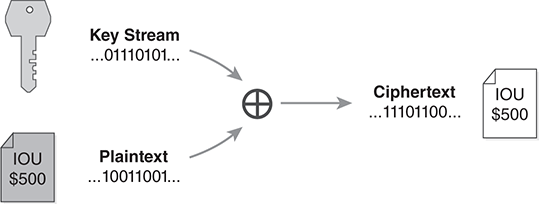
FIGURE 7.8 Vernam’s exclusive-or cipher.
Vernam’s bit combination operation is sometimes called a “half add.” More often today we call the operation exclusive or, which we abbreviate “xor” or denote with the ⊕ symbol. The recipient decrypts the message by applying the same xor operation bit by bit using the same key stream.
If we look at how xor works, we see that it produces a “0” when the data and the key stream match (both 0 or both 1). It produces a “1” when the data and the key stream differ. In the following, we encrypt a series of bits with a key stream using xor. Then we decrypt it with the same key stream:
PLAINTEXT: 00110101
Key Stream: 0101100
CIPHERTEXT: 0011001
Key Stream: 0101100
PLAINTEXT: 00110101
FIGURE 7.9 shows the effect of Vernam’s xor encryption on a binary image. The plaintext image contains the message SEND CASH handwritten in a two-dimensional field of 0 bits (white) and 1 bits (black). We show the key stream as another binary image encoded the same way. When we combine the plaintext and key stream bit by bit using xor, we produce the ciphertext shown on the right.

FIGURE 7.9 Encrypting an image with xor.
Courtesy of Dr. Richard Smith.
The encryption seems to totally disguise the message SEND CASH. However, the key stream and the ciphertext look vaguely similar. This is because we use such a simple transformation. The dark parts of the plaintext yield exact copies of the key stream, while the white parts yield a mirror image of the key stream. The plaintext remains secret as long as we keep the key stream secret, too.
Vernam found that the cipher worked best if they avoided repeating the key stream. As long as the senders did not use the exact same key stream to encrypt additional bits they sent, attackers had a hard time cracking the encryption. In fact, the encryption was easy to attack if they reused the key stream; we will look at this in Section 8.2.
7.3.2 Stream Ciphers: Another Building Block
Vernam’s cipher is the basis of the modern stream cipher (FIGURE 7.10). The heart of the cipher is an algorithm to generate the key stream, a hard-to-predict sequence of binary ones and zeros. The algorithm generates different sequences depending on the secret key. The sequence is combined with the plaintext to produce the ciphertext. The recipient uses the same key to generate a matching key stream, and then applies xor to the message and key stream to recover the plaintext.

FIGURE 7.10 Stream cipher.
The key stream algorithm is the heart of every effective stream cipher. If there is a way to guess the key or the key stream, the attacker can decrypt the ciphertext. Typically, a key stream algorithm uses the encryption key to generate a hard-to-guess sequence of bits.
If an attacker knows part of the message’s plaintext, the attacker can extract that part of the key stream. Therefore, the key stream itself should not reveal the key.
Methods to Generate a Key Stream
Recall the properties of the one-way hash we examined in Section 6.2.1. The hash output never reveals information about its input. If we were to run the encryption key through a one-way hash, the resulting hash value would not itself reveal the encryption key.
If we run that result through the hash, we get a new and different hash value. This is because the hash output should always be different from its input. Moreover, there’s no easy way to invert the hash output and derive the input that produced it. Thus, we can generate a hard-to-invert data sequence with a one-way hash (FIGURE 7.11).
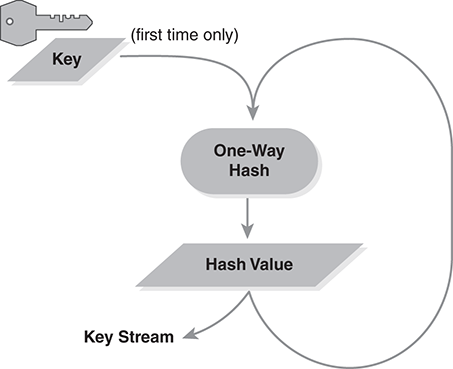
FIGURE 7.11 Key stream from a one-way hash.
The algorithm works as follows. First, we take the secret key we want to use and we hash it. That yields the first hash value, which serves as the first group of bits in our key stream. We then feed the hash value back through the one-way hash (a “feedback” loop) to generate another hash value. This serves as the next group of bits in our key stream. If the hash generates 256 bits, then we must run the one-way hash again every time we need another 256 bits of key stream.
Unfortunately, there is a serious problem with this key stream. If attackers know part of the plaintext, they can use it to find that part of the key stream. If they know enough plaintext to recover one of the hash values, they can feed it back to the one-way hash to produce the rest of the key stream. This flaw allows them to start from a part of the message they already know and decrypt the rest of the message. This is a “known plaintext” attack.
Many documents contain predictable blocks of text near the beginning. For example, an encrypted legal document from the firm “Dewey, Cheatem, & Howe” certainly contains the firm’s name somewhere near the beginning. An attacker could guess part of the key stream by applying xor to the text “Dewey, Cheatem, & Howe” and to the ciphertext. This attack requires some trial and error, but it eventually succeeds if they guess enough plaintext.
Thus, the key stream algorithm in Figure 7.11 does not produce a secure cipher. The cipher is vulnerable to a known plaintext attack.
An Improved Key Stream
We can improve the cipher by hashing the secret key along with the previous hash value in each cycle, as shown in FIGURE 7.12.

FIGURE 7.12 Improved key stream from a one-way hash.
The algorithm starts by using the key itself as the hash input. If an attacker knows some of the plaintext, he can still find that part of the key stream. Without the secret key, however, the attacker can’t generate the next word in the key stream.
Although this key stream algorithm is better than the simple one-way hash, it’s still not a good choice. One-way hash functions aren’t really designed to generate good key streams.
A better and more efficient choice would be to use a key stream generator designed for a stream cipher. For many years, a popular choice was Rivest’s Cipher 4, also known as RC4. Written in 1987 by MIT professor Ron Rivest, it has been a traditional choice in web browsers to protect messages to secure websites. RC4 requires a very simple program and it generates the key stream in 8-bit bytes. Unfortunately, RC4 has not stood the test of time. (See Section 9.2.2.)
7.3.3 Key Stream Security
When we look at the mishmash of data that makes up an encrypted message (like the right-hand block of Figure 7.9), cryptanalysis seems like an impossible task. To crack a stream cipher, we must deduce the contents of the key stream. Some key streams are relatively easy to crack, while others are very difficult. Some are impossible to crack in practice, and some are impossible both in theory and in practice. It all depends on the amount of randomness, or entropy, in the key stream.
When we use a key stream algorithm, there is a definite limit on the entropy in the key stream. Specifically, the entropy in the key stream is limited to the entropy in the secret key we use. This is the natural result of using a fixed procedure, an algorithm, to generate numerical results. The scope of possible outputs is naturally limited by the range of initial inputs.
Thus, in a worst case, we can always reproduce a message’s key stream if we know what key stream algorithm they used and we try all possible keys. This is why the DES key size was controversial. When DES was introduced, it seemed impractical to crack a 56-bit key. However, Moore’s law made it clear that key cracking would get better over the next few decades. As computer speeds increased, so did the demands for an improved, U.S. government standard cipher with a larger key.
RC4 Biases
Unfortunately, a large key is not always enough to ensure security. Few crypto designers use RC4 in modern systems even though it is often used with a 128-bit key. As researchers studied RC4, they found “biases” in its behavior. (See Section 9.2.2.)
Pseudorandom Number Generators
Our key stream generators, whether they are one-way hashes or RC4, serve as PRNGs. Most programming libraries include a PRNG function, usually named “random()” or “rand()”. Even Excel has such a function. What would happen if we used such a function to generate our key stream?
Mechanically, it seems like a practical approach. These PRNGs produce their results from an initial “seed” value. There is a function or an optional parameter that initializes the seed value. When the seed is set to a specific value, we get a predetermined sequence of pseudorandom outputs.
Remember that PRNGs are intended for games of chance, simulation, or statistical analysis. The actual sequence of values doesn’t necessarily matter to these applications as long as they are “statistically random.” In fact, some systems use a built-in, constant value for the seed. This yields the exact same sequence of pseudorandom numbers every time a program is run. This works badly for games of chance. Other systems initialize the seed automatically to a changing value like the system clock. If the system uses an unchanging “default” seed value, the game programmer must explicitly set the seed to some changing value, like the system time.
To create a stream cipher with the PRNG, we use the secret key as the seed value. Each time we call the PRNG, we use the resulting output as the next group of bits in the key stream. We xor the bits in the plaintext to bits from the key stream and emit the result as the ciphertext.
At the receiving end, we must run the same PRNG with the same secret key as the seed value. This generates the same key stream, which we xor with the ciphertext. This recovers the plaintext.
Technically, this produces a cipher. Unfortunately, it is unlikely to be a trustworthy cipher. A series of random numbers can be perfectly sufficient for statistical purposes but still exhibit biases that disclose other parts of the key stream, or even the key itself. Some PRNGs explicitly use their previous output value as the seed for producing the next value. This is the same as the key stream generator in Figure 7.11, and it suffers from the same weakness. A known plaintext attack could recover part of the key stream and use it to generate the rest of the key stream.
The Effects of Ciphertext Errors
Data storage is never perfect. As a file sits in one place on a drive or as it moves from one device to another, we risk data errors. The storage hardware and the operating system try hard to detect such errors, but this doesn’t always work.
Potential errors pose an important question as we decrypt the data: How will a broken bit in the ciphertext affect the plaintext? Fortunately, the damage is limited in stream ciphers; if an error inverts a ciphertext bit, we see the same bit inverted after we decrypt the plaintext.
On the other hand, this poses an integrity risk to our ciphertext. An attacker can change any bit in the plaintext by changing the corresponding ciphertext bit. If the text contains some sort of promise, invoice, or IOU, the attacker can make the amounts higher or lower without detection. Thus, the stream cipher doesn’t protect the data’s contents; it only protects its secrecy. We need to use a separate mechanism to detect changes to the ciphertext. We will look at that problem in Chapter 8.
7.3.4 The One-Time Pad
There is, however, a way to make this encryption theoretically impossible to crack: the one-time pad. While a stream cipher uses a key stream algorithm to generate its key stream, a one-time pad uses a truly random stream of bits for its key stream. The sender and recipient must share that key stream in secret. They then use the key stream with the xor operation to encrypt and decrypt messages.
When properly used, it is mathematically impossible to crack a message encrypted by a one-time pad. This was first described by Claude Shannon in the 1940s as part of his development of information theory. A one-time pad is impossible to crack because knowledge of the ciphertext does not reduce uncertainty about the contents of the original, plaintext message.
The one-time pad is theoretically secure because there is no way to do a trial-and-error decryption. Because the key stream can be anything, there is no way to tell if a guessed decryption is correct. If we use a key stream algorithm to generate the key stream, then we can at least theoretically decrypt any message, just by trying all possible values of the key. Because this attack isn’t practical for large secret keys, a strong, unbiased stream cipher is practical to use even if it’s theoretically breakable.
People rarely use one-time pads in practice even though they are unbreakable. The best known case today is on the “hot line” that connects leaders in Washington and Moscow. Others rarely use one-time pads because they are hard to use correctly.
Soviet Espionage and One-Time Pads
One-time pads have, however, often been used in espionage. Spies have a strong inducement to keep their messages secret, and one-time pads can be coded by hand. Soviet spies used such codes in the 1940s and 1950s. Instead of binary bits, the Soviets used a decimal number code.
The Soviets printed up the decimal one-time pads in tiny books. Each contained thousands of digits to use as key values. In both binary and decimal, the one-time pad uses “add without carry.” In the decimal code, add without carry discards the overflow, as in 7 + 7 = 4, or 8 + 8 = 6. To decrypt the decimal code we use the opposite operation: “subtract without borrow.” In the following, we encrypt a series of decimal digits using a decimal one-time pad. Then we decrypt it with the same key stream:
PLAINTEXT: 67519382
Key Stream: 52836158
CIPHERTEXT: 19345430
Key Stream: 52836158
PLAINTEXT: 67519382
After a spy encoded a message, he or she would discard the pages of used one-time pad digits. The next message would use the remaining digits. This prevented the spy from sending two or more messages using the same key—a mistake that makes the ciphertext vulnerable to attack.
Modular Arithmetic
Mathematically, we implement the one-time pad using modular arithmetic. A casual explanation might suggest that we simply “round things off” in modular arithmetic. Clearly, the decimal one-time pad example shows us discarding the tens’ overflow when encrypting. A different way to describe it is that we perform arithmetic on a “number circle.”
Children often learn conventional arithmetic by working on a “number line.” Addition or subtraction moves us to the right or left: one direction when adding and the other when subtracting.
In modular arithmetic, the results wrap around on themselves. We illustrate this most clearly on a number circle. FIGURE 7.13 shows arithmetic “modulo 10” on a number circle. This is what we used for the decimal one-time pad.
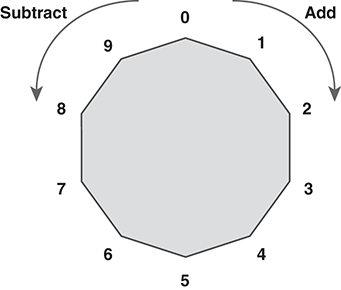
FIGURE 7.13 Modular arithmetic on a number circle.
For addition, we move clockwise around the circle. This performs the same as one-time pad encryption; we add the numbers and discard the overflow. Subtraction moves counterclockwise, the same as one-time pad decryption.
If we compare the operation of the number circle to the cipher disc in Figure 7.5, we see that it, too, performs modular calculations. Most cipher disk cryptography is easy to crack, but this is because most people use weak key streams.
Modular arithmetic plays a fundamental role in many cryptographic techniques. The xor operation is a modular operation, calculating both addition and subtraction modulo 2. We also can perform modular multiplication, division, and other operations. In fact, this is the mathematical basis for public-key cryptography (Chapter 8).
Practical One-Time Pads
As a practical matter, it is very difficult to create, manage, and protect a completely random key stream. If the stream leaks to an attacker, then the encryption is useless. There has to be exactly one digit of random key stream for every digit of traffic sent, so there has to be a periodic exchange of even more random digits. This inconvenience makes one-time pads rare in practice.
There is a lot of confusion about one-time pads. Some vendors use the term with their encryption products simply because one-time pads are provably secure. They believe that the term makes the product seem impenetrable. The crypto community has a name for products that make extravagant and inaccurate security claims like that: They call such products snake oil.
