▶ 8.3 Public-Key Cryptography
When we encrypt with a secret-key algorithm, the security resides in the key, and our data remains secret if our key remains secret. We often call this secret-key cryptography. With public-key cryptography, clever mathematics allows us to share a crypto key publicly and still keep information safe.
Here is an example with Bob and Alice:
Alice, Bob, Eve, and other friends share files through a collection of USB drives that hang on hooks on a corkboard. Different people use different crypto techniques.
Alice read up on public-key techniques, acquired some software, and has convinced Bob to use it. Alice’s software constructed two encryption keys for her. One is a private key that she keeps secret from everyone, including Bob. The other is a public key that she can share with everyone in the suite. She created a file called “Alice’s Key” that she leaves on the USB drive.
However, Alice’s keys don’t let her send secret messages; they only let her receive secret messages. To send a secret message to Alice, Bob takes her public key and encrypts the message with it. He puts the message in the shared USB drive. Alice uses her private key to decrypt the message (FIGURE 8.11).

FIGURE 8.11 Public-key encryption.
There are two essential points here. First, when the sender uses the public key, the recipient must use the private key. Eve, like Alice and Bob’s other friends, can retrieve Alice’s public key. When she tries to use it to decrypt Bob’s message, all she sees is garbage. Because we use two keys and the keys are different, we call this asymmetric cryptography.
The second essential point is that we create the private key first. We derive the public key from the private key (FIGURE 8.12). In some cases, the private key may be any random number within a particular range. In other cases, we calculate the private key from one or more randomly selected values.
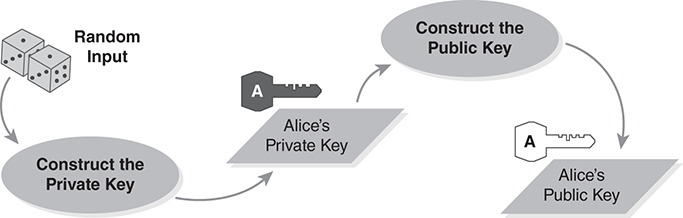
FIGURE 8.12 Constructing the public/private key pair.
The asymmetry in public-key cryptography allows us to produce digital signatures. For example, Alice can use her private key to encrypt some information; the ciphertext yields the digital signature. Anyone with Alice’s public key can decrypt one of Alice’s signatures and verify that her personal, private key had encrypted it.
TABLE 8.1 summarizes important differences between secret-key and public-key cryptography.
TABLE 8.1 Comparison of Secret-Key and Public-Key Crypto |
||
|---|---|---|
Type |
Secret Key |
Public Key |
Symmetry |
Symmetric |
Asymmetric |
Number of keys |
There is one crypto key; the sender and recipient both use it. |
There are two crypto keys; the sender uses one and the recipient uses the other. |
Key secrecy |
The secret key is always kept secret. |
The private key is kept secret. The public key is published and shared. |
Calculating efficiency |
Requires a great deal of calculation using relatively small numbers. |
Requires a great deal of calculation using very, very large numbers. |
Typical key sizes |
128–256 bits |
1024–4096 bits |
Unique identities |
Every member of the cryptonet uses the same key; it is impossible to distinguish one member from another. |
Each user may have a unique private key; only the corresponding public key works with a given private key. |
All public-key algorithms rely on a mathematical trick. The algorithms use mathematical functions that are relatively easy to calculate but very difficult to invert. Although cryptography always has had one-way functions, researchers like to call these “trapdoor one-way functions.” In other words, they have the one-way essence of cryptography, plus a second element that is easy or hard depending on the information you have.
Consider the problem of “prime factors.” All integers are either prime numbers or they are composite numbers made up of two or more primes. If we have a list of prime factors in a number (e.g., 2, 3, 5, and 11), it’s straightforward to multiply them together to yield 330. On the other hand, it takes many more computational steps—and a more subtle procedure—to undo the multiplications and retrieve the primes.
This task becomes much, much harder as the numbers grow large—and this becomes the basis of many public-key techniques. We often form the private key from one or two very large prime numbers. We form the public key by calculating a result from those primes.
When we introduced encryption in Chapter 7, we classified symmetric algorithms into categories in Figure 7.2. Asymmetric algorithms fit into categories according to the mathematics they use, but in practice, we use the names of the prevailing algorithms. This is shown in FIGURE 8.13.
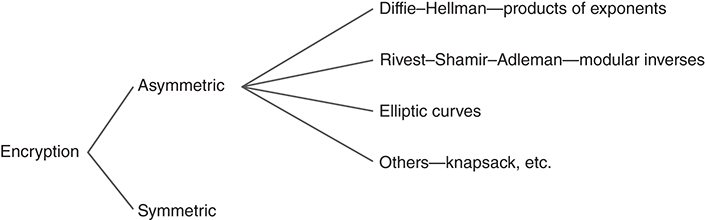
FIGURE 8.13 Asymmetric encryption algorithms.
Attacking Public Keys
Because the techniques rely on mathematical tricks, the encryption is likewise vulnerable to mathematical tricks. Most public-key techniques get their strength from the fact that it’s hard to factor very large numbers. Thus, we can attack many of these techniques by trying to factor primes. Compare this to trial-and-error attacks on secret-key algorithms: We must try every key in the range of possible keys. If we have a 200-bit secret key, we try, on average, 2199 keys to crack it. The effort to crack a secret key increases exponentially as we add more possible keys, doubling each time we add a bit.
If we have a 200-bit public key, we perform a search akin to prime factoring, which requires far fewer than 2199 trials. In fact, the effort increases logarithmically as we add more possible keys. Thus, it is much easier to crack a 200-bit public key than a 200-bit secret key. Today, recommended public-key sizes for the Diffie–Hellman and RSA algorithms may be 10 or even 20 times larger than comparable secret keys. Elliptic curve public keys are typically only twice the size of comparably strong secret keys.
Public-key cryptography does not replace secret-key cryptography. The public-key techniques do certain things very well, but they do other things very poorly. Modern systems use public keys to wrap secret keys and to construct digital signatures. Even these tasks must take place under very restricted circumstances; otherwise, attackers can use mathematical trickery to overcome the cryptographic protection.
Secret-key encryption exchanges the problem of keeping data secret for the problem of managing the secret encryption key. Public-key encryption often exchanges the problem of managing secret keys with the problem of correctly identifying the public keys. If Eve substitutes her own public key for Alice’s key, she can eavesdrop on Bob’s conversations.
8.3.1 Sharing a Secret: Diffie–Hellman
The first successful public-key algorithm was not an encryption algorithm in any normal sense. The algorithm, developed by Whitfield Diffie and Martin Hellman at Stanford University, lets two endpoints share a single secret value without sending any secrets back and forth. Although this doesn’t actually encrypt information, it provides a shared secret. We generally refer to the algorithm by its inventors’ names, Diffie–Hellman, and occasionally abbreviate it D-H. The endpoints then use the shared secret as a key in a symmetric cipher like AES. In FIGURE 8.14, we show the public key in white and the secret key in black.

FIGURE 8.14 Procedure for Diffie–Hellman secret sharing.
Unlike the earlier example, both participants must have a public and a private key pair. Each participant multiplies their own private key by the other’s public key to compute the shared secret. Even though each one has a different public and private key pair, the trapdoor nature of the computation yields an identical result.
Here’s how Bob sends Alice a message:
Alice picks a private key value and calculates the matching public-key value. She puts the public-key value on the USB drive in a file named “Alice’s Key.”
Before he can exchange messages with Alice, Bob also must produce a pair of keys. He saves his private key on his computer and puts the public key in a USB file named “Bob’s Key.”
Bob retrieves Alice’s key file from the USB drive. To find their shared secret key, he takes Alice’s public key and applies the Diffie–Hellman calculation. That yields a result that’s unique between Bob and Alice (Figure 8.14, left side).
Bob uses this unique value as a secret key to encrypt his file using AES. He names the file “To Alice.”
To recover Bob’s file, Alice does the following:
She retrieves the file from the USB drive. She also retrieves the file containing Bob’s public key.
Alice takes Bob’s public key and applies the Diffie–Hellman calculation. This yields the same secret value that Bob calculated (Figure 8.14, right side). This serves as the secret encryption key.
Alice retrieves the “To Alice” file, plugs the secret encryption key into AES, and decrypts the file.
Perfect Forward Secrecy
In Section 8.1.1, we talked about rekeying: how we need to change encryption keys regularly. If we use the same key continuously, we create more and more ciphertext that could be used to crack that key. If we produce smaller amounts of ciphertext with each key, we make the cryptanalyst’s job much harder.
Over the years, cryptographers have designed many ways to rekey. Some techniques work poorly; if attackers recover one or more keys, they can use them to find later keys. The best techniques aren’t affected if attackers recover earlier keys.
If an attacker manages to recover one of the system’s keys and that key provides no information that helps crack future keys, then the system has perfect forward secrecy. If two endpoints generate a new set of Diffie–Hellman key pairs to establish a new, shared secret key, then the system has perfect forward secrecy.
The Internet Key Exchange protocol uses Diffie–Hellman to negotiate keys. Its implementation achieves perfect forward secrecy. (See Chapter 13 for a discussion of Internet Key Exchange protocol.)
Variations of Diffie–Hellman
Although the classic Diffie–Hellman algorithm can only produce a shared secret, other variations provide encryption and digital signatures. A variant called El Gamal can encrypt data or construct digital signatures. The U.S. Digital Signature Standard (DSS) is based on a variant of El Gamal.
8.3.2 Diffie–Hellman: The Basics of the Math
Although the mathematical details of Diffie–Hellman aren’t essential to understand its use, we will provide an overview. The magic in Diffie–Hellman arises from properties of modular exponentiation. Exponentiation by itself, of course, refers to raising a number to a power. Modular arithmetic refers to arithmetic operations that are truncated relative to a particular value. The one-time pads encountered in Section 7.3.4 use modular arithmetic; the “add-without-carry” operation is a modular operation. Here’s a calculation of modular exponentiation:
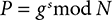
In this equation, we raise the number g to the power s. We then calculate the modulus of this based on a large prime number, N. The modulus is essentially the remainder in an integer divide operation; thus, we discard any part of the result larger than the large prime N.
In basic algebra, we learned that:
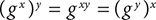
The same relation holds for modular exponentiation. However, it is incredibly more difficult to invert the modular exponentiation. The logarithm is the inverse of exponentiation, and the prime modulus operation makes exponentiation especially hard to invert. This is called the “discrete logarithm problem,” and it is as difficult in practice as factoring very large numbers. This provides the “trapdoor” so that the Diffie–Hellman result is easy to compute if you have the private key.
In a Diffie–Hellman calculation, the value s is the private key value. It is a randomly chosen value less than N. Each endpoint has its own, unique, private key, and we calculate the public key from it. The public key consists of the following:
g—the generator, a public, shared value; often g = 2
N—the modulus, a very large prime number, also shared
P—the unique public value computed from the private key s
The values g and N must be shared within the community of users. If Kevin uses different values than Alice and Bob, he can’t compute a shared key with the others. Moreover, s must be less than N.
Let’s look at what happens when Bob and Alice try to communicate. Bob has a secret value sBob, and Alice has a secret value sAlice. The following calculation produces their public keys:
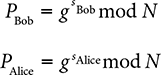
Now, Alice and Bob can share their public keys and calculate their shared secret. Both keys must use the same values for g and N. Each calculates the shared secret by raising the other’s public key by the power of their own private key. The following three steps show how the calculation reduces to identical results:
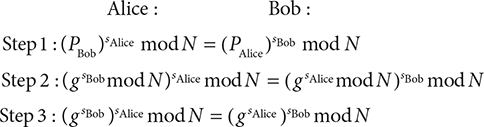
The structure of the Diffie–Hellman computation is relatively simple compared to secret-key encryption. The RC4 cipher requires two sets of loops, compared to Diffie–Hellman’s two exponentiations and a modulus. Stronger secret-key algorithms like AES are even more complex. (See Chapter 9.) Public-key calculations become challenging because they use significantly larger numbers than those in secret-key cryptography.
This simplicity opens Diffie–Hellman up to attacks unless we are very careful in the implementation. There are numerous mathematical restrictions on the numbers to use. In practice, people don’t usually use Diffie–Hellman for long-term public keys. More often, Diffie–Hellman is used to create a temporary public and private key pair for a particular transaction.
8.3.3 Elliptic Curve Cryptography
Elliptic curve cryptography has practical similarities to Diffie–Hellman, but it calculates over an elliptic curve instead of over a finite field. A discrete elliptic curve, in general, is an equation in x and y of the form:
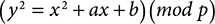
We begin by publicly sharing a particular elliptic curve with predefined values for a, b, and p. There is also a “base point” (x, y) on that curve that serves as another public parameter. These are all very large numbers; they match the key size in length.
Given the public parameters, we can establish a shared secret key using a variation of the Diffie–Hellman procedure. We also can construct a digital signature.
To construct a shared secret, for example, Bob and Alice begin by each selecting a random secret value that is less than p. Alice multiplies her secret value A by (x, y) on the discrete curve to yield her public key (xA, yA). Bob does the same with his secret multiplier B to yield his public key (xB, yB).
To construct the shared secret key, each multiplies their secret key by the other’s published product, all on the elliptic curve:
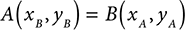
This yields the same pair of points for both Bob and Alice. They use the result to generate their shared secret key.
Finite field techniques like Diffie–Hellman are dramatically weaker, bit for bit, than comparable symmetric-key encryption. That is why Diffie–Hellman keys have at least 10 times as many bits as symmetric keys to provide comparable resistance to trial-and-error attacks.
Elliptic curve cryptography, however, resists trial-and-error attacks with much smaller key sizes. A comparable elliptic curve key may have only two to three times as many bits as a symmetric key of comparable strength. This is because the elliptic curve discrete logarithm problem is harder to solve.
In the United States, NIST and NSA have established standards for using elliptic curve cryptography in government and military applications. This is called “Suite B.” The suite includes standards for key negotiation and for digital signatures using an elliptic curve. Suite B uses the following standard curve:
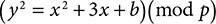
The published standards describe how to use elliptic curve cryptography with five key sizes ranging from 192 bits to 521 bits. According to NIST, the 256-bit keys provide comparable security to AES using a 128-bit key, and 384-bit keys are comparable to AES using a 192-bit key. The NIST recommendations actually suggest using slightly larger keys, but these sizes meet their minimum requirements.
8.3.4 Quantum Cryptography and Post-Quantum Cryptography
Quantum cryptography applies quantum physics to cryptographic problems. Quantum physics describes the behavior of subatomic particles such as photons and electrons. Practical applications are limited as yet, but its potential has been convincingly demonstrated in small-scale demonstrations. We briefly examine three topics here:
■ Quantum key distribution
■ Quantum cryptanalysis
■ Post-quantum cryptography
Quantum key distribution applies Heisenberg’s Uncertainty Principle to detect eavesdropping when distributing secret crypto keys. The Principle states that any measurement of a particle will affect the quantum state of the particle. If we use quantum states to encode secrets, then we can detect state changes caused by looking at those secrets. Unlike mathematical cryptography, the security strength of this technique relies on physical properties of the system. In September 2017, researchers in China and Austria used quantum key distribution to share crypto keys via an orbiting satellite.
Quantum cryptanalysis is an attack vector that uses a “quantum computer” to attack cryptographic systems. A quantum computer is built of “qubits” which, unlike conventional bits, may exist in multiple states of 0 and 1 simultaneously. This allows a quantum computation to explore vast numbers of alternative calculations simultaneously.
One technique, called Shor’s algorithm, provides a practical way to factor large numbers on a quantum computer. This provides a direct attack on Diffie–Hellman, elliptic curve, RSA, and several other public key systems. Another technique, Grover’s algorithm, greatly speeds up search algorithms such as brute force attacks on secret keys.
This attack vector is theoretical at present because practical quantum computers are currently limited to a few dozen qubits. Estimates suggest that at least a million qubits are required to attack modern public keys. Sufficiently powerful quantum computers might be built in the next few decades.
Post-quantum cryptography refers to cryptographic techniques that resist quantum cryptanalysis. Secret-key techniques can resist Grover’s algorithm by using significantly larger keys. Today’s public-key techniques may need to be entirely replaced by new, quantum-resistant algorithms.
