Chapter 1
The Thermodynamic Approach 1
1.1. Background
Despite several decades of studying microscopic modeling, no theory is yet reliable enough to explain and fully predict the behavior of perovskite in thin films although the ab initio or “from first principle” approach is beginning to give very good results [JUN 03].
However, the phenomenological approach based on thermodynamics, which is a statistical view of the problem, helps to explain a very large proportion of the numerous behaviors of perovskites. Although the case of thin films is more delicate due to extrinsic effects such as residual stresses, interfaces, composition inhomogeneities, lattice, or domain wall motion effects, it is often possible to understand, at least qualitatively, how a device that integrates a perovskite material will behave by using the thermodynamic formalism.
Therefore, in this chapter, we develop the equations that enable us to use this formalism. This energetic method is very useful to understand the several possible couplings that arise in perovskites. The general idea is to have the most general description of the system energy and, therefore, to quantify the conversions of the thermal, mechanical, electrostatic, or magnetic energies.
This theory is often referred to as Landau Ginzburg Devonshire (LGD), all three having sequentially contributed to developing it in the first half of the 20th Century. Landau’s work focused on second-order phase transitions, which are those that do not involve the latent heat of transition. This may be a ferromagnetic or ferroelectric near the Curie temperature, a superconducting material near its transition phase or a fluid near its critical point. All these transitions may behave with many similarities (“universality” concept) and are called “critical phenomena” in the literature, widely studied since the pioneering work of Landau [LIN 77]. In 1950, Landau and Ginzburg adjusted the original Landau theory to the study of transition of a superconductor. In 1949, Devonshire was inspired by this formalism to apply it to the study of ferroelectrics [DEV 49]. This global energetic approach has been a great success and is still used today, especially for thin films. It is thus possible to take into account domain walls, stresses due to the substrate and many couplings.
In this approach, the concept of symmetry is important because there is a loss of symmetry during phase transition (liquid solid, ferromagnetic paramagnetic, and ferroelectric paraelectric) nearly all the time. It is essential to be able to quantify the change in symmetry induced during transition by a parameter that characterizes the system and is called the order parameter.
Thus, in our case, it is the polarization that represents the order parameter to describe the transition between the paraelectric and ferroelectric states. Landau assumes that the free energy of the system undergoing transition can be described by an analytic function of the order parameter and precisely by an expansion in even powers of the latter. For ferroelectrics, this assumption means that the energy of the higher symmetry phase is the same whatever the sign of the applied field associated with the order parameter. This is the case because polarization is always aligned to the applied electric field in the paraelectric phase and thus the electrostatic contribution to the energy is the same irrespective of the field sign. Phase transition is also characterized by a transition temperature. The latter was introduced by Landau in his formalism so that the order parameter is zero in the high-temperature phase of high symmetry and non-zero in the low-temperature phase of lower symmetry.
We elaborate on this account by addressing thermodynamic formalism in Section 1.2.
1.2. The functions of state
This formalism has been widely described in the literature. It is repeated here to bring together the various approaches that have been proposed and to ensure consistency in the notations that we have come across. This section is largely inspired by the articles of Devonshire [DEV 49], Damjanovic [DAM 98], as well as the bookby Lines and Glass [LIN 77].
The fact that several energetic couplings are possible in many cases induces the mixing of several physical domains without a priori there being any link in the development of their respective models. In thermodynamics, such as we might have seen, the microscopic state of a system is described by the decomposition of its internal energy into several distinct contributions: mechanical, electrical, thermal, magnetic, and chemical. All these contributions correspond to global and statistical values, regardless of any microscopic description of the state of the matter in the considered system. If we are able to write the expression of this internal energy, then we can determine the state of the system based on independent macroscopic variables (for instance, the pressure or the electric field) and it becomes possible to determine its equilibrium as a function of these variables.
In the expression of internal energy, the infinitesimal amount of work δW depends on the nature of the system interactions with the external environment. Here, we consider two types of work interactions that may apply to the considered solids: mechanical and electrical. The generalization to other forms of energy (especially magnetic) may be done in the same way. The so-called conjugate pairs of variables to be considered are stresses S and strains T for the mechanical part and electric field E and electric displacement D for electrical components. The heat contribution is described by entropy σ and temperature θ as usual.
Thus, for these two types of work, by using the first principle in the case of a quasi-static transformation, the infinitesimal variation of internal energy is the sum of the infinitesimal variations of heat δQ (=θdσ) and works δW (we can note that “δ” is used for heat and work as their variations are generally not differentials):
[1.1] ![]()
We recall that the internal energy is a function of state; that is, it fully describes the energetic exchanges the system undergoes. Therefore, its variations only depend on the initial and final states of the system during a transformation. Mathematically speaking, dU isatotal differential.
To work out the infinitesimal variation of the mechanical energy (TdS), the stress is fixed and hence we consider the strain variation. For the electric energy, E is fixed and hence we concentrate on the electric displacement variation (and, therefore, electric charges). The contribution to dU is thus EdD. For the calculation of dU, the intensive variables are kept constant during the variation (temperature, stress, and electric field) and we vary the extensive variables (entropy, strain and electric displacement). An extensive variable has a value that changes depending on the size of the system whereas an intensive variable remains constant. One of the interests in the use of internal energy is to be able to characterize the equilibrium of the system with fixed entropy, strain, and electric displacement. Indeed, we then have dU = 0 according to equation [1.1], which corresponds to an extemum of U. It can be shown that this extemum is a minimum [REI 65]. It is then said that U represents the thermodynamic potential of this system for the considered transformation.
Experimentally, the external parameters which can be monitored are not always the same. It is thus interesting to be able to change the thermodynamic potential. This can be achieved by performing a Legendre transformation of the internal energy, which is equivalent to add to the latter homogeneous terms in energy, which is the product of two conjugate variables. This operation, therefore, transforms the internal energy into another function of state. Thus, it is possible to define a thermodynamic potential appropriate to each experiment.
It is very common to work at constant temperature rather than at constant entropy. On the other hand, to describe the ferroelectric-paraelectric phase transition, it is interesting to bring up polarization (and by extension electric displacement) rather than the electric field since it is the order parameter of the transition. For the mechanical part, the boundary conditions depend on the geometry of the sample. In the case of thin films, it is even common to set different boundary conditions for stresses and strains. The most common thermodynamic potentials for the study of coupled thin films are:
– Helmholtz free energy (F or A according to authors):
[1.2] ![]()
– Gibbs energy:
[1.3] ![]()
– Elastic Gibbs energy:
[1.4] ![]()
– Electric Gibbs energy:
[1.5] ![]()
NOTE: – By definition, mechanical stresses are positive when they are tensile and negative when they are compressive.
The resulting total differentials are:
[1.6] 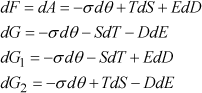
The three variables that appear in differential form in the second term of each equation correspond to the natural variables of each thermodynamic potential. Thus, the minimum of the elastic Gibbs energy G1 is reached at the equilibrium of a system for which temperature, stress, and electric displacement are constant. These three parameters represent the natural variables of G1.
All these thermodynamic potentials are functions of state. Their differential is total because all the possible contributions to the variation are considered. From a mathematical point of view, they are analytic functions that depend on several variables. They have the property to be decomposable into a Taylor series of various variables, provided that the successive derivatives exist up to the order of interest. If the second derivatives are continuous (which is true in physics most of the time), an important property follows: there is equality of cross-derivatives. Thus, this induces the Maxwell relations of thermodynamics, which play a key role. For instance, the equality of cross-derivatives for G1 gives the following relations:
[1.7] ![]()
Another interpretation of this property is that the derivative sequence for the multiple derivatives does not matter. That is to say, taking the example of G1, that we have:
[1.8] ![]()
By taking the derivative with respect to the cross-variable for each relationship, we obtain:
[1.9] 
We can represent this property by the following expression:
![]()
This property enables us to simplify the tensors that characterize the studied materials.
One last important note is that work and heat variations are usually not functions of states. In fact, the first principle says that it is their sum which is the internal energy. Therefore, their differential is generally not total.
1.3. Linear equations, piezoelectricity
It is now possible from these definitions to define the equations of state from the various thermodynamic potentials. The simplest equations correspond to an assumption of linearity of all the effects.
Let us continue with our example of the elastic Gibbs energy. To elaborate further, each variable that is conjugated along the three axes should be described, knowing that the stresses and the strains are described by tensors of rank 2, while the electric field and electric displacement are described by vectors (tensors of rank 1). dG1 hence becomes:
[1.10] ![]()
Thus, the elastic Gibbs energy, a function of state, can be expressed mathematically in the form of a Taylor series. By stopping at the second order, we obtain:
[1.11] 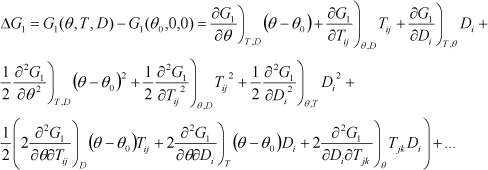
It is also possible to describe each non-natural variable by decomposing it in a Taylor series of natural variables. By stopping at the first order, we obtain the following linear equations:
[1.12] 
Each of the partial derivatives that appear in these equations represents a specific distinct physical effect for special conditions. Thus, ∂Sij/∂Dk)θ,T and ∂Ei/∂Tjk)θ,D correspond, respectively, to the indirect piezoelectric effect with temperature , and stress fixed, on the one hand, and to the direct piezoelectric effect with temperature and fixed electric displacement, on the other. However, according to the Maxwell relations of thermodynamics applied to Gibbs free energy (see equation [1.8]), these two coefficients are equal up to but the sign. So, these are actually energetic considerations that prove that the direct and indirect piezoelectric effects are identical.
Ultimately, it is possible to write a linear equation [1.12] by using the standard denominations of piezoelectricity [IEE 87]. To do this, variations of variable X are assumed to be small, which allows the approximation dX = X-X0 [LIN 77]. We obtain:
[1.13] ![]()
[1.14] ![]()
[1.15] ![]()
with:
cT,D : heat capacity of the system at fixed T and D – scalar;
![]() : thermal expansion coefficients at fixed D – tensor of rank 2;
: thermal expansion coefficients at fixed D – tensor of rank 2;
![]() :pyroelectric coefficients of field at fixed T – tensor of rank 1;
:pyroelectric coefficients of field at fixed T – tensor of rank 1;
![]() : elastic compliance coefficients at fixed θ and D – tensor of rank 4;
: elastic compliance coefficients at fixed θ and D – tensor of rank 4;
![]() : piezoelectric coefficients at fixed θ – tensor of rank 3; and
: piezoelectric coefficients at fixed θ – tensor of rank 3; and
![]() : dielectric impermittivity coefficients at fixed θ and T – tensor of rank 2.
: dielectric impermittivity coefficients at fixed θ and T – tensor of rank 2.
The coefficients that appear are tensors of various ranks ranging from 0 to 4. It should be noted that the coupling coefficients, which are those that connect variables of a different nature (![]() and
and ![]() ), are identical in their direct and indirect effects under the thermodynamic Maxwell relations, as we explained for piezoelectricity. They are thus given for a single fixed variable: the coefficient that is not part of the coupling (for instance, θ for piezoelectricity).
), are identical in their direct and indirect effects under the thermodynamic Maxwell relations, as we explained for piezoelectricity. They are thus given for a single fixed variable: the coefficient that is not part of the coupling (for instance, θ for piezoelectricity).
1.4. Nonlinear equations, electrostriction
Taylor series expansion of free energies can, of course, be done at higher orders to take into account the nonlinear effects that are common in perovskites, such as the hysteretic relationship between polarization and electric field or the electrostrictive phenomena. In 1950, Mason provided a very good example of this expansion to explain the electrostrictive effect of barium titanate ceramics [MAS 50]. It should be noted that this approach is independent of the description of the paraelectric-ferroelectric phase transition and that all insulators can theoretically be described in this way.
If we continue with our example based on the elastic Gibbs energy neglecting the thermal terms, the third-order expansion for the energy and the second order for the nonnatural variables gives the following equations:
[1.16] 
[1.17] 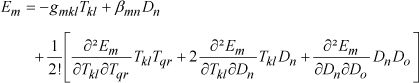
We have:
![]()
with Qijno the electrostrictive coefficients.
Electrostriction is thus represented by a tensor of order 4. The terms ∂2 Sij/∂Tkl∂Tqr correspond to the compliance variation as a function of stress, ∂2Sij/∂Tkl∂Dn to the compliance variation as a function of electric displacement, ∂2Em/∂Tkl∂Tqr to the piezoelectric coefficients’ variation as a function of stress, and ∂2Em/∂Dn∂Do to the inverse dielectric permittivity variation as a function of electric displacement.
As shown in this example, the complexity increases very quickly and the number of experiments to be carried out to determine all these coefficients can become innumerable. It is necessary to make assumptions about the predominance of certain effects over the others. As for the case of perovskites, the higher order terms that involve electric variables often predominate over those related to mechanical variables. This is because the dielectric constant is very sensitive to all experimental variables. For other materials, such as AlN, which is another remarkable piezoelectric, the variations of the coefficients as a function of variables are much more homogeneous and it is more difficult to ignore the mechanical terms.
1.5. Thermodynamic modeling of the ferroelectric-paraelectric phase transition
1.5.1. Assumption on the elastic Gibbs energy
The ferroelectric-paraelectric transition occurs at a given temperature known as the Curie temperature, TC , by analogy with ferromagnets. Thus, above the TC , the lattice is centrosymmetric (simple cubic for the perovskite) and thus no polarization can occur if the electric field is zero. Below TC , polarization can occur even at a zero field because the crystal lattice loses its center of symmetry. For bulk barium titanate (BaTiO3 aka BTO), one of the most studied perovskites, it is the tetragonal phase that occurs below TC . The polarization in this phase is along the <001> direction often called c-axis. As stated earlier, the thermodynamic description does not require any knowledge of microscopic phenomena. It is an energetic description that relies on the identification of “good macroscopic variables” selected according to experimental conditions that the system described undergoes. It follows the choice of a suitable free energy that takes a minimum value when equilibrium is reached under the principles of thermodynamics. The usual assumption then is to describe this energy by a polynomial that involves the order parameter. The order parameter is an experimental parameter whose value is zero in the higher symmetry phase and non-zero in the lower symmetry phase. It is, therefore, representative of the transition. In the paraelectric ferroelectric transition case, this order parameter is the polarization. Indeed, in the cubic phase, no polarization can occur in the absence of an electric field. Otherwise, the cubic symmetry is no longer respected [NYE 85]. In contrast, in the ferroelectric phase just below TC (tetragonal phase for BTO), the loss of symmetry allows the occurrence of a non-zero polarization in the absence of an electric field.
The polynomial order depends on the degree of nonlinearity that is required for the phenomenological description of the transition. Landau proposed an additional smart assumption: the same polynomial can describe the high- and low-temperature phase. For ferroelectrics, this is justified by the fact that, while non-centrosymmetric, the low-temperature phase lattice parameter is very close to the high-temperature lattice parameter. For example, the lattice parameter strain experienced by the BTO during phase transition is around 1%. Thus, the centrosymmetric high-temperature phase modeling called prototype phase should allow us to describe the system not only above TC but also below TC . The main limitation of this assumption is that it does not allow a perfect description of critical phenomena that occur in the transitions of the second order (without the latent heat of phase transition) [LIN 77]. However, this approach has been very satisfactory for describing most of the behaviors of perovskites, either in massive form or in thin layers.
The symmetry of the cubic phase enables us to simplify the polynomial. The odd terms of the order parameter are actually excluded. If they were present, then the energy would be different in the high symmetric phase for two polarizations exhibiting the same amplitude but a different sign, which is impossible. The accessible experimental variable corresponding to the order parameter is actually not polarization P but the electric displacement D whose derivative with respect to time gives the electrical current. However, it is common to equate polarization as the order parameter because this variable allows a better understanding of what is going on, on the scale of the crystal lattice during the transition. As D = ε0E + P and because transition occurs when P becomes non-zero for a zero electric field E, it is equivalent to the thermodynamic sense to consider P or D as a conjugate variable of E to describe the transition. However, in 1977, Lines and Glass pointed out in their description of ferroelectric materials that it is not correct to use the pair (P, E) to describe the electrical contribution in the various free energies [LIN 77]. In fact, it is not possible to experimentally control the polarization, which induces an uncertainty on the definition of the constants defined at fixed P. On the other hand, the usage of P in the energy balance leads to ignoring of the electric displacement in vacuum (ε0E). Nevertheless, most of the time this ambiguity does not play a very important role because the permittivity of perovskites is very high which, induces that D and P exhibit very similar values. However, we will adopt the classical thermodynamic approach by using the pair (D, E) of conjugate variables for describing the electrical contribution of free energies.
Thus, the conventional way to describe the ferroelectric-paraelectric transition is to use temperature, the mechanical stress, and the electric displacement as variables. Therefore, the natural variables are (θ, T and P), which correspond to the elastic Gibbs energy G1. G1 is thus the thermodynamic potential whose minimum will define the equilibrium. For simplicity, let us consider the 1D case where polarization can only take one direction (but both signs) in the non-centrosymmetric phase, which corresponds to the direction of the electric field. Under these conditions, G1 may take the form of the following polynomial [UCH 97]:
[1.18] ![]()
The 6th order is usually sufficient to describe the first- and second-order transitions for most materials. The 4th order is actually enough to describe 2nd order transitions. Recently, Vanderbilt and Cohen proposed retention of the terms up to order 12 to correctly predict the behavior of PZT in the morphotropic region of its phase diagram where several monoclinic phases occur [VAN 01]. The fourth term on the right corresponds to the elastic energy (with S = sT) and the last term is the electrostrictive term that may appear in the centrosymmetric phase. The thermal term does not appear explicitly but the temperature dependence is reflected in α.
At first glance, this equation seems inappropriate for describing the low-temperature phase because piezoelectricity does not appear explicitly. However, we see that this linear property can be described by the presence of a remnant polarization associated with the electrostrictive effect. Moreover, this approach turns out to be much closer to actual experiments by highlighting the very important influence of the dielectric constant in the piezoelectric coefficients of perovskites.
On the other hand, the signs choice in equation [1.18] does not matter a priori since they can just be corrected in the different coefficients (a, s, and Q). However, it is more appropriate to choose the signs that enable us to define positive elastic compliances sii and electrostrictive coefficients Qiijj by respecting the “natural” signs of the total differential of the elastic Gibbs energy. In fact, sii is the inverse of Young’s modulus in an isotropic material and electrostriction is often simply defined by the relationship between the strain S induced by the electrostrictive effect, and the electric displacement D by S = QD2. Experimentally, in the 1D case (for instance, along the thickness), Q is always positive for ceramics, which means that the material’s thickness increases when D is not zero.
To characterize the transition, we must follow the electric displacement as a function of temperature with zero electric field. This means that the thermodynamic potential is not G1 but G, which is Gibbs energy such that G = G1-ED. This change of thermodynamic potential may seem strange but it enables us to have both an expression that depends on the order parameter D and to set the electric field to a zero value, which is necessary to observe the transition. Therefore, it is actually G (θ, T, and E) that is minimal at the equilibrium.
The expression of E is given by the derivative of G1 with respect to D:
[1.19] ![]()
1.5.2. Second-order transition
To describe the transition as simply as possible, we will place ourselves at zero stress and consider α′ to be positive and α″ to be zero. This case corresponds to the so-called second-order transitions for which there is no latent heat associated with phase change and the order parameter varies continuously up to zero while the temperature increases until it reaches TC . Transition occurs when an electric displacement exists at a zero field, which gives from [1.19]:
[1.20] ![]()
Non-zero D is possible if the solution D2 =-α/α′ exists. Following the example of Landau, Devonshire introduced temperature in the term α as simply as possible by providing a linear dependency in the form α = θ -θC /C, where θC and C are the Curie temperature and the Curie constant, respectively. This dependency can be explained physically by the thermal expansion that occurs when temperature varies. Thus, over θC , D is zero and below ![]() . Let us note that the form of is not quite the same if α″ is not zero as we shall see later. In this simple model, the dependency of energy on temperature appears only in α. α′ and α″ are considered as constants.
. Let us note that the form of is not quite the same if α″ is not zero as we shall see later. In this simple model, the dependency of energy on temperature appears only in α. α′ and α″ are considered as constants.
The expression of β, the inverse of the dielectric χ susceptibility, is obtained by differentiating equation [1.19] with respect to D, which gives:
[1.21] ![]()
Taking the same assumptions as earlier (zero T, i.e. stress, zero α″, and positive α′), the values of χ on either side of the transition at zero field become:
[1.22] 
These expressions widely described in the literature highlight the fact that the dielectric constant ε diverges when θ = θC , in which s follows the Curie-Weiss law in the paraelectric phase and that the slope of ε versus 1/θ is twice smaller and of opposite sign in the ferroelectric phase than in the paraelectric phase.
To illustrate these properties, we take the example of a ferroelectric that might be viewed as Pb(Zr0.52Ti0.48)O3 (PZT), although the following description is more qualitative than quantitative because of many extrinsic effects that may arise during the synthesis of a real material and which is, moreover considered as a thin layer (interfaces, crystal defects, space charges, impurities). To do this, we take θC = 400°C, C = 105.ε0 F/(m.K), α′ = 8.109 m5/(F3V2), s = 1/(100 GPa) = 10-11 m2/N, and Q = 0.1 m4/C2.
Figure 1.1. (a) Elastic Gibbs energy calculated as a function of the electric displacement for second-order transitions; (b) electric displacement at equilibrium as a function of temperature
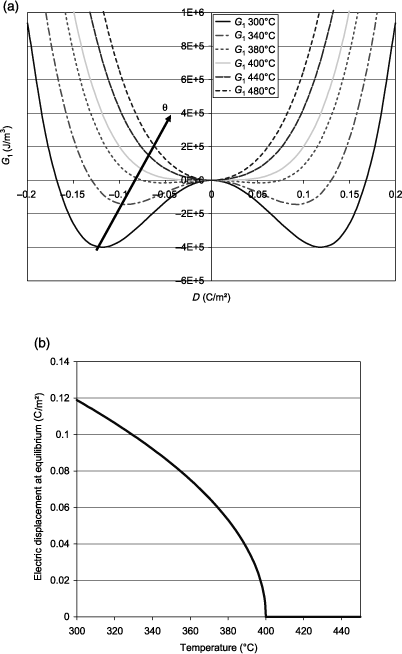
Figure 1.1(a) shows the elastic Gibbs energy calculated using equation [1.18] as a function of the electric displacement at several temperatures on either side of the transition (400°C). The absolute minimum of each curve corresponds to the equilibrium state. We observe that below θC there are two possible equilibrium states symmetrical with respect to D = 0 and that we continuously approach the equilibrium state at D = 0 when θ tends toward θC . This equilibrium is reached when θ= θC and remains the same when temperature is still increasing. The absolute value of the electric displacement D at equilibrium is illustrated in Figure 1.1(b) according to equation [1.20]. The latter continuously decreases down to zero at 400°C, which is typical for a second-order transition. The variation of the dielectric constant ε as a function of temperature is easily obtained from equation [1.22] and is not shown here. Further, ε tends to infinity when the temperature approaches 400°C. This phenomenon is sometimes called the polarization catastrophe, because setting a very low electric excitation induces an infinite polarization, only limited by the nonlinearities. More physically, it corresponds to a transverse optical phonon at very low frequency (called the soft mode), which arises in ferroelectric materials and which explains the extremely high polarizability [KIT 04]. According to the aforementioned discussion, it is often more appropriate to represent the functions that describe the transition as functions that depend on the electric field E, and hence the use of G instead of G1. Thus, Figure 1.2 shows the variation of G as a function of E at different temperatures around the transition that is calculated using equation [1.18] as well as G = G1 ED. The variation of the field begins at the most negative values, reaches its maximum value, and then goes down to its minimum value. The curve shows a hysteresis when the temperature is below θC . To describe it, it is good to rely on the curve of D, obtained as a function of E according to equation [1.19]. D is thus plotted in Figure 1.3 and it also shows a hysteresis, which characterizes ferroelectric materials. The description of the cycle is identical to that of G and is identified by numbers ranging from 1 to 7, which are plotted on both figures.
To have a good understanding of this hysteresis, we can propose a macroscopic description of a single crystalline ferroelectric material in which several ferroelectric domains can form. A ferroelectric domain is part of the material in which the value of the polarization is identical and two adjacent domains do not exhibit the same polarization. In this explanation, we will confuse the electric displacement and the polarization, which is legitimate for ferroelectrics given their very high dielectric constant. Thus, for a strong and negative field, the polarization follows the field and is therefore also negative since we are beyond of the coercive field (point 1). When the field tends toward positive values, G increases because the absolute value of ED decreases and polarization goes down due to successive switching of several ferroelectric domains in the positive direction. This gradual switching is illustrated by the nonlinear term α′. At point 2, the coercive field is almost reached and it is therefore the maximum of G since | ED | is then minimal. At point 3, the coercive field is reached and all the domains that have not yet been switched will do so to give a positive polarization in the direction of the field. | ED | again becomes large and therefore reduces G (more stable state). Energy decreases again as the electric field increases and in turn | ED | increases. Polarization grows slightly again just because of the dielectric effect (point 4). When the electric field goes down, the situation is exactly symmetrical with a gradual decrease in the polarization correlated with the increase in the free energy up to the negative coercive field (point 5). Then, there is a global switching of the polarization inducing a steep decrease of the energy at the negative coercive field (point 6), and a gradual decrease in the energy with a gradual increase in polarization as the field decreases (point 7).
Figure 1.2. Gibbs energy G as a function of the applied electric field at various temperatures for a second-order transition
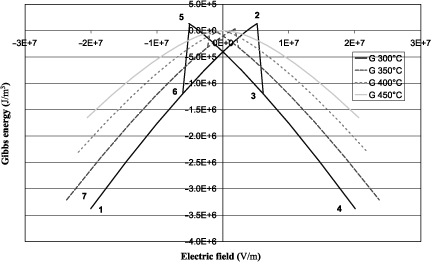
Figure 1.3. Electric displacement as a function of the applied electric field at various temperatures for a second-order transition
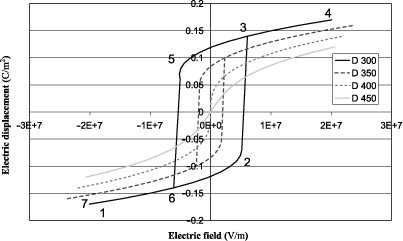
When the temperature increases, the hysteresis effect decreases and disappears completely at the Curie temperature. Beyond the latter, the nonlinear effect remains, whose microscopic origin lies in the decrease of the polarizability as the electric field grows.
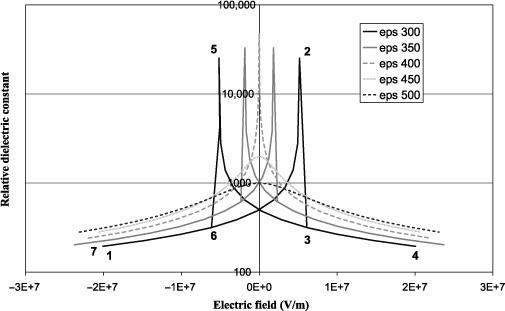
It is also possible to plot the evolution of the relative dielectric constant εr as a function of the field at various temperatures. Hysteresis is also visible in the evolution of εr when temperature is below 400°C. The maximum of εr appears at the coercive fields (points 2 and 5) corresponding to the switching of the polarization, which contributes very significantly to the polarizability of the material (infinite in the case of the model). The value of the coercive field decreases during the increase in temperature to cancel out at θC , for which εr reaches an infinite value at zero field. It is interesting to note that the variation of εr as a function of temperature is consistent with equation [1.22] at zero field because the values of εr are identical at 350°C and 500°C (factor 2 on either side of the transition). At a high field, all dielectric constants decrease because the polarizability of the material goes down. Physically, this corresponds to the hardening of the soft mode, which is an increase in its resonance frequency. Another view is to consider one of the Maxwell equations of G, which gives:
[1.23] ![]()
We have seen that D decreases with temperature at zero stress and field. According to equation [1.23], this means that entropy decreases with the electric field applied at a given stress and temperature. In other words, the number of accessible microscopic states of the system decreases with the field. Therefore, the ease of movement of the charged species that contribute to the polarization of the material decreases with the field. Thus, the dielectric constant decreases with the field.
On the other hand, Figure 1.4 shows that εr tends to be higher at high field when the temperature is greater - although at a higher temperature, the effect vanishes (not shown). This stems from the competition between the terms α and 3α′D2. In fact, α increases with temperature while 3α′D2 decreases because, for a given E, D is lower when the temperature is high. The latter observation may seem paradoxical because if D , which is often defined as D = εE, is lower, then this means ε should be lower too, whereas it is the opposite that is observed. We attribute the reason due to the fact that the phenomenological definition of ε is ∂D / ∂E, which implies that it is the variation of D as a function of E that matters.
Figure 1.4. Relative dielectric constant as a function of the applied electric field at various temperatures for a second-order transition
1.5.3. Effect of stress
The application of this model in the experiment gives very good results for bulk materials. For thin films, significant differences may appear, mainly because of extrinsic parameters such as stress.
Thus, if we keep stress at a fixed but non-zero value, equation [1.19] becomes (again with α′ positive and therefore α″ zero for a second-order transition):
[1.24] ![]()
This gives a transition when the following expression cancels out:
[1.25] 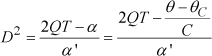
The temperature θCT at which a non-zero electric displacement occurs for a zero field when a stress is applied is therefore:
[1.26] ![]()
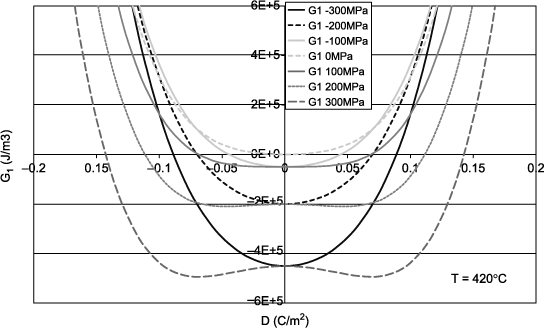
Thus, for the previous example of the PZT, the value of the term 2QCT is 35.4°C for a typical stress of 200 MPa for thin films. Figure 1.5 illustrates the impact of different stresses on the elastic Gibbs energy G1 plotted against D at 420°C, which is above the θC of the material without stress. For zero or negative stress (compression), there is only one minimum that lies at D zero. The material is, therefore, paraelectric. A tensile stress of 100 MPa induces a G1 curve that seems very close to the transition and a stress of 200 MPa clearly shows two minima, even clearer for 300 MPa. Thus, according to equation [1.26], a tensile stress stabilizes the ferroelectric phase by shifting the transition towards high temperature. Qualitatively, for the configuration of a plane capacitor vertically polarized by two electrodes, this means that an out-of-plane traction of the lattice helps to maintain a polarization at zero-field. In the case of BaTiO3, which is tetragonal just below the transition, it is easy to conceive that this traction helps to establish the c-axis off plane. Since the polarization occurs along this axis, it is therefore favored by stress. It should be noted that most discussions on the stresses in thin films involve stresses in the plane and not out-of-plane, which requires an analysis of at least two dimensions. We will have the opportunity to discuss this issue in Chapter 2.
Figure 1.5. Elastic Gibbs energy at 420°C as a function of the electric displacement at different values of applied stress
1.5.4. First-order transition
To complete this description of the transition, the case where α′ is negative and α″ is non-zero in equation [1.18] must be considered. This corresponds to a first-order transition for which the electric displacement shows a discontinuity at the transition. The presence of a latent heat of phase transition should also be noted, unlike second-order transitions. At zero stress, G1 is expressed as:
[1.27] ![]()
The definition of α is slightly different from that of a second-order transition and it is α = (θ-θ0)/C with θ0 the Curie-Weiss temperature that is not quite the same as θC for a first-order transition as we will see α′ and α″ are considered constant.
At equilibrium, when E is set to zero, G = G1–ED is minimal. At zero stress, we obtain the following relation:
[1.28] ![]()
There exists a solution to equation [1.28] for D non-zero corresponding to a minimum:
[1.29] 
The other solution, with a negative sign before the square root, exists between θ0 and θ1. The latter is the temperature that cancels the square root. However, this solution corresponds to a maximum and is therefore not an equilibrium position. θ1 also corresponds to the maximum temperature for which D can be non-zero, even beyond θC . Thus, between θC and θ1, metastable states with non-zero D may exist, as we can observe from Figure 1.6. θ1 is given by the following formula:
[1.30] ![]()
In the paraelectric phase, if E is zero, D is zero and according to equation [1.27], G1 is also zero. Therefore, the solutions with a non-zero value of D correspond to the absolute minimum of G1 if G1 is less than zero for these values of D. Thus, the transition occurs at θC when both G1 and ∂ G1/∂D are zero for a non-zero value of D. We must therefore cancel out equations [1.27] and [1.28] for a non-zero value of D. The resolution of the system gives:
[1.31] ![]()
The inverse of the dielectric susceptibility 1/χ is obtained by differentiating twice equation [1.27] with respect to D:
[1.32] ![]()
Beyond the transition (θ> 0C), D zero is the most stable solution and χ = ε-1=C/(θ-θ0) follows the Curie-Weiss law. Approaching the transition from high temperatures, we have:
[1.33] ![]()
Approaching θC from low temperatures, we can estimate the value and the slope of 1/χ by performing a Taylor expansion that gives:
[1.34] ![]()
The slope of 1/χ as a function of θ is thus eight times bigger before the transition than after (neglecting the sign change). Further, 1/χ remains finite around the transition and the ratio between the values before and after the transition is equal to 4.
To illustrate these formulas, we reconsider the previous numerical example using the following parameters: θ0 = 400°C, C = 105.ε0 F/(m.K), α′ = -8.109 m5/(F3V2), and α″ = 6.1011 m9/(F5V4). The characteristic quantities derived from the previous model are therefore θC = 417.7°C, D(θC) = 0.10 C/m2, and θ1 = 423.6°C.
Figure 1.6 shows the elastic Gibbs energy G1 as a function of D for various temperatures and a zero value of the mechanical stress. Up to 417.7°C (θC) there are two absolute minima for G1, which thus correspond to the two possible states of polarization in the ferroelectric phase (the same modulus but different directions). At 417.7°C, there are three absolute minima for which G1 and its derivative with respect to D cancel out. This is the transition. Between 417.7°C and 423.6°C (θ1), the minima at a non-zero value of D still exist but are no longer the absolute minima: they correspond to metastable equilibria. It is also observed that between 400°C (θ0) and 417.7°C, the solution D = 0 is a minimum, but not absolute. These are metastable states of the paraelectric phase below the transition. For θ > 417.7°C, there is only one absolute equilibrium, the equilibrium at D zero. Thus, at the transition, D passes suddenly from a non-zero value to a zero value.
Figure 1.6. Elastic Gibbs energy G1 as a function of the displacement electric at different temperatures around the first-order transition

To clarify the latter point, Figure 1.7 shows both D metastable and G1 at equilibrium around the transition. D metastable corresponds to the non-zero values of D for which G1(D) is a local minimum as observed in Figure 1.6.
Thus, a decrease of D correlated with an increase of G1 as we approach the transition is observed. When G1 vanishes, the absolute equilibrium is at D zero, and hence the transition takes place here at 417.7°C. The curve also provides information on the values of D for metastable equilibrium states at non-zero values of D between θC and θ1 (423.6°C).
Figure 1.7. Representation of the electric displacement D and the elastic Gibbs energy G1 at equilibrium around the transition. First-order transition case

These metastable states induce an experimental difficulty for unambiguously identifying the transition since, in the example presented above, there is a range of around 20 degrees (between θ0 and θ1) on which both polarization cases (zero and non-zero) may coexist.
Figure 1.8. Inverse of the dielectric susceptibility χ and the relative dielectric constant εr as a function of temperature for a first-order transition

Figure 1.8 clearly shows the inverse of the dielectric susceptibility 1/χ along with the relative dielectric constant εr as a function of the temperature. The most remarkable fact compared to a second-order transition is that εr is finite on either side of the transition although there is a discontinuity. The representation of 1/χ enables us to compare the slopes and the boundaries of the transition. The slopes’s ratio is -7.53 and the ratio of the values of 1/χ just before and just after the transition gives 3.92 according to the proposed simplifications in equations [1.33] and [1.34]. εr goes from 1,420 just before the transition to 5,620 just after transition and thus keeps finite values.
We will not detail the relationships between D and E for the first-order transitions because they are rare in the case of thin films. The interested reader can refer to the book by Lines and Glass [LIN 77, p. 78].
To conclude this chapter, it should be noted that thermodynamic formalism enables us to obtain the value of the phase transition’s latent heat from the value of the electric displacement at the transition. The entropy σ is given by −∂G1/∂θ at fixed T and D. Thus, according to equation [1.27] and the definition of α:
[1.35] ![]()
Thus, on either side of the transition, as D goes from D(θC) to 0, Δσis given by:
[1.36] ![]()
with Lt being the transition’s latent heat. The numerical example gives Lt = 2.36. 106J/m3.
1.6. Conclusion
In this chapter, we have discussed how the macroscopic thermodynamic approach can be developed to explain the behavior of coupled materials and notably of perovskites. In contrast, the microscopic approach is much harder to implement. The electrical, mechanical, and thermal energies are all included in this formalism. It should be noted that all the energetic contributions are valid based on this formalism (notably the magnetic one). However, we will not elaborate further in this regard with special reference to magnetic energy. This thermodynamic approach enables us not only to describe the ferroelectric-paraelectric transition but it can also be used to describe other transitions among ferroelectric phases. It is also possible to predict the dielectric, ferroelectric, piezoelectric, and electrostrictive behavior of the material, unrelated to the phase transitions.
1.7. Bibliography
[DAM 98] DAMJANOVIC D., “Ferroelectric, dielectric and piezoelectric properties of ferroelectric thin films and ceramics”, Reports on Progress in Physics, vol. 61, pp. 1267–1324, 1998.
[DEV 49] DEVONSHIRE A.F., “Theory of Baryum Titanate”, Philosophical Magazine, vol. 40, p. 1040, 1949.
[IEE 87] IEEE, Standard on piezoelectricity, vol. 176, ANSI/IEEE Std, 1987.
[JUN 03] JUNQUERA J., GHOSEZ P., “Critical thickness for ferroelectricity in perovskite ultrathin films”, Nature, no. 422, p. 506, London, 2003.
[KIT 04] KITTEL C., Introduction to Solid State Physics, 8th ed., John Wiley & Sons, New York, 2004.
[LIN 77] LINES M.E., GLASS A.M., Principles and Applications of Ferroelectrics and Related Materials, Clarendon Press, Oxford, 1977.
[MAS 50] MASON W.P., Piezoelectric Crystals and Their Application to Ultrasonics, D. Van Nostrand Company, Princeton, NJ, 1950.
[NYE 85] NYE J.F., Physical Properties of Crystals, Their Representation by Tensors and Matrices, Oxford University Press, Oxford, 1985.
[REI 65] REIF F., Statistical Physics, Berkeley Physics Course, vol. 5, McGraw-Hill, New York, 1965.
[UCH 97] UCHINO K., Piezoelectric Actuators and Ultrasonic Motors, Kluwer Academic Publishers, Dordrecht, 1997.
[VAN 01] VANDERBILT D., COHEN M.H., “Monoclinic and triclinic phases in higher-order Devonshire theory”, Physical Review, vol. B 63, p. 094108, 2001.
1 Chapter written by Emmanuel DEFAŸ.
