CHAPTER 6
YIELD MEASURES, SPOT RATES, AND FORWARD RATES
I. INTRODUCTION
Frequently, investors assess the relative value of a security by some yield or yield spread measure quoted in the market. These measures are based on assumptions that limit their use to gauge relative value. This chapter explains the various yield and yield spread measures and their limitations.
In this chapter, we will see a basic approach to computing the spot rates from the on-the-run Treasury issues. We will see the limitations of the nominal spread measure and explain two measures that overcome these limitations—zero-volatility spread and option-adjusted spread.
II. SOURCES OF RETURN
When an investor purchases a fixed income security, he or she can expect to receive a dollar return from one or more of the following sources:
1. the coupon interest payments made by the issuer
2. any capital gain (or capital loss—a negative dollar return) when the security matures, is called, or is sold
3. income from reinvestment of interim cash flows (interest and/or principal payments prior to stated maturity)
Any yield measure that purports to measure the potential return from a fixed income security should consider all three sources of return described above.
A. Coupon Interest Payments
The most obvious source of return on a bond is the periodic coupon interest payments. For zero-coupon instruments, the return from this source is zero. By purchasing a security below its par value and receiving the full par value at maturity, the investor in a zero-coupon instrument is effectively receiving interest in a lump sum.
B. Capital Gain or Loss
An investor receives cash when a bond matures, is called, or is sold. If these proceeds are greater than the purchase price, a capital gain results. For a bond held to maturity, there will be a capital gain if the bond is purchased below its par value. For example, a bond purchased for $94.17 with a par value of $100 will generate a capital gain of $5.83 ($100−$94.17) if held to maturity. For a callable bond, a capital gain results if the price at which the bond is called (i.e., the call price) is greater than the purchase price. For example, if the bond in our previous example is callable and subsequently called at $100.5, a capital gain of $6.33 ($100.50 − $94.17) will be realized. If the same bond is sold prior to its maturity or before it is called, a capital gain will result if the proceeds exceed the purchase price. So, if our hypothetical bond is sold prior to the maturity date for $103, the capital gain would be $8.83 ($103 − $94.17).
Similarly, for all three outcomes, a capital loss is generated when the proceeds received are less than the purchase price. For a bond held to maturity, there will be a capital loss if the bond is purchased for more than its par value (i.e., purchased at a premium). For example, a bond purchased for $102.50 with a par value of $100 will generate a capital loss of $2.50 ($102.50 − $100) if held to maturity. For a callable bond, a capital loss results if the price at which the bond is called is less than the purchase price. For example, if the bond in our example is callable and subsequently called at $100.50, a capital loss of $2 ($102.50 − $100.50) will be realized. If the same bond is sold prior to its maturity or before it is called, a capital loss will result if the sale price is less than the purchase price. So, if our hypothetical bond is sold prior to the maturity date for $98.50, the capital loss would be $4 ($102.50 −$98.50).
C. Reinvestment Income
Prior to maturity, with the exception of zero-coupon instruments, fixed income securities make periodic interest payments that can be reinvested. Amortizing securities (such as mortgage-backed securities and asset-backed securities) make periodic principal payments that can be reinvested prior to final maturity. The interest earned from reinvesting the interim cash flows (interest and/or principal payments) prior to final or stated maturity is called reinvestment income.
III. TRADITIONAL YIELD MEASURES
Yield measures cited in the bond market include current yield, yield to maturity, yield to call, yield to put, yield to worst, and cash flow yield. These yield measures are expressed as a percent return rather than a dollar return. Below we explain how each measure is calculated and its limitations.
A. Current Yield
The current yield relates the annual dollar coupon interest to a bond’s market price. The formula for the current yield is:
For example, the current yield for a 7% 8-year bond whose price is $94.17 is 7.43% as shown below: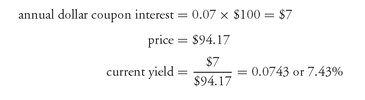
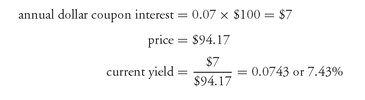
The current yield will be greater than the coupon rate when the bond sells at a discount; the reverse is true for a bond selling at a premium. For a bond selling at par, the current yield will be equal to the coupon rate.
The drawback of the current yield is that it considers only the coupon interest and no other source for an investor’s return. No consideration is given to the capital gain an investor will realize when a bond purchased at a discount is held to maturity; nor is there any recognition of the capital loss an investor will realize if a bond purchased at a premium is held to maturity. No consideration is given to reinvestment income.
B. Yield to Maturity
The most popular measure of yield in the bond market is the yield to maturity. The yield to maturity is the interest rate that will make the present value of a bond’s cash flows equal to its market price plus accrued interest. To find the yield to maturity, we first determine the expected cash flows and then search, by trial and error, for the interest rate that will make the present value of cash flows equal to the market price plus accrued interest. (This is simply a special case of an internal rate of return (IRR) calculation where the cash flows are those received if the bond is held to the maturity date.) In the illustrations presented in this chapter, we assume that the next coupon payment will be six months from now so that there is no accrued interest.
To illustrate, consider a 7% 8-year bond selling for $94.17. The cash flows for this bond are (1) 16 payments every 6-months of $3.50 and (2) a payment sixteen 6-month periods from now of $100. The present value using various semiannual discount (interest) rates is:
When a 4.0% interest rate is used, the present value of the cash flows is equal to $94.17, which is the price of the bond. Hence, 4.0% is the semiannual yield to maturity.
The market convention adopted to annualize the semiannual yield to maturity is to double it and call that the yield to maturity. Thus, the yield to maturity for the above bond is 8% (2 times 4.0%). The yield to maturity computed using this convention—doubling the semiannual yield—is called a bond-equivalent yield.
The following relationships between the price of a bond, coupon rate, current yield, and yield to maturity hold:
| Bond selling at | Relationship |
|---|---|
| par | coupon rate = current yield = yield to maturity |
| discount | coupon rate < current yield < yield to maturity |
| premium | coupon rate > current yield > yield to maturity |
1. The Bond-Equivalent Yield Convention The convention developed in the bond market to move from a semiannual yield to an annual yield is to simply double the semiannual yield. As just noted, this is called the bond-equivalent yield. In general, when one doubles a semiannual yield (or a semiannual return) to obtain an annual measure, one is said to be computing the measure on a bond-equivalent basis.
Students of the bond market are troubled by this convention. The two questions most commonly asked are: First, why is the practice of simply doubling a semiannual yield followed? Second, wouldn’t it be more appropriate to compute the effective annual yield by compounding the semiannual yield?55
The answer to the first question is that it is simply a convention. There is no danger with a convention unless you use it improperly. The fact is that market participants recognize that a yield (or return) is computed on a semiannual basis by convention and adjust accordingly when using the number. So, if the bond-equivalent yield on a security purchased by an investor is 6%, the investor knows the semiannual yield is 3%. Given that, the investor can use that semiannual yield to compute an effective annual yield or any other annualized measure desired. For a manager comparing the yield on a security as an asset purchased to a yield required on a liability to satisfy, the yield figure will be measured in a manner consistent with that of the yield required on the liability.
The answer to the second question is that it is true that computing an effective annual yield would be better. But so what? Once we discover the limitations of yield measures in general, we will question whether or not an investor should use a bond-equivalent yield measure or an effective annual yield measure in making investment decisions. That is, when we identify the major problems with yield measures, the doubling of a semiannual yield is the least of our problems.
So, don’t lose any sleep over this convention. Just make sure that you use a bond-equivalent yield measure properly.
2. Limitations of Yield-to-Maturity Measure The yield to maturity considers not only the coupon income but any capital gain or loss that the investor will realize by holding the bond to maturity. The yield to maturity also considers the timing of the cash flows. It does consider reinvestment income; however, it assumes that the coupon payments can be reinvested at an interest rate equal to the yield to maturity. So, if the yield to maturity for a bond is 8%, for example, to earn that yield the coupon payments must be reinvested at an interest rate equal to 8%.
The illustrations below clearly demonstrate this. In the illustrations, the analysis will be in terms of dollars. Be sure you keep in mind the difference between the total future dollars, which is equal to all the dollars an investor expects to receive (including the recovery of the principal), and the total dollar return, which is equal to the dollars an investor expects to realize from the three sources of return (coupon payments, capital gain/loss, and reinvestment income).
Suppose an investor has $94.17 and places the funds in a certificate of deposit (CD) that matures in 8 years. Let’s suppose that the bank agrees to pay 4% interest every six months. This means that the bank is agreeing to pay 8% on a bond equivalent basis (i.e., doubling the semiannual yield). We can translate all of this into the total future dollars that will be generated by this investment at the end of 8 years. From the standard formula for the future value of an investment today, we can determine the total future dollars as:
$94.17 × (1.04)16 = $176.38
So, to an investor who invests $94.17 for 8 years at an 8% yield on a bond equivalent basis and interest is paid semiannually, the investment will generate $176.38. Decomposing the total future dollars we see that:
Thus, any investment that promises a yield of 8% on a bond equivalent basis for 8 years on an investment of $94.17 must generate total future dollars of $176.38 or equivalently a return from all sources of $82.21. That is, if we look at the three sources of a bond return that offered an 8% yield with semiannual coupon payments and sold at a price of $94.17, the following would have to hold: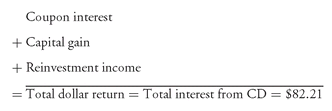
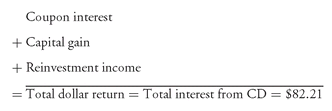
Now, instead of a certificate of deposit, suppose that an investor purchases a bond with a coupon rate of 7% that matures in 8 years. We know that the three sources of return are coupon income, capital gain/loss, and reinvestment income. Suppose that the price of this bond is $94.17. The yield to maturity for this bond (on a bond equivalent basis) is 8%. Notice that this is the same type of investment as the certificate of deposit—the bank offered an 8% yield on a bond equivalent basis for 8 years and made payments semiannually. So, what should the investor in this bond expect in terms of total future dollars? As we just demonstrated, an investment of $94.17 must generate $176.38 in order to say that it provided a yield of 8%. Or equivalently, the total dollar return that must be generated is $82.21. Let’s look at what in fact is generated in terms of dollar return.
The coupon is $3.50 every six months. So the dollar return from the coupon interest is $3.50 for 16 six-month periods, or $56. When the bond matures, there is a capital gain of $5.83 ($100 − $94.17). Therefore, based on these two sources of return we have:
Something’s wrong here. Only $61.83 is generated from the bond whereas $82.21 is needed in order to say that this bond provided an 8% yield. That is, there is a dollar return shortfall of $20.38 ($82.21 − $61.83). How is this dollar return shortfall generated?
Recall that in the case of the certificate of deposit, the bank does the reinvesting of the principal and interest, and pays 4% every six months or 8% on a bond equivalent basis. In contrast, for the bond, the investor has to reinvest any coupon interest until the bond matures. It is the reinvestment income that must generate the dollar return shortfall of $20.38. But at what yield will the investor have to reinvest the coupon payments in order to generate the $20.38? The answer is: the yield to maturity.56 That is, the reinvestment income will be $20.38 if each semiannual coupon payment of $3.50 can be reinvested at a semiannual yield of 4% (one half the yield to maturity). The reinvestment income earned on a given coupon payment of $3.50, if it is invested from the time of receipt in period t to the maturity date (16 periods in our example) at a 4% semiannual rate, is:
$3.50 (1.04)16−t − $3.50
The first coupon payment (t = 1) can be reinvested for 15 periods. Applying the formula above we find the reinvestment income earned on the first coupon payment is:
$3.50 (1.04)16−1 − $3.50 = $2.80
Similarly, the reinvestment income for all coupon payments is shown below: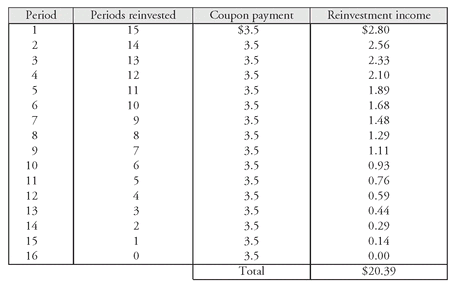
The total reinvestment income is $20.39 (differing from $20.38 due to rounding).
So, with the reinvestment income of $20.38 at 4% semiannually (i.e., one half the yield to maturity on a bond-equivalent basis), the total dollar return is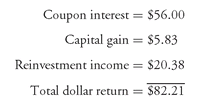
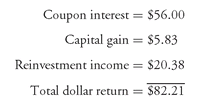
In our illustration, we used an investment in a certificate of deposit to show what the total future dollars will have to be in order to obtain a yield of 8% on an investment of $94.17 for 8 years when interest payments are semiannual. However, this holds for any type of investment, not just a certificate of deposit. For example, if an investor is told that he or she can purchase a debt instrument for $94.17 that offers an 8% yield (on a bond-equivalent basis) for 8 years and makes interest payments semiannually, then the investor should translate this yield into the following:
I should be receiving total future dollars of $176.38
I should be receiving a total dollar return of $82.21
I should be receiving a total dollar return of $82.21
It is always important to think in terms of dollars (or pound sterling, yen, or other currency) because “yield measures” are misleading.
We can also see that the reinvestment income can be a significant portion of the total dollar return. In our example, the total dollar return is $82.21 and the total dollar return from reinvestment income to make up the shortfall is $20.38. This means that reinvestment income is about 25% of the total dollar return.
This is such an important point that we should go through this one more time for another bond. Suppose an investor purchases a 15-year 8% coupon bond at par value ($100). The yield for this bond is simple to determine since the bond is trading at par. The yield is equal to the coupon rate, 8%. Let’s translate this into dollars. We know that if an investor makes an investment of $100 for 15 years that offers an 8% yield and the interest payments are semiannual, the total future dollars will be:
$100 × (1.04)30 = $324.34
Decomposing the total future dollars we see that: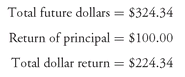
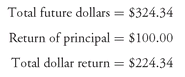
Without reinvestment income, the dollar return is:
Note that the capital gain is $0 because the bond is purchased at par value.
The dollar return shortfall is therefore $104.34 ($224.34 − $120). This shortfall is made up if the coupon payments can be reinvested at a yield of 8% (the yield on the bond at the time of purchase). For this bond, the reinvestment income is 46.5% of the total dollar return needed to produce a yield of 8% ($104.34/$224.34).57
Clearly, the investor will only realize the yield to maturity stated at the time of purchase if the following two assumptions hold:
Assumption 1: the coupon payments can be reinvested at the yield to maturity
Assumption 2: the bond is held to maturity
Assumption 2: the bond is held to maturity
With respect to the first assumption, the risk that an investor faces is that future interest rates will be less than the yield to maturity at the time the bond is purchased, known as reinvestment risk. If the bond is not held to maturity, the investor faces the risk that he may have to sell for less than the purchase price, resulting in a return that is less than the yield to maturity, known as interest rate risk.
3. Factors Affecting Reinvestment Risk There are two characteristics of a bond that affect the degree of reinvestment risk:
Characteristic 1. For a given yield to maturity and a given non-zero coupon rate, the longer the maturity, the more the bond’s total dollar return depends on reinvestment income to realize the yield to maturity at the time of purchase. That is, the greater the reinvestment risk.
The implication is the yield to maturity measure for long-term maturity coupon bonds tells little about the potential return that an investor may realize if the bond is held to maturity. For long-term bonds, in high interest rate environments, the reinvestment income component may be as high as 70% of the bond’s total dollar return.
Characteristic 2. For a coupon paying bond, for a given maturity and a given yield to maturity, the higher the coupon rate, the more dependent the bond’s total dollar return will be on the reinvestment of the coupon payments in order to produce the yield to maturity at the time of purchase.
This means that holding maturity and yield to maturity constant, bonds selling at a premium will be more dependent on reinvestment income than bonds selling at par. This is because the reinvestment income has to make up the capital loss due to amortizing the price premium when holding the bond to maturity. In contrast, a bond selling at a discount will be less dependent on reinvestment income than a bond selling at par because a portion of the return is coming from the capital gain due to accrediting the price discount when holding the bond to maturity. For zero-coupon bonds, none of the bond’s total dollar return is dependent on reinvestment income. So, a zero-coupon bond has no reinvestment risk if held to maturity.
EXHIBIT 1 Percentage of Total Dollar Return from Reinvestment Income for a Bond to Generate an 8% Yield (BEY)
The dependence of the total dollar return on reinvestment income for bonds with different coupon rates and maturities is shown in Exhibit 1.
4. Comparing Semiannual-Pay and Annual-Pay Bonds In our yield calculations, we have been dealing with bonds that pay interest semiannually. A non-U.S. bond may pay interest annually rather than semiannually. This is the case for many government bonds in Europe and Eurobonds. In such instances, an adjustment is required to make a direct comparison between the yield to maturity on a U.S. fixed-rate bond and that on an annual-pay non-U.S. fixed-rate bond.
Given the yield to maturity on an annual-pay bond, its bond-equivalent yield is computed as follows:
bond-equivalent yield of an annual-pay bond = 2[(1 + yield on annual-pay bond)0.5 − 1]
The term in the square brackets involves determining what semiannual yield, when compounded, produces the yield on an annual-pay bond. Doubling this semiannual yield (i.e., multiplying the term in the square brackets by 2), gives the bond-equivalent yield.
For example, suppose that the yield to maturity on an annual-pay bond is 6%. Then the bond-equivalent yield is:
2[(1.06)0.5 − 1] = 5.91%
Notice that the bond-equivalent yield will always be less than the annual-pay bond’s yield to maturity.
To convert the bond-equivalent yield of a U.S. bond issue to an annual-pay basis so that it can be compared to the yield on an annual-pay bond, the following formula can be used: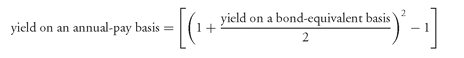
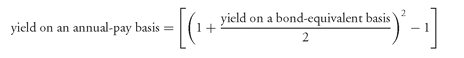
By dividing the yield on a bond-equivalent basis by 2 in the above expression, the semiannual yield is computed. The semiannual yield is then compounded to get the yield on an annual-pay basis.
For example, suppose that the yield of a U.S. bond issue quoted on a bond-equivalent basis is 6%. The yield to maturity on an annual-pay basis would be:
[(1.03)2 − 1] = 6.09%
The yield on an annual-pay basis is always greater than the yield on a bond-equivalent basis because of compounding.
C. Yield to Call
When a bond is callable, the practice has been to calculate a yield to call as well as a yield to maturity. A callable bond may have a call schedule.58 The yield to call assumes the issuer will call a bond on some assumed call date and that the call price is the price specified in the call schedule. Typically, investors calculate a yield to first call or yield to next call, a yield to first par call, and a yield to refunding. The yield to first call is computed for an issue that is not currently callable, while the yield to next call is computed for an issue that is currently callable.
Yield to refunding is used when bonds are currently callable but have some restrictions on the source of funds used to buy back the debt when a call is exercised. Namely, if a debt issue contains some refunding protection, bonds cannot be called for a certain period of time with the proceeds of other debt issues sold at a lower cost of money. As a result, the bondholder is afforded some protection if interest rates decline and the issuer can obtain lower-cost funds to pay off the debt. It should be stressed that the bonds can be called with funds derived from other sources (e.g., cash on hand) during the refunded-protected period. The refunding date is the first date the bond can be called using lower-cost debt.
The procedure for calculating any yield to call measure is the same as for any yield to maturity calculation: determine the interest rate that will make the present value of the expected cash flows equal to the price plus accrued interest. In the case of yield to first call, the expected cash flows are the coupon payments to the first call date and the call price. For the yield to first par call, the expected cash flows are the coupon payments to the first date at which the issuer can call the bond at par and the par value. For the yield to refunding, the expected cash flows are the coupon payments to the first refunding date and the call price at the first refunding date.
To illustrate the computation, consider a 7% 8-year bond with a maturity value of $100 selling for $106.36. Suppose that the first call date is three years from now and the call price is $103. The cash flows for this bond if it is called in three years are (1) 6 coupon payments of $3.50 every six months and (2) $103 in six 6-month periods from now.
The present value for several semiannual interest rates is shown in Exhibit 2. Since a semiannual interest rate of 2.8% makes the present value of the cash flows equal to the price, 2.8% is the yield to first call. Therefore, the yield to first call on a bond-equivalent basis is 5.6%.
EXHIBIT 2 Yield to Call for an 8-year 7% Coupon Bond with a Maturity Value of $100. First Call Date Is the End of Year 3, and Call Price of $103.
For our 7% 8-year callable bond, suppose that the first par call date is 5 years from now. The cash flows for computing the first par call are then: (1) a total 10 coupon payments of $3.50 each paid every six months and (2) $100 in ten 6-month periods. The yield to par call is 5.53%. Let’s verify that this is the case. The semiannual yield is 2.765% (one half of 5.53%). The present value of the 10 coupon payments of $3.50 every six months when discounted at 2.765% is $30.22. The present value of $100 (the call price of par) at the end of five years (10 semiannual periods) is $76.13. The present value of the cash flow is then $106.35 (= $30.22 + $76.13). Since the price of the bond is $106.36 and since using a yield of 5.53% produces a value for this callable bond that differs from $106.36 by only 1 penny, 5.53% is the yield to first par call.
Let’s take a closer look at the yield to call as a measure of the potential return of a security. The yield to call considers all three sources of potential return from owning a bond. However, as in the case of the yield to maturity, it assumes that all cash flows can be reinvested at the yield to call until the assumed call date. As we just demonstrated, this assumption may be inappropriate. Moreover, the yield to call assumes that
Assumption 1: the investor will hold the bond to the assumed call date
Assumption 2: the issuer will call the bond on that date
Assumption 2: the issuer will call the bond on that date
These assumptions underlying the yield to call are unrealistic. Moreover, comparison of different yields to call with the yield to maturity are meaningless because the cash flows stop at the assumed call date. For example, consider two bonds, M and N. Suppose that the yield to maturity for bond M, a 5-year noncallable bond, is 7.5% while for bond N the yield to call, assuming the bond will be called in three years, is 7.8%. Which bond is better for an investor with a 5-year investment horizon? It’s not possible to tell from the yields cited. If the investor intends to hold the bond for five years and the issuer calls bond N after three years, the total dollar return that will be available at the end of five years will depend on the interest rate that can be earned from investing funds from the call date to the end of the investment horizon.
D. Yield to Put
When a bond is putable, the yield to the first put date is calculated. The yield to put is the interest rate that will make the present value of the cash flows to the first put date equal to the price plus accrued interest. As with all yield measures (except the current yield), yield to put assumes that any interim coupon payments can be reinvested at the yield calculated. Moreover, the yield to put assumes that the bond will be put on the first put date.
For example, suppose that a 6.2% coupon bond maturing in 8 years is putable at par in 3 years. The price of this bond is $102.19. The cash flows for this bond if it is put in three years are: (1) a total of 6 coupon payments of $3.10 each paid every six months and (2) the $100 put price in six 6-month periods from now. The semiannual interest rate that will make the present value of the cash flows equal to the price of $102.19 is 2.7%. Therefore, 2.7% is the semiannual yield to put and 5.4% is the yield to put on a bond equivalent basis.
E. Yield to Worst
A yield can be calculated for every possible call date and put date. In addition, a yield to maturity can be calculated. The lowest of all these possible yields is called the yield to worst. For example, suppose that there are only four possible call dates for a callable bond, that the yield to call assuming each possible call date is 6%, 6.2%, 5.8%, and 5.7%, and that the yield to maturity is 7.5%. Then the yield to worst is the minimum of these yields, 5.7% in our example.
The yield to worst measure holds little meaning as a measure of potential return. It supposedly states that this is the worst possible yield that the investor will realize. However, as we have noted about any yield measure, it does not identify the potential return over some investment horizon. Moreover, the yield to worst does not recognize that each yield calculation used in determining the yield to worst has different exposures to reinvestment risk.
F. Cash Flow Yield
Mortgage-backed securities and asset-backed securities are backed by a pool of loans or receivables. The cash flows for these securities include principal payment as well as interest. The complication that arises is that the individual borrowers whose loans make up the pool typically can prepay their loan in whole or in part prior to the scheduled principal payment dates. Because of principal prepayments, in order to project cash flows it is necessary to make an assumption about the rate at which principal prepayments will occur. This rate is called the prepayment rate or prepayment speed.
Given cash flows based on an assumed prepayment rate, a yield can be calculated. The yield is the interest rate that will make the present value of the projected cash flows equal to the price plus accrued interest. The yield calculated is commonly referred to as a cash flow yield.59
1. Bond-Equivalent Yield Typically, the cash flows for mortgage-backed and asset-backed securities are monthly. Therefore the interest rate that will make the present value of projected principal and interest payments equal to the market price plus accrued interest is a monthly rate. The monthly yield is then annualized as follows.
First, the semiannual effective yield is computed from the monthly yield by compounding it for six months as follows:
effective semiannual yield = (1 + monthly yield)6 − 1
Next, the effective semiannual yield is doubled to get the annual cash flow yield on a bond-equivalent basis. That is,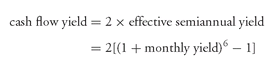
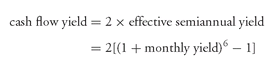
For example, if the monthly yield is 0.5%, then:
cash flow yield on a bond-equivalent basis = 2[(1.005)60 − 1] = 6.08%
The calculation of the cash flow yield may seem strange because it first requires the computing of an effective semiannual yield given the monthly yield and then doubling. This is simply a market convention. Of course, the student of the bond market can always ask the same two questions as with the yield to maturity: Why it is done? Isn’t it better to just compound the monthly yield to get an effective annual yield? The answers are the same as given earlier for the yield to maturity. Moreover, as we will see next, this is the least of our problems in using a cash flow yield measure for an asset-backed and mortgage-backed security.
2. Limitations of Cash Flow Yield As we have noted, the yield to maturity has two shortcomings as a measure of a bond’s potential return: (1) it is assumed that the coupon payments can be reinvested at a rate equal to the yield to maturity and (2) it is assumed that the bond is held to maturity. These shortcomings are equally present in application of the cash flow yield measure: (1) the projected cash flows are assumed to be reinvested at the cash flow yield and (2) the mortgage-backed or asset-backed security is assumed to be held until the final payoff of all the loans, based on some prepayment assumption. The significance of reinvestment risk, the risk that the cash flows will be reinvested at a rate less than the cash flow yield, is particularly important for mortgage-backed and asset-backed securities since payments are typically monthly and include principal payments (scheduled and prepaid), and interest. Moreover, the cash flow yield is dependent on realizing of the projected cash flows according to some prepayment rate. If actual prepayments differ significantly from the prepayment rate assumed, the cash flow yield will not be realized.
G. Spread/Margin Measures for Floating-Rate Securities
The coupon rate for a floating-rate security (or floater) changes periodically according to a reference rate (such as LIBOR or a Treasury rate). Since the future value for the reference rate is unknown, it is not possible to determine the cash flows. This means that a yield to maturity cannot be calculated. Instead, “margin” measures are computed. Margin is simply some spread above the floater’s reference rate.
Several spread or margin measures are routinely used to evaluate floaters. Two margin measures commonly used are spread for life and discount margin.60
1. Spread for Life When a floater is selling at a premium/discount to par, investors consider the premium or discount as an additional source of dollar return. Spread for life (also called simple margin) is a measure of potential return that accounts for the accretion (amortization) of the discount (premium) as well as the constant quoted margin over the security’s remaining life. Spread for life (in basis points) is calculated using the following formula: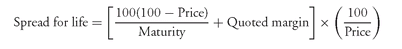
where
For example, suppose that a floater with a quoted margin of 80 basis points is selling for 99.3098 and matures in 6 years. Then,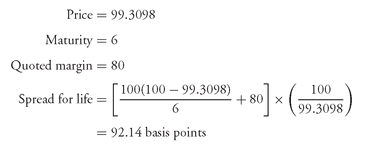
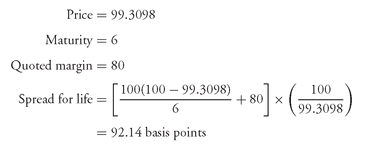
The limitations of the spread for life are that it considers only the accretion/amortization of the discount/premium over the floater’s remaining term to maturity and does not consider the level of the coupon rate or the time value of money.
2. Discount Margin Discount margin estimates the average margin over the reference rate that the investor can expect to earn over the life of the security. The procedure for calculating the discount margin is as follows:
Step 1. Determine the cash flows assuming that the reference rate does not change over the life of the security.
Step 2. Select a margin.
Step 3. Discount the cash flows found in Step 1 by the current value of the reference rate plus the margin selected in Step 2.
Step 4. Compare the present value of the cash flows as calculated in Step 3 to the price plus accrued interest. If the present value is equal to the security’s price plus accrued interest, the discount margin is the margin assumed in Step 2. If the present value is not equal to the security’s price plus accrued interest, go back to Step 2 and try a different margin.
For a security selling at par, the discount margin is simply the quoted margin in the coupon reset formula.
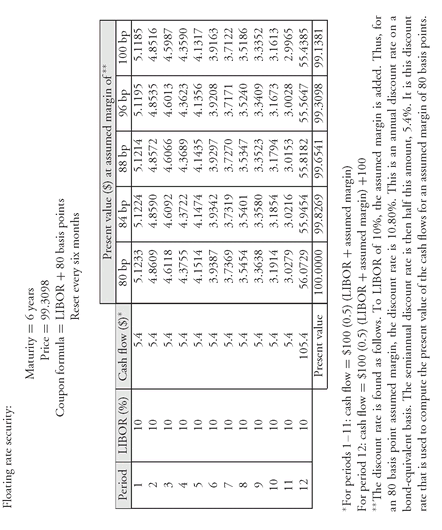
To illustrate the calculation, suppose that the coupon reset formula for a 6-year floating-rate security selling for $99.3098 is 6-month LIBOR plus 80 basis points. The coupon rate is reset every 6 months. Assume that the current value for the reference rate is 10%.
Exhibit 3 shows the calculation of the discount margin for this security. The second column shows the current value for 6-month LIBOR. The third column sets forth the cash flows for the security. The cash flow for the first 11 periods is equal to one-half the current 6-month LIBOR (5%) plus the semiannual quoted margin of 40 basis points multiplied by $100. At the maturity date (i.e., period 12), the cash flow is $5.4 plus the maturity value of $100. The column headings of the last five columns show the assumed margin. The rows below the assumed margin show the present value of each cash flow. The last row gives the total present value of the cash flows.
For the five assumed margins, the present value is equal to the price of the floating-rate security ($99.3098) when the assumed margin is 96 basis points. Therefore, the discount margin is 96 basis points. Notice that the discount margin is 80 basis points, the same as the quoted margin, when this security is selling at par.
There are two drawbacks of the discount margin as a measure of the potential return from investing in a floating-rate security. First, the measure assumes that the reference rate will not change over the life of the security. Second, if the floating-rate security has a cap or floor, this is not taken into consideration.
H. Yield on Treasury Bills
Treasury bills are zero-coupon instruments with a maturity of one year or less. The convention in the Treasury bill market is to calculate a bill’s yield on a discount basis. This yield is determined by two variables:
1. the settlement price per $1 of maturity value (denoted by p)
2. the number of days to maturity which is calculated as the number of days between the settlement date and the maturity date (denoted by NSM )
The yield on a discount basis (denoted by d ) is calculated as follows: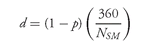
We will use two actual Treasury bills to illustrate the calculation of the yield on a discount basis assuming a settlement date in both cases of 8/6/97. The first bill has a maturity date of 1/8/98 and a price of 0.97769722. For this bill, the number of days from the settlement date to the maturity date, NSM , is 155. Therefore, the yield on a discount basis is
For our second bill, the maturity date is 7/23/98 and the price is 0.9490075. Assuming a settlement date of 8/6/97, the number of days from the settlement date to the maturity date is 351. The yield on a discount basis for this bill is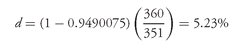
EXHIBIT 3 Calculation of the Discount Margin for a Floating-Rate Security
Given the yield on a discount basis, the price of a bill (per $1 of maturity value) is computed as follows:
p = 1 − d (NSM /360)
For the 155-day bill selling for a yield on a discount basis of 5.18%, the price per $1 of maturity value is
p = 1 − 0.0518 (155/360) = 0.97769722
For the 351-day bill selling for a yield on a discount basis of 5.23%, the price per $1 of maturity value is
p = 1 − 0.0523 (351/360) = 0.9490075
The quoted yield on a discount basis is not a meaningful measure of the return from holding a Treasury bill for two reasons. First, the measure is based on a maturity value investment rather than on the actual dollar amount invested. Second, the yield is annualized according to a 360-day year rather than a 365-day year, making it difficult to compare yields on Treasury bills with Treasury notes and bonds which pay interest based on the actual number of days in a year. The use of 360 days for a year is a convention for money market instruments. Despite its shortcomings as a measure of return, this is the method dealers have adopted to quote Treasury bills.
Market participants recognize this limitation of yield on a discount basis and consequently make adjustments to make the yield quoted on a Treasury bill comparable to that on a Treasury coupon security. For investors who want to compare the yield on Treasury bills to that of other money market instruments (i.e., debt obligations with a maturity that does not exceed one year), there is a formula to convert the yield on a discount basis to that of a money market yield. The key point is that while the convention is to quote the yield on a Treasury bill in terms of a yield on a discount basis, no one uses that yield measure other than to compute the price given the quoted yield.
IV. THEORETICAL SPOT RATES
The theoretical spot rates for Treasury securities represent the appropriate set of interest rates that should be used to value default-free cash flows. A default-free theoretical spot rate curve can be constructed from the observed Treasury yield curve. There are several approaches that are used in practice. The approach that we describe below for creating a theoretical spot rate curve is called bootstrapping. (The bootstrapping method described here is also used in constructing a theoretical spot rate curve for LIBOR.)
A. Bootstrapping
Bootstrapping begins with the yield for the on-the-run Treasury issues because there is no credit risk and no liquidity risk. In practice, however, there is a problem of obtaining a sufficient number of data points for constructing the U.S. Treasury yield curve. In the United States, the U.S. Department of the Treasury currently issues 3-month and 6-month Treasury bills and 2-year, 5-year, and 10-year Treasury notes. Treasury bills are zero-coupon instruments and Treasury notes are coupon-paying instruments. Hence, there are not many data points from which to construct a Treasury yield curve, particularly after two years. At one time, the U.S. Treasury issued 30-year Treasury bonds. Since the Treasury no longer issues 30-year bonds, market participants currently use the last issued Treasury bond (which has a maturity less than 30 years) to estimate the 30-year yield. The 2-year, 5-year, and 10-year Treasury notes and an estimate of the 30-year Treasury bond are used to construct the Treasury yield curve.
On September 5, 2003, Lehman Brothers reported the following values for these four yields:
| 2 year | 1.71% |
| 5 year | 3.25% |
| 10 year | 4.35% |
| 30 year | 5.21% |
To fill in the yield for the 25 missing whole year maturities (3 year, 4 year, 6 year, 7 year, 8 year, 9 year, 11 year, and so on to the 29-year maturity), the yield for the 25 whole year maturities are interpolated from the yield on the surrounding maturities. The simplest interpolation, and the one most commonly used in practice, is simple linear interpolation.
For example, suppose that we want to fill in the gap for each one year of maturity. To determine the amount to add to the on-the-run Treasury yield as we go from the lower maturity to the higher maturity, the following formula is used:
The estimated on-the-run yield for all intermediate whole-year maturities is found by adding the amount computed from the above formula to the yield at the lower maturity.
For example, using the September 5, 2003 yields, the 5-year yield of 3.25% and the 10-year yield of 4.35% are used to obtain the interpolated 6-year, 7-year, 8-year, and 9-year yields by first calculating:
Then,
interpolated 6-year yield = 3.25% + 0.22% = 3.47%
interpolated 7-year yield = 3.47% + 0.22% = 3.69%
interpolated 8-year yield = 3.69% + 0.22% = 3.91%
interpolated 9-year yield = 3.91% + 0.22% = 4.13%
interpolated 7-year yield = 3.47% + 0.22% = 3.69%
interpolated 8-year yield = 3.69% + 0.22% = 3.91%
interpolated 9-year yield = 3.91% + 0.22% = 4.13%
Thus, when market participants talk about a yield on the Treasury yield curve that is not one of the on-the-run maturities—for example, the 8-year yield—it is only an approximation. Notice that there is a large gap between maturity points. This may result in misleading yields for the interim maturity points when estimated using the linear interpolation method, a point that we return to later in this chapter.
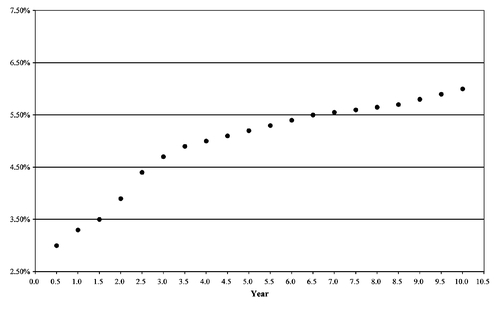
To illustrate bootstrapping, we will use the Treasury yields shown in Exhibit 4 for maturities up to 10 years using 6-month periods.61 Thus, there are 20 Treasury yields shown. The yields shown are assumed to have been interpolated from the on-the-run Treasury issues. Exhibit 5 shows the Treasury yield curve based on the yields shown in Exhibit 4. Our objective is to show how the values in the last column of Exhibit 4 (labeled “Spot rate”) are obtained.
Throughout the analysis and illustrations to come, it is important to remember that the basic principle is the value of the Treasury coupon security should be equal to the value of the package of zero-coupon Treasury securities that duplicates the coupon bond’s cash flows. We saw this in Chapter 5 when we discussed arbitrage-free valuation.
EXHIBIT 4 Hypothetical Treasury Yields (Interpolated)
EXHIBIT 5 Treasury Par Yield Curve
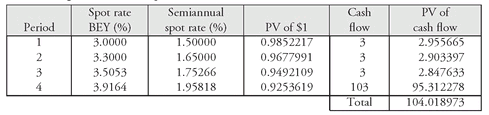
Consider the 6-month and 1-year Treasury securities in Exhibit 4. As we explained in Chapter 5, these two securities are called Treasury bills and they are issued as zero-coupon instruments. Therefore, the annualized yield (not the discount yield) of 3.00% for the 6-month Treasury security is equal to the 6-month spot rate.62 Similarly, for the 1-year Treasury security, the cited yield of 3.30% is the 1-year spot rate. Given these two spot rates, we can compute the spot rate for a theoretical 1.5-year zero-coupon Treasury. The value of a theoretical 1.5-year Treasury should equal the present value of the three cash flows from the 1.5-year coupon Treasury, where the yield used for discounting is the spot rate corresponding to the time of receipt of each six-month cash flow. Since all the coupon bonds are selling at par, as explained in the previous section, the yield to maturity for each bond is the coupon rate. Using $100 par, the cash flows for the 1.5-year coupon Treasury are:
| 0.5 year | 0.035 × $100 × 0.5 | = $1.75 |
| 1.0 year | 0.035 × $100 × 0.5 | = $1.75 |
| 1.5 years | 0.035 × $100 × 0.5 + 100 | = $101.75 |
The present value of the cash flows is then:
where
z1 = one-half the annualized 6-month theoretical spot rate
z2 = one-half the 1-year theoretical spot rate
z3 = one-half the 1.5-year theoretical spot rate
Since the 6-month spot rate is 3% and the 1-year spot rate is 3.30%, we know that:
z1 = 0.0150 and z2 = 0.0165
We can compute the present value of the 1.5-year coupon Treasury security as:
Since the price of the 1.5-year coupon Treasury security is par value (see Exhibit 4), the following relationship must hold:63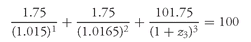 
We can solve for the theoretical 1.5-year spot rate as follows: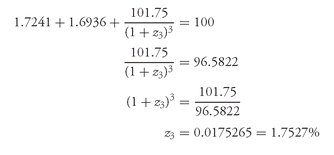
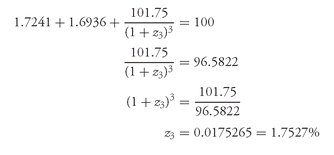
Doubling this yield, we obtain the bond-equivalent yield of 3.5053%, which is the theoretical 1.5-year spot rate. That rate is the rate that the market would apply to a 1.5-year zero-coupon Treasury security if, in fact, such a security existed. In other words, all Treasury cash flows to be received 1.5 years from now should be valued (i.e., discounted) at 3.5053%.
Given the theoretical 1.5-year spot rate, we can obtain the theoretical 2-year spot rate. The cash flows for the 2-year coupon Treasury in Exhibit 3 are:
| 0.5 year | 0.039 × $100 × 0.5 | = $1.95 |
| 1.0 year | 0.039 × $100 × 0.5 | = $1.95 |
| 1.5 years | 0.039 × $100 × 0.5 | = $1.95 |
| 2.0 years | 0.039 × $100 × 0.5 + 100 | = $101.95 |
The present value of the cash flows is then: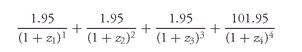
where z4 = one-half the 2-year theoretical spot rate.
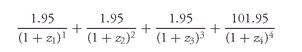
Since the 6-month spot rate, 1-year spot rate, and 1.5-year spot rate are 3.00%, 3.30%, and 3.5053%, respectively, then:
z1 = 0.0150 z2 = 0.0165 z3 = 0.017527
Therefore, the present value of the 2-year coupon Treasury security is: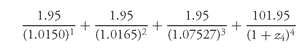
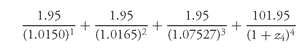
Since the price of the 2-year coupon Treasury security is par, the following relationship must hold: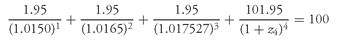
We can solve for the theoretical 2-year spot rate as follows: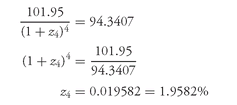
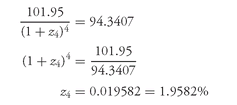
Doubling this yield, we obtain the theoretical 2-year spot rate bond-equivalent yield of 3.9164%.
One can follow this approach sequentially to derive the theoretical 2.5-year spot rate from the calculated values of z1, z2, z3, and z4 (the 6-month-, 1-year-, 1.5-year-, and 2-year rates), and the price and coupon of the 2.5-year bond in Exhibit 4. Further, one could derive theoretical spot rates for the remaining 15 half-yearly rates.
The spot rates thus obtained are shown in the last column of Exhibit 4. They represent the term structure of default-free spot rate for maturities up to 10 years at the particular time to which the bond price quotations refer. In fact, it is the default-free spot rates shown in Exhibit 4 that were used in our illustrations in the previous chapter.
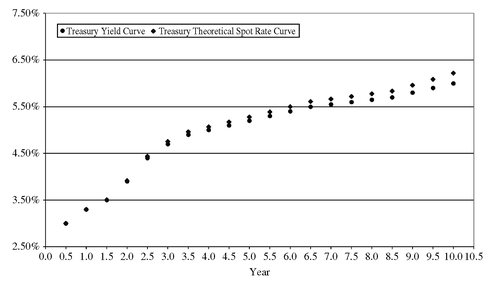
Exhibit 6 shows a plot of the spot rates. The graph is called the theoretical spot rate curve. Also shown on Exhibit 6 is a plot of the par yield curve from Exhibit 5. Notice that the theoretical spot rate curve lies above the par yield curve. This will always be the case when the par yield curve is upward sloping. When the par yield curve is downward sloping, the theoretical spot rate curve will lie below the par yield curve.
B. Yield Spread Measures Relative to a Spot Rate Curve
Traditional analysis of the yield spread for a non-Treasury bond involves calculating the difference between the bond’s yield and the yield to maturity of a benchmark Treasury coupon security. The latter is obtained from the Treasury yield curve. For example, consider the following 10-year bonds:
EXHIBIT 6 Theoretical Spot Rate Curve and Treasury Yield Curve
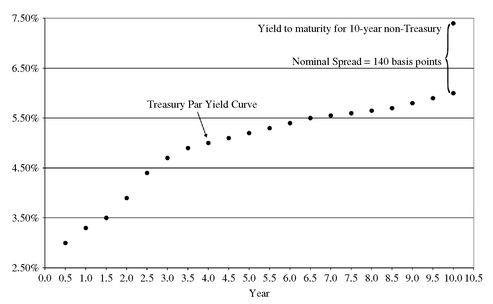
The yield spread for these two bonds as traditionally computed is 140 basis points (7.4% minus 6%). We have referred to this traditional yield spread as the nominal spread.
Exhibit 7 shows the Treasury yield curve from Exhibit 5. The nominal spread of 140 basis points is the difference between the 7.4% yield to maturity for the 10-year non-Treasury security and the yield on the 10-year Treasury, 6%.
What is the nominal spread measuring? It is measuring the compensation for the additional credit risk, option risk (i.e., the risk associated with embedded options),64 and liquidity risk an investor is exposed to by investing in a non-Treasury security rather than a Treasury security with the same maturity.
The drawbacks of the nominal spread measure are
1. for both bonds, the yield fails to take into consideration the term structure of spot rates and
2. in the case of callable and/or putable bonds, expected interest rate volatility may alter the cash flows of the non-Treasury bond.
Let’s examine each of the drawbacks and alternative spread measures for handling them.
1. Zero-Volatility Spread The zero-volatility spread or Z-spread is a measure of the spread that the investor would realize over the entire Treasury spot rate curve if the bond is held to maturity. It is not a spread off one point on the Treasury yield curve, as is the nominal spread. The Z-spread, also called the static spread, is calculated as the spread that will make the present value of the cash flows from the non-Treasury bond, when discounted at the Treasury spot rate plus the spread, equal to the non-Treasury bond’s price. A trial-and-error procedure is required to determine the Z-spread.
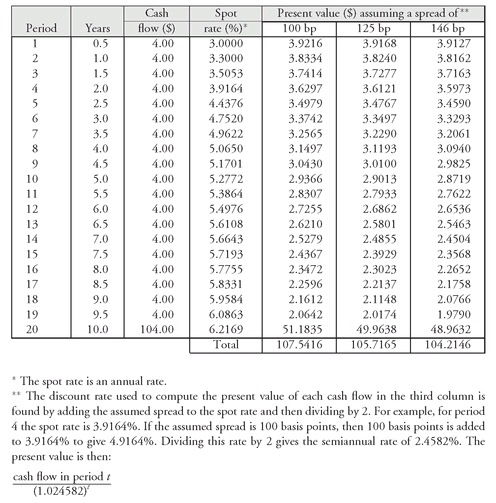
To illustrate how this is done, let’s use the non-Treasury bond in our previous illustration and the Treasury spot rates in Exhibit 4. These spot rates are repeated in Exhibit 8. The third column in Exhibit 8 shows the cash flows for the 8% 10-year non-Treasury issue. The goal is to determine the spread that, when added to all the Treasury spot rates, will produce a present value for the cash flows of the non-Treasury bond equal to its market price of $104.19.
EXHIBIT 7 Illustration of the Nominal Spread
Suppose we select a spread of 100 basis points. To each Treasury spot rate shown in the fourth column of Exhibit 8, 100 basis points is added. So, for example, the 5-year (period 10) spot rate is 6.2772% (5.2772% plus 1%). The spot rate plus 100 basis points is then used to calculate the present values as shown in the fifth column. The total present value of the fifth column is $107.5414. Because the present value is not equal to the non-Treasury issue’s price ($104.19), the Z-spread is not 100 basis points. If a spread of 125 basis points is tried, it can be seen from the next-to-the-last column of Exhibit 8 that the present value is $105.7165; again, because this is not equal to the non-Treasury issue’s price, 125 basis points is not the Z-spread. The last column of Exhibit 8 shows the present value when a 146 basis point spread is tried. The present value is equal to the non-Treasury issue’s price. Therefore 146 basis points is the Z-spread, compared to the nominal spread of 140 basis points.
A graphical presentation of the Z-spread is shown in Exhibit 9. Since the benchmark for computing the Z-spread is the theoretical spot rate curve, that curve is shown in the exhibit. Above each yield at each maturity on the theoretical spot rate curve is a yield that is 146 basis points higher. This is the Z-spread. It is a spread over the entire spot rate curve.
What should be clear is that the difference between the nominal spread and the Z-spread is the benchmark that is being used: the nominal spread is a spread off of one point on the Treasury yield curve (see Exhibit 7) while the Z-spread is a spread over the entire theoretical Treasury spot rate curve.
What does the Z-sp read represent for this non-Treasury security? Since the Z-spread is measured relative to the Treasury spot rate curve, it represents a spread to compensate for the non-Treasury security’s credit risk, liquidity risk, and any option risk (i.e., the risks associated with any embedded options).
EXHIBIT 8 Determining Z-Spread for an 8% Coupon, 10-Year Non-Treasury Issue Selling at $104.19 to Yield 7.4%
a. Divergence Between Z-Spread and Nominal Spread Typically, for standard coupon-paying bonds with a bullet maturity (i.e., a single payment of principal) the Z-spread and the nominal spread will not differ significantly. In our example, it is only 6 basis points. In general terms, the divergence (i.e., amount of difference) is a function of (1) the shape of the term structure of interest rates and (2) the characteristics of the security (i.e., coupon rate, time to maturity, and type of principal payment provision—non-amortizing versus amortizing).
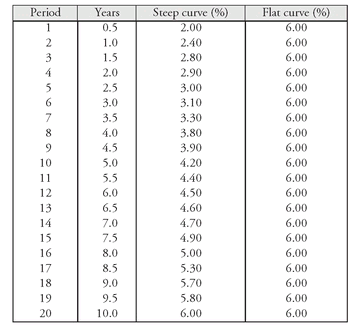
For short-term issues, there is little divergence. The main factor causing any difference is the shape of the Treasury spot rate curve. The steeper the spot rate curve, the greater the difference. To illustrate this, consider the two spot rate curves shown in Exhibit 10. The yield for the longest maturity of both spot rate curves is 6%. The first curve is steeper than the one used in Exhibit 8; the second curve is flat, with the yield for all maturities equal to 6%. For our 8% 10-year non-Treasury issue, it can be shown that for the first spot rate curve in Exhibit 10 the Z-spread is 192 basis points. Thus, with this steeper spot rate curve, the difference between the Z-spread and the nominal spread is 52 basis points. For the flat curve the Z-spread is 140 basis points, the same as the nominal spread. This will always be the case because the nominal spread assumes that the same yield is used to discount each cash flow and, with a flat yield curve, the same yield is being used to discount each flow. Thus, the nominal yield spread and the Z-spread will produce the same value for this security.
EXHIBIT 9 Illustration of the Z Spread
The difference between the Z-spread and the nominal spread is greater for issues in which the principal is repaid over time rather than only at maturity. Thus, the difference between the nominal spread and the Z-spread will be considerably greater for mortgage-backed and asset-backed securities in a steep yield curve environment. We can see this intuitively if we think in terms of a 10-year zero-coupon bond and a 10-year amortizing security with equal semiannual cash flows (that includes interest and principal payment). The Z-spread for the zero-coupon bond will not be affected by the shape of the term structure but the amortizing security will be.
EXHIBIT 10 Two Hypothetical Spot Rate Curves
b. Z-Spread Relative to Any Benchmark In the same way that a Z-spread relative to a Treasury spot rate curve can be calculated, a Z-spread to any benchmark spot rate curve can be calculated. To illustrate, suppose that a hypothetical non-Treasury security with a coupon rate of 8% and a 10-year maturity is trading at $105.5423. Assume that the benchmark spot rate curve for this issuer is the one given in Exhibit 10 of the previous chapter. The Z-spread relative to that issuer’s benchmark spot rate curve is the spread that must be added to the spot rates shown in the next-to-last column of that exhibit that will make the present value of the cash flows equal to the market price. In our illustration, the Z-spread relative to this benchmark is 40 basis points.
What does the Z-spread mean when the benchmark is not the Treasury spot rate curve (i.e., default-free spot rate curve)? When the Treasury spot rate curve is the benchmark, we said that the Z-spread for a non-Treasury issue embodies credit risk, liquidity risk, and any option risk. When the benchmark is the spot rate curve for the issuer, the Z-spread is measuring the spread attributable to the liquidity risk of the issue and any option risk.
Thus, when a Z-spread is cited, it must be cited relative to some benchmark spot rate curve. This is necessary because it indicates the credit and sector risks that are being considered when the Z-spread was calculated. While Z-spreads are typically calculated using Treasury securities as the benchmark interest rates, this need not be the case. Vendors of analytical systems commonly allow the user to select a benchmark spot rate curve. Moreover, in non-U.S. markets, Treasury securities are typically not the benchmark. The key point is that an investor should always ask what benchmark was used to compute the Z-spread.
2. Option-Adjusted Spread The Z-spread seeks to measure the spread over a spot rate curve thus overcoming the first problem of the nominal spread that we cited earlier. Now let’s look at the second shortcoming—failure to take future interest rate volatility into account which could change the cash flows for bonds with embedded options.
a. Valuation Models What investors seek to do is to buy undervalued securities (securities whose value is greater than their price). Before they can do this though, they need to know what the security is worth (i.e., a fair price to pay). A valuation model is designed to provide precisely this. If a model determines the fair price of a share of common stock is $36 and the market price is currently $24, then the stock is considered to be undervalued. If a bond is selling for less than its fair value, then it too is considered undervalued.
A valuation model need not stop here, however. Market participants find it more convenient to think about yield spread than about price differences. A valuation model can take this difference between the fair price and the market price and convert it into a yield spread measure. Instead of asking, “How much is this security undervalued?”, the model can ask, “How much return will I earn in exchange for taking on these risks?”
The option-adjusted spread (OAS) was developed as a way of doing just this: taking the dollar difference between the fair price and market price and converting it into a yield spread measure. Thus, the OAS is used to reconcile the fair price (or value) to the market price by finding a return (spread) that will equate the two (using a trial and error procedure). This is somewhat similar to what we did earlier when calculating yield to maturity, yield to call, etc., only in this case, we are calculating a spread (measured in basis points) rather than a percentage rate of return as we did then.
The OAS is model dependent. That is, the OAS computed depends on the valuation model used. In particular, OAS models differ considerably in how they forecast interest rate changes, leading to variations in the level of OAS. What are two of these key modeling differences?
• Interest rate volatility is a critical assumption. Specifically, the higher the interest rate volatility assumed, the lower the OAS. In comparing the OAS of dealer firms, it is important to check on the volatility assumption made.
• The OAS is a spread, but what is it a “spread” over? The OAS is a spread over the Treasury spot rate curve or the issuer’s benchmark used in the analysis. In the model, the spot rate curve is actually the result of a series of assumptions that allow for changes in interest rates. Again, different models yield different results.
Why is the spread referred to as “option adjusted”? Because the security’s embedded option can change the cash flows; the value of the security should take this change of cash flow into account. Note that the Z-spread doesn’t do this—it ignores the fact that interest rate changes can affect the cash flows. In essence, it assumes that interest rate volatility is zero. This is why the Z-spread is also referred to as the zero-volatility OAS.
b. Option Cost The implied cost of the option embedded in any security can be obtained by calculating the difference between the OAS at the assumed interest rate or yield volatility and the Z-spread. That is, since the Z-spread is just the sum of the OAS and option cost, i.e.,
it follows that:
Z-spread = OAS + option cost
option cost = Z-spread − OAS
The reason that the option cost is measured in this way is as follows. In an environment in which interest rates are assumed not to change, the investor would earn the Z-spread. When future interest rates are uncertain, the spread is different because of the embedded option(s); the OAS reflects the spread after adjusting for this option. Therefore, the option cost is the difference between the spread that would be earned in a static interest rate environment (the Z-spread, or equivalently, the zero-volatility OAS) and the spread after adjusting for the option (the OAS).
For callable bonds and most mortgage-backed and asset-backed securities, the option cost is positive. This is because the issuer’s ability to alter the cash flows will result in an OAS that is less than the Z-spread. In the case of a putable bond, the OAS is greater than the Z-spread so that the option cost is negative. This occurs because of the investor’s ability to alter the cash flows.
In general, when the option cost is positive, this means that the investor has sold an option to the issuer or borrower. This is true for callable bonds and most mortgage-backed and asset-backed securities. A negative value for the option cost means that the investor has purchased an option from the issuer or borrower. A putable bond is an example of this negative option cost. There are certain securities in the mortgage-backed securities market that also have an option cost that is negative.
c. Highlighting the Pitfalls of the Nominal Spread We can use the concepts presented in this chapter to highlight the pitfalls of the nominal spread. First, we can recast the relationship between the option cost, Z-spread, and OAS as follows:
Z-spread = OAS + option cost
Next, recall that the nominal spread and the Z-spread may not diverge significantly. Suppose that the nominal spread is approximately equal to the Z-spread. Then, we can substitute nominal spread for Z-spread in the previous relationship giving:
nominal spread ≈ OAS + option cost
This relationship tells us that a high nominal spread could be hiding a high option cost. The option cost represents the portion of the spread that the investor has given to the issuer or borrower. Thus, while the nominal spread for a security that can be called or prepaid might be, say 200 basis points, the option cost may be 190 and the OAS only 10 basis points. But, an investor is only compensated for the OAS. An investor that relies on the nominal spread may not be adequately compensated for taking on the option risk associated with a security with an embedded option.
3. Summary of Spread Measures We have just described three spread measures:
• nominal spread
• zero-volatility spread
• option-adjusted spread
To understand different spread measures we ask two questions:
1. What is the benchmark for computing the spread? That is, what is the spread measured relative to?
2. What is the spread measuring?
The table below provides a summary showing for each of the three spread measures the benchmark and the risks for which the spread is compensating.
| Spread measure | Benchmark | Reflects compensation for: |
|---|---|---|
| Nominal | Treasury yield curve | Credit risk, option risk, liquidity risk |
| Zero-volatility | Treasury spot rate curve | Credit risk, option risk, liquidity risk |
| Option-adjusted | Treasury spot rate curve | Credit risk, liquidity risk |
V. FORWARD RATES
We have seen how a default-free theoretical spot rate curve can be extrapolated from the Treasury yield curve. Additional information useful to market participants can be extrapolated from the default-free theoretical spot rate curve: forward rates. Under certain assumptions described later, these rates can be viewed as the market’s consensus of future interest rates.
Examples of forward rates that can be calculated from the default-free theoretical spot rate curve are the:
• 6-month forward rate six months from now
• 6-month forward rate three years from now
• 1-year forward rate one year from now
• 3-year forward rate two years from now
• 5-year forward rates three years from now
Since the forward rates are implicitly extrapolated from the default-free theoretical spot rate curve, these rates are sometimes referred to as implied forward rates. We begin by showing how to compute the 6-month forward rates. Then we explain how to compute any forward rate.
While we continue to use the Treasury yield curve in our illustrations, as noted earlier, a LIBOR spot rate curve can also be constructed using the bootstrapping methodology and forward rates for LIBOR can be obtained in the same manner as described below.
A. Deriving 6-Month Forward Rates
To illustrate the process of extrapolating 6-month forward rates, we will use the yield curve and corresponding spot rate curve from Exhibit 4. We will use a very simple arbitrage principle as we did earlier in this chapter to derive the spot rates. Specifically, if two investments have the same cash flows and have the same risk, they should have the same value.
Consider an investor who has a 1-year investment horizon and is faced with the following two alternatives:
• buy a 1-year Treasury bill, or
• buy a 6-month Treasury bill and, when it matures in six months, buy another 6-month Treasury bill.
The investor will be indifferent toward the two alternatives if they produce the same return over the 1-year investment horizon. The investor knows the spot rate on the 6-month Treasury bill and the 1-year Treasury bill. However, he does not know what yield will be on a 6-month Treasury bill purchased six months from now. That is, he does not know the 6-month forward rate six months from now. Given the spot rates for the 6-month Treasury bill and the 1-year Treasury bill, the forward rate on a 6-month Treasury bill is the rate that equalizes the dollar return between the two alternatives.
To see how that rate can be determined, suppose that an investor purchased a 6-month Treasury bill for $X . At the end of six months, the value of this investment would be:
where z1 is one-half the bond-equivalent yield (BEY) of the theoretical 6-month spot rate.
X (1 + z1)
Let f represent one-half the forward rate (expressed as a BEY) on a 6-month Treasury bill available six months from now. If the investor were to rollover his investment by purchasing that bill at that time, then the future dollars available at the end of one year from the X investment would be:
X (1 + z1)(1 + f )
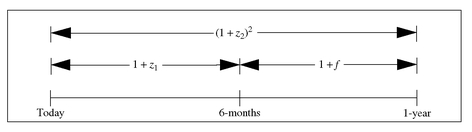
EXHIBIT 11 Graphical Depiction of the Six-Month Forward Rate Six Months from Now
Now consider the alternative of investing in a 1-year Treasury bill. If we let z2 represent one-half the BEY of the theoretical 1-year spot rate, then the future dollars available at the end of one year from the X investment would be:
X (1 + z2)2
The reason that the squared term appears is that the amount invested is being compounded for two periods. (Recall that each period is six months.)
The two choices are depicted in Exhibit 11. Now we are prepared to analyze the investor’s choices and what this says about forward rates. The investor will be indifferent toward the two alternatives confronting him if he makes the same dollar investment ($X ) and receives the same future dollars from both alternatives at the end of one year. That is, the investor will be indifferent if:
Solving for f , we get: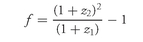
X (1 + z1)(1 + f ) = X (1 + z2)2
Doubling f gives the BEY for the 6-month forward rate six months from now.
We can illustrate the use of this formula with the theoretical spot rates shown in Exhibit 4. From that exhibit, we know that:
6-month bill spot rate = 0.030, therefore z1 = 0.0150
1-year bill spot rate = 0.033, therefore z2 = 0.0165
1-year bill spot rate = 0.033, therefore z2 = 0.0165
Substituting into the formula, we have: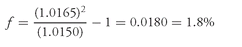
Therefore, the 6-month forward rate six months from now is 3.6% (1.8% × 2) BEY.
Let’s confirm our results. If X is invested in the 6-month Treasury bill at 1.5% and the proceeds then reinvested for six months at the 6-month forward rate of 1.8%, the total proceeds from this alternative would be:
X (1.015)(1.018) = 1.03327 X
Investment of X in the 1-year Treasury bill at one-half the 1-year rate, 1.0165%, would produce the following proceeds at the end of one year:
X (1.0165)2 = 1.03327 X
Both alternatives have the same payoff if the 6-month Treasury bill yield six months from now is 1.8% (3.6% on a BEY). This means that, if an investor is guaranteed a 1.8% yield (3.6% BEY) on a 6-month Treasury bill six months from now, he will be indifferent toward the two alternatives.
The same line of reasoning can be used to obtain the 6-month forward rate beginning at any time period in the future. For example, the following can be determined:
• the 6-month forward rate three years from now
• the 6-month forward rate five years from now
The notation that we use to indicate 6-month forward rates is 1fm where the subscript 1 indicates a 1-period (6-month) rate and the subscript m indicates the period beginning m periods from now. When m is equal to zero, this means the current rate. Thus, the first 6-month forward rate is simply the current 6-month spot rate. That is, 1f0 = z1.
The general formula for determining a 6-month forward rate is: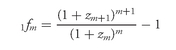
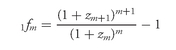
For example, suppose that the 6-month forward rate four years (eight 6-month periods) from now is sought. In terms of our notation, m is 8 and we seek 1f8. The formula is then: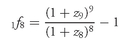
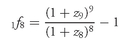
From Exhibit 4, since the 4-year spot rate is 5.065% and the 4.5-year spot rate is 5.1701%, z8 is 2.5325% and z9 is 2.58505%. Then,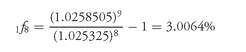
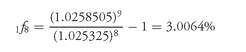
Doubling this rate gives a 6-month forward rate four years from now of 6.01%
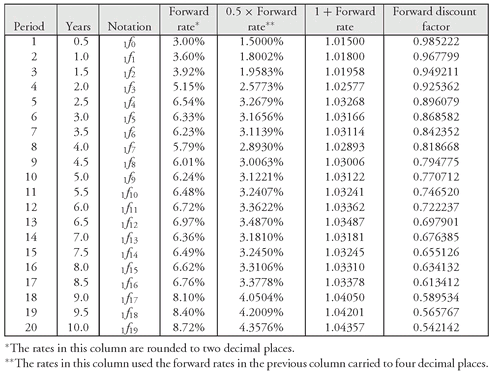
Exhibit 12 shows all of the 6-month forward rates for the Treasury yield curve shown in Exhibit 4. The forward rates reported in Exhibit 12 are the annualized rates on a bond-equivalent basis. In Exhibit 13, the short-term forward rates are plotted along with the Treasury par yield curve and theoretical spot rate curve. The graph of the short-term forward rates is called the short-term forward-rate curve. Notice that the short-term forward rate curve lies above the other two curves. This will always be the case if the par yield curve is upward sloping. If the par yield curve is downward sloping, the short-term forward rate curve will be the lowest curve. Notice the unusual shape for the short-term forward rate curve. There is a mathematical reason for this shape. In practice, analysts will use statistical techniques to create a smooth short-term forward rate curve.
EXHIBIT 12 Six-Month Forward Rates (Annualized Rates on a Bond-Equivalent Basis)
| Notation | Forward rate |
|---|---|
| 1f0 | 3.00 |
| 1f1 | 3.60 |
| 1f2 | 3.92 |
| 1f3 | 5.15 |
| 1f4 | 6.54 |
| 1f5 | 6.33 |
| 1f6 | 6.23 |
| 1f7 | 5.79 |
| 1f8 | 6.01 |
| 1f9 | 6.24 |
| 1f10 | 6.48 |
| 1f11 | 6.72 |
| 1f12 | 6.97 |
| 1f13 | 6.36 |
| 1f14 | 6.49 |
| 1f15 | 6.62 |
| 1f16 | 6.76 |
| 1f17 | 8.10 |
| 1f18 | 8.40 |
| 1f19 | 8.71 |
EXHIBIT 13 Graph of Short-Term Forward Rate Curve
B. Relationship between Spot Rates and Short-Term Forward Rates
Suppose an investor invests $X in a 3-year zero-coupon Treasury security. The total proceeds three years (six periods) from now would be:
X(1 + z6)6
The investor could instead buy a 6-month Treasury bill and reinvest the proceeds every six months for three years. The future dollars or dollar return will depend on the 6-month forward rates. Suppose that the investor can actually reinvest the proceeds maturing every six months at the calculated 6-month forward rates shown in Exhibit 12. At the end of three years, an investment of X would generate the following proceeds:
X(1 + z1)(1 +1f1)(1 +1f2)(1 +1f3)(1 +1f4)(1 +1f5)
Since the two investments must generate the same proceeds at the end of three years, the two previous equations can be equated:
X(1 + z6)6 = X(1 + z1)(1 +1f1)(1 +1f2)(1 +1f3)(1 +1f4)(1 +1f5)
Solving for the 3-year (6-period) spot rate, we have:
z6 = [(1 + z1)(1 +1f1)(1 +1f2)(1 +1f3)(1 +1f4)(1 +1f5)]1/6 − 1
This equation tells us that the 3-year spot rate depends on the current 6-month spot rate and the five 6-month forward rates. In fact, the right-hand side of this equation is a geometric average of the current 6-month spot rate and the five 6-month forward rates.
Let’s use the values in Exhibits 4 and 12 to confirm this result. Since the 6-month spot rate in Exhibit 4 is 3%, z1 is 1.5% and therefore65
z6 = [(1.015)(1.018)(1.0196)(1.0257)(1.0327)(1.03165)]1/6 − 1
= 0.023761 = 2.3761%
= 0.023761 = 2.3761%
Doubling this rate gives 4.7522%. This agrees with the spot rate shown in Exhibit 4.
In general, the relationship between a T-period spot rate, the current 6-month spot rate, and the 6-month forward rates is as follows:
zT = [(1 + z1)(1 +1f1)(1 +1f2) . . . (1 +1fT−1)]1/T − 1
Therefore, discounting at the forward rates will give the same present value as discounting at spot rates.
C. Valuation Using Forward Rates
Since a spot rate is simply a package of short-term forward rates, it will not make any difference whether we discount cash flows using spot rates or forward rates. That is, suppose that the cash flow in period T is $1. Then the present value of the cash flow can be found using the spot rate for period T as follows:
Alternatively, since we know that
then, adding 1 to both sides of the equation,
zT = [(1 + z1)(1 +1f1)(1 +1f2) · · · (1 +1fT−1)]1/T − 1
(1 + zT ) = [(1 + z1)(1 +1f1)(1 +1f2) · · · (1 +1fT−1)]1/T
Raising both sides of the equation to the T -th power we get:
(1 + zT )T = (1 + z1)(1 +1f1)(1 +1f2) · · · (1 +1fT −1)
Substituting the right-hand side of the above equation into the present value formula we get: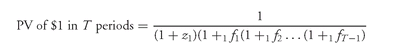
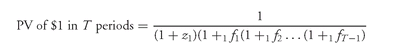
In practice, the present value of $1 in T periods is called the forward discount factor for period T.
For example, consider the forward rates shown in Exhibit 12. The forward discount rate for period 4 is found as follows: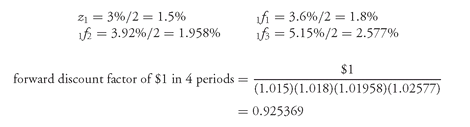
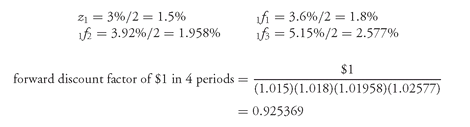
To see that this is the same present value that would be obtained using the spot rates, note from Exhibit 4 that the 2-year spot rate is 3.9164%. Using that spot rate, we find: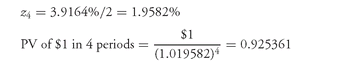
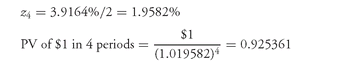
The answer is the same as the forward discount factor (the slight difference is due to rounding).
Exhibit 14 shows the computation of the forward discount factor for each period based on the forward rates in Exhibit 12. Let’s show how both the forward rates and the spot rates can be used to value a 2-year 6% coupon Treasury bond. The present value for each cash flow is found as follows using spot rates: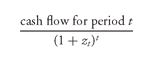
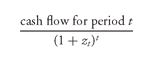
EXHIBIT 14 Calculation of the Forward Discount Factor for Each Period
The following table uses the spot rates in Exhibit 4 to value this bond:
Based on the spot rates, the value of this bond is $104.0190.
Using forward rates and the forward discount factors, the present value of the cash flow in period t is found as follows:
cash flow in period t × discount factor for period t
The following table uses the forward rates and the forward discount factors in Exhibit 14 to value this bond:
The present value of this bond using forward rates is $104.0190.
So, it does not matter whether one discounts cash flows by spot rates or forward rates, the value is the same.
D. Computing Any Forward Rate
Using spot rates, we can compute any forward rate. Using the same arbitrage arguments as used above to derive the 6-month forward rates, any forward rate can be obtained.
There are two elements to the forward rate. The first is when in the future the rate begins. The second is the length of time for the rate. For example, the 2-year forward rate 3 years from now means a rate three years from now for a length of two years. The notation used for a forward rate, f , will have two subscripts—one before f and one after f as shown below:
tfm
The subscript before f is t and is the length of time that the rate applies. The subscript after f is m and is when the forward rate begins. That is,
the length of time of the forward rate fwhen the forward rate begins
Remember our time periods are still 6-month periods. Given the above notation, here is what the following mean:
| Notation | Interpretation for the forward rate |
|---|---|
| 1f12 | 6-month (1-period) forward rate beginning 6 years (12 periods) from now |
| 2f8 | 1-year (2-period) forward rate beginning 4 years (8 periods) from now |
| 6f4 | 3-year (6-period) forward rate beginning 2 years (4 periods) from now |
| 8f10 | 4-year (8-period) forward rate beginning 5 years (10 periods) from now |
To see how the formula for the forward rate is derived, consider the following two alternatives for an investor who wants to invest for m + t periods:
• buy a zero-coupon Treasury bond that matures in m + t periods, or
• buy a zero-coupon Treasury bond that matures in m periods and invest the proceeds at the maturity date in a zero-coupon Treasury bond that matures in t periods.
The investor will be indifferent between the two alternatives if they produce the same return over the m + t investment horizon.
For $100 invested in the first alternative, the proceeds for this investment at the horizon date assuming that the semiannual rate is zm+t is
$100 (1 + zm+t )m+t
For the second alternative, the proceeds for this investment at the end of m periods assuming that the semiannual rate is zm is
$100 (1 + zm)m
When the proceeds are received in m periods, they are reinvested at the forward rate, tfm, producing a value for the investment at the end of m + t periods of
$100 (1 + zm)m(1 +tfm)t
For the investor to be indifferent to the two alternatives, the following relationship must hold:
$100 (1 + zm+t)m+t = $100 (1 + zm)m(1 +tfm)t
Solving for t fm we get:
Notice that if t is equal to 1, the formula reduces to the 1-period (6-month) forward rate.
To illustrate, for the spot rates shown in Exhibit 4, suppose that an investor wants to know the 2-year forward rate three years from now. In terms of the notation, t is equal to 4 and m is equal to 6. Substituting for t and m into the equation for the forward rate we have: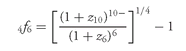
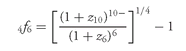
This means that the following two spot rates are needed: z6 (the 3-year spot rate) and z10 (the 5-year spot rate). From Exhibit 4 we know
then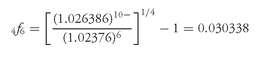
z6(the 3-year spot rate) = 4.752%/2 = 0.02376
z10(the 5-year spot rate) = 5.2772%/2 = 0.026386
z10(the 5-year spot rate) = 5.2772%/2 = 0.026386
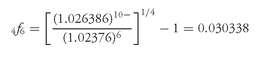
Therefore, 4f6 is equal to 3.0338% and doubling this rate gives 6.0675% the forward rate on a bond-equivalent basis.
We can verify this result. Investing $100 for 10 periods at the spot rate of 2.6386% will produce the following value:
$100 (1.026386)10 = $129.7499
Investing $100 for 6 periods at 2.376% and reinvesting the proceeds for 4 periods at the forward rate of 3.030338% gives the same value:
$100 (1.02376)6(1.030338)4 = $129.75012
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.