CHAPTER 7
INTRODUCTION TO THE MEASUREMENT OF INTEREST RATE RISK
I. INTRODUCTION
In Chapter 2, we discussed the interest rate risk associated with investing in bonds. We know that the value of a bond moves in the opposite direction to a change in interest rates. If interest rates increase, the price of a bond will decrease. For a short bond position, a loss is generated if interest rates fall. However, a manager wants to know more than simply when a position generates a loss. To control interest rate risk, a manager must be able to quantify that result.
What is the key to measuring the interest rate risk? It is the accuracy in estimating the value of the position after an adverse interest rate change. A valuation model determines the value of a position after an adverse interest rate move. Consequently, if a reliable valuation model is not used, there is no way to properly measure interest rate risk exposure.
There are two approaches to measuring interest rate risk—the full valuation approach and the duration/convexity approach.
II. THE FULL VALUATION APPROACH
The most obvious way to measure the interest rate risk exposure of a bond position or a portfolio is to re-value it when interest rates change. The analysis is performed for different scenarios with respect to interest rate changes. For example, a manager may want to measure the interest rate exposure to a 50 basis point, 100 basis point, and 200 basis point instantaneous change in interest rates. This approach requires the re-valuation of a bond or bond portfolio for a given interest rate change scenario and is referred to as the full valuation approach. It is sometimes referred to as scenario analysis because it involves assessing the exposure to interest rate change scenarios.
To illustrate this approach, suppose that a manager has a $10 million par value position in a 9% coupon 20-year bond. The bond is option-free. The current price is 134.6722 for a yield (i.e., yield to maturity) of 6%. The market value of the position is $13,467,220 (134.6722% × $10 million). Since the manager owns the bond, she is concerned with a rise in yield since this will decrease the market value of the position. To assess the exposure to a rise in market yields, the manager decides to look at how the value of the bond will change if yields change instantaneously for the following three scenarios: (1) 50 basis point increase, (2) 100 basis point increase, and (3) 200 basis point increase. This means that the manager wants to assess what will happen to the bond position if the yield on the bond increases from 6% to (1) 6.5%, (2) 7%, and (3) 8%. Because this is an option-free bond, valuation is straightforward. In the examples that follow, we will use one yield to discount each of the cash flows. In other words, to simplify the calculations, we will assume a flat yield curve (even though that assumption doesn’t fit the examples perfectly). The price of this bond per $100 par value and the market value of the $10 million par position is shown in Exhibit 1. Also shown is the new market value and the percentage change in market value.
EXHIBIT 1 Illustration of Full Valuation Approach to Assess the Interest Rate Risk of a Bond Position for Three Scenarios

In the case of a portfolio, each bond is valued for a given scenario and then the total value of the portfolio is computed for a given scenario. For example, suppose that a manager has a portfolio with the following two option-free bonds: (1) 6% coupon 5-year bond and (2) 9% coupon 20-year bond. For the shorter term bond, $5 million of par value is owned and the price is 104.3760 for a yield of 5%. For the longer term bond, $10 million of par value is owned and the price is 134.6722 for a yield of 6%. Suppose that the manager wants to assess the interest rate risk of this portfolio for a 50, 100, and 200 basis point increase in interest rates assuming both the 5-year yield and 20-year yield change by the same number of basis points. Exhibit 2 shows the interest rate risk exposure. Panel a of the exhibit shows the market value of the 5-year bond for the three scenarios. Panel b does the same for the 20-year bond. Panel c shows the total market value of the two-bond portfolio and the percentage change in the market value for the three scenarios.
In the illustration in Exhibit 2, it is assumed that both the 5-year and the 20-year yields changed by the same number of basis points. The full valuation approach can also handle scenarios where the yield curve does not change in a parallel fashion. Exhibit 3 illustrates this for our portfolio that includes the 5-year and 20-year bonds. The scenario analyzed is a yield curve shift combined with shifts in the level of yields. In the illustration in Exhibit 3, the following yield changes for the 5-year and 20-year yields are assumed:
| Scenario | Change in 5-year rate (bp) | Change in 20-year rate (bp) |
|---|---|---|
| 1 | 50 | 10 |
| 2 | 100 | 50 |
| 3 | 200 | 100 |
The last panel in Exhibit 3 shows how the market value of the portfolio changes for each scenario.
EXHIBIT 2 Illustration of Full Valuation Approach to Assess the Interest Rate Risk of a Two Bond Portfolio (Option-Free) for Three Scenarios Assuming a Parallel Shift in the Yield Curve
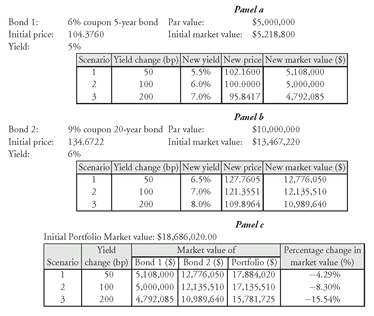
EXHIBIT 3 Illustration of Full Valuation Approach to Assess the Interest Rate Risk of a Two Bond Portfolio (Option-Free) for Three Scenarios Assuming a Nonparallel Shift in the Yield Curve

The full valuation approach seems straightforward. If one has a good valuation model, assessing how the value of a portfolio or individual bond will change for different scenarios for parallel and nonparallel yield curve shifts measures the interest rate risk of a portfolio.
A common question that often arises when using the full valuation approach is which scenarios should be evaluated to assess interest rate risk exposure. For some regulated entities, there are specified scenarios established by regulators. For example, it is common for regulators of depository institutions to require entities to determine the impact on the value of their bond portfolio for a 100, 200, and 300 basis point instantaneous change in interest rates (up and down). (Regulators tend to refer to this as “simulating” interest rate scenarios rather than scenario analysis.) Risk managers and highly leveraged investors such as hedge funds tend to look at extreme scenarios to assess exposure to interest rate changes. This practice is referred to as stress testing.
Of course, in assessing how changes in the yield curve can affect the exposure of a portfolio, there are an infinite number of scenarios that can be evaluated. The state-of-the-art technology involves using a complex statistical procedure66 to determine a likely set of yield curve shift scenarios from historical data.
It seems like the chapter should end right here. We can use the full valuation approach to assess the exposure of a bond or portfolio to interest rate changes to evaluate any scenario, assuming—and this must be repeated continuously—that the manager has a good valuation model to estimate what the price of the bonds will be in each interest rate scenario. However, we are not stopping here. In fact, the balance of this chapter is considerably longer than this section. Why? The reason is that the full valuation process can be very time consuming. This is particularly true if the portfolio has a large number of bonds, even if a minority of those bonds are complex (i.e., have embedded options). While the full valuation approach is the recommended method, managers want one simple measure that they can use to get an idea of how bond prices will change if rates change in a parallel fashion, rather than having to revalue an entire portfolio. In Chapter 2, such a measure was introduced—duration. We will discuss this measure as well as a supplementary measure (convexity) in Sections IV and V, respectively. To build a foundation to understand the limitations of these measures, we describe the basic price volatility characteristics of bonds in Section III. The fact that there are limitations of using one or two measures to describe the interest rate exposure of a position or portfolio should not be surprising. These measures provide a starting point for assessing interest rate risk.
III. PRICE VOLATILITY CHARACTERISTICS OF BONDS
In Chapter 2, we described the characteristics of a bond that affect its price volatility: (1) maturity, (2) coupon rate, and (3) presence of embedded options. We also explained how the level of yields affects price volatility. In this section, we will take a closer look at the price volatility of bonds.
A. Price Volatility Characteristics of Option-Free Bonds
Let’s begin by focusing on option-free bonds (i.e., bonds that do not have embedded options). A fundamental characteristic of an option-free bond is that the price of the bond changes in the opposite direction to a change in the bond’s yield. Exhibit 4 illustrates this property for four hypothetical bonds assuming a par value of $100.
EXHIBIT 4 Price/Yield Relationship for Four Hypothetical Option-Free Bonds

When the price/yield relationship for any option-free bond is graphed, it exhibits the shape shown in Exhibit 5. Notice that as the yield increases, the price of an option-free bond declines. However, this relationship is not linear (i.e., not a straight line relationship). The shape of the price/yield relationship for any option-free bond is referred to as convex. This price/yield relationship reflects an instantaneous change in the required yield.
The price sensitivity of a bond to changes in the yield can be measured in terms of the dollar price change or the percentage price change. Exhibit 6 uses the four hypothetical bonds in Exhibit 4 to show the percentage change in each bond’s price for various changes in yield, assuming that the initial yield for all four bonds is 6%. An examination of Exhibit 6 reveals the following properties concerning the price volatility of an option-free bond: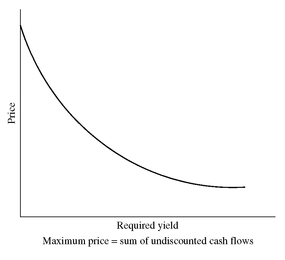

Property 1: Although the price moves in the opposite direction from the change in yield, the percentage price change is not the same for all bonds.
EXHIBIT 5 Price/Yield Relationship for a Hypothetical Option-Free Bond

EXHIBIT 6 Instantaneous Percentage Price Change for Four Hypothetical Bonds (Initial yield for all four bonds is 6%)

Property 2: For small changes in the yield, the percentage price change for a given bond is roughly the same, whether the yield increases or decreases.
Property 3: For large changes in yield, the percentage price change is not the same for an increase in yield as it is for a decrease in yield.
Property 4: For a given large change in yield, the percentage price increase is greater than the percentage price decrease.
While the properties are expressed in terms of percentage price change, they also hold for dollar price changes.
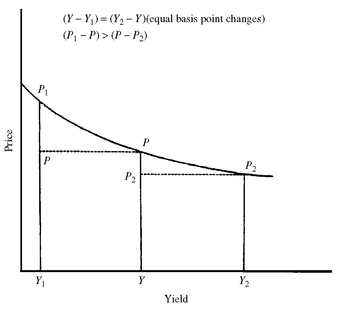
An explanation for these last two properties of bond price volatility lies in the convex shape of the price/yield relationship. Exhibit 7 illustrates this. The following notation is used in the exhibit
Y = initial yield
Y1 = lower yield
Y2 = higher yield
P = initial price
P1 = price at lower yield Y1
P2 = price at higher yield Y2
What was done in the exhibit was to change the initial yield (Y) up and down by the same number of basis points. That is, in Exhibit 7, the yield is decreased from Y to Y1 and increased from Y to Y2 such that the change is the same:
Y − Y1 = Y2 − Y
Also, the change in yield is a large number of basis points.
The vertical distance from the horizontal axis (the yield) to the intercept on the graph shows the price. The change in the initial price (P) when the yield declines from Y to Y1 is equal to the difference between the new price (P1) and the initial price (P). That is,
change in price when yield decreases = P1 − P
EXHIBIT 7 Graphical Illustration of Properties 3 and 4 for an Option-Free Bond
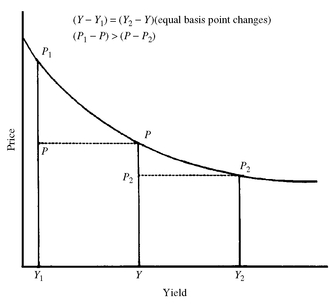
The change in the initial price (P) when the yield increases from Y to Y2 is equal to the difference between the new price (P2) and the initial price (P). That is,
As can be seen in the exhibit, the change in price when yield decreases is not equal to the change in price when yield increases by the same number of basis points. That is,
change in price when yield increases = P2 − P
P1 − P ≠ P2 − P
This is what Property 3 states.
A comparison of the price change shows that the change in price when yield decreases is greater than the change in price when yield increases. That is,
This is Property 4.
P1 − P > P2 − P
The implication of Property 4 is that if an investor owns a bond, the capital gain that will be realized if the yield decreases is greater than the capital loss that will be realized if the yield increases by the same number of basis points. For an investor who is short a bond (i.e., sold a bond not owned), the reverse is true: the potential capital loss is greater than the potential capital gain if the yield changes by a given number of basis points.
The convexity of the price/yield relationship impacts Property 4. Exhibit 8 shows a less convex price/yield relationship than Exhibit 7. That is, the price/yield relationship in Exhibit 8 is less bowed than the price/yield relationship in Exhibit 7. Because of the difference in the convexities, look at what happens when the yield increases and decreases by the same number of basis points and the yield change is a large number of basis points. We use the same notation in Exhibits 8 and 9 as in Exhibit 7. Notice that while the price gain when the yield decreases is greater than the price decline when the yield increases, the gain is not much greater than the loss. In contrast, Exhibit 9 has much greater convexity than the bonds in Exhibits 7 and 8 and the price gain is significantly greater than the loss for the bonds depicted in Exhibits 7 and 8.
EXHIBIT 8 Impact of Convexity on Property 4: Less Convex Bond
B. Price Volatility of Bonds with Embedded Options
Now let’s turn to the price volatility of bonds with embedded options. As explained in previous chapters, the price of a bond with an embedded option is comprised of two components. The first is the value of the same bond if it had no embedded option (that is, the price if the bond is option free). The second component is the value of the embedded option. In other words, the value of a bond with embedded options is equal to the value of an option-free bond plus or minus the value of embedded options.
The two most common types of embedded options are call (or prepay) options and put options. As interest rates in the market decline, the issuer may call or prepay the debt obligation prior to the scheduled principal payment date. The other type of option is a put option. This option gives the investor the right to require the issuer to purchase the bond at a specified price. Below we will examine the price/yield relationship for bonds with both types of embedded options (calls and puts) and implications for price volatility.
1. Bonds with Call and Prepay Options In the discussion below, we will refer to a bond that may be called or is prepayable as a callable bond. Exhibit 10 shows the price/yield relationship for an option-free bond and a callable bond. The convex curve given by a - a’ is the price/yield relationship for an option-free bond. The unusual shaped curve denoted by a - b in the exhibit is the price/yield relationship for the callable bond.
The reason for the price/yield relationship for a callable bond is as follows. When the prevailing market yield for comparable bonds is higher than the coupon rate on the callable bond, it is unlikely that the issuer will call the issue. For example, if the coupon rate on a bond is 7% and the prevailing market yield on comparable bonds is 12%, it is highly unlikely that the issuer will call a 7% coupon bond so that it can issue a 12% coupon bond. Since the bond is unlikely to be called, the callable bond will have a similar price/yield relationship to an otherwise comparable option-free bond. Consequently, the callable bond will be valued as if it is an option-free bond. However, since there is still some value to the call option,67 the bond won’t trade exactly like an option-free bond.
EXHIBIT 9 Impact of Convexity on Property 4: Highly Convex Bond
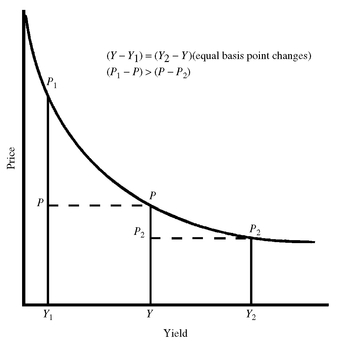
EXHIBIT 10 Price/Yield Relationship for a Callable Bond and an Option-Free Bond
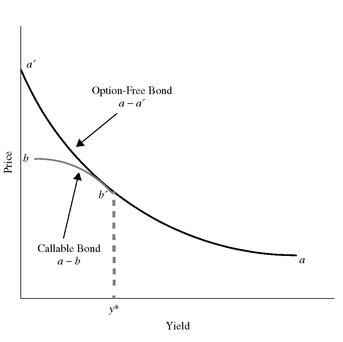
As yields in the market decline, the concern is that the issuer will call the bond. The issuer won’t necessarily exercise the call option as soon as the market yield drops below the coupon rate. Yet, the value of the embedded call option increases as yields approach the coupon rate from higher yield levels. For example, if the coupon rate on a bond is 7% and the market yield declines to 7.5%, the issuer will most likely not call the issue. However, market yields are now at a level at which the investor is concerned that the issue may eventually be called if market yields decline further. Cast in terms of the value of the embedded call option, that option becomes more valuable to the issuer and therefore it reduces the price relative to an otherwise comparable option-free bond.68 In Exhibit 10, the value of the embedded call option at a given yield can be measured by the difference between the price of an option-free bond (the price shown on the curve a - a’) and the price on the curve a - b. Notice that at low yield levels (below y* on the horizontal axis), the value of the embedded call option is high.
Using the information in Exhibit 10, let’s compare the price volatility of a callable bond to that of an option-free bond. Exhibit 11 focuses on the portion of the price/yield relationship for the callable bond where the two curves in Exhibit 10 depart (segment b’ - b in Exhibit 10). We know from our earlier discussion that for a large change in yield, the price of an option-free bond increases by more than it decreases (Property 4 above). Is that what happens for a callable bond in the region of the price/yield relationship shown in Exhibit 11? No, it is not. In fact, as can be seen in the exhibit, the opposite is true! That is, for a given large change in yield, the price appreciation is less than the price decline.
This very important characteristic of a callable bond—that its price appreciation is less than its price decline when rates change by a large number of basis points—is referred to as negative convexity.69 But notice from Exhibit 10 that callable bonds don’t exhibit this characteristic at every yield level. When yields are high (relative to the issue’s coupon rate), the bond exhibits the same price/yield relationship as an option-free bond; therefore at high yield levels it also has the characteristic that the gain is greater than the loss. Because market participants have referred to the shape of the price/yield relationship shown in Exhibit 11 as negative convexity, market participants refer to the relationship for an option-free bond as positive convexity. Consequently, a callable bond exhibits negative convexity at low yield levels and positive convexity at high yield levels. This is depicted in Exhibit 12.
As can be seen from the exhibits, when a bond exhibits negative convexity, the bond compresses in price as rates decline. That is, at a certain yield level there is very little price appreciation when rates decline. When a bond enters this region, the bond is said to exhibit “price compression.”
EXHIBIT 11 Negative Convexity Region of the Price/Yield Relationship for a Callable Bond
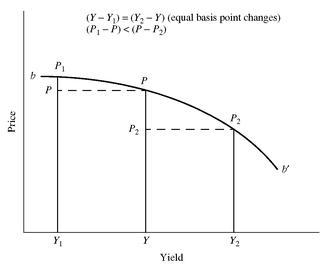
EXHIBIT 12 Negative and Positive Convexity Exhibited by a Callable Bond

2. Bonds with Embedded Put Options Putable bonds may be redeemed by the bondholder on the dates and at the put price specified in the indenture. Typically, the put price is par value. The advantage to the investor is that if yields rise such that the bond’s value falls below the put price, the investor will exercise the put option. If the put price is par value, this means that if market yields rise above the coupon rate, the bond’s value will fall below par and the investor will then exercise the put option.
EXHIBIT 13 Price/Yield Relationship for a Putable Bond and an Option-Free Bond
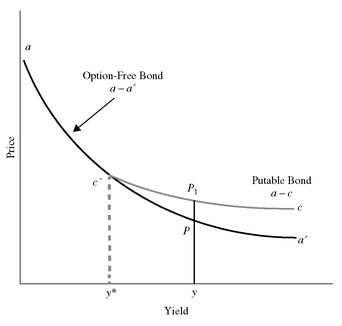
The value of a putable bond is equal to the value of an option-free bond plus the value of the put option. Thus, the difference between the value of a putable bond and the value of an otherwise comparable option-free bond is the value of the embedded put option. This can be seen in Exhibit 13 which shows the price/yield relationship for a putable bond is the curve a - c and for an option-free bond is the curve a - a’ .
At low yield levels (low relative to the issue’s coupon rate), the price of the putable bond is basically the same as the price of the option-free bond because the value of the put option is small. As rates rise, the price of the putable bond declines, but the price decline is less than that for an option-free bond. The divergence in the price of the putable bond and an otherwise comparable option-free bond at a given yield level (y) is the value of the put option (P1 - P ). When yields rise to a level where the bond’s price would fall below the put price, the price at these levels is the put price.
IV. DURATION
With the background about the price volatility characteristics of a bond, we can now turn to an alternate approach to full valuation: the duration/convexity approach. As explained in Chapter 2, duration is a measure of the approximate price sensitivity of a bond to interest rate changes. More specifically, it is the approximate percentage change in price for a 100 basis point change in rates. We will see in this section that duration is the first (linear) approximation of the percentage price change. To improve the approximation provided by duration, an adjustment for “convexity” can be made. Hence, using duration combined with convexity to estimate the percentage price change of a bond caused by changes in interest rates is called the duration/convexity approach.
A. Calculating Duration
In Chapter 2, we explained that the duration of a bond is estimated as follows: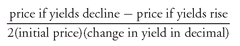
If we let
then duration can be expressed as
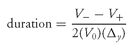
Δy = change in yield in decimal
V0 = initial price
V − = price if yields decline by Δy
V+ = price if yields increase by Δy
V0 = initial price
V − = price if yields decline by Δy
V+ = price if yields increase by Δy
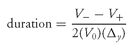
For example, consider a 9% coupon 20-year option-free bond selling at 134.6722 to yield 6% (see Exhibit 4). Let’s change (i.e., shock) the yield down and up by 20 basis points and determine what the new prices will be for the numerator. If the yield is decreased by 20 basis points from 6.0% to 5.8%, the price would increase to 137.5888. If the yield increases by 20 basis points, the price would decrease to 131.8439. Thus,
Δy = 0.002
V0 = 134.6722
V− = 137.5888
V+ = 131.8439
V0 = 134.6722
V− = 137.5888
V+ = 131.8439
Then,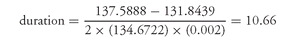
As explained in Chapter 2, duration is interpreted as the approximate percentage change in price for a 100 basis point change in rates. Consequently, a duration of 10.66 means that the approximate change in price for this bond is 10.66% for a 100 basis point change in rates.
A common question asked about this interpretation of duration is the consistency between the yield change that is used to compute duration using equation (1) and the interpretation of duration. For example, recall that in computing the duration of the 9% coupon 20-year bond, we used a 20 basis point yield change to obtain the two prices to use in the numerator of equation (1). Yet, we interpret the duration computed as the approximate percentage price change for a 100 basis point change in yield. The reason is that regardless of the yield change used to estimate duration in equation (1), the interpretation is the same. If we used a 25 basis point change in yield to compute the prices used in the numerator of equation (1), the resulting duration is interpreted as the approximate percentage price change for a 100 basis point change in yield. Later we will use different changes in yield to illustrate the sensitivity of the computed duration.
B. Approximating the Percentage Price Change Using Duration
In Chapter 2, we explained how to approximate the percentage price change for a given change in yield and a given duration. Here we will express the process using the following formula:
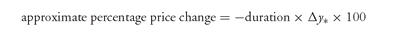 s where Δy∗ is the yield change (in decimal) for which the estimated percentage price change is sought.70 The reason for the negative sign on the right-hand side of equation (2) is due to the inverse relationship between price change and yield change (e.g., as yields increase, bond prices decrease). The following two examples illustrate how to use duration to estimate a bond’s price change.
s where Δy∗ is the yield change (in decimal) for which the estimated percentage price change is sought.70 The reason for the negative sign on the right-hand side of equation (2) is due to the inverse relationship between price change and yield change (e.g., as yields increase, bond prices decrease). The following two examples illustrate how to use duration to estimate a bond’s price change.
Example #1: small change in basis point yield. For example, consider the 9% 20-year bond trading at 134.6722 whose duration we just showed is 10.66. The approximate percentage price change for a 10 basis point increase in yield (i.e., Δy∗ = +0.001) is:
approximate percentage price change = −10.66 × (+0.001)×100 = −1.066%
How good is this approximation? The actual percentage price change is −1.06% (as shown in Exhibit 6 when yield increases to 6.10%). Duration, in this case, did an excellent job in estimating the percentage price change.
We would come to the same conclusion if we used duration to estimate the percentage price change if the yield declined by 10 basis points (i.e., Δy = −0.001). In this case, the approximate percentage price change would be +1.066% (i.e., the direction of the estimated price change is the reverse but the magnitude of the change is the same). Exhibit 6 shows that the actual percentage price change is +1.07%.
In terms of estimating the new price, let’s see how duration performed. The initial price is 134.6722. For a 10 basis point increase in yield, duration estimates that the price will decline by 1.066%. Thus, the price will decline to 133.2366 (found by multiplying 134.6722 by one minus 0.01066). The actual price from Exhibit 4 if the yield increases by 10 basis points is 133.2472. Thus, the price estimated using duration is close to the actual price.
For a 10 basis point decrease in yield, the actual price from Exhibit 4 is 136.1193 and the estimated price using duration is 136.1078 (a price increase of 1.066%). Consequently, the new price estimated by duration is close to the actual price for a 10 basis point change in yield.
Example #2: large change in basis point yield. Let’s look at how well duration does in estimating the percentage price change if the yield increases by 200 basis points instead of 10 basis points. In this case, Δy is equal to +0.02. Substituting into equation (2), we have
approximate percentage price change = −10.66 × (+0.02)×100 = −21.32%
How good is this estimate? From Exhibit 6, we see that the actual percentage price change when the yield increases by 200 basis points to 8% is −18.40%. Thus, the estimate is not as accurate as when we used duration to approximate the percentage price change for a change in yield of only 10 basis points. If we use duration to approximate the percentage price change when the yield decreases by 200 basis points, the approximate percentage price change in this scenario is +21.32%. The actual percentage price change as shown in Exhibit 6 is +25.04%.
Let’s look at the use of duration in terms of estimating the new price. Since the initial price is 134.6722 and a 200 basis point increase in yield will decrease the price by 21.32%, the estimated new price using duration is 105.9601 (found by multiplying 134.6722 by one minus 0.2132). From Exhibit 4, the actual price if the yield is 8% is 109.8964. Consequently, the estimate is not as accurate as the estimate for a 10 basis point change in yield. The estimated new price using duration for a 200 basis point decrease in yield is 163.3843 compared to the actual price (from Exhibit 4) of 168.3887. Once again, the estimation of the price using duration is not as accurate as for a 10 basis point change. Notice that whether the yield is increased or decreased by 200 basis points, duration underestimates what the new price will be. We will see why shortly.
Summary. Let’s summarize what we found in our application of duration to approximate the percentage price change: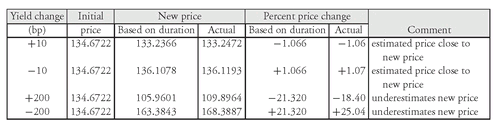

Should any of this be a surprise to you? No, not after reading Section III of this chapter and evaluating equation (2) in terms of the properties for the price/yield relationship discussed in that section. Look again at equation (2). Notice that whether the change in yield is an increase or a decrease, the approximate percentage price change will be the same except that the sign is reversed. This violates Property 3 and Property 4 with respect to the price volatility of option-free bonds when yields change. Recall that Property 3 states that the percentage price change will not be the same for a large increase and decrease in yield by the same number of basis points. Property 4 states the percentage price increase is greater than the percentage price decrease. These are two reasons why the estimate is inaccurate for a 200 basis point yield change.
Why did the duration estimate of the price change do a good job for a small change in yield of 10 basis points? Recall from Property 2 that the percentage price change will be approximately the same whether there is an increase or decrease in yield by a small number of basis points. We can also explain these results in terms of the graph of the price/yield relationship.
C. Graphical Depiction of Using Duration to Estimate Price Changes
In Section III, we used the graph of the price/yield relationship to demonstrate the price volatility properties of bonds. We can also use graphs to illustrate what we observed in our examples about how duration estimates the percentage price change, as well as some other noteworthy points.
EXHIBIT 14 Price/Yield Relationship for an Option-Free Bond with a Tangent Line
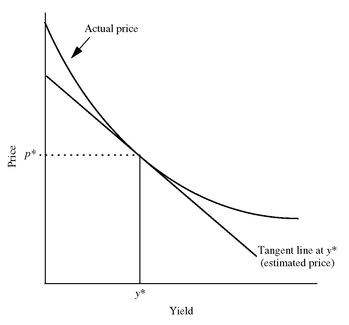
The shape of the price/yield relationship for an option-free bond is convex. Exhibit 14 shows this relationship. In the exhibit, a tangent line is drawn to the price/yield relationship at yield y∗. (For those unfamiliar with the concept of a tangent line, it is a straight line that just touches a curve at one point within a relevant (local) range. In Exhibit 14, the tangent line touches the curve at the point where the yield is equal to y∗ and the price is equal to p∗.) The tangent line is used to estimate the new price if the yield changes. If we draw a vertical line from any yield (on the horizontal axis), as in Exhibit 14, the distance between the horizontal axis and the tangent line represents the price approximated by using duration starting with the initial yield y∗.
Now how is the tangent line related to duration? Given an initial price and a specific yield change, the tangent line tells us the approximate new price of a bond. The approximate percentage price change can then be computed for this change in yield. But this is precisely what duration [using equation (2)] gives us: the approximate percentage price change for a given change in yield. Thus, using the tangent line, one obtains the same approximate percentage price change as using equation (2).
This helps us understand why duration did an effective job of estimating the percentage price change, or equivalently the new price, when the yield changes by a small number of basis points. Look at Exhibit 15. Notice that for a small change in yield, the tangent line does not depart much from the price/yield relationship. Hence, when the yield changes up or down by 10 basis points, the tangent line does a good job of estimating the new price, as we found in our earlier numerical illustration.
Exhibit 15 shows what happens to the estimate using the tangent line when the yield changes by a large number of basis points. Notice that the error in the estimate gets larger the further one moves from the initial yield. The estimate is less accurate the more convex the bond as illustrated in Exhibit 16.
EXHIBIT 15 Estimating the New Price Using a Tangent Line
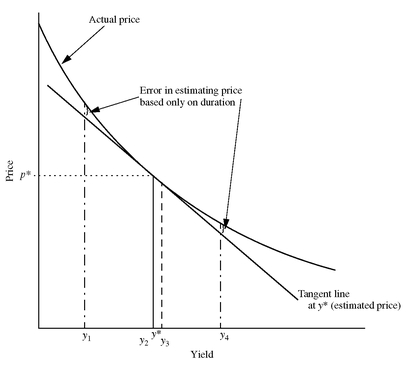
Also note that, regardless of the magnitude of the yield change, the tangent line always underestimates what the new price will be for an option-free bond because the tangent line is below the price/yield relationship. This explains why we found in our illustration that when using duration, we underestimated what the actual price will be.
The results reported in Exhibit 17 are for option-free bonds. When we deal with more complicated securities, small rate shocks that do not reflect the types of rate changes that may occur in the market do not permit the determination of how prices can change. This is because expected cash flows may change when dealing with bonds with embedded options. In comparison, if large rate shocks are used, we encounter the asymmetry caused by convexity. Moreover, large rate shocks may cause dramatic changes in the expected cash flows for bonds with embedded options that may be far different from how the expected cash flows will change for smaller rate shocks.
There is another potential problem with using small rate shocks for complicated securities. The prices that are inserted into the duration formula as given by equation (2) are derived from a valuation model. The duration measure depends crucially on the valuation model. If the rate shock is small and the valuation model used to obtain the prices for equation (1) is poor, dividing poor price estimates by a small shock in rates (in the denominator) will have a significant effect on the duration estimate.
D. Rate Shocks and Duration Estimate
In calculating duration using equation (1), it is necessary to shock interest rates (yields) up and down by the same number of basis points to obtain the values for V− and V+. In our illustration, 20 basis points was arbitrarily selected. But how large should the shock be? That is, how many basis points should be used to shock the rate?
EXHIBIT 16 Estimating the New Price for a Large Yield Change for Bonds with Different Convexities
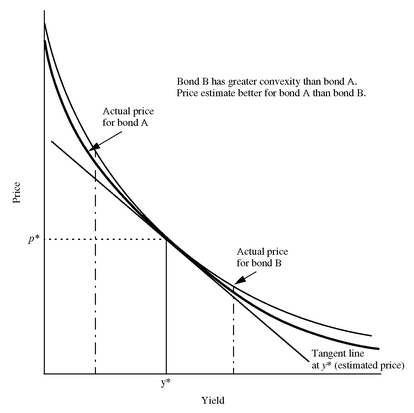
EXHIBIT 17 Duration Estimates for Different Rate Shocks Assumption: Initial yield is 6%
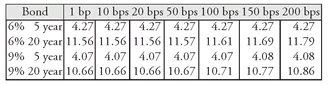
In Exhibit 17, the duration estimates for our four hypothetical bonds using equation (1) for rate shocks of 1 basis point to 200 basis points are reported. The duration estimates for the two 5-year bonds are not affected by the size of the shock. The two 5-year bonds are less convex than the two 20-year bonds. But even for the two 20-year bonds, for the size of the shocks reported in Exhibit 17, the duration estimates are not materially affected by the greater convexity.
What is done in practice by dealers and vendors of analytical systems? Each system developer uses rate shocks that they have found to be realistic based on historical rate changes.
EXHIBIT 18 Modified Duration versus Effective Duration
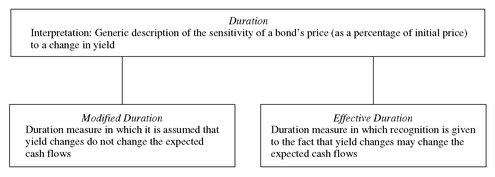
E. Modified Duration versus Effective Duration
One form of duration that is cited by practitioners is modified duration. Modified duration is the approximate percentage change in a bond’s price for a 100 basis point change in yield assuming that the bond’s expected cash flows do not change when the yield changes. What this means is that in calculating the values of V− and V+ in equation (1), the same cash flows used to calculate V0 are used. Therefore, the change in the bond’s price when the yield is changed is due solely to discounting cash flows at the new yield level.
The assumption that the cash flows will not change when the yield is changed makes sense for option-free bonds such as noncallable Treasury securities. This is because the payments made by the U.S. Department of the Treasury to holders of its obligations do not change when interest rates change. However, the same cannot be said for bonds with embedded options (i.e., callable and putable bonds and mortgage-backed securities). For these securities, a change in yield may significantly alter the expected cash flows.
In Section III, we showed the price/yield relationship for callable and prepayable bonds. Failure to recognize how changes in yield can alter the expected cash flows will produce two values used in the numerator of equation (1) that are not good estimates of how the price will actually change. The duration is then not a good number to use to estimate how the price will change.
Some valuation models for bonds with embedded options take into account how changes in yield will affect the expected cash flows. Thus, when V- and V+ are the values produced from these valuation models, the resulting duration takes into account both the discounting at different interest rates and how the expected cash flows may change. When duration is calculated in this manner, it is referred to as effective duration or option-adjusted duration. (Lehman Brothers refers to this measure in some of its publications as adjusted duration.) Exhibit 18 summarizes the distinction between modified duration and effective duration.
The difference between modified duration and effective duration for bonds with embedded options can be quite dramatic. For example, a callable bond could have a modified duration of 5 but an effective duration of only 3. For certain collateralized mortgage obligations, the modified duration could be 7 and the effective duration 20! Thus, using modified duration as a measure of the price sensitivity for a security with embedded options to changes in yield would be misleading. Effective duration is the more appropriate measure for any bond with an embedded option.
F. Macaulay Duration and Modified Duration
It is worth comparing the relationship between modified duration to the another duration measure, Macaulay duration. Modified duration can be written as:71
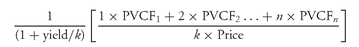 where
where

We know that duration tells us the approximate percentage price change for a bond if the yield changes.
The expression in the brackets of the modified duration formula given by equation (3) is a measure formulated in 1938 by Frederick Macaulay.72 This measure is popularly referred to as Macaulay duration. Thus, modified duration is commonly expressed as: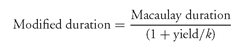
The general formulation for duration as given by equation (1) provides a short-cut procedure for determining a bond’s modified duration. Because it is easier to calculate the modified duration using the short-cut procedure, most vendors of analytical software will use equation (1) rather than equation (3) to reduce computation time.
However, modified duration is a flawed measure of a bond’s price sensitivity to interest rate changes for a bond with embedded options and therefore so is Macaulay duration. The duration formula given by equation (3) misleads the user because it masks the fact that changes in the expected cash flows must be recognized for bonds with embedded options. Although equation (3) will give the same estimate of percent price change for an option-free bond as equation (1), equation (1) is still better because it acknowledges cash flows and thus value can change due to yield changes.
G. Interpretations of Duration
Throughout this book, the definition provided for duration is: the approximate percentage price change for a 100 basis point change in rates. That definition is the most relevant for how a manager or investor uses duration. In fact, if you understand this definition, you can easily calculate the change in a bond’s value.
For example, suppose we want to know the approximate percentage change in price for a 50 basis point change in yield for our hypothetical 9% coupon 20-year bond selling for 134.6722. Since the duration is 10.66, a 100 basis point change in yield would change the price by about 10.66%. For a 50 basis point change in yield, the price will change by approximately 5.33% (= 10.66%/2). So, if the yield increases by 50 basis points, the price will decrease by about 5.33% from 134.6722 to 127.4942.
Now let’s look at some other duration definitions or interpretations that appear in publications and are cited by managers in discussions with their clients.
1. Duration Is the “First Derivative” Sometimes a market participant will refer to duration as the “first derivative of the price/yield function” or simply the “first derivative.” Wow! Sounds impressive. First, “derivative” here has nothing to do with “derivative instruments” (i.e., futures, swaps, options, etc.). A derivative as used in this context is obtained by differentiating a mathematical function using calculus. There are first derivatives, second derivatives, and so on. When market participants say that duration is the first derivative, here is what they mean. The first derivative calculates the slope of a line—in this case, the slope of the tangent line in Exhibit 14. If it were possible to write a mathematical equation for a bond in closed form, the first derivative would be the result of differentiating that equation the first time. Even if you don’t know how to do the process of differentiation to get the first derivative, it sounds like you are really smart since it suggests you understand calculus! While it is a correct interpretation of duration, it is an interpretation that in no way helps us understand what the interest rate risk is of a bond. That is, it is an operationally meaningless interpretation.
Why is it an operationally meaningless interpretation? Go back to the $10 million bond position with a duration of 6. Suppose a client is concerned with the exposure of the bond to changes in interest rates. Now, tell that client the duration is 6 and that it is the first derivative of the price function for that bond. What have you told the client? Not much. In contrast, tell that client that the duration is 6 and that duration is the approximate price sensitivity of a bond to a 100 basis point change in rates and you have told the client more relevant information with respect the bond’s interest rate risk.
2. Duration Is Some Measure of Time When the concept of duration was originally introduced by Macaulay in 1938, he used it as a gauge of the time that the bond was outstanding. More specifically, Macaulay defined duration as the weighted average of the time to each coupon and principal payment of a bond. Subsequently, duration has too often been thought of in temporal terms, i.e., years. This is most unfortunate for two reasons.
First, in terms of dimensions, there is nothing wrong with expressing duration in terms of years because that is the proper dimension of this value. But the proper interpretation is that duration is the price volatility of a zero-coupon bond with that number of years to maturity. So, when a manager says a bond has a duration of 4 years, it is not useful to think of this measure in terms of time, but that the bond has the price sensitivity to rate changes of a 4-year zero-coupon bond.
Second, thinking of duration in terms of years makes it difficult for managers and their clients to understand the duration of some complex securities. Here are a few examples. For a mortgage-backed security that is an interest-only security (i.e., receives coupons but not principal repayment) the duration is negative. What does a negative number, say, −4 mean? In terms of our interpretation as a percentage price change, it means that when rates change by 100 basis points, the price of the bond changes by about 4% but the change is in the same direction as the change in rates.
As a second example, consider an inverse floater created in the collateralized mortgage obligation (CMO) market. The underlying collateral for such a security might be loans with 25 years to final maturity. However, an inverse floater can have a duration that easily exceeds 25. This does not make sense to a manager or client who uses a measure of time as a definition for duration.
As a final example, consider derivative instruments, such as an option that expires in one year. Suppose that it is reported that its duration is 60. What does that mean? To someone who interprets duration in terms of time, does that mean 60 years, 60 days, 60 seconds? It doesn’t mean any of these. It simply means that the option tends to have the price sensitivity to rate changes of a 60-year zero-coupon bond.
3. Forget First Derivatives and Temporal Definitions The bottom line is that one should not care if it is technically correct to think of duration in terms of years (volatility of a zero-coupon bond) or in terms of first derivatives. There are even some who interpret duration in terms of the “half life” of a security.73 Subject to the limitations that we will describe as we proceed in this book, duration is the measure of a security’s price sensitivity to changes in yield. We will fine tune this definition as we move along.
Users of this interest rate risk measure are interested in what it tells them about the price sensitivity of a bond (or a portfolio) to changes in interest rates. Duration provides the investor with a feel for the dollar price exposure or the percentage price exposure to potential interest rate changes. Try the following definitions on a client who has a portfolio with a duration of 4 and see which one the client finds most useful for understanding the interest rate risk of the portfolio when rates change:
Definition 1: The duration of 4 for your portfolio indicates that the portfolio’s value will change by approximately 4% if rates change by 100 basis points.
Definition 2: The duration of 4 for your portfolio is the first derivative of the price function for the bonds in the portfolio.
Definition 3: The duration of 4 for your portfolio is the weighted average number of years to receive the present value of the portfolio’s cash flows.
Definition 1 is clearly preferable. It would be ridiculous to expect clients to understand the last two definitions better than the first.
Moreover, interpreting duration in terms of a measure of price sensitivity to interest rate changes allows a manager to make comparisons between bonds regarding their interest rate risk under certain assumptions.
H. Portfolio Duration
A portfolio’s duration can be obtained by calculating the weighted average of the duration of the bonds in the portfolio. The weight is the proportion of the portfolio that a security comprises. Mathematically, a portfolio’s duration can be calculated as follows:
where
w1D1+w2D2+w3D3+...+wKDK
wi = market value of bond i/market value of the portfolio
Di = duration of bond i
K = number of bonds in the portfolio
To illustrate this calculation, consider the following 3-bond portfolio in which all three bonds are option free:

In this illustration, it is assumed that the next coupon payment for each bond is exactly six months from now (i.e., there is no accrued interest). The market value for the portfolio is $9,609,961. Since each bond is option free, modified duration can be used. The market price per $100 par value of each bond, its yield, and its duration are given below: In this illustration, K is equal to 3 and:
| w1 = $4, 000, 000/$9, 609, 961 = 0.416 | D1 = 3.861 |
| w2 = $4, 231, 375/$9, 609, 961 = 0.440 | D2 = 8.047 |
| w3 = $1, 378, 586/$9, 609, 961 = 0.144 | D3 = 9.168 |
The portfolio’s duration is:
0.416(3.861) + 0.440(8.047) + 0.144(9.168) = 6.47
A portfolio duration of 6.47 means that for a 100 basis point change in the yield for each of the three bonds, the market value of the portfolio will change by approximately 6.47%. But keep in mind, the yield for each of the three bonds must change by 100 basis points for the duration measure to be useful. (In other words, there must be a parallel shift in the yield curve.) This is a critical assumption and its importance cannot be overemphasized.
An alternative procedure for calculating the duration of a portfolio is to calculate the dollar price change for a given number of basis points for each security in the portfolio and then add up all the price changes. Dividing the total of the price changes by the initial market value of the portfolio produces a percentage price change that can be adjusted to obtain the portfolio’s duration.
For example, consider the 3-bond portfolio shown above. Suppose that we calculate the dollar price change for each bond in the portfolio based on its respective duration for a 50 basis point change in yield. We would then have: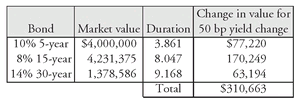

Thus, a 50 basis point change in all rates changes the market value of the 3-bond portfolio by $310,663. Since the market value of the portfolio is $9,609,961, a 50 basis point change produced a change in value of 3.23% ($310,663 divided by $9,609,961). Since duration is the approximate percentage change for a 100 basis point change in rates, this means that the portfolio duration is 6.46 (found by doubling 3.23). This is essentially the same value for the portfolio’s duration as found earlier.
V. CONVEXITY ADJUSTMENT
The duration measure indicates that regardless of whether interest rates increase or decrease, the approximate percentage price change is the same. However, as we noted earlier, this is not consistent with Property 3 of a bond’s price volatility. Specifically, while for small changes in yield the percentage price change will be the same for an increase or decrease in yield, for large changes in yield this is not true. This suggests that duration is only a good approximation of the percentage price change for small changes in yield.
We demonstrated this property earlier using a 9% 20-year bond selling to yield 6% with a duration of 10.66. For a 10 basis point change in yield, the estimate was accurate for both an increase or decrease in yield. However, for a 200 basis point change in yield, the approximate percentage price change was off considerably.
The reason for this result is that duration is in fact a first (linear) approximation for a small change in yield.74 The approximation can be improved by using a second approximation. This approximation is referred to as the “convexity adjustment.” It is used to approximate the change in price that is not explained by duration.
The formula for the convexity adjustment to the percentage price change is
 where Δy∗ = the change in yield for which the percentage price change is sought and
where Δy∗ = the change in yield for which the percentage price change is sought and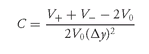
(5)
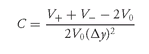
The notation is the same as used in equation (1) for duration.75
For example, for our hypothetical 9% 20-year bond selling to yield 6%, we know from Section IV A that for a 20 basis point change in yield (Δy = 0.002):
V0 = 134.6722, V− = 137.5888, and V+ = 131.8439
Substituting these values into the formula for C: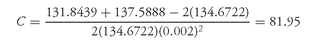
Suppose that a convexity adjustment is sought for the approximate percentage price change for our hypothetical 9% 20-year bond for a change in yield of 200 basis points. That is, in equation (4), Δy∗ is 0.02. Then the convexity adjustment is
81.95 × (0.02)2×100 = 3.28%
If the yield decreases from 6% to 4%, the convexity adjustment to the percentage price change based on duration would also be 3.28%.
The approximate percentage price change based on duration and the convexity adjustment is found by adding the two estimates. So, for example, if yields change from 6% to 8%, the estimated percentage price change would be:
| Estimated change using duration | = −21.32% |
| Convexity adjustment | = +3.28% |
| Total estimated percentage price change | = −18.04% |
The actual percentage price change is −18.40%.
For a decrease of 200 basis points, from 6% to 4%, the approximate percentage price change would be as follows:
| Estimated change using duration | = +21.32% |
| Convexity adjustment | = +3.28% |
| Total estimated percentage price change | = +24.60% |
The actual percentage price change is +25.04%. Thus, duration combined with the convexity adjustment does a better job of estimating the sensitivity of a bond’s price change to large changes in yield (i.e., better than using duration alone).
A. Positive and Negative Convexity Adjustment
Notice that when the convexity adjustment is positive, we have the situation described earlier that the gain is greater than the loss for a given large change in rates. That is, the bond exhibits positive convexity. We can see this in the example above. However, if the convexity adjustment is negative, we have the situation where the loss will be greater than the gain. For example, suppose that a callable bond has an effective duration of 4 and a convexity adjustment for a 200 basis point change of −1.2%.
The bond then exhibits the negative convexity property illustrated in Exhibit 11. The approximate percentage price change after adjusting for convexity is:
| Estimated change using duration | = −8.0% |
| Convexity adjustment | = −1.2% |
| Total estimated percentage price change | = −9.2% |
For a decrease of 200 basis points, the approximate percentage price change would be as follows:
| Estimated change using duration | = +8.0% |
| Convexity adjustment | = −1.2% |
| Total estimated percentage price change | = +6.8% |
Notice that the loss is greater than the gain—a property called negative convexity that we discussed in Section III and illustrated in Exhibit 11.
B. Modified and Effective Convexity Adjustment
The prices used in computing C in equation (4) to calculate the convexity adjustment can be obtained by assuming that, when the yield changes, the expected cash flows either do not change or they do change. In the former case, the resulting convexity is referred to as modified convexity adjustment. (Actually, in the industry, convexity adjustment is not qualified by the adjective “modified.”) In contrast, effective convexity adjustment assumes that the cash flows change when yields change. This is the same distinction made for duration.
As with duration, there is little difference between a modified convexity adjustment and an effective convexity adjustment for option-free bonds. However, for bonds with embedded options, there can be quite a difference between the calculated modified convexity adjustment and an effective convexity adjustment. In fact, for all option-free bonds, either convexity adjustment will have a positive value. For bonds with embedded options, the calculated effective convexity adjustment can be negative when the calculated modified convexity adjustment is positive.
VI. PRICE VALUE OF A BASIS POINT
Some managers use another measure of the price volatility of a bond to quantify interest rate risk—the price value of a basis point (PVBP). This measure, also called the dollar value of an 01 (DV01), is the absolute value of the change in the price of a bond for a 1 basis point change in yield. That is,
Does it make a difference if the yield is increased or decreased by 1 basis point? It does not because of Property 2—the change will be about the same for a small change in basis points.
PVBP = ∣initial price − price if yield is changed by 1 basis point∣
To illustrate the computation, let’s use the values in Exhibit 4. If the initial yield is 6%, we can compute the PVBP by using the prices for either the yield at 5.99% or 6.01%. The PVBP for both for each bond is shown below: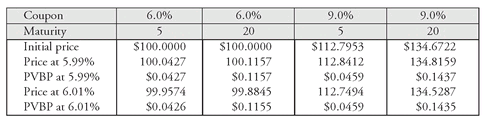

The PVBP is related to duration. In fact, PVBP is simply a special case of dollar duration described in Chapter 2. We know that the duration of a bond is the approximate percentage price change for a 100 basis point change in interest rates. We also know how to compute the approximate percentage price change for any number of basis points given a bond’s duration using equation (2). Given the initial price and the approximate percentage price change for 1 basis point, we can compute the change in price for a 1 basis point change in rates.
For example, consider the 9% 20-year bond. The duration for this bond is 10.66. Using equation (2), the approximate percentage price change for a 1 basis point increase in interest rates (i.e., Δy = 0.0001), ignoring the negative sign in equation (2), is:
10.66 × (0.0001)×100 = 0.1066%
Given the initial price of 134.6722, the dollar price change estimated using duration is
0.1066%×134.6722 = $0.1435
This is the same price change as shown above for a PVBP for this bond. Below is (1) the PVBP based on a 1 basis point increase for each bond and (2) the estimated price change using duration for a 1 basis point increase for each bond:

VII. THE IMPORTANCE OF YIELD VOLATILITY
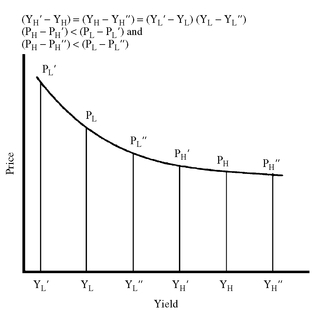
What we have not considered thus far is the volatility of interest rates. For example, as we explained in Chapter 2, all other factors equal, the higher the coupon rate, the lower the price volatility of a bond to changes in interest rates. In addition, the higher the level of yields, the lower the price volatility of a bond to changes in interest rates. This is illustrated in Exhibit 19 which shows the price/yield relationship for an option-free bond. When the yield level is high (YH , for example, in the exhibit), a change in interest rates does not produce a large change in the initial price. For example, as yields change from YH to YH ”, the price changes a small amount from PH to PH’. However, when the yield level is low and changes (YL to YL’ , for example, in the exhibit), a change in interest rates of the same number of basis points as YH to YH ” produces a large change in the initial price (PL to PL’).
This can also be cast in terms of duration properties: the higher the coupon, the lower the duration; the higher the yield level, the lower the duration. Given these two properties, a 10-year non-investment grade bond has a lower duration than a current coupon 10-year Treasury note since the former has a higher coupon rate and trades at a higher yield level. Does this mean that a 10-year non-investment grade bond has less interest rate risk than a current coupon 10-year Treasury note? Consider also that a 10-year Swiss government bond has a lower coupon rate than a current coupon 10-year U.S. Treasury note and trades at a lower yield level. Therefore, a 10-year Swiss government bond will have a higher duration than a current coupon 10-year Treasury note. Does this mean that a 10-year Swiss government bond has greater interest rate risk than a current coupon 10-year U.S. Treasury note? The missing link is the relative volatility of rates, which we shall refer to as yield volatility or interest rate volatility.
The greater the expected yield volatility, the greater the interest rate risk for a given duration and current value of a position. In the case of non-investment grade bonds, while their durations are less than current coupon Treasuries of the same maturity, the yield volatility of non-investment grade bonds is greater than that of current coupon Treasuries. For the 10-year Swiss government bond, while the duration is greater than for a current coupon 10-year U.S. Treasury note, the yield volatility of 10-year Swiss bonds is considerably less than that of 10-year U.S. Treasury notes.
EXHIBIT 19 The Effect of Yield Level on Price Volatility—Option-Free Bond
Consequently, to measure the exposure of a portfolio or position to interest rate changes, it is necessary to measure yield volatility. This requires an understanding of the fundamental principles of probability distributions. The measure of yield volatility is the standard deviation of yield changes. As we will see, depending on the underlying assumptions, there could be a wide range for the yield volatility estimates.
A framework that ties together the price sensitivity of a bond position to interest rate changes and yield volatility is the value-at-risk (VaR) framework. Risk in this framework is defined as the maximum estimated loss in market value of a given position that is expected to occur with a specified probability.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
