CHAPTER 4
Bonds
INTRODUCTION
Bonds and debentures, which we have already introduced, are referred to as fixed-income securities. They are called this because once the rate of interest is set at the onset of the period when it is due to be paid, interest is not a function of the profitability of the firm. For this reason, all bonds, including floating-rate bonds that entail the resetting of interest at the commencement of each interest payment period, are called fixed-income instruments. Interest payments are therefore contractual obligations, and failure to pay what was promised at the start of an interest computation period is tantamount to default.
A bondholder is a stakeholder in a business but is not a part owner of the business. Bondholders are entitled only to the interest that was promised and to repayment of principal at the time of maturity and do not partake in the profits of the firm. As we discussed earlier, bonds may be unsecured or secured. Unsecured debt is referred to as a debenture in the United States, and the term connotes that no specific asset(s) have been earmarked as collateral for the securities. In the case of secured debt, however, the issuer sets aside as collateral specific assets on which the investors have a claim in the event of default. Debt securities may be negotiable or nonnegotiable. A negotiable security is one that can be traded in the secondary market, whereas a nonnegotiable security cannot be endorsed by the holder in favor of another investor. Bank accounts are classic examples of nonnegotiable securities, for if investors were to open a term deposit with a commercial bank, they can always withdraw the investment and pay a third party, but they cannot transfer the ownership of the deposit.
The most basic form of a debt security is referred to as a plain-vanilla bond. It is an IOU that promises to pay a fixed rate of interest every period, which is usually every six months in the United States, and to repay the principal at maturity. Floating-rate bonds are similar except that the interest rate does not remain constant from period to period but fluctuates with changes in the benchmark to which it is linked. There are also bonds with embedded options. Convertible bonds can be converted to shares of stock by the investor. Callable bonds can be prematurely retired by the issuing company, while putable bonds can be prematurely surrendered by the bondholders in return for repayment of the principal.
Bonds provide equity shareholders with leverage. Here is a detailed illustration. Company ALPHA is entirely equity financed and has issued shares worth $1,000,000. Company BETA has raised the same amount of capital, half in the form of debt and the other half in the form of equity. The debt carries interest at the rate of 6% per annum.
Let us consider two situations, the first where both companies make a profit of $250,000 from operations, and the second where they both make a loss of $250,000. We will assume that the firm does not have to pay tax to keep matters simple.
PAT stands for profit after tax and represents what the shareholders are entitled to.
ROI is the return on investment for shareholders.
As we can see from Table 4.1, the presence of debt in the capital structure creates leverage. The profit for the shareholders is magnified from 25% to 44% when a firm is financed 50% with debt. On the other hand, any loss incurred is also magnified – in this case, from –25% to –56%. Thus, as we saw in the case of margin trading, leverage is a double-edged sword. It can also be seen from the case of BETA that the incurrence of a loss does not give the flexibility to the firm to avoid or postpone the interest due to bondholders. Thus, interest on bonds is indeed a contractual obligation.
Bonds also provide the issuing firm with a tax shield. This is because while interest on debt is a deductible expense for figuring the tax liability of a company, dividends on equity shares is not. Consequently, interest payments reduce the tax liability for the firm or, in other words, give it a tax shield. Here is an illustration using the same data as above. Both firms are assumed to have a profit of $250,000 and the applicable tax rate is assumed to be 30%.
PBT stands for Profits Before Tax.
PAT stands for Profits After Tax.
Let us analyze the last row of Table 4.2. If company BETA had been a zero-debt company like ALPHA, its shareholders would have been entitled to an income of $175,000. Because it has paid interest, though, the shareholders have received only $154,000, which is $21,000 less. Thus, from the standpoint of shareholders of BETA, they have effectively paid an interest of $21,000. So, what explains the missing $9,000, for we know that BETA did pay $30,000 to its bondholders? The answer is that by allowing the firm to deduct the interest paid as an expense prior to computing tax, the country's tax authority has forgone taxes to the extent of $9,000. Thus, the tax authority has effectively provided a subsidy to the company. The tax shield, as we term it, is equal to the product of the tax rate and the interest paid; in this case it is 0.30 × 30,000 = $9,000.
If the rules were changed and interest on debt was no longer tax deductible, BETA would have to pay tax on $250,000 and the PAT, which is what belongs to the shareholders, would be only $145,000. In this situation, the shareholders will feel the full burden of the interest paid by the firm.
TABLE 4.1 Illustration of Leverage
| Case-A | Case-A | Case-B | Case-B | |
|---|---|---|---|---|
| Firms Make a Profit | Firms Make a Profit | Firms Make a Loss | Firms Make a Loss | |
| ALPHA | BETA | ALPHA | BETA | |
| Profits from Operations | 250,000 | 250,000 | (250,000) | (250,000) |
| Less Interest | 0 | (30,000) | 0 | (30,000) |
| PAT | 250,000 | 220,000 | (250,000) | (280,000) |
| ROI | 25% | 44% | –25% | –56% |
TABLE 4.2 Illustration of a Tax Shield
| ALPHA | BETA | |
|---|---|---|
| Profit from Operations | 250,000 | 250,000 |
| Interest | NIL | 30,000 |
| PBT | 250,000 | 220,000 |
| Tax | (75,000) | (66,000) |
| PAT | 175,000 | 154,000 |
In many countries interest received from bonds is taxable at the hands of the receiver, whereas dividends received from shares are not. The reason is that since the interest is being paid out of pre-tax profits, it is not being taxed at the level of the firm. However, dividends on equity is not a tax-deductible expense for the firm and, to prevent it from being taxed twice, it is not taxed at the hands of the shareholders.
TERMS USED IN THE BOND MARKET
Face Value
The face value, also known as
- Par value
- Redemption value
- Maturity value
- Principal value
is the principal amount underlying the bond. It was the amount raised by the issuer from the first holder and is the amount repayable by the issuer to the last holder. We will denote it by the symbol M.
Term to Maturity
This is the time remaining in the life of the bond as measured at the point of evaluation. It may be perceived as the length of time after which the debt shall cease to exist, and the borrower will redeem the issue by repaying the holder. It may also be viewed as the length of time for which the borrower has to make periodic interest payments on the debt. The words maturity, term, and term to maturity are used interchangeably. We will assume that we are stationed at time zero and will denote the point of maturity by T. Thus, the number of periods until maturity is T, which is normally measured in years.
Coupon
The contractual interest payment made by the issuer is called a coupon payment. The name came about because in the earlier days, bonds were issued with a booklet of post-dated coupons. On an interest payment date, the holder was expected to detach the relevant coupon and claim his payment.
The coupon may be denoted as a rate or as a dollar value. We will denote the coupon rate by c. The dollar value, C, is therefore given by c × M. Most bonds pay interest on a semiannual basis and consequently the semiannual cash flow is c × M/2.
Consider a bond with a face value of $1,000, which pays a coupon of 8% per annum on a semiannual basis. The annual coupon rate is 0.08. The semiannual coupon payment is 0.08 × 1,000/2 = $40.
Yield to Maturity
Like the coupon rate, the yield to maturity is an interest rate. The difference is that while the coupon rate is the rate of interest paid by the issuer, the yield to maturity (YTM) is the rate of return required by the market. At a given point in time, the yield may be greater than, equal to, or less than the coupon rate. The YTM will be denoted by y and is the rate of return that a buyer will get if he were to acquire the bond at the prevailing price and hold it to maturity. We will shortly see that the YTM of a bond is equivalent to the concept of the Internal Rate of Return (IRR) used in capital budgeting. As in the case of the IRR, the YTM computation assumes that all intermediate cash flows are reinvested at the YTM itself.
VALUATION OF A BOND
To value a bond, we will first assume that we are standing on a coupon payment date. That is, we will assume that a coupon has just been received and the next coupon is exactly six months or one period away. If T is the term to maturity we have N coupons remaining where N = 2T.
We will receive N payments during the life of the bond, where each payment or cash flow is equal to C/2. This payment stream constitutes an annuity. The present value of this annuity is:
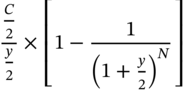
The terminal payment of the face value is a lump-sum payment. Since we are discounting the cash flows from the annuity on a semiannual basis, this payment too needs to be discounted on a similar basis. Thus, the present value of this cash flow is:

Thus, the price of the bond is given by:
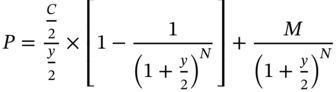
As can be seen the YTM is the discount rate that makes the present value of the cash flows from the bond equal to its price. The price of a bond is like the initial investment in a project. The remaining cash flows are similar to the inflows from the project. Consequently, the YTM is exactly analogous to the IRR.
PAR, PREMIUM, AND DISCOUNT BONDS
In the preceding illustration, the price of the bond is less than its face value. Such bonds are said to be trading at a discount to the par value and are therefore referred to as discount bonds. If the price of the bond were to be greater than its face value, then it would be said to be trading at a premium to its face value and would consequently be referred to as a premium bond. If the price is equal to the face value, then the bond is said to be trading at par.
The relationship between the price and the face value depends on whether the YTM is greater or less than the coupon. Consider the pricing equation:
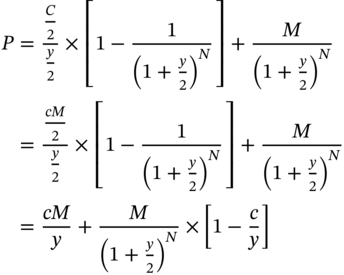
If c = y, P = M. In other words, if the coupon is equal to the YTM, the bond will always trade at par.
Why would a bond sell at a premium or at a discount? The price of a bond is the present value of all the cash flows emanating from it. If the yield is equal to the coupon, then the rate of return being demanded by investors is exactly equal to the rate of return being offered by the issuer, and consequently the bond will sell at par.
Now take a case where the yield is less than the coupon. For instance, assume that the coupon is 10% per annum while the yield is 8% per annum. An investor would be willing to pay more than its face value for it. In practice, the price would be bid up to a level where the YTM is exactly equal to 8% per annum. Finally, consider a case where the YTM is greater than the coupon. Assume that the coupon is 8% per annum while the yield is 10% per annum. Investors in these circumstances would be willing to pay only a price that is less than the face value. In practice the price would be driven down to a level where the YTM is exactly equal to 10%.
EVOLUTION OF THE PRICE
Let us consider the change in the price of a bond from one coupon date to another, assuming that the YTM remains constant.
Note: C is the annual coupon in currency terms and c is the annual coupon rate in percentage terms. Thus C = c × M.
The price of a bond with N coupons remaining is:

The price when there are N − 1 coupons left is given by:

Thus the price change between successive coupon periods is given by:
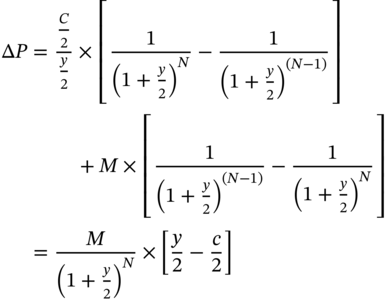
Obviously if y = c, then ΔP = 0. Thus, if the YTM were to remain constant, the price of a par bond will continue to remain at par as we go from one coupon date to the next. If the yield is greater than the coupon, then ΔP > 0. Thus, a discount bond will steadily increase in price as we go from one coupon date to the next. In the case of a premium bond, the price will steadily decline as we go from one coupon date to the next.
This is called the Pull to Par effect. The reason is the following. As we go from one coupon date to the next, one coupon drops out of the pricing equation, which pulls down the price. On the next coupon date, however, the face value is discounted for one period less, which pulls up the price. For par bonds, the two effects neutralize each other, and the price remains unchanged. For premium bonds, the first effect dominates, and the price steadily declines as we approach maturity. For discount bonds, however, the second effect dominates, and the price steadily increases from one coupon date to the next.
ZERO-COUPON BONDS
Unlike a plain-vanilla bond, which pays coupons at periodic intervals, zero-coupon bonds, also known as deep discount bonds, do not pay any interest. Such instruments are always traded at a discount to the face value, and the holder at maturity will receive the face value. For instance, consider a zero-coupon bond with a face value of $1,000 and 10 years to maturity. Assume that the required yield is 8% per annum. The price may be computed as follows.
Notice that we have chosen to discount at a rate of 4% for 20 half-yearly periods, and not at 8% for 10 annual periods. The reason is that in practice a potential investor will have a choice between plain-vanilla bonds and zero-coupon bonds. To draw meaningful inferences, it is imperative that the discounting technique be common. Since the cash flows from plain-vanilla bonds are usually discounted on a semiannual basis, we choose to do the same for zero-coupon bonds.
A zero-coupon bond will never sell at a premium. It will always trade at a discount except at the time of maturity, when it will trade for the face value. That does not mean that buyers of such a bond will always experience a capital gain. If they were to buy and hold it to maturity, then obviously they will have a capital gain. But if they choose to sell it prior to maturity they may well end up with a capital loss as we shall demonstrate.
VALUING A BOND IN BETWEEN COUPON DATES
Thus far we have assumed that we are valuing the bond on a coupon date. That is, the next coupon is exactly one period away. Now let us consider a more realistic situation where the price of the bond is sought to be calculated in between coupon dates.
Consider the timeline depicted in Figure 4.1.
As you can see, the length of time between “0” and “1” is less than one period, whereas the other coupon dates are spaced exactly one period apart.
To value the bond at time “0” we will proceed in two steps. First let us value the bond at time “1.” At this point in time, we will get a cash flow of C/2. There are N − 1 coupons left after this and the face value is scheduled to be received N − 1 periods later. The present value of the remaining cash flows at this point in time is:

Thus, the price of the bond at time “1” is:


FIGURE 4.1 Cash Flows from a Plain-Vanilla Bond
Let us denote the length of time between “0” and “1” by the symbol k. Obviously k < 1. Discounting back P1 for k periods we get:

DAY-COUNT CONVENTIONS
When valuing a bond between coupon dates the key issue is the calculation of the fractional first period. Unfortunately, there is no unique method for computing this period. Different markets, and at times different products in the same market, follow different conventions. A method of computation of the fractional period is called a day-count convention.
ACTUAL-ACTUAL
We will illustrate a convention known as the actual-actual approach. This is used for Treasury bonds in the United States. Let us go back and analyze the fractional period. In order to compute the fraction, we need to define the numerator and the denominator. The numerator is the number of days between the valuation date and the next coupon date. The denominator is obviously the number of days between the previous coupon date and the next coupon date.
As per the actual-actual method we have to actually count the exact number of days in both the numerator as well as the denominator. We will illustrate it with the help of an example.
THE TREASURY'S APPROACH
The Treasury uses a slightly different method to compute the prices of its bonds, with the difference being that it uses simple interest for the fractional period. The Treasury's formula may be stated as:

In this case, the price obtained by the Treasury will be $803.0738. The price that is computed by the Treasury for a given bond will always be lower than the value determined by Wall Street. This is because simple interest gives a higher discount rate for fractional periods as compared to compound interest.
CORPORATE BONDS
Corporate bonds in the United States are priced using a different day-count convention known as 30/360 NASD. As per this convention, the denominator, or the time period between two successive coupon dates, is always taken to be 180 days. That is, every month is assumed to consist of 30 days. The numerator, in order to compute the fractional period, is determined as follows.
Let us define the start date as D1 = (month1, day1, year1) and the end date as
D2 = (month2, day2, year2). The numerator is calculated as:
There are some additional rules which may have to be applied depending on the circumstances.
- If day1 = 31, then set it equal to 30.
- If day1 is the last day of February, whether 28 or 29, then set it equal to 30.
- If day1 is 30 or has been set equal to 30 based on the two rules listed above, then if day2 = 31, set it equal to 30.
Let us take the case of the bond maturing on 15 May (20XX+20). The valuation date as per our assumption is 21 May 20XX. The numerator for the fractional period is given by:
The value of the fractional period is 174/180 = 0.9667.
The value of the bond is therefore:
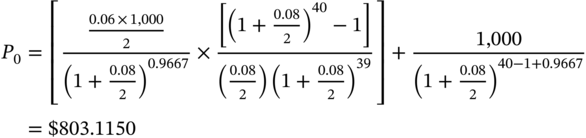
As can be seen the day-count convention does have an impact, albeit a minor one, on the price.
ACCRUED INTEREST
The value of the bond as calculated by us using the appropriate day-count convention is referred to as the full or the dirty price. This is the price that is payable by the buyer to the seller. The price includes a component called the accrued interest, which we will now explain.
When a bond is sold between two coupon dates, the next coupon will go to the buyer of the bond. The seller, having held the security for a fraction of the coupon period, is entitled to a part of the next coupon payment. This fraction of the next coupon that belongs to the seller is termed as the accrued interest. The bond pricing equation that we have just used automatically factors in the accrued interest, for it discounts all the forthcoming cash flows, from the perspective of the buyer, until the date of sale. The partial derivative of the dirty price with respect to the length of the fractional period is negative. The shorter the time remaining until the next coupon, the higher will be the accrued interest, keeping all the other variables constant; hence the higher is the dirty price.
The method for computing the accrued interest is a function of the day-count function. Let us take the case of the Treasury bond. On 21 May 20XX, it has accrued interest for 6 days. The total length of the coupon period is 184 days.1
The accrued interest is therefore:
The dirty price less the accrued interest is referred to as the clean price. In this case it is $803.0939 – 0.9783 = $802.1156.
The significance of the clean price may be demonstrated as follows. Let us consider the value of the bond on the previous coupon date, that is 15 May 20XX, assuming that the YTM is 8% per annum. The price comes out to be $802.0722.
On 15 May there is no difference between the clean price and the dirty price, since interest accrual for the next period is yet to commence. As can be seen, if the YTM is assumed to be constant, the dirty price changes by $1.0217, which amounts to more than a dollar, whereas the clean price changes only by $0.0434. Thus in the absence of a change in yield, the clean price remains relatively constant in the short run.
Look at the situation from the perspective of a bond market analyst, who knows that yield changes induce price changes. From an analysis of dirty prices, however, the analyst will be unable to discern how much of the perceived change is due to a movement in the required yield, and what is due to the change in accrued interest. Thus analysts look at prices that are not contaminated with accrued interest, or what we term as clean prices. For this reason, quoted prices in bond markets are always clean prices. However, a trader who buys a bond has to pay the full price or the dirty price. Hence when a bond is bought, the accrued interest has to be computed and added to the quoted price in order to determine the amount payable.
NEGATIVE ACCRUED INTEREST
One interesting question is, can the accrued interest be negative? Let us analyze the possible reason why accrued interest may be negative. Accrued interest represents the amount that the sellers of the bond are entitled to by virtue of the fact that they have held the bond for a part of the coupon period. Consequently, the buyer has to compensate them with this amount. Thus, negative accrued interest would correspond to a situation where the seller has to compensate the buyer, and such a case can arise when the bond trades ex-dividend.
Certain bonds trade on an ex-dividend basis close to the coupon date. We know that bonds pay coupons and not dividends, and consequently the term ex-dividend is a bit of a misnomer. But the implication is the same. Until the ex-dividend day a bond will trade cum-dividend. That is, the buyer will be entitled to the next coupon. On the ex-dividend day, however, the bond will begin to trade ex-dividend, which implies that the next coupon will go to the seller and not the buyer. However, a buyer who acquires the bond on or after the ex-dividend day is entitled to the pro-rata interest for the number of days remaining until the next coupon date. In such a situation, the seller has to share a part of the interest received with the buyer, which leads to a situation where the accrued interest is negative.
Let us consider a corporate bond maturing on 15 May (20XX+20). Assume that we are on 8 November 20XX, which is an ex-dividend date. The dirty price, just before the bond goes ex-dividend, is:
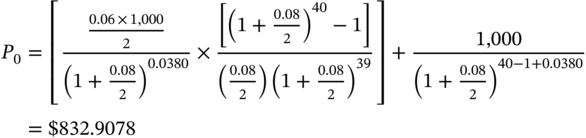
The moment the bond goes ex-dividend the price will drop by the present value of the next coupon, because the buyer is no longer entitled to it. Thus, the ex-dividend dirty price is:
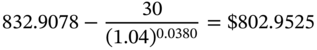
Notice that the dirty price will fall by the present value of the coupon and not by the coupon itself. This is because there is a week remaining until the next coupon and we consequently need to discount the cash flow.
The accrued interest as of 8 November 20XX is:
Thus the ex-dividend clean price is 832.9078 – 28.8587 = $804.0491. As can be seen, the ex-dividend clean price is greater than the ex-dividend dirty price by $1.0966. This is the negative accrued interest and corresponds to the accrued interest for the remaining week, which is:
YIELDS
The yield, or the rate of return from a bond, can be computed in a variety of ways. We have already referred to the YTM, which we will discuss in further detail shortly. There are a number of other yields measures that we will examine as well.
THE CURRENT YIELD
The current yield is very simple to compute, although technically it leaves a lot to be desired. It is commonly reported in practice, however, because of the ease with which it can be calculated.
To compute the current yield, we simply take the annual coupon payment (irrespective of the frequency with which the coupon is paid) and divide it by the current market price. Thus
One question is, should the price used be the clean or the dirty price? If the clean price were to be used, then the current yield will change only when there is a change in the YTM. But if the dirty price were to be used, the current yield using the dirty price will be lower than the value obtained using the clean price, if we were to calculate it prior to the ex-dividend date. This is because the dirty price in this period will be higher than the clean price. Besides, even if the YTM were to remain constant, the current yield will steadily decline along with the increase in the dirty price. In the ex-dividend period, however, the value of the current yield that we get with the dirty price will be higher than what we would get with the clean price, because the dirty price will be lower than the clean price. In this period too, if the YTM were to remain constant, the dirty price will steadily increase and consequently the current yield will steadily decline. Thus in practice if we were to plot the current yield versus the dirty price for a given YTM, we would get a sawtooth pattern.
Why do we say that the current yield is an unsatisfactory yield measure? Consider the case of investors who have a one-year investment horizon. They will get a coupon of $C in the course of the year. If we assume that P0 was the price they paid at the outset to acquire the bond, then their interest yield for the year is the same as the current yield as defined by us. But even if the investors were to have a one-year horizon, they will sell the bond at the end of the year, unless of course it were to mature at that time. They will experience a capital gain or a loss.2
If the investors had a longer-term horizon, they would get additional coupons. These can be reinvested to earn income. Besides, when multiple cash flows are involved, time value of money will enter the picture. All these facets of yield computation are totally ignored by the current yield measure.
SIMPLE YIELD TO MATURITY
The simple yield to maturity, also known as the Japanese Yield, as it is a key yield measure used in Japan, factors in the capital gain or loss that investors will get. However, it assumes that the bond will be held to maturity and that capital gains/losses occur evenly over the life of the bond. In other words, it builds in the assumption that capital gains and losses occur on a straight-line basis.
Consider the case of investors who buy the bond at a price P. If they hold it to maturity, they will get back the face value, M. The capital gain/loss over the investment horizon is given by M − P. If the bond is bought at a discount, there will be a capital gain; otherwise there will be a capital loss. If we assume that we are standing on a coupon date and that there are N coupons left, obviously there are N/2 years remaining until maturity. The capital gain/loss amortized on a straight-line basis is obviously
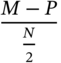
The simple YTM is given by:

Thus, for discount bonds, the simple yield to maturity will be greater than the current yield, whereas for premium bonds it will be lower. For par bonds, the two will obviously be equal.
One of the shortcomings of the Japanese yield is that it fails to take into account that investors in bonds can reinvest the coupons received by them in order to earn interest on such interest. This has the potential to significantly increase the returns from holding a bond, as we shall soon demonstrate.
YIELD TO MATURITY
The Yield to Maturity (YTM) is the internal rate of return of a bond. It is that single discount rate3 that makes the present value of the cash flows from a bond equal to its price. The bond pricing equation is a nonlinear equation. Because there is only a single change of sign in the cash flows, from Descartes' rule of signs we know that there will be a single positive real root. The pricing formula gives us a polynomial of degree “N,” assuming that the bond has N coupons remaining. To solve it, we generally require a computer program, but we can get fairly close with the Approximate Yield to Maturity (AYM) approach, which we shall demonstrate. We will show subsequently that it is a very simple matter to compute the YTM for zero-coupon bonds, and bonds with only two coupons remaining.
APPROXIMATE YIELD TO MATURITY
Consider a bond with a face value of M, a current price of P, an annual coupon of C, and with N coupons remaining until maturity.
The current investment in the bond is $P. An instant before the bond matures the investment in the security is $M. Thus the average investment is (M + P) ÷ 2.
The annual capital gain/loss computed by amortizing on a straight-line basis is

as we have seen in the case of the Japanese Yield.
The approximate YTM is defined as:

The numerator in the expression represents the annual income for the investor, assuming of course that capital gains/losses are realized on a straight-line basis. The denominator, as we have explained, is the average investment during the life of the bond.
Once the approximate yield is computed, we need to choose an interest rate band such that the upper limit gives a lower price than the observed price while the lower limit gives a higher price. The exact YTM is then obtained using linear interpolation.
ZERO-COUPON BONDS AND THE YTM
It is simple to determine the YTM for a zero-coupon bond, given its price, as the following example will illustrate.
Consider a bond with 10 years to maturity and a face value of $1,000. Assume that the current price is $475. The pricing equation is4

ANALYZING THE YTM
To better appreciate the mathematics underlying the YTM, let us consider the sources of return for investors who buy the bond at the prevailing market price and hold it to maturity.
They will obviously get N coupons, where each coupon is equal to $C/2. Each time they get a coupon they can reinvest at the market yield prevailing at that time in an asset of the same risk class. And finally, when the bond matures, they will be repaid the face value. The cash flows from the coupon payments constitute an annuity. When these cash flows are reinvested, they will earn interest. The important thing is the future value of these cash flows at the time the bond matures, which can be computed by the standard annuity formula. Let us assume that each cash flow can be reinvested at a periodic (six-monthly) rate of r/2%. For ease of exposition, we will assume that r is the same for each cash flow, or in other words, that the reinvestment rate is a constant. This is not a necessary assumption and is made purely to facilitate the presentation of the argument.
The future value of the coupons as calculated at the time of maturity is given by

Thus the total cash flow at maturity is

From the bond pricing equation
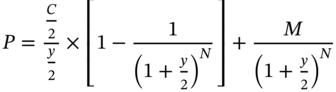
When can we make a claim that we have received a yield of y/2 per period over N periods? Only if the terminal cash flow is equal to the initial investment compounded at y/2 for N periods.
In other words, we can claim that we have obtained a semiannual yield of y/2 if

The implication is that in order to receive a periodic yield of y/2 over N periods, we need to satisfy two conditions. First, the investor must hold the bond until the maturity date. Second, y/2 must equal r/2. In other words, each intermediate cash flow obtained during the life of the bond (coupon) must be reinvested at the YTM prevailing at the time of acquisition of the bond.
Let us now analyze the consequences of relaxing this assumption.
THE REALIZED COMPOUND YIELD
We will now relax one of the two assumptions made in the previous section. We will continue to assume that the bond will be held until maturity, but we will no longer take it for granted that each coupon is reinvested at the YTM. Rather, we will assume a specific rate r, at which the coupons are assumed to be reinvested.
The following example illustrates the approach adopted to compute what is termed as the realized compound yield.
REINVESTMENT AND ZERO-COUPON BONDS
The inability to reinvest at a rate of return assumed at the outset is referred to as reinvestment risk. For coupon-paying bonds, reinvestment risk is a critical feature. Zero-coupon bonds are devoid of reinvestment risk as there are no coupons to be reinvested. Thus, in order to obtain a rate of return equal to the YTM for a zero-coupon bond, we have to satisfy only one condition: we should hold the bond to maturity.
THE HOLDING PERIOD YIELD
Now we will relax both the assumptions we made earlier in order to compute the YTM. The first change, as we did in the case of the RCY, is that we will explicitly assume a rate at which the coupons are reinvested. Second, we will no longer assume that the bond is held to maturity but will assume an investment horizon shorter than the time to maturity. The corresponding yield measure is termed as the horizon yield or the holding period yield.
The consequence of the second assumption is that it is no longer necessary that an investor will receive the face value at the end of the investment horizon. The investor will receive the market price at that time, which may be more or less than the face value, depending on the YTM prevailing at that time.
Since we need to compute the sale price prior to maturity, we need to make an assumption about the YTM that is likely to prevail at that time, if we are computing the holding period yield on an ex-ante basis.5
Let us consider the data that we used to compute the RCY. We will assume, however, that the investor has a horizon of eight years or 16 semiannual periods. We will assume that the bond can be sold at a YTM of 7.50% at the end of eight years. At that point in time, it will be a two-year bond. The corresponding price is $990.8715.
The future value of the reinvested coupons is given by6
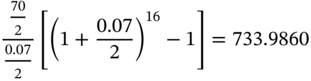
Thus, the terminal cash flow is 990.8715 + 733.9860 = 1,724.8575.
The rate of return over the eight-year period is given by

TAXABLE EQUIVALENT YIELD
Certain bonds are exempt from income taxes. In the United States both the federal and state governments are empowered to levy such taxes. In order to deal with a situation where a comparison is sought between a bond whose interest is taxable and another whose income is tax free, we need to compute the taxable equivalent yield (TEY) of the tax-free bond.
The computation of the TEY depends on the applicable taxes. Let us first consider a municipal bond which gives a yield of 6.00%. The bond is exempt from federal income tax, which we will assume is 25%. The TEY is given by
The implication is that an investor should be indifferent between a taxable bond that yields 8% and the tax-free municipal bond which yields 6%. If the taxable bond were to yield more than 8%, that would be preferable. On the other hand, if it were to yield less than 8%, the investor would prefer the municipal bond.
To make the computation more precise we need to account for the fact that both the bonds attract state income tax. This per se does not warrant an adjustment since both the bonds will be equally affected. For a bond that attracts both federal and state income taxes, however, the state tax can be deducted from the federal tax bill. This calls for the following adjustment.
Let us assume that the federal rate is 25% and the state tax rate is 8%. The adjusted federal rate is given by:
The TEY of the municipal bond is therefore:
The rationale for this correction is the following. Someone who earns $100 in income will have to pay $8 by way of state tax. The federal tax is applicable only on $92. So, the effective federal tax rate is: 0.92 × 0.25 = 0.23 ≡ 23%.
Now consider a situation where the municipal bond is exempt from both federal as well as state taxes. To make the necessary adjustment we need to compute the combined tax rate for a bond which is subject to both taxes. In our case it is 23% + 8% = 31%.
The TEY of the municipal bond in such a situation is given by
There can be a situation where the taxable bond, which is being compared with the municipal bond, is subject to federal taxes but not to state taxes. If so, we need to compute the TEY of the taxable bond and compare it with that of the municipal bond.
Assume that a T-bond with a coupon of 6.90% is being compared with a municipal bond which is exempt from both state and federal taxes. The TEY of the T-bond is:
This TEY should be compared with the TEY of the municipal bond, and the bond that offers the higher TEY will be deemed to be superior.
CREDIT RISK
Credit or default risk is the risk that the coupons and/or principal may not be paid as scheduled. Except for Treasury securities, which are backed by the full faith and credit of the federal government, all debt securities are subject to default risk, and differ only with respect to the degree of the associated risk. When a bond is issued, the borrower will release a prospectus with detailed information about its financial health and creditworthiness; however, most investors lack the required skill sets to draw meaningful conclusions from analyzing such documents. In order to give confidence to potential investors about the quality of the issue, issuers have the securities rated by credit rating agencies. These agencies specialize in evaluating the credit quality of a security issue. They not only provide a rating prior to the issue, but also continuously monitor the health of the issuer throughout the life of the security and modify their recommendations as and when required. The rating accorded to a particular issue is based on the financial health of the issuer and the quality of its management team. In the case of secured bonds, it also depends on the quality of collateral that has been specified.
The three main rating agencies in the United States are:
- Moody's Investors Service
- Standard and Poor's (S&P)
- Fitch Ratings
There are two categories of rated securities: investment grade and speculative grade. Investment-grade bonds are of higher quality and carry a lower credit risk. Non-investment grade, also known as speculative grade or junk bonds, carry a higher risk of default. Because a riskier security must offer a higher rate of return to compete with better rated securities, junk bonds carry a high coupon. Thus, investors are cautioned that they are investing at their own risk. If nothing were to go wrong, investors will walk away with higher returns.
The ratings scales adopted by the three rating agencies are depicted in Tables 4.5 and 4.6.
As discussed, the agencies may revise their ratings during the life of the security. If a rating change is being contemplated, they will signal their intentions. S&P will place the security on Credit Watch. Moody's will place the security on Under Review, while Fitch will place it on Rating Watch.
TABLE 4.5 Investment Grade Ratings
| Credit Risk | Moody's Ratings | S&P's Ratings | Fitch's Ratings |
|---|---|---|---|
| Highest Quality | Aaa | AAA | AAA |
| High Quality | Aa | AA | AA |
| Upper Medium | A | A | A |
| Medium | Baa | BBB | BBB |
TABLE 4.6 Speculative Grade Ratings
| Credit Risk | Moody's Ratings | S&P's Ratings | Fitch's Ratings |
|---|---|---|---|
| Somewhat Speculative | Ba | BB | BB |
| Speculative | B | B | B |
| Highly Speculative | Caa | CCC | CCC |
| Most Speculative | Ca | CC | CC |
| Imminent Default | C | C | C |
| Default | C | D | D |
BOND INSURANCE
A company seeking a better rating can have its issue insured in order to enhance credit quality. In such cases, the issuer will have to pay a premium to the insurance company. But this cost will be passed on to investors in the form of a lower coupon. In the case of insured bonds, the timely payment of promised cash flows is guaranteed by the insurance company. Thus, the rating of such issues would depend on the financial health of the insurer. Clearly it would make sense to get an issue insured only by a company that enjoys a better reputation than the issuer.
In the case of such bonds, the credit quality of the issuer will be appraised by two entities: the rating agency and the insurance company.
EQUIVALENCE WITH ZERO-COUPON BONDS
Consider a bond with a face value of $1,000 and two years to maturity. Assume that the coupon is 7% per annum, payable on a semiannual basis. This bond will give rise to five cash flows as per the schedule shown in Table 4.7.
Consider the first cash flow. It is like the maturity value of a zero-coupon bond with a face value of $35, maturing after six months. Similarly, the second cash flow is like the maturity value of a zero-coupon bond with a face value of $35, maturing after 12 months. Thus, the plain-vanilla bond is like a portfolio of five zero-coupon bonds. This is true for any plain-vanilla bond. If the bond has N coupons remaining until maturity, it is equivalent to a portfolio of N + 1 zero-coupon bonds.
SPOT RATES
Consider the two-year bond that we just discussed. It is equivalent to a portfolio of five zeroes. Each of the zeroes must have its own yield to maturity. The yield to maturity of a zero-coupon bond, for a given time to maturity, is referred to as the spot rate for that period. Thus, the price of the plain-vanilla bond may be expressed as
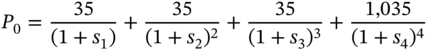
TABLE 4.7 Cash Flows from a Two-Year Bond
| Time Period | Cash Flow |
|---|---|
| 6-M | $35 |
| 12-M | $35 |
| 18-M | $35 |
| 24-M | $35 |
| 24-M | $1,000 |
The traditional pricing equation, based on the YTM, states that

Since a plain-vanilla bond is a portfolio of zeroes, the correct way to price it is by discounting each cash flow at the corresponding spot rate. When we value the cash flows by discounting at the YTM, we are using an average discount rate to capture the effect of the various spot rates. Thus, the YTM of a bond is a complex average of the underlying spot rates.
THE COUPON EFFECT
The YTM is subject to what we call a coupon effect. Consider two one-year bonds, both with a face value of $1,000. Bond A pays coupons at the rate of 7% per annum, while bond B pays a coupon at the rate of 10% per annum. Assume that the six-month spot rate is 6% per annum, while the one year spot rate is 7.25% per annum.
The price of bond A is

The YTM may be calculated as

If we solve the quadratic equation, we get y = 7.2283%.
Now consider bond B. The price is given by
The YTM comes out to be 7.2197%.
Why is it that bond A has a higher YTM than bond B? The price of one-period money is 6% per annum while that of two-period money is 7.25% per annum. Clearly, two-period money is more expensive. Bond A has

of its value locked up on one-period money. Bond B on the other hand has
of its value locked up in one-period money. Since bond B has a greater percentage of its value locked up in one-period money, which in this case is cheaper, it is not surprising that its YTM is lower than that of bond A. Thus, the YTM, which is a complex average of spot rates, is a function of the coupon rate of a bond, for a given term to maturity, which is what we term the coupon effect.
BOOTSTRAPPING
In practice we will not have price data for zero-coupon bonds expiring exactly one period apart. In other words, we will not be in a position to compute the spot rates directly from the observable prices. Bootstrapping is a technique for obtaining spot rates from price data for plain-vanilla bonds.
Consider the information given in Table 4.8. All the bonds have a face value of $1,000 and pay a coupon of 7% per annum on a semiannual basis.
The one-period spot rate is given by

We know that

Substituting for s1 we get s2 = 12.5146% per annum. Similarly, using the pricing equation for the 18-M bonds and substituting for s1 and s2, we can compute s3, and by extending the logic we can find s4. This is the essence of bootstrapping.
FORWARD RATES
Consider a person with a two-period investment horizon. He can directly invest in a two-period zero-coupon bond. Or else he can invest in a one-period bond and roll over his investment. The second approach is obviously fraught with risk, for we cannot predict at the outset as to what the one-period rate will be after one period. It may be possible, however, to enter into a forward contract at the outset which locks in a rate for the one-period investment after one period. The rate implicit in such a contract is referred to as the forward rate of interest. We will denote it as f11. The subscript indicates is that it is for a loan to be made after one period, while the superscript indicates that the loan is for one period. To rule out arbitrage it must be the case that
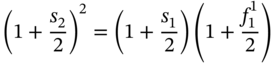
TABLE 4.8 Prices of Plain-Vanilla Bonds with Varying Times to Maturity
| Term to Maturity | Price |
|---|---|
| 6-M | 985 |
| 12-M | 950 |
| 18-M | 925 |
| 24-M | 900 |
For instance, if the one-period rate is 8% per annum while the two period rate is 8.50% per annum, then
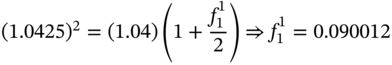
Thus, the one-period forward rate is 9.0012% per annum. In general, the forward rate symbol for an m – n period loan to be made after n periods is ![]() .
.
The relationship between the n period spot rate and the m period spot rate is given by
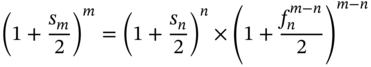
THE YIELD CURVE AND THE TERM STRUCTURE
The plot of the YTM versus the time to maturity of the bond is referred to as the Yield Curve. On the other hand, a plot of the spot rate versus the term to maturity of the bond is called the Term Structure of Interest Rates. The term structure is also known as the Zero-Coupon Yield Curve. The two will coincide if the yield curve is flat. A flat yield curve means that all the spot rates are identical. Obviously since the YTM is an average of spot rates, the YTM in such circumstances will be the same as the spot rate.
While plotting the yield curve or the term structure, it is important to ensure that the data being used pertains to bonds of the same risk class. That is, if one of the bonds is AAA, then all the bonds in the data set must be AAA, meaning that we should compare apples with apples and should not mix up data for AAA bonds with that of T-bonds.
SHAPES OF THE TERM STRUCTURE
In practice the term structure may take a variety of shapes. The commonly observed shapes are:
- Upward Sloping or Rising
- Downward Sloping or Inverted
- Humped
- U-Shaped
Rising yield curves will have a positive slope; that is, short-term yields will be lower than long-term yields. On the other hand, inverted yield curves are characterized by a negative slope; that is, short-term yields are higher than long-term yields. Humped yield curves tend to have lower rates at the short and long ends of the spectrum, and higher rates in between; the curve initially rises, peaks at the middle of the maturity spectrum, and then gradually slopes downward. U-shaped yield curves have the opposite shape; the rates are higher at the short and long ends of the spectrum and tend to be low in between. Such curves are characterized by a curve that declines initially, reaches a trough at the middle of the maturity spectrum, and then gradually slopes upwards.
THEORIES OF THE TERM STRUCTURE
A variety of theories have been expounded to explain the various observed shapes of the yield curve.
The Pure or Unbiased Expectations Hypothesis
This popular theory states that the implied forward rates computed using current spot rates are nothing but unbiased estimators of future spot rates. As per this theory, therefore, long-term spot rates are geometric averages of expected future short-term rates. This hypothesis can be used to explain any shape of the yield curve. Let us take an upward sloping curve. The expectations hypothesis would explain it with the argument that the market expects spot rates to rise. If rates are expected to rise, then holders of long-term bonds will be perturbed because the prices of such bonds are expected to decline, and they will be confronted with the possibility of a capital loss. Such investors will start selling long-term bonds and buying short-term bonds. This will lead to an increase in long-term yields and a decrease in short-term yields. The net result would be an upward-sloping yield curve.
Now consider an inverted yield curve. This would be consistent with the view that the market expects future spot rates to fall. If so, investors will seek to sell short-term bonds and invest in long-term bonds, which will push up short-term yields and lead to declining long-run yields. The net result will be an inverted yield curve.
A humped yield curve would be consistent with the expectations that investors expect short-term rates to rise and long-term rates to fall.
The expectation of the future direction of the market is primarily a function of the expected rate of inflation. If the market expects inflationary pressures in the long run, the yield curve will be upward sloped. However, if inflation rates are expected to decline in the long run, then the curve will be negatively sloped.
THE LIQUIDITY PREMIUM HYPOTHESIS
This hypothesis argues that the forward rate is not equal to the expected spot rate but is greater than the expectation of the future spot rate. The difference between the forward rate and the expectation of the future spot rate is termed the liquidity premium. This theory argues that because lenders generally prefer to lend short-term, they must be suitably compensated if induced to lend for longer terms. This compensation takes the form of a premium for a loss of liquidity. As per this hypothesis, the yield curve should invariably be upward sloping, reflecting the investors' preference for liquidity. A declining yield curve, however, can be explained by postulating that future spot rates may sharply decline, causing long-term rates to be lower than short-term rates, the liquidity premium notwithstanding.
THE MONEY SUBSTITUTE HYPOTHESIS
Per this theory short-term bonds are essentially a substitute for cash. Investors generally hold only short–term bonds because of the lower perceived risk. This drives up the demand for such securities and pushes down the yield. This explains low yields at the short end of the maturity spectrum. As far as the other end is concerned, borrowers tend to issue long-term debt, which implies that they will have to access the capital market less frequently, which minimizes the costs associated with borrowing. This leads to an excess supply at the longer end of the maturity spectrum and consequently pushes up the yield.7
THE MARKET SEGMENTATION HYPOTHESIS
The theory postulates that the market is made up of a wide variety of investors and issuers. Each class of investors or issuers has its own requirements, and consequently tends to focus on a particular range of the maturity spectrum. This theory argues that the segments of the market are compartmentalized and there are no interrelationships between them.
The observed shape of the yield curve, as per this theory, depends on the demand-supply dynamics within the market segment, and activities in a given segment have no implications for any other part of the curve. For instance, the need to constantly manage their cash leads to a situation where commercial banks primarily focus on the short end of the curve. On the other hand, institutions such as insurance companies and pension funds, whose liabilities are primarily long-term, tend to focus on the long end of the market.8 In practice there is relatively less demand for medium-dated bonds. Thus, according to this theory, yields will be relatively low at the short and long ends of the maturity spectrum and high in the middle of the term structure, which is consistent with what we call a humped yield curve.
THE PREFERRED HABITAT THEORY
A slight modification of the market segmentation hypothesis, this theory proposes that while investors do tend to concentrate on their chosen market segment, they can be persuaded to hold securities from other segments by offering them suitable inducements. For instance, while banks generally operate at the lower end of the spectrum, an increase in yields of long-dated bonds may sometimes be adequate to persuade them to hold such securities. Similarly, an increase in short-term rates may encourage pension funds and insurance companies to invest in that segment, an area of the market which they would otherwise avoid.
THE SHORT RATE
A short rate of interest is a future spot rate of interest that may evolve over time. It is usually represented as a single period rate, for the shortest period of time considered by the model under consideration. In our previous discussions, we have assumed that the shortest time period corresponds to six months.
At a given point in time we will have a vector of spot rates corresponding to various intervals of time. This vector can be used to derive a unique vector of current forward rates, as explained earlier. We cannot state with certainty, however, what the spot rate will be at a future point in time, for it may take on one of several values, each of which will have an associated probability of occurrence.
At the current instant the one-period spot rate will be equal to the one-period forward rate, which will be equal to the short rate. If we look at a longer time horizon, however, these rates will in general not be equal to each9 other.
In Figure 4.2, at each node there is a 50% probability of reaching the upper state at the end of the current period, and an equal probability of reaching the lower state. The current one-period spot rate is 6%, which is equal to the current short rate. At the end of the period there is a 50% chance that the short rate will be 6.5983% and an equal probability that it will be 4.5983%. Similarly, at the end of two periods, the short rate can take on one of three possible values, while at the end of three periods it can take on one of four possible values.
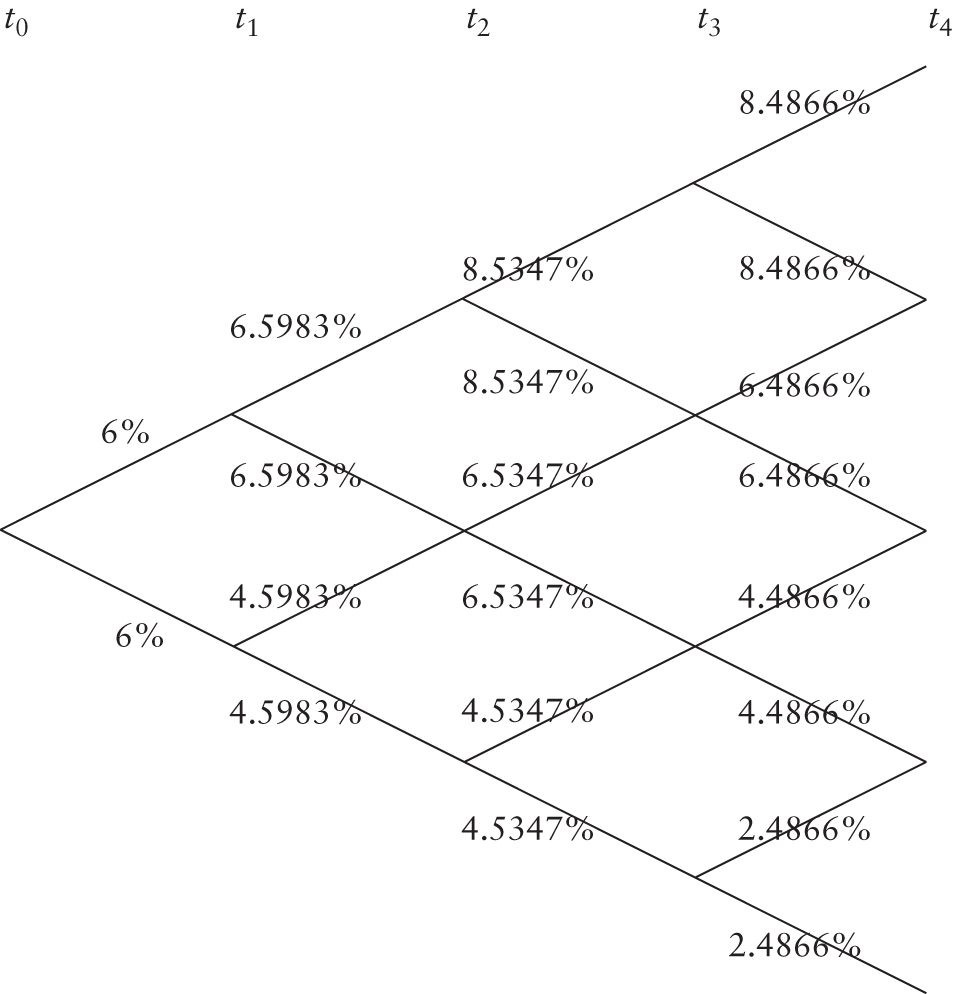
FIGURE 4.2 Evolution of the Short Rate
FLOATING RATE BONDS
Floating-rate notes and bonds, also referred to as floaters, are debt securities whose coupons are reset periodically based on a reference or benchmark rate. Typically, the coupon on such a security is defined as
For instance, consider a security whose coupon is specified as
In this case, the reference rate is the yield on a 5-year T-note and the quoted margin is 75 b.p. It should be noted that the quoted margin need not always be positive. For instance, a floater may have a coupon rate specified as
In the case of a default risk-free floating-rate bond, the price of the security will always reset to par on a coupon date, although in between two coupon dates, it may sell at a premium or at a discount.
For instance, consider a floater with a coupon equal to the 5-year T-bond rate. Assume that there are two periods to maturity. The price of the bond at the end of the first coupon period will be given by

where ![]() is the coupon rate one period before maturity, and
is the coupon rate one period before maturity, and ![]() is the required yield one period before maturity. On the coupon reset date, the YTM will be equal to the coupon since we have assumed that there is no default risk implicit in the security. Consequently, any change in the required yield, as reflected by the YTM at that point in time, will also be reflected in the coupon that is set on that day. We know that if the yield is equal to the coupon, then the bond should sell at par. Thus PT−1 = M.
is the required yield one period before maturity. On the coupon reset date, the YTM will be equal to the coupon since we have assumed that there is no default risk implicit in the security. Consequently, any change in the required yield, as reflected by the YTM at that point in time, will also be reflected in the coupon that is set on that day. We know that if the yield is equal to the coupon, then the bond should sell at par. Thus PT−1 = M.
The price at the outset is given by
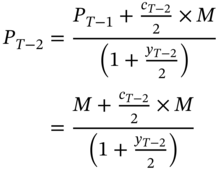
Once again at T−2, ![]() and consequently PT−2 = M. This logic can be applied to a bond with any number of coupons remaining to maturity.
and consequently PT−2 = M. This logic can be applied to a bond with any number of coupons remaining to maturity.
In between two coupon dates, however, the price of such a floater may not be equal to par. Consider the valuation of the note at time T−2+k. The price is given by
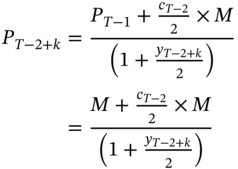
While cT−2 was set at time T−2, and is equal to yT−2, yT−2+k is determined at time T−2+k and will reflect the prevailing 5-year T-note yield at that point in time. In general, yT−2+k need not equal cT−2 and may be higher or lower. Consequently, in between two coupon dates, a floater may sell at a premium or at a discount.
Now let us consider the case of floaters characterized by default risk. In this case it is not necessary that the risk premium required by the market be constant over time. For instance, assume that when the bond was issued the required return was equal to the 5-year T-note rate + 75 b.p. The coupon was set equal to this rate and the bond was sold at par. 6-M hence, the issue is perceived to be more risky and the required return in the market is the 5-year T-note rate + 95 b.p. The coupon, however, will be reset at the prevailing T-note rate + 75 b.p. Hence this issue will not reset to par at the next coupon date.
SIMPLE MARGIN
A margin measure is essentially a yield spread measure, and such measures are used to evaluate the returns from a floater. There are various types of margins that can be computed in practice. We will consider a measure known as the simple margin.
If a floater trades at a premium or a discount, then the premium/discount needs to be factored in while computing the return. If the floater trades at a discount, then we need to account for the accretion of the discount over the life of the floater. On the contrary, if the floater trades at a premium, we need to factor in the amortization of the premium over the life of the security. The formula for the simple margin is
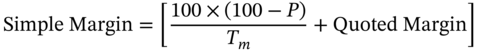
P is the market price (clean price) of the floater, as a percentage of par, and Tm is the remaining time until maturity. If it is not an integer, we need to invoke a day-count assumption. The quoted margin must be expressed in basis points and not percentage terms.
BONDS WITH EMBEDDED OPTIONS
We will consider three types of bonds with embedded options: callable, putable, and convertible bonds. All these bonds give either the issuer or the lender an option. As we have seen, an option gives the holder the right to take a course of action. Since no one will give away a right for free, the holder has to pay a price or a premium to the seller of the option. Consequently, in the case of bonds with embedded options, if the option is with the issuer, then the issuer must pay for it, and consequently the price of the bond will be less than that of a plain-vanilla bond. But if the option is with the lender, then it will manifest itself as a higher price as compared to that of a plain-vanilla bond.
CALLABLE BONDS
Such bonds contain a call option, that is, they give the issuer the right to call away the bond from the lender prior to maturity. In the case of such bonds, issuers can change the maturity of the bond by prematurely recalling it. When will such a bond be recalled? Clearly, when market interest rates are declining. Under such circumstances, the issuer can recall the existing bonds and replace them with a fresh issue with a lower coupon due to the changed circumstances.
The call provision works against lenders. This is because they may have to part with the bond when the market rates are falling, which is precisely a situation where they desire to hold on to the bonds and keep earning a high coupon. To compensate for this, lenders will demand a higher yield as compared to that of a plain-vanilla bond of the same credit quality. This will manifest itself as a lower price. Thus, whether we view it from the issuer's perspective or the lender's, a callable bond must sell at a lower price as compared to an otherwise similar plain-vanilla bond.
Such bonds may be discretely callable or continuously callable. A discretely callable bond may be recalled only at certain prespecified dates, for instance, at the coupon dates over a portion of the bond's life. A continuously callable bond may be called at any time after it becomes callable.
As we have just mentioned, a bond may be recalled only when it becomes callable. This implies that it may not be callable right from the outset. In practice, issuers generally specify a call protection period, which is a period of time during which the bond may not be recalled irrespective of what happens to the market rate of interest. Thus, a discretely callable bond can usually be recalled on any coupon payment date after the call protection period ends, while a continuously callable bond may be recalled at any time from the end of the call protection period until the maturity date of the bond. Bonds with a call protection period are referred to as deferred callable bonds and serve to provide holders with relatively greater certainty.
The price at which the bond can be recalled is referred to as the call price. In many cases a bond may be recalled at par by an issuer. But at times the issuer may specify a call premium. That is, the issuer will pay a value higher than the face value of the bonds if and when the issue is recalled. The call premium is usually set equal to one year's coupon.
Holders of callable bonds are extremely vulnerable to reinvestment risk. The likelihood that they will experience a return of cash increases in a falling interest rate environment means that they will have to face the specter of reinvesting their corpus at a lower rate of interest. Secondly, the potential for price appreciation in a falling rate environment is relatively limited as compared to a plain-vanilla bond. Why do bond prices increase in value? Because yields are declining in the market. But in the case of callable bonds this is precisely the situation where the bond can be recalled, which means the buyer of such bonds in a falling interest rate environment is constantly exposed to the risk of having to part with it at the call price. This aspect is referred to as price compression.
YIELD TO CALL
In the case of callable bonds, it is a normal practice to compute the yield to call (YTC). That is, for a given call date, all the cash flows from the current point in time until the call date are specified, and the discount rate that makes the present value of these cash flows equal to the dirty price of the bond is computed. The cash flows will be the coupons scheduled to be paid on or before the call date, and the call price. The price at which the bond is recalled may in certain cases vary with the call date; that is, the call price may be a function of the call date.
The formula for the YTC, assuming that the bond is callable after N* coupons have been paid, may be stated as

This looks similar to the pricing equation corresponding to the YTM calculation. But there are two key differences. First, M*, which is the call price, need not equal the face value. Second, N*, the number of coupons until the call dates, will be ≤ N.
PUTABLE BONDS
In the case of a putable bond, the holders have a put option. That is, they can prematurely return the bond to the issuer and claim the face value. Such an option would obviously be exercised when the market interest rates have risen. Under such circumstances the holders can return the old bonds, which are yielding a relatively lower coupon, and use the proceeds to buy bonds yielding a higher coupon. Since the option in these cases is with the holders, they have to pay for it. This will manifest itself as a higher price as compared to that for a plain-vanilla bond carrying the same coupon. Thus, a putable bond will sell for a lower yield as compared to a plain-vanilla bond.
Consider the relative coupons for plain-vanilla, callable, and putable bonds for a given risk class. The callable will have to offer the highest coupon, while the putable can be issued at the lowest coupon. After the issue, if we were to compare bonds with and without call/put options for a given coupon rate, the callable will have the lowest price or the highest yield, while the putable will have the highest price or the lowest yield.
The yield to put is typically defined as the discount rate that makes the present value of the cash flows from the bond equal to its price, assuming that the bond is held to the first put date.
CONVERTIBLE BONDS
Such bonds allow holders to convert the debt securities into shares of stock of the issuer. The number of shares that investors will receive if they were to convert the bond is known as the conversion ratio. For instance, consider a bond with a face value of $1,000 that can be converted to 50 shares of stock. The conversion ratio is obviously 50. The conversion price is the face value divided by the conversion ratio. In this case it is $20. The conversion value is the value of the shares if the bond were to be converted immediately. If we assume that the current share price is $22.50, the conversion value is $1,125.
The minimum value of a convertible is the greater of the conversion value and the value that will be obtained if the bond were to be valued under the assumption that it is a plain-vanilla bond. The latter value is termed as the straight value of the bond.
USING SHORT RATES TO VALUE BONDS
Let us consider a segment of the interest rate evolution tree that we referred to earlier. See Figure 4.3.
Consider a plain-vanilla bond maturing at t2, with a face value of $100, paying a coupon of 6% per annum on a semiannual basis. At time t2 there are three possible nodes. At each node the payoff will be $103.
The value of the bond at the upper node at t1 is:
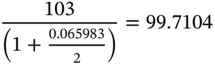
Similarly the value at the lower node at t1 is

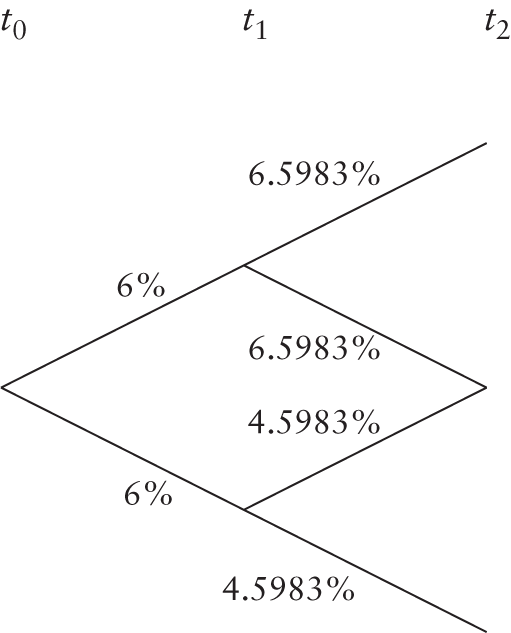
FIGURE 4.3 A Segment of the Short-Rate Tree
Given a node, the probability on an up move is equal to that of a down move, which in turn is equal to 50%, we can compute the value of the bond at t0 as
Now let us consider a callable bond, which we will assume can be called back at the face value.10 Since the value at the upper node at t1 is less than the call price, the bond will not be recalled. At the lower node, however, the value is higher than the call price and hence the issuer would like to exercise the call option. Thus, the price of the callable bond at t0 may be computed as
As can be seen, the presence of the call option leads to a reduction in the bond value. Now consider a bond with a put option. Holders will exercise it only if the value of the bond is less than its face value, assuming that they have the right to put it back at the face value. If so, the value at t0 is given by
For obvious reasons, the put option makes the bond more valuable.
PRICE VOLATILITY
It is common knowledge that prices of long-term bonds are more sensitive to a change in yield than comparable short-term bonds. This can be easily explained. The present value of a cash flow is given by ![]() .
.
The further away the cash flow – that is, the larger the value of t – the greater will be the impact of a change in the discount rate. Because long-term bonds have more cash flows coming at distant points in time, their prices are more volatile; however, subsequently a second fact was noticed. For a given term to maturity, a zero-coupon bond was more price sensitive than any coupon-paying bond with the same term to maturity. This was perplexing, as the bonds have the same term to maturity.
Frederick Macaulay came up with the concept of duration to explain this phenomenon. The crux of the idea is the following. A plain-vanilla bond, as we have seen earlier, is a portfolio of zero-coupon bonds. Each of these component zeroes will have its own term to maturity. When we state that a plain-vanilla bond has a term to maturity of T years, we are considering the term to maturity of only the last of the component zeroes. Macaulay argued that the effective term to maturity of a plain-vanilla bond ought to be a weighted average of the terms to maturity of each of the component zeroes. The weight attached to a cash flow, he postulated, should be the present value of the cash flow divided by the price of the bond. Because the price of a bond is the sum of the present values of all the cash flows received from it, the weights defined by Macaulay will add up to one. Thus, the Macaulay duration of a bond may be defined as

Following is an example of the computation of duration for a plain-vanilla bond.
A CONCISE FORMULA
For a plain-vanilla bond, we can derive a concise expression for the duration. Let us first redefine a few variables.
- c ≡ semiannual coupon rate
- y ≡ semiannual YTM
It can be shown that the duration of a bond is given by
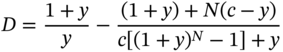
Using the data that we considered for the illustration in the example,
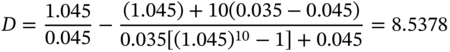
DURATION AND PRICE VOLATILITY
The rate of change of the percentage change in price with respect to yield is a function of the duration of the bond. The relationship may be expressed as

In this expression D is the duration of the bond expressed in years.
The expression ![]() is referred to as the modified duration of the bond, Dm.
is referred to as the modified duration of the bond, Dm.
We know that for a finite price change, the percentage change in price is ![]() . In the limit we can express it as dP/P. Thus, the rate of change of the percentage change in the price with respect to the yield is equal to the modified duration of the bond. Thus, it is duration, and not the term to maturity, that is an accurate measure of interest rate sensitivity.
. In the limit we can express it as dP/P. Thus, the rate of change of the percentage change in the price with respect to the yield is equal to the modified duration of the bond. Thus, it is duration, and not the term to maturity, that is an accurate measure of interest rate sensitivity.
It must be pointed out that the duration of a bond should be technically perceived as a measure of interest rate sensitivity. It cannot always be perceived as a measure of the effective average life of the bond.
PROPERTIES OF DURATION
- The duration of a bond generally increases with its term to maturity. There are two reasons for this.11 First, the principal repayment is a major component of the bond's present value, and consequently has a significant impact on its duration. As the time to maturity is increased, the repayment of principal is postponed, which serves to increase the duration. Second, as compared to a short-term bond, a long maturity bond has cash flows arising at later points in time, which serves to increase the duration.
The duration of par and premium bonds will always increase with the time to maturity; however, there could be situations where, if a bond is trading at a substantial discount, the duration may decline as the term to maturity increases.
- The duration of a bond is inversely related to its coupon rate. There are two reasons for this. First, high coupon bonds have greater amounts of cash flow occurring prior to the maturity date. This serves to reduce the relative impact of the principal repayment on duration.
Second, discounting has less impact on the earlier cash flows as compared to greater cash flows. The greater the coupon, the more is the relative present value of the earlier cash flows, which serves to reduce the duration of the security.
- Duration is inversely related to the YTM of the bond. Duration is computed by weighting the times to maturity of each coupon payment by its contribution to the present value of the bond. The higher the discount rate, the lower is the present value of a cash flow. However, increasing the discount rate has a greater impact on long-term cash flows as compared to shorter-term cash flows. Consequently, the relative weightage of shorter-term cash flows is increased as we increase the YTM, which serves to bring down the duration of the bond.
DOLLAR DURATION
The dollar duration of a bond is defined as the product of the modified duration of the bond and its price. In the illustration in Example 4.13, the price of the bond was $920.8728 and its modified duration was 4.0851 years. Consequently, the dollar duration is 920.8728 × 4.0851 = 3,761.8574.
CONVEXITY
The price-yield relationship for a plain-vanilla bond is convex in nature. Duration is a measure of the first derivative and varies along with yield. To factor in the convex nature, or curvature, of the bond we need to compute the second derivative.
FIGURE 4.4 The Price-yield Relationship
Figure 4.4 illustrates the price-yield relationship for a plain-vanilla bond. The bond was assumed to have 10 years to maturity, a face value of $1,000, and a coupon of 7% per annum payable semiannually.
From the Taylor series expansion, we can state that

where h.o.t. stands for higher order terms.
The first term on the RHS captures the duration effect. The second expression is the convexity effect. The convexity of a bond is defined as ![]() . Thus the percentage price change due to the convexity effect is
. Thus the percentage price change due to the convexity effect is
The convexity can be computed as 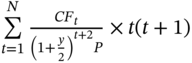 .
.
In Table 4.11, we will now calculate for the five-year bond with a coupon of 7%.
TABLE 4.11 Computation of Convexity
| Time Period | Cash Flow (CFt) | 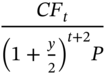 | t × (t+1) | 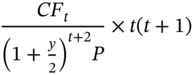 |
|---|---|---|---|---|
| 1 | 35 | 0.033306 | 2 | 0.066612 |
| 2 | 35 | 0.031872 | 6 | 0.191229 |
| 3 | 35 | 0.030499 | 12 | 0.365989 |
| 4 | 35 | 0.029186 | 20 | 0.583715 |
| 5 | 35 | 0.027929 | 30 | 0.837868 |
| 6 | 35 | 0.026726 | 42 | 1.122503 |
| 7 | 35 | 0.025575 | 56 | 1.432220 |
| 8 | 35 | 0.024474 | 72 | 1.762130 |
| 9 | 35 | 0.023420 | 90 | 2.107811 |
| 10 | 1,035 | 0.662743 | 110 | 72.90174 |
| TOTAL | 81.37182 |
The convexity in half-years is 81.37182. The convexity in annual terms can be obtained by dividing this number by 4.12 In this case the annual convexity is 20.3430.
Now consider a finite change of 100 b.p. in the annual YTM. The price at a YTM of 10% is $884.1740. The percentage price change is
The percentage price change as captured by duration is –Dm × dy. The modified duration of the bond is
Thus, the price change as captured by duration is –4.0851 × 0.01= –0.040851 ≡ –4.0851%
The price change due to the convexity effect is 0.5 × 20.3430 × (0.01)2 = 0.001017 ≡ 0.1017%.
Thus, the percentage price change as captured by both the factors combined is –4.0851% + 0.1017% = –3.9834%. As we can see, the result is fairly close to the exact percentage price change, and a combination of duration and convexity does a better job than duration alone.
A CONCISE FORMULA
There is a closed-form expression for computing the convexity of a plain-vanilla bond. It may be stated as

where as before C ≡ periodic, in our case semiannual, coupon y ≡ semiannual YTM, and N ≡ number of coupons remaining until maturity.
In our illustration, C = $35; y = 0.045; N = 10; and P = $920.8728. Substituting for the variables, we get convexity = 81.3718.
DOLLAR CONVEXITY
The dollar convexity of a bond is equal to its convexity multiplied by its price. In our illustration the price is 920.8728, and the convexity is 20.3430. Thus the dollar convexity is 18,733.3150.
PROPERTIES OF CONVEXITY
The following properties are valid for the convexity of plain-vanilla bonds.13
- As the YTM increases, the convexity decreases, and vice versa. This property of option-free bonds is referred to as positive convexity.
- For a given value of the YTM and time to maturity, the lower the coupon, the greater is the convexity of the bond. Thus, for a given yield and time to maturity, a zero-coupon bond will have the highest convexity.
- For a given value of the YTM, and modified duration, the lower the coupon, the lower is the convexity of the bond. Thus, for a given yield and modified duration, a zero-coupon bond will have the lowest convexity.
IMMUNIZATION
Consider the case of a pension fund that promises to pay a return of 4.9688% per annum compounded semiannually, on an initial investment of $100,000, after eight years. If the fund invested the corpus in a bond, it would be exposed to two types of risks. The first is reinvestment risk, or the risk that the cash flows received at intermediate stages may have to be invested at lower rates of interest. The second, called price or market risk, is the risk that interest rates could increase, causing the price of the bond to fall at the end of the investment horizon. The two risks obviously work in opposite directions. Therefore the issue is whether there is a bond that will ensure that the terminal cash flow will be equal to the amount required to satisfy the liability, irrespective of whether rates rise or fall. The process of protecting a bond portfolio against a change in the interest rate is termed as immunization.
We are considering a simple immunization strategy where we have to immunize a portfolio required to satisfy a single liability. There are two conditions that we need to satisfy in such cases. First, the present value of the liability should be equal to the amount invested in the bond at the outset. Second, the duration of the bond should be equal to the investment horizon.
Consider a bond with a face value of $1,000 and 10 years to maturity. Assume that the coupon rate is equal to the YTM and is equal to 4.9688% per annum. It can be shown that the duration is eight years.
Now consider a one-time change in interest rates right at the outset. Assume that the interest rate increases from 4.9688% per annum to 5.50% per annum. The terminal value of the coupons from the bond at the end of eight years is given by
The price at which 100 bonds can be sold, if the YTM for two-year bonds after eight years is 5.50% per annum, is 100 × 990.0681 = $99,006.8080. The total terminal cash flow is $148,108.4386. Table 4.12 gives the terminal cash flow for various values of the interest rate.
Analysis
As can be seen, the income from reinvested coupons steadily increases with the interest rate while the price of the bond at the time of sale steadily decreases with the interest rate. When there is no change in the rate, the terminal cash flow from the bond is exactly adequate to meet the liability. In all the other cases, there is a surplus. Thus, under all circumstances, the terminal cash flow from the bond is adequate to meet the liability. Thus, if the pension fund were to invest in an asset whose duration is equal to the time to maturity of its liability, then the funds received will always be adequate to meet the contractual outflow. To meet this requirement, certain conditions must be satisfied. First, the amount invested in the bonds must be equal to the present value of the liability. In this case, since the bond is assumed to be selling at par, we need to invest in 100 bonds. Second, the duration of the asset must equal the maturity horizon of the liability. Third, there must be a one-time change in the interest rate, right at the very outset. Fourth, there must be a parallel shift in the yield curve.
TABLE 4.12 An Immunized Portfolio
| Interest Rate (annualized) | Cash Flow from Reinvested Coupons | Proceeds from Sale of Bonds | Terminal Cash Flow per Bond | Terminal Cash Flow from 100 Bonds | Deviation |
|---|---|---|---|---|---|
| 0.010 | 412.7639 | 1078.394 | 1491.1576 | 149,115.76 | 1026.28 |
| 0.015 | 420.6656 | 1068.094 | 1488.7601 | 148,876.01 | 786.53 |
| 0.020 | 428.7544 | 1057.921 | 1486.6752 | 148,667.52 | 578.04 |
| 0.025 | 437.0349 | 1047.871 | 1484.9056 | 148,490.56 | 401.08 |
| 0.030 | 445.5118 | 1037.943 | 1483.4544 | 148,345.44 | 255.96 |
| 0.035 | 454.1900 | 1028.134 | 1482.3244 | 148,232.44 | 142.96 |
| 0.040 | 463.0744 | 1018.445 | 1481.5190 | 148,151.90 | 62.42 |
| 0.045 | 472.1701 | 1008.871 | 1481.0415 | 148,104.15 | 14.67 |
| 0.049688 | 480.8948 | 1000.000 | 1480.8954 | 148,089.48 | 0.00 |
| 0.050 | 481.4823 | 999.4131 | 1480.8948 | 148,089.54 | 0.06 |
| 0.055 | 491.0163 | 990.0681 | 1481.0844 | 148,108.44 | 18.96 |
| 0.060 | 500.7776 | 980.8346 | 1481.6122 | 148,161.22 | 71.74 |
| 0.065 | 510.7716 | 971.7112 | 1482.4829 | 148,248.29 | 158.81 |
| 0.070 | 521.0043 | 962.6962 | 1483.7005 | 148,370.05 | 280.57 |
| 0.075 | 531.4813 | 953.7881 | 1485.2694 | 148,526.94 | 437.46 |
| 0.080 | 542.2087 | 944.9853 | 1487.1940 | 148,719.40 | 629.92 |
| 0.085 | 553.1925 | 936.2864 | 1489.4789 | 148,947.89 | 858.41 |
| 0.090 | 564.4392 | 927.6898 | 1492.1290 | 149,212.90 | 1123.42 |
| 0.095 | 575.9551 | 919.1942 | 1495.1493 | 149,514.93 | 1425.45 |
| 0.100 | 587.7467 | 910.7981 | 1498.5448 | 149,854.48 | 1765.00 |
TREASURY AUCTIONS
The Treasury issues T-bills, T-notes, and T-bonds by way of auctions. The auction procedure is described in detail in the next chapter on money market securities. Here we will illustrate two auctions of notes and bonds to describe the salient features.
WHEN ISSUED TRADING
The when-issued (WI) market is a market for forward trading of a bond whose issue has been announced but has not yet taken place. Trades in this market take place from the date of announcement of a forthcoming auction of government securities until the actual issue date of the securities. The WI market helps potential bidders to gauge the market's interest in the security prior to the actual auction. This will obviously have ramifications for the bidding strategies of market participants and consequently will have a bearing on the outcome of the auction.
Traders can take both long and short positions in the WI market, with settlement being scheduled for the issue date. Thus, trades in this market represent forward contracts with the issue date being the settlement date. On and before the date of the auction, the issues trade on a yield basis. The actual price in dollars can be established only after the Treasury sets the coupon. For instance, a 5-year T-note is quoting in the WI market at 5%. If the coupon is set at 4.875, the price of the security will be 99.4530; however, if the coupon is set at 5.125, the price will be 100.547. Starting with the day after the auction, securities in the WI market are quoted on a price basis, since the coupon has already been established.
PRICE QUOTES
Bond prices are always quoted per $100 of face value. The reason is the following. Consider two bonds, one with a face value of $1,000 and another with a par value of $2,000. Assume that both securities are quoting at $1,500; the first is a premium bond and the second a discount bond. This cannot be discerned, however, from the observed price unless the corresponding face value is also specified. On the other hand, if the price were to be expressed for a par value of $100, any value less than 100 would signify a discount bond while a value more than 100 would connote a premium bond.
In the US market prices are quoted as a percentage of par plus 32nds. For instance, consider a quote of 97-08. This does not mean a price of $97 and 8 cents per $100 of face value. What it means is that the price per $100 of face value is 97 + 8/32 or $97.25. So if we were to buy bonds with a face value of $1MM, the amount payable will be 1,000,000 × 97.25/100 = $972,500.
The quoted prices are always clean prices. Thus, to compute the exact amount payable by the buyer, the accrued interest has to be calculated as per the prescribed convention and added to the clean price.
STRIPS
STRIPS is an acronym for Separate Trading of Registered Interest and Principal of Securities. As the name suggests, these represent zero-coupon debt securities created by selling the entitlement to each cash flow from the mother security separately. For, as we have seen earlier, a conventional bond is a portfolio of zero-coupon bonds. Thus a 10-Year T-note can be stripped into 21 zero-coupon securities, where the first 20 represent the respective coupon payments and the last represents the face value. The US Treasury does not strip eligible securities; however, a trader who holds a Treasury note or bond can seek to have the issue converted into the coupon and principal components. The request can be made at any point in time before the maturity date of the security. Once stripped, each zero-coupon component can be traded separately. Each component will have a unique CUSIP number. In practice, all interest-based strips that mature on the same day are assigned a common CUSIP number, irrespective of the mother bond from which they are created. However, principal strips that mature on a given day are assigned different CUSIP numbers.
Just as a Treasury note or a bond can be stripped, it can also be reconstituted. That is, a trader who holds the entire set of component zeroes can have the original or parent Treasury security regenerated.
Why is the STRIPS program popular? As we have seen, immunization strategies require the matching of the duration of the assets of the institution with that of its liabilities. Unlike coupon-paying bonds, whose duration is constantly changing, zero-coupon bonds always have a duration equal to their remaining term to maturity. Thus, zeroes are invaluable for implementing such a strategy. Besides, while a 30-Year note will have a duration substantially less than 30 years, by stripping it into 61 component securities, we can create zeroes with durations ranging from 6 months to 30 years.14
When a bond is stripped, the zeroes created from the coupons are referred to as C-STRIPs, while those derived from the principal are termed as P-STRIPs. The availability of P-STRIPs is higher than that of C-STRIPs corresponding to a coupon date.
INFLATION INDEXED BONDS
A plain-vanilla bond does not provide protection against inflation. The coupons are fixed in currency terms, and thus with the passage of time the purchasing power of payments received from these bonds steadily declines. There are bonds, however, whose cash flows are determined by the prevailing inflation rates; in this case, the cash flow is higher when the rate of inflation is high, and lower when the rate is low. The objective is to ensure that, in real terms, the rate of return is reasonably constant. In the United States, the Treasury issues TIPS, or Treasury Inflation-Protected Securities.
Protection against inflation may be offered in one of two ways. The first method entails the adjustment of coupons, keeping the face value constant. This is equivalent to a floating-rate bond; that is, the coupon rate is high when inflation is high and low when the change in the price level is low. Such securities are termed Coupon-Linkers or C-Linkers for short. The alternative is to keep the coupon rate constant and adjust the principal periodically for inflation to get an adjusted principal. In such cases, a fixed coupon rate is paid on the adjusted principal. These securities are termed Principal-Linkers or P-Linkers. With both security types, the cash flows per period are variable and related to the rate of inflation.
Usually, the rate of inflation will be positive, and consequently cash flows will increase. At times, however, we may have a deflationary situation, where the purchasing power of money actually increases and the rate of inflation will be negative. In such a situation, the adjusted principal for a P-Linker may be less than the original par value at maturity. If so, most governments will pay back the original par value or the terminal-adjusted principal, whichever is higher. In the case of a C-Linker, if there is a sharp decline in the price level and the inflation adjusted rate is negative, most issuers pay a coupon of zero.
COMPUTING PRICE GIVEN YIELD AND VICE VERSA IN EXCEL
If we are on a coupon date, we can compute the price given the YTM by using the PV function in Excel, and the YTM given the price by using the RATE function in Excel. Quite obviously, on a coupon date, the dirty price will be equal to the clean price.
We will illustrate the use of the functions with the help of an example.
If we are between two coupon dates, we need to use the PRICE function to compute the price of a bond given its YTM, and the YIELD function to compute the YTM of a bond given its price. The PRICE function gives the clean price of the bond. Hence to compute the dirty price, we need to separately calculate and add the accrued interest using the ACCRINT function.
The YIELD function returns the YTM given the clean price. Hence if we have the dirty price of the bond, we need to compute and subtract the accrued interest to convert it to the clean price, before invoking the YIELD function. Here are some examples.
COMPUTING DURATION IN EXCEL
Excel has a function for computing the duration of a bond. The required parameters are:
- Settlement: This is the settlement date to be input using the Date function.
- Maturity: This is the maturity date to be input using the Date function.
- Coupon: This is the annual coupon rate.
- Yield: This is the annual YTM.
- Frequency: This is 2 for bonds paying semiannual coupons.
- Basis: This represents the day-count convention.
Let us use the earlier data.
Duration(Date(2020,09,15),Date(2045,05,15),0.042,0.048,2,1) = 14.8915 years. Because the frequency has been specified as 2, the function returns the duration value in terms of number of years.
NOTES
- 1 Remember, we are using the actual-actual day-count convention.
- 2 Even if the bond were to mature after a year, there will be a capital gain or a loss.
- 3 The key term is “single.”
- 4 As explained earlier, we are pricing the bond based on 20 half-years to maturity and not on 10 years.
- 5 On an ex-post basis we will obviously know the selling price.
- 6 Notice that we have taken the coupons only for the first 16 periods.
- 7 See Choudhry (2004).
- 8 See Choudhry (2004).
- 9 Futures and Options: Concepts and Applications by Sunil Parameswaran.
- 10 In other words, there is no call premium.
- 11 See Livingston (1990).
- 12 In general, we have to divide by the square of the frequency of compounding.
- 13 See Fabozzi (1996).
- 14 See Sundaresan (2009).
