CHAPTER 9
Mortgages and Mortgage-backed Securities
INTRODUCTION
In most developed countries the right to own a home is considered to be virtually a fundamental right. But few people are in a position to pay the cost of acquisition of a home from their own personal funds. Consequently, most of the funds required to buy a home must be borrowed. A loan that is collateralized by real estate property is called a mortgage loan. The lender is called the mortgagee and the borrower is called the mortgagor. In the event of default on the part of the mortgagor, the lender can seize the property and sell it to recover the amount that is owed to it. This is called the right of foreclosure.
MARKET PARTICIPANTS
There are three categories of players in the mortgage market. These are:
- Mortgage originators
- Mortgage servicers
- Mortgage insurers
MORTGAGE ORIGINATION
Who is a mortgage originator? The original lender or the party who first extends a loan to the acquirer of the property is called the mortgage originator. Originators include:
- Thrifts or Savings & Loan Associations
- Commercial Banks
- Mortgage Bankers
- Life Insurance Companies
- Pension Funds
Income for the Originator
Originators get income from various sources. First, when a loan is granted, they will levy an origination fee. The fee is expressed in terms of points where each point is 1% of the borrowed funds. For example, if a lender were to charge 1.5 points on a loan of $200,000, the origination fee will amount to $3,000. Most originators will also levy an application fee and certain processing fees.
The second source of income is the profit that can be earned if and when the mortgage loan is sold by the originator to another party. A mortgage loan is a type of debt, and consequently is vulnerable to interest rate fluctuations. If the interest rate were to decline, such a sale would lead to a gain for the originator. This is called a secondary marketing profit. Of course, if interest rates were to rise after the loan is disbursed, the originator will incur a loss when the loan is sold.
If originators were to decide to hold the loan as an asset rather than sell it, they will earn periodic income in the form of interest.
Mortgage Servicing
Every mortgage loan must be serviced. Servicing of a mortgage loan includes the following activities:
- Collection of monthly payments and forwarding the proceeds to the owner of the loan
- Sending payment notices to mortgagors
- Reminding mortgagors whose payments are overdue
- Maintaining records of principal balances
- Administering escrow balances for real estate taxes and insurance purposes
- Initiating foreclosure proceedings if necessary
- Furnishing tax information to mortgagors when applicable
Mortgage servicers include bank-related entities; thrift-related entities; and mortgage bankers.
Escrow Accounts
An escrow account is a trust account held in the name of the homeowner to pay statutory levies like property taxes, and insurance premiums. The maintenance of such an account helps ensure that payments are made when due, for it becomes the lender's responsibility to do so.
In most cases the borrower makes deposits on a monthly basis, along with the loan payment, and the payments accrue at the lender. The amount required to be deposited every month is a function of the cost of insurance and the tax assessment of the property concerned. Consequently, it fluctuates from year to year.
Income for the Servicer
The primary source of income is the servicing fee, which is a fixed percentage of the outstanding mortgage balance. Because the mortgage loan is an amortized loan, where the outstanding principal declines with each payment, the revenue from servicing, in dollar terms, will decline over time. The second source of income arises on account of the interest that can be earned by the servicer from the escrow account that the borrower often maintains with the servicer. The third source of revenue is the float earned on the monthly mortgage payment. This opportunity arises because there is a delay that is permitted between the time the servicer receives the monthly payment and the time that the payment has to be sent to the investor.
Mortgage Insurance
There are two types of mortgage-related insurance. The first type, which is originated by the lender in order to insure against default by the borrower, is called mortgage insurance or private mortgage insurance. It is usually required by lenders on loans with a Loan to Value (LTV) ratio that is greater than 80%. The amount insured will be some percentage of the loan and may decline as the LTV declines.
What is the LTV ratio? Every borrower will have to make a down payment, which is the difference between the price of the property and the loan amount. The LTV ratio is obtained by dividing the loan amount by the market value of the property. The lower the LTV ratio, the greater is the protection for the lender in the event of default by the borrower.
The second type of mortgage-related insurance is acquired by the borrower, usually through a life insurance company, and is typically called credit life. This is not required by the lender. Such policies provide for the continuation of mortgage payments after the death of the insured person, so that survivors can continue to live in the house.
Government Insurance and PMI
As we have seen, lenders insist on insurance if the LTV ratio is more than 80%; however, low- to middle-income borrowers may not be in a position to deposit 20% of the value of the property. At the same time, their credit rating makes them ineligible to obtain insurance from private parties. To facilitate the acquisition of properties by this section of society, there are government agencies that provide loan guarantees in lieu of insurance.
Borrowers who are not eligible for loans from these agencies must obtain private mortgage insurance (PMI).
Secondary Sales
Once the loan is granted, the originator can either hold it as an asset, or sell it to an investor who may seek to either hold it as an investment, or may wish to pool many individual mortgage loans and use them as collateral for the issuance of securities. Of course, the issuance of securities backed by a pool of underlying mortgages may be undertaken by the originators themselves. When a mortgage pool is used as collateral for the issuance of a security, it is said to be securitized.
Two federally sponsored credit agencies and many private agencies buy mortgages, pool them, and issue securities backed by the pool to investors. Such agencies are referred to as conduits. The two federally sponsored agencies are:
- Federal National Mortgage Association (Fannie Mae)
- Federal Home Loan Mortgage Corporation (Freddie Mac)
Such agencies buy what they call conforming mortgages. A conforming mortgage is one that meets the underwriting criteria established by them, from the standpoint of being eligible to be included in a pool for the purpose of being securitized. A conforming mortgage must satisfy three criteria. These are:
- There must be a maximum payment to income (PTI) ratio. The PTI ratio is the ratio of monthly payments (the loan payment plus any real estate tax payments) to the borrower's monthly income. Obviously, the lower the ratio, the greater is the likelihood of the borrower being able to pay as scheduled.1
- A maximum LTV ratio
- A maximum loan amount
Mortgages that are nonconforming because they are for amounts in excess of the purchasing limit set by these agencies are termed as jumbo mortgages, whereas those which do not meet the underwriting guidelines such as credit quality or loan-to-value ratio are termed as subprime mortgages.
RISKS IN MORTGAGE LENDING
Investors who invest in mortgage loans are exposed to four main risks. These are:
- Default risk
- Liquidity risk
- Interest rate risk
- Prepayment risk
Default Risk
Default or credit risk is the risk that the borrower will default. For government-insured mortgages the risk is minimal because the insuring agencies are government sponsored. For privately insured mortgages, the risk can be gauged by the credit rating of the insurance company. For uninsured mortgages, the risk will obviously depend on the credit quality of the borrower.
Liquidity Risk
Mortgage loans tend to be rather illiquid because they are large and indivisible. Thus, while an active secondary market exists for such loans, bid–ask spreads are large relative to other debt instruments.
Interest Rate Risk
The price of a mortgage loan in the secondary market moves inversely with interest rates, just like any other debt security. Moreover, because the loans are for long terms to maturity, the impact of an interest rate change on the price of the mortgage can be significant.
Prepayment Risk
Most homeowners pay off all or a part of their mortgage balance prior to the maturity date. Payments made in excess of the scheduled principal repayments are called prepayments. Prepayments occur for one of several reasons. First, borrowers tend to prepay the entire mortgage when they sell their home. The sale of the house may be due to:
- A change of employment that necessitates moving
- The purchase of a more expensive home
- A divorce in which the settlement requires sale of the marital residence
Second, if market interest rates decline below the loan rate, the borrower may prepay the loan due to the ability to refinance at a lower rate. Third, in the case of homeowners who cannot meet their mortgage obligations, the property will be repossessed and sold. The proceeds from the sale will be used to pay off the mortgage in the case of uninsured mortgages. For an insured mortgage the insurance company will pay off the balance. Finally, if the property is destroyed by an act of God, the insurance proceeds will be used to pay off the mortgage. The effect of prepayments, irrespective of the reason, is that the cash flows from the mortgage become unpredictable.
In Example 9.1 we illustrate how to take a decision regarding the refinancing of a mortgage loan.
OTHER MORTGAGE STRUCTURES
The level payment mortgage, which entails a constant monthly payment for the life of the mortgage, is the most simple of mortgage structures. In practice there are other mortgage loans with more complex features. We will now discuss some of them.
Adjustable-Rate Mortgage (ARM)
In an adjustable-rate mortgage, the interest rate is not fixed for the life of the loan but is reset periodically. Thus, the monthly payments will rise if the interest rate at resetting is higher than it was previously, and will fall if the interest rate declines. The rate on such mortgages is linked to a benchmark such as LIBOR or the rate on Treasury securities. We will illustrate such a mortgage loan, assuming that rates are reset at the end of every year.
Option to Change the Maturity
In the case of certain adjustable-rate mortgages, the borrower may be given the option to keep the monthly installment at the initial level, and have the maturity date altered, every time the rate is reset. Let us see the implications of this for the mortgage discussed in the preceding example.
The outstanding balance after one year is $616,722.81. If we keep the equated monthly payment at $18,678.19, the life of the loan if the rate is reset at 9% is given by:
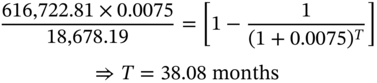
Rate Caps
In the case of ARMs, there may be a cap on how much the interest rate may increase or decrease per period. The cap may be a periodic cap or a lifetime cap. Consider a four-year mortgage with a principal of $800,000. Assume that payments are made monthly and that the interest rate every period is the prevailing LIBOR at the start of the period plus 150 b.p. The values of LIBOR observed over the next three years are as shown in Table 9.2.
Assume that there is a periodic cap of 1.5% and a lifetime cap of 9%. If so, the applicable mortgage rates for each of the periods would be as shown in Table 9.3.
TABLE 9.2 Observed Values for LIBOR
| Time in Years | LIBOR | Mortgage Rate |
|---|---|---|
| 0 | 4.20 | 5.70 |
| 1 | 6.00 | 7.50 |
| 2 | 7.00 | 8.50 |
| 3 | 8.00 | 9.50 |
TABLE 9.3 Mortgage Rates in the Presence of a Cap
| Period | Mortgage Rate |
|---|---|
| 0 | 5.70 |
| 1 | 7.20 |
| 2 | 8.50 |
| 3 | 9.00 |
Let us analyze the entries in Table 9.3. The starting mortgage rate is 5.70%, which is less than the lifetime cap of 9%. The rate at the end of the first year should be 7.50% in the absence of a periodic cap. Because there is a periodic cap of 1.5%, however, the rate cannot increase by more than 1.5%. Consequently, the rate for the second year is 7.20%, which is the rate for the first year plus 1.5%. The uncapped rate for the third year is 8.50%, which is the same as the capped rate, because 8.50% is only 1.3% more than the rate for the previous year. Finally, the rate for the fourth year in the absence of a cap should be 9.50%. This does not violate the requirement of a periodic cap, because the change is only 1% as compared to the previous year. Because there is a lifetime cap of 9%, however, the rate cannot exceed 9% in any period. Consequently, the rate for the fourth year will be 9%.
Carryovers
The presence of a rate cap may preclude the lender from increasing the coupon rate to the desired level. If, however, there is a carryover provision, the deficit can be carried over to future periods. For instance, consider a mortgage loan with a coupon of LIBOR + 1%, and a periodic cap of 1.25%. If the LIBOR at the outset is 3%, the coupon for the first year is 4%. Assume that the LIBOR at the end of the first year is 4.6%. Thus, the lenders would like to set the coupon at 5.6; however, they are constrained to set it at 5.25%. Thus, there is a deficit of 35 basis points. Assume that at the end of the second year the LIBOR is 4.80%. In the absence of a carryover facility, the coupon for the third year would have been set equal to 5.80%, which is less than the prescribed limit of 6.50%. Because of the carryover provision the coupon would be set at 6.15%, thereby adjusting the deficit that was carried over.
Payment Caps
If the adjustable-rate mortgage were to have a payment cap, there would be a limit on how much the monthly payments can increase or decrease at the end of every period. Let us take the case of the mortgage that we studied in the above example. The mortgage rate for each year is as shown in Table 9.4.
Assume that there is a payment cap of 2%. In the absence of the cap, the monthly payments in every year and the outstanding balance at the end of each year will be as given in Table 9.5.
If there is a payment cap of 2%, however, the monthly payment in the second year cannot exceed:
The interest component in the thirteenth month will be:
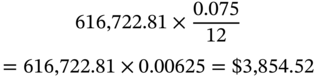
The principal repayment will therefore be only:
as compared to
in the absence of the cap. Thus, the cap leads to a slower repayment of principal. The outstanding balance at the end of the 24th month is given by:

TABLE 9.4 Observed Values for LIBOR
| Period | Mortgage Rate | Mortgage Rate |
|---|---|---|
| 0 | 4.20 | 5.70 |
| 1 | 6.00 | 7.50 |
| 2 | 7.00 | 8.50 |
| 3 | 8.00 | 9.50 |
TABLE 9.5 Monthly Payments & Outstanding Balances
| Time in Years | Monthly Payments | Outstanding Balance |
|---|---|---|
| 1 | 18,678.19 | 616,722.81 |
| 2 | 19,183.91 | 426,313.07 |
| 3 | 19,378.35 | 222,178.34 |
| 4 | 19,481.38 | 0 |
as compared to $426,313.07 in the absence of the cap. The monthly payment in year three will therefore be:

The cap for the period is:
Thus, the monthly payment in year three will be $19,432.79.
The outstanding balance at the end of the 36th month is given by:

The monthly payment for year four will therefore be:

Negative Amortization
There are times when a situation could arise wherein the capped monthly payment is less than the monthly interest due for a subsequent month. If so, instead of a reduction in the outstanding balance, the deficit in the interest payment will be added to the outstanding balance, which will cause the principal to increase in value. This is referred to as negative amortization. We will illustrate it with the help of an example.
Graduated Payment Mortgage
Young home buyers may not have the disposable income required to qualify for a conventional fixed-rate mortgage; however, many people in this age bracket have the potential to earn substantially more in the coming years. To encourage such parties to take loans, the graduated payment mortgage was designed. Such a mortgage starts with a level of payment that steadily increases every year up to a point, and then remains steady thereafter. We will illustrate it with the help of an example.
Growing Equity Mortgages (GEM)
In a growing equity mortgage, the monthly installment increases by a prescribed percentage every year; however, the installment for the first year is the same as that for a plain-vanilla mortgage. Thus, there is no negative amortization in the beginning. In contrast, we may observe negative amortization in the case of a graduated payment mortgage, which too is characterized by increasing periodic payments.
In a GEM the installment increases by a certain percentage; however, the excess payment goes toward prepayment of principal. Consequently, the principal gets paid off faster than in the case of a plain-vanilla mortgage. Thus, while the stated maturity – the time taken for the outstanding balance to go to zero – is equal to the actual maturity observed in practice for plain-vanilla mortgages and graduated payment mortgages, in the case of a growing equity mortgage the principal is fully paid off by an earlier date.
WAC and WAM
All the mortgages that constitute the pool being securitized will not have the same mortgage rate or time to maturity. Thus, it is a common practice in the market for securitized assets to take cognizance of the weighted average coupon rate and the weighted average time to maturity. The weighted average coupon (WAC) of a mortgage pool is determined by weighting the mortgage rate of each loan in the pool by the principal amount outstanding. That is, the weight for each mortgage rate is the outstanding amount of that mortgage divided by the cumulative outstanding amount of all the mortgages in the pool. Similarly, the weighted average maturity (WAM) is found by weighting the remaining number of months to maturity of each of the loans in the pool by the principal amount outstanding. We will illustrate the calculations for a hypothetical pool.
Calculation of WAC and WAM
Assume that a pool consists of 10 mortgage loans. The mortgage rate for each loan and its remaining term to maturity are given in Table 9.9.
The weight to be attached to each of the mortgage rates and terms to maturity, in order to compute the WAC and the WAM, are given in Table 9.10, as are the calculated values of the two variables.
Thus, the WAC for the pool is 6.9265% and the WAM is 301.07 months.
Pass-Through Securities
Mortgage loans are extremely illiquid. Besides, the lender faces significant exposure to credit risk as well as prepayment risk. Thus, making a secondary market for whole loans is an extremely difficult proposition. It is possible, however, to issue liquid debt securities backed by an underlying pool of mortgage loans. That is, the cash flows stemming from the underlying loans are passed through to the holders of these debt securities, and hence the name. Each holder of a pass-through security is entitled to a pro-rata undivided share of each cash flow that emanates from the underlying pool, as and when the homeowners make monthly payments. Each monthly payment will consist of an interest component, a principal component, and potentially an additional amount on account of prepayment. Any amount that constitutes a prepayment is termed as an unscheduled principal, as opposed to the scheduled or expected principal repayment. The mechanics of a pass-through may be illustrated with the help of an example.
TABLE 9.9 Mortgage Loans, Their Rates, and Times to Maturity
| S. No. | Principal Outstanding | Mortgage Rate(rs) | Term to Maturity (Ts) |
|---|---|---|---|
| 1 | 975,000 | 6.25% | 336 |
| 2 | 925,000 | 6.50% | 324 |
| 3 | 900,000 | 7.25% | 300 |
| 4 | 875,000 | 7.50% | 325 |
| 5 | 825,000 | 7.00% | 350 |
| 6 | 800,000 | 6.75% | 280 |
| 7 | 850,000 | 6.60% | 275 |
| 8 | 910.000 | 6.95% | 250 |
| 9 | 810,000 | 7.15% | 265 |
| 10 | 880,000 | 7.40% | 300 |
| Total | 8,750,000 |
TABLE 9.10 Calculation of WAC and WAM
| S. No. | Weight (ws) | rs × ws | Ts × ws |
|---|---|---|---|
| 1 | 0.1114 | 0.6964 | 37.44 |
| 2 | 0.1057 | 0.6871 | 34.25 |
| 3 | 0.1029 | 0.7457 | 30.86 |
| 4 | 0.1000 | 0.7500 | 32.50 |
| 5 | 0.0943 | 0.6600 | 33.00 |
| 6 | 0.0914 | 0.6171 | 25.60 |
| 7 | 0.0971 | 0.6411 | 26.71 |
| 8 | 0.1040 | 0.7228 | 26.00 |
| 9 | 0.0926 | 0.6619 | 24.53 |
| 10 | 0.1006 | 0.7442 | 30.17 |
| Total | 1.0000 | 6.9265% | 301.07 |
Cash Flows for a Pass-Through
Assume that the underlying pool consists of four loans of $100,000 each. Each has a rate of 9% and 360 months to maturity. Thus, the WAC will remain constant at 9% and the WAM at any point of time will be equal to the time remaining in the life of the loans. Before we can project the cash flows, we need to consider servicing and guaranteeing fees, and consider the important issue of prepayments.
The cash flow that is passed through to investors in a given period will not in practice be equal to the payment received from the underlying pool. The monthly cash flow for a pass-through is less than the monthly cash flow from the underlying loans by an amount equal to the servicing and guaranteeing fees. Thus, the coupon rate on the pass-through will be less than the mortgage rate of the underlying pool by an amount equal to the servicing and guaranteeing fees. We will assume a servicing fee of 0.5% per annum and a guaranteeing fee of 0.5% per annum. Thus, in our case, the coupon rate of the pass-through will be 8%.
Prepayment Conventions
It is impossible to predict with absolute certainty the monthly cash flow stream that a pass-through holder receives, because the timing and amount of principal that is prepaid is subject to considerable uncertainty. Because a pass-through is a debt security, we need to project the cash flows from it in order to determine its value. Such a projection entails an assumption about the prepayment behavior of the mortgage owners over the life of the pool. The prepayment rate that is assumed is called the prepayment speed.
Single Month Mortality Rate
The Single Month Mortality Rate for a given month ‘t,’ SMMt is defined as:
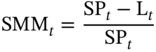
where SPt is the scheduled principal outstanding at the end of month ‘t,’ and Lt is the actual principal outstanding at the end of month ‘t.’
Thus, the actual principal at the end of month ‘t’ is given by:
Consider a mortgage with ‘N’ months to maturity, and a monthly interest rate of ‘r.’ The original loan balance is given by:
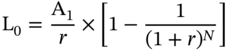
where A1 is the scheduled monthly installment for month 1. The scheduled principal at the end of the first month is given by:
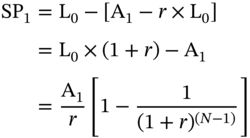
The actual balance at time ‘1’ is given by:
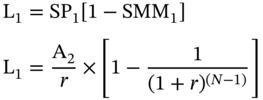
where A2 is the scheduled monthly installment for month ‘2.’

Similarly, it can be shown that:

In general, the scheduled monthly installment in month ‘t’ is given by:
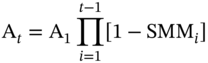
If SMMi = SMM ∀ i, then:
Let us denote the monthly payment on the original principal, in the absence of prepayments by A. Then we can state:
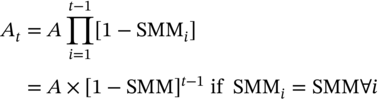
In the absence of prepayments, the interest and principal components of the tth payment and the outstanding principal at the end of “t” periods are given by:
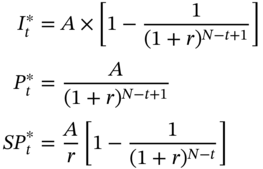
In the presence of prepayments, the actual principal outstanding at the end of ‘t −1’ is given by:
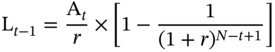
Thus, in the presence of prepayments, the interest and principal components of the tth payment are given by:

and
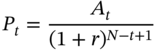
The scheduled principal at the end of the tth period is given by:
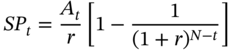
We know that
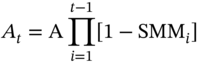
Thus:
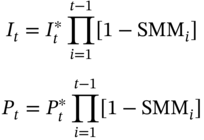
and

The actual principal at the end of ‘t’ periods is given by
Therefore:
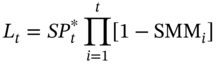
We will now give an illustration of cash flow calculations for a pass-through security with the help of a detailed example.
Average Life
Unlike a bond, which repays its principal in the form of a bullet payment at maturity, a pass-through security returns a part of its principal every month. Consequently, it is a common practice to compute the average life of a pass-through security. Let PCFt be the total principal received at time ‘t’. PCFt is obviously the sum of the scheduled principal received at time ‘t’ and the prepayment received at the same point in time. The average life may be defined as
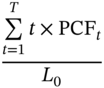
In the case of the pass-through discussed earlier, the average life in the absence of prepayments is 12.8578 months or 1.0715 years. When we assume an SMM of 2.50% per month, however, the average life declines to 10.6677 months, which is equivalent to 0.8890 years. Clearly, the higher the prepayment speed that is assumed, the shorter will be the average life of the security.
Cash Flow Yield
The cash flow yield for a pass-through is the IRR computed using the projected cash flow stream. The result is a monthly rate, which is usually converted to a bond equivalent yield to facilitate comparisons with conventional debt securities. If we denote the IRR as im, where im denotes a monthly rate, then the bond equivalent yield may be expressed as:
A Note
The average life is based on the total principal received every period, that is, the sum of the scheduled principal payment and the prepayment. Thus, it is different from bond duration, and there is no discounting of the principal payments. The cash flow yield is based on the periodic cash flow. The periodic cash flow consists of the net interest payment, that is, the gross interest payment less the servicing and guaranteeing fees, plus the scheduled principal payment, and the prepayment for the month.
Conditional Prepayment Rate
To project the cash flows from a pass-through we need to make an assumption about the prepayment behavior. The prepayment rate that is assumed for a pool of mortgages is called the conditional prepayment rate or CPR. The term conditional connotes that the rate is conditional on the remaining balance in the pool.
The CPR corresponding to the assumed prepayment speed has to be converted to the equivalent SMM. The formula for conversion is the following:
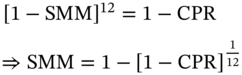
The rationale for this formula is the following. Prepaying 12 times in a year at the rate of SMM is equivalent to prepaying once a year at the rate of CPR.
PSA PREPAYMENT BENCHMARK
The public securities association (PSA) prepayment benchmark is expressed as a monthly series of annual prepayment rates.2
The PSA benchmark assumes that prepayment rates are lower for newly originated mortgages and will then speed up as the mortgages become seasoned. It has been observed that in practice, homeowners are less likely to move in the initial years of the loan. They are also less likely to refinance or make large unscheduled principal repayments. Consequently, the PSA benchmark assumes that the prepayment rate will steadily increase for the first 30 months of the loan, and stabilize thereafter.
The benchmark assumes the following CPR for 30-year mortgages:
- CPR of 0.2% for the first month
- An increase of 0.2% per month for the next 30 months until it reaches 6%
- 6% for the remaining years
This benchmark is called 100% PSA or 100PSA.
Let ‘t’ be the number of months since the mortgage was originated.
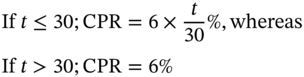
Sample calculations for the 100 PSA benchmark are given here:

Slower or faster prepayment speeds are referred to as a percentage of the standard PSA benchmark. For instance, 50 PSA means one half of the CPR of the PSA benchmark, while 150 PSA means 1.5 times the CPR of the PSA benchmark.
Thus, the case of 150 PSA, the SMM may be calculated as follows:

It should be noted that 150 PSA does not mean that the SMM for a month is 1.5 times the SMA for the same month under the 100 PSA assumption. It is the CPR for the month that is 1.5 times the CPR under the 100 PSA assumption.
Illustration of 100 PSA
Consider a pass-through backed by a single loan of $100,000 with 360 months to maturity and a mortgage rate of 9% per annum. Assume that there are no servicing or guaranteeing fees. The projected cash flows assuming 100 PSA are given in Table 9.15.
TABLE 9.15 Cash Flows Assuming 100 PSA
| Mth. | Mthly. Pmt. | Int. Pmt. | Sch. Prin. Pmt. | Sch. Out. Prin. | Pre Pmt. | Act. Out. Prin. | Cash Flow |
|---|---|---|---|---|---|---|---|
| 1 | 804.62 | 750.00 | 54.62 | 99945.38 | 16.67 | 99928.70 | 821.30 |
| 12 | 795.75 | 737.10 | 58.65 | 98221.92 | 198.64 | 98023.29 | 994.39 |
| 24 | 767.88 | 705.98 | 61.90 | 94068.57 | 384.82 | 93683.75 | 1152.70 |
| 36 | 724.49 | 660.61 | 63.88 | 88016.81 | 452.67 | 87564.14 | 1177.16 |
| 48 | 681.02 | 615.34 | 65.68 | 81979.09 | 421.62 | 81557.47 | 1102.64 |
| 60 | 640.16 | 572.62 | 67.53 | 76282.30 | 392.32 | 75889.98 | 1032.48 |
| 72 | 601.75 | 532.31 | 69.44 | 70905.39 | 364.67 | 70540.72 | 966.42 |
| 84 | 565.64 | 494.25 | 71.39 | 65828.56 | 338.56 | 65490.00 | 904.20 |
| 96 | 531.71 | 458.30 | 73.41 | 61033.16 | 313.89 | 60719.26 | 845.60 |
| 108 | 499.80 | 424.33 | 75.47 | 56501.65 | 290.59 | 56211.06 | 790.39 |
| 120 | 469.81 | 392.21 | 77.60 | 52217.54 | 268.56 | 51948.98 | 738.37 |
| 132 | 441.63 | 361.84 | 79.79 | 48165.27 | 247.71 | 47917.56 | 689.34 |
| 144 | 415.13 | 333.09 | 82.04 | 44330.24 | 227.99 | 44102.25 | 643.12 |
| 156 | 390.22 | 305.87 | 84.35 | 40698.69 | 209.31 | 40489.37 | 599.53 |
| 168 | 366.81 | 280.08 | 86.72 | 37257.64 | 191.62 | 37066.02 | 558.42 |
| 180 | 344.80 | 255.63 | 89.17 | 33994.90 | 174.84 | 33820.06 | 519.64 |
| 192 | 324.11 | 232.43 | 91.68 | 30898.98 | 158.91 | 30740.07 | 483.02 |
| 204 | 304.66 | 210.40 | 94.26 | 27959.05 | 143.79 | 27815.26 | 448.46 |
| 216 | 286.38 | 189.46 | 96.92 | 25164.92 | 129.42 | 25035.49 | 415.81 |
| 228 | 269.20 | 169.55 | 99.65 | 22506.96 | 115.75 | 22391.21 | 384.96 |
| 240 | 253.05 | 150.59 | 102.46 | 19976.14 | 102.74 | 19873.40 | 355.79 |
| 252 | 237.87 | 132.52 | 105.35 | 17563.90 | 90.33 | 17473.57 | 328.20 |
| 264 | 223.59 | 115.28 | 108.32 | 15262.20 | 78.49 | 15183.71 | 302.09 |
| 276 | 210.18 | 98.81 | 111.37 | 13063.44 | 67.19 | 12996.25 | 277.36 |
| 288 | 197.57 | 83.06 | 114.51 | 10960.45 | 56.37 | 10904.08 | 253.94 |
| 300 | 185.71 | 67.98 | 117.73 | 8946.47 | 46.01 | 8900.45 | 231.73 |
| 312 | 174.57 | 53.52 | 121.05 | 7015.10 | 36.08 | 6979.02 | 210.65 |
| 324 | 164.10 | 39.64 | 124.46 | 5160.32 | 26.54 | 5133.78 | 190.64 |
| 336 | 154.25 | 26.28 | 127.97 | 3376.42 | 17.36 | 3359.06 | 171.62 |
| 348 | 145.00 | 13.42 | 131.57 | 1658.02 | 8.53 | 1649.49 | 153.52 |
| 360 | 136.30 | 1.01 | 135.28 | 0.00 | 0.00 | 0.00 | 136.30 |
Explanation: Mth. ≡ Month; Mthly. Pmt. ≡ Monthly Payment; Int. Pmt. ≡ Interest Payment; Sch. Prin. Pmt. ≡ Scheduled Principal Payment; Sch. Out. Prin. ≡ Scheduled Outstanding Principal; Pre Pmt. ≡ Prepayment; Act. Out. Prin. ≡ Actual Outstanding Principal
The average life of the pass-through is 12.08 years.
ANALYSIS
Consider the data for the first month. The monthly payment is given by
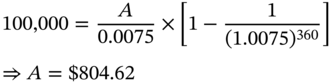
The interest component for the first month is
The scheduled outstanding principal at the end of the month is
The CPR for the first month is 0.2%. Thus, the SMM is
The prepayment for the month is
Thus, the actual outstanding principal at the end of the first month is
The cash flow for the pass-through is
Illustration of 200 PSA
Consider a pass-through backed by a single loan of $100,000 with 360 months to maturity and a mortgage rate of 9% per annum. Assume that there are no servicing or guaranteeing fees. The projected cash flows assuming 200 PSA are given in Table 9.16.
TABLE 9.16 Cash Flows Assuming 200 PSA
| Mth. | Mthly. Pmt. | Int. Pmt. | Sch. Prin. Pmt. | Sch. Out. Prin. | Pre Pmt. | Act. Out. Prin. | Cash Flow |
|---|---|---|---|---|---|---|---|
| 1 | 804.62 | 750.00 | 54.62 | 99,945.38 | 33.38 | 99,912.00 | 838.00 |
| 12 | 786.84 | 728.85 | 57.99 | 97,122.15 | 397.31 | 96,724.84 | 1,184.15 |
| 24 | 731.68 | 672.70 | 58.98 | 89,634.10 | 750.71 | 88,883.39 | 1,482.39 |
| 36 | 648.97 | 591.75 | 57.22 | 78,842.54 | 835.43 | 78,007.11 | 1,484.41 |
| 48 | 571.10 | 516.01 | 55.08 | 68,746.86 | 728.46 | 68,018.40 | 1,299.55 |
| 60 | 502.56 | 149.55 | 53.112 | 59,886.42 | 634.57 | 59,251.85 | 1,137.14 |
| 120 | 265.22 | 221.41 | 43.81 | 29,477. 80 | 312.35 | 29,165.45 | 577.57 |
| 180 | 139.96 | 103.77 | 36.20 | 13,799.60 | 146.22 | 13,653.38 | 286.19 |
| 240 | 73.86 | 43.96 | 29.91 | 5,830.94 | 61.79 | 5,769.15 | 135.65 |
| 300 | 38.98 | 14.27 | 21.71 | 1,877.81 | 19.90 | 1,857.92 | 58.88 |
| 360 | 20.57 | 0.15 | 20.42 | 0.00 | 0.00 | 0.00 | 20.57 |
Explanation: Mth. ≡ Month; Mthly. Pmt. ≡ Monthly Payment; Int. Pmt. ≡ Interest Payment; Sch. Prin. Pmt. ≡ Scheduled Principal Payment; Sch. Out. Prin. ≡ Scheduled Outstanding Principal; Pre Pmt. ≡ Prepayment; Act. Out. Prin. ≡ Actual Outstanding Principal
The average life of the pass-through is eight years. As can be seen, the more rapid prepayments lead to a reduction in the average life of the security.
Collateralized Mortgage Obligations
In the case of a pass-through, there is only one class of security that is issued, and every security is entitled to the same undivided share of the cash flows from the underlying pool. The feature of such securities is that prepayments have the same implications for all the security holders.
In real life, however, investors differ with respect to the prepayment exposure and the average security life sought by them. The securitization process can take these preferences into account by creating multiple classes of securities, or what are referred to in MBS parlance as tranches. There are clearly specified rules as to how cash flows from the underlying pool are to be directed to the holders of the various tranches. Such securities, with multiple tranches, are referred to as collateralized mortgage obligations or CMOs. We will introduce the concept by studying a very simple CMO structure known as a sequential pay CMO.
Sequential Pay CMO
Assume that a pool of mortgages consists of four loans with a principal of $100,000 each. Each loan has a maturity of 360 months and a mortgage rate of 9%. The average life of a pass-through, backed by such loans, under the assumption of 100 PSA is 12.08 years, as we have just seen.
Now assume that instead of creating a single type of security like a pass-through, four types of securities known as tranches A to D are created. All principal payments from the underlying pool, both scheduled and unscheduled, will first go to tranche A. During this time, the remaining tranches will continue to earn interest on the outstanding principal. Once tranche A is fully paid off, all subsequent principal payments, scheduled and unscheduled, will be directed to the holders of tranche B. Once again, while tranche B is being paid off, holders of tranches C and D will get interest on their outstanding principal. Extending the logic, the redemption of tranche B will see further principal payments being directed to tranche C, with holders of tranche D getting only the interest due. Finally, once tranche C securities are retired, all further principal payments will be directed to the holders of tranche D.
Let us assume that one security is issued for each tranche, with a face value of $100,000, and that there are no servicing or guaranteeing fees. The cash flow schedules for the four tranches are given in Tables 9.17 to 9.20.
Analysis – Tranche A
Consider the first month. The payment that is received from the underlying pool is
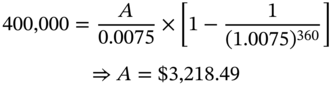
TABLE 9.17 Amortization for Tranche A
| Month | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|
| 1 | 750.00 | 285.18 | 1035.18 | 99714.82 |
| 2 | 747.86 | 353.50 | 1101.36 | 99361.32 |
| 10 | 712.36 | 895.96 | 1608.31 | 94085.02 |
| 20 | 622.99 | 1543.95 | 2166.94 | 81521.67 |
| 30 | 487.00 | 2127.57 | 2614.58 | 62806.32 |
| 40 | 330.88 | 2026.39 | 2357.27 | 42091.53 |
| 50 | 182.18 | 1930.42 | 2112.60 | 22359.64 |
| 60 | 40.49 | 1839.42 | 1879.92 | 3559.90 |
| 61 | 26.70 | 1830.58 | 1857.28 | 1729.32 |
| 62 | 12.97 | 1729.32 | 1742.29 | 0.00 |
| Month | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|
| 1 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 10 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 20 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 30 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 40 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 50 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 60 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 61 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 62 | 750.00 | 92.47 | 842.47 | 99907.53 |
| 70 | 655.48 | 1753.13 | 2408.61 | 85644.07 |
| 80 | 526.78 | 1671.32 | 2198.11 | 68566.30 |
| 90 | 404.08 | 1593.77 | 1997.85 | 52283.01 |
| 100 | 287.05 | 1520.27 | 1807.32 | 36752.77 |
| 110 | 175.40 | 1450.62 | 1626.02 | 21936.22 |
| 120 | 68.85 | 1384.63 | 1453.48 | 7795.93 |
| 125 | 17.41 | 1352.94 | 1370.35 | 968.18 |
| 126 | 7.26 | 968.18 | 975.44 | 0.00 |
| Month | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|
| 1 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 20 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 40 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 60 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 80 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 100 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 120 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 126 | 750.00 | 378.53 | 1128.53 | 99621.47 |
| 140 | 620.00 | 1262.90 | 1882.90 | 81403.49 |
| 160 | 438.49 | 1153.77 | 1592.25 | 57311.25 |
| 180 | 272.52 | 1056.02 | 1328.54 | 35280.26 |
| 200 | 120.47 | 968.57 | 1089.05 | 15094.36 |
| 210 | 49.20 | 928.41 | 977.60 | 5631.42 |
| 215 | 14.67 | 909.16 | 923.83 | 1047.35 |
| 216 | 7.86 | 905.38 | 913.23 | 141.97 |
| 217 | 1.06 | 141.97 | 143.03 | 0.00 |
TABLE 9.20 Amortization for Tranche D
| Month | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|
| 1 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 30 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 60 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 90 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 120 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 150 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 180 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 210 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 217 | 750.00 | 759.64 | 1509.64 | 99240.36 |
| 240 | 602.36 | 820.79 | 1423.15 | 79493.62 |
| 270 | 427.81 | 730.43 | 1158.23 | 56310.55 |
| 300 | 271.93 | 654.98 | 926.90 | 35601.82 |
| 330 | 131.58 | 592.44 | 724.03 | 16951.79 |
| 340 | 87.77 | 574.17 | 661.94 | 11128.88 |
| 350 | 45.29 | 557.08 | 602.37 | 5482.15 |
| 360 | 4.06 | 541.13 | 545.18 | 0.01 |
The interest component for the month is
Thus, the scheduled principal for the month is 3,218.49 – 3,000 = $218.49. This will be directed toward tranche A.
The prepayment for the month is
This will also be directed to tranche A. Thus, the total principal received by tranche A is
The interest receivable by this security for the month is
Thus, the total cash flow received by tranche A in the first month is
Now consider the second month. The monthly payment received from the underlying pool is

The interest component for the month is
Thus, the scheduled principal for the month is
The prepayment for the month is
Thus, the total principal for the month is ![]() .
.
The entire amount will obviously be directed toward tranche A. The interest receivable by this tranche for the second month is given by
Thus, the total cash flow that is directed toward tranche A at the end of the second month is ![]() .
.
At the end of the 61st month, tranche A has an outstanding principal of $1,729.32. The total principal from the underlying pool at the end of the 62nd month is $1,821.79. Of this $1,729.32 will be directed to tranche A. The balance of $92.47 will be paid to tranche B. Thus the total cash flow received by tranche A in the 62nd month is
Analysis – Tranche B
Now let us turn our attention to tranche B. For the first 61 months, tranche B will receive only interest on the outstanding principal of $100,000, which amounts to $750 per month. In the 62nd month this tranche receives $92.47 by way of principal payment, as explained. Thus, the total cash flow for this month is 750 + 92.47 = $842.47. The outstanding principal at the end of the month is 100,000 – 92.47 = $99,907.53. In the 125th month the outstanding principal for this tranche is $968.18. In the 126th month the underlying pool makes a total principal payment of $1,346.71. Thus, in this month tranche B receives $7.26 worth of interest and $968.18 of principal, which amounts to a total cash flow of $975.44. The excess principal, that is, 1,346.71 – 968.18 = $378.53, is directed to tranche C.
Analysis – Tranche C
Let us now consider tranche C. Until the 125th month this tranche receives a monthly cash flow of $750, which represents the interest on an outstanding principal of $100,000. In the 126th month there is a principal repayment of $378.53, as explained. The total cash flow for this month is therefore $1,128.53. At the end of 216 months there is an outstanding principal of $141.97. Thus, in the 217th month this tranche receives an interest payment of $1.06. In this month the total principal received from the underlying pool is $901.61. Thus, after paying $141.97 to tranche C, the excess of $759.64 is directed toward tranche D.
Analysis – Tranche D
Finally, let us analyze the last tranche. Tranche D receives interest on the initial outstanding principal until month 216, which amounts to $750 per month. In month 217 it receives a principal payment of $759.64, as explained. The tranche is fully paid off in month 360.
The average life of the collateral as calculated for a pass-through security based on the pool is 12.08 years; however, each tranche of the CMO has a different maturity and average life. The details are given in Table 9.21.
In the case of a sequential pay CMO, the average life of the mother loan is a weighted average of the average lives of the tranches. The weight attached to a tranche is its original outstanding balance, divided by the cumulative outstanding balances of all the tranches. In our illustration the weight of every tranche is 25%.
TABLE 9.21 Maturity and Average Life of the Securities
| Security | Maturity in Months | Average Life in Months |
|---|---|---|
| Collateral | 360 | 144.92 |
| Tranche A | 62 | 36.13 |
| Tranche B | 126 | 92.74 |
| Tranche C | 217 | 168.43 |
| Tranche D | 360 | 282.39 |
EXTENSION RISK AND CONTRACTION RISK
Pass-through securities and CMOs expose investors to prepayment risk. In a declining interest rate environment, prepayments affect security holders in two ways. As they are debt securities, we would expect the price of such securities to rise in a scenario where rates are declining. In the case of mortgage-backed securities, however, holders of underlying loans are likely to prepay and refinance at a lower rate when market rates go down. The overall result is price compression; that is, the rise in price will not be as large as in the case of plain-vanilla bonds. The second adverse consequence for holders of such securities is of course reinvestment risk, as is the case for all debt holders. That is, cash flows that are received in a declining interest rate environment have to be reinvested at lower rates of interest. The risk due to these two adverse consequences is termed as contraction risk.
Now let us consider a rising interest rate environment. We would clearly expect the prices of mortgage-backed securities to fall. Unlike in the case of plain-vanilla bonds, however, principal payments are likely to slow down because holders of underlying mortgage loans are less likely to refinance when mortgage rates are rising. This will exacerbate the anticipated price decline. In such a situation, the security holders would like prepayments to be high for it would afford them an opportunity to reinvest larger amounts at high rates of interest. The adverse impact for mortgage-backed securities in a rising interest rate environment is termed as extension risk.
ACCRUAL BONDS
In the case of the sequential pay CMO that we just studied, every tranche receives interest every month, based on the principal outstanding for that particular tranche at the beginning of the month. Many sequential pay CMO structures, however, do not require that every tranche should be paid interest every month based on the outstanding principal. In the case of a sequential pay CMO with an accrual bond, also termed as a Z-bond,3 however, the Z-bond will not receive any monthly interest until the previous tranches are fully retired. Therefore, the interest for the Z-bond will accrue and be added to its original principal (negative amortization) until the other classes of the CMO have been paid off. In the months prior to the retirement of the penultimate tranche, the interest that would otherwise have been paid to the Z-bond is directed to the tranche receiving principal at that point in time, and thus helps to speed up the repayment of principal.
Let us consider a CMO where tranches A, B, and C are as specified in the preceding illustration; however, the last tranche is an accrual bond. Quite obviously, the inclusion of the Z-bond will reduce the maturity and the average life of each of the three earlier tranches. (See Tables 9.22–9.26.)
Analysis
The cash flows from the underlying pool at the end of the first month are as follows.
TABLE 9.22 Amortization for Tranche A in the Presence of a Z-bond
| Month | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|
| 1 | 750.00 | 1035.18 | 1785.18 | 98964.82 |
| 2 | 742.24 | 1109.13 | 1851.36 | 97855.69 |
| 10 | 660.19 | 1698.13 | 2358.31 | 86326.76 |
| 20 | 508.59 | 2408.36 | 2916.94 | 65403.26 |
| 30 | 305.54 | 3059.04 | 3364.58 | 37679.15 |
| 40 | 77.15 | 3030.12 | 3107.27 | 7256.67 |
| 42 | 31.72 | 3025.63 | 3057.35 | 1203.21 |
| 43 | 9.02 | 1203.21 | 1212.23 | 0.00 |
TABLE 9.23 Amortization for Tranche B in the Presence of a Z-bond
| Month | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|
| 1 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 10 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 20 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 30 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 40 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 43 | 750.00 | 1820.34 | 2570.34 | 98179.66 |
| 50 | 600.57 | 3012.03 | 3612.60 | 77063.95 |
| 60 | 374.98 | 3004.94 | 3379.92 | 46991.80 |
| 70 | 149.54 | 3009.08 | 3158.61 | 16929.01 |
| 75 | 36.61 | 3015.44 | 3052.04 | 1865.71 |
| 76 | 13.99 | 1865.71 | 1879.70 | 0.00 |
TABLE 9.24 Amortization for Tranche C in the Presence of a Z-bond
| Month | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|
| 1 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 10 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 20 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 30 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 40 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 50 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 60 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 70 | 750.00 | 0.00 | 750.00 | 100000.00 |
| 76 | 750.00 | 1151.35 | 1901.35 | 98848.65 |
| 80 | 673.40 | 3024.71 | 3698.11 | 86761.89 |
| 90 | 445.69 | 3052.16 | 3497.85 | 56373.74 |
| 100 | 215.52 | 3091.80 | 3307.32 | 25644.37 |
| 109 | 5.49 | 731.83 | 737.32 | 0.00 |
| Month | Interest Due | Interest Received | Principal Received | Cash Flow | Outstanding Balance |
|---|---|---|---|---|---|
| 1 | 750 | 0.00 | 0.00 | (750.00) | 100750.00 |
| 2 | 755.63 | 0.00 | 0.00 | (755.63) | 101505.63 |
| 10 | 802.17 | 0.00 | 0.00 | (802.17) | 107758.25 |
| 20 | 864.41 | 0.00 | 0.00 | (864.41) | 116118.41 |
| 30 | 931.47 | 0.00 | 0.00 | (931.47) | 125127.18 |
| 50 | 1081.61 | 0.00 | 0.00 | (1081.61) | 145295.69 |
| 60 | 1165.52 | 0.00 | 0.00 | (1165.52) | 156568.10 |
| 70 | 1255.94 | 0.00 | 0.00 | (1255.94) | 168715.05 |
| 90 | 1458.38 | 0.00 | 0.00 | (1458.38) | 195909.25 |
| 100 | 1571.53 | 0.00 | 0.00 | (1571.53) | 211108.38 |
| 108 | 1668.33 | 0.00 | 0.00 | (1668.33) | 224112.42 |
| 109 | 1680.84 | 1680.84 | 725.59 | 2406.43 | 223386.83 |
| 120 | 1568.85 | 1568.85 | 1384.63 | 2953.48 | 207795.91 |
| 140 | 1370.00 | 1370.00 | 1262.90 | 2632.90 | 181403.48 |
| 160 | 1188.49 | 1188.49 | 1153.77 | 2342.25 | 157311.23 |
| 180 | 1022.52 | 1022.52 | 1056.02 | 2078.54 | 135280.24 |
| 200 | 870.47 | 870.47 | 968.57 | 1839.05 | 115094.34 |
| 220 | 730.86 | 730.86 | 890.46 | 1621.32 | 96557.85 |
| 240 | 602.36 | 602.36 | 820.79 | 1423.15 | 79493.59 |
| 260 | 483.75 | 483.75 | 758.78 | 1242.53 | 63740.99 |
| 280 | 373.94 | 373.94 | 703.73 | 1077.66 | 49154.44 |
| 300 | 271.93 | 271.93 | 654.98 | 926.90 | 35601.78 |
| 320 | 176.81 | 176.81 | 611.96 | 788.78 | 22962.97 |
| 340 | 87.77 | 87.77 | 574.17 | 661.94 | 11128.83 |
| 360 | 4.06 | 4.06 | 541.13 | 545.18 | (0.05) |
The outstanding principal for each of the four tranches is $100,000. Tranches A, B, and C will therefore receive an interest payment of $750 for the month. The accrual bond will obviously not receive any interest. Tranche A will receive the following amount by way of principal payment
Thus, the total cash flow for this tranche is 750 + 1,035.18 = $1,785.18. The outstanding principal at the end of the first month is 100,000 – 1,035.18 = $98,964.82.
Because the Z-bond does not receive any interest during the month there will be negative amortization. Thus, the outstanding principal for this bond at the end of the first month is $100,750.
Now let us consider the second month. The cash flows from the underlying pool are as follows. Interest = $2,997.86; Scheduled Principal = $220.09; Prepayment = $133.41. Tranche A has an outstanding principal of $98,964.82. Thus, the interest for the month for this tranche is
Tranches B and C will each receive $750 for the month by way of interest as there has been no principal repayment thus far. The principal repayment that is directed at tranche A for this month is ![]() . The outstanding principal at the end of the second month is therefore
. The outstanding principal at the end of the second month is therefore ![]() .
.
Tranche Z will not receive any cash flow during the month. The interest due is ![]() . Thus, the outstanding principal at the end of the second month is
. Thus, the outstanding principal at the end of the second month is ![]() .
.
Now let us turn to the 43rd month. The cash flows from the underlying collateral are as follows: Interest = $2,535.51; Scheduled Principal = $259.71; Prepayment = $1,737.35.
The outstanding principal for tranche A at the end of the 42nd month is $1,203.21. Thus, this tranche will receive a cash flow of ![]() . With this tranche A is retired.
. With this tranche A is retired.
Tranches B and C are entitled to an interest payment of $750 each. Thus, the principal payment that is received by tranche B during this month is ![]() . Thus, the total cash flow that is received by tranche B at the end of this month is $2,570.34. The outstanding principal is
. Thus, the total cash flow that is received by tranche B at the end of this month is $2,570.34. The outstanding principal is ![]() .
.
Similarly, tranche B is retired at the end of 76 months and tranche C at the end of 109 months. From the 109th month onwards the Z-bond starts receiving repayment of principal. The outstanding principal for the bond at the end of month 108 is $224,112.42. In the 109th month the tranche receives an interest payment of 224,112.42 × 0.0075 = $1,680.84. It also receives a principal payment of $725.59, which serves to reduce the outstanding principal to $223,386.83. The tranche is fully paid off at the end of the 360th month.
As we can see, the average life of each of the three tranches has reduced due to the presence of the Z-bond. Z-bonds have appeal to investors who are primarily concerned with the specter of reinvestment risk. Because such bonds do not entail the receipt of any cash flows until all the other classes are fully retired, reinvestment risk is totally eliminated until the Z-bond starts receiving its first cash flow.
TABLE 9.26 Maturity and Average Life of the Securities in the Presence of a Z-Bond
| Security | Maturity in Months | Average Life in Months |
|---|---|---|
| Collateral | 360 | 144.92 |
| A | 43 | 25.06 |
| B | 76 | 59.50 |
| C | 109 | 92.53 |
| Z | 360 |
FLOATING RATE TRANCHES
Floating rate bonds can be created from a fixed-rate tranche. We will illustrate this using tranche C in the previous illustration, which has a par value of $100,000 and a 9% coupon. In practice, to create a floater we have to simultaneously create an inverse floater.4 The cumulative principal of the two tranches will in this case be $100,000. There is no rule as to what the principal values of the respective tranches should be as long as their combined par value is $100,000.
Let us assume that the benchmark for the two tranches is the 3-month LIBOR and that we wish to create a floater with a par value of $60,000 and an inverse floater with a par value of $40,000. The coupon on the floater is LIBOR + m basis points while that for the inverse floater is C − L × LIBOR.
It is a common practice to specify the coupon for an inverse floater as
C is the cap or maximum interest on the inverse floater while L is referred to as the coupon leverage. The concept of a cap can be easily understood. The lower limit for LIBOR is zero. Consequently, the upper limit for the coupon on the inverse floater is C. The coupon leverage measures the rate of change of the coupon of the inverse floater with respect to the benchmark.
We know that the total annual interest available is 9% of 100,000, which is 9000. This is also the maximum interest available for the floating tranche. Thus, the cap on the floater is 9000 ÷ 60000 = 15%. The ratio of floaters to inverses is 3:2, which implies that the coupon leverage for the inverse floater is 1.50. If we assume that the coupon on the floater is LIBOR + 150 b.p., the minimum coupon on the floater is 1.50%, which would be the case if LIBOR were to be zero. The minimum interest on the floater is hence 60,000 × 0.015 = 900. Thus, the maximum interest for the inverse floater is 9,000 – 900 = $8,100. The cap on the inverse is therefore 8,100 ÷ 40,000 = 0.2025 ≡ 20.25%. We can therefore express the coupons of the two tranches as

The weighted average coupon is
For instance, if LIBOR were to be 7.50%, the weighted average will be
NOTIONAL INTEREST-ONLY TRANCHE
Let us go back to the sequential pay CMO that we studied earlier. We assumed that the underlying mortgages had a coupon rate of 9% and that each of the four tranches that we created also had a coupon of 9%. In practice, each tranche of a CMO will have a different coupon rate and there will be an excess representing the difference between the interest on the underlying collateral and the coupons on the various tranches. Therefore, it is a common practice to create a tranche that is entitled to receive only the excess coupon interest.5 Such tranches are referred to as notional interest-only securities.
We will now assume that the underlying collateral has a coupon of 9%, while the four tranches created from it have coupon rates as shown in Table 9.27.
Consider tranche A. It pays a coupon of 7.50%, while the coupon on the collateral is 9%. Thus, there is excess interest of 1.50%. Let us assume that we wish to create a notional interest-only security with a coupon of 8.40%. To find the notional amount on which the interest payable to this security will be calculated, we proceed as follows. An excess interest of 1.50% on $140,000 worth of principal can be used to pay an interest of 8.40% on a principal amount of $25,000. Similarly in the case of tranche B, an excess interest of 1.25% on a principal amount of $84,000 can be used to pay an interest of 8.40% on a principal of $12,500. Tranche C, using the same logic, generates excess interest to support $10,000 worth of principal while the last tranche is capable of servicing a principal of $8,214.2850. Thus, the excess interest generated can service a bond with a principal of ![]() . This is the notional principal for the tranche that is scheduled to receive the excess interest. The term notional connotes that this principal amount is used merely to compute the interest payable to this class for the month, and that the principal per se is not repaid.
. This is the notional principal for the tranche that is scheduled to receive the excess interest. The term notional connotes that this principal amount is used merely to compute the interest payable to this class for the month, and that the principal per se is not repaid.
The contribution of a tranche to the notional principal is in general given by the following formula.

For instance, in the case of tranche A in the earlier illustration
TABLE 9.27 Coupon Rates for a Sequential Pay CMO
| Tranche | Initial Principal | Coupon Rate |
|---|---|---|
| A | 140,000 | 7.50% |
| B | 84,000 | 7.75% |
| C | 84,000 | 8.00% |
| D | 92,000 | 8.25% |
For the first month the IO class will receive a cash flow of
Let us assume a prepayment speed of 100 PSA. The principal paid to tranche A at the end of the first month will be $285.18. This will reduce the outstanding principal for this tranche to 140,000 – 285.18 = $139,714.82. Thus, the contribution of this tranche to the notional principal for the second month is
The contributions of the other tranches will not be affected. Consequently, for the second month the notional IO class will receive interest on a principal of
Thus, the interest for this tranche for the second month will be
INTEREST-ONLY AND PRINCIPAL-ONLY STRIPS
Stripped mortgage-backed securities can be created by directing either all the principal or all the interest to a particular class. The security that is scheduled to receive only the principal is referred to as the principal-only or the PO class. The other security is obviously termed as the interest-only or IO class.
Let us first consider the PO class. The yield obtained by the security holder will depend on the speed with which the underlying pool generates prepayments. The faster the speed with which prepayments are received, the greater will be the rate of return for holders of such securities. In the case of the IO class holders, however, the desire is to have slow prepayments. This is because, given that such securities do not receive any principal payments, the interest payment income will be higher, the larger the outstanding balance on the underlying pool. This is tantamount to a slower prepayment rate.
PAC BONDS
PAC is an acronym for planned amortization class. In the case of such bonds, if the prepayment pattern falls within a prespecified range, then the cash flows received by the security are known.
PAC bonds are not created in isolation. They are accompanied by a category of bonds that are termed as support bonds. It is this category that absorbs the prepayment risk, thereby protecting the PAC bonds against extension risk as well as contraction risk.
To create a PAC bond we need to specify a range of prepayment speeds. These are referred to as the PAC collars. The PAC schedule lists the principal amount payable to the PAC bondholders if the prepayment speed is within the range provided by the lower PAC collar and the upper PAC collar. The schedule is obtained by taking the lower of the principal cash flows generated by the lower collar and the upper collar. Consider the following illustration.
NOTES
- 1 The monthly income should be taken as the take-home salary and not as the cost-to-company (CTC).
- 2 This model was developed by the Public Securities Association, which was subsequently renamed as the Bond Market Association (BMA). In 2006 the BMA merged with the Securities Industry Association to form the Securities Industry and Financial Markets Association (SIFMA); however, the prepayment benchmark is still referred to as the PSA benchmark.
- 3 Because of its similarities with a zero-coupon bond.
- 4 While the coupon of a floating rate bond moves up and down with the corresponding changes in the benchmark, the coupon of an inverse floater moves inversely with the benchmark. For instance, an inverse floater may have its coupon specified as 10% – LIBOR. Consequently, if the LIBOR were to rise, the coupon would fall and vice versa.
- 5 Note that this tranche is not entitled to any principal payments.
