Now, we will look at a variant of a prototypical network, called a Gaussian prototypical network. We just learned how a prototypical network learns the embeddings of the data points and how it builds the class prototype by taking the mean embeddings of each class and uses the class prototype for performing classification.

In a Gaussian prototypical network, along with generating embeddings for the data points, we add a confidence region around them, characterized by a Gaussian covariance matrix. Having a confidence region helps in characterizing the quality of individual data points and would be useful in the case of noisy and less homogeneous data.

So, in Gaussian prototypical networks, the output of the encoder will be embeddings, as well as the covariance matrix. Instead of using the full covariance matrix, we either include a radius or diagonal component from the covariance matrix along with the embeddings:

• Radius component: If we use the radius component of the covariance matrix, then the dimension of our covariance matrix would be 1, as the radius is just a single number.
• Diagonal component: If we use the diagonal component of the covariance matrix, then the dimension of our covariance matrix would be the same as the embedding matrix dimension.

Also, instead of using the covariance matrix directly, we use the inverse of a covariance matrix. We can convert the raw covariance matrix into the inverse covariance matrix using any of the following methods. Let S_raw be the covariance matrix and S be the inverse covariance matrix:

• S = 1 + Softplus(S_raw)
• S = 1 + sigmoid(S_raw)
• S = 1+ 4 * sigmoid(S_raw)
• S = offset + scale * softplus(S_raw/div), where offset and scale are trainable parameters

But what is the use of having the covariance matrix along with the embeddings? As said earlier, it adds the confidence region around the data points and is very useful in the case of noisy data. Look at the following diagram. Let's say we have two classes, A and B. The dark dots represent the embeddings of the data point, and the circles around the dark dots indicate the covariance matrices. A big dotted circle represents the overall covariance matrix for a class. A star in the middle indicates the class prototype. As you can see, having this covariance matrix around the embeddings gives us a confidence region around the data point and for class prototypes:

Let's better understand this by looking at the code. Let's say we have an image, X, and we want to generate embeddings for the image. Let's represent the covariance matrix by sigma. First, we select what component of the covariance matrix we want to use—that is, whether we want to use the diagonal or radius component. If we use the radius component, then our covariance matrix dimension would be just one. If we opt for the diagonal component, then the size of the covariance matrix would be same as the embedding dimension:

if component =='radius':
    covariance_matrix_dim = 1
else:
    covariance_matrix_dim = embedding_dim

Now, we define our encoder. Since our input is an image, we use a convolutional block as our encoder. So, we define the size of filters, a number of filters, and the pooling layer size:

filters = [3,3,3,3] 
num_filters = [64,64,64,embedding_dim +covariance_matrix_dim] 
pools = [2,2,2,2]

We initialize embeddings as our image, X:

previous_channels = 1 
embeddings = X 
weight = []
bias = []
conv_relu = []
conv = []
conv_pooled = []

Then, we perform the convolutional operation and get the embeddings:

for i in range(len(filters)):

    filter_size = filters[i]
    num_filter = num_filters[i]
    pool = pools[i]
    weight.append(tf.get_variable("weights_"+str(i), shape=[filter_size, filter_size, previous_channels, num_filter])
    bias.append(tf.get_variable("bias_"+str(i), shape=[num_filter]))
    conv.append(tf.nn.conv2d(embeddings, weight[i], strides=[1,1,1,1], padding='SAME') + bias[i])
    conv_relu.append(tf.nn.relu(conv[i]))
    conv_pooled.append(tf.nn.max_pool(conv_relu[i], ksize = [1,pool,pool,1], strides=[1,pool,pool,1], padding = "VALID"))

    previous_channels = num_filter
    embeddings = conv_pooled [i]

We take the output of the last convolutional layer as our embeddings and reshape the result to have embeddings, as well as the covariance matrix:

X_encoded = tf.reshape(embeddings,[-1,embedding_dim + covariance_matrix_dim ])

Now, we split the embeddings and raw covariance matrix, as we need to convert the raw covariance matrix into the inverse covariance matrix:

embeddings, raw_covariance_matrix = tf.split(X_encoded, [embedding_dim, covariance_matrix_dim], 1)

Next, we calculate the inverse of a covariance matrix using any of the discussed methods:

if inverse_transform_type == "softplus":
    offset = 1.0
    scale = 1.0
    inv_covariance_matrix = offset + scale * tf.nn.softplus(raw_covariance_matrix)


elif inverse_transform_type == "sigmoid":
    offset = 1.0
    scale = 1.0
    inv_covariance_matrix = offset + scale * tf.sigmoid(raw_covariance_matrix)


elif inverse_transform_type == "sigmoid_2":
    offset = 1.0
    scale = 4.0
    inv_covariance_matrix = offset + scale * tf.sigmoid(raw_covariance_matrix)

elif inverse_transform_type == "other":

    init = tf.constant(1.0)
    scale = tf.get_variable("scale", initializer=init)
    div = tf.get_variable("div", initializer=init)
    offset = tf.get_variable("offset", initializer=init)

    inv_covariance_matrix = offset + scale * tf.nn.softplus(raw_covariance_matrix/div)

So far, we have seen that we calculate the covariance matrix along with embeddings of an input. What's next? How can we compute the class prototype? The class prototype, , can be computed as follows:

In this equation, is the diagonal of the inverse covariance matrix, 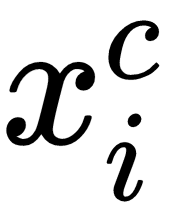denotes the embeddings and superscript c denotes the class.

After computing the prototype for each of the classes, we learn the embedding of the query point. Let  be the embedding of a query point. Then, we compute the distance between the query point embedding and class prototype as follows:

Finally, we predict the class of a query set ( ), which has the minimum distance with the class prototype: