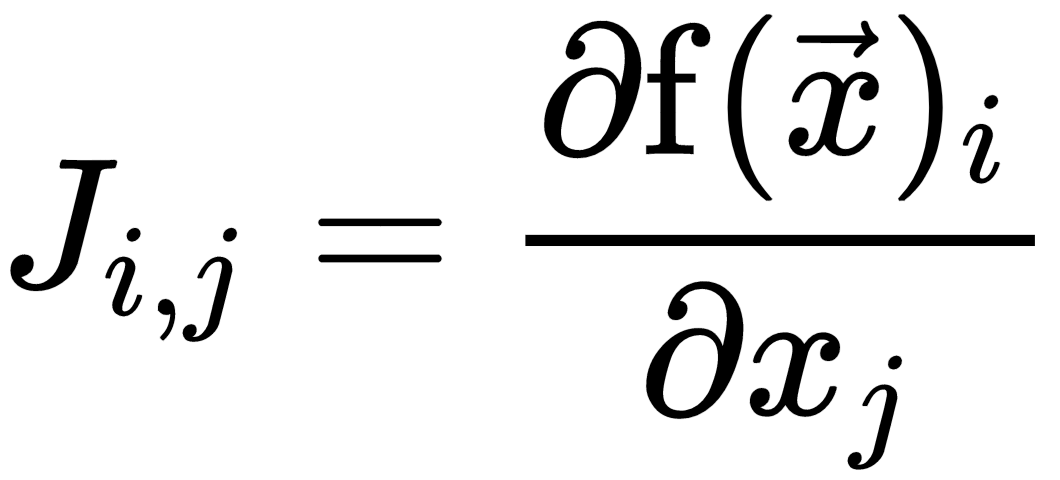Sometimes, we need to optimize functions whose input and output are vectors. So, for each component of the output vector, we need to compute the gradient vector. For , we will have m gradient vectors. By arranging them in a matrix form, we get n x m matrix of partial derivatives , called the Jacobian matrix.

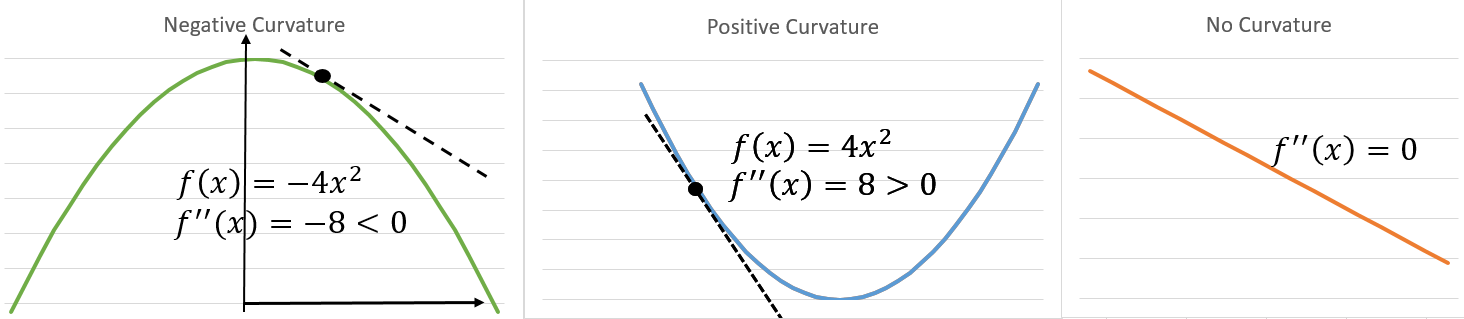
For a real-valued function of a single variable, if we want to measure the curvature of the function curve at a point, then we need to compute how first the derivative will change as we change the input. This is called the second-order derivative. A function whose second-order derivative is zero has no curvature and is a flat line. Now, for the function of several variables, there are many second derivatives. These derivatives can be arranged in a matrix called the Hessian matrix. Since the second-order partial derivatives are symmetric, that is, 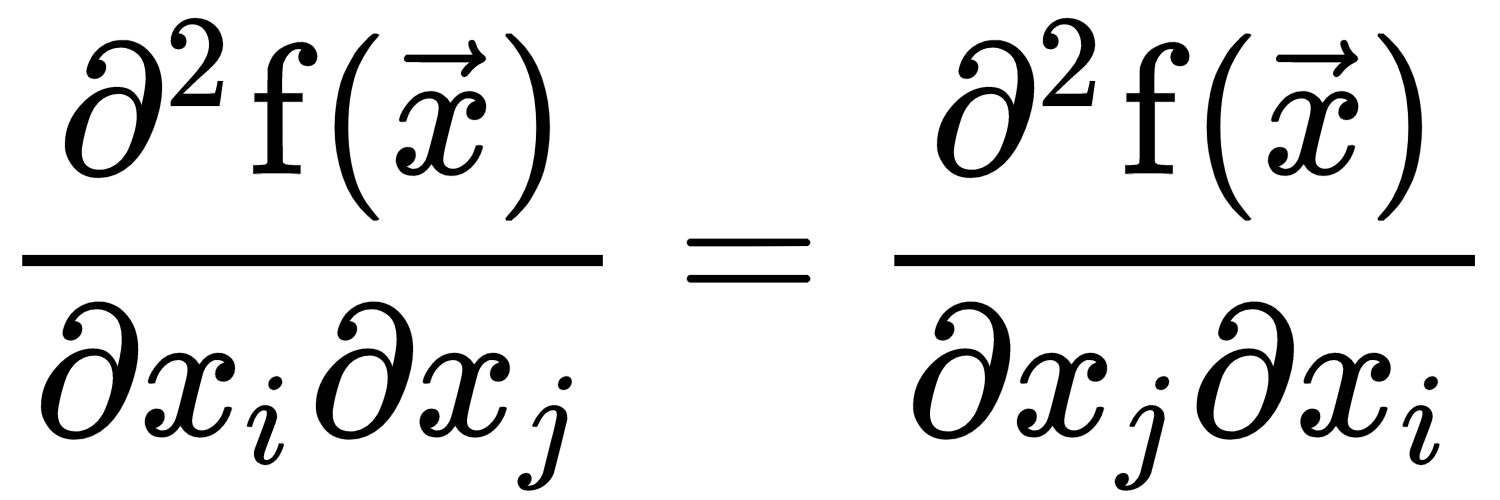, the Hessian matrix is real symmetric and thus has real eigen values. The corresponding eigen vectors represent different directions of curvature. The ratio of the magnitude of the largest and smallest eigen value is called the condition number of the Hessian. It measures how much the curvatures along each eigen dimension differ from each other. When the Hessian has a poor condition number, the gradient descent performs poorly. This is because in one direction, the derivative increases rapidly, while in another direction, it increases slowly. Gradient descent is unaware of this change and, due to this, may take a very long time to converge.

For our temperature example, the Hessian is . The direction of most curvature is two times more than the direction of least curvature. So, traversing along y, we will reach the minimum point much faster. This is also evident from the temperature contours, shown in the preceding Hot plate figure.

We can use the second-derivative curvature information to check whether an optimal point is minimum or maximum. For a single variable, f'(x) = 0, f''(x) > 0 implies x is a local minimum of f, and f' (x) = 0, f'' (x) < 0 implies x is a local maximum. This is called a second derivative test (refer to the following figure Explaining curvature). Similarly, for functions of several variables, if the Hessian is positive definite (that is, all eigen values are positive) at 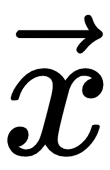, then f attains a local minimum at 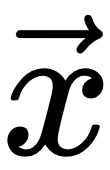. If the Hessian is negative definite at x, then f attains local maximum at x. If the Hessian has both positive and negative eigen values, then x is a saddle point for f. Otherwise, the test is inconclusive:

There are optimization algorithms based on second-order derivatives that use the curvature information. One such method is Newton's method, which can reach the optimum point in just one step for convex functions.